Abstract
We report on the experimental realization of a quasi-one-dimensional photonic graphene ribbon supporting four flat-bands (FBs). We study the dynamics of fundamental and dipolar modes, which are analogous to the s and p orbitals, respectively. In the experiment, both modes (orbitals) are effectively decoupled from each other, implying two sets of six bands, where two of them are completely flat (dispersionless). Using an image generator setup, we excite the s and p FB modes and demonstrate their non-diffracting propagation for the first time. Our results open an exciting route towards photonic emulation of higher orbital dynamics.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Recent advancement in experimental physics enabled us to emulate various semi-classical and quantum phenomena in a highly controllable environment. Ultracold atoms in optical lattices [1, 2] and periodic arrays of coupled optical waveguides (photonic lattices (PLs)) [3–5] are two parallel experimental platforms which were extensively used to observe and probe various intriguing solid-state phenomena. This includes the localization effects induced by external fields [6, 7], disorder [8, 9] and particle interactions [10, 11]. Indeed, localization is a major goal in diverse areas of physics, where the trapping and control of excitations of different nature become crucial [4]. During several years, photonics has taken a central role on this problem, being particularly intense in the context of PLs. Different fabrication techniques have been developed, being the femtosecond-laser technique probably the most flexible one in order to fabricate almost arbitrary three-dimensional configurations [12, 13]. Most of the known methods to localize energy rely on the modification of the lattice using linear or nonlinear defects, or by destroying the periodicity of the system. However, localized states in a photonic Lieb lattice [14, 15] were recently observed in the linear optical regime, due to the existence of a completely flat-band (FB). The states corresponding to the non-dispersive band occupy only a few sites and can be considered as localized states in the continuum [14, 16]. The study of FB systems has been performed for a broad community studying transport and localization phenomena in different lattice configurations. Some examples are the study of FB Hubbard models in the context of ferromagnetism [17], FBs considering excited orbitals [18], the experimental excitation of FB phenomenology in kagome and Lieb metallic lattices [19, 20], the observation of localized states in kagome photonic systems [21], FB models in driven topological lattices [22, 23] and the recent excitation of localized states in Stub quasi-one-dimensional systems [24, 25], including the idea of performing logical operations using FB localized states [26]. Unfortunately, the flatness of a given band can be modified if extra interactions are also considered in the model [27]. This is a frequent problem on several FB systems which diminishes the chances for an experimental excitation of FB localized states. However, by inspecting the discrete properties of a given system, it is possible to identify some lattices where next or even next–next nearest neighbor (NN) interactions preserve the flatness of the band. This requires a high degree of symmetry in order to effectively cancel the transport at different connector sites [28].
From an experimental point of view, most of the research devoted to the study of periodical systems has been focused on the excitation of fundamental modes on different lattice sites. This is essentially due to experimental complications of exciting higher order modes, which in some cases have been solved indirectly by selectively populating p-band states [29, 30]. However, a precise excitation of dipolar states has only been possible very recently on optical waveguide lattices using an image generator setup [31], where a well-defined contrast between the transport of fundamental and dipolar states has been shown. The possibility to experimentally excite and control higher bands excitations, in optical lattice systems, paves the venue in which the study of remarkable properties of correlated systems such as superfluidity, superconductivity, organic ferromagnetic, antiferromagnetic ordering, among others, becomes possible [32–36].
In the case of graphene ribbons, the field of research is primarily focused on its unique electronic and magnetic properties. In particular, graphene nanoribbons can exhibit edge states [37] as well as the transition from semiconductors to semi-metals, depending on the number of coupled ribbons [38, 39]. Several attempts to fabricate and characterize these graphene-like structures have been reported due to their fundamental relevance for future applications in nanoelectronics [40, 41]. This includes room-temperature ballistic transport [42], well-controlled atomic configurations [43], photonics and optoelectronic applications [44]. In the photonic platform, graphene lattices have already been induced in photorefractive crystals at the micrometer scale, where conical diffraction and nonlinear localization were experimentally observed [45]. Additionally, the observation of unconventional edge states [46], photonic floquet topological insulators [47], and pseudospin-mediated vortex generation [48] have been reported in graphene optical lattices. The ability of directly imaging the wavefunction gives an important experimental advantage for photonic setups [3–5], in comparison to solid-state physics experiments.
In this paper, we study theoretically and experimentally a graphene-like ribbon where each lattice site supports two non-degenerate modes, the fundamental and dipolar modes. This system is particularly interesting because it can possess two FBs per mode, and these bands are robust against higher-order coupling interactions. This implies that the excitation of FB states is quite stable in realistic experimental conditions, as we show below. Since these modes possess a large propagation constant detuning, the interaction between them is effectively absent in the dynamics. To the best of our knowledge, this is the first experimental realization of a static periodical system possessing multiple FBs, corroborated by the observation of the spatially localized FB states.
2. The model
The unit cell of a graphene ribbon consists of six sites as sketched in figure 1(a), where each waveguide is separated from its NN by a center-to-center distance 'a'. The interaction between lattice sites is governed by the evanescent coupling which decreases exponentially with the distance between waveguides [12, 13]. We define the nearest and next-NN coupling coefficients in figure 1(b), where the horizontal coupling is V1, the short-diagonal one is V2, the vertical coefficient is V3, and the long-diagonal one is V4. The contribution of all other long range couplings can be safely neglected for the maximum propagation distance considered here. For our laser inscribed PL, each waveguide supports elliptically oriented modes with the major axis along the vertical, implying that V2 > V1 and V3 > V4.
Figure 1. (a) A graphene-ribbon. (b) Coupling interactions represented by lines. Linear spectrum for (c) V2/V1 = 2, V3, 4/V1 = 0 and (d) V2/V1 = 2, V3, 4/V1 = 0.5.
Download figure:
Standard image High-resolution imageIn the scalar-paraxial approximation, the evolution of light waves across a graphene ribbon is governed by the following discrete linear Schrödinger-like equations [3–5]
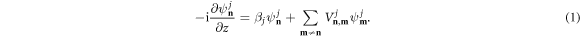
Here,  describes the field amplitude of a given mode, j = {s, p}, at the
describes the field amplitude of a given mode, j = {s, p}, at the  th site, with propagation constant βj, z corresponds to the propagation coordinate (dynamical variable) along the waveguides, and
th site, with propagation constant βj, z corresponds to the propagation coordinate (dynamical variable) along the waveguides, and  represents the coupling interactions between sites
represents the coupling interactions between sites  and
and  for mode j.
for mode j.
In model (1), it was assumed that the s and p modes are effectively decoupled. First, we consider that each waveguide supports only a single mode; i.e., the s orbital. In order to find the linear spectrum of this lattice, we first define the unit cell composed of sites A, B, C, D, E, and F as shown in figure 1(b), and insert a plane wave ansatz  , with
, with  . Here, kx and kz correspond to the transverse and longitudinal propagation constants, respectively. By solving the eigenvalue problem, we identify two FBs,
. Here, kx and kz correspond to the transverse and longitudinal propagation constants, respectively. By solving the eigenvalue problem, we identify two FBs,  , with degenerate eigenmodes, as indicated by the red horizontal lines in figures 1(c), (d). It should be highlighted that the flatness of these two bands is independent of the next-NN interactions due to the symmetry of the lattice geometry. Only for a reduced set of parameters the rest four linear bands can be expressed in a closed form. Therefore, for generality, we show the band structure in figure 1 (here, to simplify the presentation of our results, we set βs = 0) for two different cases considering (c) only NN and (d) NN plus next-NN interactions (the spectrum is shown in the corresponding Brillouin zone of size 2π/3). In both cases, one can observe two perfectly FBs, demonstrating the robustness of FB phenomena against the next-NN interactions in this lattice geometry. The compact localized states occupy only four sites (B, C, E, and F) of a unit cell, with equal intensity and the following phase distributions: {+, +, −, −} for the upper and {+, −, +, −} lower FBs, respectively. We can easily identify the destructive interference at sites An and Dn, as expected considering the properties of mini-arrays [28]. When exciting these localized FB states, the transport is absolutely canceled across the lattice due to the perfectly zero amplitude at the connector sites.
, with degenerate eigenmodes, as indicated by the red horizontal lines in figures 1(c), (d). It should be highlighted that the flatness of these two bands is independent of the next-NN interactions due to the symmetry of the lattice geometry. Only for a reduced set of parameters the rest four linear bands can be expressed in a closed form. Therefore, for generality, we show the band structure in figure 1 (here, to simplify the presentation of our results, we set βs = 0) for two different cases considering (c) only NN and (d) NN plus next-NN interactions (the spectrum is shown in the corresponding Brillouin zone of size 2π/3). In both cases, one can observe two perfectly FBs, demonstrating the robustness of FB phenomena against the next-NN interactions in this lattice geometry. The compact localized states occupy only four sites (B, C, E, and F) of a unit cell, with equal intensity and the following phase distributions: {+, +, −, −} for the upper and {+, −, +, −} lower FBs, respectively. We can easily identify the destructive interference at sites An and Dn, as expected considering the properties of mini-arrays [28]. When exciting these localized FB states, the transport is absolutely canceled across the lattice due to the perfectly zero amplitude at the connector sites.
Now, we consider that each waveguide in the lattice supports two modes, the fundamental (s) and the vertically oriented dipolar (p) modes. Note that the excitation of higher-order modes can be efficiently controlled by tuning the wavelength λ of incident light. The coupling between the two modes at the same lattice site is forbidden due to orthogonality. The large mismatch in propagation constants (defined as  ) [31] causes a negligible effective coupling interaction between the s and p modes at adjacent waveguides, as we confirmed experimentally below. The dynamical excitation of an orthogonal mode on a neighbor waveguide is proportional to the ratio Vsp/Δ β, where Vsp is the NN coupling interaction between the s and p modes. For standard elliptical waveguides [31], Vsp/Δ β ∼ 1/30. (In atomic systems, this is related to the energy difference between different energy levels. Note that the coupling interaction between the s and p modes on adjacent sites can induce interesting phenomena, such as topological edge modes [34]; however, its experimental atomic implementation is still a challenge.) By following these considerations, now we can write the dynamical equations for both modes just by identifying j = s or p in model (1) and by writing Vi as Vij, to distinguish the coupling constants for different modes (in general, as the wavefunction of the fundamental mode has a shorter evanescent tail [31, 34],
) [31] causes a negligible effective coupling interaction between the s and p modes at adjacent waveguides, as we confirmed experimentally below. The dynamical excitation of an orthogonal mode on a neighbor waveguide is proportional to the ratio Vsp/Δ β, where Vsp is the NN coupling interaction between the s and p modes. For standard elliptical waveguides [31], Vsp/Δ β ∼ 1/30. (In atomic systems, this is related to the energy difference between different energy levels. Note that the coupling interaction between the s and p modes on adjacent sites can induce interesting phenomena, such as topological edge modes [34]; however, its experimental atomic implementation is still a challenge.) By following these considerations, now we can write the dynamical equations for both modes just by identifying j = s or p in model (1) and by writing Vi as Vij, to distinguish the coupling constants for different modes (in general, as the wavefunction of the fundamental mode has a shorter evanescent tail [31, 34],  ). To simplify the description, we will consider only NN coupling such that V1, V2 ≫ V3, V4, and a detuning Δβ ≡ βs − βp ≈ 30 cm−1 [31]. In figure 2, we present an example of the composed linear spectrum for this two-mode-system (again, in order to simplify the presentation of our results, we set βp = 0). We observe four FBs located at ±V1p and Δβ ± V1s, and also the corresponding FB mode profiles. These states satisfy a destructive interference condition at connector sites (white zero amplitudes at the central row), depending on the sign of coupling constants. The relative sign of the coupling coefficients is determined by the parity symmetry of the s and p modes, considering the profiles sketched in figure 2. Whereas the fundamental coupling constants are always positive (
). To simplify the description, we will consider only NN coupling such that V1, V2 ≫ V3, V4, and a detuning Δβ ≡ βs − βp ≈ 30 cm−1 [31]. In figure 2, we present an example of the composed linear spectrum for this two-mode-system (again, in order to simplify the presentation of our results, we set βp = 0). We observe four FBs located at ±V1p and Δβ ± V1s, and also the corresponding FB mode profiles. These states satisfy a destructive interference condition at connector sites (white zero amplitudes at the central row), depending on the sign of coupling constants. The relative sign of the coupling coefficients is determined by the parity symmetry of the s and p modes, considering the profiles sketched in figure 2. Whereas the fundamental coupling constants are always positive ( ,
,  ), the dipolar ones are determined by the specific geometry: V1p > 0 and V2p < 0. In figure 2 we observe that the simplest fundamental FB mode (a) possesses the larger longitudinal propagation constant kz, while the more complex dipolar one (d) has a shorter value, for this two-modes system.
), the dipolar ones are determined by the specific geometry: V1p > 0 and V2p < 0. In figure 2 we observe that the simplest fundamental FB mode (a) possesses the larger longitudinal propagation constant kz, while the more complex dipolar one (d) has a shorter value, for this two-modes system.
Figure 2. Composed linear spectrum of a graphene-ribbon with  , V2p/V1p = −2 and
, V2p/V1p = −2 and  . (a)–(d) Intensity and phase profiles of the FB modes. Here, red (green) color represents a positive (negative) phase.
. (a)–(d) Intensity and phase profiles of the FB modes. Here, red (green) color represents a positive (negative) phase.
Download figure:
Standard image High-resolution image3. The experiment
Photonic graphene ribbons are directly fabricated inside a borosilicate substrate (Corning Eagle2000) using ultrafast laser inscription [49, 50]. Our fabrication method produces waveguides which are elongated along the vertical direction, therefore, the dipolar (p) modes are constrained to exist in that direction too. In figure 3(a), a white-light transmission micrograph of the output facet is presented, showing the vertically oriented waveguides. The laser-writing parameters are optimized to produce single-mode waveguides with low propagation losses at a 780 nm wavelength. The final lattices are inscribed in a 30 mm long substrate, with a = 17 μm waveguide spacing. In order to study the dynamics of the s and p modes, we reduced the wavelength to perform the experiment at λ = 640 nm. We implement an image generator setup [31] as shown in figure 3(b), which enables us to generate an arbitrary input state that can be launched on the PL (this is mounted on a 5-axis-stage, which is not shown in the figure). The key element of this setup is a sequence of two spatial light modulators (SLMs), that modulate the amplitude (SLM-t) and the phase (SLM-r) of an incident laser beam. Using this configuration, we launch a desired input state (with a specific intensity and/or phase distribution) at a given lattice site. For example, the inset in figure 3(b) shows a dipolar input state generated by the image generator setup. Figures 3(c), (d) present the output intensity distributions for single-site dipolar excitations at A and B sites, respectively. We observe how the energy diffracts in the lattice, due to the excitation of dispersive bands in the spectrum.
Figure 3. (a) White-light-micrograph of the output facet of a graphene ribbon. (b) Experimental setup. Here, L: lens; P: polarizer; SLM-t (SLM-r): transmission (reflection) SLM; M: Mirror; BS: Beam splitter; CCD: Camera; PL: photonic lattice. The inset shows a dipolar input state launched at an A site. (c), (d) Output intensity profiles of the dipolar excitations injected at the A and B sites, respectively, as indicated by the white circles.
Download figure:
Standard image High-resolution imageTo observe the dynamics of FB states, we use our image generator setup to excite only four desired sites of a unit cell with different spatial and phase profiles. First, to excite the fundamental FB modes, we generate two input states as sketched in figures 2(a) and (b). The observed outputs are presented in figures 4(a) and (b), respectively. We see that both FB input states propagate along the crystal without exhibiting any significant diffraction across the lattice, with an evident zero background. These states remain localized in space and occupy only four sites of the lattice, constituting two completely independent orthogonal states. To measure the phase profile of the input and output states, we implement an interferogram setup (this is not shown in figure 3(b) and simply consists on superposing the output profile with an extended tilted plane wave). The left and right insets in figures 4(a) and (b) show the input and output phase structure, respectively. As the intensity and phase profiles are preserved in the dynamics, we can confirm the first excitation of the two fundamental FB modes. Additionally, we inject an in-phase four-sites excitation pattern and observe that the energy starts to spread to the rest of the lattice by the excitation of A and D connector sites (see figure 4(c)). This input condition excites most of the linear spectrum and, therefore, for a longer propagation distance or a shorter waveguide separation, the energy would spread faster and would cover a larger transverse area, as we have confirmed numerically.
Figure 4. Output profiles for different input conditions: fundamental FB profiles at (a)  and (b) kz = Δβ − V1s, and (c) four in-phase sites. Left (right)-insets: interferogram of a tilted plane wave with input (output) profiles.
and (b) kz = Δβ − V1s, and (c) four in-phase sites. Left (right)-insets: interferogram of a tilted plane wave with input (output) profiles.
Download figure:
Standard image High-resolution imageIn the next step, we excite the dipolar (p) FB modes, which is considerably more challenging due to the complexity of the required spatial and phase profiles. Precise control of the input state, as well as its accurate overlap with the dipolar modes of the lattice sites (waveguides), is required. We generated two dipolar FB modes sketched in figures 2(c) and (d) and measured outputs are shown in figures 5(a) and (b). In both cases, we observe a spatially localized state which occupies only four sites of the lattice, with a zero background. The interferograms show that the input and output phase profiles are preserved during the propagation, confirming the excitation of p-FB modes. We probe the relevance of the phase structure, on the cancellation of the transport through connector sites [28], by injecting an input pattern composed of four in-phase dipolar waveguide modes. In figure 5(c) we show a complete destruction of the input profile, as a consequence of exciting the dispersive part of the spectrum.
Figure 5. Output profiles for different input conditions: dipolar FB profiles at (a) kz = V1p and (b) kz = −V1p, and (c) four in-phase sites. Left (right)-insets: interferogram of a tilted plane wave with input (output) profiles.
Download figure:
Standard image High-resolution image4. Conclusion
In conclusion, we studied a graphene-ribbon lattice and showed the existence of s and p FB modes in the linear optical regime. Due to the symmetry of this lattice geometry, FB states can exist even in the presence of next-NN interactions. Our lattice model possesses two FB per mode which correspond to bulk FB states, something that is particularly different to the already predicted FB edge modes in graphene-like lattices [38]. In our homogeneous lattice, fundamental and dipolar modes are effectively decoupled, showing no interaction between these modes. We carefully prepared several input states and experimentally observed a stable propagation of the four FB modes, what is confirmed by the analysis of the corresponding phase structure. This is the first experimental evidence of a controlled excitation of a system possessing two FBs per mode and, also, this is the first observation ever of a p-FB mode in any physical system. The ability to precisely control the input states in PLs gives us a unique access to investigate more complex phenomena, as it has been suggested in different areas of physics [1–5, 34–36]. It should also be highlighted that the effective coupling between the spatial modes (orbitals) can be controlled by tuning their energy (propagation constant) mismatch. Experimental realization of such engineered PLs with interacting spatial modes will enable us to investigate intriguing phenomena [34, 35] with more complex dynamics.
Acknowledgments
The authors sincerely thank financial support from Programa ICM RC130001, Millennium Institute for Research in Optics (MIRO), FONDECYT Grant No. 1151444, UK Science and Technology Facilities Council (STFC) through ST/N000625/1.








