Abstract
We introduce here the concept of establishing parity-time (PT)-symmetry through a gauge transformation involving a shift of the mirror plane for the parity operation. The corresponding unitary transformation on the system's constitutive matrix allows us to generate and explore a family of equivalent PT-symmetric systems. We further derive that unidirectional zero reflection for a reciprocal two-port system can always be associated with a passively gauged PT-symmetry. We demonstrate this experimentally using a microstrip transmission-line with magnetoelectric coupling. This study allows us to use bianisotropy as a practical route to realise and explore exceptional point behaviour of PT-symmetric or generally non-Hermitian systems.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Parity-time (PT)-symmetric Hamiltonians have been proposed as a class of non-Hermitian Hamiltonians with real eigenvalues that could possibly generalise the conventional paradigm of quantum mechanics [1–3]. At the so-called PT-symmetry breaking transition, these real eigenvalues evolve into complex conjugate pairs—a phenomenon that has triggered a series of developments, particularly in optical analogue studies, where power oscillations [4–8], coherent laser/absorbers [9–11], optical solitons in PT periodic systems [12], nonreciprocal propagation [13, 14], and wave propagation with unidirectional zero reflection (UZR), unidirectional invisibility, or constant intensity propagation [15–19], have been demonstrated. From the technological point of view, these developments have turned into a unique approach to achieve tuneable components with extreme sensitivity and unconventional behaviours [20–23]. A PT-symmetric Hamiltonian can be realised by optical components with a balanced gain/loss pair. This is understood as the ideal configuration of PT-symmetry. Further studies have shown that PT-symmetry breaking can also occur in passive systems, which can be mapped back to the ideal PT symmetric Hamiltonian by biasing the system with the averaged level of loss [4]. Such a gain/loss unbalanced situation is called a passive PT symmetry [4, 16]. More recently, PT-symmetry has also been introduced into metamaterials. With metamaterials, we can make PT-symmetric phenomena more flexible or towards the subwavelength regime. Highlights here are the possibility of unidirectional cloaking, PT-symmetric transformation optics [24–26], exceptional point-enabled polarisation manipulation [27, 28] (which is closely related to the topic of spin–orbit interaction of light [29]), the realisation of discrete breathers [30], and reversible nonreciprocity [31].
In this work, we generalise PT symmetry by gauging the parity operator through a continuous parameter, which represents the location of the mirroring plane. As we shall see, such a gauge generalisation gives us a way to generate a family of equivalent PT symmetric systems from a given seed system. It allows us to extend many of the special wave phenomena associated to PT symmetry to a much broader and equivalent family. Here, we focus on a particular phenomenon called UZR at the exceptional point of a PT-symmetric system, with zero reflectance from one side, but not from the other side of incidence [15–17]. Interestingly, UZR may be able to occur in other conventional optical systems as well, for example systems with bianisotropy, in which the forward and backward impedances are different [32–39]. Here we provide a common framework for understanding UZR in all of these different contexts by showing that UZR can actually always be interpreted as a result of passive PT-symmetry through a gauged parity operation for a reciprocal two-port system. To establish this connection between UZR and passive PT-symmetry experimentally, we use a microstrip transmission-line with bianisotropy to verify the validity of our theoretical predictions.
2. Gauged PT-symmetry condition
We start from a transmission-line system with voltage  and current
and current  for a generic discussion of one-dimensional wave propagation. Figure 1(a) shows the black-box representation of such a transmission-line system. The voltage at port 1 and port 2 are defined as
for a generic discussion of one-dimensional wave propagation. Figure 1(a) shows the black-box representation of such a transmission-line system. The voltage at port 1 and port 2 are defined as  and
and  while the currents flowing to the right at the two ports are defined by
while the currents flowing to the right at the two ports are defined by  and
and  respectively. The complex reflection amplitude for forward (backward) incidence is
respectively. The complex reflection amplitude for forward (backward) incidence is  (
( ), defined here at a common reference plane (the vertical black line), that is situated half-way in between the two ports.
), defined here at a common reference plane (the vertical black line), that is situated half-way in between the two ports.
Figure 1. (a) Transmission-line black-box representing one-dimensional wave propagation along the  -direction. Voltage at port 1 (2) is represented by
-direction. Voltage at port 1 (2) is represented by  (
( ). Current at port 1 (2) is represented by
). Current at port 1 (2) is represented by  (
( ) with positive value for current flowing to the right. The grey area denotes a black-box representation of the system. The forward (backward) complex reflection amplitude
) with positive value for current flowing to the right. The grey area denotes a black-box representation of the system. The forward (backward) complex reflection amplitude  (
( ), is defined with a common reference plane in the middle of the system, the vertical black line. (b) The gauging action by shifting the mirror action plane by
), is defined with a common reference plane in the middle of the system, the vertical black line. (b) The gauging action by shifting the mirror action plane by  in the
in the  -direction.
-direction.  and
and  are defined at the shifted plane. (c) and (d) are the trajectories of eigenvalues
are defined at the shifted plane. (c) and (d) are the trajectories of eigenvalues  of the scattering matrix and
of the scattering matrix and  (
( ) of the constitutive matrix in the complex plane for an ideal PT-symmetric system, going from the PT-symmetric phase to the broken phase through a degeneracy of eigenvalues at the exceptional point.
) of the constitutive matrix in the complex plane for an ideal PT-symmetric system, going from the PT-symmetric phase to the broken phase through a degeneracy of eigenvalues at the exceptional point.
Download figure:
Standard image High-resolution imageTo discuss PT-symmetry, we need to consider the action of parity and time-reversal operations on the various quantities. An obvious choice for the parity operation is the mirroring action with respect to the reference plane shown in figure 1(a), i.e. 
 However, by using the above black-box description, one can immediately recognise that there is a degree of freedom in where we put such a mirror plane. This degree of freedom becomes more apparent when we discuss metamaterial structures having both electric and magnetic responses in the next section as there is no obvious way to associate a mirror action plane. In light of this, figure 1(b) shows the situation if we put our mirror action plane at a location shifted from the reference plane by a distance
However, by using the above black-box description, one can immediately recognise that there is a degree of freedom in where we put such a mirror plane. This degree of freedom becomes more apparent when we discuss metamaterial structures having both electric and magnetic responses in the next section as there is no obvious way to associate a mirror action plane. In light of this, figure 1(b) shows the situation if we put our mirror action plane at a location shifted from the reference plane by a distance  in the forward propagation direction. This shifted mirroring action essentially means that we shift our reference plane for the voltages and the currents to a new reference plane (as if they are propagating on the background transmission line), then perform the mirroring action by swapping the voltages and currents on the two sides, and finally shift the reference planes back to the original position. The background transmission line in this work refers to the bare one without the two resonators. The variable
in the forward propagation direction. This shifted mirroring action essentially means that we shift our reference plane for the voltages and the currents to a new reference plane (as if they are propagating on the background transmission line), then perform the mirroring action by swapping the voltages and currents on the two sides, and finally shift the reference planes back to the original position. The background transmission line in this work refers to the bare one without the two resonators. The variable  now acts like a gauging parameter to choose the definition of the P-operator, which can now be expressed as
now acts like a gauging parameter to choose the definition of the P-operator, which can now be expressed as
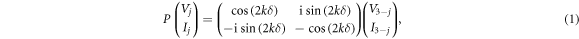
where  is the wave-number of free-space (the background transmission line, in this case). This P-operator has many of the properties of the usual parity operator (such as
is the wave-number of free-space (the background transmission line, in this case). This P-operator has many of the properties of the usual parity operator (such as  being unitary and Hermitian) so we should be able to pair it with the time-reversal operator
being unitary and Hermitian) so we should be able to pair it with the time-reversal operator
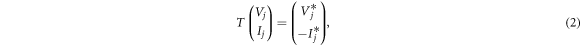
to derive a combined PT-symmetry condition with the fore-mentioned gauging parameter in the next step. On the other hand, the voltage  and current
and current  on the two sides are related to each other through a constitutive matrix description:
on the two sides are related to each other through a constitutive matrix description:
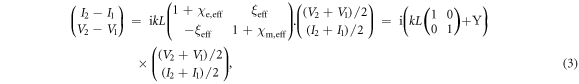
where  is the physical thickness of the system. We label the matrix elements of the constitutive matrix ϒ as
is the physical thickness of the system. We label the matrix elements of the constitutive matrix ϒ as 
 and
and  They represent the surface susceptibilities for the case of electromagnetic waves. We also limit ourselves to reciprocal systems in this work so that the two off-diagonal elements of the ϒ-matrix have same value but opposite signs. Nevertheless, equation (3), relating the difference of fields to the averaged fields, is the wave equation in the continuum limit except that we now model the system as a black-box. If the system is PT-symmetric in its response then equation (3) should be invariant after applying the combined PT-operation: [PT, ϒ] = 0. To begin with a 'conventional' case, we set
They represent the surface susceptibilities for the case of electromagnetic waves. We also limit ourselves to reciprocal systems in this work so that the two off-diagonal elements of the ϒ-matrix have same value but opposite signs. Nevertheless, equation (3), relating the difference of fields to the averaged fields, is the wave equation in the continuum limit except that we now model the system as a black-box. If the system is PT-symmetric in its response then equation (3) should be invariant after applying the combined PT-operation: [PT, ϒ] = 0. To begin with a 'conventional' case, we set  (no gauging) so that the parity operator is the usual mirror operation along the propagation direction, written as
(no gauging) so that the parity operator is the usual mirror operation along the propagation direction, written as  Invariance under this operation immediately induces the PT-symmetry condition (using [PT, ϒ] = 0) to be the requirement that the effective constitutive parameters of matrix ϒ are all real numbers. By having non-zero off-diagonal elements, we can hit the exceptional point where the two eigenvalues and the two eigenvectors of the ϒ matrix coalesce. Such a PT-symmetric constitutive matrix can be realised by stacking two dielectric slabs with the real parts of their permittivities being the same but their imaginary parts having opposite signs (e.g.
Invariance under this operation immediately induces the PT-symmetry condition (using [PT, ϒ] = 0) to be the requirement that the effective constitutive parameters of matrix ϒ are all real numbers. By having non-zero off-diagonal elements, we can hit the exceptional point where the two eigenvalues and the two eigenvectors of the ϒ matrix coalesce. Such a PT-symmetric constitutive matrix can be realised by stacking two dielectric slabs with the real parts of their permittivities being the same but their imaginary parts having opposite signs (e.g.  and
and  ). Equivalent behaviour can also be achieved by a pair of metasurfaces with shunt resistances of the same magnitude but opposite signs (gain and loss) [26]. Now, with the introduced gauging parameter
). Equivalent behaviour can also be achieved by a pair of metasurfaces with shunt resistances of the same magnitude but opposite signs (gain and loss) [26]. Now, with the introduced gauging parameter  we can define other kinds of PT-symmetry. As another typical case, we put
we can define other kinds of PT-symmetry. As another typical case, we put  for which we obtain the following PT-symmetry condition:
for which we obtain the following PT-symmetry condition:
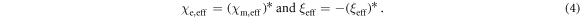
To realise this, one can again consider a pair of slabs stacked together. One slab is purely dielectric with  (real part
(real part  and imaginary part
and imaginary part  ),
),  while another slab is purely magnetic
while another slab is purely magnetic 
 This is a special case of our gauged PT-symmetry, as previously found by matching permittivity and permeability in [40]. While this double-slab system does not seem to have an obvious mirror symmetry even if we turn off the gain/loss by setting
This is a special case of our gauged PT-symmetry, as previously found by matching permittivity and permeability in [40]. While this double-slab system does not seem to have an obvious mirror symmetry even if we turn off the gain/loss by setting  it can now be considered as having PT-symmetry with a particular gauge
it can now be considered as having PT-symmetry with a particular gauge  by setting a particular location of the mirror plane. From this perspective, the gauging parameter
by setting a particular location of the mirror plane. From this perspective, the gauging parameter  actually introduces a whole family of PT-symmetric systems. For the general case, the family of PT-symmetric constitutive matrices have their family members related to each other simply through a unitary transformation:
actually introduces a whole family of PT-symmetric systems. For the general case, the family of PT-symmetric constitutive matrices have their family members related to each other simply through a unitary transformation:
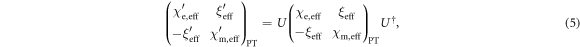
where
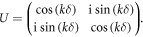
Equation (5) can be regarded as the gauge transformation subject to the gauge parameter  It means that any constitutive matrix obtained from a seed PT-symmetric constitutive matrix through a unitary transformation (the defined
It means that any constitutive matrix obtained from a seed PT-symmetric constitutive matrix through a unitary transformation (the defined  ) can be equivalently regarded as PT-symmetric, with the parity operator being gauged to another mirror action plane by a shift of distance
) can be equivalently regarded as PT-symmetric, with the parity operator being gauged to another mirror action plane by a shift of distance  We emphasise here that we put our focus on the PT-symmetry condition for the system response, i.e., on the constitutive matrix directly. This is relevant since systems whose internal system structure is not necessarily PT-symmetric (e.g. disordered systems [19, 41]), may satisfy the PT-symmetry condition in its system constitutive matrix. Consider here as an example the case of
We emphasise here that we put our focus on the PT-symmetry condition for the system response, i.e., on the constitutive matrix directly. This is relevant since systems whose internal system structure is not necessarily PT-symmetric (e.g. disordered systems [19, 41]), may satisfy the PT-symmetry condition in its system constitutive matrix. Consider here as an example the case of  for which the matrix ϒ becomes
for which the matrix ϒ becomes

with 
 and
and  being all real numbers. It is Hermitian for the case without loss and gain. One can also derive the scattering matrix S from equation (3), with convention
being all real numbers. It is Hermitian for the case without loss and gain. One can also derive the scattering matrix S from equation (3), with convention  The ϒ and S matrices are then simply related to each other through a Möbius transformation (matrix version):
The ϒ and S matrices are then simply related to each other through a Möbius transformation (matrix version):
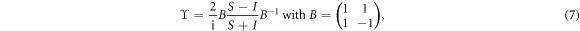
with  being the
being the  identity matrix [42, 43]. Here, the S-parameters are defined on the common reference plane (figure 1(a), or a zero thickness
identity matrix [42, 43]. Here, the S-parameters are defined on the common reference plane (figure 1(a), or a zero thickness  for the system) and the ϒ matrix obtained represents the surface susceptibilities mentioned earlier. Now, taking the example of the ϒ matrix in equation (6), as we vary the value of the gain/loss parameter
for the system) and the ϒ matrix obtained represents the surface susceptibilities mentioned earlier. Now, taking the example of the ϒ matrix in equation (6), as we vary the value of the gain/loss parameter  we can plot the eigenvalues (
we can plot the eigenvalues ( and
and  ) of the scattering matrix, as shown in figure 1(c), in the complex plane. When
) of the scattering matrix, as shown in figure 1(c), in the complex plane. When  increases from zero in the PT-symmetric phase,
increases from zero in the PT-symmetric phase,  and
and  trace out the unit circle in the complex plane, until a certain threshold when
trace out the unit circle in the complex plane, until a certain threshold when  where we have an exceptional point. In the PT-broken phase, the eigenvalues separate and deviate from the unit circle with reciprocal moduli. At the exceptional point, where eigenvalues of
where we have an exceptional point. In the PT-broken phase, the eigenvalues separate and deviate from the unit circle with reciprocal moduli. At the exceptional point, where eigenvalues of  become degenerate, UZR is realised with either
become degenerate, UZR is realised with either  or
or  going to zero. In such a case, the complex transmission coefficient
going to zero. In such a case, the complex transmission coefficient  has unit magnitude [15].
has unit magnitude [15].
On the other hand, the PT-symmetric behaviour can also be revealed if we look at the eigenvalues of the constitutive ϒ-matrix. The eigenvalues of the ϒ-matrix ( and
and  ) are related to those of the S-matrix by
) are related to those of the S-matrix by
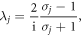
where  They are plotted in figure 1(d). These eigenvalues appear either in pairs of real numbers (PT-symmetric phase) or of two conjugate complex numbers (PT-broken phase) correspondingly. We note that this behaviour resembles that of the eigenvalues of a PT-symmetric Hamiltonian and we therefore prefer the usage of the constitutive matrix instead of the S-matrix for representation. Interestingly, equation (6) has the same form of a
They are plotted in figure 1(d). These eigenvalues appear either in pairs of real numbers (PT-symmetric phase) or of two conjugate complex numbers (PT-broken phase) correspondingly. We note that this behaviour resembles that of the eigenvalues of a PT-symmetric Hamiltonian and we therefore prefer the usage of the constitutive matrix instead of the S-matrix for representation. Interestingly, equation (6) has the same form of a  PT-symmetric Hamiltonian as that of a PT-symmetric optical waveguides pair or quantum-mechanical pair potential [1–4].
PT-symmetric Hamiltonian as that of a PT-symmetric optical waveguides pair or quantum-mechanical pair potential [1–4].
3. Bianisotropic transmission line
The above discussion on generalising the PT-symmetry condition implies that many previously considered exotic phenomena related to PT-symmetry can be immediately extended to a generalised but equivalent family. We have also proposed that PT-symmetry can be conveniently described by the constitutive matrix, which plays a similar role to that of the Hamiltonian in discussing PT-symmetry in quantum mechanics. More specifically, for the case of UZR for a two-port reciprocal system, by finding the constitutive matrix of the system, we will show that we can always associate such a system with passive PT-symmetry.
Next, we provide experimental support for validating the derived general PT-symmetry. For this purpose, we consider an electric resonating atom (a vertical bar with its far-end grounded) and a magnetic resonating atom (a split-ring resonator) coupled to a transmission line at various positions. Figure 2(a) shows a photograph of the sample when they are put at the same location. A natural choice for both the mirror and reference plane of PT-symmetry is indicated by the vertical black line. Figure 2(b) shows the case when the two atoms are put at different locations separated by a distance  chosen as 20 mm, while the extent of the losses at the two atoms can be varied by the two variable resistors mounted on the atoms. The two-ports are connected to a vector network-analyser (Agilent N5232A) for measuring the scattering parameters. For example, when we set the variable resistor at the split-ring and the vertical bar at 20
chosen as 20 mm, while the extent of the losses at the two atoms can be varied by the two variable resistors mounted on the atoms. The two-ports are connected to a vector network-analyser (Agilent N5232A) for measuring the scattering parameters. For example, when we set the variable resistor at the split-ring and the vertical bar at 20  and 0
and 0  we can extract the constitutive matrix (ϒ) from the experimentally obtained scattering parameters using equation (7). When we have metamaterial structures, it is not straightforward to identify where the interface (between freespace and metamaterial) lies. Therefore, the S-parameters here are simply defined on a common reference plane at the position of the electric atom, effectively with a zero thickness of the sample. This means that when we extract the ϒ matrix, we are only including the activity of the resonating elements and not the background transmission line. From now on, we just label the matrix elements of ϒ as
we can extract the constitutive matrix (ϒ) from the experimentally obtained scattering parameters using equation (7). When we have metamaterial structures, it is not straightforward to identify where the interface (between freespace and metamaterial) lies. Therefore, the S-parameters here are simply defined on a common reference plane at the position of the electric atom, effectively with a zero thickness of the sample. This means that when we extract the ϒ matrix, we are only including the activity of the resonating elements and not the background transmission line. From now on, we just label the matrix elements of ϒ as  for simplicity. The four matrix elements are plotted in figure 2(c), the electric response
for simplicity. The four matrix elements are plotted in figure 2(c), the electric response  constitutes a Drude-type resonance at zero frequency for the electric atom with some additional electric response from the magnetic atom. The magnetic response
constitutes a Drude-type resonance at zero frequency for the electric atom with some additional electric response from the magnetic atom. The magnetic response  is a Lorentzian, coming from the magnetic resonance of the split-ring. The bianisotropy, from the near-field coupling between the two atoms, is revealed through the non-zero values of
is a Lorentzian, coming from the magnetic resonance of the split-ring. The bianisotropy, from the near-field coupling between the two atoms, is revealed through the non-zero values of  or
or  In fact, the experimental results can be accurately represented by the following dipolar model:
In fact, the experimental results can be accurately represented by the following dipolar model:
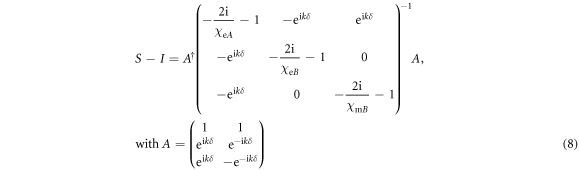
where  is the electric response of the electric atom,
is the electric response of the electric atom,  and
and  are the electric and magnetic response of the magnetic atom. The matrix
are the electric and magnetic response of the magnetic atom. The matrix  converts incident fields to local fields. The matrix in the middle is the polarizability matrix to turn local fields to dipole moments while the matrix
converts incident fields to local fields. The matrix in the middle is the polarizability matrix to turn local fields to dipole moments while the matrix  (conjugate transpose of A) converts the dipole moments to scattered waves. The phase factor
(conjugate transpose of A) converts the dipole moments to scattered waves. The phase factor  at various positions means the coupling between the electric and magnetic atoms, where
at various positions means the coupling between the electric and magnetic atoms, where  is the wavenumber of the background transmission line and
is the wavenumber of the background transmission line and  is the distance between the two resonators. By using a Lorentz model fitting on the
is the distance between the two resonators. By using a Lorentz model fitting on the 
 and
and  (see appendix for details), one can then obtain the Lorentz-model representation of the final structure and the corresponding ϒ-matrix elements are plotted as dashed lines in figure 2(c). They fit well with the measured results for the sample in figure 2(b) within the frequency range we are interested in (from 0.4 to 1 GHz) and also reveal the bianisotropy from the shifting.
(see appendix for details), one can then obtain the Lorentz-model representation of the final structure and the corresponding ϒ-matrix elements are plotted as dashed lines in figure 2(c). They fit well with the measured results for the sample in figure 2(b) within the frequency range we are interested in (from 0.4 to 1 GHz) and also reveal the bianisotropy from the shifting.
Figure 2. (a) Photo of a symmetric structure where the reference planes of the electric (upper red box) and magnetic (lower red box) resonators are aligned to the same position. (b) Photo of the structure with bianisotropy with variable resistance at the electric (magnetic) atom being set as 0 (20)  (c) ϒ-matrix elements of the bianisotropic structure with reference plane at the electric atom. The solid blue and red lines denote the real and imaginary parts of the matrix elements extracted from measurements, respectively. The light blue and dark red dashed lines are the real and imaginary parts of the corresponding matrix elements from the theoretical dipolar model, respectively.
(c) ϒ-matrix elements of the bianisotropic structure with reference plane at the electric atom. The solid blue and red lines denote the real and imaginary parts of the matrix elements extracted from measurements, respectively. The light blue and dark red dashed lines are the real and imaginary parts of the corresponding matrix elements from the theoretical dipolar model, respectively.
Download figure:
Standard image High-resolution imageNow, suppose we increase the tuneable resistance R at the electric atom while keeping the resistance of the magnetic atom set at 20  The constitutive ϒ-matrix is extracted again from the experimental results of the scattering parameters. They are shown in figure 3 for both the real and imaginary parts of the 4 matrix elements. One can see that R mostly affects
The constitutive ϒ-matrix is extracted again from the experimental results of the scattering parameters. They are shown in figure 3 for both the real and imaginary parts of the 4 matrix elements. One can see that R mostly affects  with larger imaginary part generally at larger R. It also affects the real part of
with larger imaginary part generally at larger R. It also affects the real part of  due to some induction effect (a coil structure is present within the variable resistor). The dipolar model for each value of R is fitted and serves as the model representation later.
due to some induction effect (a coil structure is present within the variable resistor). The dipolar model for each value of R is fitted and serves as the model representation later.
Figure 3. The real (left four panels) and imaginary (right four panels) parts of the experimentally extracted constitutive matrix elements as a function of the electric atom resistance (R) and the frequency in GHz (f). Reference plane is chosen to be at the electric atom.
Download figure:
Standard image High-resolution imageBy tuning the variable resistor of the electric atom, the bianisotropic transmission line can display UZR. We first locate where UZR can be obtained in the frequency-resistance phase space. The colour map in figure 4(a) shows a measure of UZR defined by  It gives a value
It gives a value  for UZR at the first point (labeld by Ex1) with
for UZR at the first point (labeld by Ex1) with  and a value
and a value  for UZR at the point (labelled by Ex2) with
for UZR at the point (labelled by Ex2) with  These two points are actually the exceptional points, i.e., the eigenvalue degeneracy of the scattering S-matrix. For example, we have plotted the trajectories of the eigenvalues of the S-matrix when the tuneable resistance is varied at fixed frequency
These two points are actually the exceptional points, i.e., the eigenvalue degeneracy of the scattering S-matrix. For example, we have plotted the trajectories of the eigenvalues of the S-matrix when the tuneable resistance is varied at fixed frequency  shown as blue colour in figure 4(b) (solid line for dipolar model results and symbols for the experimental results). The two eigenvalues cross each other and become degenerate at the exceptional point, at the tunable resistance
shown as blue colour in figure 4(b) (solid line for dipolar model results and symbols for the experimental results). The two eigenvalues cross each other and become degenerate at the exceptional point, at the tunable resistance  Similarly, we can vary the tunable resistance at
Similarly, we can vary the tunable resistance at  (plotted in red colour) to pass through the exceptional point with eigenvalue degeneracy and UZR. The UZR at exceptional point Ex1 has
(plotted in red colour) to pass through the exceptional point with eigenvalue degeneracy and UZR. The UZR at exceptional point Ex1 has  and
and  at the second exceptional point Ex2. As we have discussed, an eigenvalue degeneracy in the S matrix can be translated to an eigenvalue degeneracy in the
at the second exceptional point Ex2. As we have discussed, an eigenvalue degeneracy in the S matrix can be translated to an eigenvalue degeneracy in the  -matrix. We have plotted the eigenvalue trajectories in figure 4(c) with corresponding phenomena observed. The condition of the passive PT-symmetry, being formulated later, is plotted in advance as dashed line in figure 4(a) and it passes through the point of UZR as predicted.
-matrix. We have plotted the eigenvalue trajectories in figure 4(c) with corresponding phenomena observed. The condition of the passive PT-symmetry, being formulated later, is plotted in advance as dashed line in figure 4(a) and it passes through the point of UZR as predicted.
Figure 4. (a) Measure for UZR defined by  extracted from experimental data (color range from blue: -1, to red: +1). The dashed line shows where the system at UZR will be proved to be passive PT-symmetric in the next step. (b) Eigenvalues of S at the frequency of exceptional point 1 (blue) and exceptional point 2 (red) as a function of the tuneable resistance R. (c) Eigenvalues of ϒ at the frequency of exceptional point 1 (blue) and exceptional point 2 (red) as a function of the tuneable resistance R.
extracted from experimental data (color range from blue: -1, to red: +1). The dashed line shows where the system at UZR will be proved to be passive PT-symmetric in the next step. (b) Eigenvalues of S at the frequency of exceptional point 1 (blue) and exceptional point 2 (red) as a function of the tuneable resistance R. (c) Eigenvalues of ϒ at the frequency of exceptional point 1 (blue) and exceptional point 2 (red) as a function of the tuneable resistance R.
Download figure:
Standard image High-resolution image4. UZR as passive PT-symmetry
Up to now, we know that the exceptional point (eigenvalue degeneracy) of the ϒ-matrix is equivalent to the eigenvalue degeneracy for the S-matrix where we obtain UZR. It is well known that a conventional PT-symmetric system gives rise to UZR at an exceptional point but the converse is not a common statement, i.e. UZR does not guarantee that the system is PT-symmetric in the normal sense where P is a simple mirroring action. Here we generalise the connection between UZR and PT-symmetry by using the gauged parity operator in the following. In fact, UZR, an eigenvalue degeneracy of the ϒ-matrix, can be stated as  (reciprocity assumed so that
(reciprocity assumed so that  is always satisfied). As the eigenvalue degeneracy of the ϒ-matrix retains even if we shift to another reference plane (as it is just a unitary transformation), we can always choose the gauge such that
is always satisfied). As the eigenvalue degeneracy of the ϒ-matrix retains even if we shift to another reference plane (as it is just a unitary transformation), we can always choose the gauge such that  In such a gauge, UZR means
In such a gauge, UZR means  together with
together with  Now, we compare this to the form shown in equation (6). For a reciprocal system displaying UZR, we can therefore always write the ϒ-matrix for such a system as
Now, we compare this to the form shown in equation (6). For a reciprocal system displaying UZR, we can therefore always write the ϒ-matrix for such a system as
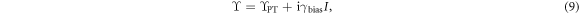
where ϒPT is PT-symmetric (in the form shown in equation (6)). Hence, we can always associate a ϒ-matrix possessing UZR to a PT-symmetric one by biasing the diagonal values with a common imaginary part  This can be called a passive PT-symmetric system, inspired by a similar nomenclature for considering PT-symmetry from a pair of optical waveguides with loss contrast [4]. Thus, we have generalised the notion of passive PT-symmetry when the parity operator is now generalised to its gauged form. We emphasise that with such a generalisation, equation (9) is the necessary and sufficient condition for obtaining UZR in a reciprocal two-port system.
This can be called a passive PT-symmetric system, inspired by a similar nomenclature for considering PT-symmetry from a pair of optical waveguides with loss contrast [4]. Thus, we have generalised the notion of passive PT-symmetry when the parity operator is now generalised to its gauged form. We emphasise that with such a generalisation, equation (9) is the necessary and sufficient condition for obtaining UZR in a reciprocal two-port system.
For the case of our bianisotropic transmission line, the real part of the ϒ-matrix elements are plotted in figure 5 in the range of frequency and tunable resistance we are considering. As we have discussed, the ϒ-matrix is now gauged to the reference plane with the real part of  and
and  being the same, as shown in figure 5(a). Figure 5(b) shows the corresponding dipolar model results with very good agreement. From the panel showing
being the same, as shown in figure 5(a). Figure 5(b) shows the corresponding dipolar model results with very good agreement. From the panel showing  or
or  the contour with zero value is identified as the dashed-lines, these lines are where the system can be regarded as passive PT-symmetric. These lines pass through the exceptional points, where also the following identities hold:
the contour with zero value is identified as the dashed-lines, these lines are where the system can be regarded as passive PT-symmetric. These lines pass through the exceptional points, where also the following identities hold:  as figure 4 shows.
as figure 4 shows.
Figure 5. The constitutive matrix after choosing a gauge to have  as a function of the electric atom resistance and the frequency f in GHz. The four panels in (a) show the real part of ϒ-matrix elements extracted from experimental results. The four panels in (b) show the corresponding model results. The passive PT-symmetry condition is indicated by the dashed line where
as a function of the electric atom resistance and the frequency f in GHz. The four panels in (a) show the real part of ϒ-matrix elements extracted from experimental results. The four panels in (b) show the corresponding model results. The passive PT-symmetry condition is indicated by the dashed line where 
Download figure:
Standard image High-resolution imageFrom the perspective of generalising PT-symmetry, it is interesting to note that our scheme and a previous scheme in establishing passive PT-symmetry [4] are both gauging actions. If the transformed system has PT-symmetry, we can say the original system is also equivalently PT-symmetric. The difference between the two schemes is in how the fields are gauged. The fields are unitarily transformed through a change of reference plane, as if the fields are propagating in a bare transmission line, in our case, while the fields are transformed through an exponential attenuation factor in the case of establishing passive PT-symmetry. On the other hand, we have used UZR to illustrate the usage of gauged PT-symmetry but there can be other PT-symmetry related phenomena generalised through such gauging. One example is a PT-symmetric laser-absorber [10]. If a PT-symmetric system supports a lasing mode at threashold with only outgoing waves, it gaurantees the PT-transformed version of such lasing mode becomes a perfect absorbing mode, in the same system, that only has incoming waves. For our gauged PT-symmetry operation, the fields on the two ports are transformed as: 


 where superscript
where superscript  indicates the forward/backward propagting amplitudes. Therefore, the roles of incoming and outgoing waves on the two ports are swapped and a gauged PT-symmetric system having a laser mode guarantees the existence of a perfectly absorbing mode in the system as well. In terms of the ϒ-matrix, a lasing mode at threshold has eigenvalue
indicates the forward/backward propagting amplitudes. Therefore, the roles of incoming and outgoing waves on the two ports are swapped and a gauged PT-symmetric system having a laser mode guarantees the existence of a perfectly absorbing mode in the system as well. In terms of the ϒ-matrix, a lasing mode at threshold has eigenvalue  (a pole of S according to equation (7)), and the PT-symemtry nature induces
(a pole of S according to equation (7)), and the PT-symemtry nature induces  (conjugate, equivalently a zero of S) as another eigenvalue indicating a perfectly absorbing mode and vice versa. We note that there are also works exploring PT-symmetry to include magnetic in addition to electric response, including chirality, bright-dark atoms configuration and ferromagnetic inclusion [44–46]. In this work, we believe the bianisotorpy being explored can provide a feasible and straight-forward route to explore exceptional point and non-Hermitian systems in general.
(conjugate, equivalently a zero of S) as another eigenvalue indicating a perfectly absorbing mode and vice versa. We note that there are also works exploring PT-symmetry to include magnetic in addition to electric response, including chirality, bright-dark atoms configuration and ferromagnetic inclusion [44–46]. In this work, we believe the bianisotorpy being explored can provide a feasible and straight-forward route to explore exceptional point and non-Hermitian systems in general.
5. Conclusion
It has been known that UZR can occur in systems both with and without PT-symmetry, but the exact relationship between these two phenomena was not clear. By considering an extension of the parity operator through gauging, we have established that a reciprocal two-port system with UZR is always equivalent to a passive PT-symmetric system through a unitary transformation of the system constitutive matrix, which effectively means a change of reference plane for the parity operator. This link will be helpful to explore systems with hidden PT-symmetry, such as the bianisotropic transmission line considered as an example in this work. Moreover, the considered gauge transformation generalises exceptional point wave phenomena associated with PT-symmetry to a broader family of equivalent systems containing exceptional points.
Acknowledgments
JL would like to acknowledge funding support from the European Union's Seventh Framework Programme (FP7) under Grant Agreement No. 630979. SR is supported by the Austrian Science Fund (FWF) through project No. F49 (SFB NextLite). LZ, YS, and HC would like to acknowledge funding support from NSFC (Grants No. 61621001 and No. 11674247).
Appendix.: Dipolar model
To model the bianisotropic structure we need to know the responses of the individual atoms. We describe the electric atom (atom A) and the magnetic atom (atom B) by the constitutive matrices  and
and  where we have assumed that
where we have assumed that  is negligible. We can then relate the susceptibilities of the A and B atoms to their polarizabilities via
is negligible. We can then relate the susceptibilities of the A and B atoms to their polarizabilities via
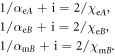
The additional imaginary constant i is the so-called radiative correction at finite frequency. The 
 and
and  can be extracted numerically through equation (7) from the S-parameters of the individual atoms shown in figure 2(a). The extracted
can be extracted numerically through equation (7) from the S-parameters of the individual atoms shown in figure 2(a). The extracted 
 and
and  can be approximately decomposed into resonance terms
can be approximately decomposed into resonance terms
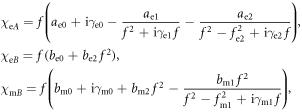
where  is the frequency in units of GHz. They are proportional to
is the frequency in units of GHz. They are proportional to  due to the definition in equation (3). The constant terms and the quadratic terms are the low-frequency Taylor series expansion contributed by the higher order modes that are not captured by the resonance terms. The various constants are extracted as
due to the definition in equation (3). The constant terms and the quadratic terms are the low-frequency Taylor series expansion contributed by the higher order modes that are not captured by the resonance terms. The various constants are extracted as 







 and
and 




 These parameters serve as the starting parameters to model of the ϒ-matrix of the final structure with a shifted distance
These parameters serve as the starting parameters to model of the ϒ-matrix of the final structure with a shifted distance  between the two atoms through the interaction dipolar model in equation (8).
between the two atoms through the interaction dipolar model in equation (8).








