Abstract
The temperature dependence of the dielectric response of ordinary ferroelectric materials exhibits a frequency-independent anomalous peak as a manifestation of the ferroelectric to paraelectric phase transition. A second anomaly in the permittivity has been reported in different ferroelectric perovskite-type systems at low temperatures, often at cryogenic temperatures. This anomaly manifests as a frequency-dependent local maximum, which exhibits similar characteristics to that observed in relaxor ferroelectrics around their phase transition. The origin of this unexpected behavior is still controversial. In order to clarify this phenomenon, a model-free route solution is developed in this work. Our findings reveal the same critical linear pattern/glass-like freezing behavior previously observed for glass-forming systems. Contrary to current thought, our results suggest that a critical-like dynamic parameterization could provide a more appropriate solution than the conventional Vogel–Fulcher–Tammann equation. The implemented methodology may open a new pathway for analyzing relaxation phenomena in other functional materials like relaxor ferroics.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The study of the temperature and frequency dependence of the dielectric response has proven to be a helpful tool in condensed matter physics. Specifically, in ferroelectric systems it has facilitated the exploration of several physical phenomena such as structural phase transitions and boundaries [1, 2], space-charge relaxations [3, 4], point defects relaxations [5], and other dielectric relaxations [6–8]. These physical phenomena are usually related to anomalous behaviors in the dielectric response. For instance, the ferroelectric to paraelectric phase transition appears as a maximum in the permittivity versus temperature curve at the transition temperature. Depending on the ferroelectric nature, this maximum shows either frequency independence (ordinary ferroelectrics) or frequency dependence (relaxor ferroelectrics) [9].
In addition to their second order phase transition, a wide variety of ordinary ferroelectric (i.e. non-relaxor) systems show a frequency-dependent low temperature dielectric anomaly. For instance, the well-known  (PZT) system shows a low temperature dielectric relaxation for different crystallographic structures (different
(PZT) system shows a low temperature dielectric relaxation for different crystallographic structures (different 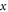 values) and dopants (donors and/or acceptors) [10–13]. A similar anomalous behavior has also been reported in NaNbO3 [14],
values) and dopants (donors and/or acceptors) [10–13]. A similar anomalous behavior has also been reported in NaNbO3 [14], 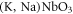 [15],
[15], 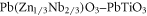 [16],
[16], 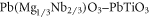 [17],
[17], 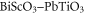 [18],
[18],  [19], and other perovskite systems. Furthermore, low temperature dielectric anomalies have also been reported in tetragonal tungsten bronze [20, 21] and Aurivillius systems [22]. Despite the phenomenon seem to be a common feature of these materials, research has been focused on understanding the specificities of each system, the results of which are usually meaningful only for the material under study. Moreover, only in a few such works have attempts been made to parameterize the observed relaxation [18, 19]; these have shown that the relaxation exhibits an unambiguous deviation from the simple Arrhenius behavior, similar to the 'super-Arrhenius' behavior displayed in most disordered systems, as in the case of relaxor ferroelectrics.
[19], and other perovskite systems. Furthermore, low temperature dielectric anomalies have also been reported in tetragonal tungsten bronze [20, 21] and Aurivillius systems [22]. Despite the phenomenon seem to be a common feature of these materials, research has been focused on understanding the specificities of each system, the results of which are usually meaningful only for the material under study. Moreover, only in a few such works have attempts been made to parameterize the observed relaxation [18, 19]; these have shown that the relaxation exhibits an unambiguous deviation from the simple Arrhenius behavior, similar to the 'super-Arrhenius' behavior displayed in most disordered systems, as in the case of relaxor ferroelectrics.
Although the low temperature dielectric relaxation displayed in ordinary ferroelectrics has been reported for a wide number of systems, the mechanisms involved are not well understood. Furthermore, the possible existence of dynamic crossovers has so far been ignored and the interpretation of the super-Arrhenius (SA) behavior has failed to take into account that several different dynamic domains could appear. Inevitably, additional theoretical and/or experimental clarifications are required to disentangle this issue. Additionally, results of recent works have indicated that investigations on low temperature dielectric relaxation are not only scientific interest, but also highly related to the outstanding room-temperature properties of ferroelectrics [23, 24]. Thus, further detailed investigations on low temperature dielectric relaxations are quite desired. In this paper, an overview of the dielectric relaxation parameterization is given, which has enabled an important question to be formulated. A new methodology has also been implemented in order to gain insights into the relaxation dynamics. Finally, a discussion of the results is provided.
2. Dielectric relaxation parameterization
Parameterization of the extraordinary increase in the primary relaxation time 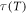 on cooling appeared to be elusive [25, 26]. It yields a dramatic increase in the activation energy, giving rise to the SA [27]:
on cooling appeared to be elusive [25, 26]. It yields a dramatic increase in the activation energy, giving rise to the SA [27]:
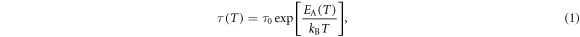
where the term EA(T) defines the temperature-dependent apparent activation energy and kB denotes the Boltzmann constant. When 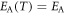 (i.e., a constant value), the simple Arrhenius relation is validated.
(i.e., a constant value), the simple Arrhenius relation is validated.
The Vogel–Fulcher–Tammann (VFT) phenomenological equation is probably the most commonly used approach for parameterizing the SA behavior in ferroelectrics. It was used for the first time in ferroelectrics to described the increase in the permittivity maximum temperature with increasing frequency in 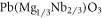 [28] and Li-doped
[28] and Li-doped 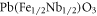 [29]. Thereafter, the VFT equation has been widely used to describe the dispersive ferroelectric to paraelectric phase transition in relaxor ferroelectrics and is often regarded as strong evidence for the existence of a static freezing temperature in the thermally activated polarization fluctuations [28].
[29]. Thereafter, the VFT equation has been widely used to describe the dispersive ferroelectric to paraelectric phase transition in relaxor ferroelectrics and is often regarded as strong evidence for the existence of a static freezing temperature in the thermally activated polarization fluctuations [28].
Despite the absence of a robust theoretical justification for the VFT equation, it is believed that its validity for the temperature maximum of the real or/and imaginary part of the dielectric permittivity implies a critical variation of the relaxation time spectrum around its singularity. However, Tangansev [30] demonstrated that a VFT-type relationship does not necessarily imply freezing in the system. By means of three parameters 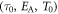 , the VFT equation describes the temperature dependence of the relaxation times in the following way:
, the VFT equation describes the temperature dependence of the relaxation times in the following way:
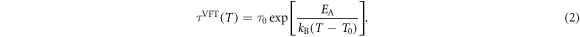
T0 being a singular divergence temperature usually regarded as the freezing temperature of a freezing phenomenon. The parameter EA denotes the Arrhenius activation energy and 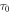 defines the relaxation time at high temperatures.
defines the relaxation time at high temperatures.
Despite the success of VFT in the relaxor ferroelectrics science community, a basic question nevertheless arises: is the divergent VFT equation suitable to describe the dynamics of the low temperature dielectric relaxation in ordinary ferroelectrics? As was stated by Hecksher et al [25], since no experiment can conclusively prove the existence of a dynamic divergence, a diverging relaxation time of VFT form will be regarded as probably correct if, and only if, the VFT equation fits data considerably better than other mathematically simple functions with the same number of fitting parameters and no dynamic divergence. Taking into account that there is no compelling evidence for the VFT prediction that the relaxation time diverges at a finite temperature, models that do not predict a dynamic divergence of the VFT form should be considered.
The impressive evidence reported by Hecksher et al [25] led to the appearance of further new, theoretically supported equation without the 'finite-temperature' divergence strengthened by the derivation made by Mauro et al [31] of the equation introduced empirically by Waterton [32]:

where  has the same meaning as in the VFT equation, while the other two parameters refer to two energies; that is, K related to an effective activation barrier and C related to the energy difference between two-states in the system. This equation is gradually gaining an increasing popularity because it provides an improved description of the relaxation time temperature relationship using the same number of VFT parameters.
has the same meaning as in the VFT equation, while the other two parameters refer to two energies; that is, K related to an effective activation barrier and C related to the energy difference between two-states in the system. This equation is gradually gaining an increasing popularity because it provides an improved description of the relaxation time temperature relationship using the same number of VFT parameters.
The subsequent analysis of experimental data confirmed the advantage of the Waterton-Mauro (WM, also called MYEGA) equation without a 'finite-temperature divergence' over the VFT equation. Nevertheless, this model does not explain the dynamic of the systems where the prevalence of the critical-like equation with the clear finite-temperature divergence is shown, such as glass-forming liquid crystals (LC) and orientationally disordered crystals (ODICs, plastic crystals), spin-glass (SG)-like systems and others [33–35], where a remarkable dynamic divergence is observed. Such systems are better described by using a power-law SG equation:

which is also a three-parameter equation, where  has a different meaning than in previous equations. Here
has a different meaning than in previous equations. Here  is the value of the relaxation time for
is the value of the relaxation time for 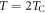 , TC being a critical temperature comparable to T0 in the VFT equation. The exponent φ is related to an order parameter, often associated to the orientational order-disorder of the system.
, TC being a critical temperature comparable to T0 in the VFT equation. The exponent φ is related to an order parameter, often associated to the orientational order-disorder of the system.
In order to answer the formulated question, an experimental fitting comparison of the three model equations should be performed to obtain statistical criteria for disentangling the predominant behavior. If the statistical comparison of the direct fitting is not clear enough to elucidate the superior model equation, a model-free approach to the experimental 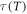 data should be performed.
data should be performed.
3. Data analysis from a model-free route
A novel procedure introduced recently for glass-forming systems [33] is implemented here in order to adopt a model-free approach for the dielectric relaxation data processing. The procedure has been successfully applied to a wide variety of experimental data-sets, ranging from low molecular weight liquids and polymers to LC and plastic crystals [36], and shows the effectiveness of this model-free route (MFR) for revealing changes in the dynamic behavior of these systems. The procedure is based on the solution of a Bernoulli-type differential equation that is obtained by taking into account that the SA behavior is described by equation (1), where the general form of the temperature-dependent activation energy EA(T) is a priori unknown.
The equation (1) can be easily transformed by the first derivative, assuming 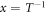 :
:
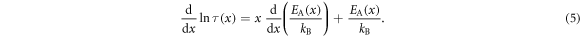
According to Drozd-Rzoska et al [37], the apparent activation enthalpy can be defined as:

Thus, the equation (5) can be rewritten as a Bernoulli-type equation:
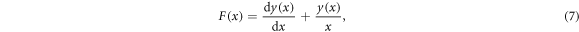
where 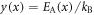 , and
, and
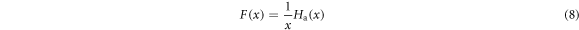
is a temperature-dependent function that can be obtained directly from dielectric relaxation data. It is important to note that the apparent activation enthalpy definition, and therefore F(x), is only valid for an isobaric process, as demonstrated by Martinez-Garcia et al [36] from a thermodynamic point of view.
The solution of the equation (7):
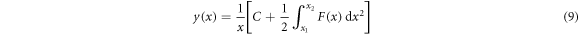
allows us to obtain the activation energy function, 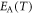 , from the experimental data, being x1 and x2 the inverse of the maximum and minimum temperatures, respectively. The constant C is evaluated by extrapolation of the experimental data at high temperatures, at which the activation energy function become a constant value.
, from the experimental data, being x1 and x2 the inverse of the maximum and minimum temperatures, respectively. The constant C is evaluated by extrapolation of the experimental data at high temperatures, at which the activation energy function become a constant value.
In the SA domain, the apparent activation energy increases with a decreasing temperature, leading to a dramatic increase from constant values to 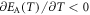 , and thus giving rise to a nonlinear behavior in the
, and thus giving rise to a nonlinear behavior in the 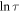 versus
versus 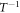 representation. This formal similarity enabled Dyre and Olsen (DO) to propose an alternative parameter of fragility to quantify the metric of the SA behavior by the 'Grüneisen-style' activation energy temperature index [38]:
representation. This formal similarity enabled Dyre and Olsen (DO) to propose an alternative parameter of fragility to quantify the metric of the SA behavior by the 'Grüneisen-style' activation energy temperature index [38]:
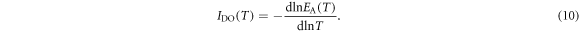
Hecksher et al [25] showed that analysis of the DO index may constitute a decisive tool for testing the validity of a given equation for fitting  experimental data. They arrived at that conclusion by comparing the experimental and theoretical values of
experimental data. They arrived at that conclusion by comparing the experimental and theoretical values of  that is, the experimental with the expected IDO(T) function from a given
that is, the experimental with the expected IDO(T) function from a given  equation for 42 relaxation time
equation for 42 relaxation time 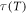 data systems by assuming two universal values of
data systems by assuming two universal values of 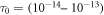 s in the calculation of
s in the calculation of 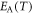 of equation (1). More recently,
of equation (1). More recently, 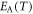 was determined without a bias assumption of
was determined without a bias assumption of 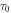 values by using the MFR, showing that the experimental values of reciprocals of DO indices yield a universal linear dependence
values by using the MFR, showing that the experimental values of reciprocals of DO indices yield a universal linear dependence 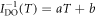 , thereby enabling a novel generalized power-law dependence for the structural entropy [33, 36]:
, thereby enabling a novel generalized power-law dependence for the structural entropy [33, 36]:
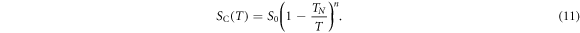
The linear regression fit of the DO index can yield experimental values of a and b without any model assumption, and subsequently the unequivocal estimations of the singular temperature  via
via 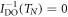 and the exponent
and the exponent 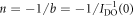 . This means that the values of a and b determined from the experimental data of
. This means that the values of a and b determined from the experimental data of 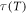 can also be used as the basic input parameters for assessing the optimal parameterization. By rescaling the equations (2)–(4) with equation (10), we obtain:
can also be used as the basic input parameters for assessing the optimal parameterization. By rescaling the equations (2)–(4) with equation (10), we obtain:
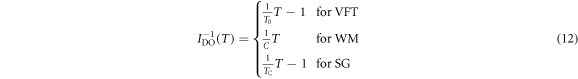
giving the theoretical values of the n parameter for each model equation, being 1 for VFT and SG, and 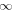 for WM. Different to VFT, the linearity for the SG is reached only in the dynamic temperature domain close to TC.
for WM. Different to VFT, the linearity for the SG is reached only in the dynamic temperature domain close to TC.
A universal temperature-linear dependence of the DO index was found for glass-forming systems [33]. Nevertheless, the functional dependence of IDO(T) is unknown for materials of the present work. If a linear behavior had been obtained, one of the three model equations investigated would have been suitable for parametrizing the SA behavior. However, the formulated question—What is the most appropriate model equation?—remains unanswered. In order to address this fundamental question, the ferroelectric DO index should be obtained from the experimental 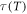 data. The exponent n and the singular temperature TN values will help to clarify the issue.
data. The exponent n and the singular temperature TN values will help to clarify the issue.
4. Results and discussion
PZT-based compositions are one of the most commonly studied ferroelectric materials because of their unique electromechanical properties. These materials are the mainstay for high performance piezoelectric actuators, sensors and transducers, occupying a dominant position in the huge piezoceramics market. PZT-based materials are therefore excellent candidates for model systems when it comes to developing a new framework in the area of ferroelectric materials. In this work, three representative unpoled PZT-based materials are selected in order to carry out a careful examination of their temperature-dependent dielectric response. Rhombohedral 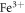 -doped
-doped  (hereafter PFZT-R) and tetragonal
(hereafter PFZT-R) and tetragonal 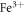 -doped
-doped 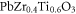 (hereafter PFZT-T) compositions are chosen as representative acceptor-doped PZTs. In addition, rhombohedral
(hereafter PFZT-T) compositions are chosen as representative acceptor-doped PZTs. In addition, rhombohedral 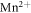 and
and 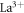 co-doped
co-doped  composition (hereafter PLMZT) is selected as a representative compositionally engineered PZT. The basic properties of these materials as well as details of their sample preparation can be found in previous works [13, 39]. Only acceptor-doped compositions are taken into account, because low temperature dielectric relaxation in these materials is clearly noticeable and therefore mathematically describable [10].
composition (hereafter PLMZT) is selected as a representative compositionally engineered PZT. The basic properties of these materials as well as details of their sample preparation can be found in previous works [13, 39]. Only acceptor-doped compositions are taken into account, because low temperature dielectric relaxation in these materials is clearly noticeable and therefore mathematically describable [10].
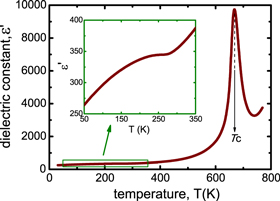
The dielectric constant as a function of the temperature, 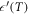 , is displayed in figure 1 for PFZT-T. As may be observed,
, is displayed in figure 1 for PFZT-T. As may be observed, 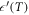 increases from an intrinsic low temperature dielectric constant close to 250 as the temperature is raised, reaching the ordinary ferro-paraelectric transition at around 670 K. Interesting features can be detected if we focus our attention on temperatures just below room temperature (figure 1, inset). In the low temperature region,
increases from an intrinsic low temperature dielectric constant close to 250 as the temperature is raised, reaching the ordinary ferro-paraelectric transition at around 670 K. Interesting features can be detected if we focus our attention on temperatures just below room temperature (figure 1, inset). In the low temperature region, 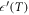 displays a plateau-like behavior between 200 and 300 K and a kink at 300 K. The temperature dependence of
displays a plateau-like behavior between 200 and 300 K and a kink at 300 K. The temperature dependence of 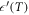 smooths out above 200 K and becomes near temperature-independent close to 300 K, above which
smooths out above 200 K and becomes near temperature-independent close to 300 K, above which 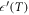 increases. This result contrasts with the expected monotonous increasing
increases. This result contrasts with the expected monotonous increasing 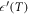 dependence that seems to be the typical feature of
dependence that seems to be the typical feature of  . This intriguing behavior is also displayed in other ordinary perovskite-type ferroelectrics such as PFZT-R and PLMZT.
. This intriguing behavior is also displayed in other ordinary perovskite-type ferroelectrics such as PFZT-R and PLMZT.
Figure 1. Dielectric constant (real permittivity) versus temperature curve from low temperature (∼20 K) to above the ferroelectric-paraelectric phase transition (∼780 K) for 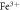 -doped
-doped  (PFZT-T). A monotonous increase of the dielectric constant from a low temperature value (∼250) to around Curie temperature, TC, seems to be the characteristic behavior. However, a careful inspection of the curve at low temperature region reveals an anomalous behavior. The insets display a zoom of the region highlighted with a green rectangle in the main panel.
(PFZT-T). A monotonous increase of the dielectric constant from a low temperature value (∼250) to around Curie temperature, TC, seems to be the characteristic behavior. However, a careful inspection of the curve at low temperature region reveals an anomalous behavior. The insets display a zoom of the region highlighted with a green rectangle in the main panel.
Download figure:
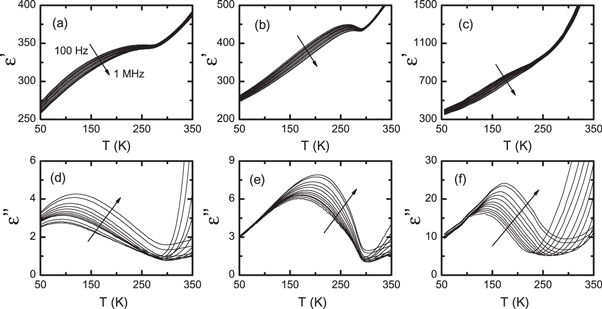
Standard image High-resolution imageAn anomalous behavior in the real permittivity usually matches with an anomaly in the imaginary permittivity. This is shown in figure 2, where the dielectric response of the three selected materials in the low temperature region is shown. In addition to the 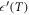 anomalous behavior displayed for all the tested materials (figures 2(a)–(c)), a frequency-dependent
anomalous behavior displayed for all the tested materials (figures 2(a)–(c)), a frequency-dependent 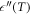 maximum is clearly exhibited. The anomaly in
maximum is clearly exhibited. The anomaly in 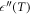 , understood as the maximum of this function, exhibits a marked frequency dispersion, thereby indicating that a dielectric relaxation phenomenon takes place. Although the physical mechanism involved is still unclear, a classical parameterization through
, understood as the maximum of this function, exhibits a marked frequency dispersion, thereby indicating that a dielectric relaxation phenomenon takes place. Although the physical mechanism involved is still unclear, a classical parameterization through  equations can be carried out to obtain information about the relaxation dynamics.
equations can be carried out to obtain information about the relaxation dynamics.
Figure 2. Real (a)–(c),  , and imaginary (d)–(f),
, and imaginary (d)–(f), 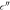 , parts of the permittivity for PFZT-T (a), (d), PFZT-R (b), (e) and PLMZT (c), (f) at several frequencies and at low temperature region. An arrow in each panel indicates the frequency increase, ranging from 100 Hz to 1 MHz.
, parts of the permittivity for PFZT-T (a), (d), PFZT-R (b), (e) and PLMZT (c), (f) at several frequencies and at low temperature region. An arrow in each panel indicates the frequency increase, ranging from 100 Hz to 1 MHz.
Download figure:
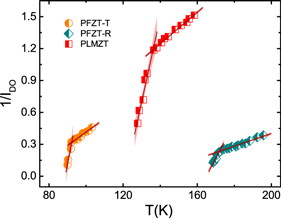
Standard image High-resolution imageThe frequency dependence of the maximum in 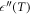 can be fitted by using equations (2)–(4). If one (at least) of these model equations fits the experimental data, the relaxation may be parameterized. Figure 3 shows one of the typical representations of the relaxation data, where relaxation times are evaluated from the measurement frequencies as
can be fitted by using equations (2)–(4). If one (at least) of these model equations fits the experimental data, the relaxation may be parameterized. Figure 3 shows one of the typical representations of the relaxation data, where relaxation times are evaluated from the measurement frequencies as 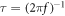 , and the temperature T corresponds to the temperature of the maximum in
, and the temperature T corresponds to the temperature of the maximum in 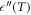 . The data fitting according to VFT, WM and SG equations is also shown.
. The data fitting according to VFT, WM and SG equations is also shown.
Figure 3. Typical relaxation data representation, logarithm of relaxation time versus temperature, for the tested ferroelectric materials. The data are fitted by using Vogel–Fulcher–Tammann (VFT), Waterton-Mauro (WM), and spin-glass (SG) equations. The data fitting to the Arrhenius equation is also shown for comparison purpose. In all cases, the confidence bands at 95% (confidence level) are exhibited.
Download figure:
Standard image High-resolution imageA visual inspection enables us to conclude that the three model equations fit well to the data. The fit to the Arrhenius equation is also shown in the graph, evidencing the non-Arrhenius behavior of the relaxation data. The apparently good fits for the non-Arrhenius equations is not a surprising result, since these are three fitting-parameter equations. A deeper analysis of the fitting may be conducted through the statistical goodness of the fits.
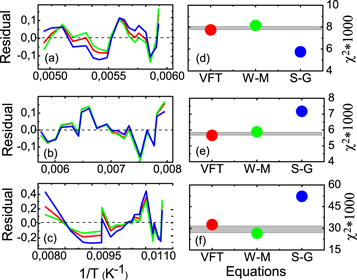
Figure 4 shows the resultant residuals of the fitting and a representation of the chi-square as a measure of the statistical goodness of fit. An equally reasonable fitting quality, within the limit of experimental error, is obtained from the three model equations. Superior fitting quality is randomly obtained (i.e., a different equation dominates for each material), thereby showing that there are no statistical criteria that make one parameterization prevail over the other two. If the classical parameterization of the dielectric relaxation does not provide compelling evidence to justify a dominant parameterization for describing the dynamic process involved, the use of a new approach appears to be mandatory.
Figure 4. Residual of the fitting (a)–(c) and chi-square,  , (d)–(f), for PFZT-R (a), (d), PLMZT (b), (e) and PFZT-T (c), (f). Similar residual and
, (d)–(f), for PFZT-R (a), (d), PLMZT (b), (e) and PFZT-T (c), (f). Similar residual and 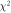 are obtained for each material without a prevalent fitting quality. The poor statistical goodness is found in PFZT-T because of its broadened
are obtained for each material without a prevalent fitting quality. The poor statistical goodness is found in PFZT-T because of its broadened 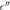 maxima (figure 2(d)).
maxima (figure 2(d)).
Download figure:
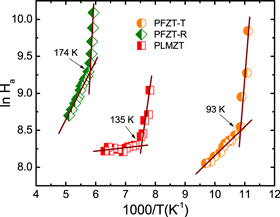
Standard image High-resolution imageThe first step is to determine the apparent enthalpy function, Ha(T), which can easily be obtained from the relaxation data by equation (6). Figure 5 shows the 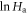 versus
versus 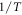 plot. Two constant slope regions emerge for this representation at 93, 135 and 174 K, depending on the tested material. As was pointed out in previous works, this slope can be interpreted as the change in the free-volume thermal expansion coefficient [40, 41], thereby evidencing the existence of two different temperature dynamic domains; that is, a dynamic crossover exists. The activation energies can subsequently be determined from the numerical solution of equation (9). The DO index is then calculated by equation (10).
plot. Two constant slope regions emerge for this representation at 93, 135 and 174 K, depending on the tested material. As was pointed out in previous works, this slope can be interpreted as the change in the free-volume thermal expansion coefficient [40, 41], thereby evidencing the existence of two different temperature dynamic domains; that is, a dynamic crossover exists. The activation energies can subsequently be determined from the numerical solution of equation (9). The DO index is then calculated by equation (10).
Figure 5. Derivative-based representation of the relaxation data for the tested materials. The logarithm of the apparent enthalpy function, 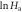 versus
versus 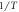 , displays a clear slope change, thereby identifying two differentiated regions. A linear fit for each region is displayed for the eyes. The crossover temperature between regions are indicated in the plot.
, displays a clear slope change, thereby identifying two differentiated regions. A linear fit for each region is displayed for the eyes. The crossover temperature between regions are indicated in the plot.
Download figure:
Standard image High-resolution imageThe inverse of the IDO are plotted as a function of the temperature in figure 6. As may be observed, a similar linear pattern known for the previtreous effect in supercooled ultraslowing/ultraviscous materials is obtained for ordinary ferroelectrics. This result may suggest that the dynamics of these materials at low temperatures could also follow the universal dynamic behavior predicted by Martinez-Garcia et al [33].
Figure 6. Temperature evolution of the inverse Dyre–Olsen (DO) index for the tested materials. Two linear domains for each material are shown, indicating the same linear pattern previously observed for glass-forming materials.
Download figure:
Standard image High-resolution imageGiven the observed linearity, the configurational structural entropy could also follow an inverse relationship as 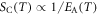 , as the Adam–Gibbs (AG) theory predicts for glass-forming systems [40]. The observed IDO linearity complemented with the AG statements strongly recall the connection of critical phenomenon to explain the dynamics of glass-forming systems. This is completely new and hitherto unexplored for ferroelectric materials.
, as the Adam–Gibbs (AG) theory predicts for glass-forming systems [40]. The observed IDO linearity complemented with the AG statements strongly recall the connection of critical phenomenon to explain the dynamics of glass-forming systems. This is completely new and hitherto unexplored for ferroelectric materials.
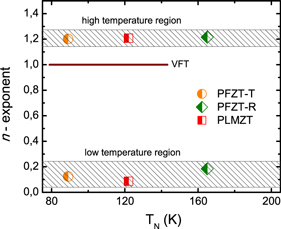
Nevertheless, the WM equation predicts a divergence state without a 'finite-temperature divergence', and follows a linear inverse IDO behavior (see equation (12)). It is therefore pertinent to ask whether the WM could also be an appropriate model equation for parametrizing the SA behavior in ordinary ferroelectrics. In order to elucidate this point, the exponent n and the singular temperature TN are computed for each material. The linear regression of the DO indices extracted from figure 6 yields the experimental values of a and b, subsequently giving the singular temperature and the exponent as 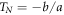 and
and 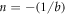 , respectively. Figure 7 shows the n-exponent plotted against its corresponding singular temperature. Two different n values (high and low temperature regions) are found for all tested materials; these two values are ascribed to the two different dynamic domains discussed previously in figure 5. An important conclusion may be reached from figure 7, where the n-exponent takes finite values for all cases, thereby revealing that the WM equation is not an appropriate model for parametrizing the SA behavior in ordinary ferroelectrics at low temperatures.
, respectively. Figure 7 shows the n-exponent plotted against its corresponding singular temperature. Two different n values (high and low temperature regions) are found for all tested materials; these two values are ascribed to the two different dynamic domains discussed previously in figure 5. An important conclusion may be reached from figure 7, where the n-exponent takes finite values for all cases, thereby revealing that the WM equation is not an appropriate model for parametrizing the SA behavior in ordinary ferroelectrics at low temperatures.
Figure 7. Experimental dependencies of the exponent n versus the divergent temperature TN obtained by the model-free approach. Two different regions with finite n-exponent value (high and low temperature regions) are shown.
Download figure:
Standard image High-resolution imageSince a model equation with 'finite-temperature divergence' should be used, a comparative estimation between the divergent temperature values TN with the singular temperatures T0 and TC obtained by direct fittings is given in figure 8. Within our modest statistical number of materials and our experimental error values of TN, we are able to claim that the divergent temperature takes values closer to TC than T0, which indicates that critical-like dynamic parameterization may be a more appropriate solution than the conventional VFT for ordinary ferroelectrics at low temperatures.
Figure 8. Comparative estimation between the divergent temperature values TN determined from the model-free approach with the singular temperatures values Tdivergent obtained by direct fittings. The critical-like parameterization (SG) seems to be a more appropriate solution to parametrize the dynamics than the conventional VFT equation.
Download figure:
Standard image High-resolution image5. Conclusions
In this report, an analysis is conducted into the dynamics of some PZT-based materials, which are one of the most broadly tested ferroelectrics studied to date. Based on conceptually different parameterizations, we have fitted the low temperature dielectric relaxation observed in these materials. The results indicate that a direct analysis of the fitting quality of 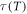 is discouraging and inconclusive, since no statistical criterion exists for considering a model equation to be predominant for the dielectric relaxation. By applying a model-free approach, our findings reveal the same linear pattern as that previously observed for the previtreous effect in supercooled ultraslowing/ultraviscous, where the existences of dynamic crossovers has been elucidated. The use of pre-established models leads to a mistaken and contradictory interpretation of the relaxation dynamics observed in ordinary ferroelectrics materials at low temperatures. The study of the dynamics with an independent-model methodology provides proof of the existence of a dynamic break that has not been reported in ferroelectrics to date. On the other hand, for these three sets of PZT-based materials we have determined the finite-temperature divergence, which could be claimed as a freezing temperature of the phenomenon involved. We conclude that a critical-like parameterization seems to be a more appropriate solution than the conventional VFT equation for parametrizing the dynamics of ordinary ferroelectrics. It is important to point out that the implemented new approach for studying dielectric relaxation in ferroelectric materials may open a new pathway for analyzing relaxation phenomena in functional materials such as relaxor ferroics.
is discouraging and inconclusive, since no statistical criterion exists for considering a model equation to be predominant for the dielectric relaxation. By applying a model-free approach, our findings reveal the same linear pattern as that previously observed for the previtreous effect in supercooled ultraslowing/ultraviscous, where the existences of dynamic crossovers has been elucidated. The use of pre-established models leads to a mistaken and contradictory interpretation of the relaxation dynamics observed in ordinary ferroelectrics materials at low temperatures. The study of the dynamics with an independent-model methodology provides proof of the existence of a dynamic break that has not been reported in ferroelectrics to date. On the other hand, for these three sets of PZT-based materials we have determined the finite-temperature divergence, which could be claimed as a freezing temperature of the phenomenon involved. We conclude that a critical-like parameterization seems to be a more appropriate solution than the conventional VFT equation for parametrizing the dynamics of ordinary ferroelectrics. It is important to point out that the implemented new approach for studying dielectric relaxation in ferroelectric materials may open a new pathway for analyzing relaxation phenomena in functional materials such as relaxor ferroics.
Acknowledgments
This work is supported by the MINECO (Spanish Government) project MAT2013-48009-C4-2-P.