Abstract
Topological superfluid is an exotic state of quantum matter that possesses a nodeless superfluid gap in the bulk and Andreev edge modes at the boundary of a finite system. Here, we study a multi-orbital superfluid driven by an attractive s-wave interaction in a rotating optical lattice. Interestingly, we find that the rotation induces the inter-orbital hybridization and drives the system into topological orbital superfluid in accordance with intrinsically chiral d-wave pairing characteristics. Thanks to the conservation of spin, the topological orbital superfluid supports four rather than two chiral Andreev edge modes at the boundary of the lattice. Moreover, we find that the intrinsic harmonic confining potential forms a circular spatial barrier which accumulates atoms and supports a mass current under the injection of small angular momentum as an external driving force. This feature provides an experimentally detectable phenomenon to verify the topological orbital superfluid with chiral d-wave order in a rotating optical lattice.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Orbital degrees of freedom play a significant role in producing various exotic quantum states in complex condensed-matter systems, such as high temperature superconductors and quantum magnetic insulators. Recent experimental realizations of multi-orbital systems with ultra-cold atoms [1–4] have promoted the theoretical studies of high orbital physics in optical lattices, where a series of exotic quantum states have been proposed [5–11] . Among them, one of the remarkable characteristics is that the orbital hybridization can play the same role as spin–orbital couplings or artificial gauge fields which are the key ingredients needed to drive topologically insulating or superconducting states [12, 13]. Therefore, topologically nontrivial many-body states can be implemented in multi-orbital systems in the absence of spin–orbital coupling. Several methods exist to induce orbital hybridization in the context of cold-atom systems, including the many-body interaction effect [5], lattice shaking [14–17], and local rotation [18]. The relevant quantum states including topological semimetal [5] and topological band insulators [10, 15, 20, 21] have been proposed.
Recently, the superfluid of bosons with chiral odd-frequency orders, i.e., p + ip-wave and f + if-wave, have been experimentally realized in multi-orbital cold-atom systems [2, 22, 23]. For fermions, however, it is still a big challenge to realize superfluid states with chiral odd-frequency orders because the atom loss is strong near the Feshbach resonance in high-frequency channels [24]. Theoretically, thanks to the Rashba spin–orbital couplings, the topological superfluids of fermions with chiral odd-frequency orders have been proposed to emerge in the s-wave channel of the Feshbach resonance [25–28]. In comparison with the well-studied chiral odd-frequency superfluids of fermions, the superfluids of fermions with chiral even-frequency orders are rarely studied, and only some candidate materials are proposed to have the chiral even-frequency orders due to the unconventional superconducting pairing in condensed-matter systems [29–32]. More recently, a checkerboard lattice in a periodic Floquet driving field was proposed to support the chiral d-wave superfluid, where the sublattice degrees of freedom plays a key role and the periodic Floquet driving field induces the hybridization of two sublattices [33]. In this paper, we propose that a superfluid state of fermions with a chiral d-wave order can be implemented in a rotating multi-orbital optical lattice. In our proposal, the key ingredients needed to drive the underlying nontrivial topology of the multi-orbital superfluid state with a chiral d-wave order come from the two orbitals that are the counterparts of spin degrees of freedom in spin–orbital coupling, and the inter-orbital hybridization is induced by the local rotation with same frequency for every individual lattice site, which can be experimentally realized [18]. Interestingly, different from conventional chiral d-wave topological superfluid which supports two chiral Andreev edge modes at the boundary of the system, the topological orbital superfluid here supports four chiral Andreev edge modes due to the conservation of spin. More importantly, we find that the spatial barrier structure spontaneously formed by the intrinsic harmonic confining potential separates the trivial and nontrivial superfluid states, accumulates cold atoms and supports a mass current under injection of small angular momentum as the external driving force. These features can be experimentally adopted to verify the topologically nontrivial superfluid states. In comparison with the chiral p-wave and f-wave topological superconductor and superfluid [25, 26, 28, 34–40], where the spin–orbital couplings are essential, the chiral d-wave topological superfluid here only requires orbital hybridization. Therefore, our proposal provides a possible route to exploring topological superfluids with chiral d-wave order in multi-orbital cold-atom systems.
The paper is organized as follows. In section 2, we discuss the implementation of the multi-orbital system with a specific configuration of laser beams and construct the effective Hamiltonian to describe the multi-orbital system. In section 3, we study the homogeneous superfluid state with self-consistent mean-field approximation, and discuss the topological properties of the homogeneous superfluid state. In section 4, we discuss the inhomogeneous superfluid state modulated by the harmonic confining potential. In section 5, we discuss the experimental scheme and present a brief summary.
2. Optical lattice and model
We consider a balanced mixture of fermion atoms with two internal states labeled by the spin index σ. The atoms are loaded in isotropic 2D square optical lattices. To introduce the couplings between different p orbital bands, one effective approach is to rotate the optical lattice with the same rotation frequency  for every individual lattice site [18]. An alternative approach would be to directly couple the states with a drive laser [19]. Finally, the trapped atoms are tuned close to a Feshbach resonance to produce attractive s-wave interactions. The lattice potential takes the form,
for every individual lattice site [18]. An alternative approach would be to directly couple the states with a drive laser [19]. Finally, the trapped atoms are tuned close to a Feshbach resonance to produce attractive s-wave interactions. The lattice potential takes the form,

Here, V1 and V2 are the optical lattice potentials and kL is the wave-vector of the laser fields. The realization of lattice potential  in equation (1) has been proposed for the case
in equation (1) has been proposed for the case  [5]. Here, we consider the case
[5]. Here, we consider the case  , and the configuration of optical lattices under the condition that
, and the configuration of optical lattices under the condition that  can be implemented through four retro-reflected laser beams as shown in figure 1(a). The electric field generated by each laser beam is
can be implemented through four retro-reflected laser beams as shown in figure 1(a). The electric field generated by each laser beam is

where  ,
,  , and
, and  are the polarization vector, the frequency, and the phase of the laser field, respectively. The parameters for each laser beams are summarized in table 1. The corresponding light-shift potential is
are the polarization vector, the frequency, and the phase of the laser field, respectively. The parameters for each laser beams are summarized in table 1. The corresponding light-shift potential is

with χ denoting the real part of the polarizability. By adopting the parameters in table 1, we can get the lattice potential shown in equation (1) with an irrelevant constant shift  . Here,
. Here,  , and
, and  . The condition
. The condition  can be achieved for arbitrary nonzero
can be achieved for arbitrary nonzero  and
and  and blue detuning with
and blue detuning with  . Here, we set
. Here, we set  and
and  .
.  is the recoil energy and a is the lattice constant.
is the recoil energy and a is the lattice constant.
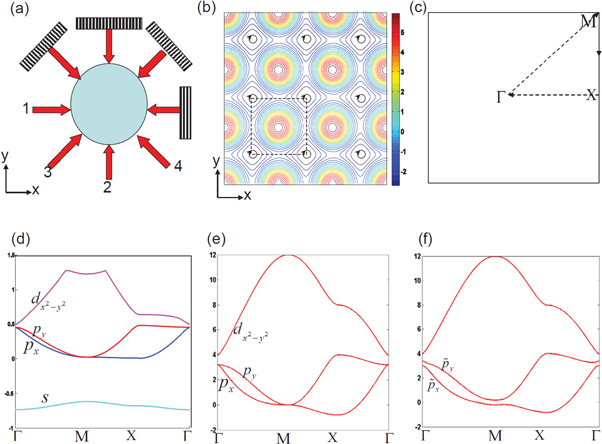
Figure 1. (a) Four retro-reflected laser beams are adopted to create the lattice potential in equation (1). (b) The contour of the lattice potential forms a 2D optical lattice, and the atoms are trapped at the minima of the potential. The small circle with an arrow at each minimum represents the on-site rotation. Here,  and
and  . (c) The Brillouin zone and high-symmetry points. (d) The single-particle energy spectrum along high-symmetry lines in the unit of ER for the four lowest bands through plane wave expansion calculation about the lattice potential. (e) and (f) The single-particle energy spectrum along high-symmetry lines from the tight-binding Hamiltonian in equation (4) without and with on-site rotation. To guarantee the consistence of the energy scales between the bands from plane wave expansion calculation about the lattice potential in (d) and the bands from tight-binding calculations in (e) and (f), the energy is measured in the unit of tpp with
. (c) The Brillouin zone and high-symmetry points. (d) The single-particle energy spectrum along high-symmetry lines in the unit of ER for the four lowest bands through plane wave expansion calculation about the lattice potential. (e) and (f) The single-particle energy spectrum along high-symmetry lines from the tight-binding Hamiltonian in equation (4) without and with on-site rotation. To guarantee the consistence of the energy scales between the bands from plane wave expansion calculation about the lattice potential in (d) and the bands from tight-binding calculations in (e) and (f), the energy is measured in the unit of tpp with  in (e) and (f). Other parameters are
in (e) and (f). Other parameters are  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  in (e) and
in (e) and  in (f).
in (f).
Download figure:
Standard image High-resolution imageTable 1. The parameters of the electric fields of four laser beams shown in figure 1(a).
| j | Ej0 |

|

|

|

|
|---|---|---|---|---|---|
| 1 |

|

|

|

|
0 |
| 2 |

|

|

|

|
0 |
| 3 |

|

|

|

|
0 |
| 4 |

|

|

|

|
0 |
The contour of  is shown in figure 1(b). The lowest four band structures from the plane wave expansion approximation upon the potential
is shown in figure 1(b). The lowest four band structures from the plane wave expansion approximation upon the potential  in equation (1) are shown in figure 1(d). It is straightforward to check that the splitting between two middle px and py bands off the high-symmetry point are induced by the coupling to the higher
in equation (1) are shown in figure 1(d). It is straightforward to check that the splitting between two middle px and py bands off the high-symmetry point are induced by the coupling to the higher  band [5]. Consider the three orbitals of px, py and
band [5]. Consider the three orbitals of px, py and  shown in figure 1(e), a tight-binding (TB) Hamiltonian can be constructed to described the band structures of the fermionic square lattice, i.e.,
shown in figure 1(e), a tight-binding (TB) Hamiltonian can be constructed to described the band structures of the fermionic square lattice, i.e.,

with



Here,  with
with

being the weak harmonic confining potential to stabilize the optical lattice.  , and
, and  are the fermion creation operators for atoms in the relevant px, py and
are the fermion creation operators for atoms in the relevant px, py and  orbitals. We first set
orbitals. We first set  to simplify the discussions and recover it later. Note that all the energy scales are measured in the unit of tpp as explained in the caption of figure 1 in the following parts of the paper if not specified. The energy spectra of TB Hamiltonian in equation (4) are shown in figures 1(e) and (f). It can be found that the TB Hamiltonian in equation (4) gives a good description of the band structures of lattice potential, and the on-site rotation in the second term in equation (6) induces the orbital hybridization to break the degeneracy of px and py bands around the Γ and M points shown in figure 1(c).
to simplify the discussions and recover it later. Note that all the energy scales are measured in the unit of tpp as explained in the caption of figure 1 in the following parts of the paper if not specified. The energy spectra of TB Hamiltonian in equation (4) are shown in figures 1(e) and (f). It can be found that the TB Hamiltonian in equation (4) gives a good description of the band structures of lattice potential, and the on-site rotation in the second term in equation (6) induces the orbital hybridization to break the degeneracy of px and py bands around the Γ and M points shown in figure 1(c).
When the fermion atoms are loaded into the two px and py bands, the attractive s-wave interactions from the Feshbach resonance provide the two-orbital attractive Hubbard interactions as follows [41]:

Here, the first term is the intra-orbital attractive interaction, and the second term is the Hund's coupling with the spin operator  and
and  . U and J take the following forms:
. U and J take the following forms:


Here, as is the s-wave scattering length with negative value, i.e.,  .
.  are the Wannier functions of the
are the Wannier functions of the  orbitals. The third term in equation (9) is the inter-orbital attractive interaction with
orbitals. The third term in equation (9) is the inter-orbital attractive interaction with  . The fourth term is the pair hopping term. Furthermore, we have
. The fourth term is the pair hopping term. Furthermore, we have  and
and  [41]. Note that the Hund's coupling and inter-orbital interaction have same amplitudes, which are different from the electron system. The interaction terms shown in equations (9)–(11) are obtained under harmonic approximation. It is shown that the anharmonicity of the optical lattice can affect the properties of the multi-orbital system [42, 43]. In particular, the intra-orbital interaction Uxx is not equal to Uyy, and the inter-orbital interaction J is off
[41]. Note that the Hund's coupling and inter-orbital interaction have same amplitudes, which are different from the electron system. The interaction terms shown in equations (9)–(11) are obtained under harmonic approximation. It is shown that the anharmonicity of the optical lattice can affect the properties of the multi-orbital system [42, 43]. In particular, the intra-orbital interaction Uxx is not equal to Uyy, and the inter-orbital interaction J is off  . Such imbalance can induce the modulations of superfluid order parameters. However, the topological superfluid is robust against such small modulations because nontrivial topology is the global feature of superfluid. For simplification, we neglect the irrelevant anharmonic effects in the present work.
. Such imbalance can induce the modulations of superfluid order parameters. However, the topological superfluid is robust against such small modulations because nontrivial topology is the global feature of superfluid. For simplification, we neglect the irrelevant anharmonic effects in the present work.
3. Homogeneous superfluid states with chirald-wave order
Now, we turn to consider the homogeneous superfluid state with  in equation (8) and the superfluid state is driven by the attractive interaction in equation (9). The spin–singlet superfluid pairing operators are defined as
in equation (8) and the superfluid state is driven by the attractive interaction in equation (9). The spin–singlet superfluid pairing operators are defined as

Then, we have

with

Note that the spin–triplet pairing parts disappear because the Hund's coupling and inter-orbital interaction have the same amplitudes. Through the mean-field approximation,  , Hint can be decoupled to be
, Hint can be decoupled to be

with

The homogeneous superfluid state can be described by the mean-field Hamiltonian on the Nambu basis: ![${\rm{\Psi }}(k)={[{d}_{k\uparrow },{p}_{x,k\uparrow },{p}_{y,k\uparrow },{d}_{k\downarrow }^{\dagger },{p}_{x,k\downarrow }^{\dagger },{p}_{y,k\downarrow }^{\dagger },{d}_{k\downarrow },{p}_{x,k\downarrow },{p}_{y,k\downarrow },{d}_{k\uparrow }^{\dagger },{p}_{x,k\uparrow }^{\dagger },{p}_{y,k\uparrow }^{\dagger }]}^{t}$](https://content.cld.iop.org/journals/1367-2630/19/8/083020/revision2/njpaa7ceaieqn70.gif) ,
,

Here, C is an operator-independent constant term.  is a 3 × 3 matrix and takes the following form:
is a 3 × 3 matrix and takes the following form:

The mean-field Hamiltonian in equation (17) can be self-consistently solved with respect to the minimum of ground state energy, i.e.,

where,  and
and  are the eigen-energy spectra of the superfluid state and normal state. Here, we focus on the filling lying in the band splitting around the M point induced by the orbital hybridization as shown in figure 2(a). The typical Fermi surface is shown in figure 2(b). From equation (18), we can find that the superfluid order parameter in the intra-px orbital channel is
are the eigen-energy spectra of the superfluid state and normal state. Here, we focus on the filling lying in the band splitting around the M point induced by the orbital hybridization as shown in figure 2(a). The typical Fermi surface is shown in figure 2(b). From equation (18), we can find that the superfluid order parameter in the intra-px orbital channel is  while the superfluid order parameter in the intra-py orbital channel is
while the superfluid order parameter in the intra-py orbital channel is  . To maximize the superfluid gap, one can find that
. To maximize the superfluid gap, one can find that  is favorable to obtain the largest amplitudes of
is favorable to obtain the largest amplitudes of  and
and  . The numerical results for the ground state energy and superfluid order parameters as functions of chemical potential
. The numerical results for the ground state energy and superfluid order parameters as functions of chemical potential  and interaction amplitude
and interaction amplitude  are shown in figures 2(c) and (d), from which the intra-orbital
are shown in figures 2(c) and (d), from which the intra-orbital  and
and  are degenerate in the whole parameter regime. This means that
are degenerate in the whole parameter regime. This means that  , and the only choice is
, and the only choice is  thanks to
thanks to  . The aforementioned analyses are consistent, and one can achieve that the superfluid ground states favor
. The aforementioned analyses are consistent, and one can achieve that the superfluid ground states favor  and
and  with the same sign to maximize the superfluid gap and to minimize the ground state energy. Furthermore, we can find that the inter-orbital
with the same sign to maximize the superfluid gap and to minimize the ground state energy. Furthermore, we can find that the inter-orbital  , which is also the matrix element in equation (18), is purely imaginary, and much smaller than
, which is also the matrix element in equation (18), is purely imaginary, and much smaller than  . The reason lies in that the inter-orbital
. The reason lies in that the inter-orbital  is induced by the orbital hybridization and modulated by
is induced by the orbital hybridization and modulated by  . It is conceivable that the strength of inter-orbital
. It is conceivable that the strength of inter-orbital  could be comparable to intra-orbital
could be comparable to intra-orbital  when
when  is large enough. However, the
is large enough. However, the  has no relation to the topological nature of the superfluid state, so we only focus on the case with
has no relation to the topological nature of the superfluid state, so we only focus on the case with  set here.
set here.
Figure 2. (a) The band structure along the high-symmetry lines, and the filling is in the shadowed regime by tuning the chemical potential. (b) The closed curve denotes the single Fermi surface. The red arrows denote the vector field of [ ,
,  ]. Here, the parameters are same as those in figure 1(f). (c) The zero-temperature ground state energy of the superfluid state as the change in chemical potential
]. Here, the parameters are same as those in figure 1(f). (c) The zero-temperature ground state energy of the superfluid state as the change in chemical potential  and interaction amplitude
and interaction amplitude  . (d) The intra-and inter-orbital superfluid order parameters as the change in chemical potential
. (d) The intra-and inter-orbital superfluid order parameters as the change in chemical potential  and interaction amplitude
and interaction amplitude  . Here,
. Here,  with
with  , and
, and  . The explicit expressions of
. The explicit expressions of  ,
,  and
and  are shown in equation (18), which are the relevant matrix elements. The mesh of
are shown in equation (18), which are the relevant matrix elements. The mesh of  .
.
Download figure:
Standard image High-resolution imageIn order to reveal the underlying topological nature of the superfluid states, we first investigate the band characteristics of the normal states. As shown in figure 1(e), the full separation between the d band and p bands guarantees the feasibility of downfolding the Hamiltonian from the space spanned by the d and p orbitals to the space spanned by the two effective  orbitals shown in figure 1(f). When
orbitals shown in figure 1(f). When  , the translation symmetry allows ones to write the TB Hamiltonian in momentum space under the effective basis
, the translation symmetry allows ones to write the TB Hamiltonian in momentum space under the effective basis ![${\tilde{\psi }}_{\sigma }(k)={[{\tilde{p}}_{x,k,\sigma },{\tilde{p}}_{y,k,\sigma }]}^{t}$](https://content.cld.iop.org/journals/1367-2630/19/8/083020/revision2/njpaa7ceaieqn112.gif) , i.e.,
, i.e.,

Here,

and


The Pauli matrices  with
with  span the two effective
span the two effective  and
and  orbital space. The effective TB Hamiltonian
orbital space. The effective TB Hamiltonian  can be rewritten in the basis spanned by the orbital angular momentum eigenstate, i.e.,
can be rewritten in the basis spanned by the orbital angular momentum eigenstate, i.e.,

Here, ![${\bar{\psi }}_{\sigma }^{\dagger }(k)=[{\bar{p}}_{+,k,\sigma }^{\dagger },{\bar{p}}_{-,k,\sigma }^{\dagger }]$](https://content.cld.iop.org/journals/1367-2630/19/8/083020/revision2/njpaa7ceaieqn118.gif) with
with ![${\bar{p}}_{\pm ,k\sigma }^{\dagger }=\tfrac{1}{\sqrt{2}}[{\tilde{p}}_{x,k\sigma }^{\dagger }\pm {i}{\tilde{p}}_{y,k\sigma }^{\dagger }]$](https://content.cld.iop.org/journals/1367-2630/19/8/083020/revision2/njpaa7ceaieqn119.gif) , and
, and

The Pauli matrices si with  span the two effective
span the two effective  and
and  orbital space. In the absence of
orbital space. In the absence of  ,
, ![$[{F}_{x}(k)=\tfrac{1}{2}{\xi }_{-}(k),{F}_{y}(k)={\xi }_{{xy}}(k)]$](https://content.cld.iop.org/journals/1367-2630/19/8/083020/revision2/njpaa7ceaieqn124.gif) forms a vector field in momentum space shown in figure 2(b). Then, the band degeneracy point at the M point can be mapped into a vortex in the momentum space with integer winding number [5], i.e.,
forms a vector field in momentum space shown in figure 2(b). Then, the band degeneracy point at the M point can be mapped into a vortex in the momentum space with integer winding number [5], i.e.,

with  . The direct calculation gives
. The direct calculation gives  in agreement with the pattern of the vector field
in agreement with the pattern of the vector field ![$[{F}_{x}(k),{F}_{y}(k)]$](https://content.cld.iop.org/journals/1367-2630/19/8/083020/revision2/njpaa7ceaieqn127.gif) as shown in figure 2(b). Note that the total winding number
as shown in figure 2(b). Note that the total winding number  should be 4 when the spin degree of freedom is taken into account. In the presence of
should be 4 when the spin degree of freedom is taken into account. In the presence of  , the induced orbital hybridization lifts the degeneracy at M point. Then, the above mapping does not work.
, the induced orbital hybridization lifts the degeneracy at M point. Then, the above mapping does not work.
In the superfluid states, quasi-particle spectra are fully gapped and the nonzero  breaks the pseudo-time-reversal symmetry. It is natural to introduce the Chern number to characterize the topological properties of the superfluid states. To show it, we consider the effective superfluid Hamiltonian spanned in the effective Nambu basis:
breaks the pseudo-time-reversal symmetry. It is natural to introduce the Chern number to characterize the topological properties of the superfluid states. To show it, we consider the effective superfluid Hamiltonian spanned in the effective Nambu basis: ![$\bar{{\rm{\Psi }}}(k)={[{\bar{p}}_{+,k,\uparrow },{\bar{p}}_{-,k,\uparrow },{\bar{p}}_{+,-k,\downarrow }^{\dagger },{\bar{p}}_{-,-k,\downarrow }^{\dagger },{\bar{p}}_{+,k,\downarrow },{\bar{p}}_{-,k,\downarrow },{\bar{p}}_{+,-k,\uparrow }^{\dagger },{\bar{p}}_{-,-k,\uparrow }^{\dagger }]}^{t}$](https://content.cld.iop.org/journals/1367-2630/19/8/083020/revision2/njpaa7ceaieqn131.gif) ,
,

with

and

Here  and
and  . Upon an unitary rotation [26], we can obtain a dual form of the Hamiltonian, i.e.,
. Upon an unitary rotation [26], we can obtain a dual form of the Hamiltonian, i.e.,

where




In the dual Hamiltonian  shown in equation (31),
shown in equation (31), ![$\left[\tfrac{{\xi }_{-}(k)}{2},{\xi }_{{xy}}(k)\right]$](https://content.cld.iop.org/journals/1367-2630/19/8/083020/revision2/njpaa7ceaieqn135.gif) resembles two components of pairing order parameters of the chiral d-wave superfluid and
resembles two components of pairing order parameters of the chiral d-wave superfluid and  corresponds to the mixed s-wave component. '
corresponds to the mixed s-wave component. ' ' is the pseudo-kinetic energy with k-independent, and resembles kinetic energy term '
' is the pseudo-kinetic energy with k-independent, and resembles kinetic energy term ' ' of the chiral d-wave superfluid when
' of the chiral d-wave superfluid when  is set to satisfy the condition
is set to satisfy the condition  . Then, the dual Hamiltonian
. Then, the dual Hamiltonian  resembles the standard Hamiltonian describing the chiral d-wave superconductors [30, 44], and belongs to class C according to the classification by Schnyder et al [45]. Here,
resembles the standard Hamiltonian describing the chiral d-wave superconductors [30, 44], and belongs to class C according to the classification by Schnyder et al [45]. Here,  by itself cannot drive the gap-closing condition because it is much smaller than
by itself cannot drive the gap-closing condition because it is much smaller than  and Fermi energy. Therefore, the small
and Fermi energy. Therefore, the small  can be absorbed and set to zero. The topological nontrivial superfluid states can be achieved under the condition [44]
can be absorbed and set to zero. The topological nontrivial superfluid states can be achieved under the condition [44] 
 when
when  , which naturally corresponds to the weak-coupling condition
, which naturally corresponds to the weak-coupling condition [34]. For the general case with arbitrary
[34]. For the general case with arbitrary  , one can obtain nontrivial superfluid states if
, one can obtain nontrivial superfluid states if  with
with  shown in equation (33), and trivial superfluid states if
shown in equation (33), and trivial superfluid states if  . The topological phase transition condition coincides with the gap-closing condition with
. The topological phase transition condition coincides with the gap-closing condition with  . The phase diagram separating the topological trivial and nontrivial superfluid phases is plotted in figure 3(d) according to phase transition condition
. The phase diagram separating the topological trivial and nontrivial superfluid phases is plotted in figure 3(d) according to phase transition condition  .
.

The nontrivial topological nature of the superfluid states can be characterized by the Chern number,

with  the Bloch functions of occupied quasi-particle states with s = up and down to label the the up-block and down-block parts of the Hamiltonian in equation (17). The straightforward calculations give
the Bloch functions of occupied quasi-particle states with s = up and down to label the the up-block and down-block parts of the Hamiltonian in equation (17). The straightforward calculations give  for
for  and
and  for
for  under the condition
under the condition  , which means the inverse local rotation corresponds to reverse chirality. From the bulk-edge correspondence, the quasi-particle spectra have two chiral gapless edge states at the open boundary shown in figure 3(a) and no gapless edge states emerge in the trivial superfluid state shown in figure 3(b). The local feature of the edge states in figure 3(a) are explicitly demonstrated through the amplitude distributions of the wave-functions shown in figure 3(c).
, which means the inverse local rotation corresponds to reverse chirality. From the bulk-edge correspondence, the quasi-particle spectra have two chiral gapless edge states at the open boundary shown in figure 3(a) and no gapless edge states emerge in the trivial superfluid state shown in figure 3(b). The local feature of the edge states in figure 3(a) are explicitly demonstrated through the amplitude distributions of the wave-functions shown in figure 3(c).
Figure 3. (a) and (b) the edge spectra of the superfluid states with  ,
,  in (a) and
in (a) and  ,
,  in (b). The relevant
in (b). The relevant  ,
,  in (a) and
in (a) and  ,
,  in (b). Here, the y direction has a periodic boundary condition while the lattice number along the x direction is set to be
in (b). Here, the y direction has a periodic boundary condition while the lattice number along the x direction is set to be  . (c) The amplitudes of wave-function of the in-gap states labeled 1–8 in (a). Note that each point is double degeneracy by taking into account the spin degree of freedom. Here, the red and blue 'o' marks label particle-like
. (c) The amplitudes of wave-function of the in-gap states labeled 1–8 in (a). Note that each point is double degeneracy by taking into account the spin degree of freedom. Here, the red and blue 'o' marks label particle-like  and hole-like
and hole-like  while the red and blue '
while the red and blue ' ' marks label particle-like
' marks label particle-like  and hole-like
and hole-like  . (d) The phase diagram of the change in chemical potential
. (d) The phase diagram of the change in chemical potential  and interaction amplitude
and interaction amplitude  .
.
Download figure:
Standard image High-resolution image4. Mass density modulation from the harmonic confining potential
Now, we consider the realistic case with nonzero harmonic confining potential in equation (8), and the pattern of  is shown in figure 4(a) with
is shown in figure 4(a) with  . We perform the self-consistent calculations about the Bogoliubov–de Gennes (BdG) Hamiltonian
. We perform the self-consistent calculations about the Bogoliubov–de Gennes (BdG) Hamiltonian  in equations (4) and (15) in lattice space. The quasi-particle spectra and the distribution of superfluid order parameters are shown in figures 4(b), (d), and (e) for two different
in equations (4) and (15) in lattice space. The quasi-particle spectra and the distribution of superfluid order parameters are shown in figures 4(b), (d), and (e) for two different  and
and  under the periodic boundary condition. We find that the amplitudes of superfluid order parameters in both cases are similar to figures 4(d) and (e), but the quasi-particle spectra are quite different from figure 4(b) with in-gap fermion modes for
under the periodic boundary condition. We find that the amplitudes of superfluid order parameters in both cases are similar to figures 4(d) and (e), but the quasi-particle spectra are quite different from figure 4(b) with in-gap fermion modes for  and without in-gap fermion modes for
and without in-gap fermion modes for  . The reason lies in that
. The reason lies in that  forms a spatial barrier structure (The position is marked with a red-dashed circle in figure 4(a)) separating the nontrivial superfluid state with
forms a spatial barrier structure (The position is marked with a red-dashed circle in figure 4(a)) separating the nontrivial superfluid state with  and trivial superfluid state with
and trivial superfluid state with  for
for  . Note that
. Note that  , thus the position of spatial barrier coincides with the gap-closing condition with
, thus the position of spatial barrier coincides with the gap-closing condition with  . For fixed
. For fixed  and Vt, one can find that
and Vt, one can find that  is always smaller than zero when
is always smaller than zero when  . The superfluid is always trivial because
. The superfluid is always trivial because  is too small to overcome the gap-closing condition
is too small to overcome the gap-closing condition  . The spatial barrier traps in-gap fermion modes and accumulates atoms when the negative energy states are occupied [44, 46]. The in-gap fermion modes trapped by the spatial barrier have the same origin as the fermion modes in spectrum of the Caroli–de Gennes–Matricon bound states in the vortex core [47].
. The spatial barrier traps in-gap fermion modes and accumulates atoms when the negative energy states are occupied [44, 46]. The in-gap fermion modes trapped by the spatial barrier have the same origin as the fermion modes in spectrum of the Caroli–de Gennes–Matricon bound states in the vortex core [47].
Figure 4. (a) The pattern of weak harmonic confining potential Vtrap with  in lattice space. The red-dashed circle denotes a spatial barrier structure of the potential, which separates the two different superfluid states. (b) The spectra of the superfluid states with the red 'o' marks and the blue '□' marks corresponding to the case with
in lattice space. The red-dashed circle denotes a spatial barrier structure of the potential, which separates the two different superfluid states. (b) The spectra of the superfluid states with the red 'o' marks and the blue '□' marks corresponding to the case with  and
and  respectively. (c) The energy levels of the in-gap fermion zero modes as function of lattice size N × N. Here, the red '□' marks and the blue 'o' marks correspond to the first and second lowest positive energy levels, and
respectively. (c) The energy levels of the in-gap fermion zero modes as function of lattice size N × N. Here, the red '□' marks and the blue 'o' marks correspond to the first and second lowest positive energy levels, and  . (d) and (e) The distributions of superfluid order parameters including intra-orbital and inter-orbital parts in lattice space with lattice size
. (d) and (e) The distributions of superfluid order parameters including intra-orbital and inter-orbital parts in lattice space with lattice size  and
and  in (c) and
in (c) and  in (d). Here, the interaction strength
in (d). Here, the interaction strength  , chemical potential
, chemical potential  , and the periodic boundary condition are applied. Other parameters are same as those in figure 1.
, and the periodic boundary condition are applied. Other parameters are same as those in figure 1.
Download figure:
Standard image High-resolution imageIn the low-energy limit, the spectrum of in-gap fermion modes in terms of the angular momentum Q takes the following form under the axisymmetric condition [44, 46]:

where  is the angular velocity of the rotation along the spatial barrier with R the radius of spatial barrier of
is the angular velocity of the rotation along the spatial barrier with R the radius of spatial barrier of  6
, a labels the ath branch, and
6
, a labels the ath branch, and  . The total number of the branches is four according to the index theorem [46] when the spin degree of freedom is taken into account. In the absence of external driving, the energy of in-gap fermion modes is
. The total number of the branches is four according to the index theorem [46] when the spin degree of freedom is taken into account. In the absence of external driving, the energy of in-gap fermion modes is  . In the square lattice space, the circular rotation symmetry SO(2) for equation (35) is broken down to C4 symmetry, and the Fermi velocity is strongly anisotropic and the superfluid order parameters are highly inhomogeneous. Qa can only take the discrete values under the constraint of C4 symmetry. Correspondingly, the energy levels of the in-gap fermion modes trapped by the spatial barrier are discrete (see figure 4(b) for details), and several energy levels close to zero usually correspond to in-gap fermion modes trapped by the spatial barrier.
. In the square lattice space, the circular rotation symmetry SO(2) for equation (35) is broken down to C4 symmetry, and the Fermi velocity is strongly anisotropic and the superfluid order parameters are highly inhomogeneous. Qa can only take the discrete values under the constraint of C4 symmetry. Correspondingly, the energy levels of the in-gap fermion modes trapped by the spatial barrier are discrete (see figure 4(b) for details), and several energy levels close to zero usually correspond to in-gap fermion modes trapped by the spatial barrier.
The localization feature of the in-gap fermion modes trapped by the spatial barrier can be reflected by the local density of states (LDOS), which is calculated by

where  and
and  are the particle-like and hole-like components of eigenstate with quasi-particle energy En at site i and orbital l. The LDOS of the five in-gap fermion modes with the highest negative energy are shown in figures 5(a1)–(a5), from which we can find that four levels with energy
are the particle-like and hole-like components of eigenstate with quasi-particle energy En at site i and orbital l. The LDOS of the five in-gap fermion modes with the highest negative energy are shown in figures 5(a1)–(a5), from which we can find that four levels with energy  are the fermion modes which are trapped by the spatial barrier. To make a comparison, the level with energy −0.0322 is the extended state. We also plot the LDOS of the the five levels with the lowest positive energy in figures 5(b1)–(b5) for comparison. Furthermore, we find that the highest negative energy level and the lowest positive energy level approach zero energy with increasing the lattice size N × N (see figure 4(c) for details).
are the fermion modes which are trapped by the spatial barrier. To make a comparison, the level with energy −0.0322 is the extended state. We also plot the LDOS of the the five levels with the lowest positive energy in figures 5(b1)–(b5) for comparison. Furthermore, we find that the highest negative energy level and the lowest positive energy level approach zero energy with increasing the lattice size N × N (see figure 4(c) for details).
Figure 5. (a1)–(a5) The distribution of LDOS defined in equation (36) for five fermion modes with negative energy close to zero. (b1)–(b5) The distribution of LDOS defined in equation (36) for five fermion modes with positive energy close to zero. (c) The distribution of change of LDOS between  and
and  . Here, the parameters are same as those in figure 4.
. Here, the parameters are same as those in figure 4.
Download figure:
Standard image High-resolution imageIn the presence of external driving, the spectrum of the in-gap fermion modes is a function of the angular momentum Q from the external driving, and the in-gap fermion modes could cross the zero energy and form the variation of the mass current. The change of the mass current trapped in the spatial barrier is [44]

where we have assumed the thickness along the z direction to be unity. The extra 1/2 in the denominator is added to compensate for the double counting due to the particle-hole symmetry. Generally, there are several external perturbations which can be introduced to be the driving force to move the in-gap fermion modes across the zero energy, such as the modulations of V1 and V2 in equation (1) to deform the  and
and  and introducing an additional laser beam to modulate the trapping potential. Here, we consider a more convenient method. From equation (35), it is straightforward to inject nonzero Q into the superfluid state through the slight modulation of local rotating frequency
and introducing an additional laser beam to modulate the trapping potential. Here, we consider a more convenient method. From equation (35), it is straightforward to inject nonzero Q into the superfluid state through the slight modulation of local rotating frequency  . As a consequence, the in-gap fermion modes can be driven to cross zero energy by the nonzero
. As a consequence, the in-gap fermion modes can be driven to cross zero energy by the nonzero  . If we further assume that all the in-gap fermion modes trapped in the spatial barrier have the relation
. If we further assume that all the in-gap fermion modes trapped in the spatial barrier have the relation  , we can obtain that the response of the change in mass current to the modulation of the rotating frequency
, we can obtain that the response of the change in mass current to the modulation of the rotating frequency 
 with the summation involving all the in-gap fermion modes across the zero energy. However, in the square lattices, we can find that the ka is different for different a-th branches from figure 5. As a good approximation, we can define an effective
with the summation involving all the in-gap fermion modes across the zero energy. However, in the square lattices, we can find that the ka is different for different a-th branches from figure 5. As a good approximation, we can define an effective  to remove the difference of different ka, and
to remove the difference of different ka, and  can be replaced with the average Fermi momentum
can be replaced with the average Fermi momentum  . Then, we can obtain that the modulation of mass current density is proportional to the change in the LDOS, i.e.,
. Then, we can obtain that the modulation of mass current density is proportional to the change in the LDOS, i.e.,

with


The pattern of  for
for  is shown in figure 5(c), from which we can find that the mass current is trapped around the spatial barrier.
is shown in figure 5(c), from which we can find that the mass current is trapped around the spatial barrier.
5. Discussion and conclusions
In terms of experiment, the fermion atoms can be selected as lithium 6Li, two internal states can be selected as  with M =
with M =  . The principal fluorescence line from 2S
. The principal fluorescence line from 2S to 2P is at 670.8 nm. Therefore, a Nd:YAG-laser with 532 nm could be selected to be the light source to realize the optical potential with the lattice constant
to 2P is at 670.8 nm. Therefore, a Nd:YAG-laser with 532 nm could be selected to be the light source to realize the optical potential with the lattice constant  nm. The recoil energy
nm. The recoil energy  kHz. The local rotation around each potential minimum has been experimentally realized through inserting electrooptic phase modulators into the beams forming the 2D lattice potential, and the relevant rotating frequency
kHz. The local rotation around each potential minimum has been experimentally realized through inserting electrooptic phase modulators into the beams forming the 2D lattice potential, and the relevant rotating frequency  can be turned with large flexibility [18]. From the energy bands in figure 1, we can estimate that it is enough for
can be turned with large flexibility [18]. From the energy bands in figure 1, we can estimate that it is enough for  KHz to satisfy the topological superfluid condition.
KHz to satisfy the topological superfluid condition.
In the presence of the harmonic trap, it has been shown that the local density approximation(LDA) breaks down for trapped non-interacting bosons in the p-orbital bands, and increasing the interactions and optical lattice potentials can suppress anisotropy of condensate density [48] . However, the picture is different for trapped non-interacting fermions in p-orbital bands due to the different statistics. It is shown that the hard-core boson known as Tonks–Girardeau boson with infinitely repulsive interactions can be mapped into non-interacting free fermion in the 1D limit [49–51]. Thus, the boson with infinitely repulsive interactions is roughly equivalent to free fermion even in a 2D system. Such effective 'repulsive interactions' can suppress the anisotropy of condensate density, and guarantee the validity of LDA in a system with trapped fermions in p-orbital bands. Furthermore, the tunability of the optical lattice potential and quite small trap potential can further reduce the anisotropy of condensate density. Though the breaking down of LDA can be suppressed, the particle density per site will inevitably vary and the s-orbital atoms will thereby shift the on-site energies for p-orbital atoms in the presence of the trap. Thanks to the small trap potential, one can expect that the density fluctuations of the both trapped s-orbital and p-orbital atoms should be small, and the main results throughout the paper are not changed qualitatively.
The change of the mass current and the accumulation of the atoms around the spatial barrier can be spatially resolved with the radio-frequency spectroscopy [52–54]. Besides the radio-frequency spectroscopy, the recently developed matter-wave interference technique [55] is a more powerful tool, which can directly represent the phase properties of the superfluid order parameter. More remarkably, one can reconstruct the spatial geometry of certain low-energy in-gap fermion modes and verify the formation of the spatial barrier structure, both of which are the key signatures in our proposal.
In summary, we propose that the superfluid states of fermions with a chiral d-wave order can be implemented in a rotating optical lattice where the orbital degrees of freedom play a key role. Our proposal presents an alternative route to realizing the topological superfluids with chiral even-frequency order in the absence of the spin–orbital coupling. Furthermore, we show that the intrinsic harmonic confining potential can form a circular spatial barrier structure which accumulates atoms and support a mass current under the injection of small angular momentum as the driving force. The mass current associated with the accumulated atoms can be experimentally detected, and provides a signature to verify the emergence of topological superfluid state with chiral d-wave order in a rotating optical lattice.
Acknowledgments
We thank S-Q Shen, S Z Zhang, D W Zhang, and G C Liu for useful discussions. This work was supported by the NSFC under Grants No. 11674331, No. 11274032, No.11625415, the Ministry of Science and Technology of China (Grant number: 2017YFA0303200), and by the 100 Talents Programme of the CAS.
Footnotes
- 6
Unlike the vortex case, where the radius of vortex has the same order of coherence length
 , the domain wall could collapse when
, the domain wall could collapse when  . Thus, the Vt should not be too large to have large R. Here, we have
. Thus, the Vt should not be too large to have large R. Here, we have  for
for  , and R is much larger than
, and R is much larger than  if the vF is estimated from the Fermi energy along
if the vF is estimated from the Fermi energy along  direction.
direction.