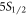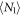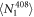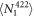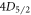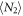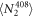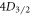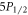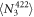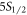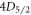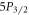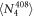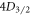Abstract
We report and demonstrate a method for measuring the branching ratios of dipole transitions of trapped atomic ions by performing nested sequences of population inversions. This scheme is broadly applicable to species with metastable lambda systems and can be generalized to find the branching of any state to lowest states. It does not use ultrafast pulsed or narrow linewidth lasers and is insensitive to experimental variables such as laser and magnetic field noise as well as ion heating. To demonstrate its effectiveness, we make the most accurate measurements thus far of the branching ratios of both 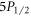 and
and 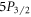 states in 88Sr+ with sub-1% uncertainties. We measure 17.175(27) for the
states in 88Sr+ with sub-1% uncertainties. We measure 17.175(27) for the 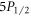 –
–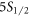 branching ratio, 15.845(71) for
branching ratio, 15.845(71) for 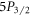 –
–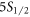 , and 0.056 09(21) for
, and 0.056 09(21) for 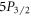 –
–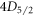 . These values represent the first precision measurement for
. These values represent the first precision measurement for 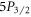 –
–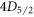 , as well as ten- and thirty-fold improvements in precision respectively for
, as well as ten- and thirty-fold improvements in precision respectively for 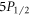 –
–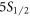 and
and 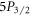 –
–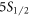 over the best previous experimental values.
over the best previous experimental values.
Export citation and abstract BibTeX RIS
1. Introduction
Empirical measurements of physical constants are fundamental to the verification and advancement of our knowledge of atoms. One important atomic property is the branching ratio of an electronic transition 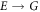 :
:
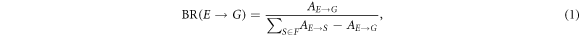
where A is the transition rate and F is the set of all states E directly decays to. Measuring these constants accurately is vital for the refinement of relativistic many-body theories and provides a crucial probe in the study of fundamental physics such as parity non-conservation [1–6].
Branching ratios for different atomic species are of great use in a wide range of fields including astrophysics, where analyzing the composition of stars contributes greatly to understanding stellar formation and evolution. Abundances of heavy elements such as strontium are essential for determining the efficiency of neutron capture processes in metal-poor stars, yet can be difficult to determine from emission spectra due to nearby transitions of other elements [7–13]. Branching ratios of these transitions are therefore vital for quantitative modeling of nucleosynthesis processes [11–13].
In addition, precise branching ratios enable the improvement of clock standards, paving the way for better global positioning systems and tests of the time-invariance of fundamental constants [14]. Atomic clocks using the optical quadrupole transition 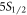 –
–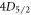 in 88Sr+, one of the secondary clock standards recommended by the International Committee for Weights and Measures [14], have achieved uncertainties at the 10−17 level [15], more accurate than the current 133Cs clock standard [16]. To further improve the precision of these systems, it is necessary to reduce uncertainty from the blackbody radiation Stark shift, a dominant source of error in many clock systems [2]. Branching ratios measured below the 1% level, combined with high-precision lifetime measurements, can improve the accuracy of static polarizabilities of clock states in 88Sr+ and many systems and thereby reduce the uncertainty in blackbody radiation shift error, in addition to providing a verification against other methods for determining polarizability [2, 17].
in 88Sr+, one of the secondary clock standards recommended by the International Committee for Weights and Measures [14], have achieved uncertainties at the 10−17 level [15], more accurate than the current 133Cs clock standard [16]. To further improve the precision of these systems, it is necessary to reduce uncertainty from the blackbody radiation Stark shift, a dominant source of error in many clock systems [2]. Branching ratios measured below the 1% level, combined with high-precision lifetime measurements, can improve the accuracy of static polarizabilities of clock states in 88Sr+ and many systems and thereby reduce the uncertainty in blackbody radiation shift error, in addition to providing a verification against other methods for determining polarizability [2, 17].
Despite their relevance, branching ratios of heavy atoms have not been precisely measured for many decades due to the large uncertainties inherent in traditional discharge chamber methods using the Hanle effect [18]. Recent astrophysical studies still use these older experimental results for fitting emission spectra [12, 13]. Only in the last decade have there been measurements of branching ratios at the 1% level [19–22] using trapped ions, which are versatile toolkits for precision spectroscopy [4, 15, 23] as well as quantum computation [24]. In particular, Ramm et al [19] established a simple method for measuring branching ratios of 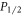 states in trapped ions with metastable lambda systems.
states in trapped ions with metastable lambda systems.
Here, we present a novel scheme for measuring the branching ratios of the 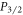 state of a trapped ion with an iterative population transfer sequence, significantly extending Ramm et al's method. As with [19], we do not require ultrafast pulsed lasers or narrow linewidth lasers for addressing quadrupole transitions, which were used by previous precision measurements of
state of a trapped ion with an iterative population transfer sequence, significantly extending Ramm et al's method. As with [19], we do not require ultrafast pulsed lasers or narrow linewidth lasers for addressing quadrupole transitions, which were used by previous precision measurements of 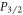 branching ratios [21, 25]. Our method uses only two lasers that pump the ion from the ground state to the
branching ratios [21, 25]. Our method uses only two lasers that pump the ion from the ground state to the 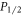 and
and 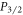 excited states and two lasers to unshelve the ion from the metastable states below
excited states and two lasers to unshelve the ion from the metastable states below 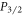 . For 88Sr+ and analogous species, these dipole-addressing lasers are already used for Doppler cooling, making this scheme broadly applicable for many trapped ion systems without the need for additional equipment. Like [19], our method is insensitive to experimental variables such as magnetic field and laser fluctuations. Furthermore, we show that the method can be extended to measure the branching ratios of an arbitrary excited state to the ground and metastable states through all intermediate states. We demonstrate the effectiveness of this method by making the first precision measurement of the
. For 88Sr+ and analogous species, these dipole-addressing lasers are already used for Doppler cooling, making this scheme broadly applicable for many trapped ion systems without the need for additional equipment. Like [19], our method is insensitive to experimental variables such as magnetic field and laser fluctuations. Furthermore, we show that the method can be extended to measure the branching ratios of an arbitrary excited state to the ground and metastable states through all intermediate states. We demonstrate the effectiveness of this method by making the first precision measurement of the 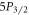 –
–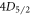 and
and 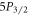 –
–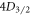 branching ratios in 88Sr+ in addition to the most accurate measurement of the
branching ratios in 88Sr+ in addition to the most accurate measurement of the 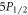 branching ratios to date.
branching ratios to date.
2. Iterative branching ratio measurement
We begin by briefly describing the procedure for measuring branching ratios of 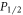 states in metastable lambda systems using the method by Ramm et al, which will be a building block for the
states in metastable lambda systems using the method by Ramm et al, which will be a building block for the  system. We use the
system. We use the 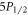 excited state in 88Sr+ as the model system (figure 1), and denote the probability of decaying to the ground
excited state in 88Sr+ as the model system (figure 1), and denote the probability of decaying to the ground 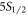 state as p and the long-lived
state as p and the long-lived 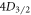 state as
state as  .
.
Figure 1. Energy levels of 88Sr+, showing the 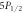 and
and 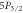 excited states and their decay channels.
excited states and their decay channels.  and
and 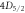 are metastable states with lifetimes much greater than the timescale of the experiment [26]. To measure the
are metastable states with lifetimes much greater than the timescale of the experiment [26]. To measure the 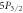 branching ratio, we need only lasers addressing the 408, 422, 1092, and 1033 nm transitions.
branching ratio, we need only lasers addressing the 408, 422, 1092, and 1033 nm transitions.
Download figure:
Standard image High-resolution imageAt the start of the experiment, the ion is initialized to the ground 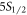 state. In the first step, the 422 nm laser is turned on to optically pump the ion to the excited
state. In the first step, the 422 nm laser is turned on to optically pump the ion to the excited 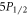 state while we record ion fluorescence at 422 nm. In the process of the ion fully shelving to the metastable
state while we record ion fluorescence at 422 nm. In the process of the ion fully shelving to the metastable  state, we detect a mean number of photons
state, we detect a mean number of photons 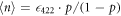 , where
, where 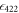 is the detection efficiency of our system at 422 nm [19]. In the second step, the 1092 nm laser is turned on to repump the ion to the excited state, during which we detect
is the detection efficiency of our system at 422 nm [19]. In the second step, the 1092 nm laser is turned on to repump the ion to the excited state, during which we detect 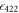 photon as it decays to the
photon as it decays to the 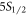 state. The branching ratio
state. The branching ratio 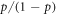 is therefore equal to the ratio of the number of photons observed during the two time intervals, independent of the collection efficiency.
is therefore equal to the ratio of the number of photons observed during the two time intervals, independent of the collection efficiency.
For the more complex 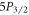 state, which decays to three instead of two states, we denote the probability of decaying to the
state, which decays to three instead of two states, we denote the probability of decaying to the 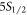 ,
,  , and
, and  states as q, r, and
states as q, r, and  respectively (figure 1). To measure the
respectively (figure 1). To measure the 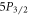 branching ratios
branching ratios 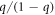 ,
,  , and
, and  , we begin with a sequence analogous to the
, we begin with a sequence analogous to the 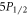 sequence, this time detecting photons at both 408 and 422 nm. Starting again with the ion in the
sequence, this time detecting photons at both 408 and 422 nm. Starting again with the ion in the  ground state, we first pump the ion into the excited
ground state, we first pump the ion into the excited 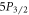 state with the 408 nm laser (Step A). We detect a mean number of photons from the ion
state with the 408 nm laser (Step A). We detect a mean number of photons from the ion
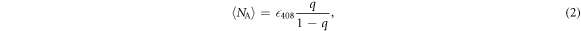
where 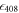 is the detection efficiency at 408 nm. We now turn on the 1033 nm laser, which drives the ion to the
is the detection efficiency at 408 nm. We now turn on the 1033 nm laser, which drives the ion to the 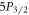 state if it was in the
state if it was in the 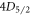 state and does nothing otherwise (Step B). We detect a mean number of 408 nm photons
state and does nothing otherwise (Step B). We detect a mean number of 408 nm photons
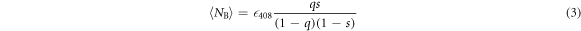
in this step. We can obtain the 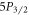 –
–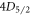 branching ratio
branching ratio  from the photon count ratio of the previous two steps.
from the photon count ratio of the previous two steps.
To measure the other two branching ratios, we note that their values are contained in the state of the ion after Step B—the population split between the 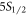 and
and 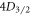 states. To obtain this information, we now turn on the 422 nm laser to pump all
states. To obtain this information, we now turn on the 422 nm laser to pump all 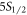 population into the
population into the 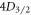 state (Step C). We detect
state (Step C). We detect
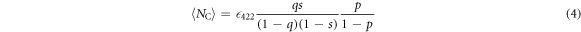
photons at 422 nm. Finally, turning on the 1092 nm laser repumps all of the population to the 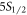 state and we detect
state and we detect 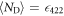 photon (Step D), which is necessary for canceling the detection efficiency
photon (Step D), which is necessary for canceling the detection efficiency 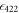 .
.
Since we can determine p experimentally with the 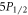 branching ratio sequence, we can solve for the
branching ratio sequence, we can solve for the 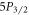 branching ratios without knowing
branching ratios without knowing 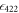 or
or 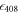 :
:
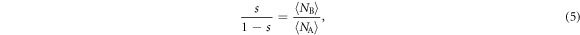
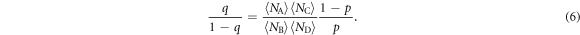
As with the 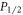 measurement scheme by Ramm et al, our sequence of population transfers is insensitive to detection efficiencies and most experimental variables. The long-lived shelving states
measurement scheme by Ramm et al, our sequence of population transfers is insensitive to detection efficiencies and most experimental variables. The long-lived shelving states 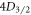 and
and 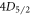 allow for the length of the measurement to far exceed the timescale needed for population transfer, rendering the measurement independent of laser power and frequency fluctuations as well as ion heating. There are no coherence effects or dark resonances since only one laser is on at a time, so our method is also insensitive to micromotion and magnetic field fluctuations. This distinguishes our method from a proposed
allow for the length of the measurement to far exceed the timescale needed for population transfer, rendering the measurement independent of laser power and frequency fluctuations as well as ion heating. There are no coherence effects or dark resonances since only one laser is on at a time, so our method is also insensitive to micromotion and magnetic field fluctuations. This distinguishes our method from a proposed 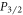 branching ratio measurement scheme [27], which not only requires an extra laser for the
branching ratio measurement scheme [27], which not only requires an extra laser for the 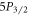 –
–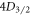 transition but also that two lasers be alternately pulsed for each step to avoid dark resonances, making the measurement sequence significantly longer.
transition but also that two lasers be alternately pulsed for each step to avoid dark resonances, making the measurement sequence significantly longer.
The branching ratios of states higher than 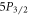 to the ground state and metastable D states are also of practical importance for calculating the scalar polarizability [2] as well as improving elemental abundance models of stars [13]. Our iterative method can be generalized to find the branching of any excited state to the lowest five states in 88Sr+ through any number of intermediate states (see
to the ground state and metastable D states are also of practical importance for calculating the scalar polarizability [2] as well as improving elemental abundance models of stars [13]. Our iterative method can be generalized to find the branching of any excited state to the lowest five states in 88Sr+ through any number of intermediate states (see
3. Experimental measurement in 88Sr+
To demonstrate our iterative method, we experimentally measure the 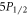 and
and 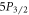 branching ratios in 88Sr+ using a trapped ion system to levels of precision over an order of magnitude over previous best values.
branching ratios in 88Sr+ using a trapped ion system to levels of precision over an order of magnitude over previous best values.
3.1. Experimental procedure
We trap single 88Sr+ ions using a surface electrode Paul trap fabricated by Sandia National Laboratories [28]. RF and DC confining fields are set such that the axial secular frequency of the ion is 600 kHz, with radial frequencies in the 3–4 MHz range and a 15° tilt in the radial plane. A magnetic field of 5.4 G is applied normal to the trap to lift the degeneracy of the Zeeman states [29]. Fluorescence from the ion is collected along the same axis by an in-vacuum 0.42 NA aspheric lens (Edmunds 49-696) into a single photon resolution photomultiplier tube (PMT, Hamamatsu H10682-210) with a filter that only passes light between 408 and 422 nm (Semrock FF01-415/10-25). The PMT signal is counted by an FPGA with arrival time binned into 2 ns intervals. The overall detection efficiency of the setup is approximately 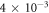 at both 422 and 408 nm. Dipole transitions of the ion are addressed using frequency-stabilized diode lasers. To execute the experimental sequence, we switch laser beams on and off using acousto-optic modulators (AOMs) driven by FPGA-controlled direct digital synthesizers.
at both 422 and 408 nm. Dipole transitions of the ion are addressed using frequency-stabilized diode lasers. To execute the experimental sequence, we switch laser beams on and off using acousto-optic modulators (AOMs) driven by FPGA-controlled direct digital synthesizers.
Each branching ratio measurement cycle begins with 100 μs of Doppler cooling using 422 and 1092 nm lasers. Subsequently, we turn on only the 1092 nm laser for 20 μs to ensure the ion is in the 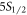 state, then perform the experimental sequence. We ran the
state, then perform the experimental sequence. We ran the 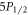 and
and 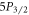 branching ratio measurement sequences for
branching ratio measurement sequences for  and
and 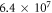 cycles respectively for a run time of 13 and 6 h each. For each step within the experimental sequence, the laser is turned on twice: first the data interval where population transfer occurs, then the background interval that is subtracted from the data interval to obtain only fluorescence from the ion. For the
cycles respectively for a run time of 13 and 6 h each. For each step within the experimental sequence, the laser is turned on twice: first the data interval where population transfer occurs, then the background interval that is subtracted from the data interval to obtain only fluorescence from the ion. For the 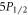 experiment, the 422 nm and 1092 nm intervals are 35 μs and 25 μs in length respectively for both data and background, with 1 μs between each interval, and the
experiment, the 422 nm and 1092 nm intervals are 35 μs and 25 μs in length respectively for both data and background, with 1 μs between each interval, and the 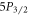 experimental sequence is depicted in figure 2.
experimental sequence is depicted in figure 2.
Figure 2. Real time-resolved fluorescence collected from the ion at 422 and 408 nm after 8 × 106 cycles of the 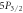 branching ratio data sequence. Counts in the background intervals (black ABCD squares) are subtracted from the data intervals (white ABCD squares) to obtain only fluorescence from the ion for each step. The length T of each interval is indicated, and the laser turn-off time is 1 μs between each interval. Atomic states losing population (dashed circle) and gaining population (solid circle) during each step are depicted.
branching ratio data sequence. Counts in the background intervals (black ABCD squares) are subtracted from the data intervals (white ABCD squares) to obtain only fluorescence from the ion for each step. The length T of each interval is indicated, and the laser turn-off time is 1 μs between each interval. Atomic states losing population (dashed circle) and gaining population (solid circle) during each step are depicted.
Download figure:
Standard image High-resolution image3.2. Error analysis
To correct for systematic effects on branching ratios, we carefully calibrated the sources of error in our experiment, which are summarized in table 1.
Table 1.
List of systematic sources of error for branching ratios of 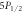 –
–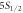 ,
, 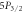 –
–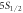 , and
, and 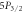 –
–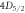 and their fractional contributions to the overall shift and uncertainty. Powers of 10 are in brackets.
and their fractional contributions to the overall shift and uncertainty. Powers of 10 are in brackets.
| Fractional shift and uncertainty | |||
|---|---|---|---|
| Error source |
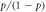
|
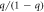
|
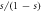
|
| Counting statistics |
![$\pm 16[-4]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn104.gif)
|
![$\pm 38[-4]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn105.gif)
|
![$\pm 33[-4]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn106.gif)
|
| Polarization alignment | — |
![$\pm 19[-4]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn107.gif)
|
![$\pm 19[-4]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn108.gif)
|
| PMT dead time |
![$46\pm 2[-5]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn109.gif)
|
![$76\pm 5[-5]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn110.gif)
|
![$-45\pm 1[-5]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn111.gif)
|
| Finite laser durations |
![$13\pm 9[-8]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn112.gif)
|
![$\pm 3[-6]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn113.gif)
|
![$-6\pm 2[-6]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn114.gif)
|
| AOM extinction ratio |
![$\pm 7[-7]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn115.gif)
|
![$\pm 3[-6]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn116.gif)
|
![$\pm 1[-6]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn117.gif)
|
| Finite D state lifetime |
![$354\pm 4[-8]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn118.gif)
|
![$-40\pm 2[-7]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn119.gif)
|
![$-124\pm 2[-7]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn120.gif)
|
 branching ratio branching ratio |
— |
![$\pm 16[-4]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn122.gif)
|
— |
| Total |
![$5\pm 16[-4]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn123.gif)
|
![$8\pm 45[-4]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn124.gif)
|
![$5\pm 38[-4]$](https://content.cld.iop.org/journals/1367-2630/18/12/123021/revision1/njpaa511dieqn125.gif)
|
The polarization alignment error arises from the Hanle effect and is a function of the magnetic field, detector position, and incident laser direction and polarization. In the 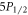 system, the
system, the  sublevels both emit radiation isotropically with 1:2 ratios of π- to σ-polarized light regardless of magnetic and electric fields, so this does not affect the measurement [30]. However, the Hanle effect is a major source of error for the
sublevels both emit radiation isotropically with 1:2 ratios of π- to σ-polarized light regardless of magnetic and electric fields, so this does not affect the measurement [30]. However, the Hanle effect is a major source of error for the 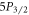 system as the ratio of emitted π- to σ-polarized photons is 0:1 for
system as the ratio of emitted π- to σ-polarized photons is 0:1 for 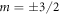 sublevels and 2:1 for
sublevels and 2:1 for 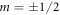 sublevels. The ratio of π to σ light emitted from Step A and Step B will therefore not be equal in general, biasing the fluorescence ratio.
sublevels. The ratio of π to σ light emitted from Step A and Step B will therefore not be equal in general, biasing the fluorescence ratio.
To resolve this problem, we linearly polarize 408 and 1033 nm light to an axis set at 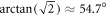 (the magic angle [31]) with respect to the magnetic field, which is set orthogonally to the laser beam. At the magic angle, the ratio of π- to σ- polarized light emitted during Steps A and B are both equal to 1:2. The difference between radiation patterns of π and σ photons and any birefringence effects in the detection system cancel out. We use a Glan-Taylor polarizer (Thorlabs GT10) with >50 dB attenuation of the orthogonal polarization to align the 408 and 1033 nm laser polarizations to within 0.2° of the magic angle. We measured the effective phase retardance
(the magic angle [31]) with respect to the magnetic field, which is set orthogonally to the laser beam. At the magic angle, the ratio of π- to σ- polarized light emitted during Steps A and B are both equal to 1:2. The difference between radiation patterns of π and σ photons and any birefringence effects in the detection system cancel out. We use a Glan-Taylor polarizer (Thorlabs GT10) with >50 dB attenuation of the orthogonal polarization to align the 408 and 1033 nm laser polarizations to within 0.2° of the magic angle. We measured the effective phase retardance 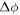 due to possible birefringence of optics and vacuum window after the polarizer to be <0.02 radians at both blue and infrared wavelengths, which does not contribute significantly to the uncertainties. The error in aligning the laser polarization with respect to the magnetic field and setting the magnetic field to be orthogonal to the laser beam accounts for the polarization alignment error in table 1.
due to possible birefringence of optics and vacuum window after the polarizer to be <0.02 radians at both blue and infrared wavelengths, which does not contribute significantly to the uncertainties. The error in aligning the laser polarization with respect to the magnetic field and setting the magnetic field to be orthogonal to the laser beam accounts for the polarization alignment error in table 1.
The effects of the other sources of systematics are accounted for by modeling the time-resolved fluorescence curves using optical Bloch equations to determine the shift and uncertainty contributed by each error source. PMT dead time, calibrated to be 20 ± 1 ns for our system using the method by Meeks and Siegel [32], leads to more undercounting in steps with higher count rates. Finite laser durations reduce the fluorescence from the ion in each step in addition to preparing states imperfectly. The small amount of laser light still present when the AOMs are switched off (extinction ratios >60 dB) leads to slight coupling between undesirable states. The finite lifetimes of the 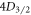 and
and 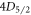 states lead to extra counts in the blue intervals and reduced counts in the IR intervals. Off-resonant excitations, where the ion is excited to the wrong state by a collision or far-detuned laser, are found to contribute negligible errors to our system based on measuring the frequency of dark events while Doppler cooling the ion. We find that these sources of systematics do not limit our current level of precision. We also verify that the fluorescence from the ion is normally distributed when binned into successive 500 000 measurement cycles.
states lead to extra counts in the blue intervals and reduced counts in the IR intervals. Off-resonant excitations, where the ion is excited to the wrong state by a collision or far-detuned laser, are found to contribute negligible errors to our system based on measuring the frequency of dark events while Doppler cooling the ion. We find that these sources of systematics do not limit our current level of precision. We also verify that the fluorescence from the ion is normally distributed when binned into successive 500 000 measurement cycles.
The largest source of error for both 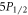 and
and 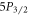 branching ratios is from counting statistics. This can be improved via either more measurement cycles, more ions, or greater collection efficiency, though for the latter two methods it is important to take into account the increased error from PMT dead time. Other errors can also be reduced via improvement of the experimental apparatus, such as more accurate alignment of the laser polarization and using a PMT with less dead time. The only fundamental limitation to the accuracy of the technique is the uncertainty on the finite lifetimes of the
branching ratios is from counting statistics. This can be improved via either more measurement cycles, more ions, or greater collection efficiency, though for the latter two methods it is important to take into account the increased error from PMT dead time. Other errors can also be reduced via improvement of the experimental apparatus, such as more accurate alignment of the laser polarization and using a PMT with less dead time. The only fundamental limitation to the accuracy of the technique is the uncertainty on the finite lifetimes of the  and
and 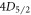 states, which restricts the length of the population inversion sequence, but the limit is many orders of magnitude below the current level of accuracy.
states, which restricts the length of the population inversion sequence, but the limit is many orders of magnitude below the current level of accuracy.
After correcting for systematic shifts and propagating uncertainties, we obtain for the 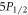 branching ratio
branching ratio  and for the
and for the 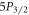 branching ratios
branching ratios 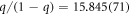 ,
, 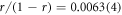 , and
, and 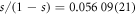 , with errors representing 1σ bounds. The corresponding branching fractions are
, with errors representing 1σ bounds. The corresponding branching fractions are 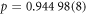 ,
, 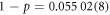 ,
, 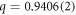 ,
,  , and
, and 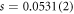 .
.
3.3. Comparison with previous works
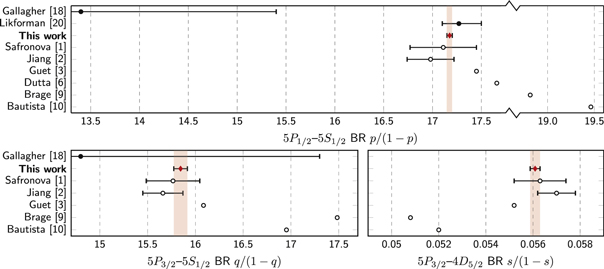
The uncertainty of our results is at a level smaller than the discrepancy between previous experimental and theoretical results, as shown in figure 3. Our value for the 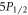 –
–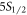 branching ratio is in agreement with the recent measurement done by Likforman et al [20] with trapped ions, as well as theoretical values of Safronova [1] and Jiang et al [2], while it is 1.9 σ away from the gas discharge chamber experiment by Gallagher [18]. For
branching ratio is in agreement with the recent measurement done by Likforman et al [20] with trapped ions, as well as theoretical values of Safronova [1] and Jiang et al [2], while it is 1.9 σ away from the gas discharge chamber experiment by Gallagher [18]. For 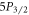 , only the
, only the 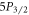 –
–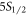 branching ratio has been previously reported, also by Gallagher, which our value is in agreement with. We are also in agreement with theory values of Safronova and Jiang et al for all
branching ratio has been previously reported, also by Gallagher, which our value is in agreement with. We are also in agreement with theory values of Safronova and Jiang et al for all 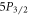 branching ratios. We note that Safronova's theoretical values have been found to be in good agreement with precision measurements of branching ratios and dipole matrix elements in other elements [19, 23, 33–35]. We obtain a ten-fold improvement in precision for the
branching ratios. We note that Safronova's theoretical values have been found to be in good agreement with precision measurements of branching ratios and dipole matrix elements in other elements [19, 23, 33–35]. We obtain a ten-fold improvement in precision for the 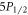 branching ratios over Likforman et al and a thirty-fold improvement for the
branching ratios over Likforman et al and a thirty-fold improvement for the 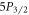 –
–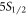 branching ratio over the early results of Gallagher.
branching ratio over the early results of Gallagher.
Figure 3. Branching ratios (BR) for the 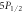 and
and 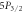 excited states in Sr+ obtained by this work (red diamond) and previous experimental (filled circle) and theoretical (empty circle) works. Error bars are included whenever uncertainties are provided by the source.
excited states in Sr+ obtained by this work (red diamond) and previous experimental (filled circle) and theoretical (empty circle) works. Error bars are included whenever uncertainties are provided by the source.
Download figure:
Standard image High-resolution imageFor improving the precision of 88Sr+ atomic clocks, it is important to have accurate rates for transitions to the 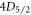 and
and 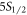 levels. Using the 6.63(7) ns
levels. Using the 6.63(7) ns 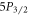 lifetime value measured by Pinnington et al [36], we obtain transition rates
lifetime value measured by Pinnington et al [36], we obtain transition rates 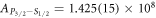 s−1 and
s−1 and  s−1 using our measured branching ratios. These are significantly more accurate compared to previous best-known transition rates of
s−1 using our measured branching ratios. These are significantly more accurate compared to previous best-known transition rates of 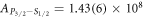 s−1 and
s−1 and 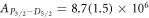 s−1 from Gallagher [18]. The uncertainty in transition rates is now dominated by the uncertainty in the
s−1 from Gallagher [18]. The uncertainty in transition rates is now dominated by the uncertainty in the 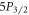 lifetime.
lifetime.
4. Conclusion and outlook
In summary, we have introduced a novel method for measuring the branching ratio of the 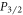 state in ions with metastable lambda systems and demonstrated its effectiveness with measurements in 88Sr+ at the sub-1% level. Our scheme, as with the Ramm et al method for
state in ions with metastable lambda systems and demonstrated its effectiveness with measurements in 88Sr+ at the sub-1% level. Our scheme, as with the Ramm et al method for 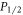 states, uses only dipole transition addressing lasers and is insensitive to detector efficiencies, laser and magnetic field fluctuations, as well as ion heating and micromotion. We further describe how to extend this population transfer sequence to measure the branching of any excited state to the
states, uses only dipole transition addressing lasers and is insensitive to detector efficiencies, laser and magnetic field fluctuations, as well as ion heating and micromotion. We further describe how to extend this population transfer sequence to measure the branching of any excited state to the 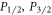 , and ground and metastable states through all intermediate states with the addition of a few more lasers. This scheme is also broadly applicable to excited states in other elements with a similar lambda structure of decaying into a ground state and long-lived states, such as secondary clock standards 199Hg+ and 171Yb+, for which greater branching ratio and lifetime precision can reduce uncertainty from blackbody radiation as well [37, 38].
, and ground and metastable states through all intermediate states with the addition of a few more lasers. This scheme is also broadly applicable to excited states in other elements with a similar lambda structure of decaying into a ground state and long-lived states, such as secondary clock standards 199Hg+ and 171Yb+, for which greater branching ratio and lifetime precision can reduce uncertainty from blackbody radiation as well [37, 38].
Acknowledgments
The authors acknowledge helpful discussions with Hartmut Häffner, Christian Roos, and Luca Guidoni. This work was supported in part by the IARPA MQCO program and by the NSF Center for Ultracold Atoms.
Appendix. Generalization of branching ratio measurement to arbitrary excited states
Denote the set of the five lowermost states in 88Sr+, 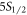 ,
, 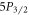 ,
, 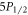 ,
, 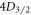 , and
, and 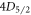 , as S. Define the set of all states that state E decays to through any number of intermediate states to be
, as S. Define the set of all states that state E decays to through any number of intermediate states to be 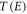 . We define the base branching fraction
. We define the base branching fraction 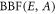 of
of 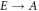 for
for 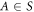 to be the probability of state E decaying to A while only ever occupying intermediate states from the set
to be the probability of state E decaying to A while only ever occupying intermediate states from the set 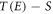 . We label the base branching fractions of E to
. We label the base branching fractions of E to 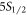 ,
, 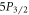 ,
, 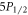 ,
,  , and
, and 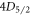 to be a, b, c, d, and
to be a, b, c, d, and  respectively, as shown in figure A1
.
respectively, as shown in figure A1
.
Figure A1. The base branching ratios of an arbitrary state E in 88Sr+, effectively the branching ratios of the set of states consisting of E and all states higher than the five lowermost states that E decays to. Only detecting 422 and 408 nm photons from various population transfers is sufficient for measuring base branching ratios.
Download figure:
Standard image High-resolution imageIt follows that 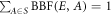 , as all end states (ground and metastable) of 88Sr+ are in S. We define base branching ratios to be
, as all end states (ground and metastable) of 88Sr+ are in S. We define base branching ratios to be 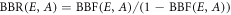 . Under the assumption that E and all states in
. Under the assumption that E and all states in 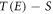 decay much faster than the lifetime of
decay much faster than the lifetime of 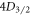 and
and 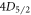 , it is possible to measure base branching ratios of any E.
, it is possible to measure base branching ratios of any E.
As all higher states of 88Sr+ have nonzero probability of eventually decay to 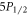 or
or  , there will always be 422 or 408 nm photons emitted after the ion is excited to E. In fact, base branching ratios can be measured by the same experimental setup for measuring
, there will always be 422 or 408 nm photons emitted after the ion is excited to E. In fact, base branching ratios can be measured by the same experimental setup for measuring 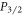 branching ratios, with the addition of appropriate dipole-addressing lasers as well as the minor modification of detecting 422 and 408 nm photons separately. A scheme which solves for the base branching ratios of any state
branching ratios, with the addition of appropriate dipole-addressing lasers as well as the minor modification of detecting 422 and 408 nm photons separately. A scheme which solves for the base branching ratios of any state 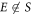 is as follows:
is as follows:
- (i)Pump the ion from
 to E, collect
to E, collect  photons total,
photons total,  at 408 nm and
at 408 nm and  at 422 nm.
at 422 nm. - (ii)Pump from
 to E, collect
to E, collect  photons total,
photons total,  at 408 nm and
at 408 nm and  photons at 422 nm.
photons at 422 nm. - (iii)Pump from
 to
to  , collect
, collect  photons.
photons. - (iv)Pump the ion from
 to E.
to E. - (v)Pump from
 to
to  , collect
, collect  photons.
photons. - (vi)Pump from
 to
to  , collect
, collect  photons.
photons.
The base branching ratios can be calculated from the experimental results as follows:
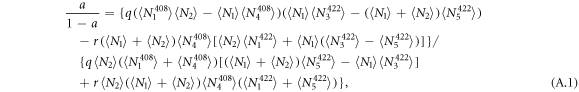
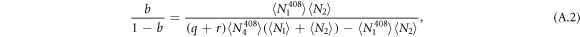
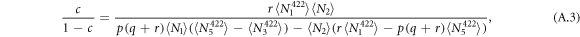
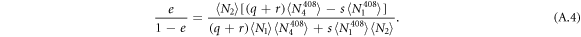
This scheme is insensitive to the same experimental variables as the 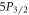 measurement scheme. Aside from the lasers needed for transferring the ion population from
measurement scheme. Aside from the lasers needed for transferring the ion population from 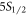 and
and 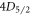 to E, no other additional equipment is necessary. With some adjustments, it can be used to solve for base branching ratios of other analogous species with long-lived metastable states.
to E, no other additional equipment is necessary. With some adjustments, it can be used to solve for base branching ratios of other analogous species with long-lived metastable states.