Abstract
Two-mode squeezed states, generated via non-degenerate parametric down-conversion, are invariably revealed via their entangled vacuum or correlated thermal fluctuations. Here, two-mode thermal squeezed states, generated in an electromechanical system, are made bright by means of degenerate parametric amplification of their constituent modes to the point where they are almost perfect, even when seeded from low intensity non-degenerate parametric down-conversion. More dramatically, activating the degenerate parametric resonances of the underlying modes yields perfect correlations which can be resolved via the coordinated switching of their phase bi-stable vibrations, without recourse to monitoring their thermal fluctuations. This ability to enhance the two-mode squeezed states and to decipher them without needing to observe their intrinsic noise is supported by both analytical and numerical modelling and it suggests that the technical constraints to making this phenomenon more widely available can be dramatically relaxed.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Two-mode squeezed states generated via non-degenerate parametric down-conversion are routinely observed in the lab via their vacuum noise principally due to the widespread availability of efficient detectors for optical photons [1–3]. On the other hand two-mode vacuum squeezed states realised with microwave photons in superconducting circuits are more challenging to observe due to their small energy thus requiring the development efficient amplifiers [4–6]. This challenge is further magnified when extended to phonons, usually localised in low frequency mechanical resonators, with the dual requirement of operation in their vacuum state combined with the ability to detect their miniscule fluctuations [7, 8]. Indeed only recently has it become possible to create entangled phonons via the two-mode squeezer interaction and even then in a hybrid system composed of photons and phonons [9, 10]. Alternatively two-mode squeezing with a system composed purely of phonons has also been realised but was limited to thermal populations yielding correlated states [11–13].
Here a protocol is developed to increase the visibility of the two-mode thermal squeezed states from phonons which concomitantly furnishes perfect correlations and it has the potential to be extended to vacuum squeezed states. It is based on degenerately parametrically amplifying the two-mode thermal squeezed states that are engendered from the non-degenerate parametric down-conversion. Specifically this is achieved by modulating the spring constants of the modes, underpinning the two-mode squeezed states, at twice their natural frequency [14]. On the other hand large gains from the degenerate parametric amplification results in the constituent modes parametrically resonating, with bi-stable phases, and in this regime the two-mode squeezed states can instead be identified from the correlated vibration phases of the underlying modes rather than from their more usual intrinsic noise [15]. Indeed this latter regime offers the tantalising prospect of more readily resolving the correlations between modes, from the two-mode squeezing, which could be harnessed for technological applications. In many respects these observations are analogous to the readout of superconducting quantum bits [16] via a Josephson parametric amplifier [17] when operated in the amplification [18, 19] or in the oscillation regime [20] thus suggesting the applicability of this protocol to two-mode vacuum squeezed states with phonons in an electromechanical system [21].
2. Experimental
The prototype electromechanical system in which these concepts are explored is shown in figure 1(a) and it consists of two GaAs based mechanical beams of length, width and thickness of 80 μm, 20 μm and 800 nm respectively which are strongly intercoupled via the exaggerated overhangs between them. Piezoelectric transducers are also incorporated into the clamping points of both mechanical elements, consisting of a doped GaAs layer and gold electrodes sandwiching an insulating GaAs/AlGaAs superlattice, and they enable the strain in the electromechanical system to be dynamically modulated [15]. The motion of the mechanical beams, at room temperature and in a high vacuum, is transduced via a laser Doppler interferometer and both the device and the measurement setup are detailed elsewhere [11].
Figure 1. (a) A raw electron micrograph of the coupled mechanical beams sustaining the symmetric and asymmetric vibration modes whose profiles are shown in the upper and lower insets respectively that are extracted from a finite element method simulation. (b)–(d) The thermal motion of the symmetric and asymmetric modes as they are non-degenerately and degenerately amplified when the electromechanical system's spring constant is modulated at either the sum frequency of both modes or at twice the frequency of the symmetric or asymmetric mode respectively.
Download figure:
Standard image High-resolution imageThe strongly coupled beams in the electromechanical system sustain two spectrally closely spaced vibration modes labelled symmetric (S) and asymmetric (A), as shown in figure 1(a), and they can be identified by their thermal Langevin force driven random motion with natural frequencies 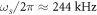 and
and 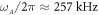 and quality factors
and quality factors 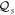 = 1300 and
= 1300 and 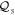 = 2300 respectively, as shown in figures 1(b)–(d) at 0 Vrms. Non-degenerate parametric amplification can be activated in the electromechanical system by modulating the spring constants of both modes at their sum frequency via piezoelectrically pumped (
= 2300 respectively, as shown in figures 1(b)–(d) at 0 Vrms. Non-degenerate parametric amplification can be activated in the electromechanical system by modulating the spring constants of both modes at their sum frequency via piezoelectrically pumped (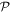 ) strain
) strain 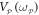 which results in the simultaneous amplification of the random displacement fluctuations of both modes as shown in figure 1(b). The simultaneous generation of phonons in both modes from this process amplifies and correlates their displacement fluctuations resulting in a two-mode thermally squeezed state namely the classical analogue of entanglement from parametric down-conversion [11–13]. On the other hand degenerate parametric amplification can also be activated in the electromechanical system by piezoelectrically modulating the spring constant of either mode at twice their natural frequency via
which results in the simultaneous amplification of the random displacement fluctuations of both modes as shown in figure 1(b). The simultaneous generation of phonons in both modes from this process amplifies and correlates their displacement fluctuations resulting in a two-mode thermally squeezed state namely the classical analogue of entanglement from parametric down-conversion [11–13]. On the other hand degenerate parametric amplification can also be activated in the electromechanical system by piezoelectrically modulating the spring constant of either mode at twice their natural frequency via 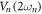 where
where 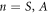 as shown in figures 1(c) and (d). This process not only amplifies the thermally driven random displacement fluctuations of either mode [14, 22] but once the phonon generation rate from this process exceeds the rate of loss, from either mode, it results in a parametric resonance [15, 23].
as shown in figures 1(c) and (d). This process not only amplifies the thermally driven random displacement fluctuations of either mode [14, 22] but once the phonon generation rate from this process exceeds the rate of loss, from either mode, it results in a parametric resonance [15, 23].
3. Theoretical
The Hamiltonian of this electromechanical system can then be expressed as
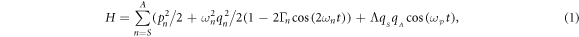
where the summation expresses the kinetic and potential energies from both modes in terms of their position qn and momentum pn [11, 15, 24]. The potential energy term contains two contributions, the second arising from the periodic modulation of the mechanical spring constant with amplitude 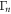 at twice the natural mode frequency, namely
at twice the natural mode frequency, namely 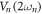 experimentally, which yields degenerate parametric amplification and parametric resonance [14, 23]. The last term in equation (1) describes non-degenerate parametric down-conversion from the pump with amplitude Λ at
experimentally, which yields degenerate parametric amplification and parametric resonance [14, 23]. The last term in equation (1) describes non-degenerate parametric down-conversion from the pump with amplitude Λ at 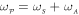 , namely
, namely 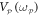 experimentally, which results in both modes being amplified and correlated yielding a two-mode squeezed state [11, 25].
experimentally, which results in both modes being amplified and correlated yielding a two-mode squeezed state [11, 25].
This Hamiltonian can be translated into the rotating frame following standard procedure [26] with the introduction of canonically conjugate variables P and Q defined as
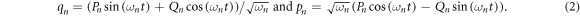
The effective Hamiltonian in these variables is then given by
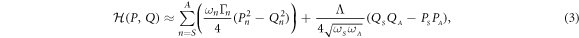
where all the fast off-resonance terms have been neglected. In order to solve this equation with damping 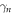 , the corresponding equations of motion are first extracted from
, the corresponding equations of motion are first extracted from 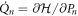 and
and 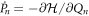 which yields
which yields
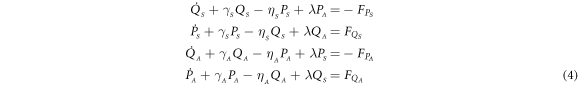
with the thermal Langevin force, decomposed into in-phase and quadrature components namely 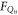 and
and 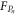 , driving both modes within their bandwidths i.e.
, driving both modes within their bandwidths i.e. 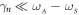 , where
, where
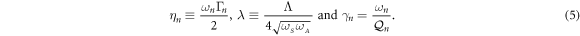
3.1. Numerical solutions
The equations of motion in (4) are first numerically solved using the Runge–Kutta method for the in-phase Qn and quadrature components Pn where four independent random number generators are used to mimic 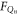 and
and 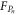 , in all four equations, driving both modes at 300 K. The equations are solved 6000 times, with
, in all four equations, driving both modes at 300 K. The equations are solved 6000 times, with 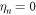 , as a function Λ and the two-mode squeezed states from this interaction can be unveiled by reconstructing the phase portrait from the cross-quadrature
, as a function Λ and the two-mode squeezed states from this interaction can be unveiled by reconstructing the phase portrait from the cross-quadrature 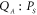 (the phase portrait from
(the phase portrait from 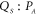 is similar and not shown throughout) and is shown in the inset to figure 2(a). This reveals a squashed distribution which implies that the vibrations in the two modes have become correlated from the non-degenerate parametric down-conversion as experimentally observed previously [11–13]. This assertion can be statistically confirmed by evaluating the corresponding correlation coefficient
is similar and not shown throughout) and is shown in the inset to figure 2(a). This reveals a squashed distribution which implies that the vibrations in the two modes have become correlated from the non-degenerate parametric down-conversion as experimentally observed previously [11–13]. This assertion can be statistically confirmed by evaluating the corresponding correlation coefficient  where the numerator describes the covariance and σ is the standard deviation. The results of this analysis as a function of Λ are shown in figure 2(a) which reveals that this metric tends to 1 indicating perfectly correlated vibrations between the symmetric and asymmetric modes.
where the numerator describes the covariance and σ is the standard deviation. The results of this analysis as a function of Λ are shown in figure 2(a) which reveals that this metric tends to 1 indicating perfectly correlated vibrations between the symmetric and asymmetric modes.
Figure 2. (a) The inset shows the phase portrait reconstructed from the numerically calculated cross-quadrature 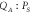 from equation (4) as a function of Λ, where this magnitude is colour coded in the main figure which details the corresponding correlation coefficient. (b) The inset shows the phase portrait reconstructed from the numerically calculated cross-quadrature
from equation (4) as a function of Λ, where this magnitude is colour coded in the main figure which details the corresponding correlation coefficient. (b) The inset shows the phase portrait reconstructed from the numerically calculated cross-quadrature  from equation (4) with
from equation (4) with 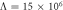 as function of both
as function of both 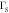 and
and  whose magnitudes are colour coded in the main figure which details the corresponding correlation coefficient. This analysis reveals that the weak correlation generated via the non-degenerate parametric down-conversion can be enhanced by the degenerate parametric amplification of the constituent modes and can even be made perfect when
whose magnitudes are colour coded in the main figure which details the corresponding correlation coefficient. This analysis reveals that the weak correlation generated via the non-degenerate parametric down-conversion can be enhanced by the degenerate parametric amplification of the constituent modes and can even be made perfect when 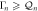 namely via their parametric resonance. (c) The analytically derived correlation coefficient between the cross-quadrature
namely via their parametric resonance. (c) The analytically derived correlation coefficient between the cross-quadrature 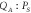 as function of pump intensity (
as function of pump intensity (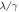 ) for degenerate parametric amplification ranging from
) for degenerate parametric amplification ranging from 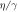 = 0–0.9 in 0.1 increments to 0.975. Even a weak correlation from
= 0–0.9 in 0.1 increments to 0.975. Even a weak correlation from  can be enhanced via
can be enhanced via  and be made perfect i.e. 1 via the degenerate parametric amplification with
and be made perfect i.e. 1 via the degenerate parametric amplification with 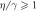 .
.
Download figure:
Standard image High-resolution imageGiven the system Hamiltonian in equation (1), it is interesting to investigate how the two-mode squeezed states behave in the presence of degenerate parametric amplification namely 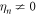 . To that end a value of Λ is selected that yields a weakly correlated state and then equations (4) are solved again but now as function of
. To that end a value of Λ is selected that yields a weakly correlated state and then equations (4) are solved again but now as function of 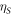 and
and 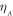 which are both simultaneously increased to the threshold for parametric resonance i.e.
which are both simultaneously increased to the threshold for parametric resonance i.e.  [15]. Again the cross-quadratures from the resultant
[15]. Again the cross-quadratures from the resultant 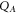 and
and 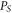 solutions are reconstructed in phase space and the corresponding correlation coefficient is also extracted with both being shown in figure 2(b). The numerical simulations reveal that even weak correlations generated between the two modes from Λ can be enhanced via
solutions are reconstructed in phase space and the corresponding correlation coefficient is also extracted with both being shown in figure 2(b). The numerical simulations reveal that even weak correlations generated between the two modes from Λ can be enhanced via 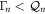 namely in the amplification regime and even be made perfect when
namely in the amplification regime and even be made perfect when 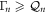 that is when both constituent modes parametrically resonate.
that is when both constituent modes parametrically resonate.
3.2. Analytical solutions
To confirm that the enhancement in the two-mode squeezing via degenerate parametric amplification is not an artefact of the numerical simulations, the equations of motion in (4) are also analytically solved with 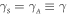 and
and 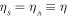 . The Langevin equations in this form can then be solved by linear combinations of variables
. The Langevin equations in this form can then be solved by linear combinations of variables 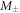 and
and 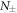 which are defined as
which are defined as
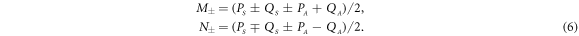
From equations (4) and (6), four independent Langevin equations can then be derived as
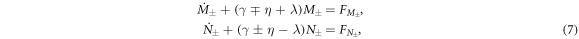
where the decomposed thermal Langevin forces are now given by
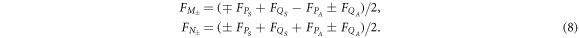
Consequently the correlation functions for variables 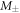 and
and 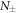 , driven by the thermal Langevin forces
, driven by the thermal Langevin forces 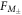 and
and  respectively, can then readily be extracted as
respectively, can then readily be extracted as

where kB is the Boltzmann constant, T is the temperature and the frequency difference between the two modes is assumed to be small so that 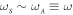 . The correlation coefficient between the cross-quadratures
. The correlation coefficient between the cross-quadratures 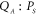 , for instance, can then be analytically derived using equations (6) and (9) which yields
, for instance, can then be analytically derived using equations (6) and (9) which yields

The resultant correlation coefficient as a function of the non-degenerate parametric pump intensity 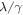 for a range of degenerate parametric amplification amplitudes
for a range of degenerate parametric amplification amplitudes 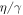 is plotted in figure 2(c). This reveals that the analytical solutions confirm the numerical results namely even weak correlations from the two-mode squeezing can be enhanced and made perfect by the degenerate parametric amplification and resonance of the constituent modes.
is plotted in figure 2(c). This reveals that the analytical solutions confirm the numerical results namely even weak correlations from the two-mode squeezing can be enhanced and made perfect by the degenerate parametric amplification and resonance of the constituent modes.
3.3. Physical interpretation
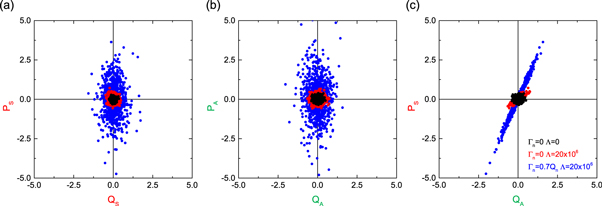
The above numerical and analytical analysis can be more intuitively interpreted as follows: the non-degenerate parametric down-conversion not only amplifies the constituent modes, leading to larger circular distributions in phase-space for both modes (see red points in figures 3(a) and (b)), but it also creates a two-mode squeezed state which can be resolved in the cross-quadrature phase portrait (see red points in figure 3(c)). On the other hand the degenerate parametric amplification of both modes is phase sensitive and it amplifies the quadrature component while the in-phase component is nominally unaffected (see blue points in figures 3(a) and (b)). Note the degenerate parametric amplification can yield squeezing below the thermal noise in the in-phase components of both modes with more modest 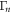 excitations. Alternatively the in-phase component can also be amplified while the quadrature component is squeezed, or any arbitrary orthogonal combination in phase space, by simply adjusting the phase of the degenerate parametric amplification. The cross-quadrature phase portrait reconstructed from the non-degenerate parametric down-conversion with degenerate parametric amplification exhibits further squeezing (see blue points in figure 3(c)). This effect is identified as enhanced correlations between the modes as quantified by the correlation coefficient in figure 2(b). This enhancement is a consequence of the squashed thermal fluctuation distributions of the constituent modes where the quadrature components are stretched and these underlying geometries naturally lead to narrower two-mode squeezed distributions.
excitations. Alternatively the in-phase component can also be amplified while the quadrature component is squeezed, or any arbitrary orthogonal combination in phase space, by simply adjusting the phase of the degenerate parametric amplification. The cross-quadrature phase portrait reconstructed from the non-degenerate parametric down-conversion with degenerate parametric amplification exhibits further squeezing (see blue points in figure 3(c)). This effect is identified as enhanced correlations between the modes as quantified by the correlation coefficient in figure 2(b). This enhancement is a consequence of the squashed thermal fluctuation distributions of the constituent modes where the quadrature components are stretched and these underlying geometries naturally lead to narrower two-mode squeezed distributions.
Figure 3. (a) and (b) The phase portraits of the symmetric and asymmetric modes numerically calculated from equation (4) with  = 0, Λ = 0 yielding their thermal noise distribution (black points). Activating non-degenerate parametric down-conversion with
= 0, Λ = 0 yielding their thermal noise distribution (black points). Activating non-degenerate parametric down-conversion with 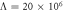 phase insensitively amplifies the thermal distribution of both modes (red points). Activating degenerate parametric amplification simultaneously in both modes with
phase insensitively amplifies the thermal distribution of both modes (red points). Activating degenerate parametric amplification simultaneously in both modes with 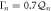 phase sensitively amplifies the non-degenerately amplified thermal noise with large gain in the quadrature component and negligible gain in the in-phase component yielding squashed distributions (blue points). (c) The cross-quadrature phase portrait
phase sensitively amplifies the non-degenerately amplified thermal noise with large gain in the quadrature component and negligible gain in the in-phase component yielding squashed distributions (blue points). (c) The cross-quadrature phase portrait 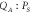 reconstructed from the above calculations reveals that the two-mode squeezed state from the non-degenerate parametric down-conversion is enhanced via the degenerate parametric amplification as evidenced by the narrower and more squashed distribution (blue points) with respect to the latter (red points).
reconstructed from the above calculations reveals that the two-mode squeezed state from the non-degenerate parametric down-conversion is enhanced via the degenerate parametric amplification as evidenced by the narrower and more squashed distribution (blue points) with respect to the latter (red points).
Download figure:
Standard image High-resolution image4. Results
Before these expectations can be tested, the availability of thermomechanical two-mode squeezed states in this electromechanical system needs to be verified. To that end, the spring constant of both modes is pumped with voltage  which simultaneously amplifies the thermomechanical displacement fluctuations of both modes as shown in figure 1(b) [27]. In this configuration all four in-phase and quadrature components of the fluctuations from both modes are simultaneously acquired over a period of 300 s with a 50 ms sampling rate. From this measurement the phase portrait from the cross-quadrature
which simultaneously amplifies the thermomechanical displacement fluctuations of both modes as shown in figure 1(b) [27]. In this configuration all four in-phase and quadrature components of the fluctuations from both modes are simultaneously acquired over a period of 300 s with a 50 ms sampling rate. From this measurement the phase portrait from the cross-quadrature 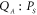 can be reconstructed and the corresponding correlation coefficient (from both sets of cross-quadratures) can be extracted, as a function of pump voltage, and is shown in figure 4(a). The phase portrait reveals a squashed distribution which implies that the motion from both modes is intertwined and this is statistically confirmed from the correlation coefficient which tends to 0.9 as
can be reconstructed and the corresponding correlation coefficient (from both sets of cross-quadratures) can be extracted, as a function of pump voltage, and is shown in figure 4(a). The phase portrait reveals a squashed distribution which implies that the motion from both modes is intertwined and this is statistically confirmed from the correlation coefficient which tends to 0.9 as 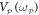 approaches 500 mVrms. However when
approaches 500 mVrms. However when 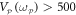 mVrms, both modes begin to self-oscillate and amplification due to non-degenerate parametric down-conversion is no longer available [11, 28, 29]. The phase portrait shown in the inset to figure 4(a) also enables the noise squeezing below the thermal level to be quantified as detailed in [11]. In this case starting with thermal populations of approximately 107 phonons in each mode at 300 K with
mVrms, both modes begin to self-oscillate and amplification due to non-degenerate parametric down-conversion is no longer available [11, 28, 29]. The phase portrait shown in the inset to figure 4(a) also enables the noise squeezing below the thermal level to be quantified as detailed in [11]. In this case starting with thermal populations of approximately 107 phonons in each mode at 300 K with 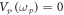 Vrms (black points in the inset to figure 4(a)), noise squeezing of −1.55 dB below the thermal level is achieved with
Vrms (black points in the inset to figure 4(a)), noise squeezing of −1.55 dB below the thermal level is achieved with 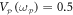 Vrms (red points in the inset to figure 4(a)).
Vrms (red points in the inset to figure 4(a)).
Figure 4. (a) The inset shows the phase portrait reconstructed from the cross-quadrature 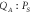 with
with 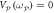 and 0.5 Vrms and are colour coded in the main figure which details the corresponding correlation coefficient (points). This reveals that the two modes become almost indistinguishable as the pump amplitude is increased. Also shown is the correlation coefficient extracted from the numerical simulations where Λ is used as a fitting parameter (line). (b) The inset shows the
and 0.5 Vrms and are colour coded in the main figure which details the corresponding correlation coefficient (points). This reveals that the two modes become almost indistinguishable as the pump amplitude is increased. Also shown is the correlation coefficient extracted from the numerical simulations where Λ is used as a fitting parameter (line). (b) The inset shows the 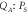 phase portrait measured on-resonance with
phase portrait measured on-resonance with 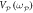 = 0.2Vrms (blue points). The initially weak squeezing can be enhanced with the degenerate parametric amplification of both modes whose magnitude is colour coded in the main figure which details the corresponding correlation coefficient (points) and it statistically confirms the enhancement from this process. Also shown is the correlation coefficient extracted from the numerical simulations as a function of
= 0.2Vrms (blue points). The initially weak squeezing can be enhanced with the degenerate parametric amplification of both modes whose magnitude is colour coded in the main figure which details the corresponding correlation coefficient (points) and it statistically confirms the enhancement from this process. Also shown is the correlation coefficient extracted from the numerical simulations as a function of 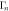 where
where  (line).
(line).
Download figure:
Standard image High-resolution imageNext the correlations between the two modes generated from the non-degenerate parametric down-conversion are experimentally investigated while undergoing degenerate parametric amplification. To that end first a weakly correlated state is created with 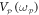 = 0.2 Vrms and then
= 0.2 Vrms and then 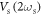 and
and 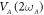 are both simultaneously increased from 0 to 0.35 Vrms in 0.05 Vrms increments. The cross-quadrature phase portrait from
are both simultaneously increased from 0 to 0.35 Vrms in 0.05 Vrms increments. The cross-quadrature phase portrait from 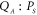 reconstructed from this measurement reveals that the initially weakly correlated symmetric and asymmetric modes becoming more strongly entwined as evidenced by the increasingly squashed distribution and this is quantitatively confirmed via their correlation coefficient which tends to unity as shown in figure 4(b). This measurement also yields enhanced squeezing of −3 dB below the thermal level when
reconstructed from this measurement reveals that the initially weakly correlated symmetric and asymmetric modes becoming more strongly entwined as evidenced by the increasingly squashed distribution and this is quantitatively confirmed via their correlation coefficient which tends to unity as shown in figure 4(b). This measurement also yields enhanced squeezing of −3 dB below the thermal level when 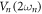 = 0.35 Vrms (red points in the inset to figure 4(b)). These experimental observations confirm the theoretical expectation in figure 2(b) and they naturally suggest the possibility of perfect correlations, even with
= 0.35 Vrms (red points in the inset to figure 4(b)). These experimental observations confirm the theoretical expectation in figure 2(b) and they naturally suggest the possibility of perfect correlations, even with 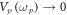 , if
, if 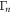 (from
(from 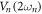 ) can be increased sufficiently as shown in figure 2(c).
) can be increased sufficiently as shown in figure 2(c).
Experimentally a large  implies that the thermal fluctuations of both modes are being degenerately amplified to such an extent that they parametrically resonate as, shown in figures 1(c) and (d), when
implies that the thermal fluctuations of both modes are being degenerately amplified to such an extent that they parametrically resonate as, shown in figures 1(c) and (d), when  Vrms and
Vrms and 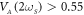 Vrms respectively [15, 23]. However a unique feature of the parametric resonance is that it can only vibrate with one of two phases separated by π radians [30]. Consequently the cross-quadrature phase portraits and indeed the language of two-mode squeezing is no longer available and relevant respectively in this regime as the steady state parametric resonances of the constituent modes with a particular phase will simply yield a single point far from the origin (the opposite phase will yield point with a π phase rotation) with almost no distribution as this vibration amplitude is orders of magnitude larger than both the thermomechanical noise of the mechanics and the electrical noise in the detection circuit see figures 1(c) and (d). Additionally the statistics of the resultant correlation will also be unavailable in this configuration as it essentially constitutes a single sample.
Vrms respectively [15, 23]. However a unique feature of the parametric resonance is that it can only vibrate with one of two phases separated by π radians [30]. Consequently the cross-quadrature phase portraits and indeed the language of two-mode squeezing is no longer available and relevant respectively in this regime as the steady state parametric resonances of the constituent modes with a particular phase will simply yield a single point far from the origin (the opposite phase will yield point with a π phase rotation) with almost no distribution as this vibration amplitude is orders of magnitude larger than both the thermomechanical noise of the mechanics and the electrical noise in the detection circuit see figures 1(c) and (d). Additionally the statistics of the resultant correlation will also be unavailable in this configuration as it essentially constitutes a single sample.
To that end an alternative strategy is developed where the bi-stable phase of the parametric resonance from both modes is monitored via the in-phase component of their vibrations. To observe this phase bi-stability, both modes are simultaneously and repeatedly activated via 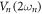 with a period of 0.3 Hz and the resultant in-phase components of their vibrations are monitored over a period of 1000 s and are shown in figure 5(a). This measurement confirms the phase bi-stability of the parametric resonance [15, 30] and it also indicates the absence of correlations between the modes as the choice of vibration phase in one of the modes is random and completely unrelated to the vibration phase in the other mode. On the other hand if this measurement is repeated in the presence of continuous-wave non-degenerate parametric down-conversion with
with a period of 0.3 Hz and the resultant in-phase components of their vibrations are monitored over a period of 1000 s and are shown in figure 5(a). This measurement confirms the phase bi-stability of the parametric resonance [15, 30] and it also indicates the absence of correlations between the modes as the choice of vibration phase in one of the modes is random and completely unrelated to the vibration phase in the other mode. On the other hand if this measurement is repeated in the presence of continuous-wave non-degenerate parametric down-conversion with 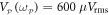 it results in the outputs shown in figure 5(b) which reveals that both modes always vibrate with same phase as the actuation of their degenerate parametric resonance is periodically modulated. This observation indicates that the two modes have become correlated from the non-degenerate parametric down-conversion and indeed the corresponding correlation coefficient extracted from this measurement yields a value of unity. Evaluating the correlation coefficient from this protocol as function of
it results in the outputs shown in figure 5(b) which reveals that both modes always vibrate with same phase as the actuation of their degenerate parametric resonance is periodically modulated. This observation indicates that the two modes have become correlated from the non-degenerate parametric down-conversion and indeed the corresponding correlation coefficient extracted from this measurement yields a value of unity. Evaluating the correlation coefficient from this protocol as function of 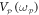 yields the data in figure 5(c) which indicates that correlations can be observed via the parametric resonances of both modes with a
yields the data in figure 5(c) which indicates that correlations can be observed via the parametric resonances of both modes with a 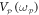 amplitude that is three orders of magnitude smaller than the equivalent measurement utilising thermomechanical noise fluctuations as shown in figure 4(a).
amplitude that is three orders of magnitude smaller than the equivalent measurement utilising thermomechanical noise fluctuations as shown in figure 4(a).
Figure 5. (a) The temporal response of the symmetric and asymmetric modes via the in-phase component of their parametric resonance, when both are simultaneously and periodically pulsed at 0.3 Hz with 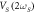 =
= 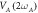 = 0.7 Vrms while
= 0.7 Vrms while 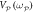 = 0 Vrms, reveals that the two modes always vibrate with phases whose polarity is random and independent of each other. (b) The temporal response of both modes acquired with the same conditions as in (a) but now with
= 0 Vrms, reveals that the two modes always vibrate with phases whose polarity is random and independent of each other. (b) The temporal response of both modes acquired with the same conditions as in (a) but now with 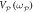 = 600 μVrms reveals that they always vibrate with same phase. (c) The correlation coefficient extracted from the switching outputs detailed above as a function of
= 600 μVrms reveals that they always vibrate with same phase. (c) The correlation coefficient extracted from the switching outputs detailed above as a function of 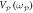 indicates that perfect correlations from non-degenerate parametric down-conversion can be accessed with a miniscule pump intensity namely three orders of magnitude smaller than in figure 4(a). Note the coloured points correspond to the data in (a) and (b) with the same colouration.
indicates that perfect correlations from non-degenerate parametric down-conversion can be accessed with a miniscule pump intensity namely three orders of magnitude smaller than in figure 4(a). Note the coloured points correspond to the data in (a) and (b) with the same colouration.
Download figure:
Standard image High-resolution imageAn intuitive insight to these observations can be gleaned by interpreting the non-degenerate parametric down-conversion, which generates phonons in the underlying modes at their natural frequency, as breaking symmetry of the double-well potentials which underpin the phase bi-stable parametric resonances [24]. This in turn results in a given mode preferentially vibrating with one of the two available phases. However since the parametric down-conversion simultaneously generates a pair of phonons in both modes, which are intertwined, this naturally results in the symmetry breaking in the double-well potential of the counterpart mode correlating with the first mode and it results in it vibrating with a coordinated phase.
5. Summary
The enhancement of thermomechanical two-mode squeezing, via phonon ensembles in two vibration modes, in an electromechanical system is investigated. Both numerical and analytical analysis indicates that the resultant squeezing can not only be enhanced via degenerate parametric amplification of the constituent modes but the resultant correlated mechanical vibrations can also be made more visible via their parametric resonance. The experimental measurements based on this analysis confirm these expectations where the non-degenerate parametric amplification amplitude necessary to generate correlations can be reduced by three orders of magnitude while simultaneously yielding bright and perfectly correlated vibrations in the underlying mechanical modes.
The ability to not only enhance the thermomechanical two-mode squeezed states via the degenerate parametric resonances of the constituent modes but also to simultaneously increase their visibility suggests an alternative approach to identifying mechanical vacuum squeezed states which could prove pivotal in detecting a macroscopic all-mechanical entanglement [21]. Meanwhile these protocols make the two-mode squeezing phenomenon with phonons in electromechanical systems [11–13] more widely available by bringing the resultant bright correlations, namely the classical analogue of entanglement, a step closer to being exploited in technological applications.
Acknowledgments
The authors are grateful to Y Ishikawa, K Onomitsu for growing the heterostructure. This work was partly supported by MEXT KAKENHI Grant No. 15H05869.