Abstract
The radical pair model of the avian magnetoreceptor relies on long-lived electron spin coherence. Dephasing, resulting from interactions of the spins with their fluctuating environment, is generally assumed to degrade the sensitivity of this compass to the direction of the Earth's magnetic field. Here we argue that certain spin relaxation mechanisms can enhance its performance. We focus on the flavin–tryptophan radical pair in cryptochrome, currently the only candidate magnetoreceptor molecule. Correlation functions for fluctuations in the distance between the two radicals in Arabidopsis thaliana cryptochrome 1 were obtained from molecular dynamics (MD) simulations and used to calculate the spin relaxation caused by modulation of the exchange and dipolar interactions. We find that intermediate spin relaxation rates afford substantial enhancements in the sensitivity of the reaction yields to an Earth-strength magnetic field. Supported by calculations using toy radical pair models, we argue that these enhancements could be consistent with the molecular dynamics and magnetic interactions in avian cryptochromes.
Export citation and abstract BibTeX RIS
1. Introduction
The rates and yields of free radical reactions are often sensitive to applied magnetic fields, a phenomenon known as the radical pair mechanism [1, 2]. It has been suggested [3] that migratory birds sense the direction of the Earth's magnetic field [4–7] by means of radical pairs formed photochemically in cryptochrome proteins located in their retinas [8]. Experimental and theoretical support for a radical pair mechanism of compass magnetoreception is accumulating (reviewed in [9–17]) although it is not yet clear whether cryptochrome is actually the sensor.
In vitro photo-excitation of the flavin adenine dinucleotide (FAD) cofactor in cryptochromes leads to the formation of radical pairs via sequential electron transfers along the 'Trp-triad', a chain of three tryptophan residues within the protein [18–21]. Donation of an electron to the excited singlet state of the FAD leads to the flavin radical, FAD•−, and the radical form of the terminal tryptophan,  (supplementary figure S1). This [FAD•−
(supplementary figure S1). This [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn2.gif) radical pair in both Arabidopsis thaliana cryptochrome-1 (AtCry1) and a closely related DNA photolyase has been shown to respond to weak magnetic fields (∼1 mT) and has at least some of the properties required of a magnetic compass sensor [22, 23]. The origin of the magnetic field effect lies in a combination of the spin dynamics of the radical pair and its spin-selective recombination reactions, figures 1(a) and (b) and supplementary figure S1 [9].
radical pair in both Arabidopsis thaliana cryptochrome-1 (AtCry1) and a closely related DNA photolyase has been shown to respond to weak magnetic fields (∼1 mT) and has at least some of the properties required of a magnetic compass sensor [22, 23]. The origin of the magnetic field effect lies in a combination of the spin dynamics of the radical pair and its spin-selective recombination reactions, figures 1(a) and (b) and supplementary figure S1 [9].
Figure 1. Radical pair reaction schemes. S and T are the singlet and triplet states of the radical pair. The curved orange arrows indicate the coherent interconversion of the S and T states by hyperfine and Zeeman interactions. kS, kT, kb, and kf are rate constants. The electron Zeeman interaction alters the extent and timing of S ↔ T interconversion in the radical pair so that the final yields of the reaction products, once all the radicals have reacted, depend on the orientation of the radical pair with respect to the magnetic field. (a) A generic radical pair reaction scheme in which the S and T states are able to react spin-selectively to form singlet and triplet products, PS and PT, respectively. (b) A reaction scheme for [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn3.gif) (RP1) in AtCry1 in which triplet recombination cannot occur. Instead, the S and T states undergo a non-spin-selective reaction (protonation of FAD•−, deprotonation of
(RP1) in AtCry1 in which triplet recombination cannot occur. Instead, the S and T states undergo a non-spin-selective reaction (protonation of FAD•−, deprotonation of  or both) with the same rate constant to form a product PF. (c) An extension of (b) in which RP0 ([FAD•−
or both) with the same rate constant to form a product PF. (c) An extension of (b) in which RP0 ([FAD•− ![${{{\rm{TrpH}}}_{{\rm{B}}}}^{\bullet +}])$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn5.gif) is formed reversibly by electron hopping (TrpHB
is formed reversibly by electron hopping (TrpHB 
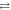
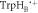 TrpHC) during the lifetime of RP1. In both (b) and (c), the singlet product, PS, is the ground state of the protein.
TrpHC) during the lifetime of RP1. In both (b) and (c), the singlet product, PS, is the ground state of the protein.
Download figure:
Standard image High-resolution imageVarious spin interactions determine the magnetic field effect. The hyperfine interactions [24] of the electron spins with magnetic nuclei (mainly 1H and 14N) result in coherent, oscillatory interconversion of the electronic singlet and triplet states of the radical pair. The electronic Zeeman interaction with the external magnetic field modifies this time-dependence, altering the probability of spin-dependent radical recombination and changing the yields of the reaction products (figures 1(a) and (b)). The anisotropy of the hyperfine interactions causes the effect of the external field to depend on its direction, as required for a compass sensor. Two other important interactions—usually neglected in this context—are the electron–electron exchange and dipolar couplings [25, 26], both of which depend on r, the distance between the centres of electron spin density in the two radicals. The exchange interaction is usually assumed to have the exponential form:
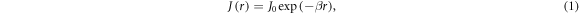
with a range parameter β = 14 nm−1 for radicals embedded in a protein [25, 27]. The strength of the interaction, J0, has a complex dependence on the electronic properties of the radicals and is difficult to calculate with any accuracy. The dipolar interaction, however, can reliably be obtained by assuming the electron spins to be point dipoles (normally an excellent approximation for radical pairs [25]):
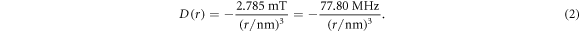
In the absence of other spin interactions, J(r) and D(r) remove the degeneracy of the singlet (S) and the three triplet (T+1, T0, T−1) states:
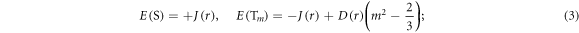
(m, the magnetic quantum number of the triplet, equals 0 or ±1). These interactions hinder efficient singlet–triplet interconversion and so degrade the sensitivity of the radical pair to the geomagnetic field [25].
The magnetically sensitive [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn9.gif) radical pair in AtCry1 [23] has r = 1.90 nm [28], giving D(r) = −11 MHz and
radical pair in AtCry1 [23] has r = 1.90 nm [28], giving D(r) = −11 MHz and 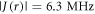 (assuming
(assuming 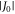 ≈ 8.0 × 107 T and β = 14 nm−1 [25]). Experimental measurements of J(r) for [FAD•−
≈ 8.0 × 107 T and β = 14 nm−1 [25]). Experimental measurements of J(r) for [FAD•− 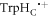 ] in two DASH-type cryptochromes are in rough agreement with this estimate: +2.0 MHz for Xenopus laevis [29] and +4.2 MHz for Synechocystis [30]. A more exact calculation of D(r), avoiding the point-dipole approximation, confirmed the −11 MHz value to within 0.6 MHz [25]. It is therefore clear that both
] in two DASH-type cryptochromes are in rough agreement with this estimate: +2.0 MHz for Xenopus laevis [29] and +4.2 MHz for Synechocystis [30]. A more exact calculation of D(r), avoiding the point-dipole approximation, confirmed the −11 MHz value to within 0.6 MHz [25]. It is therefore clear that both 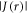 and
and 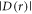 are likely to be larger than the electron Zeeman interaction (∼1.4 MHz) with the Earth's magnetic field (∼50 μT), and cannot therefore be dismissed.
are likely to be larger than the electron Zeeman interaction (∼1.4 MHz) with the Earth's magnetic field (∼50 μT), and cannot therefore be dismissed.
Although values of 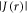 or
or 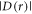 larger than a few MHz would be sufficient to mar the performance of a radical pair as a geomagnetic sensor, the effects of the two interactions can partially cancel under certain circumstances, specifically when D(r)/J(r) ≈ +6 or −3 [25]. Using estimates of
larger than a few MHz would be sufficient to mar the performance of a radical pair as a geomagnetic sensor, the effects of the two interactions can partially cancel under certain circumstances, specifically when D(r)/J(r) ≈ +6 or −3 [25]. Using estimates of 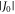 derived from data on photosynthetic reaction centre proteins [31–33], it has been argued that such ratios can be expected when r ≈ 2.0 ± 0.2 nm, i.e. a separation close to that of FAD•− and
derived from data on photosynthetic reaction centre proteins [31–33], it has been argued that such ratios can be expected when r ≈ 2.0 ± 0.2 nm, i.e. a separation close to that of FAD•− and 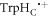 in cryptochromes (∼1.9 nm) [25]. However, the values of J(r) and D(r) are not known for any of the four avian cryptochromes, and it has not been established how effective the cancellation would be for radicals as complex as flavin and tryptophan. It is therefore appropriate to ask whether the damaging effects of J(r) and D(r) could be circumvented in some other way. One possibility, discussed later, is that 'the quantum Zeno effect immunises the avian compass against the deleterious effects of exchange and dipolar interactions' [34]. Here, we examine whether electron spin relaxation could come to the rescue.
in cryptochromes (∼1.9 nm) [25]. However, the values of J(r) and D(r) are not known for any of the four avian cryptochromes, and it has not been established how effective the cancellation would be for radicals as complex as flavin and tryptophan. It is therefore appropriate to ask whether the damaging effects of J(r) and D(r) could be circumvented in some other way. One possibility, discussed later, is that 'the quantum Zeno effect immunises the avian compass against the deleterious effects of exchange and dipolar interactions' [34]. Here, we examine whether electron spin relaxation could come to the rescue.
Spin relaxation, the process that drives the electron–nuclear spin system of the radical pair towards thermal equilibrium [24], is normally expected to attenuate the sensitivity of the compass by destroying the spin coherence that is essential for its operation [35]. It seems plausible that the optimum performance would require negligible loss of coherence during the lifetime of the radical pair. There have been several theoretical treatments of spin relaxation in the context of magnetoreception, almost all of which have dealt with generic relaxation mechanisms furnished with phenomenological rate constants [36–41]. Intriguingly, a few of these studies have indicated that the compass sensitivity could be enhanced by the inclusion of certain abstract spin relaxation pathways [37, 38, 40, 42, 43]. In the following, we discuss the spin relaxation that arises from realistic spin interactions modulated by realistic protein dynamics. Specifically, we show that the time dependence of J(r) and D(r) arising from stochastic fluctuations in the separation of the FAD•− and 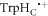 radicals in cryptochrome has the potential to boost the magnetic field effect and so counteract the detrimental effects these interactions would have in the absence of molecular motion.
radicals in cryptochrome has the potential to boost the magnetic field effect and so counteract the detrimental effects these interactions would have in the absence of molecular motion.
2. J-modulation by fluctuations in r
We start by establishing the principle that the harmful effect of an exchange interaction on a radical pair compass can be alleviated by fluctuations in the strength of that interaction. To do so, we chose the simplest possible radical pair comprising two electron spins, one of which is coupled to a single spin- nucleus via an anisotropic hyperfine interaction. The eigenvalues of the anisotropic hyperfine tensor [24],
nucleus via an anisotropic hyperfine interaction. The eigenvalues of the anisotropic hyperfine tensor [24], 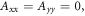
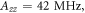 were chosen to resemble the hyperfine tensor of the N5 interaction in FAD•− [44]. Singlet and triplet pairs were allowed to react to form distinct products (figure 1(a)) with identical rate constants, k = kS = kT = 106 s−1, such that the radical pair lifetime was 1 μs. At time t = 0, the radical pair was in a pure singlet state with no nuclear polarisation. The performance of this toy compass was judged by the anisotropy of the singlet yield:
were chosen to resemble the hyperfine tensor of the N5 interaction in FAD•− [44]. Singlet and triplet pairs were allowed to react to form distinct products (figure 1(a)) with identical rate constants, k = kS = kT = 106 s−1, such that the radical pair lifetime was 1 μs. At time t = 0, the radical pair was in a pure singlet state with no nuclear polarisation. The performance of this toy compass was judged by the anisotropy of the singlet yield:

where 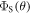 is the final yield of the singlet product (PS in figure 1(a)) and θ is the angle between the external magnetic field (50 μT) and the symmetry axis of the hyperfine tensor.
is the final yield of the singlet product (PS in figure 1(a)) and θ is the angle between the external magnetic field (50 μT) and the symmetry axis of the hyperfine tensor.
 was determined using the equation of motion for the radical pair density operator,
was determined using the equation of motion for the radical pair density operator, 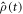 :
:
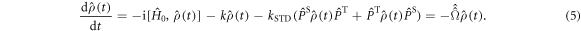
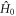 is the time-independent part of the spin Hamiltonian:
is the time-independent part of the spin Hamiltonian:

in which the three terms are, respectively, the electron Zeeman, electron–nuclear hyperfine, and average exchange interactions. 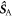 and
and 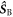 are the electron spin angular momentum operators of the two radicals, and
are the electron spin angular momentum operators of the two radicals, and 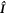 is the spin operator of the nucleus in radical A.
is the spin operator of the nucleus in radical A. 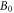 = 50 μT is the strength of the external magnetic field. The other terms in equation (5) account for the radical recombination reactions and the effects of fluctuations in J(r). The latter is derived in appendix
= 50 μT is the strength of the external magnetic field. The other terms in equation (5) account for the radical recombination reactions and the effects of fluctuations in J(r). The latter is derived in appendix 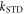 is the rate constant of the spin relaxation caused by J-modulation, and
is the rate constant of the spin relaxation caused by J-modulation, and 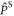 and
and 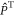 are the singlet and triplet projection operators. If the fluctuations in the exchange interaction occur on a faster timescale than the coherent spin dynamics,
are the singlet and triplet projection operators. If the fluctuations in the exchange interaction occur on a faster timescale than the coherent spin dynamics, 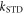 is given by (appendix
is given by (appendix
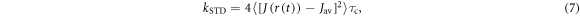
where  indicates a time average,
indicates a time average,  =
= 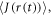 and the correlation time
and the correlation time  characterises the timescale of the fluctuations in r. The rate of relaxation is thus proportional to the mean square deviation of the exchange parameter from its mean value and is faster the slower the fluctuations. It is clear from equation (5) that J-modulation relaxes density matrix elements of the type
characterises the timescale of the fluctuations in r. The rate of relaxation is thus proportional to the mean square deviation of the exchange parameter from its mean value and is faster the slower the fluctuations. It is clear from equation (5) that J-modulation relaxes density matrix elements of the type 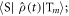 it is therefore referred to as a 'singlet–triplet dephasing' (STD) mechanism [45]. We note that the relaxation term in equation (5) can also be obtained phenomenologically using Lindblad noise operators,
it is therefore referred to as a 'singlet–triplet dephasing' (STD) mechanism [45]. We note that the relaxation term in equation (5) can also be obtained phenomenologically using Lindblad noise operators, 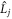 [36, 46]:
[36, 46]:
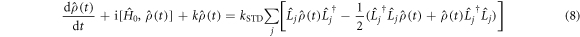
with 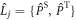 or
or 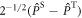 .
.
Finally, the singlet yield once all radicals have recombined is:
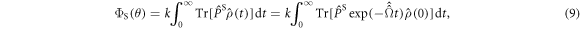
where the superoperator 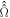 is defined in equation (5) and
is defined in equation (5) and 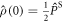 .
.
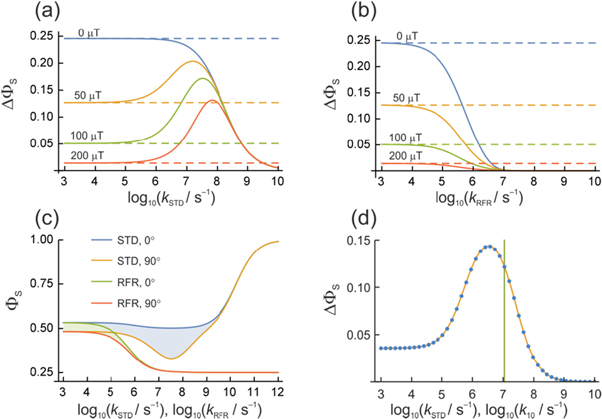
Figure 2(a) plots the anisotropy 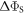 (equation (4)) versus
(equation (4)) versus 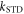 for four values of
for four values of 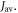 When
When 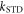 is small (e.g. 103 s−1), there is essentially no relaxation during the 1 μs lifetime of the radicals. In this limit,
is small (e.g. 103 s−1), there is essentially no relaxation during the 1 μs lifetime of the radicals. In this limit, 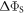 is dramatically reduced when the average exchange interaction is comparable to or stronger than the geomagnetic field (50 μT). However, when
is dramatically reduced when the average exchange interaction is comparable to or stronger than the geomagnetic field (50 μT). However, when 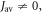 values of
values of 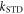 greater than ∼106 s−1 cause ΔΦS to rise towards the values appropriate for
greater than ∼106 s−1 cause ΔΦS to rise towards the values appropriate for 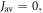 When the relaxation is faster still (
When the relaxation is faster still (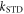 > 108 s−1),
> 108 s−1), 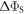 drops towards zero. Fluctuations in J(r) resulting in intermediate relaxation rates (106 s−1 <
drops towards zero. Fluctuations in J(r) resulting in intermediate relaxation rates (106 s−1 < 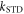 < 108 s−1) therefore boost the compass sensitivity well above the level expected for a time-independent exchange interaction (dashed lines in figure 2(a)). Similar behaviour was found for modulation of the dipolar interaction (appendix
< 108 s−1) therefore boost the compass sensitivity well above the level expected for a time-independent exchange interaction (dashed lines in figure 2(a)). Similar behaviour was found for modulation of the dipolar interaction (appendix
Figure 2. Anisotropy of the singlet yield 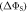 of a toy radical pair as a function of the spin relaxation rate constant. The solid lines in (a) and (b) show
of a toy radical pair as a function of the spin relaxation rate constant. The solid lines in (a) and (b) show 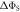 (equation (4)) for the STD and RFR mechanisms, respectively, for four values of Jav. The dashed lines are
(equation (4)) for the STD and RFR mechanisms, respectively, for four values of Jav. The dashed lines are 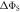 in the absence of spin relaxation. (c) The singlet yield,
in the absence of spin relaxation. (c) The singlet yield, 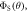 when the magnetic field is parallel
when the magnetic field is parallel 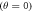 and perpendicular
and perpendicular 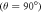 to the symmetry axis of the hyperfine interaction, for the STD and RFR mechanisms with Jav = 100 μT. (d)
to the symmetry axis of the hyperfine interaction, for the STD and RFR mechanisms with Jav = 100 μT. (d) 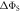 for the STD relaxation mechanism induced by electron hopping. Blue dots:
for the STD relaxation mechanism induced by electron hopping. Blue dots: 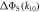 calculated with explicit two-site electron hopping; orange line:
calculated with explicit two-site electron hopping; orange line: 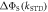 calculated using equation (9). The green line indicates the value of k10 (1.1 × 107 s−1) determined from experiments on AtCry1 [23]. (a)–(c) D = 0, magnetic field = 50 μT, principal components of the hyperfine interaction, (Axx, Ayy, Azz) = (0.0, 0.0, +1.5) mT, recombination rate constants = kS = kT = 106 s−1 (figure 1(a)). (d) As for (a)–(c), with J(RP0) = 800 mT, J(RP)1 = 0.1 mT, k01 = 1.0 × 1010 s–1, kb = 4.9 × 105 s–1, kf = 2.5 × 105 s−1 (see figure 1(b) for definitions of the rate constants).
calculated using equation (9). The green line indicates the value of k10 (1.1 × 107 s−1) determined from experiments on AtCry1 [23]. (a)–(c) D = 0, magnetic field = 50 μT, principal components of the hyperfine interaction, (Axx, Ayy, Azz) = (0.0, 0.0, +1.5) mT, recombination rate constants = kS = kT = 106 s−1 (figure 1(a)). (d) As for (a)–(c), with J(RP0) = 800 mT, J(RP)1 = 0.1 mT, k01 = 1.0 × 1010 s–1, kb = 4.9 × 105 s–1, kf = 2.5 × 105 s−1 (see figure 1(b) for definitions of the rate constants).
Download figure:
Standard image High-resolution imageTo put figure 2(a) in context, J-modulation was compared with a 'random fields' relaxation (RFR) mechanism in which unspecified, uncorrelated molecular motions cause the expectation values of all three spin angular momentum operators (
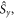 and
and 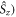 of both electrons to relax independently with the same rate constant,
of both electrons to relax independently with the same rate constant, 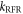 (appendix
(appendix 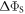 but causes it to fall towards zero at much smaller values of the rate constant than was the case in figure 2(a). Clearly, not all relaxation mechanisms are able to rescue the sensitivity of a radical pair compass.
but causes it to fall towards zero at much smaller values of the rate constant than was the case in figure 2(a). Clearly, not all relaxation mechanisms are able to rescue the sensitivity of a radical pair compass.
To shed light on the differences between figures 2(a) and (b), figure 2(c) plots 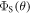 for
for  and
and 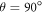 as a function of the relaxation rate constant for the two mechanisms (with
as a function of the relaxation rate constant for the two mechanisms (with 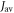 = 100 μT). It can be seen that very fast relaxation (>1010 s−1) destroys the anisotropy either by locking the radical pair into its initial singlet state (STD) or by relaxing the spins to the equilibrium state in which the singlet probability is 0.25 (RFR). For rate constants between 106 s−1 and 108 s−1, STD is much less effective at relaxing
= 100 μT). It can be seen that very fast relaxation (>1010 s−1) destroys the anisotropy either by locking the radical pair into its initial singlet state (STD) or by relaxing the spins to the equilibrium state in which the singlet probability is 0.25 (RFR). For rate constants between 106 s−1 and 108 s−1, STD is much less effective at relaxing 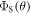 towards 0.25 when the magnetic field is parallel to the hyperfine axis (
towards 0.25 when the magnetic field is parallel to the hyperfine axis (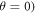 than when it is perpendicular (
than when it is perpendicular (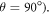 For the STD mechanism, therefore, the anisotropy in the reaction yield is considerably larger when 106 s−1
For the STD mechanism, therefore, the anisotropy in the reaction yield is considerably larger when 106 s−1 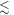
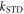
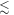 108 s−1 than in the absence of relaxation (
108 s−1 than in the absence of relaxation ( < 104 s−1). The RFR mechanism, by contrast, relaxes the spins isotropically and so drives
< 104 s−1). The RFR mechanism, by contrast, relaxes the spins isotropically and so drives 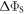 monotonically to zero as
monotonically to zero as 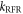 is increased.
is increased.
3. J-modulation by electron hopping
STD has been invoked to account for the observed magnetic-field dependence of the flavin–tryptophan radical pair reaction in AtCry1 [23]. J-modulation was considered to arise from reversible electron hopping between the distal and medial members of the Trp-triad, i.e. [FAD•− TrpHB 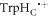 ]
] 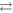 [FAD•−
[FAD•− 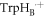 TrpHC] (figure 1(c)). As described above, the former (denoted RP1) has r1 = 1.90 nm and exchange and dipolar interactions of a few MHz; the latter (denoted RP0) has a centre-to-centre distance r0 = 1.32 nm in AtCry1 and estimated interactions:
TrpHC] (figure 1(c)). As described above, the former (denoted RP1) has r1 = 1.90 nm and exchange and dipolar interactions of a few MHz; the latter (denoted RP0) has a centre-to-centre distance r0 = 1.32 nm in AtCry1 and estimated interactions: 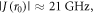 D(r0) = −34 MHz [25]. With such a large exchange interaction in RP0, reversible electron hopping results in strong modulation of
D(r0) = −34 MHz [25]. With such a large exchange interaction in RP0, reversible electron hopping results in strong modulation of 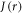 and potentially rapid relaxation of singlet–triplet coherences in RP1. Provided k01, the electron hopping rate constant for RP0 → RP1, is not much larger than
and potentially rapid relaxation of singlet–triplet coherences in RP1. Provided k01, the electron hopping rate constant for RP0 → RP1, is not much larger than 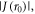 then every time RP1 is converted into RP0 the coherence experiences a large phase shift before the electron jumps back. Under these conditions, the dephasing rate constant kSTD in equation (5) is expected to be equal to k10, the rate constant for RP0 ← RP1 [23].
then every time RP1 is converted into RP0 the coherence experiences a large phase shift before the electron jumps back. Under these conditions, the dephasing rate constant kSTD in equation (5) is expected to be equal to k10, the rate constant for RP0 ← RP1 [23].
This prediction can be verified with a toy model similar to that used above. Figure 2(d) shows the singlet yield anisotropy determined (i) as a function of kSTD using equation (5) and (ii) as a function of k10 by solving a Liouville equation containing explicit reversible electron hopping between RP0 and RP1, coherent spin dynamics in both radical pairs, and spin-selective recombination for RP1 (figure 1(c) and appendix ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn89.gif) in AtCry1 [23]. The two calculations are in excellent agreement confirming that the dephasing rate constant is indeed given by k10. Note also that the value of k10 (= 1.1 × 107 s–1) determined from the magnetic field effects on AtCry1 [23] corresponds to a position in figure 2(d) close to the maximum enhancement of
in AtCry1 [23]. The two calculations are in excellent agreement confirming that the dephasing rate constant is indeed given by k10. Note also that the value of k10 (= 1.1 × 107 s–1) determined from the magnetic field effects on AtCry1 [23] corresponds to a position in figure 2(d) close to the maximum enhancement of 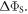 However, this should be treated with caution because of our use of a grossly simplified spin system for figure 2(d) (one nuclear spin instead of ∼10; eight spin states instead of ∼212).
However, this should be treated with caution because of our use of a grossly simplified spin system for figure 2(d) (one nuclear spin instead of ∼10; eight spin states instead of ∼212).
4. J-modulation in cryptochrome
We now turn to STD spin relaxation for the [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn91.gif) radical pair in cryptochrome. Fluctuations in the separation and relative orientation of the two radicals were characterised by means of all-atom molecular dynamics (MD) simulations [47]. The calculations were performed using a modified version of the crystal structure of AtCry1 (PDB ID 1U3C [28]) containing the flavin radical, FAD•−, and the radical form of the terminal residue of the Trp-triad,
radical pair in cryptochrome. Fluctuations in the separation and relative orientation of the two radicals were characterised by means of all-atom molecular dynamics (MD) simulations [47]. The calculations were performed using a modified version of the crystal structure of AtCry1 (PDB ID 1U3C [28]) containing the flavin radical, FAD•−, and the radical form of the terminal residue of the Trp-triad,  (W324) with force-field parameters and atomic charges as in [48]. The protein was solvated in an aqueous solution of 50 mM NaCl in a periodic box of dimensions 103 × 111 × 99 Å3 containing a total of 113 455 atoms. After extensive equilibration, seven statistically independent MD trajectories, three spanning 300 ns and four covering 100 ns, were accumulated for the microcanonical ensemble at 300 K. The initial configuration of the system was identical in the seven simulations; stochastic behaviour emerged from the Langevin thermostat [49], as implemented in NAMD [50]. The protein dynamics were sampled at intervals of 0.5 or 5 ps. The accumulated trajectories cover 1.3 μs. Because the motions of the radicals are considerably faster than both spin relaxation and radical recombination, it is not necessary for the simulations to include the reactions or to span the lifetime of the radicals. Electron hopping between TrpHB and TrpHC [23] was not included. Further details of the simulations can be found in [47].
(W324) with force-field parameters and atomic charges as in [48]. The protein was solvated in an aqueous solution of 50 mM NaCl in a periodic box of dimensions 103 × 111 × 99 Å3 containing a total of 113 455 atoms. After extensive equilibration, seven statistically independent MD trajectories, three spanning 300 ns and four covering 100 ns, were accumulated for the microcanonical ensemble at 300 K. The initial configuration of the system was identical in the seven simulations; stochastic behaviour emerged from the Langevin thermostat [49], as implemented in NAMD [50]. The protein dynamics were sampled at intervals of 0.5 or 5 ps. The accumulated trajectories cover 1.3 μs. Because the motions of the radicals are considerably faster than both spin relaxation and radical recombination, it is not necessary for the simulations to include the reactions or to span the lifetime of the radicals. Electron hopping between TrpHB and TrpHC [23] was not included. Further details of the simulations can be found in [47].
Motional correlation functions, calculated from the MD trajectories, were used to obtain spectral densities and hence a Redfield relaxation superoperator [51, 52] which, when combined with (i) electron Zeeman and hyperfine interactions, (ii) average exchange and dipolar interactions, and (iii) spin-selective recombination reactions, allowed calculation of the singlet yield 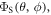 where the polar angles θ and ϕ specify the direction of the external 50 μT magnetic field (appendix
where the polar angles θ and ϕ specify the direction of the external 50 μT magnetic field (appendix  was calculated as the difference between the maximum and minimum values of
was calculated as the difference between the maximum and minimum values of  Spin relaxation induced by fluctuations in the hyperfine interactions was the subject of [47] and is not treated here. The forward electron transfer steps along the Trp-triad are complete within a nanosecond which is too fast for singlet–triplet coherence to be generated in the intermediate radical pairs [FAD•−
Spin relaxation induced by fluctuations in the hyperfine interactions was the subject of [47] and is not treated here. The forward electron transfer steps along the Trp-triad are complete within a nanosecond which is too fast for singlet–triplet coherence to be generated in the intermediate radical pairs [FAD•− ![${{{\rm{TrpH}}}_{{\rm{A}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn96.gif) and [FAD•−
and [FAD•− ![${{{\rm{TrpH}}}_{{\rm{B}}}}^{\bullet +}].$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn97.gif) Consequently, STD relaxation is expected to occur only in [FAD•−
Consequently, STD relaxation is expected to occur only in [FAD•− 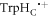 ].
].
Figures 3(a)–(c) show the variation in r, J(r) and D(r) over the course of MD trajectories spanning 1.3 μs in total. J(r) and D(r) were calculated using equations (1) and (2), with  = 8 × 107 T and β = 14 nm−1. The mean distance between the centres of spin density (± standard deviation; see supplementary figure S4) is rav = 1.89 ± 0.05 nm. The mean interaction strengths (± standard deviation) are
= 8 × 107 T and β = 14 nm−1. The mean distance between the centres of spin density (± standard deviation; see supplementary figure S4) is rav = 1.89 ± 0.05 nm. The mean interaction strengths (± standard deviation) are 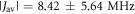 and
and 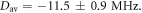 The maximum and minimum separations are rmax = 2.43 nm and rmin = 1.69 nm, so that
The maximum and minimum separations are rmax = 2.43 nm and rmin = 1.69 nm, so that 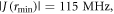
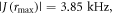 D(rmin) = −16.1 MHz, and
D(rmin) = −16.1 MHz, and  = −5.5 MHz.
= −5.5 MHz.
Figure 3. Variation in (a) the radical separation, (b) the exchange interaction and (c) the dipolar interaction of [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn105.gif) in AtCry1. The MD trajectories were sampled every 5 ps. The different colours indicate different MD runs starting from the same configuration. The horizontal lines in the three panels give the mean values: rav, Jav, and Dav. Shown on the right-hand side of (a)–(c) are the corresponding distribution functions. (d) Auto-correlation functions,
in AtCry1. The MD trajectories were sampled every 5 ps. The different colours indicate different MD runs starting from the same configuration. The horizontal lines in the three panels give the mean values: rav, Jav, and Dav. Shown on the right-hand side of (a)–(c) are the corresponding distribution functions. (d) Auto-correlation functions, 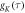 (equation (10)), for the exchange (pink) and dipolar (green) interactions in [FAD•− TrpH•+] in AtCry1, calculated from the MD trajectories. The dashed black lines are the multi-exponential fits used to calculate the relaxation superoperator; both have been extrapolated back to τ = 100 fs.
(equation (10)), for the exchange (pink) and dipolar (green) interactions in [FAD•− TrpH•+] in AtCry1, calculated from the MD trajectories. The dashed black lines are the multi-exponential fits used to calculate the relaxation superoperator; both have been extrapolated back to τ = 100 fs.  decays to ∼0.79 within the first 500 fs; motions on this timescale are far too fast to cause spin relaxation.
decays to ∼0.79 within the first 500 fs; motions on this timescale are far too fast to cause spin relaxation.
Download figure:
Standard image High-resolution imageFigure 4 gives an impression of the positions of the two radicals in AtCry1 in the average structure and in the two extreme conformations, r = rmin and r = rmax. The variation in the radical separation is mainly attributable to the greater mobility of the  radical compared to the more snugly bound FAD•− radical located in the centre of the protein. Representations of the semi-occupied molecular orbitals and the spin densities in the two radicals are shown in supplementary figure S4.
radical compared to the more snugly bound FAD•− radical located in the centre of the protein. Representations of the semi-occupied molecular orbitals and the spin densities in the two radicals are shown in supplementary figure S4.
Figure 4. Molecular dynamics structures of AtCry1 in the region of the FAD and Trp triad. The positions of the two components of the radical pair (FAD•− and  the proximal and medial tryptophans (TrpHA and TrpHB), and the backbone in the average structure (rav = 1.89 nm) are shown in green and grey. The positions of the two radicals, and the backbone in the region of
the proximal and medial tryptophans (TrpHA and TrpHB), and the backbone in the average structure (rav = 1.89 nm) are shown in green and grey. The positions of the two radicals, and the backbone in the region of 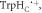 are shown in red and blue for the structures with, respectively, the largest (rmax = 2.43 nm) and smallest (rmin = 1.69 nm) radical separations. The curved arrow indicates the range of motion of
are shown in red and blue for the structures with, respectively, the largest (rmax = 2.43 nm) and smallest (rmin = 1.69 nm) radical separations. The curved arrow indicates the range of motion of 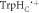 .
.
Download figure:
Standard image High-resolution imageGiven the uncertainty in the value of J0 (equation (1)), we henceforth treat 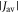 as an adjustable parameter and model the exchange interaction as
as an adjustable parameter and model the exchange interaction as 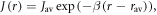 with β = 14 nm−1 and rav = 1.89 nm as above. Except for very small values of
with β = 14 nm−1 and rav = 1.89 nm as above. Except for very small values of 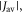 the fluctuations in
the fluctuations in 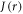 are much larger than those in
are much larger than those in 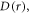 meaning that J-modulation should be the dominant source of spin relaxation.
meaning that J-modulation should be the dominant source of spin relaxation.
The auto-correlation functions
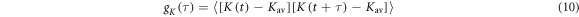
(K = r, J, or D, and  that characterise the relevant motions of the radical pair are highly non-exponential as a result of motions on timescales ranging from picoseconds to nanoseconds (figure 3(d)). The average time constant for the decay of
that characterise the relevant motions of the radical pair are highly non-exponential as a result of motions on timescales ranging from picoseconds to nanoseconds (figure 3(d)). The average time constant for the decay of 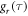 (8.5 ns) is determined mainly by low-amplitude components in the range τ ≥ 10 ns. In combination with the large fluctuations in
(8.5 ns) is determined mainly by low-amplitude components in the range τ ≥ 10 ns. In combination with the large fluctuations in  noted above, these comparatively slow motions tend to dominate the spin relaxation. By contrast, the rapidly decaying components of
noted above, these comparatively slow motions tend to dominate the spin relaxation. By contrast, the rapidly decaying components of 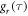 (τ < 500 fs) are of minor importance. The average time constants for
(τ < 500 fs) are of minor importance. The average time constants for 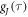 and
and 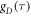 are 8.5 ns and 7.6 ns, respectively, reflecting the different r-dependence of the two interactions.
are 8.5 ns and 7.6 ns, respectively, reflecting the different r-dependence of the two interactions.
Figures 5(a) and (b) show, respectively, the singlet yield averaged over all directions of the magnetic field, 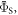 and the relative anisotropy,
and the relative anisotropy, 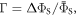 both as functions of
both as functions of 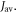 The lifetime of the radical pair (
The lifetime of the radical pair (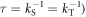 was 1 μs. When
was 1 μs. When 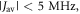 the protein dynamics have a minimal effect on
the protein dynamics have a minimal effect on 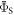 (figure 5(a)). For larger
(figure 5(a)). For larger 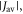 relaxation tends to reduce
relaxation tends to reduce 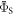 towards the statistical value of 0.25. The effect of spin relaxation on the anisotropy (figure 5(b)) is small when
towards the statistical value of 0.25. The effect of spin relaxation on the anisotropy (figure 5(b)) is small when 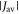 is outside the range 2 MHz <
is outside the range 2 MHz < 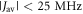 but shows a complex behaviour within this range. For most of these intermediate values of
but shows a complex behaviour within this range. For most of these intermediate values of 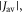 STD boosts the anisotropy above that found when relaxation is excluded. Γ is particularly strongly enhanced for positive values of the exchange interaction (7 MHz <
STD boosts the anisotropy above that found when relaxation is excluded. Γ is particularly strongly enhanced for positive values of the exchange interaction (7 MHz < 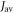 < 18 MHz).
< 18 MHz).
Figure 5. Dependence of (a) the average singlet yield 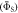 and (b) the fractional anisotropy of the singlet yield
and (b) the fractional anisotropy of the singlet yield 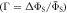 on the mean exchange interaction, Jav. (c) Dependence of Γ on the radical pair lifetime for selected values of Jav. The green and orange lines are for radical pairs respectively with and without the spin relaxation caused by fluctuations in the exchange and dipolar interactions. For all three panels, the magnetic field was 50 μT. In (a) and (b) the radical pair lifetime was
on the mean exchange interaction, Jav. (c) Dependence of Γ on the radical pair lifetime for selected values of Jav. The green and orange lines are for radical pairs respectively with and without the spin relaxation caused by fluctuations in the exchange and dipolar interactions. For all three panels, the magnetic field was 50 μT. In (a) and (b) the radical pair lifetime was  = 1 μs. [FAD•−
= 1 μs. [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn138.gif) was modelled by including the N5 and N10 hyperfine interactions of FAD•− in one radical and no hyperfine interactions in the other radical (i.e. a total of 36 spin states). The hyperfine and average electron–electron dipolar interaction tensors are given in the supporting information of [47]. The relaxation effects in the lower two panels in (c) arise entirely (left) and mostly (right) from D-modulation.
was modelled by including the N5 and N10 hyperfine interactions of FAD•− in one radical and no hyperfine interactions in the other radical (i.e. a total of 36 spin states). The hyperfine and average electron–electron dipolar interaction tensors are given in the supporting information of [47]. The relaxation effects in the lower two panels in (c) arise entirely (left) and mostly (right) from D-modulation.
Download figure:
Standard image High-resolution imageFigure 5(c) offers additional insight by plotting the relative singlet yield anisotropy Γ against the radical pair lifetime for a few representative values of Jav. In the absence of relaxation (orange lines), Γ is small for very short lifetimes (τ < 10 ns), grows as τ approaches the reciprocal of the Larmor period (∼700 ns), and eventually reaches a plateau when τ > ∼10 μs. When relaxation is included (green lines) and  is small (e.g. 0.0 and −0.75 MHz), the anisotropy is always less than or equal to that in the absence of relaxation. For larger Jav however (e.g. +16.8 MHz and +9.0 MHz), the relaxation causes a substantial increase in Γ for radical pairs with intermediate lifetimes (10 ns < τ < 1 μs). For example, when Jav = +16.8 MHz, and τ = 100 ns, the STD mechanism boosts Γ by a factor of 34. No enhancement of any magnitude was found in our earlier study of the relaxation resulting from fluctuations in the hyperfine interactions in FAD•− and
is small (e.g. 0.0 and −0.75 MHz), the anisotropy is always less than or equal to that in the absence of relaxation. For larger Jav however (e.g. +16.8 MHz and +9.0 MHz), the relaxation causes a substantial increase in Γ for radical pairs with intermediate lifetimes (10 ns < τ < 1 μs). For example, when Jav = +16.8 MHz, and τ = 100 ns, the STD mechanism boosts Γ by a factor of 34. No enhancement of any magnitude was found in our earlier study of the relaxation resulting from fluctuations in the hyperfine interactions in FAD•− and 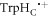 [47].
[47].
In summary, unless the mean exchange interaction is too large or too small, the thermal fluctuations in the separation of the FAD•− and 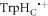 radicals in cryptochrome can induce spin relaxation of such a rate as to enhance the magnetic sensitivity, sometimes quite substantially.
radicals in cryptochrome can induce spin relaxation of such a rate as to enhance the magnetic sensitivity, sometimes quite substantially.
5. Discussion
In the following paragraphs we discuss other ways in which Nature might have avoided the problems posed by exchange and dipolar interactions in a [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn142.gif) cryptochrome magnetosensor. We then comment on possible reasons why the sensitivity enhancements afforded by fluctuations in the radical separation might not be manifested in cryptochrome.
cryptochrome magnetosensor. We then comment on possible reasons why the sensitivity enhancements afforded by fluctuations in the radical separation might not be manifested in cryptochrome.
5.1. Asymmetric recombination rates
Dellis and Kominis have suggested that harmful effects of exchange and dipolar interactions may be avoided if the radical recombination kinetics are highly asymmetric [34]. They argued that the anisotropy  can be larger when the rate constants for recombination of the singlet and triplet states (figure 1(a)) are such that kT
can be larger when the rate constants for recombination of the singlet and triplet states (figure 1(a)) are such that kT  kS rather than kT = kS. We believe this is unlikely to occur in a cryptochrome magnetoreceptor, for two reasons. First, our experience with toy models (supplementary figure S5) suggests that any benefit arising from the condition kT
kS rather than kT = kS. We believe this is unlikely to occur in a cryptochrome magnetoreceptor, for two reasons. First, our experience with toy models (supplementary figure S5) suggests that any benefit arising from the condition kT  kS only accrues when the average exchange and/or dipolar interactions are stronger than the effective hyperfine interactions in both radicals, viz. 39 MHz ≡ 1.40 mT for FAD•− and 54 MHz ≡ 1.94 mT for
kS only accrues when the average exchange and/or dipolar interactions are stronger than the effective hyperfine interactions in both radicals, viz. 39 MHz ≡ 1.40 mT for FAD•− and 54 MHz ≡ 1.94 mT for 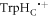 [23]. A value of
[23]. A value of 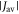 in excess of 40–50 MHz would result in such a small singlet yield anisotropy (see, e.g., figure 5(b)) that it would probably be beyond rescue by even the most favourable kinetics [53]. Second, a reaction scheme in which singlet and triplet radical pair states both recombine spin selectively to give distinct products (figure 1(a)) is not appropriate for [FAD•−
in excess of 40–50 MHz would result in such a small singlet yield anisotropy (see, e.g., figure 5(b)) that it would probably be beyond rescue by even the most favourable kinetics [53]. Second, a reaction scheme in which singlet and triplet radical pair states both recombine spin selectively to give distinct products (figure 1(a)) is not appropriate for [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn148.gif) because there is no energetically accessible molecular triplet state in cryptochrome to which the triplet radical pair could recombine [23]. Rather, one should consider a scheme (figure 1(b)) in which the singlet recombines spin selectively (to form the ground state of the protein, with rate constant kb) in competition with a reaction such as (de)protonation of one or both of the radicals [23] whose rate constant (kf) is independent of the spin state of the pair. For such a reaction scheme, there is no advantage to be gained from highly asymmetric rate constants (supplementary figure S5).
because there is no energetically accessible molecular triplet state in cryptochrome to which the triplet radical pair could recombine [23]. Rather, one should consider a scheme (figure 1(b)) in which the singlet recombines spin selectively (to form the ground state of the protein, with rate constant kb) in competition with a reaction such as (de)protonation of one or both of the radicals [23] whose rate constant (kf) is independent of the spin state of the pair. For such a reaction scheme, there is no advantage to be gained from highly asymmetric rate constants (supplementary figure S5).
5.2. Alternative radical pairs
Despite the finding that [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn149.gif) in isolated AtCry1 in vitro responds to relatively weak magnetic fields [23], it is not clear that this radical pair would necessarily be the sensor in an in vivo cryptochrome magnetoreceptor. Protein–protein and protein–ligand interactions in a cellular environment could result in a different, and possibly more sensitive, radical pair via an alternative or extended electron transfer pathway [44, 54, 55]. It is therefore important to ask whether Nature could have contrived a cryptochrome-based magnetic sensor in which the exchange and dipolar interactions are so weak that they do not adversely affect its performance. This is a complex question with no clear answer. Using equation (1) with β = 14 nm−1, an increase in r of only 0.33 nm would result in a 100-fold reduction in J(r), making it negligibly small. This might be achieved if a fourth tryptophan residue were involved in the electron transfer chain that creates the magnetically sensitive radical pair [56, 57]. However such an increase in the separation of the radicals would also slow down the reverse electron transfer reaction by about two orders of magnitude, prolong the lifetime of the radical pair and make it much more vulnerable to loss of coherence by spin relaxation. This problem could be avoided by multi-step reverse electron transfer along the Trp-triad, e.g. [FAD•− TrpHB
in isolated AtCry1 in vitro responds to relatively weak magnetic fields [23], it is not clear that this radical pair would necessarily be the sensor in an in vivo cryptochrome magnetoreceptor. Protein–protein and protein–ligand interactions in a cellular environment could result in a different, and possibly more sensitive, radical pair via an alternative or extended electron transfer pathway [44, 54, 55]. It is therefore important to ask whether Nature could have contrived a cryptochrome-based magnetic sensor in which the exchange and dipolar interactions are so weak that they do not adversely affect its performance. This is a complex question with no clear answer. Using equation (1) with β = 14 nm−1, an increase in r of only 0.33 nm would result in a 100-fold reduction in J(r), making it negligibly small. This might be achieved if a fourth tryptophan residue were involved in the electron transfer chain that creates the magnetically sensitive radical pair [56, 57]. However such an increase in the separation of the radicals would also slow down the reverse electron transfer reaction by about two orders of magnitude, prolong the lifetime of the radical pair and make it much more vulnerable to loss of coherence by spin relaxation. This problem could be avoided by multi-step reverse electron transfer along the Trp-triad, e.g. [FAD•− TrpHB 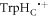 ] → [FAD•− TrpHB•+ TrpHC] → FAD + TrpHB + TrpHC, although it is not clear that this would be energetically feasible [58, 59]. Such electron hopping could be accompanied by strong J-modulation as discussed in section 3.
] → [FAD•− TrpHB•+ TrpHC] → FAD + TrpHB + TrpHC, although it is not clear that this would be energetically feasible [58, 59]. Such electron hopping could be accompanied by strong J-modulation as discussed in section 3.
Turning now to the dipolar interaction, 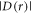 only becomes comparable to the Zeeman interaction with the geomagnetic field (50 μT ≡ 1.4 MHz) when r = 3.8 nm (equation (2)). In the x-ray structure of AtCry1 [28], the tryptophan and tyrosine residues that are furthest from the FAD are W447 at 2.90 nm and Y170 at 2.44 nm (edge-to-edge distances between aromatic rings). Neither is far enough away to have
only becomes comparable to the Zeeman interaction with the geomagnetic field (50 μT ≡ 1.4 MHz) when r = 3.8 nm (equation (2)). In the x-ray structure of AtCry1 [28], the tryptophan and tyrosine residues that are furthest from the FAD are W447 at 2.90 nm and Y170 at 2.44 nm (edge-to-edge distances between aromatic rings). Neither is far enough away to have 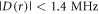 and neither is part of an obvious electron transport chain linking it to the FAD. One way to realise a radical-radical separation exceeding 3.8 nm would be if the ultimate electron donor were located on another (unknown) protein complexed to the cryptochrome. Once again, a sequential reverse electron transfer pathway would be needed to allow fast enough singlet recombination. Finally, an effective radical separation as large as 3–4 nm could conceivably be contrived if the FAD•− inside the cryptochrome were paired with a freely diffusing radical formed, for example, by electron transfer to the Trp radical in [FAD•−
and neither is part of an obvious electron transport chain linking it to the FAD. One way to realise a radical-radical separation exceeding 3.8 nm would be if the ultimate electron donor were located on another (unknown) protein complexed to the cryptochrome. Once again, a sequential reverse electron transfer pathway would be needed to allow fast enough singlet recombination. Finally, an effective radical separation as large as 3–4 nm could conceivably be contrived if the FAD•− inside the cryptochrome were paired with a freely diffusing radical formed, for example, by electron transfer to the Trp radical in [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}].$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn153.gif) Ascorbic acid has been discussed in this context [44].
Ascorbic acid has been discussed in this context [44].
In summary, although one can imagine cryptochrome-derived radical pair magnetic sensors in which Jav and Dav are small enough that they do not present a problem, such arrangements do not, at present, seem very likely.
5.3. Relaxation-enhanced compass sensitivity in cryptochrome
The results presented in figure 5 suggest that the anisotropic response of [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn154.gif) in AtCry 1 is particularly strongly enhanced for positive
in AtCry 1 is particularly strongly enhanced for positive 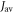 in the range ∼7 MHz to ∼18 MHz. These values are of the same sign but somewhat larger than the only experimental measurements of this quantity (in different cryptochromes): 2.0 MHz [29] and 4.2 MHz [30]. However, it should be borne in mind that the exchange interaction depends on the separation of the radicals and the surrounding amino acid residues and could be larger in an avian magnetoreceptor cryptochrome than in a cryptochrome with a different biological function.
in the range ∼7 MHz to ∼18 MHz. These values are of the same sign but somewhat larger than the only experimental measurements of this quantity (in different cryptochromes): 2.0 MHz [29] and 4.2 MHz [30]. However, it should be borne in mind that the exchange interaction depends on the separation of the radicals and the surrounding amino acid residues and could be larger in an avian magnetoreceptor cryptochrome than in a cryptochrome with a different biological function.
Although we have focussed here on the modulation of exchange and dipolar interactions, this is not the only source of spin relaxation. The other obvious contributors are (i) modulation of anisotropic hyperfine interactions by librational motions of the radicals within their binding sites and (ii) modulation of isotropic hyperfine interactions by conformational fluctuations, in particular in dihedral angles [47]. Further work will be needed to determine (a) whether the enhancements discussed here survive in the presence of these other spin-relaxation pathways and (b) the consequences of J-modulation and electron hopping occurring in tandem.
The simulations of [FAD•− ![${{{\rm{TrpH}}}_{{\rm{C}}}}^{\bullet +}]$](https://content.cld.iop.org/journals/1367-2630/18/6/063007/revision1/njpaa285dieqn156.gif) described here were performed using a drastically simplified spin system, comprising two electron spins and two nuclear spins whose hyperfine tensors are those of the two 14N nuclei (N5 and N10) in the central ring of the FAD•− isoalloxazine ring system [44]. These two interactions—strongly axially anisotropic with parallel symmetry axes—dominate the spin dynamics of FAD•− and arguably make flavin radicals near-optimal as components of a magnetic compass sensor [44, 60]. However, the influence of other nuclear spins cannot be discounted. In particular, a number of the hyperfine interactions in
described here were performed using a drastically simplified spin system, comprising two electron spins and two nuclear spins whose hyperfine tensors are those of the two 14N nuclei (N5 and N10) in the central ring of the FAD•− isoalloxazine ring system [44]. These two interactions—strongly axially anisotropic with parallel symmetry axes—dominate the spin dynamics of FAD•− and arguably make flavin radicals near-optimal as components of a magnetic compass sensor [44, 60]. However, the influence of other nuclear spins cannot be discounted. In particular, a number of the hyperfine interactions in  are significantly anisotropic and of lower symmetry [44]. It seems likely that the lower the overall anisotropy of the radical pair, the less scope there would be for J-modulation to relax the spins anisotropically. Unfortunately it is difficult to explore this without much more efficient techniques for simulating large spin systems [61, 62]. Extending this line of argument, we speculate that the enhancement arising from J-modulation is more likely to be observed for a radical pair in which the
are significantly anisotropic and of lower symmetry [44]. It seems likely that the lower the overall anisotropy of the radical pair, the less scope there would be for J-modulation to relax the spins anisotropically. Unfortunately it is difficult to explore this without much more efficient techniques for simulating large spin systems [61, 62]. Extending this line of argument, we speculate that the enhancement arising from J-modulation is more likely to be observed for a radical pair in which the 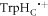 radical has been replaced by a radical with fewer, smaller, more isotropic hyperfine interactions (e.g. the ascorbyl radical [44]). Another reason in favour of a magnetically simpler partner for the FAD•− radical is that any enhancement resulting from J-modulation would be less likely to be obscured by hyperfine-induced spin relaxation.
radical has been replaced by a radical with fewer, smaller, more isotropic hyperfine interactions (e.g. the ascorbyl radical [44]). Another reason in favour of a magnetically simpler partner for the FAD•− radical is that any enhancement resulting from J-modulation would be less likely to be obscured by hyperfine-induced spin relaxation.
6. Conclusions
Previous work on radical pair magnetoreceptors has sought to identify, and in some cases quantify, the factors that control their sensitivity to the direction of the geomagnetic field. These properties include the identity of the radicals [44, 63, 64], their separation [25] and relative orientation [65], their hyperfine interactions [39, 44, 60, 66, 67], and their chemical kinetics [9, 67, 68]. Clearly, the molecular dynamics of the radicals must be added to this list given the profound effects electron spin relaxation can have on the spin-coherence. As argued here, modulation of spin interactions by molecular motions does not always simply degrade the performance of the sensor by destroying coherence. Under some circumstances, protein dynamics and appropriate magnetic interactions combine to produce anisotropic spin relaxation pathways that enhance the response of the compass to the direction of the geomagnetic field. Intermediate spin relaxation rates were found to be most effective. Evolution, acting through random mutations in the sequence of an avian cryptochrome, could have tuned not only its structural, magnetic and kinetic properties but also its dynamics for the purpose of magnetic sensing. In this regard, magnetoreception is no different from many other protein functions in which dynamics as well as structure play an essential role [69]. As in other areas of 'quantum biology' [70–72], interactions of the quantum system with a fluctuating environment appear to be critical for the quantum behaviour [58, 71]. An example, with a clear parallel to the present work, is 'environment assisted quantum transport' in which intermediate dephasing rates enhance the efficiency of photosynthetic energy transfer [73, 74].
Acknowledgments
We are grateful to Ye Jin and Jonathan Manouch for preliminary calculations. We thank the University of Oxford Advanced Research Computing (ARC) facility (http://dx.doi.org/10.5281/zenodo.22558) and the DeiC National HPC Center, University of Southern Denmark for generous allocation of CPU time. IAS is grateful for financial support from the Lundbeck Foundation and the Russian Science Foundation (Grant No. 14-12-00342). PJH thanks the European Research Council (under the European Union's 7th Framework Programme, FP7/2007-2013/ERC Grant Agreement No. 340451) and the Air Force Office of Scientific Research (Air Force Materiel Command, USAF Award No. FA9550-14-1-0095) for financial support.
Appendix A.: Spin relaxation arising from J-modulation
Equation (7) and the STD term in equation (5) can be derived as follows. We start with the equation of motion of the radical pair density operator, 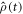 :
:
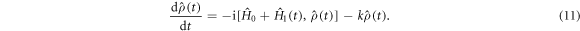
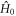 is the time-independent part of the spin Hamiltonian containing the Zeeman and hyperfine interactions and the average exchange interaction. k (= kS = kT) is the rate constant for the formation of reaction products from the singlet and triplet states of the radical pair (figure 1(a)).
is the time-independent part of the spin Hamiltonian containing the Zeeman and hyperfine interactions and the average exchange interaction. k (= kS = kT) is the rate constant for the formation of reaction products from the singlet and triplet states of the radical pair (figure 1(a)). 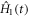 contains the time-dependence of the exchange interaction arising from fluctuations in the radical separation:
contains the time-dependence of the exchange interaction arising from fluctuations in the radical separation:
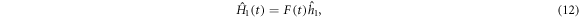
where
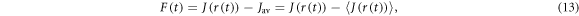
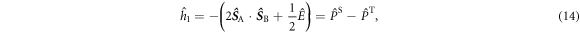
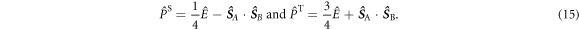
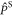 and
and 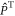 are the singlet and triplet projection operators,
are the singlet and triplet projection operators, 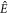 is the identity operator, and
is the identity operator, and 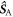 and
and 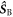 are the electron spin angular momentum operators of the two radicals. We assume that the correlation function for
are the electron spin angular momentum operators of the two radicals. We assume that the correlation function for 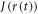 decays exponentially with a correlation time
decays exponentially with a correlation time 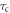 ,
,
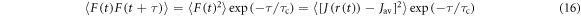
and that the fluctuations in  are fast enough that
are fast enough that
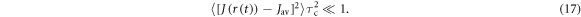
Then, in the extreme narrowing limit , 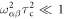 (
(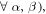 where
where  are
are 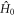 eigenvalue-differences, equation (11) becomes:
eigenvalue-differences, equation (11) becomes:
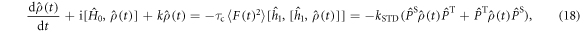
with 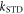 given by equation (7). The operator part of equation (18) can be obtained using equations (14) and (19) and
given by equation (7). The operator part of equation (18) can be obtained using equations (14) and (19) and
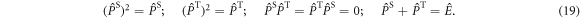
We note that this approach could be extended to somewhat slower fluctuations, i.e. outside the extreme narrowing limit, using standard Redfield relaxation theory.
For the toy radical pair discussed in sections 2 and 3, the time-independent spin Hamiltonian is given by equation (6). More generally, for a radical pair with multiple, non-diagonal, rhombic hyperfine interactions, 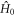 has the form
has the form

where K = 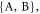 and
and 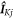 and
and 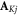 are the nuclear spin angular momentum operator and hyperfine tensor of nucleus j in radical K. NK is the number of nuclear spins in radical K. Note that the spatial degrees of freedom are included in the spin Hamiltonian by means of effective parameters such as
are the nuclear spin angular momentum operator and hyperfine tensor of nucleus j in radical K. NK is the number of nuclear spins in radical K. Note that the spatial degrees of freedom are included in the spin Hamiltonian by means of effective parameters such as 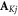 and
and  .
.
A rough estimate of kSTD may be obtained by assuming a Gaussian distribution of separations, centred at 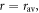 with standard deviation, σ:
with standard deviation, σ:
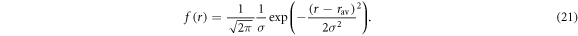
Then, using equations (1) and (7):
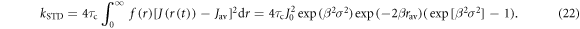
When J0 = 8 × 107 T, β = 14 nm−1, rav = 1.9 nm, σ = 0.1 nm, and τc = 1 ns, equation (22) gives kSTD = 2.7 × 108 s−1.
Appendix B.: Spin relaxation arising from D-modulation
The relaxation arising from fluctuations in the dipolar interaction may be treated in the same way as J-modulation. The analogous expressions to equations (13) and (14) are:
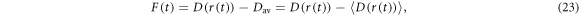
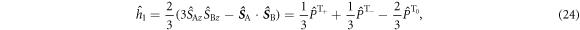
where 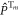 is the projection operator for the
is the projection operator for the 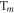 triplet state (m = 0, ±1). The evolution of the density operator is:
triplet state (m = 0, ±1). The evolution of the density operator is:
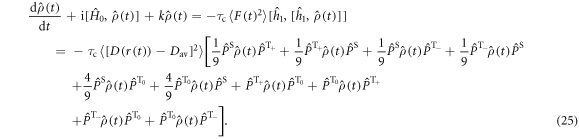
It can be seen from equation (25) that D-modulation leads not only to STD but also to triplet–triplet dephasing; density matrix elements such as 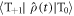 and
and  (but not
(but not 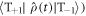 are relaxed.
are relaxed. 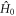 in equation (25) is given by equations (6) or (20) with the exchange term replaced by
in equation (25) is given by equations (6) or (20) with the exchange term replaced by 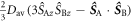 .
.
Using rav = 1.9 nm, σ = 0.1 nm, and τc = 1 ns (as above, equation (21)), the dipolar relaxation rate constant is:
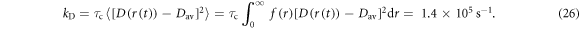
This value is substantially smaller than the corresponding estimate of kSTD for J-modulation (2.7 × 108 s−1) because the dipolar interaction has a much weaker dependence on r.
Appendix C.: Spin relaxation arising from the random fields mechanism
A corresponding treatment of the 'random fields' relaxation mechanism proceeds as follows. The time-dependent part of the spin Hamiltonian is

with
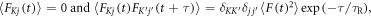
where 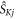 is the j-component (j = x, y, z) of the electron spin operator for radical K (K = A, B). Hence:
is the j-component (j = x, y, z) of the electron spin operator for radical K (K = A, B). Hence:
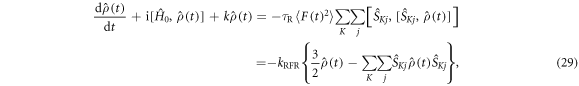
with

Appendix D.: Spin relaxation arising from electron hopping
The effects of the J-modulation caused by electron hopping between RP0 and RP1 (figure 1(c)) were modelled by means of coupled Liouville equations for the two density operators:
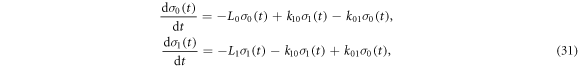
in which k10 and k01 are the first order rate constants for RP1 → RP0 and RP0 → RP1 respectively and 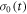 and
and 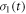 are the vector representations of the two density operators,
are the vector representations of the two density operators,  and
and 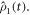 The matrix representations of the two Liouvillian superoperators are
The matrix representations of the two Liouvillian superoperators are
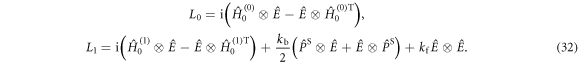
The rate constants 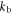 and
and 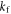 are defined in figure 1(c). Superscript T denotes transpose. The two spin Hamiltonians are
are defined in figure 1(c). Superscript T denotes transpose. The two spin Hamiltonians are
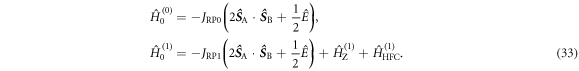
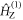 and
and  are the Zeeman and hyperfine interactions in RP1 (see equation (6)). It was assumed that
are the Zeeman and hyperfine interactions in RP1 (see equation (6)). It was assumed that 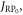 the exchange interaction in RP0, is so large that the Zeeman and hyperfine interactions in RP0 have a negligible effect on its spin dynamics. The singlet product yield was calculated by assembling a joint Liouville space for the two sites:
the exchange interaction in RP0, is so large that the Zeeman and hyperfine interactions in RP0 have a negligible effect on its spin dynamics. The singlet product yield was calculated by assembling a joint Liouville space for the two sites:
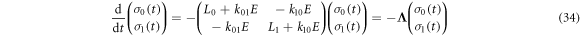
so that
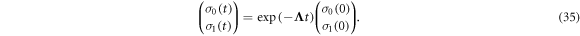
The singlet yield is then
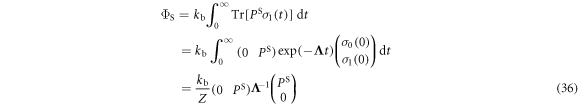
using the initial condition 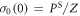 where Z is the total number of nuclear spin configurations.
where Z is the total number of nuclear spin configurations.