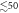Convection and segregation in fluidised granular systems exposed to two-dimensional vibration

C R K Windows-Yule

doi:10.1088/1367-2630/18/3/033005

1. Introduction

Assemblies of multiple, individual macroscopic particles, collectively known as granular materials, are ubiquitous in the world around us, playing vital rôles in innumerable industrial and natural processes [1–3]. When exposed to an energy source, granular media are known to demonstrate numerous different physical states, and to exhibit a wide variety of interesting and often surprising dynamical phenomena [4, 5], both with and without parallel in classical, molecular materials.

While there exist various manners in which energy may be provided to a granular system [6–8], our focus here is on the provision of energy through vibrational excitation, whereby the particles comprising a granular bed gain energy through collisions with a massive, oscillating surface [9]. The study of vibrated systems is of direct relevance to various industrial processes including, but by no means limited to, the drying [10], mixing [11] and sorting [12] of various materials, the separation of valuable substances from electronic waste [13], and the construction of dampers used in fields ranging from aerospace engineering to architecture [14]. Vibrated granular media also provide valuable canonical systems in which the collisional interactions between particles may be studied on a fundamental level. More recently, these systems have been used to provide easily studied analogues to microscale, nanoscale and even biological systems [15, 16]. These nascent applications hold much promise for future study in a number of diverse fields.

However, before the potential of any of the above applications can be fully achieved, there remains much work to be done understanding vibrated granular materials on a fundamental level. Despite the utility and versatility of vibrofluidised granular systems, they remain, on the whole, poorly understood and under-researched as compared to classical, molecular systems. In particular, it is notable that in the vast majority of prior studies, vibration is applied only in one direction; while the application of (mono-directional) vertical and (mono-directional) horizontal vibration has been extensively researched, there exist only a handful of studies in which the effects of two- [17] or three-dimensional [18–21] vibrational excitation are explored. Moreover, these studies deal exclusively with highly dense, weakly excited systems. To the best of the author's knowledge, there exist no studies investigating the effects of multi-directional driving on more energetic liquid- or gas-like systems. This is surprising as, unlike in molecular systems, the dissipative nature of granular liquids and gases means that the exact manner of energy input may carry numerous consequences [22–24] which are not apparent in classical fluids. In other words, by neglecting the case of strong, multi-directional driving, it is highly probable that the community has thus far overlooked the existence of potentially interesting phenomena unique to these systems.

In this paper, we take a first step towards understanding the effects of multi-dimensional driving in the case of energetic, highly fluidised granulates. Specifically, we study a simulated system driven in two spatial dimensions by four oscillating sidewalls. In doing so, we demonstrate numerous novel system states, phase transitions and dynamical behaviours unobserved in unilaterally driven systems and undocumented in the existing literature. We focus in particular on two phenomena of particular relevance to 'real-world' systems—granular convection [25, 26] and granular segregation [9, 27]. We present phase diagrams showing the diverse phenomena and physical states exhibited over a wide range of parameter space for both single-component systems and binary mixtures.

We demonstrate that the application of multi-dimensional driving allows the state and behaviour of a system to be deliberately manipulated in various manners, of which many are not possible using only a single vibration direction. Nonetheless, our results also provide insight into the convective and segregative behaviours observed in these more conventional systems, in particular the interactions and competition between the various segregation mechanisms present in vibrated beds.

The paper is ordered as follows: in the remainder of this section, we provide an introduction to the three topics which form the main focus of our work: granular convection (section 1.1), granular segregation (section 1.2), and the phase behaviour of the systems studied (section 1.3). We then provide details of the simulations from which our data are acquired (section 2) before detailing and analysing our results (section 3). Finally, in section 4 we summarise our major findings and conclusions.

1.1. Sidewall-driven convection

The convective motion observed within granular systems can be broadly categorised into two main types: frictionally driven convection [25, 26] in dense systems where contacts are enduring and frictional forces dominate the system's behaviour, and 'thermal' or 'buoyancy-driven' convection [28, 29] in systems where collisional interactions predominate. While frictionally driven convection is typically strongly coupled to the specific motion of the vibrating base [30], for thermally convective systems, the vibrating walls can be considered simply as an energy source—thus allowing a much closer analogy to thermodynamic systems. Indeed, it has been shown that thermal convection can be reproduced in simulations [29] and hydrodynamic models [31] where vibrating walls are replaced by a static energy source. Since our current interest lies predominantly in the behaviours of energetic, fluid-like systems we will focus our discussion primarily on thermal convection.

Thermal convection is so named due to its dependence on the granular analogue to temperature, T_g, which is related to the fluctuation of particle velocities about a mean value [32]—a greater fluctuating kinetic energy is equivalent to a higher 'granular temperature¹ '. The granular temperature is defined as ${T}_{{\rm{g}}}=m\langle {(v-{v}_{0})}^{2}\rangle$ , where m is the average mass of a particle, 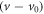$(v-{v}_{0})$ gives the deviation of a given particle velocity, v, from the mean value, v₀, and the brackets $\langle \rangle$ represent an ensemble average over all particles within a given volume.

Due to the fact that granular materials are inherently dissipative, a granular assembly driven by a single, vertically vibrating wall placed at the system's base will spontaneously develop a vertical (granular) temperature gradient. This gradient in T_g renders the system susceptible to convective instabilities, with analogy often drawn between thermal granular convection and Rayleigh-Bénard convection in conventional fluids [33, 34]. In experimental systems, the observed thermal convection is often sidewall-driven [35]—in systems with dissipative sidewalls, the greater collision rate for particles near these lateral boundaries leads to a localised increase in the rate of energy loss, and hence a lower granular temperature in these regions. With this lower temperature comes a simlarly reduced granular pressure, causing an increased flux of particles to this region. This, in turn, leads to a further augmented collision rate and a still more rapid loss of energy. As this positive feeback loop continues, the increasingly dense and 'cold' regions near the system's sidewalls will tend to sink downward through the system. Due to the conservation of mass flow, this downward motion must be balanced by a net upward flux of 'hotter' particles near the system's centre, clearly leading to the formation of a symmetric pair of convection rolls whose sense is upward in the system's centre and downward near its side-boundaries. A typical example of this form of convective motion may be seen in figure 1.

**Figure 1.** *Left:* velocity vector field showing the archetypal flow pattern pattern exhibited by systems which are subject to sidewall-induced convection. The data shown correspond to a system of 600 particles driven with a dimensionless peak amplitude $A/d=0.1$ . *Right:* the corresponding granular temperature field for the same system, demonstrating both the vertical and horizontal temperature gradients necessary to produce the convection rolls shown in the adjacent image. The values shown are normalised such that the maximal temperature exhibited by the system is given by a value of unity, while zero corresponds to T_g = 0.
Download figure:
Standard image High-resolution image

**Figure 1.** *Left:* velocity vector field showing the archetypal flow pattern pattern exhibited by systems which are subject to sidewall-induced convection. The data shown correspond to a system of 600 particles driven with a dimensionless peak amplitude $A/d=0.1$ . *Right:* the corresponding granular temperature field for the same system, demonstrating both the vertical and horizontal temperature gradients necessary to produce the convection rolls shown in the adjacent image. The values shown are normalised such that the maximal temperature exhibited by the system is given by a value of unity, while zero corresponds to T_g = 0.
Download figure:
Standard image High-resolution image

Previous simulational [36] and experimental [37] studies have shown a clear connection between the strength of sidewall-induced convection and the dissipative properties of the the vertical walls themselves, with more dissipative walls producing stronger convection. Such a connection is perhaps unsurprising—a more dissipative side boundary will more rapidly remove energy from particles in its vicinity, thus amplifying and expediting the effects described above and hence producing a greater rate of convection. In short, it is clear both from previous work and from simple reason that a greater disparity in density and temperature between the horizontal centre and lateral extremities of a system will lead to stronger convective flow.

The preceding discussion raises an interesting question: what if, rather than acting as an energy sink, the sidewalls of a system were instead to provide an energy source —for instance if these walls were caused to oscillate also? In this case, simple granular temperature and pressure considerations would immediately imply a reversal of the conventional situation described above, with a more dilute, energetic region in the locality of the system's lateral boundaries and a denser, cooler mass of particles nearer the centre of the system. In this situation, we can surely expect the sense of our convection rolls to be inverted. Moreover, the ability to vary the sidewall vibration intensity can potentially allow us to control the strength of convection within the system by altering the energy input from the walls.

Despite the simplicity of the the argument presented, the proposed inverse sidewall-driven convection has, to the authors' knowledge, not been previously observed. In section 3.2.2 of this paper, we put the above hypotheses to the test, exploring the relationship between sidewall driving and convection strength for a range of systems.

1.2. Granular segregation

The term 'granular segregation' refers to the partial or complete separation of a multicomponent particulate system into its individual constituents. The segregation of excited granular mixtures occurs spontaneously, based on differences in, for instance, size [38, 39], density [40, 41], geometry [42, 43] or elastic [44, 45] or frictional [46] properties between particles. In the current work, we focus on density-driven segregation, investigating systems of particles possessing identical sizes, geometries and contact properties, differing only in their densities and, hence, masses.

Density-induced segregation has been previously observed in a number of diverse granular systems, including not only vibrated beds but also rotating drum geometries [47], and gravitationally driven flows [48–50]. The density-segregation observed within these various systems may be driven by any of a number of mechanisms (or combinations thereof), such as simple buoyancy [47] or more complex shear-driven segregation [49]. While a perusal of the papers cited will certainly allow the reader a broader view of the granular segregation phenomenon in general, in the current work, for brevity, we focus on the segregation mechanisms most relevant to the strongly excited, vibrationally riven systems detailed here.

Previous studies have proposed multiple mechanisms by which density segregation may occur; for the sake of brevity, we will discuss here only those most relevant to the strongly excited, vibrationally driven systems detailed in this article.

We consider firstly the relatively simple case of a bidisperse-by-density system driven in such a manner that the bed is fluidised, but exhibits no strong temperature gradients. Under these conditions, granular systems have been shown to obey simple Archimedean buoyancy [51, 52]—i.e. smaller or (as in our case) more dense particles will 'sink' towards the lower regions of a system, while larger or less dense particles will migrate upwards.

When the temperature of a system can no longer be considered uniform, simple buoyancy can no longer be assumed. In these instances, kinetic theory predictions [53, 54] strongly suggest that heavy or large particles will migrate towards areas of lower temperature and lighter or smaller particles towards 'cooler' regions; this prediction is well supported by experimental [55] and simulational [56] results.

The theoretical frameworks mentioned above are only valid for non-convective systems—as indeed are, to the best of the authors' knowledge, all other published models concerning the segregation of dilute granular materials. Nonetheless, the broad, qualitative outcome of these models—namely the segregation of heavier particles toward lower-T_g (i.e. lower-energy) regions—seemingly holds also for systems in which convection is present. Specifically, various experimental and simulational studies of convective multicomponent systems show a definite tendency for denser particles to migrate towards less-active regions of a convective bed [57–59].

Later experimental studies [60] systematically explored the effect of convection in dilute sytems subject to strong temperature gradients, demonstrating a seemingly universal qualitative trend relating the strength of convection within a dilute, convective system to the steady-state degree of segregation achieved. Specifically, it was shown that weak to moderate convection strengths would act to augment segregation, while highly intense convection would actually act in opposition to the segregative mechanism detailed above, actively re-mixing the system.

In section 3.3, we demonstrate the variety of flow patterns and segregated system configurations, both known and novel, produced by our system, and attempt to explain their origins within the context of the mechanisms described above. In doing so, we also provide new insight into the mechanisms themselves, including an examination of their respective ranges of validity in the parameter space explored.

1.3. Phase transitions in granular media

A knowledge of the phase states available to a system and the conditions under which transitions between these states may be expected to occur is highly important to our understanding of any physical system, be it nanoscale, colloidal, polymeric or granular. As such, there exist several important papers detailing the phase behaviour of vibrated granular systems under a variety of excitation conditions.

The 1996 paper of Umbanhower et al [61], for example, demonstrated the formation of various ordered structures or 'patterns' by grains in a vertically vibrated monolayer. The paper constructed the phase boundaries between different configurational states in a Γ–f parameter space, where f is the frequency of the driving oscillations and 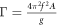${\rm{\Gamma }}=\frac{4{\pi }^{2}{f}^{2}A}{g}$ is the non-dimensionalised peak acceleration of these oscillations, with A the vibratory amplitude and g the magnitude of the gravitational acceleration.

In a paper highly relevant to the current work, Aoki et al [33], also in 1996, studied the transitions between differing frictionally driven convection modes for dense, vertically vibrated systems. It was shown that by varying the system's driving strength, Γ, or the number of particles within the system, N, it is possible to reverse the direction of segregation, or even to produce multiple pairs of convection rolls. Specifically, Aoki et al demonstrated transitions between a state exhibiting a single pair of convection rolls, a chaotic state with no obervable convection, and a state possessing two pairs of horizontally adjacent rolls. In this paper (see section 3.2.1), we perform a similar analysis to that of Aoki et al, focussing instead on the more dilute, strongly excited regime dominated by collisional, as opposed to frictional, interactions. We also extend our investigation to the bidisperse case, showing that the introduction of additional particle species can strongly affect the behaviour of, and states exhibited by, a granular system.

In 1997, Ristow et al [62] investigated the phase behaviour of a horizontally vibrated system, focussing specifically on the transition from a solid-like state to a fluidised state. Their results strongly suggested that, for a fixed particle number, the transition point is determined by the peak acceleration of the driving vibration, Γ.

More recently, in 2007, Eshuis et al [63], using a quasi-two-dimensional, vertically driven system, conducted a study utilising a considerably wider parameter space than had been previously explored and, consequently, observed a number of transitions involving a range of different phenomena and system states. Their results for weak excitation agreed well with the prior study of Ristow et al [62], demonstrating once again Γ to be the key energy-input control parameter determining a system's state. However, for stronger shaking and hence more dilute, energetic particles (i.e. in systems where particle motion becomes decoupled from that of the vibrating base-wall), a new dimensionless control parameter, 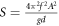$S=\frac{4{\pi }^{2}{f}^{2}{A}^{2}}{{gd}}$ , is required to characterise the observed phase transitions. Since it is this latter regime which forms the focus of our current work, our results will be presented in terms of S, as opposed to Γ. In addition to the energy input parameter S, Eshuis et al [63] also considered the effect of a varying particle number, N, plotting their data in a two-dimensional S–F phase space, where 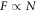$F\propto N$ is the number of layers of particles formed by the system in a resting state (i.e. S = 0).

Although there exist many other publications dealing with the phase behaviour of granular systems, the above provide an informative cross-section of the types of systems which have been explored thus far—both dense and dilute, vertically and horizontally vibrated, as well as deep, shallow and monolayer. However, to the best of the authors' knowledge, there currently exist no such studies concerning multi-dimensional driving, an omission which we redress in this manuscript (see section 3.1.1). We also present what is, to the best of our knowledge, a first set of phase diagrams for a bidisperse granular medium (section 3.1.2), detailing not only transitions between dynamic states but also configurational states (section 3.3), highlighting the areas of parameter space in which segregation is strong, weak, or indeed entirely absent—potentially valuable information for both future research and various practical applications.

2. Simulations

2.1. Simulation details

Our system is simulated using the open-source MercuryDPM discrete particle method software package² [64–66]. The normal and tangential forces acting between colliding particles are modelled using a frictional spring-dashpot model with a linear elastic and a linear dissipative contribution. The code used in this study takes a user-defined coefficient of restitution, ε, and contact time, t_c, which are used to calculate appropriate values for the normal spring constant, kⁿ, and damping constant, 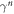${\gamma }^{n}$ , respectively, as [67, 68]:

$\begin{eqnarray}&&{k}^{n}={m}_{{ij}}\left[{\left(\displaystyle \frac{\pi }{{t}_{{\rm{c}}}}\right)}^{2}-{\left(\displaystyle \frac{\mathrm{log}\varepsilon }{{t}_{{\rm{c}}}}\right)}^{2}\right]\end{eqnarray} \tag{ 1 }$

and

$\begin{eqnarray}&&{\gamma }^{n}=-2{m}_{{ij}}\left(\displaystyle \frac{\mathrm{log}\varepsilon }{{t}_{{\rm{c}}}}\right).\end{eqnarray} \tag{ 2 }$

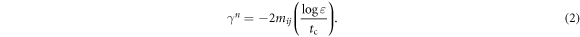
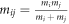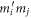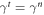In the above equations, m_ij is simply the reduced mass, ${m}_{{ij}}=\frac{{m}_{i}{m}_{j}}{{m}_{i}+{m}_{j}}$ , where ${m}_{i}^{\prime }{m}_{j}$ are the masses of two colliding particles. The equivalent coefficients for the tangential components of the spring and damping constants are determined as ${k}^{t}=\frac{2}{7}{k}^{n}$ and ${\gamma }^{t}={\gamma }^{n}$ , respectively.

The constants defined above can then be used to calculate the inter-particle forces, f_ij, acting between particles i and j in the normal and tangential directions as [67, 68]:

$\begin{eqnarray}&&{f}_{{ij}}^{n}={k}^{n}{\delta }_{{ij}}^{n}{\hat{{\bf{n}}}}_{{ij}}-{\gamma }^{n}{{\bf{v}}}_{{ij}}^{n}\end{eqnarray} \tag{ 3 }$

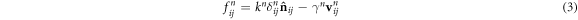
and

$\begin{eqnarray}&&{f}_{{ij}}^{t}=-{k}^{t}{\delta }_{{ij}}^{t}-{\gamma }^{t}{{\bf{v}}}_{{ij}}^{t},\end{eqnarray} \tag{ 4 }$

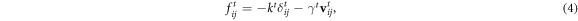
where 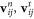${{\bf{v}}}_{{ij}}^{n},{{\bf{v}}}_{{ij}}^{t}$ are the normal and tangenetial components of the relative velocity between the interacting particles and ${{\boldsymbol{\delta }}}_{{ij}}^{t}$ is the elastic tangential displacement (described in detail in [69]). A static yield criterion is applied in such a manner as to truncate the magnitude of ${{\boldsymbol{\delta }}}_{{ij}}^{t}$ such that the inequality ${f}_{{ij}}^{t}\leqslant \mu {f}_{{ij}}^{n}$ is satisfied, where μ is the relevant frictional coefficient. All particles within the system are subject to a gravitational field which acts downwards in the negative (vertical) z direction (the relevant coordinate system is shown in figure 2).

**Figure 2.** Schematic diagram of the system modelled, visually detailing the system and particle dimensions and the coordinate system used throughout this manuscript. Dotted lines represent the direction of the vibrational motion to which the system's four mobile walls are exposed, illustrating the fact that each of these walls oscillates with an equal amplitude, A.
Download figure:
Standard image High-resolution image

2.2. The simulated system

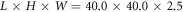Our typical system comprises a number $N\in [200,5000]$ of spherical particles housed within a domain of dimension $L\times H\times W=40.0\times 40.0\times 2.5$ particle diameters. The minimum value of N explored corresponds, for the geometry chosen, to approximately two resting layers of particles, ensuring that an equally weighted binary system may theoretically achieve complete vertical segregation even for the smallest N tested. The geometry of the domain is chosen to provide a system which is shallow in the horizontal y-direction, but not strictly quasi-two-dimensional—the width is adequate to allow particles to easily pass one another in the x–y plane, thus maintaining three-dimensional dynamics in an effectively two-dimensional system. The chosen system size is advantageous in that it allows the large volume of individual data sets required for the present study to be performed within a feasible time frame. A schematic diagram of our system may be seen in figure 2.

The experimental domain is bounded by six solid walls. For both particles and walls, the frictional coefficient is taken as 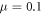$\mu =0.1$ , a value which has been shown to accurately reproduce experimental results in vibrated systems using the same software employed here [70, 71]. The implementation of this value of μ also adds to the generality of our results, as a number of easily available materials which are commonly used in experiment (for example glass, steel, acrylic) share a similar friction coefficient of 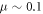$\mu \sim 0.1$ [72]. As such, our choice of μ makes our findings not only more directly comparable to those of previous studies, but also ensures that our simulated results may be relatively easily and cost-effectively reproduced in experiment. For similar reasons, the particle and wall coefficients of restitution, ε, used in our simulations were implemented as 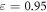$\varepsilon =0.95$ , a value that is once again appropriate to the modelling of various frequently studied materials, e.g. Delrin, steel, acrylic or glass [72].

Both mono- and bi-disperse systems are modelled. For the binary case, we set the values of 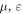$\mu ,\varepsilon$ , and the particle diameter, d, equal for both species in order to specifically isolate effects due to differences in particle density. The implementation of an equal diameter for both species also means that the volume fraction of a given species is, by definition, equal to the number fraction, making the interpretation of our results considerably clearer and less ambiguous, as compared to a bidisperse-by-size particle assembly. For all binary systems explored, the relative fraction of each species is held equal, i.e. 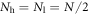${N}_{{\rm{h}}}={N}_{{\rm{l}}}=N/2$ , where the subscripts h and l denote values corresponding to the 'heavy' (higher-density) and 'light' (lower-density) species, respectively. A fixed density ratio, 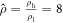$\hat{\rho }=\frac{{\rho }_{{\rm{h}}}}{{\rho }_{{\rm{l}}}}=8$ is maintained for all binary systems. The specific value was chosen to be high enough to ensure that effects due to density differences are strong and hence clearly observable, yet small enough that a similar ratio can be realistically achieved in experiment. It is worth noting here that previous studies have demonstrated that, for vibrated systems such as those explored here, the behaviour of a bed which is bidisperse-by-density is dependent only on the relative mass of particles—not the absolute mass [73]. In other words, the findings here can be generalised to any binary system with the same 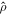$\hat{\rho }$ , irrespective of the specific masses and densities of the individual constituents.

The walls of the system lying in the x–y and y–z planes are vibrated at a fixed frequency, f, in the direction normal to their respective planes about a fixed central position. A value of f = 200 Hz is used in all experiments; this relatively high frequency is chosen such that the particle dynamics of the system are decorrelated from the motion of the system's walls [74]—i.e. the oscillating walls can be treated simply as an energy source for the system. Experiments are conducted using various values of vibrational amplitude, A, in the the range 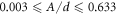$0.003\leqslant A/d\leqslant 0.633$ , resulting in a wide range of excitation strengths (see section 1.3) 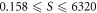$0.158\leqslant S\leqslant 6320$ . Since, as previously noted, the vibration of the walls acts only to provide energy to the system, the results obtained here for any given S value can be expected to apply to any arbitrary combination of f and A which produce the same S provided the f chosen is sufficiently high to decouple particle motion from base motion. The specific range of A and f used in this experiment were deliberately chosen to allow a wide range of S to be produced while ensuring that the frequency and amplitude values both remain accessible to contemporary experimental and industrial apparatus.

The four dynamic walls of the system oscillate with the same 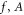$f,A$ and hence S. The reasons for this choice are twofold: firstly, by implementing the same values for all walls, the system's driving can be characterised by a single, scalar value, making the discussion and presentation of our results more easily intelligible. Secondly, as such a condition is arguably the easiest to practically implement in an experimental or industrial set-up, it seems sensible to conduct our simulations accordingly, such that our results may be easily translated to real systems.

The oscillations of the walls were also chosen to be in-phase, once again emulating the most likely experimental realisation of our system. Since, as has been repeatedly stated, the specific details of the vibratory energy input are unimportant to the dynamics of the system, the relative phases of the walls are in fact inconsequential to the behaviour of the granular system being driven. Nonetheless, preliminary tests were conducted for a variety of N and S values using in-phase, out-of-phase and antiphase oscillations, with no apparent differences in system state or dynamics observed. The in-phase method of vibration employed carries the additional advantage that the system maintains a constant volume throughout all experiments.

Since we are interested primariliy in the steady-state behaviour of our systems, all data shown are time-averaged over a period 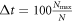${\rm{\Delta }}t=100\frac{{N}_{\mathrm{max}}}{N}$ s, starting from a time t₀ at which our system can safely be assumed to have reached a steady state³ . In other words, the behaviour of our largest systems (N = 5000) is averaged over a period of 100 s, with the measurement duration increasing proportionately with each reduction in N so as to ensure good statistics for all data sets acquired.

In summary, care has been taken to ensure consistency between all individual data sets acquired in terms of all major parameters which may affect system behaviour, leaving only the key control parameters S and N as our independent variables. Thus, we are able to explore a two-dimensional parameter space equivalent to those studied in the highly informative works of Aoki et al [33] and Eshuis et al [63].

3. Results

3.1. The granular phase diagram for two-dimensionally driven systems

3.1.1. Monodisperse beds

For the system geometry and parameter space explored within this work, the range of phenomena observed can be categorised into five main states:

(i)
Dense chaotic: Particles exhibit chaotic, randomised motion, behaving similarly to a simple, incompressible liquid.
(ii)
Dense convective: Particles maintain a dense, liquid-like state, but begin to exhibit convection, which may be localised to the upper regions of the bed, or pervade the entire system.
(iii)
Convective Leidenfrost: A 'cloud' of densely packed particles is supported from below by a dilute 'gas' of more energetic particles in a manner analogous to the Leidenfrost effect observed in molecular fluids [75]. Unlike the granular Leidenfrost effect first observed by Eshuis et al [76], the application of multi-directional driving also acts to prevent direct contact between the dense particle cloud and the oscillating side- and upper-walls, in essence making this a 'two-dimensional Leidenfrost state'. Convection is, in all cases, observed throughout the entire system.
(iv)
Dilute convective: Particles from a fully convective, dilute, gas-like phase.
(v)
Dilute chaotic: Particles form a dilute, gaseous phase, exhibiting no clear coordinated motion.

Visual examples of all states described above are provided in figure 4. Having briefly introduced all of the major states observed in our monoodisperse system, we now discuss in greater detail some of the more remarkable and unexpected features of these states, and the transitions between them.

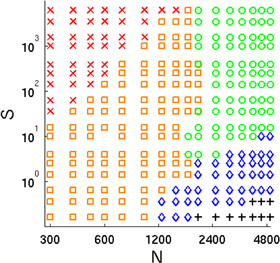
The ranges of the N–S parameter space corresponding to each state may be seen in figure 3. For relatively weakly driven (low S) and/or large (high N) granular assemblies, our systems exist in the dense chaotic phase. As noted previously, our interest here lies in more energetic, fluidised systems, where comparatively little prior research has been conducted. As such, the system parameters, and the ranges thereof, are carefully chosen such that fluid-like behaviour is induced for all systems explored. Specifically, the use of a large vibrational frequency, f, ensures that even for small S, the value of Γ remains relatively high. Since Γ is known to be the key control parameter governing the solid–liquid phase transition in both vertically and horizontally vibrated systems [77, 78], we can thus ensure that fluidisation is achieved for all systems studied.

**Figure 3.** Phase diagram showing the various states achieved by a monodisperse system for differing combinations of dimensionless driving strength, S, and particle number, N. The states depicted are as follows: dense chaotic (black crosses, +), dense convective (blue diamonds, ), dilute convective (orange squares, ), convective Leidenfrost (green circles, ) and dilute chaotic (red crosses, ). The states are described in detail in section 3.1.1 of the main text.
Download figure:
Standard image High-resolution image

As the driving strength, S, is increased, the system may enter either the dense convective phase (for relatively high N) or the dilute convective phase (for relatively low N). The two, respectively liquid-like and gaseous, states can be distinguished by their vertical density distributions. Systems in the dense convective phase possess either an approximately uniform distribution of particles or a slight, uniformly decreasing vertical density gradient. Systems in the dilute convective phase, meanwhile, clearly demonstrate the 'humped' or exponentially decaying density profiles characteristic of the gaseous state [79, 80]. We shall discuss first this latter state, due to its relative simplicity and strong similarity to the more well-known convective state observed in dilute, unilaterally driven systems. Indeed, the dilute convective state is, in essence, directly equivalent—in terms of its underlying mechanism—to the sidewall-driven convective state discussed in section 1.1. The only difference between the two cases is that in conventional, unilaterally driven systems, the system walls typically act to remove energy from the system, while in our present system, these same walls act to inject energy into the system. This difference (as outlined in section 1.1) manifests itself as an inversion of the flow direction (see the leftmost panel of figure 1 and the centre-right panel of figure 4). This same flow orientation is clearly observed for all systems in the dilute convective regime, thus providing strong support for the validity of our hypothesis. The validity of our second conjecture from section 1.1, that one may be able to control the convection rate by varying the strength of driving, will be tested in section 3.2.2.

**Figure 4.** Examples of the typical steady-state packing density and velocity fields for the 5 main states discussed within this manuscript. For each region of the system, the local, time-averaged packing fraction, η, is given by the colour scale adjacent to each individual image. The direction of the mean flow velocity for each area of the system is represented by the orientations of the arrows superimposed onto the density map, thus showing the typical steady-state flow patterns, if any, exhibited by the system in the various states shown. For clarity, due to the wide ranges of velocities presented by the various systems, the arrows are all of fixed length—i.e. the *magnitude* of the velocity in each region is not represented. *Top left:* dense chaotic state. *Top right:* dense convective state. *Centre left:* convective Leidenfrost state. *Centre right:* dilute convective state. *Bottom left:* dilute chaotic (gaseous) state. *Bottom right:* dilute convective state with colour scale adjusted to illustrate density variations.
Download figure:
Standard image High-resolution image

Our observations in the dense convective regime are both more complex and perhaps more unexpected than for its dilute counterpart. Firstly, the convection observed in this regime is, for weak driving and large N (i.e. beds possessing a large aspect ratio), limited only to the upper regions of the bed, as may be observed in figure 3. As S is increased the convective region grows, eventually encompassing the entire particle assembly. On the surface, this observation is not unusual—indeed it agrees well [81] with our expectations for denser, more weakly excited systems in which convection is driven by frictional effects [26]. However, surprisingly, we find the observed convection to persist even when all frictional coefficients within the system are set to zero. The continued presence of convection in the absence of friction strongly suggests that the observed motion is due to thermal convection, as the conventionally accepted mechanisms for convection in dense vibrated systems are all reliant, in some manner, on frictional effects. This conjecture is further supported by the widths and, more importantly, positions, of the upward- and downward-flowing regions in these dense systems. As would be expected from our discussion in section 1.1, upward motion occurs only in the narrow region of low-density near the system's energy-providing sidewalls (see figure 4, top right). This marks a stark contrast to the dilute convective case (see figure 4, bottom right), where there exists a larger low-density region, and correspondingly a significantly wider upward-flowing region.

This is an important result—while previous studies have routinely demonstrated thermal convection in dilute and moderately dense systems [29, 35, 36, 82–85] this is, to the best of our knowledge, the first direct evidence of thermal convection in highly dense systems where collisionally driven effects would typically not be considered important. Moreover, our observations provide valuable information regarding the onset of thermal convection: a comparison of the two topmost panels of figure 4 shows the non-convective state to possess a near-uniform density in all directions, while the partially convective state demonstrates a small but significant density gradient, which is enough to trigger a degree of thermal convection. This observation holds true for all similar data sets observed. Thus, our results strongly imply that the onset condition for thermal convection is simply the presence of some degree of compressibility. It should be noted that, in our current system, this condition is seemingly both necessary and sufficient, in simple vertically vibrated geometries, there exists also a dependence on various particle and wall properties [84]. Nonetheless, we can assert with some confidence that, with the exception of highly dilute gases approaching the non-interacting regime, any compressible vibrated system can be expected to be susceptible to thermal convection.

As the driving strength S is increased, a system in the dense convective state will, for relatively small N, transition to the dilute convective regime discussed previously or, for larger N, attain instead the convective Leidenfrost state. The observed Leidenfrost-like phenomenon differs both from its classical, molecular counterpart and the previously observed granular Leidenfrost regime for unilaterally driven systems [76, 86] in that the state invariably exhibits convective motion across the entire parameter range explored. The unusual ability of this state to sustain both convective motion and density-inversion can perhaps be ascribed to the fact that the convection is driven by an excess of energy near the walls as opposed to a reduction in energy, as is the case for 'normal' buoyancy-driven convection. To put it differently, consider a system possessing perfectly elastic sidewalls which exists in a carefully balanced Leidenfrost state. If, with all other parameters held constant, the walls are rendered more dissipative, the densification of the region near the now-dissipative walls will lead to a previously absent downflow of material, and also a net loss of energy within the system. This will create an instability, causing the formation of (previously absent) convection rolls, and a collapse of the density-inverted, phase-separated state into a simple, convective fluid [63]. Consider now the case in which energy is added to the system at the boundaries. As discussed extensively already, the presence of these active boundaries will induce thermal convection rolls. However, in this latter case, the system experiences a net gain in energy, preventing the collapse of the density inverted phase. Conversely, the introduction of additional energy is, due to the increased pressure from the our system's confining walls and upper boundary, less likely to simply cause the system to evaporate into a dilute, gaslike phase. Thus, our systems demonstrate a stable, convective Leidenfrost state for a relatively wide range of parameter space (see figure 3). It should be noted that, by carefully controlling the relevant parameters, it is in fact possible to achieve a similar state in conventional, unilaterally driven systems [87]. However, as is clear from our discussion, the range of parameter space for which such a phase may occur is considerably more limited in these systems.

As mentioned in the definition of the Leidenfrost state at the start of this section, the dense phase of the system is 'supported' on four sides by the dilute gaseous phase induced by the system sidewalls. By varying the vibration strength of one or more walls independently of the others, it is possible to deliberately alter the position of the dense phase. The ability to deliberately move and position the main bulk of material within a system may potentially carry various practical applications.

It is notable from our phase diagram (figure 3) that the parameter space corresponding to the Leidenfrost-like state observed here differs considerably from the observations of Eshuis et al [63]. Specifically the line delineating the transition between this state and the purely convective state shows a monotonic relation between N and S in the phase diagram of [63], but a distinctly non-monotonic trend in the equivalent diagram presented here. Specifically, we observe that—unlike in [63]—for certain N values, as S is increased at fixed N, a system will transition from the Leidenfrost-like state, into a single-phase, purely convective state and then, with further increasing S, return to the Leidenfrost state. This observation, and the discrepancy between our results and those of Eshuis et al [63] may be explained by the confined nature of our system, as opposed to the 'open' geometry explored in [63]. Specifically, for intense driving and an adequately large particle number, the augmented granular temperature induced by the system boundaries will act to compress and hence densify the central region, causing the bed to 're-enter' the Leidenfrost state.

For smaller particle numbers, N, increasing S will simply cause a transition from the convective Leidenfrost state to the dilute convective state and then, as opposed to returning the system to the Leidenfrost state, will cause it to enter the dilute chaotic state. While the gaseous state is, in itself, rather unremarkable, it is interesting to note that the phase boundary between the convective and chaotic gaseous regimes for our system differs considerably from the observations of Eshuis et al [63]. Specifically, whereas in [63] the gaseous phase is strictly limited to very low-N systems, in the present work, we see from figure 3 that the gaseous phase encroaches considerably further into the higher-N regions of the parameter space studied.

There are two likely explanations for this divergence. Firstly, we consider here significantly greater values of the vibrational strength, S, than were experimentally accessible in [63]—i.e. if the system of Eshuis et al were driven more strongly, a similar phase behaviour may also have been observed in their system. Secondly, the confined nature of our system will, at high S and for adequately dilute systems (i.e. low N), act to provide a more uniform (and vertically symmetric) temperature field than the open system of Eshuis et al, as illustrated in figure 5. The lack of a significant granular temperature gradient will, by definition, act to suppress thermal convection, in particular for cases in which the driving is such that the peak acceleration of the oscillating base significantly outwieghs gravity, i.e. 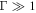${\rm{\Gamma }}\gg 1$ . In reality, the observed discrepancy is likely due to a combination of both of the above.

**Figure 5.** Two-dimensional, depth-averaged temperature distributions for a constrained, two-dimensionally driven system such as those discussed throughout this manuscript (*left*) and an equivalent open, vertically vibrated system. Both systems contain N = 500 particles and are excited with a dimensionless driving strength S = 262.7. For ease of comparison, the granular temperature, T_g, is normalised in both cases such that 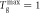${T}_{{\rm{g}}}^{\mathrm{max}}=1$ .
Download figure:
Standard image High-resolution image

**Figure 5.** Two-dimensional, depth-averaged temperature distributions for a constrained, two-dimensionally driven system such as those discussed throughout this manuscript (*left*) and an equivalent open, vertically vibrated system. Both systems contain N = 500 particles and are excited with a dimensionless driving strength S = 262.7. For ease of comparison, the granular temperature, T_g, is normalised in both cases such that ${T}_{{\rm{g}}}^{\mathrm{max}}=1$ .
Download figure:
Standard image High-resolution image

3.1.2. Bidisperse beds

The phase diagram shown in figure 6 corresponds to data acquired from bidisperse-by-density systems comprising a 1:1 ratio of dense or 'heavy' (h) particles and less-dense or 'light' (l) particles possessing a density ratio, 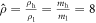$\hat{\rho }=\frac{{\rho }_{{\rm{h}}}}{{\rho }_{{\rm{l}}}}=\frac{{m}_{{\rm{h}}}}{{m}_{{\rm{l}}}}=8$ . Other than their binary nature, the systems explored here are identical to those whose behaviours were detailed in section 3.1.1 ⁴ . In figure 6, we show the distribution in S–N phase space of the same major states discussed in the previous section. This diagram is broadly similar to that presented in figure 3, although there exist two main differences, which we discuss below.

**Figure 6.** Phase diagram showing the various states achieved by a bidisperse system for differing combinations of S, and N. The states are denoted in the diagram as follows: dense chaotic (black crosses, +), dense convective (blue diamonds, ), dilute convective (orange squares, ), convective Leidenfrost (green circles, ) and dilute chaotic (red crosses, ). The states are described in detail in section 3.1.1.
Download figure:
Standard image High-resolution image

Firstly, the transition from the dense chaotic state to the dense or dilute convective states occurs, for fixed N, at markedly lower S values for the bidisperse case as opposed to the monodisperse. This 'earlier' transition can be explained as follows: the dense convective phases are higher energy states than the dense chaotic. As will be discussed in further detail in section 3.3, for relatively low excitation strengths, S, the system is segregated such that denser particles line the bottom of the container, i.e. a greater proportion of heavier particles lie in the immediate vicinity of the system's vibrating walls. Since the system's walls are infinitely massive (a modelling assumption which has been repeatedly shown to provide an accurate representation of real, experimental systems [73, 88]) a given particle-wall collision will impart a fixed velocity (as opposed to a fixed energy) to the colliding particle, irrespective of the particle's mass. As such, heavier particles will acquire more energy from the system's walls, resulting in a greater energy flux into the system [73, 88]. Thus, a system with a greater proportion of collisions between heavy particles and the oscillating boundaries will acquire a greater energy per particle as compared to an equivalent, monodisperse system. Consider also that, at low S, the system is segregated such that lighter particles, which are more susceptible to convection [51, 60], occupy the upper regions of the bed (which, as discussed in section 3.2.2 is the first to become convective), it stands to reason that a bidisperse-by-density will exhibit convective motion for lower excitation strengths than a similar unary system.

For increasing S values, as the bed begins to expand, the relative number of energy-injecting particle-wall collisions experienced by the lighter species will increase, and particle velocities will begin to equilibrate [89], explaining the strong similarity between the monodisperse and bidisperse phase diagrams for large S.

A second difference between the monodisperse and bidisperse phase diagrams is that the onset of the (convective) Leidenfrost state with increasing S is also delayed. This can be relatively simply explained by the fact that, due to the known tendency in dilute systems for heavier particles to migrate to lower-T_g regions and lighter particles to dominate 'hotter' regions [53], the dilute gaseous phase will be comprised of predominantly of l particles—as may be clearly seen in figure 7. For the Leidenfrost state to form, this dilute gaseous phase must support the mass of the dense particle cloud which, due to the excess of light particles in the gaseous phase must, by definition, contain a greater relative fraction of the heavier species. Clearly, a gas of light particles supporting a comparatively heavy dense phase will require a higher kinetic energy per unit mass than is necessary for the monodisperse case in which all particles are equally massive—i.e. binary systems will require a greater S in order to achieve a Leidenfrost-like state, as observed. Following a similar argument, the system will also be slower to transition out of the Leidenfrost state and into the single-phase dilute convective state, as the lower-energy l particles are less likely to be able to 'break up' the dense central region without a greater increase in S as compared to the monodisperse case [63].

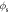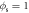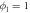**Figure 7.** *Left:* two-dimensional plot showing the average local volume fraction, ${\phi }_{{\rm{s}}}$ , of light-species particles for all given regions of the experimental system. Data is shown for a system of N = 3500 particles driven with S = 394.8, producing a convective Leidenfrost state. A value ${\phi }_{{\rm{s}}}=1$ (red) denotes a region occupied solely by l particles, while ${\phi }_{{\rm{l}}}=1$ (blue) corresponds a region entirely dominated by particles of the heavier (h) species. *Right:* the distribution of densities, η, for the same system. A comparison of the two images clearly shows a preponderance of h particles in the dense phase and a dilute phase containing predominantly l particles.
Download figure:
Standard image High-resolution image

**Figure 7.** *Left:* two-dimensional plot showing the average local volume fraction, ${\phi }_{{\rm{s}}}$ , of light-species particles for all given regions of the experimental system. Data is shown for a system of N = 3500 particles driven with S = 394.8, producing a convective Leidenfrost state. A value ${\phi }_{{\rm{s}}}=1$ (red) denotes a region occupied solely by l particles, while ${\phi }_{{\rm{l}}}=1$ (blue) corresponds a region entirely dominated by particles of the heavier (h) species. *Right:* the distribution of densities, η, for the same system. A comparison of the two images clearly shows a preponderance of h particles in the dense phase and a dilute phase containing predominantly l particles.
Download figure:
Standard image High-resolution image

In summary, we observe a broad, qualitative agreement between the phase behaviours presented here and those detailed by Eshuis et al [63]. Specifically, although the individual states observed often differ in their internal flow dynamics (those observed here being more prone to convective motion) we find that the gas-like, dilute convective, phase-inverted (Leidenfrost-like) and relatively dense states observed by both authors occupy the same limits of the phase space explored. The lack of a quantitative agreement, and the presence of certain discrepancies in the observed forms of the phase boundaries, are to be expected: there exist marked differences between the two studies in terms of the system parameters employed, the system geometry, and in particular the manner of energy injection. The agreement that is observed, however, provides a measure of validation for our results. The phase diagrams presented here, and the associated discussion explaining the relevant states and their transitions, give a valuable insight into the little-explored systems detailed within this paper, hopefully fuelling further research into these scientifically interesting and potentially practically useful systems.

3.2. Convective behaviours

3.2.1. Convective phase diagram

Figure 8 demarcates the regions of parameter space corresponding to the several different convective modes observed in our two-dimensionally vibrated, bidisperse system—several of which are not present in the monodisperse case, and one of which is indeed without parallel in conventional, unilaterally driven systems. It is immediately interesting to note that the presence of the differing convection modes seemingly does not influence the specific state of the system, as can be observed by comparing figures 6 and 8 and noting the significant overlap in the phase boundaries observed between the differing states and those separating the dissimilar convective modes. For example, the 'dual convection' mode (defined below) denoted in the rhs diagram by pentagramal symbols can be observed in the dense convective, dilute convective and convective Leidenfrost regimes. This apparent decoupling of the system's phase states and flow regimes is a highly interesting and potentially important observation.

**Figure 8.** Phase diagram showing the different convective modes exhibit by a binary system for various combinations of driving intensity, S and particle number, N. The modes shown are as follows: non-convective (black dots, ·), single species convection (blue triangles, ), dual convection, (green pentagrams, ), combined convection (orange squares, ) and asymmetric convection (red hexagrams, ). Details of the various states may be found in section 3.2.1 of the main text.
Download figure:
Standard image High-resolution image

The full set of convective modes observed within the binary system can be broadly grouped into the following four distinct classifications:

(i)
Single-species convection: Convective motion is limited to the lighter of the two species present.
(ii)
Dual convection: Each species exhibits its own distinct convection roll pair, with a single pair of horizontally adjacent convection rolls comprising predominantly lighter-species particles 'stacked' on top of a second pair of convection rolls comprising almost exclusively particles belonging to the heavier species.
(iii)
Combined convection: Both particle species are entrained in a single pair of convection rolls.
(iv)
Asymmetric convection: Convection rolls are unstable with, at any point in time, between 1 and 5 distinct rolls present.

With the exception of the 'asymmetric' case, convection rolls occur in symmetric pairs, with upward orientations at the sidewalls and downward at or near the system's horizontal centre. Images corresponding to the various convection modes may be seen in figure 9.

**Figure 9.** Two-dimensional velocity vector fields superimposed onto two-dimensional packing density distributions, demonstrating archetypal examples of each of the four main convective modes demonstrated by the binary systems discussed here. *Upper left:* the single species convection mode. *Upper right:* the dual convection mode. *Lower left:* the combined convection mode. *Lower right:* the asymmetric convection mode. Details of each convective regime are given in the main text (section 3.2.1).
Download figure:
Standard image High-resolution image

The existence of the single-species convective mode, and its presence in exclusively low-S regions of the parameter space presented in figure 8 can be explained by the mass difference between particles and the resultant segregation observed within the system, as outlined in section 3.1.2. In short, since lighter particles will segregate towards the free surface of the system (i.e. are less constrained by pressure) and gain a larger kinetic energy relative to their mass as compared to their heavier counterparts, they will naturally possess faster dynamics, and therefore be the first to exhibit convective motion [89]. Thus, for granular beds in which the balance between the energy injected into the system, S, and the energy dissipated by the system (a function of N) is such that full convection is not energetically possible, only the l species will exhibit convective motion, resulting in the single-species convection mode observed.

As the rate of energy injection to the system is increased, the system will reach a point at which there exists enough energy for both species to exhibit convective motion, at which point the system will transition out of the single-species convection mode. For S values relatively close to the transition point, the h-species particles forming the lower phase of the system will remain adequately densely packed that the lighter particles above are incapable of penetrating into this lower region. As such, the system will form two separate pairs of convection rolls for the light-particle phase and the dense-particle phase, 'stacked' one atop the other—the dual convection phase. Although the observation of different particle species possessing differing net flow rates is not a new one [51, 60] this is, to the best of our knowledge, the first time that such a state—possessing two entirely separate thermal convection roll pairs for dissimilar species—has been observed.

As S is further increased and the system as a whole becomes more dilute, lighter particles are more easily able to penetrate into the lower regions of the bed, thus leading both heavy and light particles to be entrained in a single convection roll. It is worth noting—as is clearly illustrated in figure 9, and will be discussed further in section 3.3—that this does not necessarily mean that the two species will become mixed, as may perhaps be expected from previous studies [57, 90].

Finally, in the high-N limit, we observe a convective mode in which, unlike all other states heretofore discussed, displays a convection pattern which is both asymmetric and unstable in time—i.e. no steady-state convection pattern is observed. For the vast majority of systems explored, a steady convective state is achieved in under 10 s. However, for systems in the asymmetric convection regime, a steady convective state is not observed even after runs two orders of magnitude longer than this. Rather, the system is observed to continually evolve, exhibiting varying numbers of convection rolls with varying orientations.

The aymmetric mode exists almost uniquely in the Leidenfrost state, and it is this observation that may potentially provide a clue as to its origin. We hypothesise that an uneven distribution of particle masses in the central dense region may lead to an imposed shift towards or away from a given wall, breaking the symmetry of the system and thus setting up an asymmetric convection pattern. The occurrence of this new convection pattern will, in turn, lead to a redistribution of heavy and light particles, once more shifting the mass centre of the system's dense phase, and thus repeating the above process, leading to the observed unstable system. Although, for brevity, we will not discuss this state further in the current paper, the interesting and complex dynamics observed here are worthy of future study.

3.2.2. Convection strength

One of the main aims of this work was to establish whether inverse wall-induced thermal convection could be achieved through the application of multi-dimensional vibrational excitation. In the preceding sections, we have demonstrated emphatically that the induction of such convective motion is indeed possible, and demonstrated the (considerable) range of phase-space for which it is observable. In the introduction to this work (section 1.1), we also raised the question as to whether by using energy-imparting walls to induce convection, one could alter the convection strength within the system simply by adjusting the wall driving strength, leaving all other parameters constant.

In figure 10, we plot 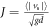$J=\frac{\langle | {v}_{{\rm{s}}}| \rangle }{\sqrt{{gd}}}$ , the non-dimensionalised mean streamwise velocity, v_s, of particles entrained in the convective flow, as a function of the system driving strength, S. This plot shows several interesting features; firstly, and most obviously, we see a clear, strong dependence of the flow rate on the driving strength, S, as predicted in section 1.1; this in itself is potentially a highly useful observation, as it demonstrates that it is possible to both induce and control the strength of convection within a system, an ability with various potential applications.

We additionally observe that the relation between J and S is decidedly non-monotonic. Once the threshold S-value for convective motion has been reached, a further increase in S initially produces a higher convection rate. For still stronger driving, increasing S causes the convection strength, J to pass through a maximum, from which it seemingly monotonically decreases as 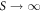$S\to \infty$ . While one might, perhaps, naively expect J to increase with S ad infinitum, the mon-monotonic behaviour observed in practice can actually be relatively easily explained. In short, the main factor governing the strength of convection in our system is the relative density of regions neighbouring the oscillating sidewalls and those nearer the system's centre. For very low excitation strengths, the material near the wall will only be weakly excited and hence only experience a small increase in temperature and a correspondingly minor decrease in density, resulting in weak convection. As S is increased, material near the sidewalls will become significantly 'hotter' and more dilute than that in the central region, leading to an increase in convection strength. However, as S is further increased, the heating effect of the walls will pervade the entire system, resulting in a significant expansion of the central region also, and hence a reduced relative density between the different horizontal regions of the system as the system approaches a more homogeneous gaseous state⁵ . Clearly, from this argument, we can expect the most pronounced convection for some intermediate value of S, as we indeed observe.

Finally, and perhaps most strikingly, the maxima in the plot of convection strength versus driving strength are approximately coincident for all values of N, the second key control parameter in our experiment. Despite the similarity of the observed trends for differing N values, however, the various curves cannot, it seems, be collapsed through normalisation by any single constant value or simple function of N. The authors will attempt to address in detail the relationship between the intensity with which our system is driven and the strength of the convective motion induced in a future publication.

Although further work, which is beyond the scope of this current work, is required to fully understand the relationship between J and S, the analysis presented here has nonetheless yielded two important results.

Firstly, we have provided a direct demonstation that two-dimensional vibration can be used to both induce and control the strength of buoyancy-driven granular convection. Such an ability may, for instance, prove highly useful in a number of industrial processes involving multicomponent particulate systems, due to the known ability of convective motion to influence both the mixing and separation of materials [39]. The ability to induce and 'tune' convection may also prove a valuable asset to future scientific studies in which such motion is either prerequisite or, conversely, undesirable.

Secondly, we have shown the existence of an apparent universal maximum in the relationship between convection strength and vibrational energy input. The existence of such a relationship suggests that, for a given system, by determining the S value corresponding to the maximal convection rate for any single particle number, N, one automatically knows the value required to induce the strongest possible convection in any arbitrary convective system. As with the above, this new knowledge may prove highly beneficial to any future research or industrial process where convective motion is of importance.

3.3. Segregation

The final topic to be discussed in this paper is that of granular segregation, a phenomenon with applicability to a wide variety of real-world processes [1–3, 91–94], and which has been heavily investigated for several decades. Yet in spite of the importance of this phenomenon, and the wealth of publications dedicated to its study, to the best of the author's knowledge, it has—until now—never been studied for the case of vertical, two-dimensionally driven systems such as those explored here.

The degree of segregation exhibited by our systems is determined by subdividing the experimental volume into a number N_c of individual cells and, for each of these cells, determining the time-averaged volume fraction, 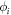${\phi }_{i}$ (where 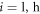$i={\rm{l}},{\rm{h}}$ ) of a given system component. The scalar quantity I_s, the segregation intensity, can then be determined as [95]:

$\begin{eqnarray}&&{I}_{{\rm{s}}}={\left[\displaystyle \frac{{\displaystyle \sum }_{i=1}^{i={N}_{{\rm{c}}}}{({\phi }_{i}-{\phi }_{m})}^{2}}{{N}_{c}}\right]}^{\frac{1}{2}},\end{eqnarray} \tag{ 5 }$

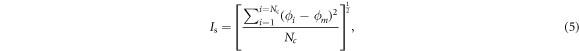
where 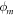${\phi }_{m}$ is the mean particle concentration of the system as a whole. For our system, in which a 1:1 ratio of light to heavy particles is implemented, 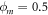${\phi }_{m}=0.5$ . In such a system, the maximal value of I_s, corresponding to a completely segregated system, is also 0.5, with a value I_s = 0 representing a system which is perfectly mixed.

Figure 11 shows the variation in the strength of segregation observed for the S–N phase space explored in this study. Previous simulational and experimental investigations of strongly fluidised, bidisperse-by-density systems have shown that increasing driving strength and/or decreasing N (i.e. reducing the packing density of a system) will act to reduce segregation [37, 57, 96], with a strong, monotonically decreasing relationship between the system density, η, and the segregation intensity, I_s.

The variation in segregation strength depicted in figure 11, however, displays a considerably more complex relationship between I_s and the key control parameters N and S—as may be expected due to the comparative complexity of the system itself and the expansive parameter space investigated. Thus, in order to provide an explanation for the segregative behaviours of our system across the entirety of the phase space explored, we cannot rely on a single driving factor, but must instead consider the action of several distinct segregation mechanisms.

Let us first consider the limit of large N and weak driving, where the system exists in a dense, liquid-like state and S is low enough that gravity may still be considered a dominant force within the system. In this limit, we can expect the system to be subject to simple, pseudo-Archimedean buoyancy [52, 97].

As S increases or, equivalently, N decreases, and convection becomes more pervasive within the system, we must additionally consider the effect of this convective flow on the system's segregative behaviours. In systems driven by weak and/or low-frequency vibration, the frictionally driven convection observed will normally act to induce mixing [57, 90]. However, in the strongly excited, high-f, collisional regime considered here, convection can actually drive segregation [60], as discussed in section 1.2. As such, for low-to-moderate S values, the convective and buoyant mechanisms will both act to induce segregation, explaining the consistently strong segregation observed even as the system undergoes the transition from a non-convective, incompressible-fluid-like state to a fully convective state (see figures 8 and 11).

It is important to reiterate, however, that the convective segregation mechanism detailed in [60] does not vary monotonically with convection strength, J, but rather—for very large values of J—actually favours mixing. It is interesting to observe that the S value corresponding to the local minimum in I_s for large N corresponds closely to the maximum in J in figure 10—a strong indication that this mechanism is indeed active in our system.

Considering next the limit of strong driving and low particle number, we observe a very high degree of intermixing between species, with an effectively homogeneously mixed system for the extremal values. This observation is not surprising as, in this limit, the system is not only non-convective (see figures 6, 8), eliminating the convective segregation mechanism, but also highly dilute (see figure 12), meaning that buoyancy forces will be negligible. The lack of significant temperature gradients in the gaseous regime will also act to suppress the thermal diffusion mechanisms predicted by kinetic theory (see section 1.2).

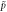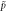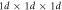**Figure 12.** Variation of packing density, η (*left*) and the non-dimensionalised pressure, $\tilde{p}$ (*right*) across the S–N parameter space explored. The system averages of η and $\tilde{p}$ values shown are calculated by determining the time-averaged local value of the relevant parameter for a series of overlapping $1d\times 1d\times 1d$ volumes within the experimental system and taking the average across all volumes which are occupied by particles for at least 10% of the experiment duration.
Download figure:
Standard image High-resolution image

**Figure 12.** Variation of packing density, η (*left*) and the non-dimensionalised pressure, $\tilde{p}$ (*right*) across the S–N parameter space explored. The system averages of η and $\tilde{p}$ values shown are calculated by determining the time-averaged local value of the relevant parameter for a series of overlapping $1d\times 1d\times 1d$ volumes within the experimental system and taking the average across all volumes which are occupied by particles for at least 10% of the experiment duration.
Download figure:
Standard image High-resolution image

Finally, we consider the limit of high S and N. Somewhat surprisingly, we observe the presence of relatively strong segregation for the uppermost values of the key control parameters, where neither buoyancy nor convection would be intuitively expected to play a strong role—or, more accurately, their strength should not increase with S, as is observed. Taking the extremal example, for N = 5000, we see an increase in I_s as 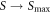$S\to {S}_{\mathrm{max}}$ , despite the fact that, as 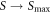$S\to {S}_{\mathrm{max}}$ , the system's average density remains constant and 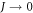$J\to 0$ (resulting in a diminished contribution to segregation from convective effects). The final piece to the puzzle that is our two-dimesnional segregation field can potentially be provided through the consideration of the granular pressure, p, within the system.

In the limit of strong driving, our system can be assumed to be subject to a granular equivalent of kinetic theory [98], allowing us to define a simple granular analogy to pressure for any given volume within the system as 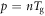$p={{nT}}_{{\rm{g}}}$ , where T_g is the now familiar granular temperature and n the local number density of particles [99].

In the right-hand panel of figure 12, we plot the non-dimensionalised pressure, 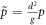$\tilde{p}=\frac{{d}^{2}}{g}p$ as a function of S and N. A comparison of this plot with the segregation intensity field shown in figure 11 shows a distinct region of high pressure in the high-S, high-N limit, where the incongruous region of strong segregation discussed above is observed. This marked increase in pressure will, naturally, lead to an increase in buoyant forces within the system, thus leading to the observed upturn in segregation.

4. Conclusions

We have provided a first insight into the dynamics and phase behaviours of strongly fluidised, two-dimensionally vibrated granular systems. We have observed, detailed and explained the origins of a wide variety of phenomena, both entirely novel and with strong parallels in conventional, unilaterally driven particle assemblies.

The manuscript presents a series of phase diagrams for both monodisperse and binary granular assemblies. Through these diagrams, we have gained a first insight into the manner in which the key driving parameters of the systems studied may be expected to affect a granular bed's state, convective regime and tendency towards phase-separation.

We have detailed multiple novel system states and flow regimes currently unobserved in conventional, unidirectionally vibrated systems.

It has been demonstrated that the convective flow rate of a system may be deliberately altered through a variation in the strength, S, of two-dimensional driving to which the system is exposed. Further, we have shown the existence of a maximum in the relationship between convection rate and driving strength whose position is—for a given system geometry—seemingly invariant with the number, N, of particles within the system. We have also shown the manner in which the system's segregative and mixing behaviours are influenced by the key control parameters S and N. These observations may both potentially prove valuable to industry and in future research.

Our work has also provided new insight into the onset of thermally driven convection, providing a strong suggestion that the susceptibility of a bed to thermal convection depends only on the compressibility of the granular bed—i.e. the onset of convective motion is (under otherwise conducive circumstances) coincident with the onset of compressibility. As such, we observe thermal convection to be important even in relatively dense systems where its presence is typically neglected. These observations are likely to be applicable also to unilaterally driven systems.

Despite the numerous novel states and phenomena documented and significant new insights provided, the work detailed here represents only a first step towards our understanding of the systems explored, providing great scope for future research.

Acknowledgments

The author would like to thank H M Amos for valuable discussions, and to acknowledge the Dutch Technology Foundation STW for its financial support of STW-Vidi project 13472, Shaping Segregation: Advanced Modelling of Segregation and its Application to Industrial Processes.

Convection and segregation in fluidised granular systems exposed to two-dimensional vibration

Article metrics

Author e-mails

Author affiliations

Dates

Abstract