Abstract
In this work, we study the acoustically mediated interaction forces among multiple well-separated spherical particles trapped in the same node or antinode plane of a standing wave. An analytical expression of the acoustic interaction force is derived, which is accurate even for the particles beyond the Rayleigh limit. Interestingly, the multi-particle system can be decomposed into a series of independent two-particle systems described by pairwise interactions. Each pairwise interaction is a long-range interaction, as characterized by a soft oscillatory attenuation (at the power exponent of n = −1 or −2). The vector additivity of the acoustic interaction force, which is not well expected considering the nonlinear nature of the acoustic radiation force, is greatly useful for exploring a system consisting of a large number of particles. The capability of self-organizing a big particle cluster can be anticipated through such acoustically controllable long-range interaction.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
After the pioneering discovery of optical trapping [1, 2], Burns et al [3] observed a series of optically-induced bound states between two polystyrene spheres. Different from the optical trapping generated by the gradient of an external field directly, the optical binding effect occurs even in a plane wave field without any gradient. Since then, extensive efforts have been devoted to the light-mediated particle-particle interaction [4–12]. The optical binding force alternates between attraction and repulsion with the inter-particle separation, which leads to a light-mediated self-organization of particle clusters. The interaction between objects can also be induced by acoustic waves, as reported theoretically [13–24] and experimentally [25–28]. Comparing with its optical counterpart, less progress has been made on the sound-mediated interaction. To the best of our knowledge, most of the current theoretical studies focus on the acoustic interaction between two objects [14–20].
The acoustic radiation force (ARF), as a second order quantity of the acoustic field, relies on an accurate calculation of the self-consistent field distribution in the presence of the particles. The self-consistent sound field can be solved by various techniques, such as the finite-element method, the finite difference time domain simulation, and the multiple-scattering theory (MST). For spherical particles, the MST approach has been proved to be the most efficient since the sound field can be precisely captured by a finite number of spherical basis functions. It has been successfully developed to calculate the acoustic interaction between two spherical particles [14, 15]. Although a system involving multiple particles [21–23] can also be handled, the MST method becomes inefficient as the growth of the particle number, owing to the overloaded memory and time consumption. Recently, for the particles much smaller than the acoustic wavelength (i.e., Rayleigh particles), a simple formula of the pairwise interaction force has been derived based on a scalar potential theory [24]. Together with a mean-field approximation, this approach is further demonstrated to be powerful in treating a great number of the Rayleigh particles. It is worth pointing out that, the acoustic interaction among the Rayleigh particles is very weak, which could be hidden in the gradient force induced by a tiny defect of the external sound field.
Based on a single prior scattering approximation, here we present a theoretical study on the sound-mediated interactions among the multiple spherical particles distributed sparsely in the same node or antinode plane of a plane standing wave (PSW) field. Particularly, we focus on the particle size comparable with the acoustic wavelength, in which the acoustic interaction is anticipated to be much stronger than that in the Rayleigh situation. We derive a concise form for the total interaction force exerting on any given particle. It consists of a series of independent pairwise interactions between the particle and the others. Therefore, the multi-particle system is reduced into a two-body problem, which greatly simplifies the computation comparing with the rigorous MST method. Interestingly, we find that each pairwise interaction is a conservative force and thus the whole system could be described by a potential energy. This result is unusual for the particle beyond the Rayleigh limit. Besides, the pairwise force is oscillatory at a factor of cosine function and decays at a power exponent of n = −1 or −2. The oscillatory long-range interaction, controlled by the external sound field, could facilitate the self-organization of a two-dimensional (2D) cluster involving a large number of particles.
The remainder of this paper is organized as follows. In section 2, an analytical formula responsible for the long-distance acoustic interaction is derived, followed by a detailed discussion on the formula. In section 3 we check first the accuracy of our formula by some few-particle systems, and then study the system involving a large number of particles. Finally, a brief summary is made in the last section.
2. Theoretical derivation of the long-range acoustic interaction
PSW is a good external field for exploring the acoustically mediated particle–particle interaction. The node or antinode plane forms a natural potential well to confine the particles tightly in the same plane without any transversal field gradient. Assume that the acoustic PSW field is described by 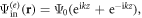 where
where 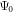 characterizes the amplitude of the PSW field. In this case, the interaction force survives only in the xy plane owing to the symmetry of the external field.
characterizes the amplitude of the PSW field. In this case, the interaction force survives only in the xy plane owing to the symmetry of the external field.
As schematically depicted in figure 1, for an arbitrary spherical particle  the total velocity potential function can be written as a superposition of the incident wave
the total velocity potential function can be written as a superposition of the incident wave 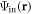 and the scattering wave
and the scattering wave  i.e.,
i.e.,
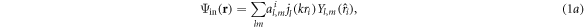
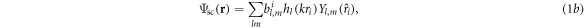
where 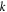 is the wavenumber in the host fluid, the vector
is the wavenumber in the host fluid, the vector 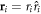 refers to any probe position
refers to any probe position 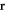 measured from the center of a given sphere
measured from the center of a given sphere  and
and 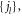
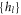 and
and 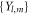 are the spherical Bessel functions, the spherical Hankel functions of the first kind and the spherical harmonics, respectively.
are the spherical Bessel functions, the spherical Hankel functions of the first kind and the spherical harmonics, respectively.
Figure 1. Spherical particles distributed in the same node or antinode plane of an acoustic PSW field consisting of two counter-propagating plane waves. Each color arrow labels a position vector measured from the origin or a given sphere center.
Download figure:
Standard image High-resolution imageThe incident coefficient 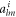 can be decomposed into two parts,
can be decomposed into two parts,
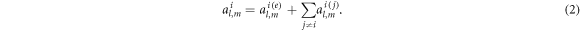
The first part 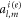 stems from the external incidence (PSW field here),
stems from the external incidence (PSW field here),
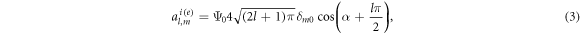
with 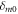 being a Kronecker delta. The value of
being a Kronecker delta. The value of 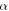 depends on the location of the particle ensemble:
depends on the location of the particle ensemble: 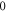 for the antinode plane and
for the antinode plane and 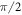 for the node plane of the acoustic PSW field. The second part stems from the scattering of the other particles
for the node plane of the acoustic PSW field. The second part stems from the scattering of the other particles  Each component
Each component 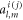 can be derived according to the addition theorem of the spherical functions [29], i.e.,
can be derived according to the addition theorem of the spherical functions [29], i.e.,
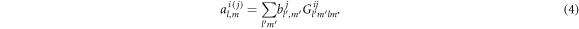
Here 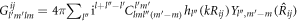 with the coefficient
with the coefficient 
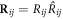 represents the position vector of the spherical center
represents the position vector of the spherical center  measured from the spherical center
measured from the spherical center  .
.
For a homogeneous spherical particle, the incident and scattering coefficients can be related by a diagonal scattering matrix  i.e.,
i.e.,  according to the continuum boundary condition on the surface of the particle. Substituting this relation into equation (4) and using equation (2), we obtain a linear equation system
according to the continuum boundary condition on the surface of the particle. Substituting this relation into equation (4) and using equation (2), we obtain a linear equation system
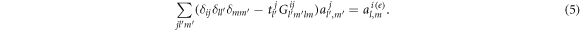
Solving this linear problem gives the incident coefficient 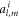 and further gives the total self-consistent acoustic field according to equation (1). In this procedure, multiple scatterings among the particles are taken into account rigorously. However, the computational time and memory cost increase rapidly with the growth of the particle number. If the particles are distributed sparsely
and further gives the total self-consistent acoustic field according to equation (1). In this procedure, multiple scatterings among the particles are taken into account rigorously. However, the computational time and memory cost increase rapidly with the growth of the particle number. If the particles are distributed sparsely  a single prior scattering approximation can be used to avoid solving the linear problem. Now the scattering contribution from the sphere
a single prior scattering approximation can be used to avoid solving the linear problem. Now the scattering contribution from the sphere  to
to 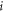 is dominated by a single prior scattering event, i.e.,
is dominated by a single prior scattering event, i.e.,  which finally gives rise to
which finally gives rise to
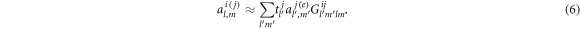
Combining the equations (1), (2) and (6) with the relation 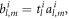 we can obtain the field distribution in the presence of particles. The ARF exerted on any particle
we can obtain the field distribution in the presence of particles. The ARF exerted on any particle 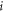 can be calculated by integrating the time-averaged radiation stress tensor
can be calculated by integrating the time-averaged radiation stress tensor  over an arbitrary surface
over an arbitrary surface  enclosing the particle, i.e.,
enclosing the particle, i.e.,
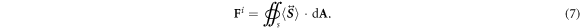
Specifically, the time-averaged radiation stress tensor 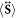 can be written as
can be written as
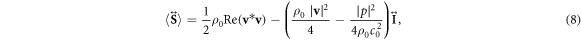
with 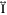 being a unit tensor,
being a unit tensor, 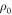 and
and 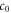 being the static mass density and sound velocity of the fluid background, and
being the static mass density and sound velocity of the fluid background, and 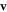 and
and 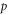 denoting the first-order velocity and pressure fields, respectively. If an infinitely large contour is selected, the integral form of the ARF
denoting the first-order velocity and pressure fields, respectively. If an infinitely large contour is selected, the integral form of the ARF 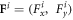 can be rewritten as a series [30, 31]
can be rewritten as a series [30, 31]

where the coefficient ![${\mu }_{l,m}=\sqrt{[(l-m)(l-m-1)]/[(2l-1)(2l+1)]}.$](https://content.cld.iop.org/journals/1367-2630/18/11/113034/revision1/njpaa48cbieqn44.gif) Using the relation
Using the relation  equation (9) can be reorganized into
equation (9) can be reorganized into
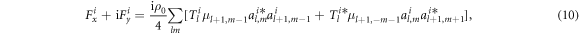
where the factor 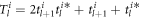 characterizes the scattering property of the particle
characterizes the scattering property of the particle 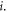 Substituting equation (2) into equation (10), the acoustic interaction can be divided into three parts
Substituting equation (2) into equation (10), the acoustic interaction can be divided into three parts
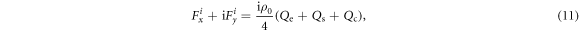
where
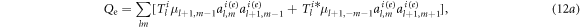
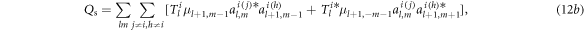
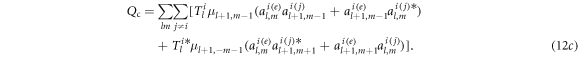
The first term 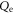 involves only the external field
involves only the external field  which is always zero because
which is always zero because 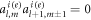 (see equation (3)). This stems inherently from the translational invariance of the external PSW field in the xy plane. The second term
(see equation (3)). This stems inherently from the translational invariance of the external PSW field in the xy plane. The second term  involving only
involving only  is contributed by the scattering from the other particles
is contributed by the scattering from the other particles  and the third term
and the third term 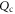 is a cross term that involves the external incidence
is a cross term that involves the external incidence 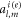 and the scattering
and the scattering 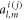 simultaneously. It is straight to prove that
simultaneously. It is straight to prove that 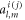 becomes negligibly small with respect to
becomes negligibly small with respect to 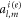 as the inter-particle separation increases. Therefore, the cross term
as the inter-particle separation increases. Therefore, the cross term 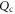 is dominant for the dilute particle suspension.
is dominant for the dilute particle suspension.
Using the approximation 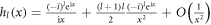 for
for 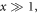
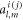 in equation (6) can be reshaped as
in equation (6) can be reshaped as
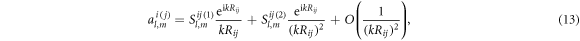
where the coefficients
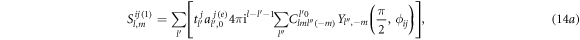
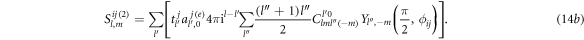
with 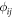 denoting the azimuthal angle of
denoting the azimuthal angle of 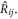 Especially, one may prove that
Especially, one may prove that 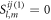 if the particles are positioned on the node plane of the PSW field, since
if the particles are positioned on the node plane of the PSW field, since 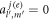 for even
for even  (see equation (3)) and
(see equation (3)) and 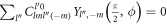 for odd
for odd 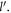 Therefore, the total interaction force exerting on the sphere
Therefore, the total interaction force exerting on the sphere 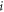 can be approximately written as
can be approximately written as
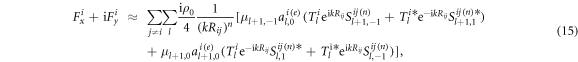
where n = 1 and n = 2 correspond to the antinode and node planes, respectively.
Note that here only the terms 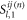 and
and 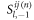 are involved, because
are involved, because 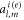 is nonzero only for m = 0 (see equation (3)).
is nonzero only for m = 0 (see equation (3)).
To further simplify equation (15), we substitute the definition of the spherical harmonics 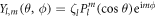 into equation (14), with
into equation (14), with 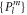 being the associated Legendre polynomials and
being the associated Legendre polynomials and ![${\zeta }_{l}=\sqrt{[(2l+1)(l+1)!]/[4\pi (l-1)!]}.$](https://content.cld.iop.org/journals/1367-2630/18/11/113034/revision1/njpaa48cbieqn76.gif) This gives rise to
This gives rise to
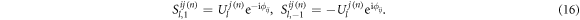
with

Combining equation (15) with equation (16), we derive a relatively simple and compact form
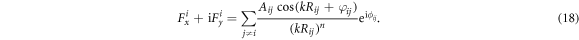
The amplitude factor 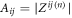 and the phase shift
and the phase shift 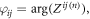 where the complex quantity
where the complex quantity  is defined by
is defined by
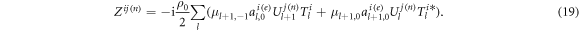
Interestingly, for Rayleigh particles 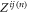 can be simplified further by considering the lowest two scattering channels only. This gives rise to
can be simplified further by considering the lowest two scattering channels only. This gives rise to 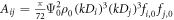 and
and 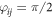 for the antinode plane, and
for the antinode plane, and 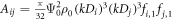 and
and 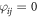 for the node plane, where
for the node plane, where 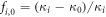 and
and  are the monopole and dipole scattering factors of the Rayleigh particle
are the monopole and dipole scattering factors of the Rayleigh particle  respectively. Here
respectively. Here 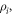
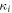 and
and  are the mass density, the bulk modulus and the diameter of the particle
are the mass density, the bulk modulus and the diameter of the particle  respectively, and
respectively, and 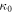 is the bulk modulus of the background fluid. The result responsible for the Rayleigh limit is consistent with that derived by Silva and Bruus (see equations (22b) and (23b) in reference [24]).
is the bulk modulus of the background fluid. The result responsible for the Rayleigh limit is consistent with that derived by Silva and Bruus (see equations (22b) and (23b) in reference [24]).
Below we give a summary on the property of the acoustic interaction among the sparsely distributed multiple particles. (i) The total force (see equation (18)) exerting on the sphere 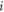 can be viewed as a vector addition of all pairwise interactions labeled by
can be viewed as a vector addition of all pairwise interactions labeled by 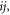 since the quantity
since the quantity 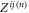 in equation (19) depends on the scattering property of the particles
in equation (19) depends on the scattering property of the particles 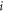 and
and  only. The additivity of the interaction does not hold naturally since the ARF is a second order quantity of the sound field. In this case, the conclusion stems from the negligible contribution of the interference among the scattering fields (see equation (12b)). As a consequence, a multi-body system can be simply decomposed into a series of independent two-body problems, which will greatly simplify the computation of a dilute particle ensemble involving a large number of particles. (ii) For each pairwise interaction, the orientation of the force component depends on the azimuthal angle of
only. The additivity of the interaction does not hold naturally since the ARF is a second order quantity of the sound field. In this case, the conclusion stems from the negligible contribution of the interference among the scattering fields (see equation (12b)). As a consequence, a multi-body system can be simply decomposed into a series of independent two-body problems, which will greatly simplify the computation of a dilute particle ensemble involving a large number of particles. (ii) For each pairwise interaction, the orientation of the force component depends on the azimuthal angle of 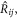 i.e.,
i.e., 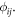 This means that the pairwise interaction is a 2D central force and thus is conservative, as long as the particle pair is tightly bounded on the node or antinode plane. Therefore, we can use a potential energy function to characterize the multi-particle system, considering the additivity of the pairwise force. (iii) As a whole, the pairwise interaction decays at a power exponential factor
This means that the pairwise interaction is a 2D central force and thus is conservative, as long as the particle pair is tightly bounded on the node or antinode plane. Therefore, we can use a potential energy function to characterize the multi-particle system, considering the additivity of the pairwise force. (iii) As a whole, the pairwise interaction decays at a power exponential factor 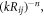 where
where 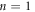 or
or  corresponds to the case of the antinode plane or the node plane. Similar to the Coulomb force or the gravitational force, the acoustically mediated interaction decays moderately and is a long-range force. Besides, the cosine-like oscillation factor
corresponds to the case of the antinode plane or the node plane. Similar to the Coulomb force or the gravitational force, the acoustically mediated interaction decays moderately and is a long-range force. Besides, the cosine-like oscillation factor 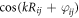 suggests a binding effect between the two particles: there exists a series of stable configurations occurring at
suggests a binding effect between the two particles: there exists a series of stable configurations occurring at  with
with 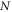 denoting an integer. The periodicity exhibited in the inter-particle separations of the bound states originate inherently from the distance dependent factor
denoting an integer. The periodicity exhibited in the inter-particle separations of the bound states originate inherently from the distance dependent factor 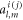 (see equation (13)) involved in the dominant force component
(see equation (13)) involved in the dominant force component 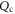 (see equation (12c)). Although a similar formula has been reported in optic systems [3, 5, 9], which involves the dipole–dipole interaction only, the present form of the pairwise acoustic interaction is not obvious since all scattering channels are considered here.
(see equation (12c)). Although a similar formula has been reported in optic systems [3, 5, 9], which involves the dipole–dipole interaction only, the present form of the pairwise acoustic interaction is not obvious since all scattering channels are considered here.
3. Numerical results and discussions
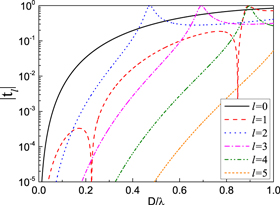
The sound-mediated interaction is closely related to the scattering property of the particles. In the following paper, the particles are assumed to be identical despite the fact that equation (18) can deal with an ensemble of particles with different geometry and material parameters. Intentionally, the water-immersed polystyrene particle is under consideration. The system carries rich scattering resonances at a wavelength comparable with the diameter 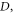 as revealed by figure 2, the size-dependent magnitudes of the scattering matrix elements
as revealed by figure 2, the size-dependent magnitudes of the scattering matrix elements 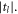 The material parameters involved are: the mass density
The material parameters involved are: the mass density 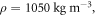 the longitudinal velocity
the longitudinal velocity 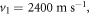 and the transverse velocity
and the transverse velocity 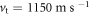 for polystyrene; the mass density
for polystyrene; the mass density 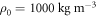 and the sound speed
and the sound speed 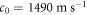 for water. For the convenience of presentation, below all lengths are scaled by the operation wavelength
for water. For the convenience of presentation, below all lengths are scaled by the operation wavelength 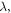 and the interaction force is scaled by
and the interaction force is scaled by 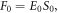 where
where 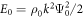 is the energy density of a single plane wave, and
is the energy density of a single plane wave, and 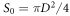 is the cross-section area of the spherical particle.
is the cross-section area of the spherical particle.
Figure 2. Magnitudes of the lowest six orders of the scattering matrix elements for a water-immersed polystyrene particle, plotted as a function of the dimensionless particle size 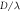 .
.
Download figure:
Standard image High-resolution image3.1. The system involving few particles
We first provide a numerical validation for the formula of pairwise interaction. According to equation (18), the normalized interaction force  between a pair of particles
between a pair of particles 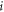 and
and 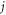 with a large separation
with a large separation 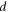 can be expressed as
can be expressed as
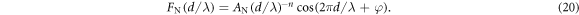
where the amplitude factor ![${A}_{{\rm{N}}}=| {Z}^{ij(n)}| /[{(2\pi )}^{n}{F}_{0}],$](https://content.cld.iop.org/journals/1367-2630/18/11/113034/revision1/njpaa48cbieqn124.gif) the phase shift
the phase shift 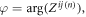 and the power attenuation factor
and the power attenuation factor  or
or 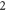 corresponds to the antinode or node plane. The positive (negative) sign of
corresponds to the antinode or node plane. The positive (negative) sign of 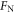 corresponds to a repulsive (attractive) force. Figure 3 shows the pairwise interaction force plotted as a function of the dimensionless inter-particle separation
corresponds to a repulsive (attractive) force. Figure 3 shows the pairwise interaction force plotted as a function of the dimensionless inter-particle separation  where the red dashed and black solid lines provide the comparative results obtained through the theoretical prediction and the rigorous MST approach, respectively. Three different particle sizes are considered, one close to the Rayleigh limit and the other two comparable with the acoustic wavelength. Depending on the stability of a single particle in the
where the red dashed and black solid lines provide the comparative results obtained through the theoretical prediction and the rigorous MST approach, respectively. Three different particle sizes are considered, one close to the Rayleigh limit and the other two comparable with the acoustic wavelength. Depending on the stability of a single particle in the 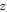 direction, the pair of particles are placed on the same node or antinode plane. It is observed that, the accuracy of equation (20) depends on the particle size and the inter-particle separation simultaneously. A remarkable deviation occurs at the first several wavelengths, especially for the big particles. As the inter-particle separation grows, the analytical results always capture well the MST data for all particle sizes. Without data presented here, we have also studied the pairwise interactions for the non-Rayleigh particles made of, e.g., steel, olive, and air, which carry strikingly different acoustic properties. Again, excellent accuracy of our analytical approach has been revealed by comparing with the MST results, as long as the inter-particle separation is larger than several wavelengths.
direction, the pair of particles are placed on the same node or antinode plane. It is observed that, the accuracy of equation (20) depends on the particle size and the inter-particle separation simultaneously. A remarkable deviation occurs at the first several wavelengths, especially for the big particles. As the inter-particle separation grows, the analytical results always capture well the MST data for all particle sizes. Without data presented here, we have also studied the pairwise interactions for the non-Rayleigh particles made of, e.g., steel, olive, and air, which carry strikingly different acoustic properties. Again, excellent accuracy of our analytical approach has been revealed by comparing with the MST results, as long as the inter-particle separation is larger than several wavelengths.
Figure 3. Distance dependence of the pairwise interaction force for three different particle sizes. The black solid and red dashed lines correspond to the results calculated by the rigorous MST method and the analytical formula equation (20), respectively. In (a) and (b), the insets indicate the enlarged forces for the large inter-particle distance.
Download figure:
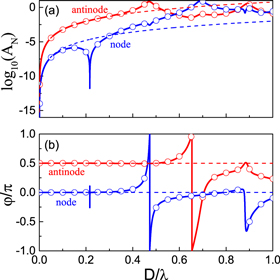
Standard image High-resolution imageWithout resorting to strict MST calculations, the equation (20) enables a direct understanding of the long-range pairwise interaction. In addition to the well-defined power decay factor, the acoustic interaction can be described by two independent quantities, i.e., the dimensionless amplitude factor 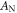 and the phase shift
and the phase shift 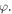 Figure 4 shows
Figure 4 shows 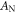 and
and 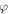 for a pair of polystyrene particles located on the same node plane (blue solid lines) or the antinode plane (red solid lines) of the PSW field, plotted as a function of the particle size
for a pair of polystyrene particles located on the same node plane (blue solid lines) or the antinode plane (red solid lines) of the PSW field, plotted as a function of the particle size 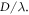 For small particles
For small particles 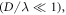 as predicted in the Rayleigh limit (dashed lines),
as predicted in the Rayleigh limit (dashed lines), 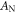 grows fast because of the rapidly enhanced scattering, accompanying with a nearly constant
grows fast because of the rapidly enhanced scattering, accompanying with a nearly constant 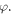 As
As  increases,
increases, 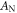 becomes nonmonotonic and
becomes nonmonotonic and 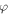 varies sharply (where the latter suggests that the stable configuration is very sensitive to the particle size near the resonance). These features can be understood directly from the characteristics of the scattering matrix elements (see figure 2) and the incident coefficient
varies sharply (where the latter suggests that the stable configuration is very sensitive to the particle size near the resonance). These features can be understood directly from the characteristics of the scattering matrix elements (see figure 2) and the incident coefficient 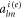 (which is zero for either odd or even
(which is zero for either odd or even 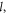 depending on the position of the particle, see equation (3)). For comparison, we have also calculated the pairwise interaction by using the rigorous MST method, and fit the parameters
depending on the position of the particle, see equation (3)). For comparison, we have also calculated the pairwise interaction by using the rigorous MST method, and fit the parameters 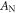 and
and 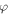 according to equation (20). The fitted data agree well with the analytical ones again, as shown in figure 4 by the blue and red circles.
according to equation (20). The fitted data agree well with the analytical ones again, as shown in figure 4 by the blue and red circles.
Figure 4. The amplitude factor 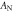 (a) and the phase shift
(a) and the phase shift 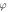 (b) of the long-range acoustic interaction between a pair of polystyrene spheres located on the node plane (blue) or the antinode plane (red), plotted as the function of the dimensionless particle size
(b) of the long-range acoustic interaction between a pair of polystyrene spheres located on the node plane (blue) or the antinode plane (red), plotted as the function of the dimensionless particle size  Here the solid lines are analytical results from equation (20), the dashed lines correspond to the Rayleigh limit, and the circles are fitted from the MST method, respectively.
Here the solid lines are analytical results from equation (20), the dashed lines correspond to the Rayleigh limit, and the circles are fitted from the MST method, respectively.
Download figure:
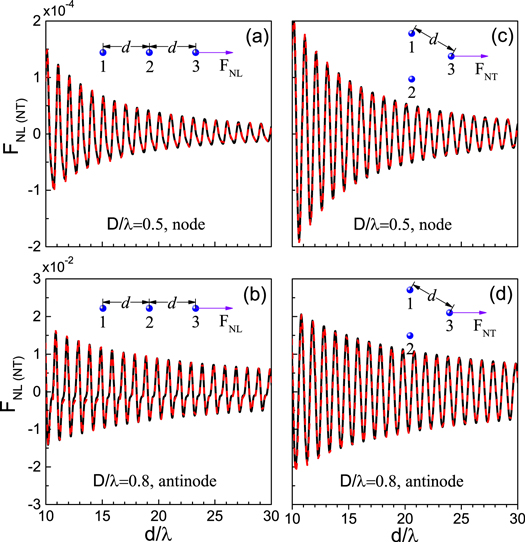
Standard image High-resolution imageNow we check the vector additivity of the long-range acoustic interaction among multiple spherical particles. Without losing generality, we consider three identical polystyrene particles arranged into an equidistant linear array or a regular triangle array. As shown by the insets in figure 5, both configurations can be defined by the separation between adjacent particles. We consider the total force exerted on the third particle, which is along the x direction due to the symmetry of the system. It is easy to derived that for the linear and triangular configurations, the dimensionless total forces labeled by 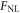 and
and 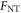 can be expressed as
can be expressed as
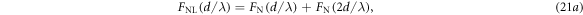
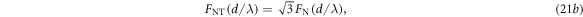
where 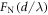 is the pairwise interaction in equation (20). In figure 5 we present the analytical results (red dashed lines) for both configurations, together with the MST (black solid lines) for comparison. The particles with sizes
is the pairwise interaction in equation (20). In figure 5 we present the analytical results (red dashed lines) for both configurations, together with the MST (black solid lines) for comparison. The particles with sizes 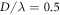 and
and 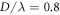 are considered, respectively. Excellent agreements between the two approaches confirm well the vector additivity of the sound-mediated long-range interaction.
are considered, respectively. Excellent agreements between the two approaches confirm well the vector additivity of the sound-mediated long-range interaction.
Figure 5. Verification of the vector additivity for the acoustically mediated long-range interaction, where (a) and (b) correspond to linear configurations, and (c), (d) represent regular triangle configurations. The black solid and red dashed lines correspond to the results calculated by the rigorous MST method and the analytical formula, respectively.
Download figure:
Standard image High-resolution image3.2. The system involving a large number of particles
Below we consider the systems involving many particles. Figure 6(a) shows 91 particles (diameter 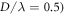 located on the node plane of the PSW field and arranged in a hexagonal lattice. We have calculated the total ARFs exerting on two of the particles (labeled by 1 and 2), one close to the center and the other near the boundary of the particle array, respectively. For these two particles, only the x-component is nonzero because of the mirror symmetry of the system. Figure 6(b) shows the comparative results for one hundred of configurations with different lattice constants
located on the node plane of the PSW field and arranged in a hexagonal lattice. We have calculated the total ARFs exerting on two of the particles (labeled by 1 and 2), one close to the center and the other near the boundary of the particle array, respectively. For these two particles, only the x-component is nonzero because of the mirror symmetry of the system. Figure 6(b) shows the comparative results for one hundred of configurations with different lattice constants 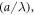 evaluated by our analytical formula (solid lines) and the rigorous MST method (circles). Excellent agreement can be observed. (Note that in both calculations, the cutoff of the angular quantum number
evaluated by our analytical formula (solid lines) and the rigorous MST method (circles). Excellent agreement can be observed. (Note that in both calculations, the cutoff of the angular quantum number 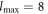 is used.) In the MST approach, ∼28 h is paid to finish the calculation, in which solving the linear problem is time-consuming and requires large memory storage. In contrast, only ∼1.0 s is cost in our analytical method, associated with a negligible memory requirement. It is worth pointing out that, the particle cluster will be eventually driven into a mechanically stable configuration by the nonzero force, as shown by the green circles in figure 6(a), which slightly deviates from the initial configuration of hexagonal lattice.
is used.) In the MST approach, ∼28 h is paid to finish the calculation, in which solving the linear problem is time-consuming and requires large memory storage. In contrast, only ∼1.0 s is cost in our analytical method, associated with a negligible memory requirement. It is worth pointing out that, the particle cluster will be eventually driven into a mechanically stable configuration by the nonzero force, as shown by the green circles in figure 6(a), which slightly deviates from the initial configuration of hexagonal lattice.
Figure 6. (a) A finite hexagonal lattice array of the polystyrene particles (labeled by black circles) located on the node plane of the PSW field. The green circles display a final configuration driven by the nonzero force, starting from an initial state with lattice constant of 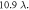 (b) The total interaction forces exerted on the particles 1 (blue) and 2 (red) labeled in (a), evaluated by the analytical formula (solid lines) and the rigorous MST method (circles).
(b) The total interaction forces exerted on the particles 1 (blue) and 2 (red) labeled in (a), evaluated by the analytical formula (solid lines) and the rigorous MST method (circles).
Download figure:
Standard image High-resolution imageThe significant optimization in computation time and memory cost also allows the analytic method to handle a system involving a huge number of particles, which is unattainable by the conventional MST approach. For instance, we consider a system consisting of 101 × 101 particles 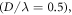 arranged by a square lattice in the node plane of the PSW field. The lattice constant is taken as
arranged by a square lattice in the node plane of the PSW field. The lattice constant is taken as 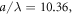 one of the stable distances in the corresponding two-particle system. Obviously, the particle arrangement does not guarantee the stability of the whole system. For every particle, we have calculated the total interaction force exerted by the other particles. Figure 7(a) shows the force amplitudes for all particles. Interestingly, one can observe a much weaker force for the inner particle, comparing with the case near the boundary. Physically, the screening effect of the acoustic interaction can be understood by the cancelation of many pairwise interactions of relatively short distance. For example, as indicated in figure 7(a), the pairwise interaction
one of the stable distances in the corresponding two-particle system. Obviously, the particle arrangement does not guarantee the stability of the whole system. For every particle, we have calculated the total interaction force exerted by the other particles. Figure 7(a) shows the force amplitudes for all particles. Interestingly, one can observe a much weaker force for the inner particle, comparing with the case near the boundary. Physically, the screening effect of the acoustic interaction can be understood by the cancelation of many pairwise interactions of relatively short distance. For example, as indicated in figure 7(a), the pairwise interaction 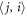 can be balanced by
can be balanced by 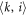 if the position vector satisfies
if the position vector satisfies 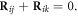 A similar screening effect can be seen in figure 7(b) for the case of
A similar screening effect can be seen in figure 7(b) for the case of 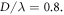 Comparing with figure 7(a), the force attenuation from the boundary is much slower, since the particles are located on the antinode plane now (n = 1).
Comparing with figure 7(a), the force attenuation from the boundary is much slower, since the particles are located on the antinode plane now (n = 1).
Figure 7. (a) The force pattern for 101x101 polystyrene particles (with diameter 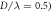 arranged in a square lattice (with lattice constant
arranged in a square lattice (with lattice constant 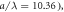 where the color shows the amplitude of the total force exerting on the particle located at the corresponding position. The dashed rectangle frame indicates a particle region that contributes zero force to the particle i. (b) The same as (a), but for the particle size
where the color shows the amplitude of the total force exerting on the particle located at the corresponding position. The dashed rectangle frame indicates a particle region that contributes zero force to the particle i. (b) The same as (a), but for the particle size 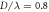 and the lattice constant
and the lattice constant 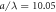 .
.
Download figure:
Standard image High-resolution image4. Conclusion
Starting from a single prior scattering approximation, we have derived a compact analytical formula for the sound-mediated interaction among sparsely distributed particles. The formula, confirmed by the rigorous MST method, reveals that a multi-particle system can always be reduced to a two-particle problem, irrelevant to the size of particles. A combination of our analytical method with the MST approach could be helpful to further handle a big particle cluster with arbitrary inter-particle separations. The possibility of such new type of oscillatory long-range interactions in creating thermodynamically stable 2D colloidal crystals is also of great interest4 .
Acknowledgments
This work is supported by the National Basic Research Program of China (Grant No. 2015CB755500); National Natural Science Foundation of China (Grant Nos. 11374233, 11534013, 11674250, and 11547310).
Footnotes
- 4
Here we give a brief comment on the energy barrier between two adjacent bound states in the pairwise interaction. Consider the wave frequency 11 MHz and the pressure amplitude 0.045 MPa [32]. The energy barrier, decaying as 1/d or 1/d2 again, is high enough to overcome the thermal effect. For instance, the energy barriers between two adjacent bound states (with d/λ ∼ 20) are ∼102kBT for D/λ = 0.5 and ∼105kBT for D/λ = 0.8. Here kB is the Boltzmann constant and T = 300 K is the room temperature. This reveals the possibility of binding particles at large distance through acoustic waves.