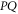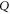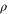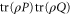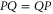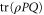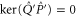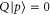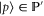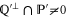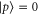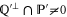Abstract
It is known that non-commuting observables in quantum mechanics do not have joint probability. This statement refers to the precise (additive) probability model. I show that the joint distribution of any non-commuting pair of variables can be quantified via upper and lower probabilities, i.e. the joint probability is described by an interval instead of a number (imprecise probability). I propose transparent axioms from which the upper and lower probability operators follow. The imprecise probability depend on the non-commuting observables, is linear over the state (density matrix) and reverts to the usual expression for commuting observables.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Non-commuting observables in quantum mechanics do not have a joint probability [1–5] (see appendix
As a possible alternative to quasi-probabilities, one can relax the requirement that the sought joint probability correctly reproduces the marginals3
. This is done when studying joint measurements of non-commuting variables [4, 5, 21–26]. Such measurements have to be approximate, since they operate on an arbitrary initial state [4, 5]. They produce positive probabilities for the measurement results, but it is not clear to which extent these probabilities are intrinsic [27], i.e. to which extent they characterize the system itself, and not approximate measurements employed. Alternatively, one can consider two consecutive measurements of the non-commuting observables [28, 29]. These two-time probabilities do not (generally) qualify for the joint probability of the non-commuting observables; see appendix
It is assumed that the sought joint probability is linear over the state (density matrix). If this condition is skipped, there are positive probabilities that correctly reproduce marginals for non-commuting observables [20, 24], e.g. simply the product of two marginals [13]. However, they do not reduce to the usual form of the joint quantum probability for commuting observables4 ; hence their physical meaning is unclear [13].
The statement on the non-existence of joint probability concern the usual precise and additive probability. This is not the only model of uncertainty. It was recognized since early days of probability theory [49] that the probability need not be precise: instead of being a definite number, it can be a definite interval [51–54]; see [55] for an elementary introduction5 .
Instead of a precise probability for an event E, the measure of uncertainty is now an interval ![$[\underline{p}(E),\bar{p}(E)]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn7.gif) , where
, where 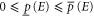 are called lower and upper probabilities, respectively. Qualitatively,
are called lower and upper probabilities, respectively. Qualitatively, 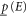 (
(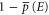 ) is a measure of a sure evidence in favor (against) of E. The event E is surely more probable than E', if
) is a measure of a sure evidence in favor (against) of E. The event E is surely more probable than E', if 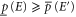 . The usual probability is recovered for
. The usual probability is recovered for 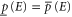 . Two different pairs
. Two different pairs ![$[\underline{p}(E),\bar{p}(E)]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn13.gif) and
and ![$[\underline{p}^{\prime} (E),\bar{p}^{\prime} (E)]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn14.gif) can hold simultaneously (i.e. they are consistent), provided that
can hold simultaneously (i.e. they are consistent), provided that 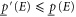 and
and 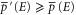 for all E. In particular, every imprecise probability is consistent with6
for all E. In particular, every imprecise probability is consistent with6
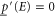 ,
, 
It is not assumed that for all E there is a true (precise, but unknown) probability that lies in ![$[\underline{p}(E),\bar{p}(E)]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn19.gif) . This assumption is frequently (but not always [34]) made in applications7
[52, 53], and it did motivate the generalized Kolmogorovian axiomatics of imprecise probability [54]; see appendix
. This assumption is frequently (but not always [34]) made in applications7
[52, 53], and it did motivate the generalized Kolmogorovian axiomatics of imprecise probability [54]; see appendix
My purpose here is to propose a transparent set of conditions (axioms) that lead to quantum lower and upper joint probabilities. They depend only on the involved non-commuting observables (and on the quantum state).
The next section discusses previous attempts to introduce imprecise probability in quantum physics. Section 3 recalls standard linear algebra notations employed in this work. Section 4 describes physical conditions that are imposed on the sought imprecise probability. Section 5 outlines the main linear-algebra tool (CS-representation for projection operators) that is employed for finding the imprecise probability operators. Details of this representation are outlined in appendix
2. Previous work
In 1967 Prugovecki tried to describe the joint probability of two non-commuting observables in a way that resembles imprecise probabilities [30]. But his expression was not correct, since it still can be negative [13]; cf footnote 1 and see also [18] in this context.
In 1991 Suppes and Zanotti proposed a local upper probability model for the standard setup of Bell inequalities (two entangled spins) [31]; see also [32, 33]. The formulation was given in the classical event space of hidden variables, and it is not unique even for the particular case considered. It violates classical observability conditions for the imprecise probability [31, 34, 54]. In particular, no lower probability exists in this scheme. Despite of such drawbacks, the pertinent message of [31] is that one should attempt at quantum applications of the upper probabilities that go beyond its classical axioms.
More recently, Galvan attempted to empoy (classical) imprecise probabilities for describing quantum dynamics in configuration space [37]. For a general discussion on quantum versus classical probabilities see [38].
3. Notations
All operators (matrices) live in a finite-dimensional Hilbert space 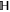 . For two Hermitean operators Y and Z,
. For two Hermitean operators Y and Z, 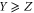 means that all eigenvalues of
means that all eigenvalues of 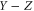 are non-negative, i.e.
are non-negative, i.e.  for any
for any 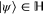 . The direct sum
. The direct sum 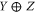 of two operators refers to the following block-diagonal matrix:
of two operators refers to the following block-diagonal matrix:
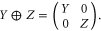
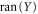 is the range of Y (set of vectors
is the range of Y (set of vectors  , where
, where  ).
). 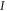 is the unity operator of
is the unity operator of 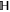 .
. 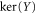 is the subspace of vectors
is the subspace of vectors 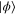 with
with 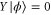 .
.
 and 0n are the n × n unity and zero matrices, respectively.
and 0n are the n × n unity and zero matrices, respectively.
In the direct sum of two sub-spaces,  it is always understood that
it is always understood that  and
and 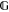 are orthogonal. The vector sum of (not necessarily orthogonal) sub-spaces
are orthogonal. The vector sum of (not necessarily orthogonal) sub-spaces 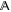 and
and 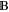 will be denoted as
will be denoted as  . This space is formed by all vectors
. This space is formed by all vectors 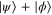 , where
, where 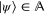 and
and  .
.
4. Axioms for quantum imprecise probability
Existing axioms for imprecise probability are formulated on a classical event space with usual notions of con- and disjunction and complemention [51, 51–54]; see appendix
The usual quantum probability can be defined over (Hermitean) projectors 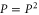 [39, 40]. A projector generalizes the classical notion of characteristic function. Each
[39, 40]. A projector generalizes the classical notion of characteristic function. Each 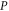 uniquely relates to its eigenspace
uniquely relates to its eigenspace 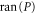 .
.  refers to a set of Hermitean operators
refers to a set of Hermitean operators 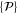 :
:
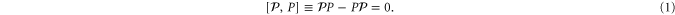
 is a projector to an eigenspace of
is a projector to an eigenspace of 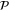 or to a direct sum of such eigenspaces, i.e.
or to a direct sum of such eigenspaces, i.e. 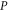 refers to an eigenvalue of
refers to an eigenvalue of 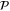 or to a union of several eigenvalues. The quantum (precise and additive) probability to observe
or to a union of several eigenvalues. The quantum (precise and additive) probability to observe 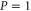 is
is ![$\mathrm{tr}[\rho P]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn54.gif) , where the density matrix
, where the density matrix  defines the quantum state [4, 5, 39, 40].
defines the quantum state [4, 5, 39, 40].
Let 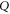 be another projector which refers to the set
be another projector which refers to the set 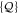 of observables. Generally,
of observables. Generally, ![$[P,Q]\ne 0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn58.gif) . Given the density matrix ρ, we seek upper and lower joint probabilities of
. Given the density matrix ρ, we seek upper and lower joint probabilities of 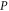 and
and  (i.e. of the corresponding eigenvalues of
(i.e. of the corresponding eigenvalues of 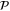 and
and 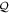 ):
):
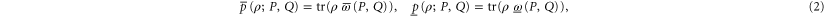
where 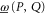 and
and 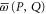 are Hermitean operators. Note that the upper and lower probabilities in (2) are assumed to have the usual Born's form, as far as their dependence on ρ is concerned.
are Hermitean operators. Note that the upper and lower probabilities in (2) are assumed to have the usual Born's form, as far as their dependence on ρ is concerned.
We impose the following conditions (axioms):


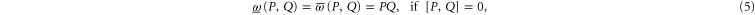

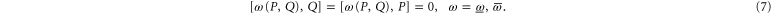
Equation (2) implies that 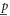 and
and 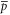 depend on
depend on 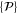 and
and  only through
only through  and
and 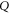 . This non-contextuality feature holds also for the ordinary (one-variable) quantum probability [43, 44]. Provided that the operators
. This non-contextuality feature holds also for the ordinary (one-variable) quantum probability [43, 44]. Provided that the operators  and
and 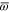 are found,
are found,  and
and 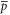 can be determined in the usual way of quantum averages.
can be determined in the usual way of quantum averages.
Conditions (3) stem from 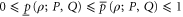 that are demanded for all density matrices ρ. Equation (4) is the symmetry condition necessary for the joint probability. Equation (5) is reversion to the commuting case. In particular, (5) ensures
that are demanded for all density matrices ρ. Equation (4) is the symmetry condition necessary for the joint probability. Equation (5) is reversion to the commuting case. In particular, (5) ensures 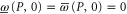 and
and

Since 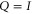 means that
means that 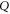 is anywhere, (8) is the reproduction of the marginal probability. The latter cannot be recovered by summation, since the very probability model is not additive.
is anywhere, (8) is the reproduction of the marginal probability. The latter cannot be recovered by summation, since the very probability model is not additive.
For ![$[P,Q]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn81.gif) the joint probability is
the joint probability is  . This expression is well-defined (i.e. positive, symmetric and additive) also for
. This expression is well-defined (i.e. positive, symmetric and additive) also for ![$[\rho ,Q]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn83.gif) or
or ![$[\rho ,P]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn84.gif) (but not necessarily
(but not necessarily ![$[P,Q]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn85.gif) ). If
). If ![$[\rho ,Q]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn86.gif) , one obtains
, one obtains 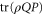 by measuring
by measuring 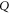 (ρ is not disturbed) and then
(ρ is not disturbed) and then 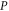 . Alternatively, one can obtain it by measuring the average of an Hermitean observable
. Alternatively, one can obtain it by measuring the average of an Hermitean observable 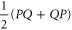 . Thus (5), (6) demands that
. Thus (5), (6) demands that  and
and 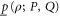 are consistent with the joint probability
are consistent with the joint probability 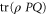 , whenever the latter is well-defined.
, whenever the latter is well-defined.
Finally, equation (7) means that 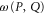 (
( ) can be measured simultaneously and precisely with
) can be measured simultaneously and precisely with 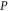 or with
or with  (on any quantum state), a natural condition for the joint probability (operators)8
.
(on any quantum state), a natural condition for the joint probability (operators)8
.
If there are several candidates satisfying (3)–(7) we shall naturally select the ones providing the largest lower probability and the smallest upper probability.
5. CS-representation
This representation will be our main tool. Given the projectors  and Q, Hilbert space
and Q, Hilbert space 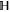 can be represented as a direct sum [45–47] (see appendix
can be represented as a direct sum [45–47] (see appendix

where the sub-space 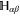 of dimension
of dimension 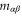 is formed by common eigenvectors of
is formed by common eigenvectors of 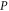 and
and 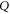 having eigenvalue α (for
having eigenvalue α (for  ) and β (for Q). Depending on
) and β (for Q). Depending on  and
and 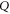 every sub-space can be absent; all of them can be present only for
every sub-space can be absent; all of them can be present only for 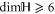 . Now
. Now  is the intersection of the ranges of
is the intersection of the ranges of 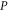 and
and 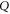 .
. 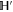 has even dimension 2
has even dimension 2 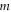 [46, 47], this is the only sub-space in (9) that is not formed by common eigenvectors of
[46, 47], this is the only sub-space in (9) that is not formed by common eigenvectors of 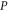 and
and  . There exists a unitary transformation
. There exists a unitary transformation
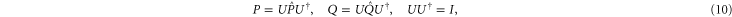
so that 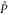 and
and 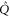 get the following block-diagonal form related to (9) [46]:
get the following block-diagonal form related to (9) [46]:
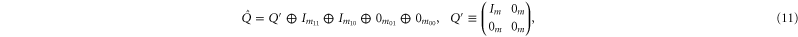
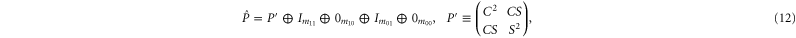
where C and S are invertible square matrices of the same size holding
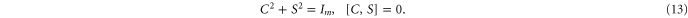
Now 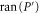 and
and 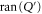 are sub-spaces of
are sub-spaces of 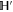 . One has
. One has 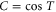 and
and 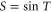 , where T is the operator analogue of the angle between two spaces.
, where T is the operator analogue of the angle between two spaces. 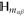 are absent, if P and Q do not have any common eigenvector. This, in particular, happens in
are absent, if P and Q do not have any common eigenvector. This, in particular, happens in  .
.
6. The main result
Note that if (3)–(7) holds for 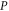 and Q, they hold as well for
and Q, they hold as well for 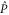 and
and 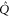 , because
, because 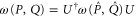 for
for 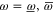 . Appendix
. Appendix 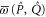 and
and 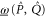 from (3)–(7) and (11), (12):
from (3)–(7) and (11), (12):
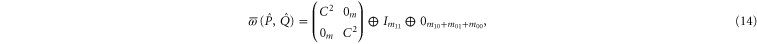
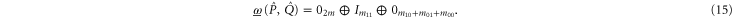
Let  be the projector onto intersection
be the projector onto intersection 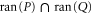 of
of 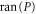 and
and 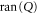 . We now return from (10), (14) and (15) to original projectors
. We now return from (10), (14) and (15) to original projectors 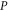 and
and 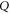 (see appendix
(see appendix


For ![$[P,Q]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn137.gif) ,
, 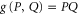 , and we revert to
, and we revert to 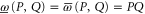 . Note that
. Note that ![$[P,{(P-Q)}^{2}]=[Q,{(P-Q)}^{2}]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn140.gif) .
.
7. Physical meaning of upper and lower probability operators
When looking for a joint probability defined over two projectors 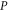 and
and 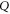 one wonders whether it is just not some (operator) mean of
one wonders whether it is just not some (operator) mean of 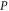 and
and  . For ordinary numbers
. For ordinary numbers 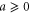 and
and 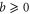 there are three means: arithmetic
there are three means: arithmetic  , geometric
, geometric  and harmonic
and harmonic 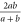 . Now (16) is precisely the operator harmonic mean of
. Now (16) is precisely the operator harmonic mean of  and
and 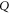 [57]
[57]
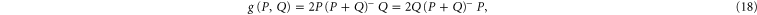
where 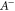 is the inverse of A if it exists, otherwise it is the pseudo-inverse; see appendix
is the inverse of A if it exists, otherwise it is the pseudo-inverse; see appendix 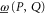 and
and 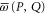 . More familiar formula is
. More familiar formula is
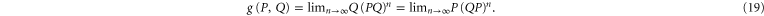
The intersection projector 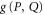 appears in [39–43]. It was stressed that
appears in [39–43]. It was stressed that 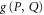 cannot be a joint probability for non-commutative
cannot be a joint probability for non-commutative 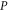 and
and 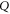 [21]. Its meaning is clear by now: it is the lower probability for
[21]. Its meaning is clear by now: it is the lower probability for  and
and 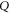 . Note that
. Note that
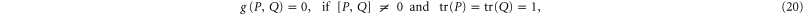
since two different rays ( and
and 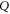 ) cross only at zero. Thus,
) cross only at zero. Thus, 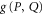 is non-zero for
is non-zero for ![$[P,Q]\ne 0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn164.gif) , only if
, only if  (or
(or 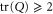 ). I consider this as a natural features of the quantum lower probability, because the classical case—where the lower probability is expected to be non-zero and close to the upper probability—can be generically reached due to the coarse-graining, i.e. due to
). I consider this as a natural features of the quantum lower probability, because the classical case—where the lower probability is expected to be non-zero and close to the upper probability—can be generically reached due to the coarse-graining, i.e. due to 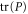 (or
(or  , or both) being sufficiently larger than 1.
, or both) being sufficiently larger than 1.
Let us now turn to 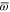 . The transition probability between two pure states is determined by the squared cosine of the angle between them:
. The transition probability between two pure states is determined by the squared cosine of the angle between them: 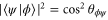 . Equation (14) shows that
. Equation (14) shows that  depends on
depends on  , where T is the operator angle between
, where T is the operator angle between  and
and 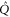 . Note from (11), (12) that the eigenvalues λ of
. Note from (11), (12) that the eigenvalues λ of 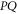 , which hold
, which hold 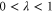 are the eigenvalues of C2, and
are the eigenvalues of C2, and 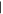 as seen from (14)—they are also (doubly-degenerate) eigenvalues of
as seen from (14)—they are also (doubly-degenerate) eigenvalues of 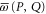 . Thus we have a physical interpretation not only for
. Thus we have a physical interpretation not only for  (transition probability), but also for eigenvalues of
(transition probability), but also for eigenvalues of 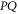 (
(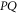 and
and  have the same eigenvalues).
have the same eigenvalues).
Equations (10), (14) and (15) imply that the upper and lower probability operators can be measured simultaneously on any state (cf (7)):
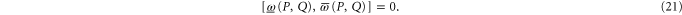
The operator  quantifies the uncertainty for joint probability, the physical meaning of this characteristics of non-commutativity is new.
quantifies the uncertainty for joint probability, the physical meaning of this characteristics of non-commutativity is new.
Appendix
Note that the conditional (upper and lower) probabilities are straighforward to define, e.g. (cf (2)):  .
.
The distance between two probability intervals ![$[\underline{p},\bar{p}]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn185.gif) and
and ![$[\underline{p}^{\prime} ,\bar{p}^{\prime} ]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn186.gif) can be calculated via the Haussdorff metric [56]
can be calculated via the Haussdorff metric [56]

which nullifies if and only if  and
and  , and which reduces to the ordinary distance
, and which reduces to the ordinary distance  for usual (precise) probabilities.
for usual (precise) probabilities.
Let us see when we can use the notion of 'surely more probable'. Now
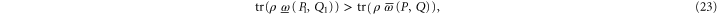
means that the pair of projectors 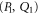 is surely more probable (on ρ) than
is surely more probable (on ρ) than  ; see appendix
; see appendix
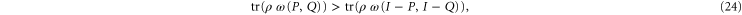
holds for 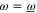 , then it also hods for
, then it also hods for  (and vice versa). Though in a weaker sense than (23), (24) means that
(and vice versa). Though in a weaker sense than (23), (24) means that 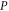 and
and 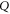 together is more probable than neither of them together (which is the pair
together is more probable than neither of them together (which is the pair 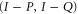 ). equations (23), (24) are examples of comparative (modal) probability statements; see [36] in this context.
). equations (23), (24) are examples of comparative (modal) probability statements; see [36] in this context.
Further features of  and
and  are uncovered when looking at a monotonic change of their arguments; see appendix
are uncovered when looking at a monotonic change of their arguments; see appendix
8. Coordinate and momentum
Coordinate x and momentum p operators, ![$[x,p]={\rm{i}}$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn199.gif) (
(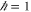 ) is the most known example of non-commutativity in quantum mechanics. Hence I shall illustrate the upper and lower probability for this example. In the (one-dimensional) x-representation, x-operator amounts to multiplication, while
) is the most known example of non-commutativity in quantum mechanics. Hence I shall illustrate the upper and lower probability for this example. In the (one-dimensional) x-representation, x-operator amounts to multiplication, while 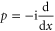 . For intervals
. For intervals 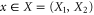 and
and 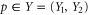 the corresponding projectors read in the coordinate representation
the corresponding projectors read in the coordinate representation
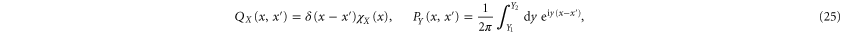
where 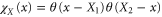 is the characteristic function of interval X. Recall that QY and PY are linked via the Fourier transform:
is the characteristic function of interval X. Recall that QY and PY are linked via the Fourier transform:
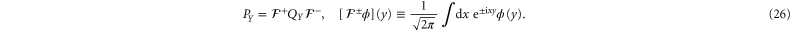
The first thing to note is that if X and Y are finite intervals, then  , i.e.
, i.e. 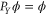 and
and 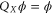 lead to
lead to 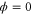 . This is a well-known result in the Fourier analysis; see, e.g. [61–63]. The simplest way to show it is to note (from (26)) that
. This is a well-known result in the Fourier analysis; see, e.g. [61–63]. The simplest way to show it is to note (from (26)) that  has a finite support, hence
has a finite support, hence 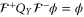 is analytic. On the other hand, ϕ should have a finite support. Thus
is analytic. On the other hand, ϕ should have a finite support. Thus 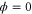 . This argument extends to the case, where (say) Y is semi-infinite, e.g.
. This argument extends to the case, where (say) Y is semi-infinite, e.g. 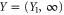 , while X differs from
, while X differs from 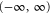 by a finite (or semi-infinite) interval [63]. Indeed, now
by a finite (or semi-infinite) interval [63]. Indeed, now =\frac{1}{\sqrt{2\pi }}\int {\rm{d}}\xi \;{{\rm{e}}}^{{\rm{i}}x\xi }[{Q}_{Y}{{\mathcal{F}}}^{-}\phi ](\xi )$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn214.gif) is analytic for
is analytic for 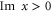 , while from
, while from 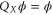 it follows that
it follows that 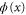 is zero in a finite interval at least.
is zero in a finite interval at least.
Thus, for finite (or at least one semi-infinite) intervals X and Y the lower probability for the joint distribution of the coordinate and momentum is zero (cf (16) )
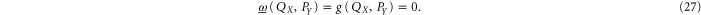
However, if both X and Y are finite intervals, 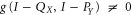 , e.g. the above analiticity argument does not work. Moreover,
, e.g. the above analiticity argument does not work. Moreover, 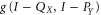 has a discrete spectrum, and its range is infinite-dimensional [61, 62]. We shall avoid this complication by looking at those case, where (at least) one of X and Y is semi-infinite. Then (27) still holds, while the upper probability operator
has a discrete spectrum, and its range is infinite-dimensional [61, 62]. We shall avoid this complication by looking at those case, where (at least) one of X and Y is semi-infinite. Then (27) still holds, while the upper probability operator  reduces to (cf (17))
reduces to (cf (17))
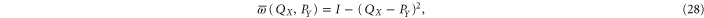
and is straightforward to calculate via (25). Several examples of the upper probability calculated from (28) are presented in figure 1.
Figure 1. The upper probability 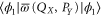 , where
, where  is given by (28) with
is given by (28) with 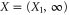 and
and ![$Y=[-0.5,0.5]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn224.gif) (red curve),
(red curve), ![$Y=[-1,1]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn225.gif) (blue curve),
(blue curve), ![$Y=[-1.5,1.5]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn226.gif) (green curve),
(green curve), ![$Y=[-2,2]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn227.gif) (black curve). Here
(black curve). Here 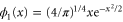 is the wave-function of the first excited level for the harmonic oscillator with Hamiltonian
is the wave-function of the first excited level for the harmonic oscillator with Hamiltonian 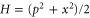 . This example of
. This example of  is chosen, because the Wigner function for the excited states of the harmonic oscillator is negative [8] and thus cannot serve for probabilistic reasoning. Note that for small values of X1 (left plateau on the figure),
is chosen, because the Wigner function for the excited states of the harmonic oscillator is negative [8] and thus cannot serve for probabilistic reasoning. Note that for small values of X1 (left plateau on the figure), 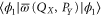 tends to
tends to 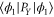 , while for large values of X1 it tends to
, while for large values of X1 it tends to 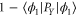 . For the eigen-functions of
. For the eigen-functions of 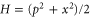 , the (marginal) distributions of the coordinate and momentum are equal, e.g.
, the (marginal) distributions of the coordinate and momentum are equal, e.g. 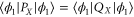 .
.
Download figure:
Standard image High-resolution image9. Summary and open problems
The main message of this work is that while joint precise probability for non-commuting observables does not exist, there are well-defined operator expressions for upper and lower imprecise probabilities. They are not additive, but otherwise they do satisfy a number of reasonable conditions: positivity, reproduction of correct marginals, direct observability via quantum averages, consistency with the (effectively) commuting case, where the joint probability is well-defined etc.
Several open questions are suggested by this research. First of all, it is not clear what is the suitable way of defining averages over the imprecise probability. This would be necessary for defining various correlation functions. Recall that the average 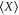 of a random variable X that has a precise probability is defined via two conditions (see e.g. [60]): linearity,
of a random variable X that has a precise probability is defined via two conditions (see e.g. [60]): linearity, 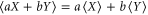 , and monotonicity,
, and monotonicity, 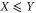 implies
implies  . Presumably, these conditions are to be modified for imprecise probability; in addition the sought average should reduce to the usual one when averaging over a single observable. This question should be clarified before the imprecise probability can be efficiently applied in quantum statistical mechanics.
. Presumably, these conditions are to be modified for imprecise probability; in addition the sought average should reduce to the usual one when averaging over a single observable. This question should be clarified before the imprecise probability can be efficiently applied in quantum statistical mechanics.
Another open issue relates to the point (see (6)) that whenever the joint probability 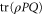 for non-commuting projectors
for non-commuting projectors  and
and  is well defined due to e.g.
is well defined due to e.g. ![$[\rho ,P]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn243.gif) (see the discussion after (8)), the upper and lower probabilities
(see the discussion after (8)), the upper and lower probabilities 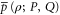 and
and 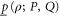 are merely consistent with the exact probability
are merely consistent with the exact probability  , but are not equal to it, which would be a more desired outcome. It is thus not completely clear whether the found imprecise probabilities cannot be made more precise by looking at more general conditions (axioms), e.g. those that involve a nonlinear dependence on the density matrix ρ; cf (2). Such a dependence might however impede the direct observability of imprecise probabilities; the resulting issues need further investigations.
, but are not equal to it, which would be a more desired outcome. It is thus not completely clear whether the found imprecise probabilities cannot be made more precise by looking at more general conditions (axioms), e.g. those that involve a nonlinear dependence on the density matrix ρ; cf (2). Such a dependence might however impede the direct observability of imprecise probabilities; the resulting issues need further investigations.
In a more remote perspective, one can ask about the joint imprecise probability of 3 (and more) non-commuting observables. In contrast to the previous two open problems, where the progress looks to be feasible, this is a difficult problem, because no analogue of the CS-representation for 3 (or more) non-commuting projectors seems to exists; see however [64].
Acknowledgments
I thank KV Hovhannisyan for discussions. I was supported by COST network MP1209.
Appendices
All 6 appendices can be read independently from each other.
Appendices A–C recall, respectively, the no-go statements for the joint quantum probability, generalized axiomatics for the imprecise probability and the CS-representation. This material is not new, but is presented in a focused form, adapted from several different sources.
Appendix D contains the derivation of the main result, while appendices E and F demonstrate various feature of quantum imprecise probability.
Appendix G illustrates it with simple physical examples.
Appendix A.: Non-existence of (precise) joint probability for non-commuting observables
A.1. The basic argument
Given two sets of non-commuting Hermitean projectors:
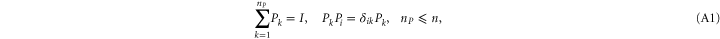

we are looking for non-negative operators 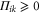 such that for an arbitrary density matrix ρ
such that for an arbitrary density matrix ρ
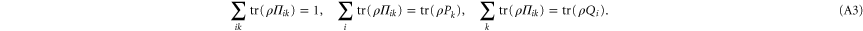
These relations imply
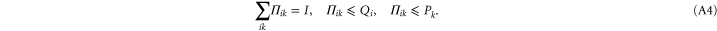
Now the second (third) relation in (A4) implies  (
( ). Hence
). Hence 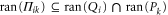 .
.
Thus, if 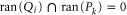 (e.g. when Pk and Qi are one-dimensional (1D)), then
(e.g. when Pk and Qi are one-dimensional (1D)), then 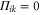 , which means that the sought joint probability does not exist.
, which means that the sought joint probability does not exist.
If 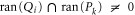 , then the largest
, then the largest 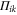 that holds the second and third relation in (A4) is the projection
that holds the second and third relation in (A4) is the projection 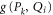 on
on 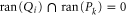 . However, the first relation in (A4) is still impossible to satisfy (for
. However, the first relation in (A4) is still impossible to satisfy (for ![$[{P}_{i},{Q}_{k}]\ne 0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn257.gif) ), as seen from the superadditivity feature (F1):
), as seen from the superadditivity feature (F1):
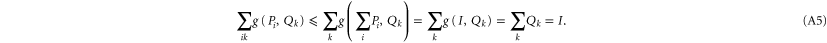
A.2. Two-time probability (as a candidate for the joint probability)
Given (A1), (A2), we can carry out two successive measurements. First (second) we measure a quantity, whose eigen-projections are  (
( ). This results to the following joint probability for the measurement results (ρ is the density matrix)
). This results to the following joint probability for the measurement results (ρ is the density matrix)
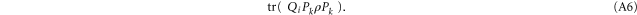
Likewise, if we first measure 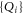 and then
and then 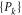 , we obtain a quantity that generally differs from (A6):
, we obtain a quantity that generally differs from (A6):
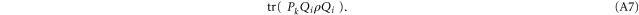
If we attempt to consider (A7) (or (A6)) as a joint additive probability for Pi and Qk, we note that (A7) (and likewise (A6)) reproduces correctly only one marginal:
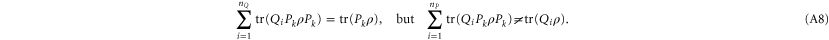
One can attempt to interpret the mean of (A6), (A7)

as a non-additive probability. This object is linear over ρ, symmetric (with respect to interchanging Pk and Qi), non-negative, and reduces to the additive joint probability for ![$[{P}_{k},{Q}_{i}]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn262.gif) . The relation
. The relation  can be interpreted as consistency with the correct marginals (once
can be interpreted as consistency with the correct marginals (once 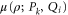 is regarded as a non-additive probability, there is no point in insisting that the marginals are obtained in the additive way).
is regarded as a non-additive probability, there is no point in insisting that the marginals are obtained in the additive way).
However, the additive joint probability 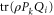 is well-defined also for
is well-defined also for ![$[\rho ,{P}_{k}]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn266.gif) (or for
(or for ![$[\rho ,{Q}_{i}]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn267.gif) ). If
). If ![$[\rho ,{P}_{k}]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn268.gif) holds,
holds,  is not consistent with
is not consistent with 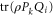 , i.e. depending on ρ, Pk and Qi both
, i.e. depending on ρ, Pk and Qi both
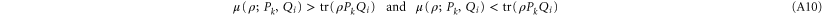
are possible.
To summarize, the two-time measurement results do not qualify as the additive joint probability, first because they are not unique (two different expressions (A6) and (A7) are possible), and second because they do not reproduce the correct marginals. If we take the mean of two expressions (A6) and (A7) and attempt to interpret it as a non-additive probability, it is not compatible with the joint probability, whenever the latter is well-defined.
Appendix B.: Axioms for classical imprecise probability
B.1. Generalized Kolmogorov's axioms
Given the full set of events Ω, 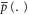 and
and 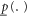 defined over sub-sets
defined over sub-sets 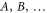 of Ω (including the empty set
of Ω (including the empty set  ) satisfy [52–54]:
) satisfy [52–54]:
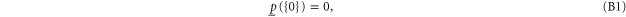
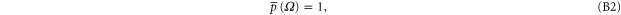
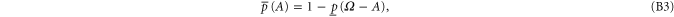
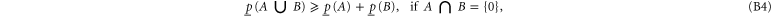
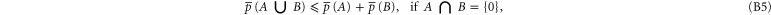
where  includes all elements of Ω that are not in A, and where
includes all elements of Ω that are not in A, and where 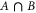 means intersection of two sets;
means intersection of two sets; 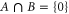 holds for elementary events.
holds for elementary events.
Here are some direct implications of (B1)–(B5)
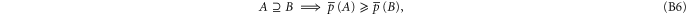
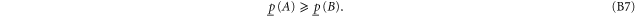
Equation (B7) follows directly from (B4). Equation (B6) follows from (B4), (B3). Next relation:

which, in particular, implies
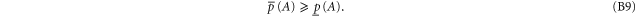
To derive (B8), note that (B4), (B3) imply 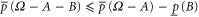 or
or  , which is the first inequality in (B8). The second inequality is derived via (B5), (B3).
, which is the first inequality in (B8). The second inequality is derived via (B5), (B3).
The following inequality generalizes the known relation of the additive probability theory
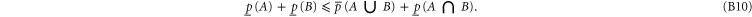
To prove (B10), we denote 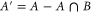 , which means
, which means 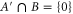 . Now
. Now
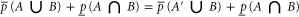
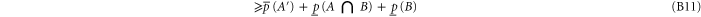
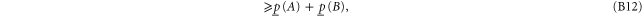
where in (B11) (resp. in (B12)) we applied the first (resp. the second) inequality in (B8).
Note that the (non-negative) difference  between the upper and lower probabilities also holds the super-additivity feature (cd (B5))
between the upper and lower probabilities also holds the super-additivity feature (cd (B5))
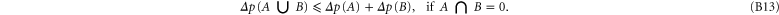
Employing (B8) one can derive [58] for arbitrary A1 and A2:

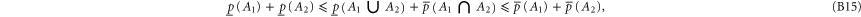
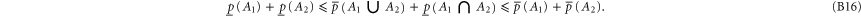
B.2. Joint probability
The joint probabilities of A and B are now defined as
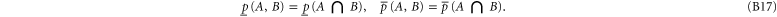
Employing the distributivity feature

which holds for any triple  , we obtain from (B4), (B5) for
, we obtain from (B4), (B5) for 

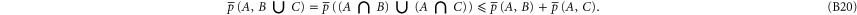
B.3. Dominated upper and lower probability
The origin of (B1)–(B5) can be related to the simplest scheme of hidden variable(s) [52]. One imagines that there exists a precise probability  , where the parameter θ is not known. Only the extremal values over the parameter are known:
, where the parameter θ is not known. Only the extremal values over the parameter are known:
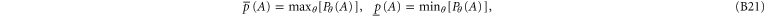
However, it is generally not true that (B1)–(B5) imply the existence of a precise probability  that holds (B21) [53].
that holds (B21) [53].
Appendix C.: Derivation of the CS-representation
C.1. The main theorem
Let 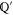 and
and  are two subspaces of Hilbert space
are two subspaces of Hilbert space  that hold (
that hold (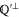 is the orthogonal complement of
is the orthogonal complement of  )
)
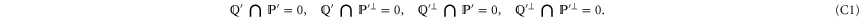
The simplest example realizing (C1) is when 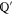 and
and  are 1D subspaces of a two-dimensional (2D)
are 1D subspaces of a two-dimensional (2D) 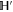 .
.
Let 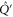 and
and  be projectors onto
be projectors onto 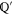 and
and 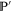 respectively. Now
respectively. Now  is the projector of
is the projector of 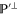 , and let
, and let 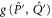 be the projector
be the projector  . Employing the known formulas (see e.g. [47])
. Employing the known formulas (see e.g. [47])
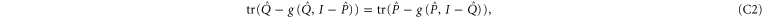
we get from (C1)

which means that 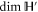 should be even for (C1) to hold9
.
should be even for (C1) to hold9
.
Here is the statement of the CS-representation [46]: after a unitary transformation 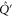 and
and  can be presented as
can be presented as
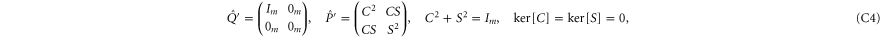
where all blocks in (C4) have the same dimension m.
To prove (C4), note that 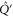 and
and  can be written as (cf (C3))
can be written as (cf (C3))
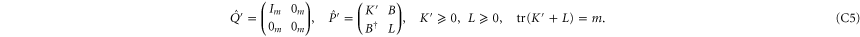
Next, let us show that

Since 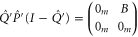 , we need to show that for any
, we need to show that for any  ,
, 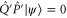 means
means 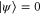 . Indeed, we have
. Indeed, we have 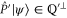 , which together with
, which together with 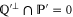 (see (C1)) leads to
(see (C1)) leads to 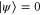 . Equation (C6) implies that there is the well-defined polar decomposition (
. Equation (C6) implies that there is the well-defined polar decomposition (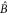 is Hermitean, while V is unitary)
is Hermitean, while V is unitary)

We transform as

where  . We shall now employ the fact that the last matrix in (C8) is a projector:
. We shall now employ the fact that the last matrix in (C8) is a projector:

The first and second relations in (C9) show that ![$[K,\hat{B}]=[L,\hat{B}]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn329.gif) . Then the third relations produces
. Then the third relations produces 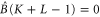 . Since
. Since 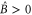 (due to
(due to  ), we conclude that
), we conclude that  . The rest is obvious.
. The rest is obvious.
C.2. Joint commutant for two projectors
Given (C4), we want to find matrices that commute both with 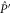 and
and 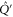 [46]. Matrices that commute with
[46]. Matrices that commute with 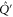 read
read
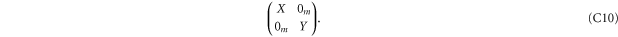
Employing (C4), we get that (C10) commutes with  if
if
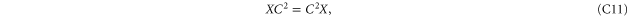
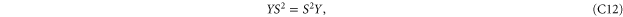
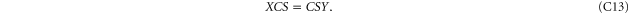
Since C and S are invertible, (C11), (C12) imply that ![$[X,S]=[X,C]=[Y,S]=[Y,C]=0$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn338.gif) . And then (C13) implies that X = Y. Hence
. And then (C13) implies that X = Y. Hence
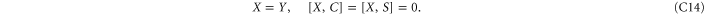
C.3. General form of the CS representation
The above derivation of (C4) assumed conditions (C1). More generally, the Hilbert space  can be represented as a direct sum [45–47]
can be represented as a direct sum [45–47]
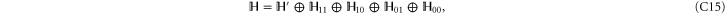
where the sub-space  of dimension
of dimension 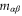 is formed by common eigenvectors of
is formed by common eigenvectors of 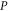 and
and 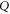 having eigenvalue α (for
having eigenvalue α (for 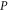 ) and β (for Q). Depending on
) and β (for Q). Depending on  and
and  every sub-space can be absent; all of them can be present only for
every sub-space can be absent; all of them can be present only for  . Now
. Now  .
. 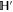 has even dimension
has even dimension  [46, 47], this is the only sub-space that is not formed by common eigenvectors of
[46, 47], this is the only sub-space that is not formed by common eigenvectors of 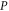 and
and 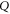 .
.
After a unitary transformation
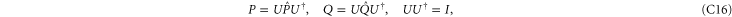
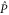 and
and  get the following block-diagonal form that is related to (C15) [46] and that generalizes (C4):
get the following block-diagonal form that is related to (C15) [46] and that generalizes (C4):
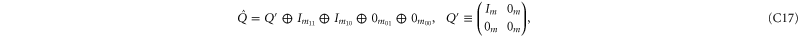
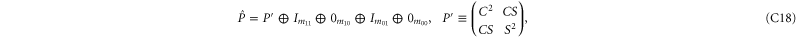
where C and S are invertible square matrices of the same size holding
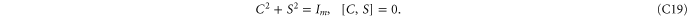
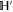 refers to P' and Q'. If
refers to P' and Q'. If 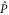 and
and  do not have any common eigenvector,
do not have any common eigenvector, 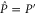 and
and  .
.
Appendix D.: Derivation of the main result (equations (16), (17) of the main text)
We start with representation (C17), (C18) and axioms (3)–(7) of the main text. These axioms hold for 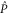 ,
, 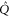 and
and  (see (C16)) instead of
(see (C16)) instead of 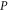 ,
, 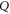 and ρ, because
and ρ, because  for
for 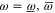 (recall that
(recall that  and
and 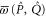 are Taylor expandable). Hence we now search for
are Taylor expandable). Hence we now search for  and
and 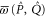 .
.
The block-diagonal form (C17), (C15) remains intact under addition and multiplication of 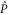 and
and  . Hence
. Hence  and
and 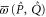 have the block-diagonal form similar to (C17), where the diagonal blocks are to be determined. Let now
have the block-diagonal form similar to (C17), where the diagonal blocks are to be determined. Let now  be the projector on
be the projector on 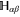 . We get [
. We get [ ]
]
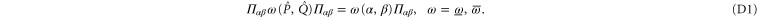
Hence condition (5) of the main text implies [for 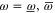 and
and  ]
]
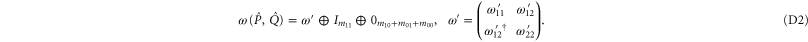
Aiming to apply (6) of the main text, we write down (C17) explicitly as
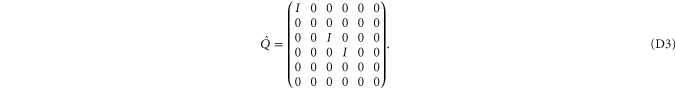
The most general density matrix 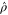 that commutes with
that commutes with 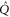 reads (in the same block-diagonal form)
reads (in the same block-diagonal form)

Now 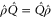 is seen from the fact that after permutations of rows and columns,
is seen from the fact that after permutations of rows and columns, 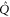 and
and 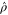 become
become  and
and 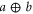 , respectively. Note that
, respectively. Note that 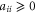 and
and 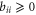 .
.
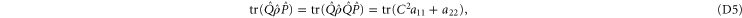
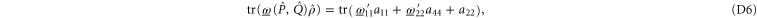
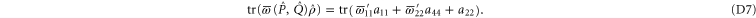
Condition (7) (of the main text) and (C14) imply
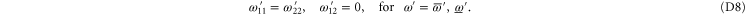
Recall condition (6) of the main text. It amounts to (D5) 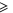 (D6) that should hold for arbitrary aik and bik. Hence we deduce:
(D6) that should hold for arbitrary aik and bik. Hence we deduce: 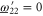 and hence
and hence 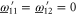 . Likewise, (D7)
. Likewise, (D7)  (D5) leads to
(D5) leads to  ,
, 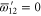 ; recall that we want the smallest upper probability. Now (4) (of the main text) holds, since
; recall that we want the smallest upper probability. Now (4) (of the main text) holds, since
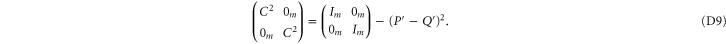
Thus (cf (C15))
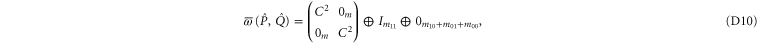
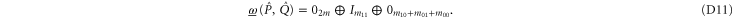
Now  is the projector onto
is the projector onto  . To return from (D10), (D11) to original projectors
. To return from (D10), (D11) to original projectors  and Q, we note via (C17), (C18) (recall that
and Q, we note via (C17), (C18) (recall that 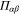 is the projector onto
is the projector onto 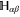 ):
):
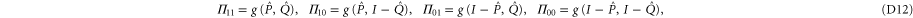
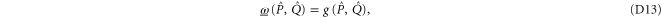
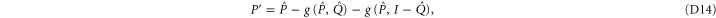
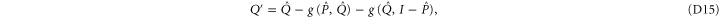
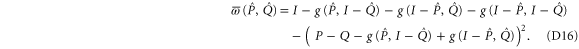
We act back by U, e.g.  , and get finally
, and get finally
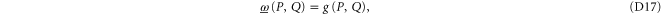

Appendix E.: Various representations of upper and lower probability operators
E.1. Representations for the upper probability operator
Let us turn into a more detailed investigation of (D18). Note from (C17), (C18) and (D12) that  is the projector to
is the projector to  , where
, where  is the vector sum of two sub-spaces. Note the following representation [48]:
is the vector sum of two sub-spaces. Note the following representation [48]:
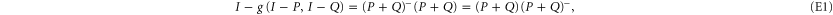
where  is the pseudo-inverse of Hermitean A, i.e. if
is the pseudo-inverse of Hermitean A, i.e. if  (where V is unitary:
(where V is unitary:  ), then
), then 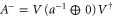 .
.
The third equality in (E1) is the obvious feature of the pseudo-inverse. The first equality in (E1) follows from the fact that 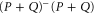 is the projector on
is the projector on  and the known relation [48]:
and the known relation [48]:
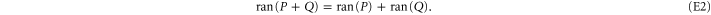
Employing  ,
,  can be presented as a function of
can be presented as a function of 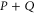 (cf (E1)):
(cf (E1)):
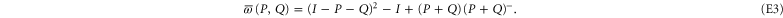
Note another representation for the projector to  [40]
[40]
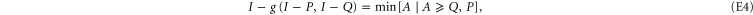
where  equals to the minimal Hermitean operator A that holds two conditions after
equals to the minimal Hermitean operator A that holds two conditions after  .
.
E.2. Representations for the lower probability operator
Let us first show that the projector 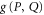 into
into  holds [57]
holds [57]
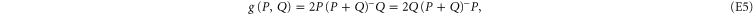
where  is the pseudo-inverse of A (cf (E1)).
is the pseudo-inverse of A (cf (E1)).
The last equality in (E5) follows from the fact that 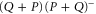 is the projector to
is the projector to 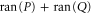 (see (E1), E2)), which then leads to
(see (E1), E2)), which then leads to 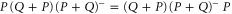 .
.
The first equality in (E5) is shown as follows. Let  . Then using (E5):
. Then using (E5):
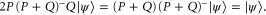
Thus, 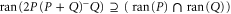 . On the other hand,
. On the other hand,  and
and 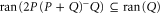 , where the first relation follows from the implication: if
, where the first relation follows from the implication: if 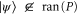 , then
, then 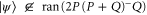 .
.
There are two other (more familiar) representations of 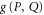 (see e.g. [40, 48]):
(see e.g. [40, 48]):
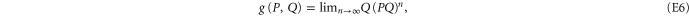

Equation (E6) can be interpreted as a result of (infinitely many) successive measurements of 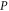 and
and  . Equation (E7) should be compared to (E4).
. Equation (E7) should be compared to (E4).
Yet another representation is useful in calculations, since it explicitly involves a 2 × 2 block-diagonal representation [57]:
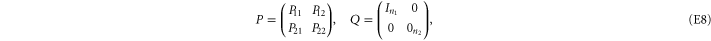

where  ,
, 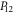 ,
, 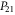 and
and  are, respectively,
are, respectively,  ,
,  ,
, 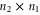 ,
, 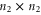 matrices.
matrices.
E.3. Direct relation between the eigenvalues of  and
and 
We can now prove directly (i.e. without employing the CS representation) that there is a direct relation between the eigenvalues of 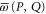 and
and 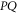 . Let
. Let 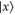 be the eigenvector of Hermitean operator
be the eigenvector of Hermitean operator 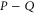 :
:
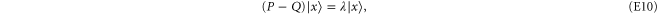
where 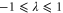 is the eigenvalue. Multiplying both sides of (E10) by
is the eigenvalue. Multiplying both sides of (E10) by 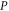 (by Q) and using
(by Q) and using 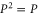 (
(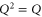 ) we get
) we get
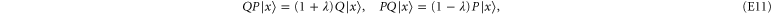
which then implies
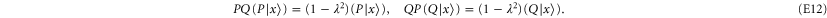
Thus 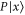 (
(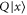 ) is an eigenvector of
) is an eigenvector of 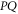 (
(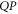 ) with eigenvalue
) with eigenvalue 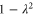 .
.
As seen from (E11), the 2D linear space 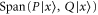 formed by all superpositions of
formed by all superpositions of 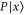 and
and 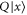 remains invariant under action of both
remains invariant under action of both 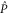 and
and  . Together with
. Together with  this means that if (E10) holds, then
this means that if (E10) holds, then 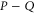 has eigenvalue
has eigenvalue 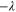 with the eigen-vector living in
with the eigen-vector living in 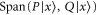 .
.
Further details on the relation between 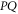 and
and 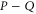 can be looked up in [59].
can be looked up in [59].
Appendix F.: Additivity and monotonicity
We discuss here the behavior of 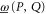 and
and 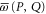 (given by (D17), (D18)) with respect to a monotonic change of their arguments. For two projectors
(given by (D17), (D18)) with respect to a monotonic change of their arguments. For two projectors  and Q,
and Q,  means
means 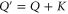 , where
, where  and
and  . Now (D17), (D18) and (E7) imply that
. Now (D17), (D18) and (E7) imply that  is operator superadditive
is operator superadditive
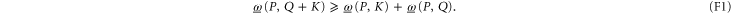
Likewise,  is operator subadditive, but under an additional condition:
is operator subadditive, but under an additional condition:
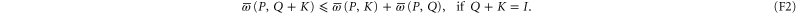
They are the analogues of classical features (B4) and (B5), respectively. Note that (F1) and (B4) are valid under the same conditions, since  is the analogue of
is the analogue of  . In that sense the correspondence between (F2) and (B5) is more limited, since
. In that sense the correspondence between (F2) and (B5) is more limited, since 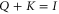 is more restrictive than
is more restrictive than 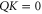 .
.
We focus on deriving (F1), since (F2) is derived in the same way. Note from (E7) that  and
and 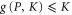 imply
imply 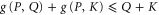 . Since
. Since  ,
,  . Using (E7) for
. Using (E7) for 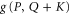 we obtain (F1).
we obtain (F1).
Note as well that both  and
and 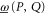 are monotonous [
are monotonous [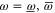 ]:
]:

Equation (F3) for 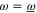 follows from (F1). For
follows from (F1). For  it is deduced as follows (cf (E4), (E7)):
it is deduced as follows (cf (E4), (E7)):
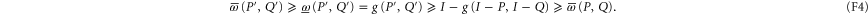
Let us now discuss whether (F2) can hold under the same condition  as (F1). Now
as (F1). Now
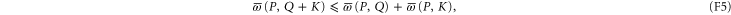
amounts to
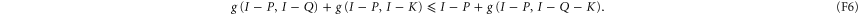
First of all note that for  and
and 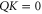 we get
we get 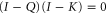 and (F6) does hold for the same reason as (F1).
and (F6) does hold for the same reason as (F1).
For 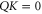 , equation (F6) is invalid in 3D space (as well as for larger dimensional Hilbert spaces). Indeed, let us assume that
, equation (F6) is invalid in 3D space (as well as for larger dimensional Hilbert spaces). Indeed, let us assume that 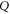 and
and  are 1D:
are 1D:
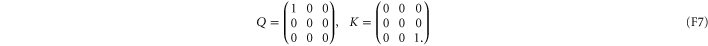
Given  as
as

we get (cf (E9))
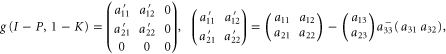
where  is the pseudo-inverse of a33.
is the pseudo-inverse of a33.
Likewise

Now  , since
, since  is a 1d projector. We can now establish that generically
is a 1d projector. We can now establish that generically
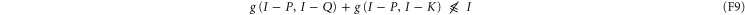
(let alone (F6)), because the difference has both positive and negative eigenvalues.
The message (F9) is that the function 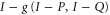 is not sub-additive.
is not sub-additive.
Now consider (F5), (F6), but under additional condition that  . Now (F6) amounts to
. Now (F6) amounts to
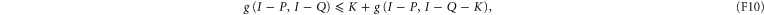
which holds as equality since 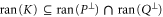 .
.
Appendix G.: Upper and lower probabilities for simple examples
G.1. 2D Hilbert space
It should be clear from (D10), (D11) that in 2D Hilbert space, any lower probability operator  is zero (since two rays overlap only at zero), while the upper probability operator
is zero (since two rays overlap only at zero), while the upper probability operator  just reduces to the transition probability (i.e. to a number)
just reduces to the transition probability (i.e. to a number) 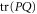 . Thus for the present case both
. Thus for the present case both 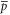 and
and 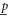 do not depend on ρ.
do not depend on ρ.
G.2. Spin 1
G.2.1. Projectors
The 3 × 3 matrices for the spin components read
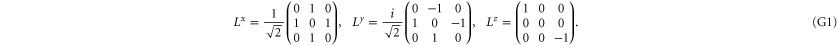
Now 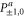 for
for 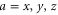 are the 1D projectors to the eigenspace with eigenvalues ± 1 or 0 of La:
are the 1D projectors to the eigenspace with eigenvalues ± 1 or 0 of La:
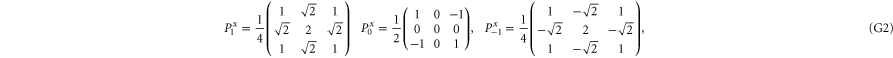
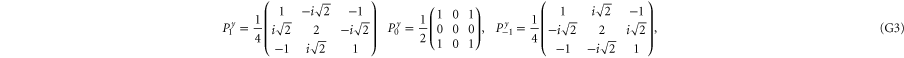
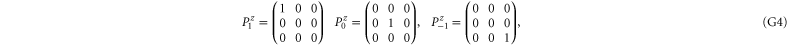
where the zero components are orthogonal to each other:

Other overlaps are simple as well 
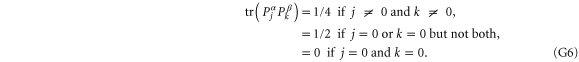
Given two projectors P and Q, we defined  as the projector on
as the projector on 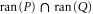 . For calculating
. For calculating 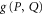 we employ (E5).
we employ (E5).
G.2.2. Fine-grained joint probabilities for  and
and 
Here are upper probability operators for joint values of  and
and 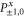 :
:
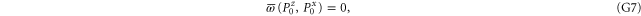
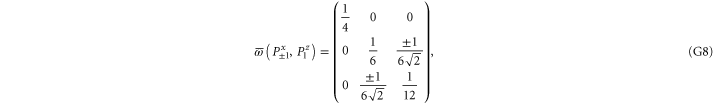
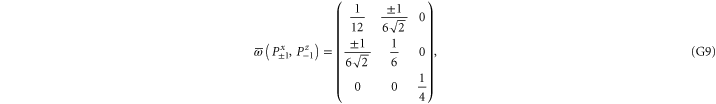
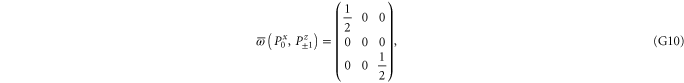
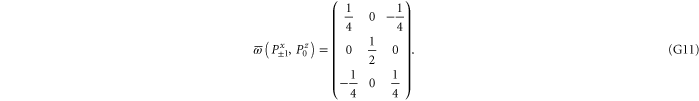
Since 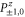 and
and 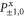 are 1D projectors, all the lower probability operators nullify. Equation (G7) means that the precise probability of Pz0 and Px0 is zero; cf (G5).
are 1D projectors, all the lower probability operators nullify. Equation (G7) means that the precise probability of Pz0 and Px0 is zero; cf (G5).
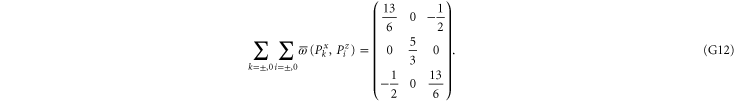
This matrix is larger than 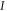 , since its eigenvalues are
, since its eigenvalues are  ,
,  and
and  .
.
Note from (C17), (C18) that for 3 × 3 matrices  , while
, while 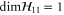 (if this sub-space is present at all). Hence the eigenvalues of
(if this sub-space is present at all). Hence the eigenvalues of  relate to transition probabilities (G6). Indeed, the eigenvalues of matrices in (G8), (G9) (resp. in (G10), (G11)) is
relate to transition probabilities (G6). Indeed, the eigenvalues of matrices in (G8), (G9) (resp. in (G10), (G11)) is  (resp.
(resp.  ). Hence the maximal probability interval
). Hence the maximal probability interval ![$[\frac{1}{4},0]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn529.gif) that can be generated by (G8), (G9) is smaller than the maximal interval
that can be generated by (G8), (G9) is smaller than the maximal interval ![$[\frac{1}{2},0]$](https://content.cld.iop.org/journals/1367-2630/17/8/085005/revision1/njp516246ieqn530.gif) generated by (G10), (G11). As an example, let us take the upper probabilities generated on eigenstates of Ly (
generated by (G10), (G11). As an example, let us take the upper probabilities generated on eigenstates of Ly ( ):
):
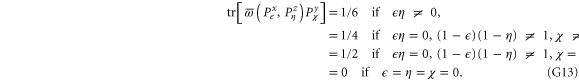
G.2.3. Coarse-grained joint probabilities for  and
and 
Let us now turn to joint probabilities, where the lower probability is non-zero
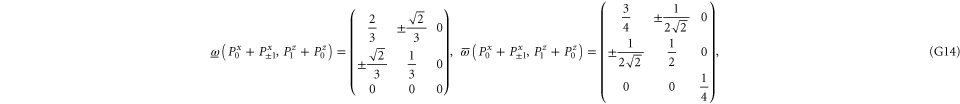
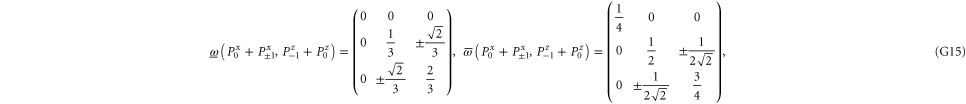
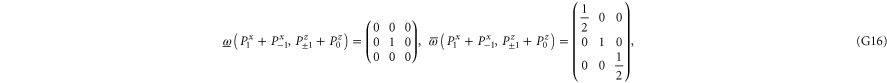
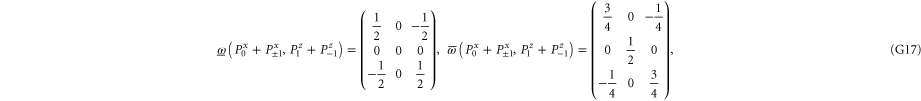
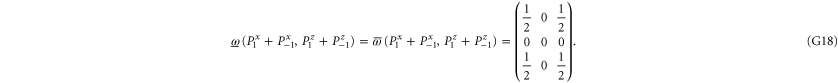
Now  for (G14), (G15) has eigenvalues
for (G14), (G15) has eigenvalues 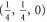 , while for for (G16), (G17) this matrix has eigenvalues
, while for for (G16), (G17) this matrix has eigenvalues  (the last case (G18) refers to the commutative situation). Hence the probabilities for (G16), (G17) are more uncertain.
(the last case (G18) refers to the commutative situation). Hence the probabilities for (G16), (G17) are more uncertain.
Next, let us establish whether certain combinations can be (surely) more probable than others. Note that
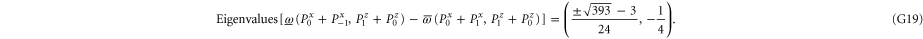
Once there is (one) positive eigenvalue, there is a class of states ρ for which
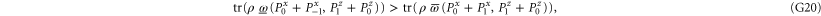
i.e. 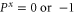 and
and 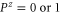 is more probable than
is more probable than 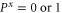 and
and 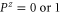 . Note that
. Note that
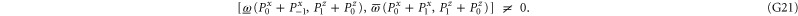
Such examples can be easily continued, e.g.
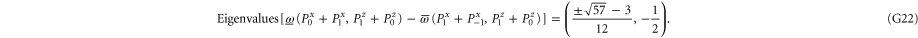
Footnotes
- 1
Negative probabilities were not found to admit a direct physical meaning [14] (what can be less possible, than the impossible?). In certain cases what seemed to be a negative probability was later on found to be a local value of a physical quantity, i.e. physically meaningful, but not a probability [14]. Mathematical meaning of negative probability is discussed in [18, 19].
- 2
One should stress here that the usage of quasi-probabilities in statistical mechanics is frequently implicit, but is nevertheless essential. For instance, the routine introduction of symmetrized correlators of non-commuting variables [17] implies an implicit choice of the underlying Terletsky–Margenau–Hill quasi-probability, because the symmetrized correlators are the 'real' correlators with respect to this quasi-probability. This point is seen in the standard quantum fluctuation–dissipation theorem [17].
- 3
Employing instead the unbiasedness: the averages of the non-commuting quantities are reproduced correctly [22].
- 4
Given two projectors
 and
and  and state
and state  , this product is
, this product is  , while the correct form for
, while the correct form for  is
is  .
. - 5
Ellsberg's paradox is an example in psychology, where the ordinary probability theory does not apply, while imprecise probabilities can be used fruitfully for explaining experimental results on human decision making [50].
- 6
This 'nothing is known' situation cannot be represented by usual probabilities, the simplest example showing that imprecise probabilities can model types of uncertainty that are not captured by the precise model.
- 7
- 8
- 9