Abstract
We show that all Dirichlet series, linear combinations of them and their analytical continuations represent probability amplitudes for measurements on time-dependent quantum systems. In particular, we connect an arbitrary Dirichlet series to the time evolution of an appropriately prepared quantum state in a non-linear oscillator with logarithmic energy spectrum. However, the realization of a superposition of two Dirichlet sums and its analytical continuation requires two quantum systems which are entangled, and a joint measurement. We illustrate our approach of implementing arbitrary Dirichlet series in quantum systems using the example of the Riemann zeta function and relate its non-trivial zeros to the interference of two quantum states reminiscent of a Schrödinger cat.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The representation of a function in terms of a power series [1] is a mathematical tool employed in almost all branches of physics. In contrast, ordinary Dirichlet series [2]
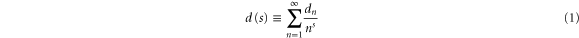
which are central to number theory [3, 4] are extremely rare in physics. In the present paper we show that this disregard by physics is unjustified since Dirichlet series are intimately connected to quantum mechanics [5] through (i) the time evolution governed by the Schrödinger equation, and (ii) joint measurements [6].
This observation allows us to construct a quantum system whose dynamics provides us with a single Dirichlet series, a combination of two Dirichlet series or even the analytical continuation [1] of a Dirichlet series to the complete complex plane. It is remarkable that in the latter cases we can no longer restrict ourselves to a single quantum system and its time evolution, but we must consider joint measurements on an entangled system similar to the generation of Schrödinger cats [7]. This connection suggests an intriguing analogy between two key concepts of complex analysis and quantum theory: analytical continuation and entanglement [8].
The most famous example for a Dirichlet series is the Riemann zeta function ζ [3] which plays a key role in number theory [4]. Indeed, the distribution of its non-trivial zeros determines the distribution of the prime numbers p in the sea of natural numbers n, expressed by the prime number theorem [2, 9]. However, even today, the location of these zeros has not been proven mathematically although the first 10 billion of zeros [10, 11] have been found to be on the critical line  where they should lie according to the Riemann hypothesis [12].
where they should lie according to the Riemann hypothesis [12].
Our paper is organized as follows: in section 2 we show that a single Dirichlet series corresponds to a probability amplitude for a measurement on a time-dependent anharmonic oscillator with a logarithmic energy spectrum. We then turn in section 3 to the problem of a sum of two Dirichlet series and generalize our approach in section 4 to two series where the coefficients cn also depend on the argument s, like in the analytical continuation of the Riemann zeta function. In section 5 we illustrate our approach by employing the representations of ζ in the different regions of the complex plane. The dynamics of the states provides us with ζ along any line in the complex plane parallel to the imaginary axis. In particular, we show that the non-trivial zeros of ζ are a consequence of a superposition of two quantum states. (For a different approach to the Riemann hypothesis based on the Newton Flow see [13].) Finally, we conclude in section 6 by presenting a brief summary and an outlook.
Since our analysis relies on the existence of a non-linear oscillator with a logarithmic energy spectrum we briefly outline in appendix
2. Single Dirichlet series: single probability amplitude
Our construction of a physical system to realize an ordinary Dirichlet series starts from the observation that the definition (1) is equivalent to
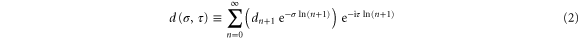
with complex-valued expansion coefficients  . Hence, the phase factor
. Hence, the phase factor ![$\mathrm{exp}[-{\rm{i}}\tau \mathrm{ln}(n+1)]$](https://content.cld.iop.org/journals/1367-2630/17/6/063040/revision1/njp513909ieqn4.gif) is reminiscent of the unitary time evolution of an energy eigenstate of a quantum system with a logarithmic energy spectrum. Here τ plays the role of a dimensionless time and the terms
is reminiscent of the unitary time evolution of an energy eigenstate of a quantum system with a logarithmic energy spectrum. Here τ plays the role of a dimensionless time and the terms ![$\left|{d}_{n+1}\right|\mathrm{exp}[-\sigma \mathrm{ln}(n+1)]\;\mathrm{exp}\left({\rm{i}}{\varphi }_{n+1}\right)$](https://content.cld.iop.org/journals/1367-2630/17/6/063040/revision1/njp513909ieqn5.gif) are similar to the initial probability amplitudes of the nth energy eigenstate.
are similar to the initial probability amplitudes of the nth energy eigenstate.
In [14] we have constructed a non-linear oscillator whose energy eigenstates  have the eigenvalues
have the eigenvalues
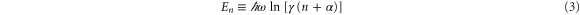
where  is a unit of energy, and γ and α are dimensionless parameters. For a suggestion of how to realize such an unusual oscillator we refer to [15] and to appendix
is a unit of energy, and γ and α are dimensionless parameters. For a suggestion of how to realize such an unusual oscillator we refer to [15] and to appendix
With  the time-evolution of the initial state
the time-evolution of the initial state
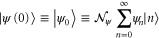
containing the constant complex-valued expansion coefficients  reads
reads
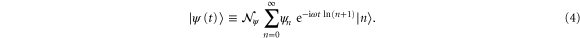
In order to ensure the Born probability interpretation [5] for  we require
we require
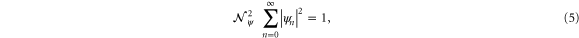
where we have chosen the normalization constant  real.
real.
Hence, from (4) we obtain the probability amplitude
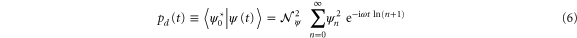
to find in  the phase-conjugated initial state
the phase-conjugated initial state
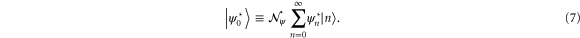
A comparison of (6) with (2), or more precisely
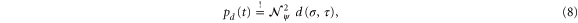
immediately yields the identifications  and
and
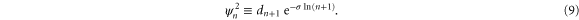
Thus the real part σ of s together with the coefficients  determines the degree of occupation of the individual states
determines the degree of occupation of the individual states  , and the probability amplitude
, and the probability amplitude  to find the phase-conjugated initial state
to find the phase-conjugated initial state  in the time-evolved state
in the time-evolved state  involving the non-linear oscillator with logarithmic eigenvalues reads out the Dirichlet series
involving the non-linear oscillator with logarithmic eigenvalues reads out the Dirichlet series  .
.
Moreover, since the expansion coefficients  are independent of τ, the whole dependence of
are independent of τ, the whole dependence of  on the imaginary part τ of the argument s is governed by the time evolution. Therefore, with
on the imaginary part τ of the argument s is governed by the time evolution. Therefore, with  we actually can read out the Dirichlet series
we actually can read out the Dirichlet series  along a line parallel to the imaginary axis with real part σ.
along a line parallel to the imaginary axis with real part σ.
Needless to say, if the coefficients dn are real (9) provides  and the phase-conjugated initial state is identical to the initial state. Then, the probability amplitude (6) simplifies to
and the phase-conjugated initial state is identical to the initial state. Then, the probability amplitude (6) simplifies to  which is the auto-correlation function.
which is the auto-correlation function.
Due to the realization of the Dirichlet series d by  and
and  via (8) there must be an intimate connection between the domain of definition of d and the properties of the states. Indeed, when we consider the normalization
via (8) there must be an intimate connection between the domain of definition of d and the properties of the states. Indeed, when we consider the normalization  given by (5) we get with (9)
given by (5) we get with (9)
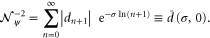
Hence, the states are only defined in the region where the Dirichlet series (2) is absolutely convergent (see [16] and
3. Sum of Dirichlet series: interfering probability amplitudes
The probability amplitude pd assumes complex values. The absolute value  manifests itself in the probability
manifests itself in the probability  to find
to find  in
in  . However, the phase of pd can only be determined in an interference arrangement, that is relative to another probability amplitude. For this reason we now concentrate on the sum of two Dirichlet series and show that they represent the sum of two probability amplitudes. Here we restrict ourselves to a particular combination which appears frequently in number theory. Indeed, we now concentrate on the complex function
. However, the phase of pd can only be determined in an interference arrangement, that is relative to another probability amplitude. For this reason we now concentrate on the sum of two Dirichlet series and show that they represent the sum of two probability amplitudes. Here we restrict ourselves to a particular combination which appears frequently in number theory. Indeed, we now concentrate on the complex function
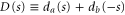
which consists of the sum of two Dirichlet series defined by (2) where da contains the argument s and db has the argument  .
.
We emphasize that the minus sign in db leads to a positive sign in the exponent of the phase factor ![$\mathrm{exp}[+{\rm{i}}\tau \mathrm{ln}(n+1)]$](https://content.cld.iop.org/journals/1367-2630/17/6/063040/revision1/njp513909ieqn34.gif) instead of the negative one appearing in the Dirichlet series da(s). For this reason a single quantum system does not suffice anymore to create the function
instead of the negative one appearing in the Dirichlet series da(s). For this reason a single quantum system does not suffice anymore to create the function

We recall [17] that a similar combination of phase factors appears in the time evolution created by the interaction Hamiltonian
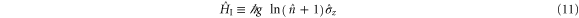
between a two-level atom characterized by the Pauli-spin matrix  of the excited and ground state
of the excited and ground state  and
and  , respectively, and a far off-resonant harmonic oscillator with energy eigenstates
, respectively, and a far off-resonant harmonic oscillator with energy eigenstates  , such that
, such that  . Here g is the interaction strength. We emphasize that
. Here g is the interaction strength. We emphasize that  is in the interaction picture.
is in the interaction picture.
Since in [17] we have proposed a method how to realize such an interaction we now assume that  can indeed be implemented. Hence, we find for the initial state
can indeed be implemented. Hence, we find for the initial state
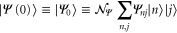
with  and the probability amplitudes
and the probability amplitudes  for the oscillator as well as the atom, the time-evolved state
for the oscillator as well as the atom, the time-evolved state
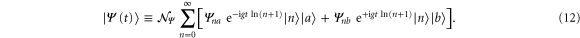
The real-valued normalization constant  is introduced by the requirement
is introduced by the requirement
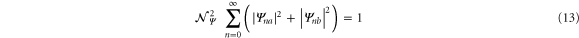
which ensures that the state  is normalized.
is normalized.
Here the two contributions to  in (12) differ in their time evolution due to the two internal states. Whereas the excited state
in (12) differ in their time evolution due to the two internal states. Whereas the excited state  undergoes the familiar clockwise motion in phase space, the ground state
undergoes the familiar clockwise motion in phase space, the ground state  exhibits a counter-clockwise rotation. This behavior is reminiscent of the celebrated approach [18–20] of creating Schrödinger cats of a single mode of the radiation field in a cavity, or in the motion of an ion stored in a trap. The only difference is that in these cases the logarithmic operator
exhibits a counter-clockwise rotation. This behavior is reminiscent of the celebrated approach [18–20] of creating Schrödinger cats of a single mode of the radiation field in a cavity, or in the motion of an ion stored in a trap. The only difference is that in these cases the logarithmic operator  in the Hamiltonian (11) is replaced by its linear limit
in the Hamiltonian (11) is replaced by its linear limit  .
.
In order to connect the state  given by (12) to the sum D of the two Dirichlet series (10) we calculate the probability amplitude
given by (12) to the sum D of the two Dirichlet series (10) we calculate the probability amplitude
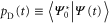
to find the phase-conjugated initial state
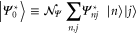
in the time-evolved state  which yields
which yields
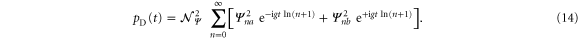
When we compare (10) and (14) by examining
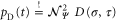
we arrive at the connection  between the time t and the imaginary part τ of s and the probability amplitudes fulfill the relations
between the time t and the imaginary part τ of s and the probability amplitudes fulfill the relations
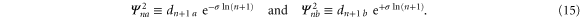
Hence, the phase of  is created by the relative motion between the probability amplitudes connected to the excited state and the ones connected to the ground state. Like in the case of a single Dirichlet sum
is created by the relative motion between the probability amplitudes connected to the excited state and the ones connected to the ground state. Like in the case of a single Dirichlet sum  the dependence of
the dependence of  on the imaginary part τ is again solely governed by the time evolution.
on the imaginary part τ is again solely governed by the time evolution.
The normalization determined by the requirement (13) and the probability amplitudes in (15) now read

Therefore, the states are restricted to the region where both Dirichlet sums da(s) and db(−s) are absolutely convergent.
Since in general the analytical continuation of a Dirichlet series beyond the line of convergence cannot be represented by another Dirichlet series or a superposition of Dirichlet series we discuss in the next section a generalization of our approach.
4. Analytical continuation
In the next section the example of the Riemann zeta function will show that we can only reach into the part of the complex plane where the non-trivial zeros of ζ are located when we employ its analytical continuation represented by a sum of Dirichlet-like series
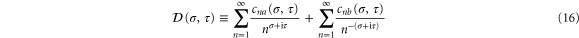
where the coefficients  depend on the real part σ as well as the imaginary part τ of the argument s.
depend on the real part σ as well as the imaginary part τ of the argument s.
The function  can of course be realized by (14), that is the overlap between the phase-conjugated initial state
can of course be realized by (14), that is the overlap between the phase-conjugated initial state  and the time-evolved state
and the time-evolved state  , however, the probability amplitudes must then fulfill the requirement
, however, the probability amplitudes must then fulfill the requirement

Hence, the time evolution does not determine the complete dependence of the Dirichlet-like series  on the imaginary part τ, in contrast to the realization of the Dirichlet series
on the imaginary part τ, in contrast to the realization of the Dirichlet series  and the sum
and the sum  in the previous sections.
in the previous sections.
To avoid the appearance of τ in the probability amplitudes  we can use the projection
we can use the projection  of a reference state
of a reference state
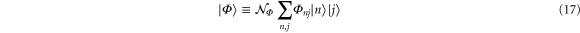
with real-valued normalization constant  onto the time-evolved state
onto the time-evolved state  , given by (12), which yields
, given by (12), which yields
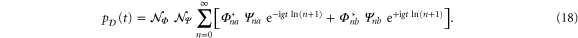
The comparison
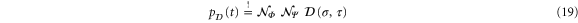
between (16) and (18) then shows that the connection between the time t and the imaginary part τ of s is again given by  , and the probability amplitudes must satisfy the relations
, and the probability amplitudes must satisfy the relations
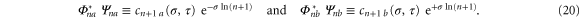
Here we can transfer the dependence of cnj on the imaginary part τ completely to the reference state by choosing  . Hence, we can again read out the function
. Hence, we can again read out the function  on the whole positive axis with real part σ parallel to the imaginary axis by
on the whole positive axis with real part σ parallel to the imaginary axis by  whose dependence on τ is entirely governed by the time evolution, and an appropriately chosen reference state which explicitly depends on the imaginary part τ.
whose dependence on τ is entirely governed by the time evolution, and an appropriately chosen reference state which explicitly depends on the imaginary part τ.
Before we illustrate this approach for the example of the Riemann zeta function, we recall that the states  and
and  given by (12) and (17), respectively, are derived in the interaction picture. In the Schrödinger picture, the time-evolved state
given by (12) and (17), respectively, are derived in the interaction picture. In the Schrödinger picture, the time-evolved state

contains the additional time-dependent phase factors  due to the transformation
due to the transformation
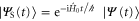
with the free Hamiltonian  leading to the energies
leading to the energies  determined by
determined by  .
.
Hence, if we want to interpret the sum of two Dirichlet-like series as the probability amplitude of a joint measurement of the states  and
and  in the same way as in (18) we have to include these additional phases in the probability amplitudes of the reference state, that is
in the same way as in (18) we have to include these additional phases in the probability amplitudes of the reference state, that is
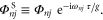
Needless to say, this phase must also be included when we choose  as probability amplitudes of the reference state. In what follows we return to the description in the interaction picture.
as probability amplitudes of the reference state. In what follows we return to the description in the interaction picture.
5. Application to Riemann zeta function
In order to illustrate our results we now turn to the Riemann zeta function ζ and make contact with the representations analyzed in sections 2 and 4. Indeed, depending on the argument of ζ the function is either given by a single Dirichlet series or a sum of Dirichlet-like series representing its analytical continuation.
5.1. Dirichlet series
For  , that is for arguments s in the complex plane to the right of the line
, that is for arguments s in the complex plane to the right of the line  , the Riemann zeta function ζ is defined by the Dirichlet series [3]
, the Riemann zeta function ζ is defined by the Dirichlet series [3]
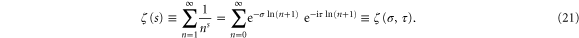
In this case we find from (2) that dn = 1 and consequently the phase conjugated initial state  , given by (7), is identical to the initial state
, given by (7), is identical to the initial state
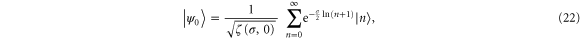
that is  . Hence, the condition (8) reduces to the probability amplitude
. Hence, the condition (8) reduces to the probability amplitude
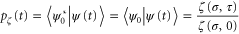
of the initial quantum state (22) moving in the non-linear oscillator with the logarithmic spectrum. A detailed description of the phase space behavior of these states is given in [17].
5.2. Alternating Dirichlet series
The most elementary analytical continuation [3] of ζ beyond  is given by the alternating representation
is given by the alternating representation
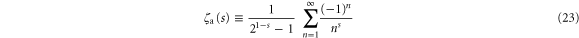
which is convergent for  . However, the initial state
. However, the initial state
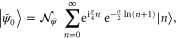
which creates the alternating Dirichlet sum on the right-hand side of (23) by the auto-correlation function  is only defined in the region of the complex plane where
is only defined in the region of the complex plane where  . Indeed, the normalization of
. Indeed, the normalization of  reads
reads
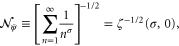
involving the Riemann zeta function defined by the Dirichlet sum (21).
The reason for this constraint is the fact that the line of absolute convergence  is identical for the sums in (21) and (23) as we show in
is identical for the sums in (21) and (23) as we show in  with a single physical system [21].
with a single physical system [21].
5.3. Berry–Keating representation
Yet, there exist many other representations [3] of ζ for  . The most relevant ones to the present discussion are in terms of the sum of two Dirichlet-like series with a positive and a negative argument. We now concentrate on the Berry–Keating formula [22]
. The most relevant ones to the present discussion are in terms of the sum of two Dirichlet-like series with a positive and a negative argument. We now concentrate on the Berry–Keating formula [22]
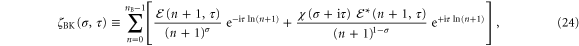
where
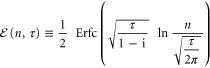
and
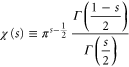
are defined in terms of the complementary error function [23]  and the gamma function [24] Γ, respectively. Although (24) only differs from the approximation given by Carl Ludwig Siegel [25] by the additional function
and the gamma function [24] Γ, respectively. Although (24) only differs from the approximation given by Carl Ludwig Siegel [25] by the additional function  and the summation limit
and the summation limit ![$\left[\sqrt{\frac{\tau }{2\pi }}\right]\leqslant {n}_{{\rm{B}}}$](https://content.cld.iop.org/journals/1367-2630/17/6/063040/revision1/njp513909ieqn95.gif) , where
, where ![$[x]$](https://content.cld.iop.org/journals/1367-2630/17/6/063040/revision1/njp513909ieqn96.gif) denotes the floor function, it provides a much better approximation of ζ in the critical strip
denotes the floor function, it provides a much better approximation of ζ in the critical strip  . However, we emphasize that our interpretation in terms of interfering probability amplitudes of joint measurements works for both formulae. The results for the Riemann-Siegel representation are given in [17].
. However, we emphasize that our interpretation in terms of interfering probability amplitudes of joint measurements works for both formulae. The results for the Riemann-Siegel representation are given in [17].
When we now compare  with
with  defined by (16) and (24), respectively, we can identify the coefficients
defined by (16) and (24), respectively, we can identify the coefficients
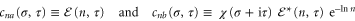
for  of the sum of two Dirichlet-like series. Hence, we can realize the Berry–Keating representation (24) by using
of the sum of two Dirichlet-like series. Hence, we can realize the Berry–Keating representation (24) by using

which is in complete analogy to the comparison (19) of the projection  to the function
to the function  . The probability amplitudes of of the time-evolved state
. The probability amplitudes of of the time-evolved state  and the reference state
and the reference state  given by (12) and (17), respectively, fulfill the relations (20), that is
given by (12) and (17), respectively, fulfill the relations (20), that is
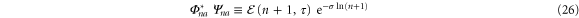
and
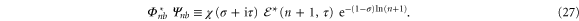
Since only the products  and
and  have to vanish for
have to vanish for  to realize the right-hand side of (25), it suffices to choose
to realize the right-hand side of (25), it suffices to choose  or
or  for
for  in the physical picture to eliminate the redundant summands.
in the physical picture to eliminate the redundant summands.
We emphasize that there are many valid choices for the probability amplitudes  , however, we consider now
, however, we consider now
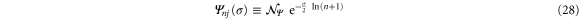
for  and
and  with the normalization
with the normalization
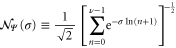
as the probability amplitudes of the state  as suggested in [17]. This choice provides three significant advantages: (i) Since
as suggested in [17]. This choice provides three significant advantages: (i) Since  , we start from a product state which gets entangled by the time-evolution. (ii) As long as
, we start from a product state which gets entangled by the time-evolution. (ii) As long as  the state
the state  can represent ζ in the whole complex plane. Needless to say, the restriction to a finite summation limit ν vanishes for
can represent ζ in the whole complex plane. Needless to say, the restriction to a finite summation limit ν vanishes for  due to the convergence of the Dirichlet sum (21) defining ζ in this region. (iii) With
due to the convergence of the Dirichlet sum (21) defining ζ in this region. (iii) With  the indirect dependence
the indirect dependence ![$\left[\sqrt{\frac{\tau }{2\pi }}\right]\leqslant {n}_{{\rm{B}}}$](https://content.cld.iop.org/journals/1367-2630/17/6/063040/revision1/njp513909ieqn114.gif) of the summation limit
of the summation limit  on τ is transferred to the reference state.
on τ is transferred to the reference state.
Using (28), we finally get from (20)
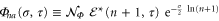
and
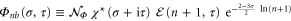
for  . The normalization of the reference state then reads
. The normalization of the reference state then reads
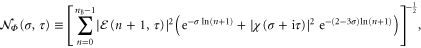
where we have used that  for
for  to ensure the truncation of the Dirichlet-like sums at
to ensure the truncation of the Dirichlet-like sums at  .
.
It is shown in [21] that the reference state is entangled for all σ due to the contributions of the function  . Nevertheless, the absolute values
. Nevertheless, the absolute values  and
and  are the same on the critical line
are the same on the critical line  since
since  . Hence, the absolute values of the contributions (26) and (27) to the Dirichlet-like sums become equal on the critical line and thus can lead to a complete destructive interference, that is to a zero of the function (24). This analysis suggests that the non-trivial zeros of ζ are a consequence of the interference of two probability amplitudes corresponding to the sum of two Dirichlet-like series, that is of the superposition of two quantum states similar to a Schrödinger cat, and thus might open a new avenue towards the long-standing problem of the Riemann hypothesis.
. Hence, the absolute values of the contributions (26) and (27) to the Dirichlet-like sums become equal on the critical line and thus can lead to a complete destructive interference, that is to a zero of the function (24). This analysis suggests that the non-trivial zeros of ζ are a consequence of the interference of two probability amplitudes corresponding to the sum of two Dirichlet-like series, that is of the superposition of two quantum states similar to a Schrödinger cat, and thus might open a new avenue towards the long-standing problem of the Riemann hypothesis.
6. Conclusion
Dirichlet series interpreted as interfering probability amplitudes for measurement outcomes in quantum systems: this phrase summarizes the main result of our paper. Obviously both Dirichlet series as well as probability amplitudes are complex-valued functions. However, there is one feature which makes this connection unique. The imaginary part τ of the argument s of the Dirichlet series appears in the argument of a phase factor which is reminiscent of the appearance of time in the evolution of an energy eigenstate.
In this picture the non-trivial zeros of the Riemann zeta function are a consequence of interference, that is of the superposition of two quantum states similar to a Schrödinger cat. Indeed, since we focus on the dynamics of a quantum system which provides us with ζ directly the energy eigenvalues of our system are unrelated to the zeros of ζ but are constructed in such a way as to obtain the representation of ζ either as a single Dirichlet series, or a combination of two Dirichlet-like series.
Hence, our approach is quite different from the Pólya-Hilbert approach towards the Riemann hypothesis which searches for a bridge between eigenvalues of a physical problem and the non-trivial zeros. It emerged from the collaboration of György Pólya with David Hilbert, who developed the theory of eigenvalue equations, as a response to the question of the number theorist Edmund Landau of whether Pólya would know a physical system [26] that displays ζ.
One such bridge appears is random matrix theory [27] and quantum chaos [28]. Here the nearest-neighbor statistics of the eigenvalues of random matrices is identical to that of the non-trivial zeros. Other physical systems where ζ manifests itself [29] in the spirit of Landau are, for example, the inverted harmonic oscillator [30] resulting from the non-Hermitian combination  of the position and momentum operator
of the position and momentum operator  and
and  , quantum graphs [31], and the quantum Mellin transform [32].
, quantum graphs [31], and the quantum Mellin transform [32].
Moreover, our approach shows that quantum systems can serve as analogue computers for all complex function which can be represented as combinations of Dirichlet-like series. In this way we could establish a link between the seemingly disjoint fields of number theory and quantum mechanics.
Acknowledgments
We thank W Arendt, M Freyberger, H Maier and W H Zurek for many fruitful discussions. WPS gratefully acknowledges the support by a Texas A&M University Institute for Advanced Study (TIAS) Faculty Fellowship.
Appendix A.: Oscillator with logarithmic energy spectrum
In this appendix we briefly outline two ideas of how to realize an anharmonic oscillator with a logarithmic energy spectrum. The first one relies on an atom moving in an appropriately tailored potential and has been discussed in great detail in [15] and the second one employs the analogy between the time-independent Schrödinger equation and the Helmholtz equation of classical electrodynamics. In both cases we do not go into details but focus on the key features. We conclude by briefly addressing the question of entangled quantum systems.
A.1. Atom in an external field
The motion of a particle of mass μ and coordinate x moving in a potential  along a line is governed by the time-independent Schrödinger equation
along a line is governed by the time-independent Schrödinger equation
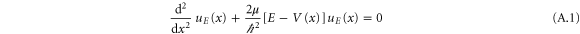
for the energy eigenfunctions  with eigenvalue E. In [15] we have constructed a potential such that the resulting energy spectrum is of the form (3). For this purpose we have solved the inverse spectrum problem using semi-classical approximations as well as exact numerical techniques based on the Hellmann–Feynman theorem.
with eigenvalue E. In [15] we have constructed a potential such that the resulting energy spectrum is of the form (3). For this purpose we have solved the inverse spectrum problem using semi-classical approximations as well as exact numerical techniques based on the Hellmann–Feynman theorem.
The remaining question is how to realize this so-obtained potential in an experiment. Here we recall [6] that an atom that interacts with a classical electric field whose frequency is far-detuned from the atomic transition frequency feels a potential whose spatial dependence is determined by that of the intensity I, that is  . Hence, an atom moving in a potential provided by a far-detuned light field with a spatial distribution found from the inversion problem leads us via the time-independent Schrödinger equation (A.1) to the logarithmic energy spectrum (3). For a more detailed discussion, and in particular, the question of how to realize a one-dimensional motion we refer to [15].
. Hence, an atom moving in a potential provided by a far-detuned light field with a spatial distribution found from the inversion problem leads us via the time-independent Schrödinger equation (A.1) to the logarithmic energy spectrum (3). For a more detailed discussion, and in particular, the question of how to realize a one-dimensional motion we refer to [15].
A.2. Graded index wave guide
The second method to obtain the spectrum (3) takes advantage of the familiar analogy between the paraxial wave equation and the Schrödinger equation. Here we consider the propagation of a classical electromagnetic field along a given space direction which plays the role of time and the transverse space variables represent the two space variables. Moreover, the potential V of (A.1) is replaced by the transverse index of refraction.
Hence, we can realize the time-evolution of the wave packet in the non-linear oscillator with logarithmic energy spectrum by light pulses propagating along a wave guide whose transverse direction displays a graded index profile determined by the potential V. In this case the transverse mode functions take the role of the energy wave functions.
A.3. Entanglement
In section 3 we consider two quantum systems interacting with each other according to the Hamiltonian (11) which also contains a logarithmic dependence. Unfortunately, in this case we cannot employ the two techniques discussed in the previous sections, because they are limited to an individual system. However, in [17] we have already outlined an approach how to implement (11) based on a generalization of the Jaynes–Cummings Hamiltonian [6]. Here we consider the interaction of a single ion moving in a one-dimensional trap with a classical electromagnetic field in a mode function which we tailor as to obtain the desired Hamiltonian. For more details we refer to [17].
Appendix B.: Dirichlet series
In this appendix we give a more general definition of the Dirichlet series. Moreover, we discuss the difference between convergence and absolute convergence of the series.
B.1. General Definition
The most general definition of a Dirichlet series of the type  for complex-valued argument
for complex-valued argument  is given by [16]
is given by [16]
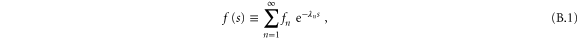
where fn are complex numbers and the exponents  are a sequence of real increasing numbers whose limit is infinity.
are a sequence of real increasing numbers whose limit is infinity.
In this article we concentrate on the series with exponents  , that is
, that is

which are called ordinary Dirichlet series.
B.2. Convergence
The behavior of the Dirichlet series (B.1) in the complex plane is described by the elementary theorem [16]:
If the series f(s) is convergent for
, then it is convergent for any value of s whose real part is greater than
.
Hence, the Dirichlet series is convergent on the half plane with  with the line of convergence at
with the line of convergence at  as left border.
as left border.
Moreover, when we recall [24] that an infinite series
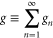
with complex components gn is absolutely convergent in the region where the series
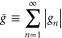
of the absolute values of the components gn converges, the series
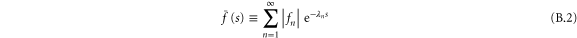
is absolutely convergent on the half plane with  . We therefore call
. We therefore call  the line of absolute convergence. As a consequence, the Dirichlet series f(s), defined by (B.1), possesses a line of absolute convergence at
the line of absolute convergence. As a consequence, the Dirichlet series f(s), defined by (B.1), possesses a line of absolute convergence at  which is evidently on, or to the right of the line of convergence
which is evidently on, or to the right of the line of convergence  , that is
, that is  .
.
The difference between the line of convergence and the line of absolute convergence becomes immediately clear when we have a closer look on the Dirichlet sum and the alternating representation of ζ, given by (21) and (23), respectively.
The first one is convergent as well as absolutely convergent for  due to
due to
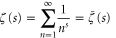
where  is defined according to (B.2). That is, the line of convergence and the line of absolute convergence are identical.
is defined according to (B.2). That is, the line of convergence and the line of absolute convergence are identical.
In contrast, the sum
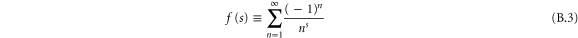
in definition (23) is convergent for  . However, the corresponding sum
. However, the corresponding sum
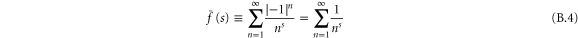
is convergent only if  . Hence, the line of absolute convergence of (B.3) and therefore of
. Hence, the line of absolute convergence of (B.3) and therefore of  is at
is at  which is to the right of the line of convergence
which is to the right of the line of convergence  .
.
As a consequence, the alternating states defined in section 5.2 are restricted to the region with  since their normalization involves the sum
since their normalization involves the sum  defined by (B.4). This property emphasizes the intimate connection of the physical requirement of normalization to the mathematical property of absolute convergence which forbids the realization of the alternating representation
defined by (B.4). This property emphasizes the intimate connection of the physical requirement of normalization to the mathematical property of absolute convergence which forbids the realization of the alternating representation  by a single quantum system in the critical strip
by a single quantum system in the critical strip  .
.





