Abstract
A new mechanism for electromagnetic emission in the terahertz (THz) frequency regime from laser-plasma interactions is described. A localized and long-lasting transverse current is produced by two counter-propagating short laser pulses in weakly magnetized plasma. We show that the electromagnetic wave radiating from this current source, even though its frequency is close to cut-off of the ambient plasma, grows and diffuses towards the plasma-vacuum boundary, emitting a strong monochromatic THz wave. With driving laser pulses of moderate power, the THz wave has a field strength of tens of MV m−1, a frequency of a few THz and a quasi-continuous power that exceeds all previous monochromatic THz sources. The novelty of the mechanism lies in a diffusing electromagnetic wave close to cut-off, which is modelled by a continuously driven complex diffusion equation.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Far-infrared light has been expected to be uniquely advantageous for probing and imaging the structure and dynamics of matter compared with other light sources. However, the characteristics of the radiation sources in that frequency regime have not been satisfactory with respect to various requirements. Enormous efforts are now being made to fill the perceived terahertz (THz) gap with the development of high power THz sources because of their potential high-impact applications in science and technology. Diverse sources have been developed using both electronic and optical methods, for example the laser-plasma-based schemes [1–20], which promise compact THz sources with notably high field amplitude over a wide range of frequencies, and conventional beam driven vacuum sources such as gyrotrons, backward wave oscillators etc.
Linear mode conversion and two-colour schemes are known to yield short-duration and wide-band THz pulses with remarkably high amplitude. The latter is especially attractive because a high THz amplitude up to 2 GV m−1 can be expected [21]. In this scheme, a slow component of a strong photocurrent is efficiently yielded by phase-controlled photoionization at each laser field extremum [22, 23], which is essential in generating a broad-band THz pulse.
While the peak power of these wide-band THz sources is increasing rapidly, the average power of available narrow-band THz sources remains very low. A monochromatic THz source based on laser-plasma interactions and wakefields is feasible [6]. By converting the longitudinal current of the wakefield to a transverse one using an external magnetic field, this Cherenkov wake scheme extends the pulse duration and increases the emission power [18–20]. However, the field amplitude or power from such a monochromatic THz source is still low compared with wide-band schemes. Considering the numerous important applications such as high-contrast imaging [24–26] or interferometry of Tokamak plasmas [27], it is necessary to provide suitable monochromatic sources that have high tunability, compactness, and above all, high power.
In this paper, we propose a new mechanism of generating high-intensity monochromatic THz radiation from laser-plasma interactions. The fundamental idea is to evoke a strong, localized, long-lasting electron oscillation in plasma, which acts as a radiating antenna emitting a continuous THz wave. In practice, the radiation current source can be generated by the strong ponderomotive force from two short laser pulses colliding at a desired position inside the plasma [28]. The current generated in this way is maintained for a long time by the plasma oscillation mechanism even after the passage of the driving laser pulses. The longitudinal current induced in this way oscillates electrostatically. To obtain electromagnetic radiation, i.e. the THz wave, some fraction of the longitudinal electron oscillation is converted to a transverse one by a weak transverse external magnetic field. Because the radiation from this current source oscillates at the plasma frequency, the electromagnetic fields are at the cut-off of the ambient plasma and cannot propagate under normal conditions, which is indeed the very reason why plasma oscillations cannot be easily converted to transverse electromagnetic waves in laser-plasma systems. However, we have discovered that if the electromagnetic wave is constantly driven near cut-off, as in our case, the field grows as its energy is fed by the driving current. Furthermore, both electric and magnetic components of the field diffuse strongly into the plasma. As a consequence, the diffusing electromagnetic field eventually propagates across the plasma-vacuum boundary and is converted to an electromagnetic wave emitted into free space. This concept of THz generation is shown schematically in figure 1. Our scheme shares a common feature with the Cherenkov wake driven by a single pulse in using the external magnetic field to convert a longitudinal oscillation to a transverse one. However, the stronger, local electron oscillation by colliding pulses, and the diffusion-growth mechanism are two unique features of our scheme.
Figure 1. Schematic of terahertz emission from a current source generated by two counter-propagating laser pulses.
Download figure:
Standard image High-resolution imageAs the plasma frequency can be easily controlled in the few-THz regime, this mechanism can be utilized as a new THz radiation source. As we will show later through numerical simulations, the resultant amplitude of the THz emission reaches tens of MV m−1 and has a sub-nanosecond pulse duration. Such high amplitudes in the regime of narrow-band THz pulses with long pulse duration are not readily obtained with conventional methods in compact systems. Note that from wide-band THz sources, such as the two-colour scheme, short THz pulses with peak amplitudes higher by two orders of magnitude are available [21].
This paper is organised as follows. In section 2, we describe the diffusion and growth of the electromagnetic field near cutoff theoretically and using simulations. In section 3, a theoretical scaling law for the THz emission amplitude as a function of the amplitude of the driving pulse is derived. Then, in section 4 we give a summary and conclusions.
2. Electromagnetic diffusion and growth near cutoff
The diffusion of the electromagnetic field, which is a key factor for enhanced THz emission in our scheme, is apparent in the field evolution modelled by a constantly driven complex diffusion equation. Such diffusion of the electromagnetic wave is quite different from the well-known magnetic field diffusion into conducting material, where just the slowly varying magnetic component diffuses while the electric component remains negligibly small. To describe electromagnetic diffusion near cut-off, we start from the wave equation:
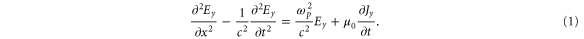
Similar equations describing the field evolution in the two-colour scheme can be found in [29]. Equation (1) differs from those in so far as, firstly, Jy originates from the ponderomotive force of the laser pulses rather than from photoionization, and secondly, the role of the laser pulses in our scheme is limited to an initial source current Jy. Thus Ey in equation (1) includes just the THz field without the laser field. Note that the first term on the right-hand side is the self-current induced by Ey itself, while the second term is a constant driving current. Assuming that the electric field amplitude evolves slowly, the electric field Ey can be written as 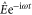 , where
, where 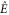 is a slowly evolving function of time. Since
is a slowly evolving function of time. Since 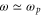 , i.e. Ey is nearly at cut-off, the first term on the right-hand side cancels out the second time derivative of
, i.e. Ey is nearly at cut-off, the first term on the right-hand side cancels out the second time derivative of 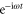 on the left-hand side. Neglecting the second time derivative of
on the left-hand side. Neglecting the second time derivative of  in accordance with the slowly varying assumption, we obtain a constantly driven diffusion-like equation of the electric field:
in accordance with the slowly varying assumption, we obtain a constantly driven diffusion-like equation of the electric field:
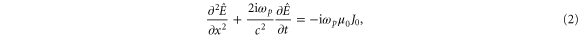
where J0 is the current amplitude defined by 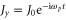 . The transverse current Jy is induced by the external magnetic field (B0) from the longitudinal current Jx, which is driven by the beat of two counter-propagating laser pulses. Because the pulse duration is very short, a few tens of femtoseconds, the longitudinal current Jx is generated almost instantaneously at the moment of pulse collision. Once Jx is formed, it continues to oscillate by the regular plasma oscillation mechanism. Since the conversion rate from Jx to Jy is very small for
. The transverse current Jy is induced by the external magnetic field (B0) from the longitudinal current Jx, which is driven by the beat of two counter-propagating laser pulses. Because the pulse duration is very short, a few tens of femtoseconds, the longitudinal current Jx is generated almost instantaneously at the moment of pulse collision. Once Jx is formed, it continues to oscillate by the regular plasma oscillation mechanism. Since the conversion rate from Jx to Jy is very small for 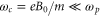 , Jx acts as feeding Jy constantly. Thus J0 can be considered temporally quasi-constant, leading to
, Jx acts as feeding Jy constantly. Thus J0 can be considered temporally quasi-constant, leading to 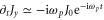 . The THz pulse generated by such a constantly oscillating current is expected to have a long pulse duration, as will be confirmed later. Note that equation (2) takes the familiar form of a driven diffusion equation, except that the diffusion coefficient, which is
. The THz pulse generated by such a constantly oscillating current is expected to have a long pulse duration, as will be confirmed later. Note that equation (2) takes the familiar form of a driven diffusion equation, except that the diffusion coefficient, which is 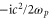 , is imaginary.
, is imaginary.
By applying Laplace and inverse Laplace transforms to equation (2), the solution can be represented in integral form as follows:
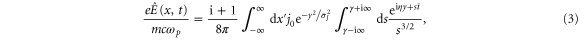
where the variables are normalized as  ,
, 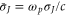 ,
, 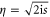 ,
,  , and
, and 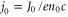 . In deriving equation (3) we have assumed that the transverse current amplitude J0 takes on a very narrow Gaussian form,
. In deriving equation (3) we have assumed that the transverse current amplitude J0 takes on a very narrow Gaussian form, 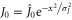 . Here
. Here 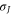 is the spatial length of the current source, which corresponds to half the laser pulse duration.
is the spatial length of the current source, which corresponds to half the laser pulse duration.
Approximate solutions of equation (3) can be obtained in certain limits. First, for  , i.e. far from the current source and temporally in the early stage, applying the steepest descent method leads to
, i.e. far from the current source and temporally in the early stage, applying the steepest descent method leads to
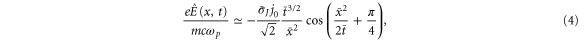
with  . Second, for x = 0, i.e. at the oscillation centre of the current, by applying Watson's lemma to the first order term we obtain an asymptotic form as a function of t as follows:
. Second, for x = 0, i.e. at the oscillation centre of the current, by applying Watson's lemma to the first order term we obtain an asymptotic form as a function of t as follows:
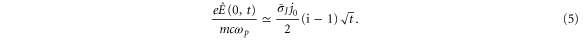
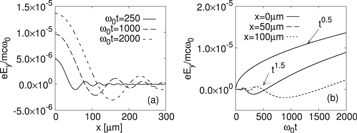
Figure 2(a) are snapshots of the diffusing fields at different times, obtained from numerical integration of equation (2). As the field diffuses, its modulation length shrinks with increasing distance for fixed time, while growing at a fixed position as can be predicted from the cosine term in equation (4). This temporal behaviour is presented in figure 2(b), where the result of numerical integration of equation (2) is plotted at  (current centre), 5, and 10. The central field increases monotonically by
(current centre), 5, and 10. The central field increases monotonically by 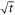 as expected from equation (5), while the off-central field initially follows
as expected from equation (5), while the off-central field initially follows  obeying equation (4), but eventually reduces to
obeying equation (4), but eventually reduces to 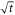 as the central peaked region of the field expands.
as the central peaked region of the field expands.
Figure 2. (a) Spatial profile of the diffusing field at different times and (b) its temporal growth at different positions, where 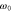 is the laser angular frequency.
is the laser angular frequency.
Download figure:
Standard image High-resolution imageThe simultaneous diffusion and growth of the field can be utilized as a method to convert the plasma oscillation into an electromagnetic wave in free space. As the growing field eventually hits the plasma-vacuum boundary through diffusion, radiation will be emitted into free space with temporally increasing amplitude. Indeed, this field growth driven by the diffusion mechanism is the major advantage of our scheme in producing strong THz emission. To confirm this scenario of THz radiation, we have performed one- and two-dimensional particle-in-cell (PIC) simulations. A trapezoidal shape has been chosen for the plasma density profile, with two different densities in the flat region,  and
and 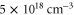 (10 and 20 THz, respectively). To reduce any mismatch of radiation impedance, a density ramp-up over 100
(10 and 20 THz, respectively). To reduce any mismatch of radiation impedance, a density ramp-up over 100  was added to the flat plasma. An additional important effect of the density gradient is that the field growth indicated by equation (4) is sustained for a longer time, eventually leading to stronger THz emission. The two counter-propagating pulses are arranged so that they collide at 25 or 50 μm from the knee of the density gradient. The wavelength of one of the pulses is 870 nm, which is typical for Ti:sapphire lasers, and the other is detuned so that their beat resonantly drives the plasma oscillation. In the two-dimensional simulation, the pulses focus at the colliding point with 50 μm spot radius. The normalized vector potential of the pulse is 0.05, for which
was added to the flat plasma. An additional important effect of the density gradient is that the field growth indicated by equation (4) is sustained for a longer time, eventually leading to stronger THz emission. The two counter-propagating pulses are arranged so that they collide at 25 or 50 μm from the knee of the density gradient. The wavelength of one of the pulses is 870 nm, which is typical for Ti:sapphire lasers, and the other is detuned so that their beat resonantly drives the plasma oscillation. In the two-dimensional simulation, the pulses focus at the colliding point with 50 μm spot radius. The normalized vector potential of the pulse is 0.05, for which 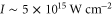 and
and 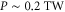 .
.
Figure 3(a) is an image of the THz emission obtained from two-dimensional PIC simulations. The diffusion and growth of the field measured on the axis, figure 3(b), takes on a very similar shape to the theoretical model. To observe the long-time behaviour of the signals, several one-dimensional PIC simulations have also been performed with the same parameters, varying the distance from the plasma edge to the pulse collision point as shown in figure 3(c). In this figure, THz emission grows as 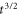 initially, but soon evolves into a
initially, but soon evolves into a  dependence, which is exactly the same feature as in figure 2(b). When the pulse collision occurs further into the plasma, it takes longer for the emission to grow, but eventually it reaches a comparable level (red and blue). Note that, due to the density gradient, a strong, but short duration emission by linear mode conversion [10] emerges simultaneously in the early stage. Though not fully plotted in the figure, the emission usually lasts up to an order of a hundred pico-seconds, which produces quite a monochromatic frequency spectrum as shown in figure 3(d). In the PIC simulations, collisions between charged particles are neglected, since the collisional rate is very small compared with the plasma frequency for the given density. Furthermore, we did not consider collisions between charged and neutral particles, assuming the plasma is prepared one hundred percent ionized by discharge or field ionization. If the ionization is not complete, collisions can reduce the lifetime of the current oscillation, leading to a shortened THz pulse.
dependence, which is exactly the same feature as in figure 2(b). When the pulse collision occurs further into the plasma, it takes longer for the emission to grow, but eventually it reaches a comparable level (red and blue). Note that, due to the density gradient, a strong, but short duration emission by linear mode conversion [10] emerges simultaneously in the early stage. Though not fully plotted in the figure, the emission usually lasts up to an order of a hundred pico-seconds, which produces quite a monochromatic frequency spectrum as shown in figure 3(d). In the PIC simulations, collisions between charged particles are neglected, since the collisional rate is very small compared with the plasma frequency for the given density. Furthermore, we did not consider collisions between charged and neutral particles, assuming the plasma is prepared one hundred percent ionized by discharge or field ionization. If the ionization is not complete, collisions can reduce the lifetime of the current oscillation, leading to a shortened THz pulse.
Figure 3. (a) Diffusion of the transverse electromagnetic field inside a magnetized plasma ( ) and THz radiation with
) and THz radiation with 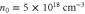 , a0 = 0.05, and the pulse duration
, a0 = 0.05, and the pulse duration 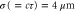 . The snapshot was captured at 1.3 ps after the pulse collision. (b) The field measured on the axis. (c) Temporal growth and saturation of the THz field for different collision points (L), and (d) the corresponding spectra of the THz electric field, with
. The snapshot was captured at 1.3 ps after the pulse collision. (b) The field measured on the axis. (c) Temporal growth and saturation of the THz field for different collision points (L), and (d) the corresponding spectra of the THz electric field, with 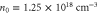 ,
,  (31.4 fs at full-width-half-maximum (FWHM), red, blue), and
(31.4 fs at full-width-half-maximum (FWHM), red, blue), and  ,
, 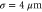 (15.7 fs at FWHM, green). The normalization factor of the electric field,
(15.7 fs at FWHM, green). The normalization factor of the electric field, 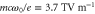 .
.
Download figure:
Standard image High-resolution image3. Scaling of the THz amplitude
To obtain a scaling law for the field strength of the THz emission as a function of the driving pulse amplitude, we calculate the radiation current source, i.e. the J0 term in equation (2). Since the current is driven by the beat of two counter-propagating pulses, the electron oscillation is spatially fast-varying, so that a linear portion of the oscillation is averaged out. However, the remaining smooth, nonlinear component can still be strong [31], forming a bunched longitudinal current oscillating at the plasma frequency. Once this average longitudinal current is generated, it induces a transverse current oscillation via the external magnetic field.
If the right- and left-going laser pulses are represented by  and
and 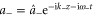 , respectively, their beat is proportional to
, respectively, their beat is proportional to  . Thus, they exert a ponderomotive force on the electrons which yields a density perturbation
. Thus, they exert a ponderomotive force on the electrons which yields a density perturbation 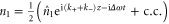 . Because the spatial average of n1 disappears, the linear current
. Because the spatial average of n1 disappears, the linear current 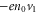 does not contribute significantly to the electromagnetic radiation. However, a non-vanishing second-order current remains, given by
does not contribute significantly to the electromagnetic radiation. However, a non-vanishing second-order current remains, given by
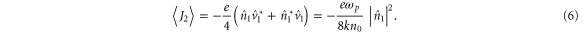
Here, we have used the continuity relation between n1 and v1, and assumed resonant driving, i.e.  . This spatially smooth nonlinear current, together with the linear self-current, drives the longitudinal electric field oscillations via the relation
. This spatially smooth nonlinear current, together with the linear self-current, drives the longitudinal electric field oscillations via the relation 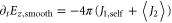 . Calculating the self-current using the linearized equation of motion for the electron plasma, we obtain
. Calculating the self-current using the linearized equation of motion for the electron plasma, we obtain

Note that 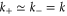 , so
, so  . To obtain the solution of equation (7) we evaluate the temporal evolution of
. To obtain the solution of equation (7) we evaluate the temporal evolution of 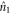 driven by the beat of the counter-propagating pulses
driven by the beat of the counter-propagating pulses
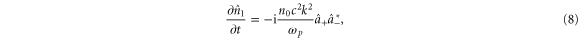
where n0 represents the unperturbed plasma density. In deriving equation (8), we neglect the magnetic force term, because we consider a very weakly magnetized plasma, i.e.  . In the case where the plasma oscillation is driven by the beat of counter-propagating pulses, as in equation (8), the transverse component of the ponderomotive force is commonly neglected [31]. The transverse force is proportional to
. In the case where the plasma oscillation is driven by the beat of counter-propagating pulses, as in equation (8), the transverse component of the ponderomotive force is commonly neglected [31]. The transverse force is proportional to  , where w is the pulse spot size, while the longitudinal one by the counter-beat is
, where w is the pulse spot size, while the longitudinal one by the counter-beat is 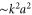 . Since
. Since  under usual circumstances, the longitudinal ponderomotive force is dominant. For laser pulses assumed to be longitudinally Gaussian with equal maximum amplitude a0 and pulse duration τ, the pulse amplitudes can be written as
under usual circumstances, the longitudinal ponderomotive force is dominant. For laser pulses assumed to be longitudinally Gaussian with equal maximum amplitude a0 and pulse duration τ, the pulse amplitudes can be written as ![${{\hat{a}}_{\pm }}={{a}_{0}}{\rm exp} \left[ -{{(t\mp (z\pm L)/c)}^{2}}/{{\tau }^{2}} \right]$](https://content.cld.iop.org/journals/1367-2630/17/4/043045/revision1/njp511945ieqn53.gif) . Note that it is arranged for the peaks of the pulses to overlap at z = 0 after propagation by distance L. Then, applying the Green function method to equation (7), we obtain
. Note that it is arranged for the peaks of the pulses to overlap at z = 0 after propagation by distance L. Then, applying the Green function method to equation (7), we obtain

where
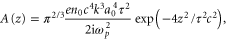
and  . Finally, the spatially averaged amplitude of the longitudinal oscillation becomes
. Finally, the spatially averaged amplitude of the longitudinal oscillation becomes
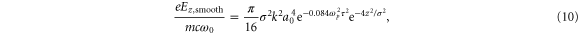
where 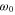 is the laser frequency and
is the laser frequency and 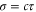 is the spatial length of the laser pulse. An interesting feature of this equation is that the longitudinal field depends only weakly on the plasma density via the exponential term, which is quite different from the single-pulse-driven wakefield.
is the spatial length of the laser pulse. An interesting feature of this equation is that the longitudinal field depends only weakly on the plasma density via the exponential term, which is quite different from the single-pulse-driven wakefield.
By applying an external magnetic field in the transverse direction, the longitudinal electric field given by equation (10) can be partially converted to a transverse field oscillating with the same frequency  . Here the ratio of the transverse oscillation to the longitudinal one is given by
. Here the ratio of the transverse oscillation to the longitudinal one is given by  , where
, where  , leading to
, leading to
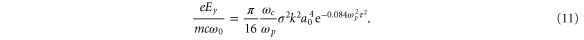
The radiation source current is then calculated from the relation 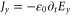 .
.
If the plasma-vacuum boundary is sharp, and the pulse collision point is located exactly at the edge of the plasma, the transverse field given by equation (11) is coupled to the vacuum without experiencing the diffusion and growth. Thus equation (11) gives the scaling of the minimum THz amplitude as a function of the driving pulse amplitude. An interesting point in this scaling is that the THz amplitude is proportional to 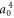 , corresponding to P2, where P is the power of the driving laser pulse. This is significantly different from the single-pulse driven systems, where the emission amplitude is proportional just to P [30]. From this different scaling, and due to the k2-factor, one of which is replaced by a much smaller value
, corresponding to P2, where P is the power of the driving laser pulse. This is significantly different from the single-pulse driven systems, where the emission amplitude is proportional just to P [30]. From this different scaling, and due to the k2-factor, one of which is replaced by a much smaller value 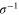 in the single-pulse case, we expect the counter-propagating pulse scheme to generate a much stronger THz wave than the single-pulse driven schemes, even with very moderate laser power. More detailed comparison between equation (11) and the single-pulse scaling shows that the effect of colliding pulses dominates the single-pulse effect when
in the single-pulse case, we expect the counter-propagating pulse scheme to generate a much stronger THz wave than the single-pulse driven schemes, even with very moderate laser power. More detailed comparison between equation (11) and the single-pulse scaling shows that the effect of colliding pulses dominates the single-pulse effect when 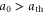 , where
, where
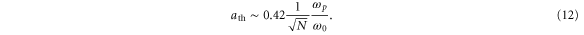
Here N, which represents the number of oscillations of the laser field within the pulse duration, is usually 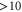 , and
, and 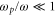 , thus this condition is satisfied even for small a0.
, thus this condition is satisfied even for small a0.
Figure 4 shows theoretical curves of the THz amplitudes from the two different schemes for  and
and  , corresponding to 20 and 10 THz, respectively.
, corresponding to 20 and 10 THz, respectively.
In figure 4, the simulation data (circles) exhibits saturation, which arises from wave-breaking of the spatially fast varying wave. One major effect of wave-breaking is the suppression of the plasma current by kinetic detuning [32]. From the fact that it occurs when the electron fluid velocity, which is 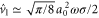 according to the linearized continuity equation, exceeds the phase velocity of the plasma wave, we estimate the laser amplitude for saturation to be
according to the linearized continuity equation, exceeds the phase velocity of the plasma wave, we estimate the laser amplitude for saturation to be
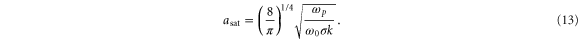
In addition, though not as apparent in the figure, the scaling for very low a0, less than ath, obeys 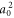 rather than
rather than  As a consequence, operating with a0 between ath and asat may yield optimum energy conversion from laser to THz emission.
As a consequence, operating with a0 between ath and asat may yield optimum energy conversion from laser to THz emission.
Figure 4. Amplitude of the terahertz emission as a function of a0 for the counter-propagating pulse scheme and the single-pulse scheme with magnetic field  . (a) The case for
. (a) The case for 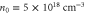 (20 THz) and
(20 THz) and  (15.7 fs at FWHM). (b) The case for
(15.7 fs at FWHM). (b) The case for  (10 THz) and
(10 THz) and 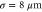 (31.4 fs at FWHM). The vertical bars represent the theoretical wave-breaking points from equation (13).
(31.4 fs at FWHM). The vertical bars represent the theoretical wave-breaking points from equation (13).
Download figure:
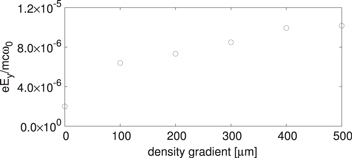
Standard image High-resolution imageAs mentioned above in the discussion of figure 3(b), the density gradient helps the diffusing field to grow and to yield much stronger THz emission than for the sharp boundary case. This feature is verified by the PIC simulations, as shown in figure 5, where a significant enhancement due to the density gradient is apparent. Indeed, the positive effect of the density gradient is one of the advantages of the field diffusion mechanism. Because every realistic plasma from a gas-jet or capillary discharge used for laser-plasma interactions has a natural density ramp-up, the experimental conditions can be greatly relaxed in our diffusion-growth scheme. Furthermore, even though a varying density is employed, the radiation frequency is not influenced much by that since our scheme is based on the local oscillation of the plasma. Note that for a density gradient the THz frequency is usually chirped when driven by a single pulse, leading to broad-band emission.
Figure 5. Dependence of the amplitude of THz emission on the length of the density gradient for 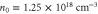 (10 THz), a0 = 0.05,
(10 THz), a0 = 0.05, 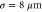 , and
, and 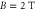 .
.
Download figure:
Standard image High-resolution image4. Conclusions
In summary, we have proposed and investigated a novel method for obtaining strong THz emission based on a driven-diffusion mechanism. We obtain, analytically, the temporal growth of the diffusing electromagnetic field by solving the constantly driven complex diffusion equation. For the driving term of the diffusing field a long lasting localized current source for the radiation can be produced by two counter-propagating laser pulses colliding in a weakly magnetized plasma. From analytic theory, we find that the THz amplitude scales with P2, where P is the power of the driving pulse, which is verified by one-dimensional PIC simulations. This scaling gives much stronger emission than for single-pulse driven systems, for which it is proportional just to P. Such significant enhancement of the THz amplitude arises from two factors: one is the stronger ponderomotive force produced by counter-propagating pulses compared with a single pulse for a given total energy of the pulses. The other is the growth of the emission by a driven-diffusion mechanism of the electromagnetic field.
Finally, we have confirmed the feasibility of the proposed scheme for experimental realization by showing that it does not impose any strict condition on the plasma or lasers such as a sharp plasma edge or the exact pulse collision point. Moreover, we have discovered that the density gradient positively enhances the emission amplitude. From these results, we note that the experimental conditions can be significantly relaxed. We suggest the following proof-of-principle experimental parameters: a couple of millimetres plasma with density of order 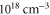 and density-ramp-up over
and density-ramp-up over  , which is readily available from gas jet or capillary discharge. The intensity of the laser pulses with 30 fs FWHM pulse duration used in our simulation is
, which is readily available from gas jet or capillary discharge. The intensity of the laser pulses with 30 fs FWHM pulse duration used in our simulation is  , which yields a THz amplitude of 50 MV m−1. Therefore we expect that pulses with a few TW power and 200
, which yields a THz amplitude of 50 MV m−1. Therefore we expect that pulses with a few TW power and 200  spot radius (pulse energy ∼0.2 J) may yield a THz power of order 0.1 MW.
spot radius (pulse energy ∼0.2 J) may yield a THz power of order 0.1 MW.
Acknowledgments
This research was supported by the Basic Science Research Program through the National Research Foundation (NRF) of Korea funded by the Ministry of Science, ICT and Future Planning (Grant number NRF-2014M1A7A1A01030175 and NRF-2013R1A1A2006353, NRF-2014M1A7A1A01030173). We acknowledge the support of the UK EPSRC (grant no. EP/J018171/1), the ECs LASERLAB-EUROPE (grant agreement no. 284464, Seventh Framework Programme), EuCARD-2 (grant no. 312453, FP7) and the Extreme Light Infrastructure (ELI) European Project. We greatly appreciate Prof Z -M Sheng for useful comments on our work.