Abstract
Recently, a class of interesting strategies, named extortion strategies, has attracted considerable attention since such extortion strategies can dominate any opponent in a repeated prisoner's dilemma game. In this paper, we investigate the influence of the strategy-selection timescale on the evolution of extortion and cooperation in networked systems. Through connecting the lifetime of individuals' strategies with their fitness, we find that extortioners can form long-term stable relationships with cooperative neighbors, whereas the lifetime of a defection strategy is short according to the myopic best response rule. With the separation of interaction and strategy-updating timescales, the extortioners in a square lattice are able to form stable, cross-like structures with cooperators due to the snowdrift-like relation. In scale-free networks the hubs are most likely occupied by extortioners, who furthermore induce their low-degree neighbors to behave as cooperators. Since extortioners in scale-free networks can meet more cooperators than their counterparts in the square lattice, the latter results in higher average fitness of the whole population than the former. The extortioners play the role of a catalyst for the evolution of cooperation, and the diversity of strategy-selection timescale furthermore promotes the maintenance of extortioners with cooperators in networked systems.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Game theory provides a powerful framework to understand the ubiquitous cooperative behaviors in social and biological systems [1]. The famous Prisoner's dilemma (PD) game describes the conflict among cooperation and defection [2]. Although mutual cooperation can provide more benefit to participants than mutual defection, selfish individuals tend to select defection strategy if the PD game is played only once. The situation may change if participants can interact repeatedly. The question of what kind of strategy can allow a participant to obtain an advantage over his/her opponent poses an interesting and challenging problem. Recently, Press and Dyson showed a novel class of strategies via a two-person repeated PD game, so-called zero-determinant (ZD) strategies, which can enforce a linear relationship between two participants' long-term payoffs [3]. In particular, a subset of ZD strategies, extortion strategies, have attracted considerable attention. An extortioner can unilaterally ensure that his/her surplus is χ-fold ( ) that of his/her opponent. The famous tit-for-tat strategy is a fair strategy with χ = 1. Hence, the ZD strategy theory provides a new perspective to comprehend strategy evolution in the repeated PD game [4, 5].
) that of his/her opponent. The famous tit-for-tat strategy is a fair strategy with χ = 1. Hence, the ZD strategy theory provides a new perspective to comprehend strategy evolution in the repeated PD game [4, 5].
Although an extortioner can exploit an unwitting opponent, he/she gets nothing if his/her opponent is an extortioner or a defector. From an evolutionary perspective, the extortion strategy is neutral with the defection strategy in a well-mixed population. Hence the extortion strategy is evolutionarily unstable [6]. Hilbe et al showed that the extortion strategy can stably exist in small populations. Although the extortion strategy is unstable in a large population, he/she can act as catalyst for the evolution of cooperation [7]. Therefore, understanding the evolution of extortioners in large populations is both very interesting and important.
The networked reciprocity is an efficient mechanism to support the evolution of cooperation in a population [8–11]. Previous investigations showed that cooperators can form tight clusters to defend against the invasion of defectors in regular or complex networks if strategies are updated in terms of imitation dynamics [12–17]. Many important factors, such as degree heterogeneity [13–17], environment noise [18–20], individual aspiration [21, 22], teaching activity [23–25], migration [26–29], interdependence of networks [30–34], percolation phase transition [35, 36], etc., exert key influences on the evolution and maintenance of cooperation in networks. Szolnoki and Perc [37, 38] recently showed that if strategy updating is guided by the myopic best response rule, the extortion strategy can stably exist with other strategies in a structured population, which furthermore promotes the emergence of cooperation. Through the aspiration-driven strategy updating rule [21], Wu and Rong [39] showed that the involvement of extortioners facilitates the boom of cooperators in a square lattice.
There are two time scales in game dynamics: the interaction timescale, which depicts how frequently individuals play games with each other; and the strategy-selection timescale, which characterizes how frequently they update their strategies. The two processes are interdependent, and many previous investigations consider that they have the same timescale, i.e., every individual immediately updates his/her behavior after one round of the game. However, the evolution of cooperation changes if individuals in a well-mixed or structured population own nonidentical timescales [40–44]. Specifically, by investigating the evolution of extortioners in well-mixed population, Hilbe et al [7] showed that the extortion strategy can also exist in two distinct well-mixed populations if the two populations evolve in different timescales, i.e., extortioners can be dominant in the population with a slow timescale and exploit individuals in another population with a fast timescale. Rong et al [42, 43] also previously studied the coevolution of timescale and cooperation in a networked PD game, and found that cooperation can be promoted if one permits an individual with a high payoff to hold onto his/her successful strategy for longer. This motivates us to investigate how the extortion strategy evolves in networked systems where individuals can adaptively adjust their strategy-selection time scales.
2. Model
Consider each individual occupying one site on a network. Each individual can play the donation game (a popular form of the PD game) with his/her neighbors, i.e., a cooperator pays the cost c for each his/her partner, who will thus receive the benefit b. A defector obtains benefit from cooperator without providing help. Therefore, the reward of mutual cooperation is  and the punishment of mutual defection is 0. If a cooperator meets a defector, the former pays
and the punishment of mutual defection is 0. If a cooperator meets a defector, the former pays  and the latter receives b. Consider that each individual has three choices, i.e., unconditional cooperation (C), unconditional defection (D) or extortion (
and the latter receives b. Consider that each individual has three choices, i.e., unconditional cooperation (C), unconditional defection (D) or extortion ( ); the long-term payoff matrix among the three strategies can be written as follows [7, 37]:
); the long-term payoff matrix among the three strategies can be written as follows [7, 37]:
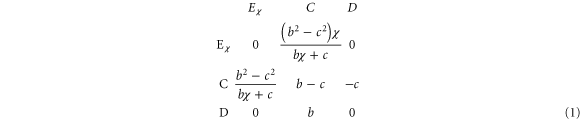
An extortioner can obtain  -fold of surplus compared with his/her cooperative partner. Therefore, an extortioner and a cooperator can form a snowdrift-like relation, i.e., the best response of the partner of the extortioner is to choose the cooperation strategy instead of the extortion strategy for
-fold of surplus compared with his/her cooperative partner. Therefore, an extortioner and a cooperator can form a snowdrift-like relation, i.e., the best response of the partner of the extortioner is to choose the cooperation strategy instead of the extortion strategy for  . However, when an extortioner meets a defector, they can get nothing and thus the relation between extortioner and defector is neutral. If setting
. However, when an extortioner meets a defector, they can get nothing and thus the relation between extortioner and defector is neutral. If setting  , there are only two parameters in the payoff matrix, i.e., the benefit factor
, there are only two parameters in the payoff matrix, i.e., the benefit factor  and the extortion factor
and the extortion factor  . If the benefit factor b is increased, the payoffs between extortioner and cooperator will also increase, whereas with an increase of the extortion factor
. If the benefit factor b is increased, the payoffs between extortioner and cooperator will also increase, whereas with an increase of the extortion factor  , the extortioner can obtain more surplus from his/her cooperative partner.
, the extortioner can obtain more surplus from his/her cooperative partner.
In social and biological systems, individuals tend to adopt the behavior with high fitness, which can be characterized by his/her payoff. For every round t, each individual i obtains the accumulated payoff Pi via playing the donation game with his/her neighbors. With probability pi(t), which will be defined later, an individual i will change his/her behavior from the current strategy si to another randomly selected strategy  with probability q in terms of the myopic best response rule [37], i.e.,
with probability q in terms of the myopic best response rule [37], i.e.,
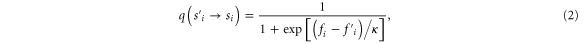
where the fitness fi corresponding to strategy si is obtained by  , and ki is the degree of individual i. This implies that individuals update their behaviors according to normalized payoff, and
, and ki is the degree of individual i. This implies that individuals update their behaviors according to normalized payoff, and  is the fitness of the same individual adopting strategy
is the fitness of the same individual adopting strategy  to play the game within the same neighborhood. The parameter κ represents the noise of the environment and is set as 0.05 following the previous paper [37].
to play the game within the same neighborhood. The parameter κ represents the noise of the environment and is set as 0.05 following the previous paper [37].
In this paper, we consider the strategy-selection timescale to be longer than the interaction timescale, which indicates that individuals can hold onto their current strategies and play the game with neighbors for several rounds before they modify their behaviors. This implies that the strategy has a lifetime. From social and biological points of view, the lifetime of a strategy is related to the fitness that an individual obtains through the strategy. If an individual has positive fitness in the current generation, he/she tends to hold his/her current advantageous behavior for longer. However, for an individual obtaining negative fitness in the current generation, he/she will try other possible behaviors. Therefore, in this paper we consider the case where an individual i updates his/her behavior with probability  . The timescale parameter
. The timescale parameter  adjusts the time it takes for individuals to update their behaviors. The case of
adjusts the time it takes for individuals to update their behaviors. The case of  corresponds to the original networked game model where individuals immediately update their strategies after one round of the game. For
corresponds to the original networked game model where individuals immediately update their strategies after one round of the game. For  , behaviors with higher fitness have a longer lifetime. Below we will investigate how individuals evolve their strategies under the control of parameter η in different networked systems.
, behaviors with higher fitness have a longer lifetime. Below we will investigate how individuals evolve their strategies under the control of parameter η in different networked systems.
3. Results and analysis
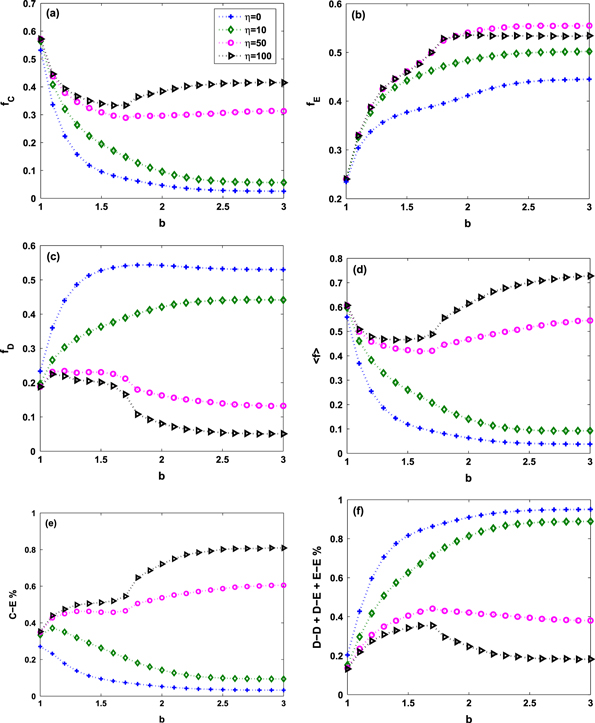
We first study how the timescale parameter η affects the evolution of cooperation in a square lattice with periodic boundary conditions, where the average degree  = 4. Initially, individuals have equal probability to choose the cooperation, defection or extortion strategy. Figures 1(a)–(c) show the evolution of cooperators, extortioners and defectors in the square lattice with the increase of the benefit factor b for different values of η. When η = 0, which means the strategy-selection timescale is identical to the interaction timescale, the frequency of cooperators (
= 4. Initially, individuals have equal probability to choose the cooperation, defection or extortion strategy. Figures 1(a)–(c) show the evolution of cooperators, extortioners and defectors in the square lattice with the increase of the benefit factor b for different values of η. When η = 0, which means the strategy-selection timescale is identical to the interaction timescale, the frequency of cooperators ( ) monotonically decreases, whereas the frequencies of extortioners (
) monotonically decreases, whereas the frequencies of extortioners ( ) and defectors (
) and defectors ( ) increase when cooperators distribute more benefit. In contrast, the fractions of both cooperators and extortioners increase with the increase of η, which implies that the number of defectors decreases if an advantageous strategy has a longer lifetime. It is very interesting that when η is sufficiently large (such as η = 100), the frequency of cooperators changes non-monotonically versus b and the number of extortioners decreases slightly in the square lattice, which cannot be disclosed through the mean-field approximation method [39] (see section 2 of the supplementary information for details). This is different from the traditional results in networked game theory, where the frequency of cooperators usually changes monotonically. Moreover, it is shown in figure 1(d) that, with the increase of cooperation level, the average fitness of the whole system will also increase.
) increase when cooperators distribute more benefit. In contrast, the fractions of both cooperators and extortioners increase with the increase of η, which implies that the number of defectors decreases if an advantageous strategy has a longer lifetime. It is very interesting that when η is sufficiently large (such as η = 100), the frequency of cooperators changes non-monotonically versus b and the number of extortioners decreases slightly in the square lattice, which cannot be disclosed through the mean-field approximation method [39] (see section 2 of the supplementary information for details). This is different from the traditional results in networked game theory, where the frequency of cooperators usually changes monotonically. Moreover, it is shown in figure 1(d) that, with the increase of cooperation level, the average fitness of the whole system will also increase.
Figure 1. The frequencies of (a) cooperators ( ), (b) extortioners (
), (b) extortioners ( ), and (c) defectors (
), and (c) defectors ( ) as a function of the benefit factor b for different values of η in the square lattice. (d) shows the change of average fitness
) as a function of the benefit factor b for different values of η in the square lattice. (d) shows the change of average fitness  versus b. (e) and (f) show the percentage of cooperator–extortioner (C–E) pairs and the pairs that bring punishment, i.e., defector–defector (D–D), defector–extortioner (D–E) and extortioner–extortioner (E–E). The data are obtained from 5000 generations after a transient time of 1000 generations in the square lattice with 10,000 individuals when the extortion factor χ = 5.
versus b. (e) and (f) show the percentage of cooperator–extortioner (C–E) pairs and the pairs that bring punishment, i.e., defector–defector (D–D), defector–extortioner (D–E) and extortioner–extortioner (E–E). The data are obtained from 5000 generations after a transient time of 1000 generations in the square lattice with 10,000 individuals when the extortion factor χ = 5.
Download figure:
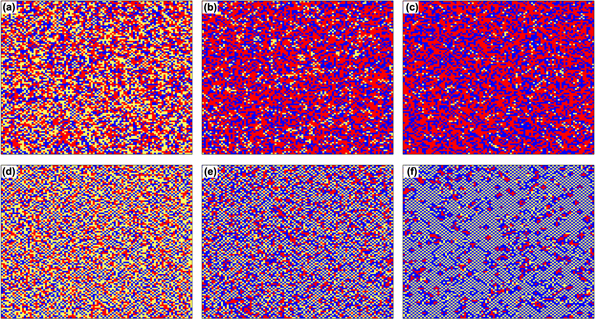
Standard image High-resolution imageHere we will explain the evolution of cooperators and extortioners in the square lattice from the perspective of pattern formation and strategy pairs. It is shown from Equation (1) that extortioners are neutral with defectors and they coexist in the square lattice, whereas the snowdrift-like relation between extortioners and cooperators makes the partner of extortioner more likely to turn into a cooperator under the myopic best response rule, and extortioners can invade cooperative clusters. It is displayed in figures 2(a)–(c) that, following the increase of b for η = 0, the cooperators will lose more and tend to become an extortioner or defector, and for a larger value of b, cooperators can only loosely disperse near extortioners and large cooperative clusters disappear in the square lattice. In addition, as shown in figure 1(f), the pairs between defectors and extortioners, as well as themselves, are dominant for η = 0. When introducing the timescale factor and increasing the parameter η, there are distinctive results for defectors, extortioners and cooperators. A defector can obtain high payoff from his/her cooperative neighbors, but leave negative payoff as a return to them. As a consequence, those neighboring cooperators of defectors will be prone to adopting either the defection or the extortion strategy in the subsequent rounds, which in turn diminishes the gains for defectors, hence leading to the short-term lifetime of the defection strategy. In contrast, those neighboring cooperators of extortioners are much better off since they can obtain some tiny positive payoffs, irrespective of being extorted by them. Consequently, when the strategy's lifetime is related to his/her fitness, extortioners can form stable relationships with cooperators in the long term. As shown in figures 2(d)–(f), for a large value of η = 100, extortioners can form cross-like structures with cooperators, which leads to the boom of both cooperators and extortioners in the square lattice. This is also validated by the plentiful cooperator–extortioner pairs in the square lattice when η = 100 as shown in figure 1(e). Following the increase of b, the frequency of cooperators will first decrease since the increase of b enables a defector to obtain more from a cooperator. However, with an increase of b that allows the payoffs between extortioner and cooperators to increase, extortioners have sufficient time to invade clusters of defectors and induce more cooperators around them. Therefore, the frequency of cooperators will then increase and a large number of cross-like structures between extortioners and cooperators emerges in the square lattice. Hence, introducing the timescale factor can form the stable existence of extortioners as well as enhancing the cooperation level and system fitness in the square lattice.
Figure 2. The typical snapshots of individuals in a 100 × 100 square lattice at the 6000th generation for (a) b = 1.1, (b) b = 1.5, (c) b = 2.0 when η = 0, and (d) b = 1.1, (e) b = 1.5, (f) b = 2.0 when η = 100. The extortion factor χ = 5.0. The yellow, red and blue colors represent the cooperator, defector as well as extortioner, respectively.
Download figure:
Standard image High-resolution imageWe then turn to study how the extortion factor χ affects the evolution of extortioners and cooperators in the square lattice. The cooperators obtain less with the increase of χ, as they are exploited more by extortioners. It is shown from figures 3(a)–(c) that, for η = 0, the frequency of cooperators monotonically decreases with the increase of χ, which is mostly replaced by extortioners. For  , the evolution of cooperation and extortion will become nontrivial, which can be understood through strategy pairs as shown in figures 3(e) and (f). Following the increase of η, there are more extortioners replacing defectors in the square lattice since extortioners can invade clusters of defectors and induce more cooperators around them, which is validated by figures 3(e) and (f), where there are more cooperator–extortioner pairs, replacing pairs that bring punishment, i.e., defector–defector pairs, defector–extortioner pairs and extortioner–extortioner pairs. Moreover, for a low value of χ, which implies an extortioner tending to share the benefit with his/her partner fairly, an extortioner obtains low surplus from a neighboring cooperator and has a short lifetime. Therefore, the number of pairs that bring punishment will first ascend with the increase of
, the evolution of cooperation and extortion will become nontrivial, which can be understood through strategy pairs as shown in figures 3(e) and (f). Following the increase of η, there are more extortioners replacing defectors in the square lattice since extortioners can invade clusters of defectors and induce more cooperators around them, which is validated by figures 3(e) and (f), where there are more cooperator–extortioner pairs, replacing pairs that bring punishment, i.e., defector–defector pairs, defector–extortioner pairs and extortioner–extortioner pairs. Moreover, for a low value of χ, which implies an extortioner tending to share the benefit with his/her partner fairly, an extortioner obtains low surplus from a neighboring cooperator and has a short lifetime. Therefore, the number of pairs that bring punishment will first ascend with the increase of  4, which leads to the decrease of
4, which leads to the decrease of  . For a large value of χ, an extortioner can obtain more benefit from cooperators and leave a tiny positive payoff to his/her partner, which promotes the emergence of more extortioner–cooperator cross-like structures in the square lattice for η = 100. Therefore, for a large value of η, the frequency of cooperators will increase with the increase of extortioners, which also improves the total fitness of the system as shown in figure 3(d). Hence, the timescale factor can play a nontrivial role in the evolution of cooperation in the square lattice.
. For a large value of χ, an extortioner can obtain more benefit from cooperators and leave a tiny positive payoff to his/her partner, which promotes the emergence of more extortioner–cooperator cross-like structures in the square lattice for η = 100. Therefore, for a large value of η, the frequency of cooperators will increase with the increase of extortioners, which also improves the total fitness of the system as shown in figure 3(d). Hence, the timescale factor can play a nontrivial role in the evolution of cooperation in the square lattice.
Figure 3. The frequencies of (a) cooperators, (b) extortioners, (c) defectors and (d) the average fitness as a function of the extortion factor χ for different values of η in the 100 × 100 square lattice. (e) and (f) are the percentage of cooperator–extortioner (C–E) pairs and the pairs that bring punishment, i.e., defector–defector (D–D), defector–extortioner (D–E) and extortioner–extortioner (E–E). The data are obtained from 5000 generations after a transient time of 1000 generations when b = 2.0.
Download figure:
Standard image High-resolution imageNow, we move on to studying the evolution of cooperation and extortion in scale-free networks. If only cooperators and defectors exist, traditional results in networked game theory show that, when considering the accumulated payoff, these high-degree hubs can obtain more payoff than low-degree individuals [13–15]. A hub tends to be a stable cooperator under the influence of a positive feedback mechanism between the number of cooperative neighbors around a hub and the payoff of the hub, which promotes the boom of cooperation in heterogeneous scale-free networks. However, in the framework of normalized payoff, which means individuals divide their accumulated payoff by degree, a hub has less normalized payoff than low-degree nodes. The cooperative behavior is more likely to disappear in scale-free networks under a normalized payoff framework if no efficient mechanism works [45]. Rong et al [43] show that when introducing the timescale factor, cooperators can also boom in scale-free networks with the normalized payoff framework because of the efficient feedback mechanism between strategy lifetime and learning information. Here, we investigate how the timescale factor works in scale-free networks when introducing extortioners.
Figure 4 shows the evolution of game dynamics as a function of the benefit factor b in the Barabási–Albert (BA) scale-free network [46]. For the case of η = 0, which corresponds to the original network game model [37], the change of game behaviors in the scale-free network is similar to that of the square lattice. When introducing the timescale factor, the situation is changed. Compared with the result in the square lattice (figure 1), the cooperative behavior in the scale-free network can be greatly enhanced, the frequency of extortioners will decrease and the frequency of defectors will rapidly decrease. Therefore, the networked structure plays a nontrivial role in the evolution of game behaviors under the influence of timescale.
Figure 4. The frequencies of (a) cooperators  , (b) extortioners
, (b) extortioners  , (c) defectors
, (c) defectors  as well as (d) system average fitness
as well as (d) system average fitness  as a function of the benefit factor, b, for different values of η in BA scale-free networks. (e) and (f) show the percentage of cooperator–extortioner (C–E) pairs and the pairs that bring punishment. The data are obtained by averaging 5000 generations after a transient time of 1000 generations in BA scale-free networks with 10000 nodes and average degree
as a function of the benefit factor, b, for different values of η in BA scale-free networks. (e) and (f) show the percentage of cooperator–extortioner (C–E) pairs and the pairs that bring punishment. The data are obtained by averaging 5000 generations after a transient time of 1000 generations in BA scale-free networks with 10000 nodes and average degree  = 4. The data are obtained by averaging over 10 different BA scale-free networks with 2 runs for each network. Here,
= 4. The data are obtained by averaging over 10 different BA scale-free networks with 2 runs for each network. Here,  .
.
Download figure:
Standard image High-resolution imageLet us understand the strategy evolution through investigating the relation between an individual's degree and the length of time that they hold onto different strategies during steady state as well as strategy pairs. It is shown in figure 5 that for η = 0, the behavior with high fitness has the same lifetime compared to that with low fitness. The hubs can meet more neighbors and find that choosing the defection or extortion strategy can obtain higher fitness than the cooperation strategy and the pairs that bring punishment are dominant in scale-free networks as shown in figure 4(f). If  , an individual can hold his/her advantageous strategy for longer. If a hub chooses the defection strategy, his/her cooperative neighbors obtain negative fitness and thus become defectors or extortioners, which decreases the fitness of the defective hub. In contrast, if a hub is extortioner, he/she can stimulate his/her neighbors to become cooperators since they can obtain positive fitness and other behaviors will obtain nothing from extortioners. This forms a positive feedback that encourages more neighbors to become cooperators; a hub with the extortion strategy will obtain more fitness and hold onto this strategy for a longer time, which leads to the stable reciprocity relationship between extortioner hubs and cooperative low-degree individuals. Hence, with the increase of η, more individuals with both medium- and high-degrees tend to become extortioners that induce a large number of low-degree individuals choosing the cooperation strategy and promote cooperative behavior in scale-free networks. Moreover, it is shown in figure 6 that for a low value of b = 1.5, individuals with medium-degrees tend to choose the extortion strategy instead of the defection strategy, and the defective behavior also booms in hubs since hubs can meet many neighbors and obtain benefit from their cooperative low-degree neighbors, which leads to the decrease in the frequency of cooperators as well as the increase in the frequencies of extortioners and defectors. However, with an increase of b that increases the benefit of both extortioner and cooperator, the high-degree individuals gradually adopt extortion instead of defection behaviors under the influence of the timescale factor, and it is shown in figure 4(e) that the stable cooperator–extortioner pairs flourish in scale-free networks that increase the frequencies of both cooperators and extortioners. Since those hubs tend to extort their cooperative low-degree individuals, the average fitness of the whole population in scale-free networks (figure 4(d)) will decrease compared with that in the square lattice (figure 1(d)).
, an individual can hold his/her advantageous strategy for longer. If a hub chooses the defection strategy, his/her cooperative neighbors obtain negative fitness and thus become defectors or extortioners, which decreases the fitness of the defective hub. In contrast, if a hub is extortioner, he/she can stimulate his/her neighbors to become cooperators since they can obtain positive fitness and other behaviors will obtain nothing from extortioners. This forms a positive feedback that encourages more neighbors to become cooperators; a hub with the extortion strategy will obtain more fitness and hold onto this strategy for a longer time, which leads to the stable reciprocity relationship between extortioner hubs and cooperative low-degree individuals. Hence, with the increase of η, more individuals with both medium- and high-degrees tend to become extortioners that induce a large number of low-degree individuals choosing the cooperation strategy and promote cooperative behavior in scale-free networks. Moreover, it is shown in figure 6 that for a low value of b = 1.5, individuals with medium-degrees tend to choose the extortion strategy instead of the defection strategy, and the defective behavior also booms in hubs since hubs can meet many neighbors and obtain benefit from their cooperative low-degree neighbors, which leads to the decrease in the frequency of cooperators as well as the increase in the frequencies of extortioners and defectors. However, with an increase of b that increases the benefit of both extortioner and cooperator, the high-degree individuals gradually adopt extortion instead of defection behaviors under the influence of the timescale factor, and it is shown in figure 4(e) that the stable cooperator–extortioner pairs flourish in scale-free networks that increase the frequencies of both cooperators and extortioners. Since those hubs tend to extort their cooperative low-degree individuals, the average fitness of the whole population in scale-free networks (figure 4(d)) will decrease compared with that in the square lattice (figure 1(d)).
Figure 5. The relations between individuals' degree k and average time of (a) cooperation  , (b) extortion
, (b) extortion  , (c) defection
, (c) defection  , in scale-free networks for different values of
, in scale-free networks for different values of  when b = 2, where
when b = 2, where  ,
,  and
and  are the number of generations for which individuals hold onto the responding strategies during the steady state, with length Ts = 5000 in this paper. The other parameters are the same as those in figure 4.
are the number of generations for which individuals hold onto the responding strategies during the steady state, with length Ts = 5000 in this paper. The other parameters are the same as those in figure 4.
Download figure:
Standard image High-resolution imageFigure 6. The relations between individuals' degree k and average time of (a) cooperation  , (b) extortion
, (b) extortion  , (c) defection
, (c) defection  , in scale-free networks for different values of b when χ = 5 and
, in scale-free networks for different values of b when χ = 5 and  = 100. The other parameters are the same as those in figure 5.
= 100. The other parameters are the same as those in figure 5.
Download figure:
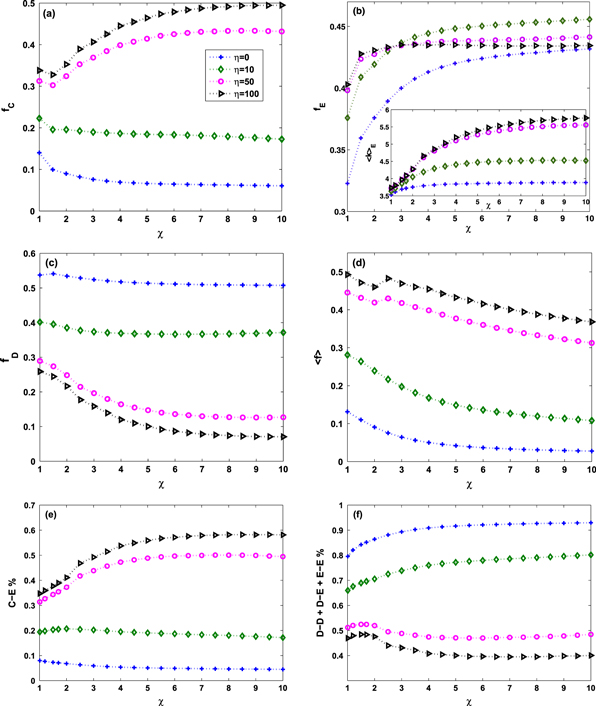
Standard image High-resolution imageFinally, we study the evolution of game behaviors by changing the extortion factor χ. It is shown in the inset of figure 7(b) that, with the increase of χ, which means extortioners become more greedy, the average degree of extortioners in scale-free networks will increase with the increase of η. This implies that individuals with medium/high degrees tend to choose extortion and induce more low-degree neighbors to choose the cooperation strategy, cooperator–extortioner pairs are promoted, and the pairs that bring punishment are inhibited with the increase of χ as shown in figures 7(e) and (f). It is exhibited in figures 7(a) and (c) that the frequency of cooperators increases and that of defectors decreases following the increase of χ for a large value of η. However, we observe in figure 7(d) that the average fitness will decrease with the increase of χ since more cooperators are extorted by those greedy hubs, which is different from the case of the square lattice.
Figure 7. The frequencies of (a) cooperation  , (b) extortion
, (b) extortion  , (c) defection
, (c) defection  and (d) average fitness
and (d) average fitness  as a function of the extortion factor χ for different values of η in BA scale-free networks when b = 2.0. (e) and (f) show the percentage of cooperator–extortioner (C–E) pairs and the pairs that bring punishment, i.e., defector–defector (D–D), defector–extortioner (D–E) and extortioner–extortioner (E–E). The inset of (b) shows the average degree of extortioners evolving with the extortion factor χ.
as a function of the extortion factor χ for different values of η in BA scale-free networks when b = 2.0. (e) and (f) show the percentage of cooperator–extortioner (C–E) pairs and the pairs that bring punishment, i.e., defector–defector (D–D), defector–extortioner (D–E) and extortioner–extortioner (E–E). The inset of (b) shows the average degree of extortioners evolving with the extortion factor χ.
Download figure:
Standard image High-resolution image4. Conclusions and discussion
In this paper, we have investigated the influence of the separation of interaction and strategy-updating timescales on the evolution of extortioners in networked systems. Our investigation shows that if a strategy's lifetime is related to its fitness, it is easy for the extortioners to invade the clusters of defectors, and form stable relationships with cooperative neighbors. Therefore, introducing the timescale factor into game dynamics promotes the stable existence of extortioners and furthermore enhances the cooperation level in networked systems. Particularly, different from the traditional networked game theory where cooperators can form tight clusters to defend from the invasion of defectors in PD game, the snowdrift-like relation between extortioner and cooperator leads to cross-like structures in a square lattice.
Moreover, when linking the lifetime of a strategy with fitness, extortioners are prone to occupying the hubs in scale-free networks, and induce more cooperative neighbors around hubs, which means hubs obtain more fitness and stick to the extortion strategy for a longer period. The positive feedback mechanism between the lifetime of a strategy with fitness is enhanced with the increase of η, which leads to more cooperators located at low-degree nodes being exploited by hubs. Therefore, the average fitness of the whole population in scale-free networks reduces compared with that in the square lattice.
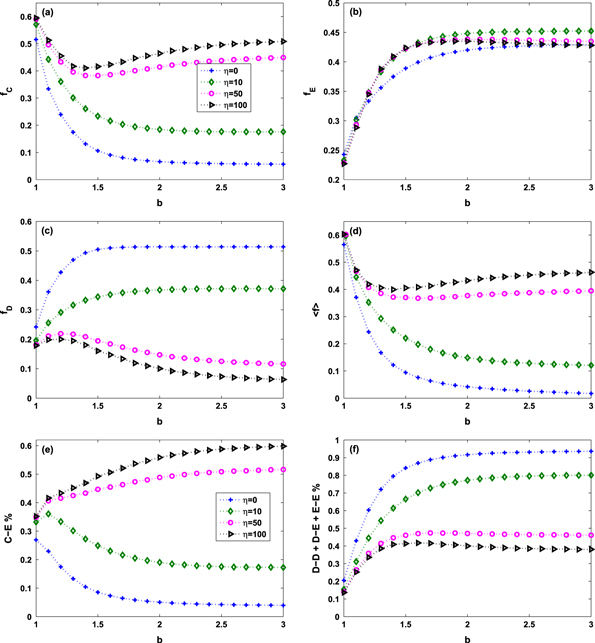
Furthermore, we also validate the results in a well-mixed population, lattice and scale-free network with more density. It is shown from figure 8 that comparing with the case of η = 0, the cooperation behavior in the well-mixed population slightly decreases for a large value of η = 100. This is due to the fact that, when cooperators interact with defectors and extortioners in the well-mixed population, each individual can interact with all other individuals, and introducing the timescale factor offers a defector or an extortioner a long lifetime in which to exploit a neighboring cooperator. The result in the well-mixed population is different from that in the spatial structure, where introducing the timescale can promote the emergence of cooperation. This indicates that the structure can promote the emergence and maintenance of cooperation with extortion under the influence of the timescale factor. In this paper we mainly investigate the evolution of strategies with timescale in the square lattice and BA scale-free networks with average degree  = 4. In figure 8 we also show the results in denser networks, i.e., the Moore lattice and BA scale-free networks with
= 4. In figure 8 we also show the results in denser networks, i.e., the Moore lattice and BA scale-free networks with  = 8. It is shown that introducing the timescale can promote the emergence of cooperation in denser networks, whereas the cooperation behavior is inhibited and the non-monotonic behavior of
= 8. It is shown that introducing the timescale can promote the emergence of cooperation in denser networks, whereas the cooperation behavior is inhibited and the non-monotonic behavior of  may disappear when the network becomes denser. This is because these low-degree individuals can meet more neighbors, which promotes the maintenance of defectors and inhibits the emergence of cooperation level in denser networks (see section 3 of the supplementary information for details).
may disappear when the network becomes denser. This is because these low-degree individuals can meet more neighbors, which promotes the maintenance of defectors and inhibits the emergence of cooperation level in denser networks (see section 3 of the supplementary information for details).
Figure 8. The frequencies of cooperation  , extortion
, extortion  , defection
, defection  evolve in a well-mixed population in terms of (a) b and (b) χ, the Moore lattice with
evolve in a well-mixed population in terms of (a) b and (b) χ, the Moore lattice with  = 8 in terms of (c) b and (d) χ and the BA scale-free network with
= 8 in terms of (c) b and (d) χ and the BA scale-free network with  = 8 in terms of (e) b and (f) χ. The population size is N = 10,000. The extortion factor is χ = 5 in (a), (c) and (e). The benefit factor is b = 1.2 in (b) and b = 2 in (d) and (f).
= 8 in terms of (e) b and (f) χ. The population size is N = 10,000. The extortion factor is χ = 5 in (a), (c) and (e). The benefit factor is b = 1.2 in (b) and b = 2 in (d) and (f).
Download figure:
Standard image High-resolution imageWe also notice that there is another class of ZD strategies, namely generosity strategies, which allows participants to obtain the payoff of mutual cooperation [4, 47–49, 51]. The famous 'generous tit-for-tat' strategy is a subset of generosity strategies. The evolution of the generosity strategy with the extortion strategy deserves a through investigation in future. Moreover, individuals usually interact in group formation. Recent results have shown that ZD strategies also exist in multi-player games, such as the public goods game [51–53]. This provides a clue to understanding the evolution among extortion and generous behaviors in networked systems with group interactions.
Acknowledgments
The authors thank the anonymous reviewers for their constructive suggestions to help improve this paper. This work was supported by the National Natural Science Foundation of China (No. 61273223, 11135001, 61374053 and 61473060), the Research Foundation of UESTC and Hong Kong Scholars Program (No. XJ2013019 and G-YZ4D), the Fundamental Research Funds for the Central Universities (Grant No. lzujbky-2014–28).