Abstract
We observe Wannier–Stark (W–S) localization in curved photonic lattices, realized using arrays of evanescently coupled optical waveguides. By correctly tuning the strength of inter-site coupling in the lattice, we observe that W–S states become increasingly localized, and eventually fully localized to one site, as the curvature of the lattice is increased. We then demonstrate that tunneling can be successfully restored in the lattice by applying a resonant sinusoidal modulation to the lattice position, an effect that is a direct analogue of photon-assisted tunneling. This precise tuning of the tunneling matrix elements, through resonant modulation-assisted tunneling, opens a novel route for the creation of gauge fields in laser-fabricated photonic lattices.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Quantum matter or light propagating in engineered lattices offer versatile platforms for the quantum simulation of new states of matter, such as topological phases [1–5]. This approach relies on novel technologies allowing for the tuning of microscopic parameters that characterize lattice models of interest, such as on-site interactions and tunneling matrix elements. In fact, generating complex-valued tunneling matrix elements can potentially induce non-trivial gauge structures in the lattice, e.g. artificial magnetic fields and non-Abelian gauge potentials [1, 5, 6], offering an interesting route for quantum simulation [7]. In this context, photon-assisted tunneling, a powerful method by which tunneling can be controlled in lattice systems, has been recently exploited in cold gases [8–14] and ion traps [15, 16]; this led to the experimental realization of the Hofstadter model [17, 18] and to the detection of the topological Chern number [19] with cold atomic gases.
The photon-assisted-tunneling method relies on two main ingredients [10, 13–15]: (a) an artificial electric field generating a large energy offset Δ between neighboring sites, hence inhibiting the bare hopping, and (b) a time-modulation of the on-site energy, whose frequency is resonant with respect to the static offset 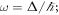 this restores the tunneling in an efficient and tunable manner. In this paper, we experimentally demonstrate the realization of modulation-assisted tunneling, an analogue of photon-assisted-tunneling, in arrays of coupled optical waveguides.
this restores the tunneling in an efficient and tunable manner. In this paper, we experimentally demonstrate the realization of modulation-assisted tunneling, an analogue of photon-assisted-tunneling, in arrays of coupled optical waveguides.
The transport of light in a system of coupled optical waveguides, a photonic lattice, can be described by a Schrödinger-like equation. As a result, photonic lattices can be used to observe phenomena known from solid state physics. In recent years photonic lattices have been used to study fundamental solid state phenomena including Bloch oscillations [20, 21], dynamic localization [22–24], Bloch–Zener dynamics [25], and Landau–Zener dynamics [26]. These phenomena are each related to the manner in which a charged particle behaves in a periodic potential and external electric field. In such a system, a static electric field destroys the translational symmetry of the lattice, and the delocalized Bloch states become localized in space. These states are known as Wannier–Stark (W–S) states, originally predicted by Wannier in 1960 [27].
In the absence of an external electric field, the eigenstates of an electron in a periodic potential are the Bloch states. A static electric field ( ) destroys the degeneracy of these spatially delocalized Bloch states. In this situation, the eigenstates and energies are [28, 29]
) destroys the degeneracy of these spatially delocalized Bloch states. In this situation, the eigenstates and energies are [28, 29]
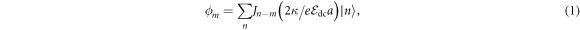
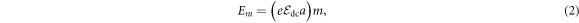
where 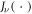 is the Bessel function of order ν, a is the lattice spacing,
is the Bessel function of order ν, a is the lattice spacing,  is the bandwidth, e is the electronic charge and
is the bandwidth, e is the electronic charge and 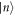 are the Wannier states. The span of the first Brillouin zone is
are the Wannier states. The span of the first Brillouin zone is  In the limit
In the limit 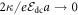 there is only one term in equation (1), i.e. the eigenstates exactly correspond to the localized Wannier states
there is only one term in equation (1), i.e. the eigenstates exactly correspond to the localized Wannier states 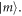 In fact, in a strong external electric field and weak inter-site interaction i.e.
In fact, in a strong external electric field and weak inter-site interaction i.e.  the spatial width of W–S state is less than the inter-site separation, a. In this limit, the W–S states will be localized to a single lattice site, indicating that the energy offset
the spatial width of W–S state is less than the inter-site separation, a. In this limit, the W–S states will be localized to a single lattice site, indicating that the energy offset 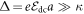 generated by the static electric field inhibits the bare hopping between neighboring sites. Importantly, when driving the system, the strongly localized electronic states on individual lattice sites can interact through photons and tunnel to the nearest lattice sites. This type of tunneling with discrete energy exchange is known as photon-assisted tunneling; it has been observed in superconducting diodes [30], semiconductor superlattices [31], quantum dots [32], and also with cold atoms trapped in optical lattices [33].
generated by the static electric field inhibits the bare hopping between neighboring sites. Importantly, when driving the system, the strongly localized electronic states on individual lattice sites can interact through photons and tunnel to the nearest lattice sites. This type of tunneling with discrete energy exchange is known as photon-assisted tunneling; it has been observed in superconducting diodes [30], semiconductor superlattices [31], quantum dots [32], and also with cold atoms trapped in optical lattices [33].
In this paper, we use photonic lattices, fabricated using the technique of ultrafast laser inscription, as a powerful platform to investigate the dynamics of W–S states in a strong static electric field and weak inter-site interaction. We demonstrate strong localization of the W–S state, seen for the first time using curved photonic lattices, where the curvature is analogous to the inverse of a static electric field in the electronic case. When the electric field exceeds a threshold value, we observe that the W–S state becomes localized to a single lattice site. Importantly, we then also demonstrate that a strongly localized W–S state becomes delocalized when an appropriate (specific frequencies and amplitudes) sinusoidal modulation is applied to the lattice. The latter result constitutes the first photonic-crystal analogue of photon-assisted tunneling, based on fabricated sinusoidal modulations, offering a promising method for the generation of gauge fields in photonic lattices.
2. The photonic lattice
The propagation of the electric field envelope  in the material is governed by
in the material is governed by
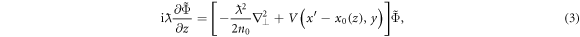
where  depends on
depends on  and z,
and z, 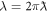 is the free-space wavelength and
is the free-space wavelength and 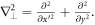
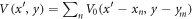 describes the refractive index modulation in the transverse cross section where
describes the refractive index modulation in the transverse cross section where 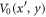 is the refractive index profile of a single waveguide at position xn, yn. The function
is the refractive index profile of a single waveguide at position xn, yn. The function  determines the transverse shift of the whole lattice depending on the propagation distance z. By making a change of reference frame
determines the transverse shift of the whole lattice depending on the propagation distance z. By making a change of reference frame 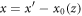 equation (3) can be rewritten as
equation (3) can be rewritten as

with 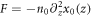 and where
and where 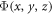 is the consequently transformed state [23, 34]. The transport of light in a circularly curved one-dimensional (1D) photonic lattice, with sinusoidal modulation (figure 1(c)) is then governed by the paraxial equation [23, 34]
is the consequently transformed state [23, 34]. The transport of light in a circularly curved one-dimensional (1D) photonic lattice, with sinusoidal modulation (figure 1(c)) is then governed by the paraxial equation [23, 34]
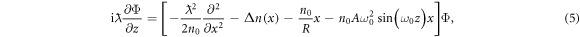
where the lattice is bending along the x direction with a radius of curvature R. The amplitude and frequency of the z-dependent 'ac' modulation are A and ω0 respectively, n0 is the refractive index of the substrate material and 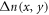 is the transverse refractive index profile. Equation (5) is analogous to the Schrödinger equation of a particle with effective mass n0 and charge e moving in a 1D periodic potential
is the transverse refractive index profile. Equation (5) is analogous to the Schrödinger equation of a particle with effective mass n0 and charge e moving in a 1D periodic potential 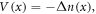 with an external (artificial) electric field
with an external (artificial) electric field 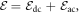 where
where 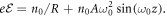 Here, z plays the role of time,
Here, z plays the role of time,  and
and  (see equations (1) and (2)).
(see equations (1) and (2)).
Figure 1. Schematic diagrams of (a) an array of straight optical waveguides, (b) an array of circularly curved optical waveguides, (c) an array of circularly curved optical waveguides with a sinusoidal modulation. (d) Schematic diagram of the ultrafast laser inscription technique. (e) White-light transmission micrograph of the facet of an array of straight waveguides. Lattice constant a = 16 μm. Each waveguide is single-mode at 780 nm wavelength. The central waveguide, indicated with the red circle, was excited for all measurements.
Download figure:
Standard image High-resolution imageFor well-confined single-mode waveguides, equation (5) can be solved using the tight-binding approximation. For a 1D photonic lattice, and supposing that only the lowest band is excited, equation (5) gives the coupled-mode equations
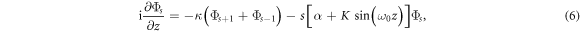
where Φs is the electric field amplitude in the sth waveguide, κ is the nearest-neighbor coupling constant along the x direction,  is the strength of the external linear potential (i.e. the artificial dc electric field) and
is the strength of the external linear potential (i.e. the artificial dc electric field) and 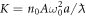 is the strength of the artificial ac modulation.
is the strength of the artificial ac modulation.
In the absence of the ac field, K = 0, and considering the regime where the energy offset α inhibits tunneling between neighboring sites, 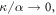 a state excited at the input becomes perfectly localized to a single lattice site. This is W–S localization. When adding the artificial ac field, the analogue of photon-assisted-tunneling occurs when the resonance condition
a state excited at the input becomes perfectly localized to a single lattice site. This is W–S localization. When adding the artificial ac field, the analogue of photon-assisted-tunneling occurs when the resonance condition

is satisfied. Hence, for a photonic lattice satisfying  tunneling between neighboring sites is restored. This leads to an effective coupling constant,
tunneling between neighboring sites is restored. This leads to an effective coupling constant,  whose amplitude is given by (see [10, 14] and section 5)
whose amplitude is given by (see [10, 14] and section 5)
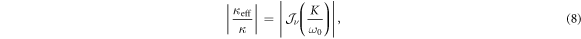
where  is the Bessel function of order ν; see also figure 6. Let us point out that the real part of the effective coupling constant
is the Bessel function of order ν; see also figure 6. Let us point out that the real part of the effective coupling constant  is allowed to take positive, but also negative values. This effect has a simple semi-classical interpretation based on the micro-motion associated with the ac field, and which generates oscillations in quasi-momentum space, see [14, 35]. Let us consider the case ν = 0 for simplicity, and suppose that a wave packet is prepared in the vicinity of the band's ground-state at k = 0. For weak modulations
is allowed to take positive, but also negative values. This effect has a simple semi-classical interpretation based on the micro-motion associated with the ac field, and which generates oscillations in quasi-momentum space, see [14, 35]. Let us consider the case ν = 0 for simplicity, and suppose that a wave packet is prepared in the vicinity of the band's ground-state at k = 0. For weak modulations 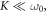 the oscillations in quasi-momentum space are small, and the wave packet essentially remains localized around k = 0; the effective tunneling rate
the oscillations in quasi-momentum space are small, and the wave packet essentially remains localized around k = 0; the effective tunneling rate  is only slightly affected. For strong modulations, the micro-motion oscillations become comparable to the size of the Brillouin zone, and the wave packet often visits the high-energy regions of the band at
is only slightly affected. For strong modulations, the micro-motion oscillations become comparable to the size of the Brillouin zone, and the wave packet often visits the high-energy regions of the band at 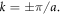 This situation is consistent with a change of sign of the tunneling rate, i.e.
This situation is consistent with a change of sign of the tunneling rate, i.e. 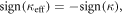 as described by the Bessel function
as described by the Bessel function  This semi-classical picture generalizes to arbitrary
This semi-classical picture generalizes to arbitrary 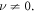
3. W–S localization
To investigate W–S localization, fifteen 1D lattices (lattice constant a = 16 μm) were fabricated using ultrafast laser inscription, figure 1(d). In these lattices, no modulation was created (A = 0), however the radius of curvature of the lattice was varied between 1.5 and 0.1 m (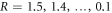 m), see figure 1(b). An additional straight lattice was also fabricated (
m), see figure 1(b). An additional straight lattice was also fabricated (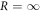 ), see figure 1(a). The white-light transmission micrograph of the facet of a lattice is shown in figure 1(e). The refractive index profile of each waveguide was controlled using the 'slit-beam' shaping method [36]. Each waveguide was inscribed by translating the 30 mm long glass sample (Corning Eagle2000), at a translation speed of 8 mm s−1, once through the focus of a 500 kHz train of 1030 nm femtosecond laser pulses. The laser inscription parameters were optimized to produce waveguides that were single-mode and well confined at 780 nm. For a more detailed description of the waveguide fabrication procedure, see [37]. It should be highlighted that although the propagation loss of a waveguide depends on its curvature, we do not expect this to be important in our discussion since all waveguides in each lattice have the same bend radius at a given value of z. In other words, there is no site dependent loss for a given lattice.
), see figure 1(a). The white-light transmission micrograph of the facet of a lattice is shown in figure 1(e). The refractive index profile of each waveguide was controlled using the 'slit-beam' shaping method [36]. Each waveguide was inscribed by translating the 30 mm long glass sample (Corning Eagle2000), at a translation speed of 8 mm s−1, once through the focus of a 500 kHz train of 1030 nm femtosecond laser pulses. The laser inscription parameters were optimized to produce waveguides that were single-mode and well confined at 780 nm. For a more detailed description of the waveguide fabrication procedure, see [37]. It should be highlighted that although the propagation loss of a waveguide depends on its curvature, we do not expect this to be important in our discussion since all waveguides in each lattice have the same bend radius at a given value of z. In other words, there is no site dependent loss for a given lattice.
The nearest-neighbor coupling, κ, was measured to be 0.072 mm−1. The next-nearest neighbor coupling strength, κN, was insignificant for the 30 mm long lattices with 16 μm lattice constant. Figure 2 shows the output intensity distribution measured for the lattices with radii of curvature 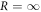 (i.e. the straight lattice), 1.5, 1.2, 0.5 0.3 and 0.2 m. It is clear from figure 2 that the light becomes increasingly localized as the radius of curvature is reduced, as would be expected from equation (1). To investigate this phenomenon further, we fabricated 10 mm long 2D lattices with a lattice constant a = 15 μm along both x and y axes, where each lattice curves only along the x direction. For these lattices, the measured coupling strengths along the x and y axes were 0.085 mm
(i.e. the straight lattice), 1.5, 1.2, 0.5 0.3 and 0.2 m. It is clear from figure 2 that the light becomes increasingly localized as the radius of curvature is reduced, as would be expected from equation (1). To investigate this phenomenon further, we fabricated 10 mm long 2D lattices with a lattice constant a = 15 μm along both x and y axes, where each lattice curves only along the x direction. For these lattices, the measured coupling strengths along the x and y axes were 0.085 mm  and 0.095
and 0.095 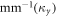 respectively. From simulations, the estimated value of next-nearest-neighbor coupling was 0.019
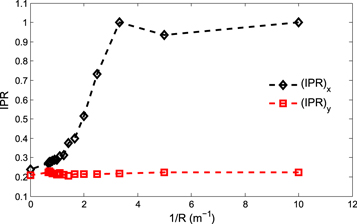
respectively. From simulations, the estimated value of next-nearest-neighbor coupling was 0.019 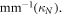 As can be seen from figure 3, localization occurs only along the x axis, the direction of the artificial electric field. To quantify localization along the two axes, the inverse participation ratio (IPR) was calculated. The IPR is a measure of localization and is defined as the inverse of the absolute value of the average of the fourth power of the wave function. For our purpose, the IPR for the x axis was obtained by summing all the intensity values in each column to obtain a vector of values along the x axis. The IPR was then calculated using this vector. The IPR along the y axis was calculated using the same procedure, but by summing the rows rather than columns. For a localized state, the IPR is equal to 1. As can be seen from figure 4, there is no effect of electric field along the y axis, as would be expected, but complete localization is observed along the x axis once the artificial electric field exceeds a threshold value.
As can be seen from figure 3, localization occurs only along the x axis, the direction of the artificial electric field. To quantify localization along the two axes, the inverse participation ratio (IPR) was calculated. The IPR is a measure of localization and is defined as the inverse of the absolute value of the average of the fourth power of the wave function. For our purpose, the IPR for the x axis was obtained by summing all the intensity values in each column to obtain a vector of values along the x axis. The IPR was then calculated using this vector. The IPR along the y axis was calculated using the same procedure, but by summing the rows rather than columns. For a localized state, the IPR is equal to 1. As can be seen from figure 4, there is no effect of electric field along the y axis, as would be expected, but complete localization is observed along the x axis once the artificial electric field exceeds a threshold value.
Figure 2. Intensity distribution at the output of 30 mm long circularly curved 1D lattices with radii of curvature (a)  (i.e. straight lattice), (b)
(i.e. straight lattice), (b) 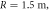 (c)
(c)  (d)
(d)  (e)
(e) 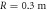 and (f)
and (f) 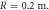 Here
Here 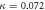 mm−1,
mm−1, 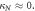 In each case, light was launched into the central waveguide (as indicated by the white circle).
In each case, light was launched into the central waveguide (as indicated by the white circle).
Download figure:
Standard image High-resolution imageFigure 3. (a) Micrograph of the facet of a finite square lattice. For all measurements, light was launched into the circled waveguide. (b)–(g) Intensity distribution at the output of 10 mm-long circularly curved square lattice with radii of curvature (b)  (i.e. straight lattice), (c) R = 1 m, (d)
(i.e. straight lattice), (c) R = 1 m, (d)  (e)
(e)  (f)
(f) 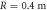 and (g)
and (g) 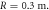
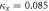
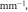
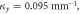
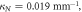 lattice constant a = 15 μm.
lattice constant a = 15 μm.
Download figure:
Standard image High-resolution imageFigure 4. Inverse participation ratio (IPR) is a measure of localization and is defined as the average of the absolute value of the fourth power of the wave function. The IPRs along the x and y directions, (IPR)x and (IPR)y respectively, have been plotted as a function of the inverse of curvature radius R which is a measure of the strength of dc electric field. There is no effect of electric field along the y direction. Complete localization (IPR = 1) is observed in the x direction as the electric field exceeds a threshold value.
Download figure:
Standard image High-resolution imageThe localization phenomenon can also be explained using the theory of waveguide optics. It can be shown [34], using a conformal transformation, that a 1D array of circularly curved waveguides with periodic transverse refractive index profile is equivalent to an array of straight waveguides with a new refractive index profile. In the limit 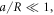 the new refractive index profile is the superposition of the original periodic index profile and a linear ramp of refractive index, and the radius of curvature controls this ramp. In other words, the mode supported by each waveguide in the curved array has a different propagation constant β. As R decreases, the difference in β increases, resulting in partial transfer of light into the nearest waveguides via evanescent coupling. After a threshold value of R, there is no significant coupling between the nearest waveguides resulting in a complete spatial localization.
the new refractive index profile is the superposition of the original periodic index profile and a linear ramp of refractive index, and the radius of curvature controls this ramp. In other words, the mode supported by each waveguide in the curved array has a different propagation constant β. As R decreases, the difference in β increases, resulting in partial transfer of light into the nearest waveguides via evanescent coupling. After a threshold value of R, there is no significant coupling between the nearest waveguides resulting in a complete spatial localization.
4. Analog photon-assisted tunneling
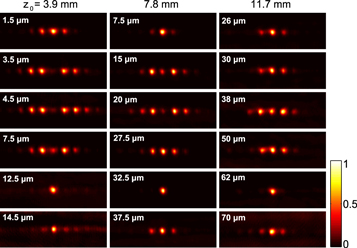
To observe the effect analog to photon-assisted tunneling, three sets of 30 mm long lattices were fabricated with a sinusoidal modulation (figure 1(c)). For sets 1, 2 and 3, the periods  were set to 3.9 mm, 7.8 mm and 11.7 mm respectively, corresponding to ν = 1, 2 and 3 in equation (7). For all sets, the radius of curvature and inter-site separation were set to R = 120 mm and a = 16 μm respectively. For each set, 15 lattices were fabricated and the amplitude of oscillation, A, was varied; 0.5 μm
were set to 3.9 mm, 7.8 mm and 11.7 mm respectively, corresponding to ν = 1, 2 and 3 in equation (7). For all sets, the radius of curvature and inter-site separation were set to R = 120 mm and a = 16 μm respectively. For each set, 15 lattices were fabricated and the amplitude of oscillation, A, was varied; 0.5 μm  14.5 μm (for set 1), 5.0 μm
14.5 μm (for set 1), 5.0 μm 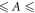 40.0 μm (for set 2) and 14 μm
40.0 μm (for set 2) and 14 μm  70 μm (for set 3). The measured output intensity distributions are shown in figure 5. The effective coupling of a modulated lattice, for a given value of A, z0 and R, was evaluated by simulating a 30 mm long straight photonic lattice, and varying the coupling strength to optimally fit the observed output intensity distributions. The normalized effective coupling strength (
70 μm (for set 3). The measured output intensity distributions are shown in figure 5. The effective coupling of a modulated lattice, for a given value of A, z0 and R, was evaluated by simulating a 30 mm long straight photonic lattice, and varying the coupling strength to optimally fit the observed output intensity distributions. The normalized effective coupling strength (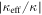 ) is plotted graphically as a function of
) is plotted graphically as a function of 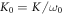 in figure 6, where it can be seen that the normalized effective coupling strength has a characteristic (Bessel-function) dependency on K0, as predicted by equation (8). This is clear evidence that the tunneling has been partially restored through an analogue of photon-assisted tunneling. As a final note, it should be stressed that simulations performed using the experimentally evaluated parameters indicate that significant tunneling is absent when z0 was not an integer multiple of 3.9 mm.
in figure 6, where it can be seen that the normalized effective coupling strength has a characteristic (Bessel-function) dependency on K0, as predicted by equation (8). This is clear evidence that the tunneling has been partially restored through an analogue of photon-assisted tunneling. As a final note, it should be stressed that simulations performed using the experimentally evaluated parameters indicate that significant tunneling is absent when z0 was not an integer multiple of 3.9 mm.
Figure 5. Intensity distribution at the output of circularly curved lattices with sinusoidal modulation. Spatial periods of oscillation are 3.9 mm (1st column), 7.8 mm (2nd column) and 11.7 mm (3rd column). For each period the amplitude of oscillation, A, was varied as shown. Here 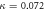 mm−1 and
mm−1 and 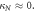 In each case, light was launched into the central waveguide. See also figure (6) for a graphical representation.
In each case, light was launched into the central waveguide. See also figure (6) for a graphical representation.
Download figure:
Standard image High-resolution imageFigure 6. Graphical representation of figure 5. Variation of the normalized effective coupling strength with  The periods are
The periods are  corresponding to ν = 1, 2 and 3 in equation (7), respectively. The solid lines are the absolute values of Bessel functions
corresponding to ν = 1, 2 and 3 in equation (7), respectively. The solid lines are the absolute values of Bessel functions  and
and 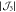 respectively, which were predicted theoretically from equation (8).
respectively, which were predicted theoretically from equation (8).
Download figure:
Standard image High-resolution image5. Application: artificial magnetic fluxes
Photon-assisted tunneling constitutes a powerful method to generate artificial gauge structures in lattice systems [13–15]. To illustrate this concept, let us start with a simplified version of the system described by equations (6), (7). Consider a two-level system 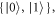 i.e. two sites of a lattice treated in a single-band tight-binding approximation, with energy offset
i.e. two sites of a lattice treated in a single-band tight-binding approximation, with energy offset 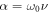 and resonant 'time' modulation with frequency
and resonant 'time' modulation with frequency 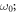 here
here 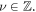 The Hamiltonian is taken to be of the form
The Hamiltonian is taken to be of the form

which is indeed strictly equivalent to restricting the Schrödinger equation in equations (6), (7) to two lattice sites  Note that we have introduced the phase of the modulation ϕ, and we note that
Note that we have introduced the phase of the modulation ϕ, and we note that  in the strong-driving regime. We tackle the Schrödinger equation by first performing a unitary transformation
in the strong-driving regime. We tackle the Schrödinger equation by first performing a unitary transformation
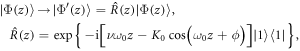
which results in the modified z-dependent Hamiltonian

where we used the Jacobi–Anger expansion, 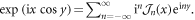 To lowest order in
To lowest order in  the effective Hamiltonian [14, 35] is well approximated by the time-average over one period (i.e. j = 0 in equation (9)), which yields
the effective Hamiltonian [14, 35] is well approximated by the time-average over one period (i.e. j = 0 in equation (9)), which yields
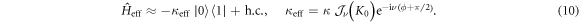
Importantly, the effective coupling elements 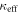 are now complex-valued for
are now complex-valued for 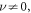 with a phase factor
with a phase factor 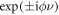 that explicitly depends on the phase of the modulation ϕ. The two-site result in equation (10) directly generalizes to the full modulated W-S ladder (equations (6), (7)), which is then well described by the effective Hamiltonian
that explicitly depends on the phase of the modulation ϕ. The two-site result in equation (10) directly generalizes to the full modulated W-S ladder (equations (6), (7)), which is then well described by the effective Hamiltonian
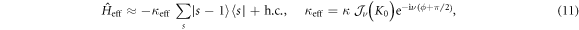
as already announced in equation (8) for ϕ = 0.
While the phase factor  in equation (11) is irrelevant in the 1D geometries considered in this work (i.e. the phase is associated with a constant gauge potential; see [38–40] for physical consequences), it can potentially lead to dramatic effects in 2D geometries if it is made explicitly space-dependent [13–15]. Indeed, let us consider a modulated W–S ladder aligned along the x direction, with sites labeled by the index sx, and let us assume that the phase of the modulation
in equation (11) is irrelevant in the 1D geometries considered in this work (i.e. the phase is associated with a constant gauge potential; see [38–40] for physical consequences), it can potentially lead to dramatic effects in 2D geometries if it is made explicitly space-dependent [13–15]. Indeed, let us consider a modulated W–S ladder aligned along the x direction, with sites labeled by the index sx, and let us assume that the phase of the modulation 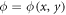 can be controlled in a space-dependent manner. If an additional lattice is aligned along the y direction, with lattice sites labeled by sy, then the 2D effective Hamiltonian will be of the form [13–15, 41, 42]
can be controlled in a space-dependent manner. If an additional lattice is aligned along the y direction, with lattice sites labeled by sy, then the 2D effective Hamiltonian will be of the form [13–15, 41, 42]
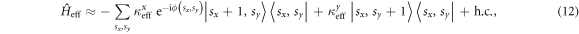
where 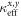 are real-valued tunneling rates along the x and y directions, respectively, and where we considered the case ν = 1 for simplicity. If the phase is designed to be in the form
are real-valued tunneling rates along the x and y directions, respectively, and where we considered the case ν = 1 for simplicity. If the phase is designed to be in the form 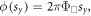 then the system realizes the Harper–Hofstadter Hamiltonian [41–43]: a 2D lattice penetrated by a uniform magnetic flux
then the system realizes the Harper–Hofstadter Hamiltonian [41–43]: a 2D lattice penetrated by a uniform magnetic flux 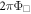 per plaquette. Indeed, the wavefunction of a particle circulating around any plaquette of the lattice acquires an Aharanov-Bohm phase associated with the flux
per plaquette. Indeed, the wavefunction of a particle circulating around any plaquette of the lattice acquires an Aharanov-Bohm phase associated with the flux  Hence, engineering the spatial dependence of the phase of the modulation ϕ, which still constitutes an experimental challenge, would allow for the creation of synthetic fluxes in photonic lattice systems, opening an interesting route for photonic quantum-Hall (topological) physics.
Hence, engineering the spatial dependence of the phase of the modulation ϕ, which still constitutes an experimental challenge, would allow for the creation of synthetic fluxes in photonic lattice systems, opening an interesting route for photonic quantum-Hall (topological) physics.
6. Conclusion
In this paper, we have demonstrated that an appropriately designed array of evanescently coupled curved optical waveguides can be used to observe a W–S state that is fully localized on a single lattice site. From the perspective of solid state physics, the localization is due to an analogue of a strong external dc electric field that breaks the degeneracy of the Bloch states and results in a W–S ladder. We also demonstrate that tunneling in such photonic lattices can be restored by applying an analogue of an ac electric field, and that the strength of this tunneling obeys a characteristic dependency on the frequency and amplitude of the ac modulation, which is in excellent agreement with the existing theory of photon-assisted tunneling. By further tuning the spatial dependence of the laser-fabricated modulation, this method could be used to produce effective magnetic fluxes [13–15, 44] in 2D photonic lattices; this goes beyond the realization of artificial electric fields, as presented and exploited in this work. The interplay between such artificial fields and the presence of nonlinearities opens a promising route for the study of interacting particles in large magnetic fields and topological phenomena.
Acknowledgments
RRT gratefully acknowledges funding from the UK Science and Technology Facilities Council (STFC) in the form of an STFC Advanced Fellowship (ST/H005595/1) and through the STFC Project Research and Development (STFC-PRD) scheme (ST/K00235X/1). RRT also thanks the European Union for funding via the OPTICON Research Infrastructure for Optical/IR astronomy (EU-FP7 226604). SM thanks Heriot-Watt University for a James Watt PhD Scholarship. SM also thanks David Maclachlan and Frauke Izdebski for helpful discussions. AS acknowledges support from the EPSRC CM-DTC. NG is financed by the FRS-FNRS Belgium and by the Belgian Science Policy Office under the Interuniversity Attraction Pole project P7/18 DYGEST. We acknowledge helpful discussions with Manuel Valiente.