Abstract
The anhydrous alum KTi(SO4)2, where the Ti3+ (d1, S = 1/2) ions form an anisotropic triangular lattice, has been prepared by a new hydrothermal route and characterized by magnetic susceptibility and neutron scattering measurements. Contrary to expectations, fits to the magnetic susceptibility indicate that the spins are isotropic (i.e. Heisenberg) and that the frustrating couplings are weak; indeed, the system is well modelled by nearly isolated chains. The inelastic neutron scattering data furthermore shows excellent agreement with an exact theoretical calculation for the one-dimensional spinon continuum. The unexpected magnetic properties of KTi(SO4)2 are explained in the light of density functional calculations, which reveal an unusual orbital ground state for the Ti3 + ion.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Considered a cornerstone of quantum many-body physics for many decades [1], the antiferromagnetic S = 1/2 Heisenberg chain model (AQHC) continues to attract experimental and theoretical attention. This enduring appeal can be traced back to the model's richness, as well as its exact solvability. In zero magnetic field, the celebrated Bethe ansatz solution [2, 3] for the ground state is an entangled singlet characterized by algebraically decaying spin–spin correlations. Its excitations are S = 1/2 quasi-particles known as spinons [4, 5], which may be pictured as propagating domain walls arising from spin flips; because each flip produces an even number of spinons, they are observed in continua when using experimental techniques like inelastic neutron scattering. The recent availability of, on the one hand, large single crystals of systems which approximate the AQHC, and on the other, accurate calculations for the two and four-spinon dynamical scattering functions [6], has lead to several detailed neutron scattering measurements of spinon continua. Highlights include studies on SrCuO2 [7], Cu(SO4) · 5(H2O) [8], and KCuF3 [9], where careful data treatment and analysis permit a quantitative comparison with theory. In parallel with these works, there has also been considerable interest in the effect of perturbations on the AQHC, particularly relating to quantum criticality [10, 11] and geometric frustration. Regarding the latter, the most commonly considered model is the S = 1/2 Heisenberg anisotropic triangular lattice (QHAT), where intra- and interchain couplings generate a network of isosceles triangles [12–14] (figure 1). Perhaps the best known realizations of this model are found in the family of Cs2CuX4 (X = Cl, Br) materials [15–19]. In Cs2CuCl4, where the ratio of the intrachain to interchain coupling J/J' ≃ 3, neutron scattering has revealed the coexistence of a spinon continuum with a bound state induced by the interchain coupling [17, 18], as well as incommensurate spiral order at low temperatures [16].
Figure 1. (Right) The structure of KTi(SO4)2 viewed along the c* axis. The TiO6 octahedra are displayed in blue and the SO4 tetrahedra in yellow. The interplane K+ ions have been left out for clarity. The anisotropic triangular magnetic lattice has been plotted on top of the structure, with J represented as solid black lines along 〈010〉 and J' as dashed lines along  respectively. (left) A magnified view of a single TiO6 octahedron. The isosurface represents the Ti3+ ground-state Wannier orbital φ1 drawn at arbitrary probability, and the black arrows denote the x'and y'directions in the rotated local coordinate frame. The dominant superexchange pathway proceeds through the equatorial oxygens, lying at the Ti–O distance 2.044(1) Å. The figure was obtained using the VESTA software [20].
respectively. (left) A magnified view of a single TiO6 octahedron. The isosurface represents the Ti3+ ground-state Wannier orbital φ1 drawn at arbitrary probability, and the black arrows denote the x'and y'directions in the rotated local coordinate frame. The dominant superexchange pathway proceeds through the equatorial oxygens, lying at the Ti–O distance 2.044(1) Å. The figure was obtained using the VESTA software [20].
Download figure:
Standard image High-resolution imageNearly twenty years ago, Bramwell et al proposed the anhydrous alums AM(SO4)2 (A = K, Rb, M = Ti, Fe) as an alternative set of compounds to represent both the anisotropic and isotropic (J = J') triangular lattice models [21]. Among these, KTi(SO4)2 is the only compound which realizes the quantum limit S = 1/2, in this case arising from the single unpaired electron in the d-shell of Ti3 + . KTi(SO4)2 is isomorphous with the naturally occurring mineral yavapaiite, KFe(SO4)2, which crystallizes in the monoclinic C2/m space group [22]. The structure consists of sheets of octahedrally coordinated Ti3+ ions bridged by (SO4)2 − ions to form an anisotropic triangular lattice in the ab plane. The Ti–Ti nearest-neighbour distances along the 〈010〉 and  directions are 5.24 Å and 4.88 Å, respectively, with the corresponding exchanges labelled J and J' (figure 1). Because superexchange between neighbouring Ti3+ proceeds along a Ti–O–S–O–Ti pathway in both cases, J and J' are expected to be small. Furthermore, because each nearest neighbour bond contains an inversion centre, no Dzyaloshinskii–Moriya terms are allowed (unlike in Cs2CuCl4). The triangular lattice [Ti(SO4)2]− sheets are well separated by K+ ions along the c direction, with the interlayer distance corresponding to 7.74 Å. In [21], the magnetic susceptibility χ(T) of KTi(SO4)2 is found to show a broad shoulder indicating short range correlations at 7 K, followed by a sharp Curie-like increase, possibly caused by a paramagnetic impurity, at lower temperatures. Based on the small Curie constant (and hence magnetic moment) attained from fits to the high temperature data, it was speculated that the Ti3+ moment possesses an Ising anisotropy, as has been observed in the fully hydrated alum Cs[Ti:Al](SO4)
directions are 5.24 Å and 4.88 Å, respectively, with the corresponding exchanges labelled J and J' (figure 1). Because superexchange between neighbouring Ti3+ proceeds along a Ti–O–S–O–Ti pathway in both cases, J and J' are expected to be small. Furthermore, because each nearest neighbour bond contains an inversion centre, no Dzyaloshinskii–Moriya terms are allowed (unlike in Cs2CuCl4). The triangular lattice [Ti(SO4)2]− sheets are well separated by K+ ions along the c direction, with the interlayer distance corresponding to 7.74 Å. In [21], the magnetic susceptibility χ(T) of KTi(SO4)2 is found to show a broad shoulder indicating short range correlations at 7 K, followed by a sharp Curie-like increase, possibly caused by a paramagnetic impurity, at lower temperatures. Based on the small Curie constant (and hence magnetic moment) attained from fits to the high temperature data, it was speculated that the Ti3+ moment possesses an Ising anisotropy, as has been observed in the fully hydrated alum Cs[Ti:Al](SO4) H2O, where
H2O, where 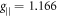 and g⊥ = 0.230 [23].
and g⊥ = 0.230 [23].
In this paper, we will show that KTi(SO4)2 is in fact an excellent realization of the AQHC. This change in interpretation has been made possible by the availability of higher quality samples synthesized by a new hydrothermal route. Standard analysis of the magnetic susceptibility yields nearly the full spin-only moment for S = 1/2, which may be understood in the context of an unusual orbital ground state revealed by DFT calculations. This ground state also explains the strong one-dimensionality of the magnetism, confirmed by fits to series expansion results for the QHAT and exact diagonalizations for the the isolated AQHC. Finally, time-of-flight neutron spectroscopy results are in near perfect agreement with the exact two- and four-spinon cross section for the AQHC, despite the use of a powder sample.
2. Synthesis and magnetic interactions
We begin by briefly discussing the sample synthesis: the literature route to KTi(SO4)2 involves vacuum dehydration of a stoichiometric solution of Ti2(SO4)3 and K2SO4, followed by regrinding and annealing [21]. As stated previously, this protocol appears to also generate a large paramagnetic impurity and/or lattice defects. To prepare the present samples of KTi(SO4)2, we instead begin with a solution of Ti2(SO4)3 and K2SO4 (molar ratio 3.5: 1) in H2SO4 (1.9 mol dm3)6 . The solution is enclosed in a 35 ml thick-walled teflon-stoppered pyrex tubes (Ace glass) and heated to 155 °C for 48 h, before slowly cooling to room temperature over 24 h. Small (∼0.1 mm3) crystals of KTi(SO4)2 are found on the sides of the vessel alongside a moderate amount of non-magnetic TiO2 (anatase) powder, which may be partly removed by washing. X-ray diffraction confirms the monoclinic space group of KTi(SO4)2 , and yields room temperature lattice parameters a = 8.2894(3) Å, b = 5.2257(2) Å, c = 7.8441(3) Å, and β = 94.645(2)°. Refinements of neutron diffraction data taken at 2 K on the D1A diffractomer at the Institut Laue–Langevin (ILL) (see figure S1 in the supplementary material) indicate that a and c contract from their room temperature values to 8.2402(2) Å and 7.7678(1) Å, respectively. More surprisingly, b shows a slight expansion to 5.23511(9) Å. The phase fraction of anatase is estimated by the same refinement to be ∼10 %.
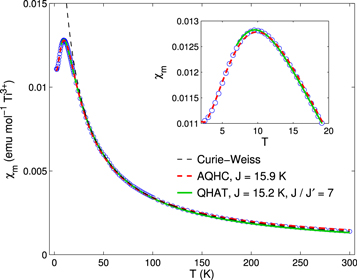
A few clusters of crystals (in total 126.9 mg) were selected for magnetic susceptibility measurements, carried out in an applied magnetic field H = 1000 Oe using a Quantum Design MPMS-5 magnetometer; the temperature dependence of the molar susceptibility χm(T) is shown in figure 2. At high temperature, χm(T) follows the Curie–Weiss law χm(T) = C/(T − θCW ) + χ0, where 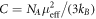 and θCW are, respectively, the Curie and the Weiss constants, and χ0 is a T-independent background. Fitting in the temperature range 50 − 300 K yields values of θCW = −11(2) K and an effective magnetic moment μeff = 1.68(2) μB, indicating weak antiferromagnetic couplings and a nearly full S = 1/2 spin-only moment [geff = 1.94(3)]. The relatively large background χ0 = 3 × 10−4 originates from the core diamagnetism of KTi(SO4)2 and the plastic sample holder. At lower temperatures, a broad, symmetric maximum characteristic of short range order appears around Tp = 10 K (figure 2(inset)). No signs of either a large Curie tail, as seen in [21], nor a magnetic long range ordering anomaly are observed.
and θCW are, respectively, the Curie and the Weiss constants, and χ0 is a T-independent background. Fitting in the temperature range 50 − 300 K yields values of θCW = −11(2) K and an effective magnetic moment μeff = 1.68(2) μB, indicating weak antiferromagnetic couplings and a nearly full S = 1/2 spin-only moment [geff = 1.94(3)]. The relatively large background χ0 = 3 × 10−4 originates from the core diamagnetism of KTi(SO4)2 and the plastic sample holder. At lower temperatures, a broad, symmetric maximum characteristic of short range order appears around Tp = 10 K (figure 2(inset)). No signs of either a large Curie tail, as seen in [21], nor a magnetic long range ordering anomaly are observed.
Figure 2. Magnetic susceptibility χm(T) of Ti-yavapaiite. The experimental data recorded at 1000 Oe is plotted with blue circles, while the fits to the Curie–Weiss law, the AQHC, and the QHAT are indicated by black dashed, red dashed, and green solid lines, respectively. The latter is only plotted down to 8 K ≃ 0.8Tp due to the divergence of the [5,5] Padé approximant below this temperature. The inset shows a magnified region around the low temperature peak.
Download figure:
Standard image High-resolution imageBased on the arrangement of Ti3+ ions in KTi(SO4)2, the most obvious starting point to fit χm(T) is the QHAT, described by the Hamiltonian  where
where 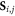 are the Heisenberg spin operators on pairs sites i, j within (first term) and between (second term) chains. To this end, we calculate the Padé approximants of the 10th order high-T series expansion derived for
are the Heisenberg spin operators on pairs sites i, j within (first term) and between (second term) chains. To this end, we calculate the Padé approximants of the 10th order high-T series expansion derived for  by Zheng et al [25] using the continued fraction quotient-difference algorithm [26]. All approximants are found to diverge at temperatures below T ≃ 0.8 Tp for J/J' > 5, which is therefore used as the lower limit for the fitting range. Remarkably, the best fit (χ2 = 6.0) to the experimental curve is achieved for J = 15.2 K and J/J' = 9(1), very close to the isolated one-dimensional chain limit. Indeed, decreasing J/J' to 6 leads to an appreciable asymmetry in the peak, reflected by a poorer χ2 = 18.0. Given the large ratio of J/J', we also attempt a fit to exact diagonalization results7
for the isolated AQHC (J' = 0) model with a small paramagnetic tail, yielding the red curve in figure 2. While χ2 = 40.2 is worse than for both QHAT fits, the peak (in particular its symmetry) at Tp is nonetheless well described. We will return to the role of the interchain coupling in the context of our neutron scattering results further on in this manuscript.
by Zheng et al [25] using the continued fraction quotient-difference algorithm [26]. All approximants are found to diverge at temperatures below T ≃ 0.8 Tp for J/J' > 5, which is therefore used as the lower limit for the fitting range. Remarkably, the best fit (χ2 = 6.0) to the experimental curve is achieved for J = 15.2 K and J/J' = 9(1), very close to the isolated one-dimensional chain limit. Indeed, decreasing J/J' to 6 leads to an appreciable asymmetry in the peak, reflected by a poorer χ2 = 18.0. Given the large ratio of J/J', we also attempt a fit to exact diagonalization results7
for the isolated AQHC (J' = 0) model with a small paramagnetic tail, yielding the red curve in figure 2. While χ2 = 40.2 is worse than for both QHAT fits, the peak (in particular its symmetry) at Tp is nonetheless well described. We will return to the role of the interchain coupling in the context of our neutron scattering results further on in this manuscript.
3. Orbital ground state and superexchange
To understand the large measured moment and apparent one-dimensionality of the magnetism in KTi(SO4)2, we return to its structure, and in particular, the geometry of the Ti3+ octahedra. In d1 compounds, the interplay of crystal field terms and spin–orbit coupling are crucially important for determining the single-ion magnetic properties. For perfect octahedral coordination (point group Oh), the 2D free ion state is split into the usual set of t2g and eg levels, with the lone electron populating the former. The three-fold degeneracy of the crystal field ground state is lifted by LS-coupling to an effective L = −1 orbital momentum, resulting in a non-Kramers pair of doublets in the ground state, both with  [23]. Lowering the symmetry to tetragonal (D4h), the symmetry and magnitude of the magnetic moment become dependent on the sign and magnitude, δ, of the tetragonal distortion; when the octahedron is axially compressed (δ < 0), the orbital ground state is based on the dxy orbital, which yields a Kramers doublet ground state with g = 2, i.e. Heisenberg spins. The nearly tetragonal (C2h) local environment of Ti3+ in KTi(SO4)2 indeed appears to fulfil this condition, with two short axial and four long equatorial Ti–O distances (2.000(1) Å versus 2.044(1) Å from neutron diffraction) and O–Ti–O angles close to 90° (figure 1). The resulting dxy orbital order is anticipated to produce dominant exchange along the b-direction, along which the Ti–O orbital overlap is large. Both the observation of a nearly full S = 1/2 moment and the one-dimensionality thus appear to be accounted for.
[23]. Lowering the symmetry to tetragonal (D4h), the symmetry and magnitude of the magnetic moment become dependent on the sign and magnitude, δ, of the tetragonal distortion; when the octahedron is axially compressed (δ < 0), the orbital ground state is based on the dxy orbital, which yields a Kramers doublet ground state with g = 2, i.e. Heisenberg spins. The nearly tetragonal (C2h) local environment of Ti3+ in KTi(SO4)2 indeed appears to fulfil this condition, with two short axial and four long equatorial Ti–O distances (2.000(1) Å versus 2.044(1) Å from neutron diffraction) and O–Ti–O angles close to 90° (figure 1). The resulting dxy orbital order is anticipated to produce dominant exchange along the b-direction, along which the Ti–O orbital overlap is large. Both the observation of a nearly full S = 1/2 moment and the one-dimensionality thus appear to be accounted for.
This simple picture is challenged by density-functional (DFT) calculations performed in the local density approximation (LDA) [28] using the FPLO code [29]. The orbital energies are extracted by fitting Wannier functions to the resulting d-bands, which comprise the t2g states around the Fermi level and the eg states 2 eV higher in energy (figure S3). Using the orthogonalized local coordinate frame with x, y, and z directed along the Ti–O bonds, we find  xy = 0.203 eV and
xy = 0.203 eV and  yz =
yz =  xz = 0.135 eV. While this splitting is compatible with the crystal-field scheme for D4h described above, the orbitals are ordered contrary to the expectation for δ < 0. Before addressing this discrepancy, we consider the effect of lowering the site symmetry to C2h, which entails an additional small splitting between the dyz and dxz states. This splitting becomes visible when the local
xz = 0.135 eV. While this splitting is compatible with the crystal-field scheme for D4h described above, the orbitals are ordered contrary to the expectation for δ < 0. Before addressing this discrepancy, we consider the effect of lowering the site symmetry to C2h, which entails an additional small splitting between the dyz and dxz states. This splitting becomes visible when the local  axis is directed along the two-fold rotation axis between two adjacent oxygen atoms in the xy plane. In the new x'y'z coordinate frame, effectively the original frame with x and y axes turned by 45° (figure 1), the dxy orbital has (x')2 − (y')2 symmetry, and the orbital energies become
axis is directed along the two-fold rotation axis between two adjacent oxygen atoms in the xy plane. In the new x'y'z coordinate frame, effectively the original frame with x and y axes turned by 45° (figure 1), the dxy orbital has (x')2 − (y')2 symmetry, and the orbital energies become 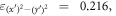
 y'z = 0.112, and
y'z = 0.112, and  x'z = 0.083 eV.
x'z = 0.083 eV.
The result that  x'z <
x'z <  y'z is again at odds with the geometry of the Ti3+ octahedron, which implies
y'z is again at odds with the geometry of the Ti3+ octahedron, which implies  x'z >
x'z >  y'z. This arrangement is expected from the scissor-like distortion of the O atoms in the xy plane, where the O–Ti–O angles are 88° and 92°, respectively. The closer proximity of the O2 − ions to x', which bisects the smaller angle, then suggests
y'z. This arrangement is expected from the scissor-like distortion of the O atoms in the xy plane, where the O–Ti–O angles are 88° and 92°, respectively. The closer proximity of the O2 − ions to x', which bisects the smaller angle, then suggests  x'z >
x'z >  y'z. Taking this and the unexpectedly high energy of the (x')2 − (y')2 orbital into account, it appears that the ions beyond the nearest-neighbour oxygens play the decisive role in the ordering of the t2g orbitals. This is perhaps not surprising given the small magnitude of the distortion of the Ti3+ octahedron; the difference between axial and equatorial Ti–O bond lengths is only 0.2%. In the present case, the dx'z-orbital may be stabilized by the positively charged K+ ions along the x'-direction, located at a Ti–K distance of 3.88 Å. It may also be envisaged that the second-neighbour oxygens within the SO4 tetrahedra contribute; these are more remote from Ti3+ along the x'-direction (Ti–O2 distance of 4.30 Å) than along the y'-direction (Ti–O1 distance of 3.45 Å and Ti–O3 distance of 4.09 Å). While these oxygens may also be responsible for the high energy of the (x')2 − (y')2 orbital in energy, this is less evident.
y'z. Taking this and the unexpectedly high energy of the (x')2 − (y')2 orbital into account, it appears that the ions beyond the nearest-neighbour oxygens play the decisive role in the ordering of the t2g orbitals. This is perhaps not surprising given the small magnitude of the distortion of the Ti3+ octahedron; the difference between axial and equatorial Ti–O bond lengths is only 0.2%. In the present case, the dx'z-orbital may be stabilized by the positively charged K+ ions along the x'-direction, located at a Ti–K distance of 3.88 Å. It may also be envisaged that the second-neighbour oxygens within the SO4 tetrahedra contribute; these are more remote from Ti3+ along the x'-direction (Ti–O2 distance of 4.30 Å) than along the y'-direction (Ti–O1 distance of 3.45 Å and Ti–O3 distance of 4.09 Å). While these oxygens may also be responsible for the high energy of the (x')2 − (y')2 orbital in energy, this is less evident.
To investigate the orbital ground state of Ti3+ in KTi(SO4)2 under more realistic conditions, we extend the above calculations by adding a Hubbard U at the mean-field level (LSDA+U). Occupations of d-orbitals are varied as to minimize the total energy under the presence of the Hubbard term 8
. These calculations yield an insulating state with a band gap of 2.3 eV and a ground-state orbital wave-function 
 obtained by diagonalizing the d-orbital occupation matrix.
obtained by diagonalizing the d-orbital occupation matrix.
We now perform the Wannier fit to the original LDA bands using an orthonormal basis containing the  orbital (figure 1) together with
orbital (figure 1) together with 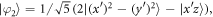
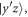 and the two eg states. The energies of the t2g orbitals become
and the two eg states. The energies of the t2g orbitals become  φ1 = 0.064,
φ1 = 0.064,  y'z = 0.112, and
y'z = 0.112, and  φ2 = 0.235 eV; the
φ2 = 0.235 eV; the  orbital indeed has the lowest energy at the LDA level (figure S3). The nearest-neighbour Ti–Ti hoppings of this state corresponding to the pathways for the exchange couplings J and J' are t = −0.045 eV and t' = 0.023 eV, respectively. Using the full five-band tight-binding model and adding an effective Hubbard Ueff = 4 eV and Hund's coupling
orbital indeed has the lowest energy at the LDA level (figure S3). The nearest-neighbour Ti–Ti hoppings of this state corresponding to the pathways for the exchange couplings J and J' are t = −0.045 eV and t' = 0.023 eV, respectively. Using the full five-band tight-binding model and adding an effective Hubbard Ueff = 4 eV and Hund's coupling  we compute exchange couplings from the Kugel–Khomskii model [31, 32] and arrive at J = 18.3 K and J' = 5.1 K (J/J' = 3.6) in reasonable agreement with the susceptibility fits. Alternatively, we obtain J = 16 K and J' = 7 K (J/J' = 2.3) from LSDA+U total energies of ferromagnetic and antiferromagnetic spin configurations (the so-called supercell method). However, these LSDA+U-based values appear to be strongly dependent on the choice of the Hubbard U and on the double-counting correction method in LSDA+U.
we compute exchange couplings from the Kugel–Khomskii model [31, 32] and arrive at J = 18.3 K and J' = 5.1 K (J/J' = 3.6) in reasonable agreement with the susceptibility fits. Alternatively, we obtain J = 16 K and J' = 7 K (J/J' = 2.3) from LSDA+U total energies of ferromagnetic and antiferromagnetic spin configurations (the so-called supercell method). However, these LSDA+U-based values appear to be strongly dependent on the choice of the Hubbard U and on the double-counting correction method in LSDA+U.
KTi(SO4)2 may thus be said to feature a well-defined but rather unexpected orbital state described by 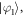 which is triggered by the weak crystal-field splitting of the t2g states. This splitting is not consistent with the local distortion of the TiO6 octahedron and reflects a complex interplay of ionic charges surrounding the Ti3+ ion in the crystal structure. A similar inversion of the orbital energies with respect to crystal-field predictions for nearest-neighbour oxygens has also recently been demonstrated in the iridate compound Sr2IrO4 [33]. Finally, the ground-state orbital yields quasi-one-dimensional magnetism with the dominant exchange along the b direction, thus revealing the origin of the behaviour observed in our magnetic susceptibility measurements. We will confirm that the b-axis is the one-dimensional axis in the following section.
which is triggered by the weak crystal-field splitting of the t2g states. This splitting is not consistent with the local distortion of the TiO6 octahedron and reflects a complex interplay of ionic charges surrounding the Ti3+ ion in the crystal structure. A similar inversion of the orbital energies with respect to crystal-field predictions for nearest-neighbour oxygens has also recently been demonstrated in the iridate compound Sr2IrO4 [33]. Finally, the ground-state orbital yields quasi-one-dimensional magnetism with the dominant exchange along the b direction, thus revealing the origin of the behaviour observed in our magnetic susceptibility measurements. We will confirm that the b-axis is the one-dimensional axis in the following section.
4. Magnetic excitations
To address the unsettled question of the interchain couplings (and more generally, the magnetic excitations) in KTi(SO4)2, we carried out a time-of-flight neutron scattering on the IN5 spectrometer at the ILL. Approximately 10 g of polycrystalline KTi(SO4)2 (the same sample as used for neutron diffraction on D1A) were loaded in a cylindrical Cu can of diameter 11 mm, which was connected to the end of an ILL-built dilution refrigerator with a base temperature of 50 mK. Around 1 bar (at 298 K) of 4He exchange gas was admitted into the can to thermalize the sample at sub-Kelvin temperatures. Given the energy scale extracted from the fits to χm(T), wavelengths of λi = 3 Å(Ei = 9.09 meV) and 5 Å(Ei = 3.27 meV) were selected by a pair of counter-rotating disk choppers. For both wavelengths, the choppers were spun at 17000 rpm to yield full-width half-maximum E-resolutions at the elastic line of 0.31 meV and 0.07 meV, respectively. The data were corrected for detector efficiency using a vanadium standard, the E-dependent self-attenuation of the sample, as well as background from the sample environment. Unfortunately, it was not possible to fully subtract a component arising from the beam stop, which manifests itself as strong spurious scattering at small angle in the entire energy transfer window for both wavelengths (figure 3(a))9 .
Figure 3. (a) The background-subtracted experimental S(Q, E) of KTi(SO4)2 measured at 50 mK on the IN5 spectrometer (ILL) using 5 Å neutrons. The grey bar and grey square correspond to the position of spurious features due to scattering from the beam-stop, while the red line corresponds to the lower bound of the two-spinon continuum Es(Q) (see text). (b) The powder-averaged two- and four-spinon dynamical scattering function 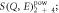 qualitative agreement with (a) is excellent for J = 15.2 K. The black line marks the boundary of the experimental (Q, E) window at λi = 5 Å.
qualitative agreement with (a) is excellent for J = 15.2 K. The black line marks the boundary of the experimental (Q, E) window at λi = 5 Å.
Download figure:
Standard image High-resolution imageThe dynamical scattering function 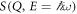 at 50 mK for λi = 5 Å is shown in figure 3(a). A clear branch of excitations is observed dispersing from the vicinity of the antiferromagnetic position
at 50 mK for λi = 5 Å is shown in figure 3(a). A clear branch of excitations is observed dispersing from the vicinity of the antiferromagnetic position  up to ∼2 meV. Upon initial inspection, the powder averaging renders it difficult to distinguish whether this represents conventional magnons or a spinon continuum. However, the sharp onset of the scattering, particularly at small E (figure 4(a)), can be associated with a powder averaged one-dimensional dispersion. Furthermore, the lower bound of the spinon continuum is expected to be found at
up to ∼2 meV. Upon initial inspection, the powder averaging renders it difficult to distinguish whether this represents conventional magnons or a spinon continuum. However, the sharp onset of the scattering, particularly at small E (figure 4(a)), can be associated with a powder averaged one-dimensional dispersion. Furthermore, the lower bound of the spinon continuum is expected to be found at 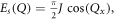 where Qx is the component of the wave-vector transfer Q along the chain direction. Choosing J = 1.31 meV = 15.2 K and
where Qx is the component of the wave-vector transfer Q along the chain direction. Choosing J = 1.31 meV = 15.2 K and 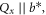 as inferred from our fits to χm(T) and electronic structure calculations, we find excellent agreement with the observed dispersion. The semi-classical spin wave solution, on the other hand, indicates a zone-boundary energy of J = 1.32 meV, clearly inconsistent with the data. It also predicts an absence of scattering beyond the dispersion maximum, which a Q-integrated slice of the 3 Å data verifies is not the case (figure 4(f)).
as inferred from our fits to χm(T) and electronic structure calculations, we find excellent agreement with the observed dispersion. The semi-classical spin wave solution, on the other hand, indicates a zone-boundary energy of J = 1.32 meV, clearly inconsistent with the data. It also predicts an absence of scattering beyond the dispersion maximum, which a Q-integrated slice of the 3 Å data verifies is not the case (figure 4(f)).
Figure 4. (a)–(d) E-integrated strips at selected energies for λi = 5 Å. In each, the fit to  is indicated by a solid red line, and the background by the shaded region. (e) The E-dependence of the fitting amplitude. The black line represents the average amplitude
is indicated by a solid red line, and the background by the shaded region. (e) The E-dependence of the fitting amplitude. The black line represents the average amplitude  from which the highest E points deviates by around 10%. (f) A Q-integrated slice taken from the λi = 3 Å data. Again, the fit to
from which the highest E points deviates by around 10%. (f) A Q-integrated slice taken from the λi = 3 Å data. Again, the fit to 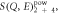 here convoluted with an E-dependent resolution, is indicated by a solid red line.
here convoluted with an E-dependent resolution, is indicated by a solid red line.
Download figure:
Standard image High-resolution imageWe now attempt to put our claim that the observed scattering represents a spinon continuum on a more quantitative footing. The two- and four-spinon dynamical structure factor S(Q, E)2+4 for the QHCA has been obtained exactly by Caux and Hagemans [6] from an algebraic treatment based on the observation that even-spinon states are eigenstates of the AQHC Hamiltonian. Using this result as a starting point, spherical (powder) averaging was carried out assuming no dispersion or modulation of the intensity perpendicular to Qx. To achieve a uniform sampling on the constant-Q sphere, random Cartesian coordinates were selected from a Gaussian distribution and normalized to the sphere radius. The S(Q, E)pow2 + 4 resulting from this procedure is shown in figure 3(b). The Q-dependence of the experimental S(Q, E) was extracted by integrating over a series of 0.2 meV wide strips between E = 0.5 and 2.1 meV (figures 4(a)–(d)). These strips were then fitted to the corresponding section of the powder-averaged S(Q, E)2 + 4pow; for each strip, the background and amplitude A(E) were adjustable parameters, while J was considered a global parameter. Regions in Q contaminated by scattering from the beam-stop were not included in the fitting range. The fits for selected energies up to 2.1 meV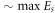 are shown in figures 4(a)–(d), with A(E) given in figure 4(e). Excellent agreement between experiment and theory is found for all strips using J = 1.32(2) meV = 15.3(2) K. Furthermore, A(E) is broadly consistent across the full energy range, but shows a ∼10% drop from its average value
are shown in figures 4(a)–(d), with A(E) given in figure 4(e). Excellent agreement between experiment and theory is found for all strips using J = 1.32(2) meV = 15.3(2) K. Furthermore, A(E) is broadly consistent across the full energy range, but shows a ∼10% drop from its average value  for the highest energy strip (figure 4(e)). Although a small J'could explain this small deviation [18], we will show that the likeliest explanation is the imperfect correction of the experimental data.
for the highest energy strip (figure 4(e)). Although a small J'could explain this small deviation [18], we will show that the likeliest explanation is the imperfect correction of the experimental data.
To verify the robustness of the AQHC with respect to our fits, we turn to the E-dependent strip through the 3 Å data-set discussed above (figure 4(f)). As the scattering up to ∼1 Å−1 contains a strong contribution from the background, we integrate S(Q, E) over the range 1.5–2.0 Å−1. This range furthermore covers Q ≃ 1.7 Å−1, where J' is expected to cause a large redistribution of intensity from the powder-averaging of the inter-chain dispersion. In order to fit S(Q, E)2 + 4pow to the experimental data, we convolute it pixel-by-pixel with an E-dependent resolution calculated from the expression given in [34]. Again, the agreement with the model is nearly perfect (figure 4(f)) for J = 1.38(2) meV = 16.0(2) K, close to the value extracted from our 5 Å dataset and susceptibility fit. This indicates that slight variation in A(E) observed at the longer neutron wavelength λ = 5 Å is probably an experimental artefact, with the self-attenuation correction, which neglects the absorption in the walls of the Cu can, the most likely source of the error. Based on the above, as well as the fact that no asymmetry is observed in the dispersion, it thus appears that KTi(SO4)2 is close to an ideal realization of the AQHC, fulfilling the condition 
Finally, we search for evidence of magnetic order below 1.8 K by comparing our 50 mK data to higher temperature datasets; subtraction of datasets collected in the range 1.3–10 K do not result in any systematic changes in the elastic scattering consistent with magnetic order (see figure S2, supplemental material). Using the intensity of the (001) nuclear Bragg peak, the statistical error of our data, and assuming collinear Néel order propagating with 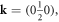 we estimate an upper limit for the ordered moment of μo ∼ 0.1 μB for any magnetic moment direction. Despite the small magnitude of this estimate, magnetic order cannot be excluded in KTi(SO4)2; in fact, strongly suppressed ordered moments (and Néel temperatures, TN) are a general feature of one-dimensional materials. Indeed, several quasi-1D systems, including Sr2CuO3 and Ca2CuO3, show μo < 0.1 μB [35]. The small ordered moments and Néel temperatures can be partly understood in the context of quantum field theory calculations, which yield
we estimate an upper limit for the ordered moment of μo ∼ 0.1 μB for any magnetic moment direction. Despite the small magnitude of this estimate, magnetic order cannot be excluded in KTi(SO4)2; in fact, strongly suppressed ordered moments (and Néel temperatures, TN) are a general feature of one-dimensional materials. Indeed, several quasi-1D systems, including Sr2CuO3 and Ca2CuO3, show μo < 0.1 μB [35]. The small ordered moments and Néel temperatures can be partly understood in the context of quantum field theory calculations, which yield  where Jc is an unfrustrated interchain coupling, and TN ∼ C2Jc (ignoring logarithmic corrections). C1 and C2 are constants, and correspond to ∼1 and ∼0.8 for a cubic arrangement of spin chains [36, 37]. Similar calculations on stacked anisotropic triangular planes (as in KTi(SO4)2) show that the latter relation still holds, but that the constant C2 is reduced by a factor ∼2; this is presumably because the frustration within the planes reduces the effective number of nearest neighbour chains from four (in the cubic case) to two. The reduction in C1 should correspondingly be
where Jc is an unfrustrated interchain coupling, and TN ∼ C2Jc (ignoring logarithmic corrections). C1 and C2 are constants, and correspond to ∼1 and ∼0.8 for a cubic arrangement of spin chains [36, 37]. Similar calculations on stacked anisotropic triangular planes (as in KTi(SO4)2) show that the latter relation still holds, but that the constant C2 is reduced by a factor ∼2; this is presumably because the frustration within the planes reduces the effective number of nearest neighbour chains from four (in the cubic case) to two. The reduction in C1 should correspondingly be 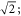 from this, we may estimate an interchain coupling between adjacent planes of Jc < 0.02J = 0.3 K, and thus TN < 0.4 K [38]. This is consistent with the Jc = 0.05 K (J/Jc ≃ 300) extracted from our DFT calculations. Regardless of the presence or absence of magnetic order in KTi(SO4)2, the excitation spectrum is expected to remain largely unchanged except at very low energies <0.25 meV, where transverse spin waves and a gapped longitudinal spin-wave mode may occur [39–43].
from this, we may estimate an interchain coupling between adjacent planes of Jc < 0.02J = 0.3 K, and thus TN < 0.4 K [38]. This is consistent with the Jc = 0.05 K (J/Jc ≃ 300) extracted from our DFT calculations. Regardless of the presence or absence of magnetic order in KTi(SO4)2, the excitation spectrum is expected to remain largely unchanged except at very low energies <0.25 meV, where transverse spin waves and a gapped longitudinal spin-wave mode may occur [39–43].
5. Conclusion
To conclude, the recent preparation of high-quality samples of the anhydrous alum KTi(SO4)2 have allowed us to re-evaluate its magnetic properties. Fits to both magnetic susceptibility and inelastic neutron scattering data indicate that it is an excellent realization of the AQHC, with J = 15.3(2) K = 1.32(2) meV, and g ≃ 2. These properties appear to arise from an unusual orbital order on the Ti3+ site, which results in moderate antiferromagnetic superexchange along the crystallographic b-direction and weak exchange along other directions. A few points remain to to be clarified, however, most prominently the possible presence of magnetic order at T < 0.4 K due to interchain couplings. This problem is most appropriately dealt with by inelastic or polarized neutron scattering at lower energies than presented here, as well as muon spin rotation.
Acknowledgments
We are grateful to S T Bramwell, M Mourigal, and A R Wildes for useful discussions and J -S Caux for helpful comments and for supplying the dynamical structure factor data. The experimental work was supported by the Swiss National Science foundation and its Synergia network Mott Physics Beyond the Heisenberg Model. AT was funded by the Federal Ministry for Education and Research through the Sofja Kovalevskaya award of the Alexander von Humboldt Foundation. DK acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG) within Forschergruppe (FOR) 1346.
Footnotes
- 6
The composition of the starting solution and the reaction conditions are similar to those used in the synthesis of the monohydrate KTi(SO4)2·H2O, another low dimensional magnetic system [24].
- 7
The simulation was carried out using the ALPS package [27] on a chain of 20 spins with periodic boundary conditions.
- 8
We used the on-site Hubbard repulsion Ud = 4 eV and Hund's exchange Jd = 1 eV following our recent study of KTi(SO4)2 · 2H2O in [30].
- 9
This issue has since been resolved.