Abstract
In this article, we show that eigenenergies and eigenstates of a system consisting of four one-dimensional hard-core particles with masses 6m, 2m, m, and 3m in a hard-wall box can be found exactly using Bethe Ansatz. The Ansatz is based on the exceptional affine reflection group  associated with the symmetries and tiling properties of an octacube—a Platonic solid unique to four-dimensions, with no three-dimensional analogues. We also uncover the Liouville integrability structure of our problem: the four integrals of motion in involution are identified as invariant polynomials of the finite reflection group F4, taken as functions of the components of momenta.
associated with the symmetries and tiling properties of an octacube—a Platonic solid unique to four-dimensions, with no three-dimensional analogues. We also uncover the Liouville integrability structure of our problem: the four integrals of motion in involution are identified as invariant polynomials of the finite reflection group F4, taken as functions of the components of momenta.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The relationship between exactly solvable quantum one-dimensional multi-particle problems and kaleidoscopes has been long appreciated [1]. A kaleidoscope is a system of mirrors where none of the multiple images of the original object is broken at the mirror junctions. A viewer situated inside a kaleidoscopic cavity has no means of distinguishing the images of objects from the original. For a broad class of boundary conditions, the eigenmodes of a kaleidoscopic cavity are represented by finite superpositions of plane waves; they can be found exactly, using the method of images [2]. When a many-body problem reduces to an exactly solvable kaleidoscope, the resulting solution is known as the (coordinate) Bethe Ansatz solution [3, 4]. The list of particle systems solvable using Bethe Ansatz is so far exhausted by: equal mass hard-core bosons, on an open line, on a circle or in between walls [5]; δ-interacting, equal-mass, generally distinguishable particles on a line and on a circle [6–8]; this includes bosons [9], which could also be in the presence of one or two walls [1]; systems of two hard-core particles with masses m and  interacting with a wall, for both wall-m-
interacting with a wall, for both wall-m- and wall-
and wall- -m spatial orders were briefly commented on in [6], but discarded as inferior to the problems with finite strength interactions.
-m spatial orders were briefly commented on in [6], but discarded as inferior to the problems with finite strength interactions.
It has been long conjectured that no exceptional—specific to a given number of spatial dimensions—kaleidoscopes lead to exactly solvable particle problems with realistic interactions [1, 3]. The search for physical realizations was limited to systems of particles of the same mass, with a possible addition of immobile walls. In this Letter, we show that the exceptional closed kaleidoscope 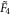 induces a novel quantum integrable system: four one-dimensional quantum hard-core particles with different masses,
induces a novel quantum integrable system: four one-dimensional quantum hard-core particles with different masses, 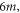
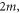 m, and
m, and 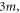 in a hard-wall box. The solution utilizes the symmetries of an octacube, a Platonic solid unique to four dimensions.
in a hard-wall box. The solution utilizes the symmetries of an octacube, a Platonic solid unique to four dimensions.
2. Identifying the particle problem generated by the Coxeter diagram 
Consider six hard-core (i.e. impenetrable) particles on a line, with masses m0, m1, m2, m3, m4, and m5. Their coordinates will be denoted as x0, x1, x2, x3, x4, and x5 respectively. The natural coordinate transformation
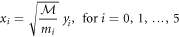
reduces the system to a single six-dimensional particle of mass 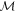 (to be fixed later) whose motion is constrained by the following set of five inequalities:
(to be fixed later) whose motion is constrained by the following set of five inequalities: 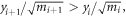 for
for 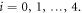
Consider now the affine Coxeter diagram 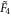 [10] depicted in the top line of figure 1. It encodes the geometry of a particular simplex-shaped four-dimensional kaleidoscope. The vertices label its five mirrors: the three-faces (represented by three-dimensional simplexes) of the four-dimensional simplex. The edges—the links—of the diagram (and their absences) encode the angles between the corresponding mirrors, i.e. the angles between their normals. When two vertices are not linked by an edge, the respective mirrors are orthogonal to each other. An edge with no numbers above it corresponds to an angle of
[10] depicted in the top line of figure 1. It encodes the geometry of a particular simplex-shaped four-dimensional kaleidoscope. The vertices label its five mirrors: the three-faces (represented by three-dimensional simplexes) of the four-dimensional simplex. The edges—the links—of the diagram (and their absences) encode the angles between the corresponding mirrors, i.e. the angles between their normals. When two vertices are not linked by an edge, the respective mirrors are orthogonal to each other. An edge with no numbers above it corresponds to an angle of 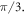 A number n above an edge would produce an angle of
A number n above an edge would produce an angle of 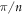 between the corresponding mirrors. The meaning of the mark inside the leftmost vertex will be explained later. In our case, the non-right angles between the mirrors are
between the corresponding mirrors. The meaning of the mark inside the leftmost vertex will be explained later. In our case, the non-right angles between the mirrors are 
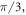
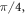 and
and 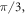 in the order of their appearance on the Coxeter diagram, left to right.
in the order of their appearance on the Coxeter diagram, left to right.
Figure 1. The  kaleidoscope and its particle realization. From top to bottom: the affine Coxeter diagram
kaleidoscope and its particle realization. From top to bottom: the affine Coxeter diagram 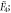 the angles between the mirrors; the four particles with masses
the angles between the mirrors; the four particles with masses 
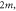 m, and
m, and 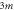 between two hard walls at
between two hard walls at 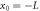 and
and  the particle–particle and particle-wall hyperplanes of contact in all three coordinate systems used in the main text.
the particle–particle and particle-wall hyperplanes of contact in all three coordinate systems used in the main text.
Download figure:
Standard image High-resolution imageLet us try to identify the five consecutive vertices of the Coxeter diagram with the five hyperplanes of contact between neighboring particles: 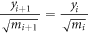 for
for 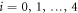 (see the particle diagrams in figure 1). This choice is natural: contact hyperplanes for two non-overlapping pairs of neighboring particles are indeed orthogonal to each other. Then the four edges of the diagram correspond to the four triplets of consecutive particles.
(see the particle diagrams in figure 1). This choice is natural: contact hyperplanes for two non-overlapping pairs of neighboring particles are indeed orthogonal to each other. Then the four edges of the diagram correspond to the four triplets of consecutive particles.
For three consecutive particles, i, 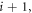 and
and  the angle between the i versus
the angle between the i versus 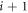 and
and 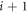 versus
versus 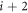 contact hyperplanes is given by
contact hyperplanes is given by
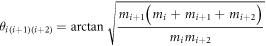
(see e.g. [6]). Notice that these angles do not depend on the overall mass scale. Therefore, any constraints on these angles can only lead to relationships between the five mass ratios, 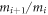 for
for 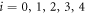 alone, with no overall mass scale involved. On the other hand, for our six-body system to lead to the
alone, with no overall mass scale involved. On the other hand, for our six-body system to lead to the 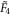 kaleidoscope, the angles between the hyperplanes of contact must satisfy four equations only,
kaleidoscope, the angles between the hyperplanes of contact must satisfy four equations only,
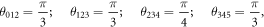
thus being seemingly underdetermined. Nevertheless, once the non-negativity of the masses (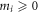 for
for 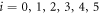 ) is invoked, a single solution (up to an overall scale m) survives:
) is invoked, a single solution (up to an overall scale m) survives:
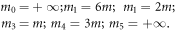
In retrospect, that both the leftmost and the rightmost mass should be infinite could have been predicted from the onset: this is probably the only way to map six particles on an open line to a single four-dimensional particle in a closed cavity.
Without loss of generality, we can place the infinitely massive particles at
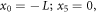
where L is the size of the resulting hard-wall box (see the hyperplanes of contact in terms of the original x-coordinates in figure 1). Now observe that  and L appear to be convenient mass and length scales, and ℏ a natural scale of action. From now on, we will be using the system of units where
and L appear to be convenient mass and length scales, and ℏ a natural scale of action. From now on, we will be using the system of units where
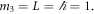
Also, it will become clear from what follows that the choice 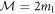 allows us to respect the existing conventions on the size of the octacube.
allows us to respect the existing conventions on the size of the octacube.
Figure 1 also shows the corresponding formulae for the contact hyperplanes expressed through the transformed coordinates y1, y2, y3, and y4. These hyperplanes form the boundaries of the  kaleidoscope we have in mind:
kaleidoscope we have in mind: 
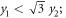
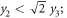
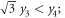

The coordinate transformation 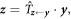 with the rotation-inversion matrix
with the rotation-inversion matrix 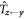 given by
given by
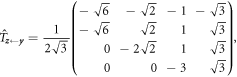
brings the domain of our  kaleidoscope to the conventional form [2, 3, 11–15]:
kaleidoscope to the conventional form [2, 3, 11–15]:
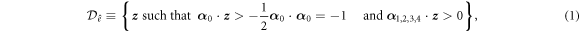
where 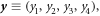 and
and  According to this convention, the kaleidoscope (1) is a four-dimensional simplex with five 3-faces (mirrors) defined by five inward normals
According to this convention, the kaleidoscope (1) is a four-dimensional simplex with five 3-faces (mirrors) defined by five inward normals 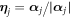 for
for  with
with 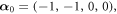
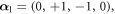
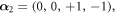
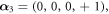
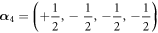 being the so-called minimal (or negative of maximal) root (j = 0) and the simple roots (
being the so-called minimal (or negative of maximal) root (j = 0) and the simple roots (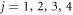 ) of the corresponding finite reflection group F4[16]. The mirrors from 1 to 4 pass through the origin; the 0th mirror (marked by a dot in the Coxeter diagram of figure 1) passes through the point
) of the corresponding finite reflection group F4[16]. The mirrors from 1 to 4 pass through the origin; the 0th mirror (marked by a dot in the Coxeter diagram of figure 1) passes through the point 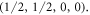 The hyperplanes that define the inequalities (1) are also identified in figure 1. In equation (1), the subscript
The hyperplanes that define the inequalities (1) are also identified in figure 1. In equation (1), the subscript 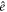 in
in 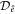 has the meaning of the identity element of the finite group F4, a convention whose meaning will become clear from what follows. Note that the 'natural coordinates'
has the meaning of the identity element of the finite group F4, a convention whose meaning will become clear from what follows. Note that the 'natural coordinates' 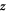 can be expressed through the particle coordinates
can be expressed through the particle coordinates 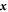 as
as  with
with
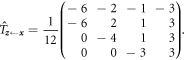
3. Periodic tiling by consecuitive reflections
The key to Bethe Ansatz solvability of the closed kaleidoscopic billiards lies in their ability to periodically tile the full space—with neither holes nor overlaps—via consecutive reflections about their faces3
[2]. Consider the 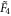 kaleidoscope (1). A union of the figures produced by sequential reflections of (1) about its three-faces from the 1st to the 4th ('simple root' mirrors),
kaleidoscope (1). A union of the figures produced by sequential reflections of (1) about its three-faces from the 1st to the 4th ('simple root' mirrors),

with
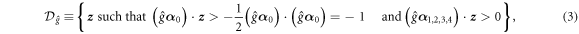
leads to the so-called octacube, otherwise known as the 24-cell [10]; it is the only four-dimensional Platonic solid that does not have any three-dimensional analogues. Its 24 vertices lie at points given by all coordinate permutations and sign choices applied to 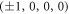 and
and 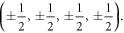 Its 24 octahedron-shaped three-faces are centered at all coordinate permutations and sign choices of
Its 24 octahedron-shaped three-faces are centered at all coordinate permutations and sign choices of 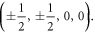 Sequential reflections about the 'simple root' mirrors of the
Sequential reflections about the 'simple root' mirrors of the 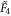 kaleidoscope form the symmetry group of the octacube, the reflection group F4. (The same label is used to mark both an open kaleidoscope, where the 0th, 'minimal root' mirror is absent and the corresponding simple, 'non-affine' Coxeter diagram.) The union in (2) runs over all elements
kaleidoscope form the symmetry group of the octacube, the reflection group F4. (The same label is used to mark both an open kaleidoscope, where the 0th, 'minimal root' mirror is absent and the corresponding simple, 'non-affine' Coxeter diagram.) The union in (2) runs over all elements  of the group F4. The 'physical' domain (1) is the identity member of the set (3).
of the group F4. The 'physical' domain (1) is the identity member of the set (3).
The four-dimensional space can be periodically tiled by identical octacubes; the centers of the octacubical cells lie on all points with integer coordinates whose coordinates sum to an even number: 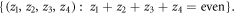 The very same tiling can be obtained by a consecutive reflection of the (1) simplex about all five of its mirrors, including the 'minimal root' one. Transformations generated by these reflections form the symmetry group of the octacubical tiling— the affine reflection group
The very same tiling can be obtained by a consecutive reflection of the (1) simplex about all five of its mirrors, including the 'minimal root' one. Transformations generated by these reflections form the symmetry group of the octacubical tiling— the affine reflection group  homonymous to the corresponding closed kaleidoscope.
homonymous to the corresponding closed kaleidoscope.
We choose the lattice vectors 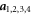 to be proportional to the four simple roots (in an unconventional order) of the reflection group D4[16], closely associated with4
F4 :
to be proportional to the four simple roots (in an unconventional order) of the reflection group D4[16], closely associated with4
F4 : 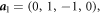
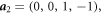
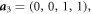 and
and  The reciprocal lattice vectors are thus
The reciprocal lattice vectors are thus 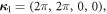
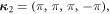
 and
and 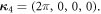 Any plane wave whose wavevector is equal to an integer-coefficient linear superposition of the reciprocal lattice vectors will be periodic on the original spatial lattice.
Any plane wave whose wavevector is equal to an integer-coefficient linear superposition of the reciprocal lattice vectors will be periodic on the original spatial lattice.
Let us briefly describe the parallel structures in the case of a much simpler two-dimensional kaleidoscope,  —a right triangle with angles
—a right triangle with angles 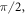
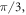 and
and 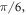 which allows one to solve the two-body problem with particles of mass m and
which allows one to solve the two-body problem with particles of mass m and 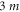 in between two hard walls [6]. In this case, the minimal root wall will be represented by the shortest of the two catheti (sides enclosing the right angle). The other cathetus and the hypothenuse would give the simple-root walls. Consecutive reflections about the latter produce a hexagonal periodicity cell, an analogue of the octacubical cell (2). The lattice vectors are given by the simple roots of the reflection group A2: two equal-length vectors at an angle
in between two hard walls [6]. In this case, the minimal root wall will be represented by the shortest of the two catheti (sides enclosing the right angle). The other cathetus and the hypothenuse would give the simple-root walls. Consecutive reflections about the latter produce a hexagonal periodicity cell, an analogue of the octacubical cell (2). The lattice vectors are given by the simple roots of the reflection group A2: two equal-length vectors at an angle  between them.
between them.
4. Finding the eigenenergies and eigenstates of the problem
In general, finding the eigenenergies and eigenstates of a D-dimensional kaleidoscopic billiard amounts to solving a system of D nonlinear algebraic equations—the so-called Bethe Ansatz equations [2, 3, 11–15]. However, in the case of hard-core interactions, the problem greatly simplifies (see corollary 3.2 in [13]). The eigenstates acquire the form
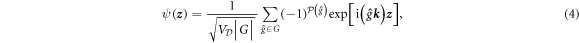
where 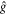 are the members of the finite reflection group G(
are the members of the finite reflection group G(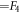 in our case) generated by sequential reflections about the 'simple root' mirrors of the kaleidscope in question;
in our case) generated by sequential reflections about the 'simple root' mirrors of the kaleidscope in question; 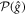 is the parity of the number of the elementary reflections needed to reach
is the parity of the number of the elementary reflections needed to reach 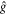 from the identity transformation;
from the identity transformation; 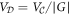 (
(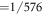 in our case) is the kaleidoscope volume;
in our case) is the kaleidoscope volume; ![${V}_{{\mathcal{C}}}=| \mathrm{det}[({{\boldsymbol{a}}}_{1},{{\boldsymbol{a}}}_{2},{{\boldsymbol{a}}}_{3},\ldots )]| $](https://content.cld.iop.org/journals/1367-2630/17/10/105005/revision1/njp520660ieqn95.gif) is the unit cell volume;
is the unit cell volume; 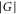 (
(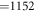 for F4) is the order, i.e. the number of elements, of the group G. The conjecture contained in theorem 1 in [15] indicates that the wavefunction (4) is normalized to unity:
for F4) is the order, i.e. the number of elements, of the group G. The conjecture contained in theorem 1 in [15] indicates that the wavefunction (4) is normalized to unity: 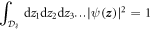 when integrated over the corresponding kaleidoscope
when integrated over the corresponding kaleidoscope 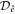 ((1) in the case of
((1) in the case of 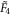 ). This conjecture covers not only the case of the hard-wall boundary conditions but also a much more general class of boundary conditions, associated with finite strength interactions. The wavevectors k are simply drawn from the reciprocal lattice of the corresponding tiling5
. In order to prevent both double counting and the formal appearance of the eigenstates that are identically zero, the wavevectors k must be further restricted to those lying inside the open kaleidoscope associated with the kaleidoscope in question, obtained by removing the 'minimal root' mirror:
). This conjecture covers not only the case of the hard-wall boundary conditions but also a much more general class of boundary conditions, associated with finite strength interactions. The wavevectors k are simply drawn from the reciprocal lattice of the corresponding tiling5
. In order to prevent both double counting and the formal appearance of the eigenstates that are identically zero, the wavevectors k must be further restricted to those lying inside the open kaleidoscope associated with the kaleidoscope in question, obtained by removing the 'minimal root' mirror: 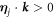 for
for 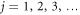 (see the end of section 3 of [13]).
(see the end of section 3 of [13]).
For the case of the hard-wall boundary conditions, the normalization formula used above can also be proven directly without resorting to the conjecture [15]. Observe that the octacube (2) is a unit cell of the lattice spanned by the lattice vectors 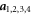 and that the 'seed' wavevector
and that the 'seed' wavevector  along with all its images
along with all its images  belong to the respective reciprocal lattice. In that case, any two distinct plane waves with wave vectors
belong to the respective reciprocal lattice. In that case, any two distinct plane waves with wave vectors 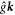 and
and 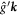 will be orthogonal to each other if integrated over the whole cell:
will be orthogonal to each other if integrated over the whole cell:

with
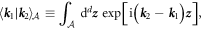
where 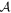 is an area of space. The normalization integral in question can now be evaluated as
is an area of space. The normalization integral in question can now be evaluated as
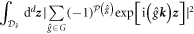
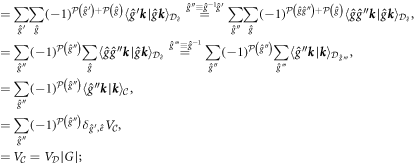
this result justifies the choice of the normalization factor in the expression (4). Above, we used  and
and 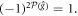
We are now in the position to write down the spectrum of our system explicitly. Starting from this point we abandon the 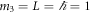 system of units. The eigenenergies,
system of units. The eigenenergies, 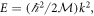 and the eigenstates (4), with
and the eigenstates (4), with 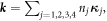
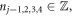 and
and 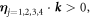 are then given by
are then given by

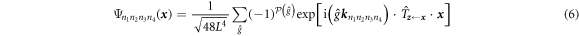
for 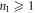 and
and  , where
, where
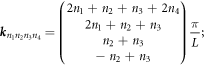
the sum in (6) runs over all 1152 members 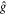 of the reflection group F4 [17] (transformations generated by consecutive reflections about the four 'simple root' mirrors of the
of the reflection group F4 [17] (transformations generated by consecutive reflections about the four 'simple root' mirrors of the  kaleidoscope);
kaleidoscope); ![${{\rm{\Psi }}}_{{n}_{1}{n}_{2}{n}_{3}{n}_{4}}({\boldsymbol{x}})\equiv \sqrt{| \mathrm{det}[{\hat{T}}_{{\boldsymbol{z}}\leftarrow {\boldsymbol{x}}}]| }{\psi }_{{n}_{1}{n}_{2}{n}_{3}{n}_{4}}({\hat{T}}_{{\boldsymbol{z}}\leftarrow {\boldsymbol{x}}}\cdot {\boldsymbol{x}})$](https://content.cld.iop.org/journals/1367-2630/17/10/105005/revision1/njp520660ieqn120.gif) are the eigenstates of the system expressed through the particle coordinates
are the eigenstates of the system expressed through the particle coordinates 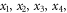 normalized as
normalized as 
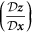 is the Jacobian matrix of the
is the Jacobian matrix of the 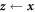 transformation.
transformation.
At high energies, the spectrum converges to the Weyl law prediction for the number of states with energies below a given energy E: 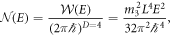 where
where  is the classical phase-space volume occupied by points with energies below E, and D is number of spatial dimensions (see figure 2).
is the classical phase-space volume occupied by points with energies below E, and D is number of spatial dimensions (see figure 2).
Figure 2. Exact energy spectrum for four particles of mass 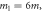
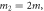
 and
and 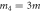 in a hard-wall box of length L (red solid line). Weyl's law prediction for the spectrum of this system (blue dashed line).The energies up to
in a hard-wall box of length L (red solid line). Weyl's law prediction for the spectrum of this system (blue dashed line).The energies up to 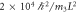 are shown.
are shown.
Download figure:
Standard image High-resolution imageThe ground state energy is
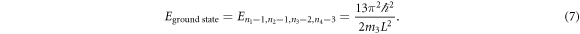
The ground state wave function can be obtained from equation (6), using
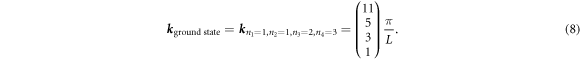
figure 3 shows a particular section of the ground state density distribution within the  simplex, along with its space-tiling mirror images.
simplex, along with its space-tiling mirror images.
Figure 3. The ground state of our four-body system. The plot is performed using the z coordinates, relevant to the tiling. The image is produced by first intersecting the four-dimensional density distribution by the three-plane and the three-sphere indicated in the upper left and upper right corners, respectively (the formulas, however, are given in x coordinates, in which the three-sphere becomes a three-ellipsoid). The result is a two-sphere centered at the origin. Considering now this two-sphere as living in the usual 3D space, we pick, in this 3D space, a (2D) plane that does not intersect the two-sphere, and project onto it the two-sphere's hemisphere closest to the plane; this projection is what is shown in the image. The circles on the two-sphere are the sections of the 3D hyperplanes of the original 4D space; the great circles come from the hyperplanes that pass through the origin, and the other circles come from the hyperplanes that do not. The lighter triangle in the middle corresponds to a section of the 'physical' four-dimensional simplex to which the particle coordinates are bounded; the remainder of the sphere is a section of the entire four-dimensional space when this space is octacubically tiled with the mirror images of the original 'physical' simplex. The existence of this tiling ensures the applicability of the Bethe Ansatz [2]. Remark that even though the images of the 'physical' simplex are identical (up to a rotation) in the full four-dimensional space, the two three-surfaces indicated in the upper corners cross different images at different points and at different angles: thus, different images appear differently at this figure.
Download figure:
Standard image High-resolution imageThe first excitation,  has an energy
has an energy 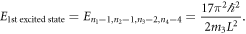 The first degeneracy unites the 14th and the 15th excited states. All degeneracies appear to be purely 'number-theoretical,' i.e. not associated with the symmetries of the system. While the rich symmetry and the tiling properties of the octacubical periodicity cell constitute the very reason for the existence of the exact solutions, the actual kaleidoscope—of whose mirror images the cell consists—does not possess any relevant symmetry.
The first degeneracy unites the 14th and the 15th excited states. All degeneracies appear to be purely 'number-theoretical,' i.e. not associated with the symmetries of the system. While the rich symmetry and the tiling properties of the octacubical periodicity cell constitute the very reason for the existence of the exact solutions, the actual kaleidoscope—of whose mirror images the cell consists—does not possess any relevant symmetry.
5. Integrals of motion
The Bethe Ansatz integrability of our system can be also reinterpreted in terms of the Liouville integrability. To construct the three additional integrals of motion in involution with the Hamiltonian and each other, we suggest invoking the invariant polynomials of the group in question [18]: finite polynomials of coordinates 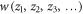 that remain invariant under the group action,
that remain invariant under the group action,
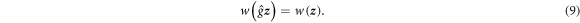
Consider now an operator 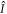 that is constructed by taking an invariant polynomial w as a function of the momenta associated with the
that is constructed by taking an invariant polynomial w as a function of the momenta associated with the 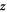 coordinates:
coordinates:
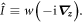
Let us show that any eigenstate (4) of the kaleidoscope associated with the group in question is at the same time an eigenstate of 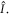 Indeed,
Indeed,
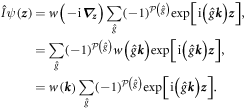
Q.E.D. for the reflection group F4, the four lowest power functionally independent invariant polynomials read [19]:

Accordingly, the four fundamental integrals of motion for our system read

with
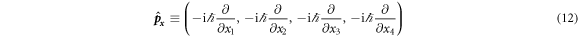
being the particle momenta, corresponding to the particle coordinates x1, x2, x3, x4. Above,  stands for the transpose of a matrix. Note that the first integral of motion is proportional to the Hamiltonian of the system:
stands for the transpose of a matrix. Note that the first integral of motion is proportional to the Hamiltonian of the system: 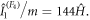
6. Summary and outlook
In this Letter, we obtain—using Bethe Ansatz—an exact expression for the eigenenergies and eigenfunctions of four hard-core particles with mass ratios 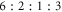 in a hard-wall box. The Ansatz is induced by a hidden symmetry of the system related to the symmetries of the tiling of a four-dimensional space by octacubes. The exact spectrum stands in good agreement with the approximate Weyl's law prediction.
in a hard-wall box. The Ansatz is induced by a hidden symmetry of the system related to the symmetries of the tiling of a four-dimensional space by octacubes. The exact spectrum stands in good agreement with the approximate Weyl's law prediction.
The following observation may serve as a seed for a longer research program. The procedure, outlined in this Letter, for identifying a few-body problem relevant to a particular Coxeter diagram [17] is not unique to 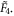 Any diagram, affine or not, that does not have bifurcations can potentially be used to generate a solvable few-body hard-core problem. The
Any diagram, affine or not, that does not have bifurcations can potentially be used to generate a solvable few-body hard-core problem. The 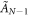 (N identical hard-cores on a circle) and
(N identical hard-cores on a circle) and 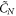 (N identical hard-cores in a hard-wall box) diagrams have been already successfully introduced in the first years of many-body Bethe Ansatz, in [5] and [1], respectively. The
(N identical hard-cores in a hard-wall box) diagrams have been already successfully introduced in the first years of many-body Bethe Ansatz, in [5] and [1], respectively. The 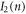 diagrams were explored in [20], albeit classically, still awaiting a quantum treatment: for each integer n a continuous one-parametric family of solvable three-body mass ratios (on a line with no boundary conditions) was obtained. A system of two hard-core particles with mass ratio 3:1 in a box (whose one-wall version was explored in [6]) is expected to exhibit an exact solution associated with the
diagrams were explored in [20], albeit classically, still awaiting a quantum treatment: for each integer n a continuous one-parametric family of solvable three-body mass ratios (on a line with no boundary conditions) was obtained. A system of two hard-core particles with mass ratio 3:1 in a box (whose one-wall version was explored in [6]) is expected to exhibit an exact solution associated with the 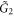 Coxeter diagram. It can be conjectured that H3 and H4 Coxeter diagrams lead to solvable four- and five-body problems on a line, respectively.
Coxeter diagram. It can be conjectured that H3 and H4 Coxeter diagrams lead to solvable four- and five-body problems on a line, respectively.
The true challenge is posed by the Coxeter diagrams (affine or otherwise) with bifurcations, most notably the 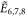 series. At the moment, it is not clear if there are any respective realistic 6-, 7-, or 8-body problems that can be solved using these symmetries. (Some examples of 'unphysical' few-body realizations of Coxeter diagrams—e.g. those where a given particle can interact with an empty point in between the other two—are given in [3].)
series. At the moment, it is not clear if there are any respective realistic 6-, 7-, or 8-body problems that can be solved using these symmetries. (Some examples of 'unphysical' few-body realizations of Coxeter diagrams—e.g. those where a given particle can interact with an empty point in between the other two—are given in [3].)
The potential empirical context for this and further planned explorations is one-dimensional cold gas mixtures in optical lattices where the dynamics is governed by an effective (rather than physical) mass, controlled at will [21].
Acknowledgments
We are profoundly indebted to late Marvin Girardeau for guidance and inspiration. We are thanking Jean-Sébastien Caux for reading the manuscript and for the comments that followed. The impact of the numerous in-depth discussions of the subject with Dominik Schneble can not be overestimated. This work was supported by grants from National Science Foundation (PHY-1402249) and the Office of Naval Research (N00014-12-1-0400).
Footnotes
- 3
Regardless of the geometry, all faces are assumed to be distinct. For example, an isosceles triangle with angles 2π/3, π/6, and π/6 does tile a two-dimensional plane via consequitive reflections about its sides. However, if its legs (equal length sides) are labeled, there exists no tiling with edges (boundaries between the tiles) uniquely labeled by the legs that created them: for a particular tiling edge, its label would be different for different orders of the tiling sequence.
- 4
The roots of D4 are the so-called long roots of F4 [16].
- 5
Construction of solution for problems leading to open simplexes with the 'minimal root' wall removed is very similar: simple, inftead of affine, Coxeter diagrams are used to label kaleidoscopes; the simple roots only are used to construct the mirrors; any wavevector can be used to construct a solution, so no quantization is required.