Abstract
The second law of thermodynamics normally prescribes that heat tends to disperse, but in certain cases it instead implies that heat will spontaneously concentrate. The spontaneous formation of stars out of cold cosmic nebulae, without which the universe would be dark and dead, is an example of this phenomenon. Here we show that the counter-intuitive thermodynamics of spontaneous heat concentration can be studied experimentally with trapped quantum gases, by using optical lattice potentials to realize weakly coupled arrays of simple dynamical subsystems, so that under the standard assumptions of statistical mechanics, the behavior of the whole system can be predicted from ensemble properties of the isolated components. A naive application of the standard statistical mechanical formalism then identifies the subsystem excitations as heat in this case, but predicts them to share the peculiar property of self-gravitating protostars, of having negative micro-canonical specific heat. Numerical solution of real-time evolution equations confirms the spontaneous concentration of heat in such arrays, with initially dispersed energy condensing quickly into dense 'droplets'. Analysis of the nonlinear dynamics in adiabatic terms allows it to be related to familiar modulational instabilities. The model thus provides an example of a dictionary mesoscopic system, in which the same non-trivial phenomenon can be understood in both thermodynamical and mechanical terms.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
GENERAL SCIENTIFIC SUMMARY Introduction and background. Without the temperature gradients that stars supply, life as we know it would not exist in the universe. Stars form from spontaneous hotspots in cold nebulae, but how can such hotspots form and intensify, when the Second Law of Thermodynamics normally implies that energy must disperse? The theoretical answer is that, because of their own gravitational attraction, protostars have the unusual thermodynamic property of negative specific heat. Negative specific heat turns the world upside down, thermodynamically; it implies that entropy increases when heat flows from lower to higher energy subsystems, opposite to the usual direction.
Main results. Here we show that negative specific heat can also occur in cold atomic vapors, allowing experimental study of the rare and important phenomenon of spontaneous energy concentration here on Earth, by using optical lattice potentials to realize weakly coupled arrays of simple dynamical subsystems which have negative micro-canonical specific heat. In such systems initially dispersed heat quickly condenses into dense `droplets'.
Wider implications. Besides the thermodynamic interpretation such systems also allow for a purely mechanical picture of this condensation process of heat in terms of an adiabatic theory of the underlying nonlinear dynamics. We therefore propose laboratory studies of negative specific heat as an elusive but fundamentally important aspect of thermodynamics, which may shed fresh light on the general problem of how thermodynamics emerges from mechanics.
 Figure. Local particle number (left) and local two-mode energy (right) of an 512×512-array of two-mode Bose–Hubbard systems after short evolution after an initial excitation. Each pixel in the plots corresponds to one two-mode system. The local initial excitations relax radiating away sound waves while 'droplets' of maximally excited two-mode subsystem form. Spontaneous concentration of heat occurs due to the surprising thermodynamic effect of negative specific heat.
Figure. Local particle number (left) and local two-mode energy (right) of an 512×512-array of two-mode Bose–Hubbard systems after short evolution after an initial excitation. Each pixel in the plots corresponds to one two-mode system. The local initial excitations relax radiating away sound waves while 'droplets' of maximally excited two-mode subsystem form. Spontaneous concentration of heat occurs due to the surprising thermodynamic effect of negative specific heat.
Stars form when cold cosmic nebulae spontaneously develop hot spots that steadily intensify until they reach fusion temperatures [1]. The formation of protostars has been much discussed [2–7], however, for it appears to violate the second law of thermodynamics, which normally implies that heat disperses. We show how laboratory experiments can illuminate this apparent paradox, which is as fundamental in origin as it is important in consequence, by studying spontaneous heat concentration in trapped quantum gases ('cold atoms'). This represents an advance within the current broad enterprise of using quantum gases to probe the mechanical underpinnings of thermodynamics, for example by studying the relationship between integrability and the onset of equilibration [8], exploring concepts like pre-thermalization [9] and realizing negative temperature [10].
The unprecedented controllability of cold atom systems is a powerful tool for the longstanding task of reducing thermodynamic behavior to its fundamental mechanical basis. This task, which began with Boltzmann in the 19th century, remains unfinished despite the immense successes of statistical mechanics. Those very successes sometimes even obscure the basic fact that every thermodynamic effect must always have an alternative description in mechanical terms, simply because every thermodynamic effect occurs in a physical system, however large, which obeys the fundamental laws of mechanics. The problem is that the language of thermodynamics contains important terms, such as entropy, whose purely mechanical meaning remains unclear, but in the large systems for which thermodynamics is usually invoked, translation between the two languages faces an immense barrier of complexity.
What may be possible with studies on highly controlled mesoscopic systems is to find dictionaries, in which non-trivial phenomena can be fully understood in both thermodynamical and mechanical terms simultaneously, so that a tentative lexicon may be established, which can then be expanded by gradually turning on more complex effects. This kind of analysis may provide more thorough understanding of fundamental processes like equilibration, but there is no reason it cannot also be pursued for more dramatic thermodynamic phenomena. In this paper we present a theoretical example of such a dictionary system, which may be implemented with a cold atom setup of weakly coupled two-mode subsystems. The dramatic thermodynamical phenomenon our system exhibits is the instability of spontaneous heat concentration, which plays a vital role in the formation of stars and of geologically active planets [11]. We show how this phenomenon may be understood explicitly in the standard terms of statistical mechanics, as a manifestation of negative specific heat; we then show how, with the help of adiabatic theory, it may also be understood mechanically, as a modulational instability [12] of adiabatically conserved excitations.
Within thermodynamics, the paradox of spontaneous heat concentration admits a simple resolution: negative specific heat [3]. The second law of thermodynamics says that entropy cannot decrease, which is often summarized by saying that heat cannot flow from colder systems to hotter. This summary is correct if hotter and colder are interpreted as higher and lower temperature, but it is not necessarily valid in reference to systems containing more or less heat. The rate at which temperature changes with energy—the specific heat CV —is normally positive, so that higher temperature implies higher energy, and heat flow from high to low temperature redistributes energy more evenly throughout aggregate systems, tending toward uniform equilibrium. If CV should be negative, however, the world of thermodynamics turns upside down: higher temperature corresponds to lower thermal energy, and increasing entropy requires that systems with less energy lose heat to systems with more energy. In aggregates of many subsystems, negative CV thus implies instability toward spontaneous heat concentration (see the supplementary material, available from stacks.iop.org/NJP/16/013013/mmedia).
In the case of star formation, the negative work done by self-gravitation is an essential element in the dynamics underlying negative specific heat; but a simpler realization of negative specific heat can in principle be achieved in systems dominated by pure heat transport, where work plays very little role, and heat can essentially be identified with total energy. The work-free special case is in fact the standard one in much of condensed matter theory, where statistical mechanics compares different ensembles with a fixed Hamiltonian, and hence classifies all energy changes as heat transfer [13, 14]. Pursuing laboratory models for negative CV , therefore, we will henceforth not distinguish between heat and energy. For comparison with gravitational systems, our statements about energy must be interpreted more specifically in terms of heat.
It has been debated whether or under which circumstances negative CV without gravity is really possible, however [15–20]. Recent experiments have reported negative specific heat in melting atomic clusters [21, 22] and fragmenting nuclei [23], but these arguably represent transient phenomena outside the proper scope of thermodynamics. Some classic thermodynamics texts state flatly that systems with negative CV cannot exist [24], while others discuss the issue at more cautious length [25]. In fact thermodynamics does not prescribe such features of any system. It is the discipline of statistical mechanics that strives to predict them, by representing the effect of complex mechanical interactions in terms of probability distributions, and identifying statistical properties of these distributions with thermodynamical quantities like CV . According to the workhorse probability distribution of statistical mechanics, the so-called canonical ensemble (CE), negative CV is indeed impossible for any system:
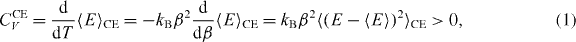
where the expectation value of the energy in thermal equilibrium according to the CE is given by
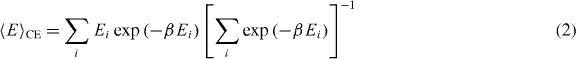
and β = 1/(kBT). This theorem does not hold, however, in the alternative probability distribution of the micro-canonical ensemble (μC), in which the system's energy is fixed, rather than fluctuating randomly as in the CE. It has been argued that the canonical ensemble is invalid whenever the micro-canonical ensemble yields negative CV [4]. These discrepancies between ensembles point to the fact that statistical mechanics remains a comparatively weak link in the chain of physics.
It is nonetheless a tremendously important link, and ensemble inequivalence [18, 26] and concepts such as non-extensive micro-canonical thermodynamics in small systems [27, 28] are subjects of active research. The assumptions of statistical mechanics can moreover be tested today as never before, with experiments on tightly controlled mesoscopic systems whose dynamics can be followed closely [8]. Trapped quantum gases offer an especially promising laboratory for such tests. The observation of Bose–Einstein condensation was a scientific landmark because it confirmed one dramatic prediction of statistical mechanics, the cessation of thermal motion by a large fraction of gas atoms at a temperature above absolute zero. Can trapped quantum gases test another dramatic statistical mechanical prediction, spontaneous heat concentration as in star formation, by realizing an aggregate of systems with negative specific heat?
They can. The two-mode BH model with repulsive interactions has been highly studied as a model system, representing bosonic particles that quantum mechanically tunnel back and forth between two potential wells [29–32]. It has also been realized as such in experiments [33–36]. In the formalism of so-called second quantization, where the canonical operators 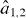 remove atoms from wells 1 and 2, and their conjugate operators
remove atoms from wells 1 and 2, and their conjugate operators 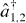 replace the atoms correspondingly, the Hamiltonian of a single two-mode BH system reads
replace the atoms correspondingly, the Hamiltonian of a single two-mode BH system reads
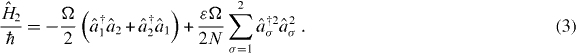
For repulsively interacting trapped bosons, the constants Ω > 0 and ε > 0 are determined by the details of the trapping potential and of interparticle scattering, respectively. N is chosen equal to the expectation value of 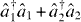 , which represents the total number of particles in both wells together, and is conserved by time evolution under
, which represents the total number of particles in both wells together, and is conserved by time evolution under 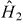 .
.
A system with only two degrees of freedom like this is not normally treated statistically, but if we consider a large collection of many such systems, weakly coupled together using optical lattice potentials [37, 38] as sketched in figure 1, then applying statistical mechanics to the individual two-mode systems is much like the standard textbook case of deducing the thermodynamic properties of a dilute gas from the statistical mechanics of a single non-interacting particle, or of modeling the effect on a system of interactions with a reservoir by means of an ensemble—in which the interactions themselves are not incorporated. Naively applying the same logic, we obtain the quantum statistical mechanical entropy of two-mode BH in the microcanonical ensemble as

where ZΔE(E) is the number of eigenstates of 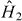 with eigenvalues in the range (E,E + ΔE), and kB is Boltzmann's constant. Here the ground state energy and entropy have both been set to zero by shifting all energies and entropies uniformly, as one is free to do in thermodynamics. In the thermodynamic limit of a dense energy spectrum, where this definition is normally applied, ΔE must be chosen great enough for ZΔE(E) to be large and relatively smooth as a function of E, but small enough for ZΔE(E) to be linearly proportional to ΔE for all E, so that SΔE(E) → S(E) becomes independent of ΔE.
with eigenvalues in the range (E,E + ΔE), and kB is Boltzmann's constant. Here the ground state energy and entropy have both been set to zero by shifting all energies and entropies uniformly, as one is free to do in thermodynamics. In the thermodynamic limit of a dense energy spectrum, where this definition is normally applied, ΔE must be chosen great enough for ZΔE(E) to be large and relatively smooth as a function of E, but small enough for ZΔE(E) to be linearly proportional to ΔE for all E, so that SΔE(E) → S(E) becomes independent of ΔE.
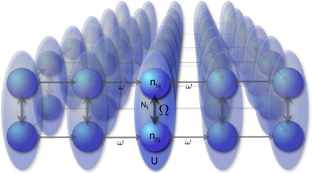
Figure 1. Two-mode Bose–Hubbard (BH) systems weakly coupled in a two-dimensional (2D) sheet. Atoms oscillate between modes within each subsystem at the tunneling Rabi rate Ω, as well as between the subsystems at ω ≪ Ω.
Download figure:
Standard image High-resolution imageThe two-mode BH spectrum becomes dense in the limit of large total boson number N, which is also the regime most easily attained in experiments [33, 39], and in this semiclassical limit the eigenspectrum is given accurately, except for classical orbits too near an unstable fixed point, by Bohr–Sommerfeld quantization. This involves constructing canonical action–angle variables J,ϕ for the quantum system's classical analogue, expressing the classical Hamiltonian H2 as E(J), and then determining the quantum eigenenergies as 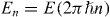 for n a whole number. The limit of a dense spectrum is obtained for large N, and implies
for n a whole number. The limit of a dense spectrum is obtained for large N, and implies 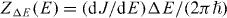 . For the classical analogue of
. For the classical analogue of 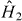 the derivative dJ/dE may be calculated analytically in closed form (see the supplementary material, available from stacks.iop.org/NJP/16/013013/mmedia), yielding the entropy
the derivative dJ/dE may be calculated analytically in closed form (see the supplementary material, available from stacks.iop.org/NJP/16/013013/mmedia), yielding the entropy

where K(k) is the complete elliptic integral of the first kind, and we define the functions

Here Emax(N,Ω,ε) denotes the highest energy of the classical system for fixed N, so that  is the normalized energy. The entropy turns out only to depend on N and Ω by depending on
is the normalized energy. The entropy turns out only to depend on N and Ω by depending on  . (In this sense the two-mode BH entropy is non-extensive with particle number N, but this should not be surprising, since what is expected is extensivity in the number of two-mode systems that are coupled together in a large aggregate system.) The specific heat may then be calculated microcanonically in terms of derivatives of S(E): CμCV = −(∂S/∂E)2/(∂2S/∂E2).
. (In this sense the two-mode BH entropy is non-extensive with particle number N, but this should not be surprising, since what is expected is extensivity in the number of two-mode systems that are coupled together in a large aggregate system.) The specific heat may then be calculated microcanonically in terms of derivatives of S(E): CμCV = −(∂S/∂E)2/(∂2S/∂E2).
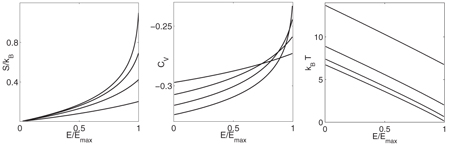
The thermodynamic quantities S, CμCV and the temperature T = (∂S/∂E)−1 are plotted versus  for different values of ε in figure 2. Note that CμCV is always negative. For ε = 1, CμCV diverges at
for different values of ε in figure 2. Note that CμCV is always negative. For ε = 1, CμCV diverges at 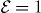 , but at this point Bohr–Sommerfeld quantization breaks down for any N because the maximum energy classical orbit is a dynamically unstable fixed point. This actually means that the two-mode entropy is always a purely convex function of the energy as long as the system is superfluid and below the self-trapping transition. Therefore, the interaction strength can be chosen arbitrarily from a wide range of possible values; it may be quite large and still retain a convex entropy function. For ε < 1 and large N, the statistical mechanical result is definite: an array of weakly coupled two-mode BH systems, as in figure 1, is an aggregate of interacting subsystems that all have negative CV . In contrast to the canonical temperature which can be negative when the energy is bounded from above [10], the micro-canonical temperature of the two-mode BH system turns out to be positive. The micro-canonical temperature is, however, monotonically decreasing with energy. This unusual fact, as well as the drastic inequivalence of the two ensembles regarding temperature, again reflects the unusual behavior of systems with negative CV .
, but at this point Bohr–Sommerfeld quantization breaks down for any N because the maximum energy classical orbit is a dynamically unstable fixed point. This actually means that the two-mode entropy is always a purely convex function of the energy as long as the system is superfluid and below the self-trapping transition. Therefore, the interaction strength can be chosen arbitrarily from a wide range of possible values; it may be quite large and still retain a convex entropy function. For ε < 1 and large N, the statistical mechanical result is definite: an array of weakly coupled two-mode BH systems, as in figure 1, is an aggregate of interacting subsystems that all have negative CV . In contrast to the canonical temperature which can be negative when the energy is bounded from above [10], the micro-canonical temperature of the two-mode BH system turns out to be positive. The micro-canonical temperature is, however, monotonically decreasing with energy. This unusual fact, as well as the drastic inequivalence of the two ensembles regarding temperature, again reflects the unusual behavior of systems with negative CV .
Figure 2. Thermodynamical properties of the two-mode BH system. Left: microcanonical entropy S(E) of the two-mode BH system in units of kB as a function of normalized energy for ε = 0.2,0.4,0.6 and 0.8 (bottom to top), where ground state energy and entropy are both set to zero. Middle: microcanonical heat capacity CV (E) of a single two-mode system as a function of energy for the same values of ε (top to bottom at the left of the graph). Right: microcanonical temperature T = (∂S/∂E)−1 of the two-mode system as a function of energy for the same values of ε (top to bottom).
Download figure:
Standard image High-resolution imageRealizing a large array of two-mode BH subsystems, each weakly coupled to its neighbors, is certainly possible in current laboratories that trap cold bosons in so-called optical lattice potentials, induced by standing waves of laser light [33]. The weak coupling, which allows the subsystems to exchange both atoms and energy with their neighbors, is provided by quantum tunneling, just as between the two wells within each two-mode subsystem, except that a slower frequency ω ≪ Ω is imposed, by making the potential barriers higher. This possibility, of coupling many simple subsystems together weakly, makes the thermodynamical treatment of the two-mode BH system physically meaningful, for it is the basic assumption of statistical mechanics that weak interactions in large aggregate systems effectively redistribute energy incoherently, allowing exact states to be mimicked with ensembles of simplified systems, where the simplification often consists precisely in neglecting the very interactions (collisions, for example, or coupling to a bath) that have been invoked to justify the procedure.
From the mechanical point of view, on the other hand, weak coupling establishes a separation of time scales between intra-sub-system dynamics and within-system evolution. And finally from the thermodynamic point of view, weak coupling justifies the assumption of local (quasi-)equilibrium, because local equilibration occurs faster than heat transport between subsystems. In our case each isolated system is automatically and trivially in equilibrium, in the sense that its time evolution rapidly explores the entire surface of constant energy, because the surface of constant energy is one-dimensional (1D). Adding weak perturbations between our subsystems is thus adding a weak coupling between subsystems that are in local equilibrium. Controllable weak coupling between large aggregates of simple subsystems is thus an essential tool for investigating the emergence of thermodynamics and statistical mechanics from mechanics. Such control is a basic feature of cold atom systems, and with the prospect of new experiments in this fundamental subject, the task of theory also shifts toward identifying outstanding targets for experiment, based on simple ideas.
Negative specific heat is a particularly apt target for investigations of the roots of thermodynamics, precisely because the instability toward spontaneous energy concentration tends to steepen temperature gradients, rather than smoothing them out: when systems holding less heat have higher temperature, the spontaneous flow of heat from high temperature to low tends to amplify temperature differences rather than reduce them. This instability raises questions about basic concepts of equilibrium, and even of ensembles. For example, cases where heat concentrates in one subsystem or another may be equally likely (by symmetry), but the time scale for fluctuations between the two macroscopically distinct cases can easily be so long that it ceases to make sense to regard the cases as two ensemble elements in a single macrostate; they should rather be classed as two distinct macrostates. The thermodynamics and statistical mechanics of negative specific heat in general requires difficult extensions of standard theory. In particular the scaling of effects with system size (extensivity) is a major issue, because of the basic instability toward inhomogeneity.
Many questions can be raised about such systems, and many simple quantum systems may formally possess negative CV , at least in some energy range, but the merit of the cold atom realization we propose is that its controllable coupling and system size open many of the basic thermodynamic and statistical mechanical questions raised by negative CV to highly controlled terrestrial experiments. Sophisticated theoretical tools can also be applied to BH systems, allowing more rigorous first-principles results than may be available for other real systems. In advance of such detailed theoretical or experimental studies, however, it is not difficult to take the first step of simply applying our CV calculation for a single two-mode BH, to naively predict the behavior of a large aggregate system. Negative CV for local subsystems would thermodynamically imply that energy initially distributed across the lattice will concentrate, as heat does in star-producing nebulae, rather than dispersing as heat usually does. This is a strong prediction of dramatic behavior in a large and complex dynamical system, and it is made without any detailed consideration of the very inter-component interactions that make the system complex; even qualitative agreement between this naive theory and real time evolution is a significant victory for statistical mechanics.
In the same semi-classical limit in which our entropy calculation is performed, a large aggregate of many coupled BH subsystems may be evolved accurately under mean field theory, which can easily be simulated numerically. Our numerical simulations indeed show a dramatic and robust tendency for initially broad distributions of excitation energy to concentrate spontaneously, into tight 'droplets'. Moreover this result tends to justify the naive extrapolation from two-mode subsystem thermodynamics to the larger system, as being self-consistent in hindsight: the system quickly relaxes into a configuration where almost all subsystems are either close to maximally or close to minimally excited, with only small fluctuations. Within each of the two types of domains that thus emerge, the behavior of each subsystem is similar, and in this sense the aggregate behavior is well represented by the individual example.
The Hamiltonian for our large aggregate system reads
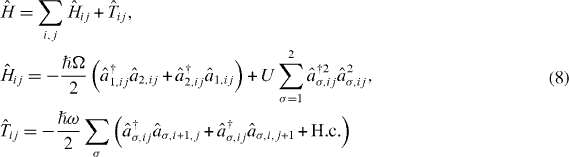
in which we recognize 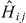 as a 2D array of
as a 2D array of 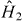 forms, with the nonlinearity constant written with U rather than
forms, with the nonlinearity constant written with U rather than 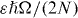 because N → Nij can now vary in time, as the
because N → Nij can now vary in time, as the 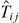 term lets particles tunnel between neighboring subsystems. In the experimentally attainable limit where all the Nij remain large, the complex quantum many-body dynamics of
term lets particles tunnel between neighboring subsystems. In the experimentally attainable limit where all the Nij remain large, the complex quantum many-body dynamics of 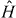 can be well approximated with classical mean-field theory [40]. Even the classical dynamics is chaotic, but it can be integrated numerically. The results for a 512 × 512 array of two-mode BH systems are shown in figure 3, as three 'stills' from video 1 available in the supplementary material (available from stacks.iop.org/NJP/16/013013/mmedia).
can be well approximated with classical mean-field theory [40]. Even the classical dynamics is chaotic, but it can be integrated numerically. The results for a 512 × 512 array of two-mode BH systems are shown in figure 3, as three 'stills' from video 1 available in the supplementary material (available from stacks.iop.org/NJP/16/013013/mmedia).
Figure 3. Evolution of local particle number and energy; each pixel in the plots corresponds to one two-mode BH system. Left column: total particle number in each two-mode system Nij at three points in time (t = 0τ,92τ and 697τ, where τ = 2π/ω). Right column: normalized energy of the two-mode system E/Emax at each site at the same points in time. System parameters: 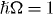 ,
,  , U = 2 and N = 1024, lattice size: 512 × 512. We start with uniformly distributed atoms and diffuse clouds of excitation defined by simulated phase imprinting. These clouds concentrate into maximally excited droplets.
, U = 2 and N = 1024, lattice size: 512 × 512. We start with uniformly distributed atoms and diffuse clouds of excitation defined by simulated phase imprinting. These clouds concentrate into maximally excited droplets.
Download figure:
Standard image High-resolution imageAs initial state we choose a configuration in which all of the atoms are distributed uniformly over the whole array of two-mode subsystems. We moderately excite this state locally by phase imprinting, i.e. in some regions we externally change the local two-mode energy by adjusting the local relative phase between the two modes. The relative phases between the subsystems are not involved in the excitation process. This non-equilibrium initial state, which includes only weak energetic inhomogeneity, relaxes by excitation of sound waves, i.e. waves in the number distribution Nij, seen in the left column of figure 3. Some of the initial energy thus disperses into these complex low-amplitude waves; but the majority of the two-mode energy concentrates into bright droplets of maximum excitation, seen in the right column of the figure. The regions of energy concentration behave very much like droplets, with positive surface tension. They can also move (see the supplementary video). The droplet boundaries are also visible in the left column as domain-wall-like depressions in the local particle number, which extend over several lattice sites. Their thickness is on the order of the characteristic 'healing' length of the mean-field theory [40]. Their formation is a continuum limit phenomenon, rather than a lattice effect, since the inverses of all their characteristic length scales are well inside the first Brillouin zone. The results shown in figure 3 and video 1 are robust and typical over a wide range of parameters and initial conditions and also hold in other dimensions. The numerical analysis presented here therefore confirms the dramatic statistical mechanical prediction of spontaneous energy concentration in the semiclassical limit. This is our first major result.
In a 1D chain of two-mode BH subsystems the energy concentration effect is also present, but it is slower and less dramatic because local equilibration by sonic radiation is less efficient. A detailed discussion of the 1D system is presented in [41]. The corresponding three-dimensional system is expected to show energy concentration even more cleanly than in 2D, because radiation is still more efficient at establishing local equilibrium, but this case is of course more demanding computationally, and also more difficult to display clearly.
Our 2D mean field simulation is also sufficient to provide a second major result. In addition to observing the formation of 'droplets of heat', we are able to follow it in detail as a dynamical process. At least in the regime we have analyzed here, we can thereby 'reverse engineer' the thermodynamics of energy concentration, in the sense that we can identify the dynamical mechanisms underlying the phenomenon.
The weak coupling limit ω ≪ Ω implies a time scale separation, such that when two neighboring subsystems exchange energy, the sum of their two action variables J is a so-called adiabatic invariant. In a Bohr–Sommerfeld semiclassical sense, this implies that quanta of local two-mode BH energy are approximately conserved. A resummed Bogoliubov transformation [42, 43] shows the same result perturbatively, rather than semi-classically. One can then derive a low-frequency effective theory for the evolution of atoms and plasmon-like two-mode excitations, as two species of separately conserved quasi-particles. This comes near to reviving the 18th century caloric theory of heat [44, 45], in a quantum mechanical re-interpretation.
Expanding the full Hamiltonian 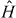 in terms of these new quasi-particles, we find that the leading interactions among the plasmon-like energy quasi-particles are attractive whenever those among the physical particles are repulsive [42, 43]. This possibly surprising result is, at least in the semi-classical limit, merely a restatement of the fact that classically the energy grows sub-linearly with the action. The action corresponds to quasi-particle number, and so linear dependence of energy on action implies non-interacting quasi-particles, while any nonlinear dependence of energy on action corresponds to interactions. If the energy grows more slowly than linearly with action, then the nonlinear corrections are negative, and hence the interactions are attractive. For the two-mode case this simply corresponds to the well-known fact that the period of Josephson oscillations lengthens with amplitude [30]. When adiabatically conserved excitation quasi-particles attract each other, while particles continue to repel, the instability towards concentration of excitations within a uniform distribution of particles becomes easy to understand in mechanical terms. In repulsive BH systems, energy concentrates spontaneously because local energy excitations attract each other. Damping supplied by coupling to long-wavelength density waves can then quickly draw high-frequency excitations together.
in terms of these new quasi-particles, we find that the leading interactions among the plasmon-like energy quasi-particles are attractive whenever those among the physical particles are repulsive [42, 43]. This possibly surprising result is, at least in the semi-classical limit, merely a restatement of the fact that classically the energy grows sub-linearly with the action. The action corresponds to quasi-particle number, and so linear dependence of energy on action implies non-interacting quasi-particles, while any nonlinear dependence of energy on action corresponds to interactions. If the energy grows more slowly than linearly with action, then the nonlinear corrections are negative, and hence the interactions are attractive. For the two-mode case this simply corresponds to the well-known fact that the period of Josephson oscillations lengthens with amplitude [30]. When adiabatically conserved excitation quasi-particles attract each other, while particles continue to repel, the instability towards concentration of excitations within a uniform distribution of particles becomes easy to understand in mechanical terms. In repulsive BH systems, energy concentrates spontaneously because local energy excitations attract each other. Damping supplied by coupling to long-wavelength density waves can then quickly draw high-frequency excitations together.
Within purely mechanical adiabatic theory, the 'heat droplets' predicted by statistical mechanics thus appear as structures like the spin domains seen in spinor condensates [46], which are understood in terms of purely mechanical instabilities. It is important to note, however, that the instability to heat concentration which we describe is not identical to familiar modulational instabilities [12], as known in nonlinear (atom) optics: it is only energy that concentrates spontaneously here, while the total atom density remains nearly uniform. Neither is the formation of heat droplets identical to spin domain formation, as seen in spinor condensates [46], for in our model there is no nonlinear interaction between the two modes of each subsystem, and in this regime spinor condensates are normally miscible rather than domain-forming. Also unlike ordinary spin domains, our droplets form only in highly excited states of our system—they are droplets of high excitation. The true ground state of our system is uniform and trivial. The modulational instability we describe occurs among energy-carrying quasi-particles which are only adiabatically conserved. It is closely similar to other well known modulational instabilities, and in this sense counts as a fully understood mechanical phenomenon; but it appears in a non-trivial adiabatic context, for highly excited states, in which it is simultaneously recognizable as the thermodynamic instability associated with negative specific heat.
We have therefore achieved, at least in one example, the goal of finding a system which exhibits a non-trivial thermodynamic phenomenon which can also be fully understood in mechanical terms. Such a simultaneous description on both mechanical and thermodynamical levels must in principle always be possible, for any system; the simplicity of the many-body models which are realizable with ultracold atoms has allowed both descriptions to be made explicit in this case. This promising adiabatic insight into the microphysical basis of an important thermodynamic phenomenon has only been achieved in a simple limit, however. Beyond the mean-field or perturbative regimes, the quantum many-body theory of large BH arrays with large particle number and high excitation is extremely challenging, even with the best available computations. Spontaneous energy concentration is a robust enough mean-field effect, however, that it must surely extend in some form into more strongly quantum mechanical regimes, which can be probed experimentally.
We also note that, although dynamical chaos is often invoked as a justification for the emergence of thermodynamic behavior from pure mechanics, its role is far from understood [47]. Our two-mode subsystems are perfectly integrable in isolation, but the large aggregate system in which many of them are coupled can certainly feature chaotic dynamics. Our study thus neither challenges nor supports the importance of chaos in the emergence of thermodynamics; but it does suggest that only rather weak chaos may turn out to be needed. Comparison of our case with models in which the weakly coupled subsystems are themselves non-integrable would be interesting.
With these views toward further investigations of stronger chaotic and quantum effects, our main contribution here is to have shown how much there is to be learned about the mesoscopic interplay between (quantum) mechanics and thermodynamics, by exploring the dramatic phenomenon of spontaneous energy concentration, with quantum gas experiments on coupled BH systems. We can bring the heat that kindles suns into the ultracold laboratory.