Abstract
The classification of topological states of matter depends on spatial dimension and symmetry class. For non-interacting topological insulators and superconductors, the topological classification is obtained systematically and non-trivial topological insulators are classified by either integer or Z2. The classification of interacting topological states of matter is much more complicated and only special cases are understood. In this paper we study a new class of topological superconductors in (2 + 1) dimensions which has time-reversal symmetry and a 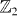 spin conservation symmetry. We demonstrate that the superconductors in this class are classified by
spin conservation symmetry. We demonstrate that the superconductors in this class are classified by 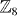 when electron interaction is considered, while the classification is
when electron interaction is considered, while the classification is 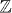 without interaction.
without interaction.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Topological states of matter (TSM) are ground states of gapped quantum systems which cannot be adiabatically tuned to a topologically trivial state without going across a phase transition. The first TSM discovered in nature are integer and fractional quantum Hall states [1, 2]. Many TSM have gapless surface states on the boundary which are topologically protected within the given symmetry class. For example, the integer quantum Hall states have chiral fermion edge states which propagate unidirectionally along the edge of the two-dimensional (2D) system, and are robust against arbitrary perturbation as long as the bulk remains gapped. The number of chiral channels is an integer which determines the Hall conductance and characterizes the corresponding quantum Hall state.
Since the recent discovery of time-reversal invariant topological insulators [3–5]. TSM has been understood much more systematically in generic spatial dimensions and symmetries [6–8]. For gapped non-interacting fermion systems, i.e. band insulators without electron correlation and gapped superconductors in the mean-field theory sense, there are ten symmetry classes in each spatial dimension [9, 10] if we only consider symmetries that preserve the positions of electrons, such as time-reversal symmetry and particle–hole symmetry. In each spatial dimension, TSM exist in five of the ten symmetry classes, which always include three classes with integer classification and two classes with Z2 classification [7, 8]. The topological classification depends on the spatial dimension and symmetry class in a periodic way [8] which originates from the Bott periodicity [11]. When electron interaction is considered, the problem is much more complicated and the topological classification in generic dimensions and symmetry classes has not been completely understood. Topological invariants based on a single-particle Green's function has been proposed for interacting TSM [12–15]. In one dimension (1D), the classification of gapped states has been studied systematically by making use of matrix product states and entanglement spectrum [16, 17]. In particular, Fidkowski and Kitaev [18] proposed an explicit example of 1D time-reversal invariant superconductors for which the topological classification is 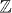 for non-interacting states but is reduced to
for non-interacting states but is reduced to 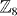 when interaction is considered. In dimensions higher than one, a systematical approach of constructing interacting symmetry-protected topological states (defined as the TSM in a certain symmetry class which becomes trivial when the symmetry is broken) in spin models has been proposed based on group cohomology [19]. The relation between such states and the non-interacting TSMs in generic cases remains an open question1.
when interaction is considered. In dimensions higher than one, a systematical approach of constructing interacting symmetry-protected topological states (defined as the TSM in a certain symmetry class which becomes trivial when the symmetry is broken) in spin models has been proposed based on group cohomology [19]. The relation between such states and the non-interacting TSMs in generic cases remains an open question1.
In this paper, we propose a new class of TSM (labeled by D') which in 2Ds is classified by 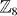 . This symmetry class is defined by two discrete symmetries, the time-reversal symmetry and an additional global
. This symmetry class is defined by two discrete symmetries, the time-reversal symmetry and an additional global 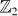 symmetry. Physically, this symmetry class consists of time-reversal invariant superconductors of spinful fermions with the number of spin-up electrons (and also that of spin-down electrons) conserved modular 2. Without interaction, the topological classification is
symmetry. Physically, this symmetry class consists of time-reversal invariant superconductors of spinful fermions with the number of spin-up electrons (and also that of spin-down electrons) conserved modular 2. Without interaction, the topological classification is 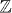 , the same as time-reversal breaking superconductors (class D) in 2D [20]. With electron interactions, we show that the classification is reduced to
, the same as time-reversal breaking superconductors (class D) in 2D [20]. With electron interactions, we show that the classification is reduced to 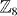 , by analyzing the edge states and topological defects. This state can be considered as a higher dimensional generalization of the
, by analyzing the edge states and topological defects. This state can be considered as a higher dimensional generalization of the 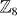 topological superconductor (TSC) proposed in [18].
topological superconductor (TSC) proposed in [18].
2. Definition of the symmetry class and the classification of non-interaction systems
Consider a 2D electron system with the generic Hamiltonian H = H(ciσ,c†iσ), with σ = ↑,↓ two spin components, and i labels the lattice sites. The symmetries we consider are time-reversal symmetry defined by

and the 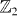 spin conservation symmetry named by R:
spin conservation symmetry named by R:

It should be noticed that T is an anti-unitary symmetry and R is a unitary symmetry. In an explicit form R = (−1)N↓ with N↓ the total number of spin-down electrons. An equivalent definition of T and R symmetries which is basis independent is
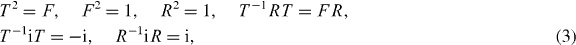
in which F = (−1)N↑+N↓ is the fermion number parity. The second line means that T is anti-unitary and R is unitary. We label the symmetry class defined by symmetries T and R as class D' due to its relation to the class D of time-reversal symmetry breaking superconductors, which will be made clear in the later part of the draft.
Now we consider the simple situation when the Hamiltonian is quadratic in ciσ,c†iσ. Apparently, any term mixing spin-up and -down electrons such as c†i↑cj↓ and ci↑cj↓ is odd under the 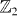 symmetry R, such that the quadratic Hamiltonian Hquad is decoupled into a direct sum of that of the spin-up and -down subsystems:
symmetry R, such that the quadratic Hamiltonian Hquad is decoupled into a direct sum of that of the spin-up and -down subsystems:
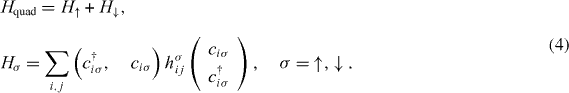
The single-particle Hamiltonians h↑ij and h↓ij are related by the time-reversal invariance condition

Thus all non-interacting states in this class are direct products of spin-up and -down superconductor ground states, and the spin-down state is determined by the spin-up state due to time-reversal symmetry. Consequently, the topological classification of Hquad reduces to that of the spin-up subsystem H↑, which is a Hamiltonian of a generic 2D superconductor, without time-reversal symmetry. (The time-reversal symmetry is recovered only when the spin-down state is also included.)
It is well known that the 2D time-reversal breaking superconductors are classified by integer, in the same way as integer quantum Hall states [20]. The topological invariant characterizing this class of TSC is the Chern number of the single-particle Hamiltonian. For a translation-invariant system, if we denote |n,k〉 as the eigenstates of the single-particle Hamiltonian h↑, with correspondingly eigenvalues En(k), the Chern number is defined as the total flux of the Berry phase gauge field in the Brillouin zone:  with
with  . For a system with Chern number C1 = N, on an open boundary there are N channels of chiral Majorana edge states, described by the following Hamiltonian:
. For a system with Chern number C1 = N, on an open boundary there are N channels of chiral Majorana edge states, described by the following Hamiltonian:

with k the momentum along the edge and η↑ak the edge state quasiparticle operator which is a superposition of electron and hole operators. η↑ak satisfies the Majorana condition η†↑ak = η↑a,−k so that the edge state fermion is its own anti-particle. In particular, η↑a,k=0 = η†↑a,k=0 is a Majorana zero mode, carrying half of the degree of freedom of a complex fermion [20, 21]. For N > 0 (N < 0) v is positive (negative) respectively, corresponding to left and right moving edge states. For simplicity, we have set the velocity of the Majorana edge states to be the same. Generically the velocity can be different for different a but it does not change the topological properties. According to equation (5) determined by time-reversal symmetry, it can be shown straightforwardly that h↓ and h↑ have opposite Chern number. Correspondingly the edge states of them consist of the same number of Majorana edge states with opposite chirality. For C↑1 = −C↓1 = N > 0, the edge theory of the whole system is
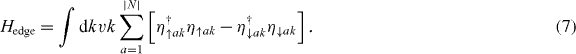
Since η↑(↓)ak is a superposition of c↑(↓), the action of R symmetry on η↑(↓)ak is R−1η↑akR = η↑ak, R−1η↓akR = −η↓ak. Consequently, no mixing term such as η†↑akη↓ak' is allowed in the Hamiltonian Hedge if we consider generic perturbations preserving the R symmetry.
In summary, from the analysis above we conclude that the 2D superconductors with T, R symmetries are classified by integer, and the class labeled by integer N has an edge theory of |N| flavors of non-chiral Majorana fermions, which are protected to be gapless by the two symmetries.
3. The reduction of  to
to  with interaction
with interaction
Now we consider the effect of electron interaction in this system. With interaction the terms mixing spin-up and -down electrons are allowed by the R symmetry, such as a pair hopping term 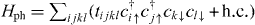 with h.c. denotes the Hermitian conjugate of the first term. The time-reversal symmetry leads to some requirements on the matrix elements tijkl = tklij. Other terms such as c†i↑c†j↑c†k↓c†k↓ can also be considered. To see the consequence of such interaction terms on the
with h.c. denotes the Hermitian conjugate of the first term. The time-reversal symmetry leads to some requirements on the matrix elements tijkl = tklij. Other terms such as c†i↑c†j↑c†k↓c†k↓ can also be considered. To see the consequence of such interaction terms on the 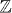 topological invariant, it is most convenient to study the stability of the edge states described by the Hamiltonian (7) under interaction [22].2 In the following we will show that the Hamiltonian (7) with N = 8 can be gapped by an interacting term without breaking the T,R symmetries, so that the classification of the bulk topological states can at most be
topological invariant, it is most convenient to study the stability of the edge states described by the Hamiltonian (7) under interaction [22].2 In the following we will show that the Hamiltonian (7) with N = 8 can be gapped by an interacting term without breaking the T,R symmetries, so that the classification of the bulk topological states can at most be 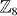 .
.
This conclusion is obtained based on the results of [18] in (1 + 1)-dimensions. It was shown explicitly in [18] that the following interacting term induces a mass to eight channels of free Majorana fermions given by equation (7):
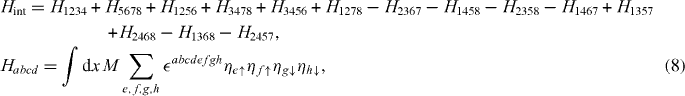
in which the indices a,b,...,h run from 1 to 8, and  abcdefgh is the eight-dimensional totally antisymmetric tensor. For eight Majorana fermions with the same velocity, there is an SO(8) symmetry between the Majorana fermions generated by the operators
abcdefgh is the eight-dimensional totally antisymmetric tensor. For eight Majorana fermions with the same velocity, there is an SO(8) symmetry between the Majorana fermions generated by the operators ![$J_{ab}=\frac 1{4\mathrm {i}}([\eta _{a\uparrow },\eta _{b\uparrow }]+[\eta _{a\downarrow },\eta _{b\downarrow }])$](https://content.cld.iop.org/journals/1367-2630/15/6/065002/revision1/nj465428ieqn24.gif) , and the Majorana fermion operators ηa form vector representation of this SO(8). The interaction term given above breaks the SO(8) symmetry to SO(7), but the SO(7) subgroup is not the one which preserves some vector na of SO(8), but the one which preserves some spinor ψα of SO(8). In the appendix A we provide an explicit explanation why the interaction term (8) leads to such a non-conventional symmetry breaking.
, and the Majorana fermion operators ηa form vector representation of this SO(8). The interaction term given above breaks the SO(8) symmetry to SO(7), but the SO(7) subgroup is not the one which preserves some vector na of SO(8), but the one which preserves some spinor ψα of SO(8). In the appendix A we provide an explicit explanation why the interaction term (8) leads to such a non-conventional symmetry breaking.
It is straightforward to verify that Hint defined in equation (8) preserves both T and R symmetries. The existence of such a mass term suggests that the quadratic Hamiltonian (4) with Chern number N = 8 for spin-up electrons is topologically trivial, since it can be adiabatically deform to a trivial state with N = 0. The adiabatic deformation path can be constructed by considering the N = 8 system on a closed manifold, and creating a trivial N = 0 region on the manifold. By moving the boundary between the two regions one can expand the trivial region until it covers the whole manifold. Since the edge states between the N = 0 and 8 regions can be completely gapped, the whole system remains gapped during this process, so that the N = 8 state is equivalent to N = 0.3 For N > 8 one can add the same mass term for any eight of the Majorana fermions, leading to the conclusion that the Hamiltonians with Chern number N and N − 8 have topologically equivalent edge states. If the edge states for N < 8 is stable, one is lead to the conclusion that the topological classification of T,R invariant TSC is 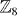 rather than
rather than 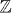 .
.
4. Dimensional reduction and the stability of  classification
classification
Now we present further evidence that the systems with Chern number N = 0,1,...,7 are indeed topologically distinct from each other. Consider an open boundary system and add the following spatially inhomogeneous mass term to the Hamiltonian:

Here 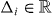 is finite in a neighborhood of the edge, and vanishes in the bulk. The Hamiltonian (9) is a special pairing term where each electron creation or annihilation operator is paired with its time reversal:
is finite in a neighborhood of the edge, and vanishes in the bulk. The Hamiltonian (9) is a special pairing term where each electron creation or annihilation operator is paired with its time reversal: ![$H_\Delta =\sum _{i\sigma }\frac {\mathrm {i}\Delta _i}2[c_{i\sigma }^\dagger \left (T^{-1}c_{i\sigma }^\dagger T\right )+c_{i\sigma } (T^{-1}c_{i\sigma }T)]$](https://content.cld.iop.org/journals/1367-2630/15/6/065002/revision1/nj465428ieqn29.gif) . Such a generic definition of this pairing term is basis independent [23]. Therefore in the low-energy edge theory (7), the pairing term leads to a mass term
. Such a generic definition of this pairing term is basis independent [23]. Therefore in the low-energy edge theory (7), the pairing term leads to a mass term 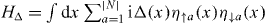 .
.
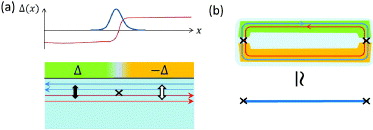
In particular, consider the configuration of Δ(x) with a domain wall where Δ(x) changes its sign, as shown in figure 1(a). This configuration corresponds to a Josephson junction between two s-wave superconductors in proximity with the TSC, as shown in figure 1(a). As is well known, such a mass term domain wall leads to Majorana zero modes localized on the domain wall [24]. For Chern number N there are |N| zero modes on the domain wall. As is known for other symmetry classes, such as the quantum spin Hall state with T-breaking domain wall on the edge [25], such a domain wall of a symmetry breaking mass term can carry fractional quantum numbers (i.e., projective representation of remaining symmetries), in which case it can be used as a probe of the TSM even if electron interaction is considered. For example, in the case of quantum spin Hall insulator the T-breaking mass domain wall on the edge traps a fractional charge [25]. In the current system, to see if the zero modes carry fractional quantum numbers, one can first analyze the symmetry of the system with the domain wall. The mass term HΔ in equation (9) breaks both T and R symmetries, but preserves the combined symmetry 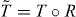 . From the definition of T and R in equations (1) and (2) one can see that
. From the definition of T and R in equations (1) and (2) one can see that 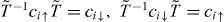 , so that
, so that 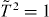 . Thus
. Thus 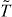 can be considered as the time-reversal symmetry for spinless fermions, which is the symmetry defining the BDI symmetry class [9, 10]. The domain wall zero modes are thus topologically equivalent to the edge zero modes of a 1D TSC in the BDI class [18]. The relation between the domain wall zero modes and the edge state of 1D TSC can be seen most explicitly in the geometry shown in figure 1(b). A strip of 2D TSC with the upper and lower surface states gapped by opposite mass Δ and −Δ can be considered as a 1D TSC in the BDI class. With open boundary in the horizontal direction, the end of the 1D system becomes a mass domain wall between Δ and −Δ which has Majorana zero modes if the topological invariant is N ≠ 0 mod 8. In [16, 17, 26] it was shown that the edge zero modes of a 1D system are classified by projective representations of the symmetry group, or equivalently, the second cohomology of the symmetry group. Here the symmetries of the system are
can be considered as the time-reversal symmetry for spinless fermions, which is the symmetry defining the BDI symmetry class [9, 10]. The domain wall zero modes are thus topologically equivalent to the edge zero modes of a 1D TSC in the BDI class [18]. The relation between the domain wall zero modes and the edge state of 1D TSC can be seen most explicitly in the geometry shown in figure 1(b). A strip of 2D TSC with the upper and lower surface states gapped by opposite mass Δ and −Δ can be considered as a 1D TSC in the BDI class. With open boundary in the horizontal direction, the end of the 1D system becomes a mass domain wall between Δ and −Δ which has Majorana zero modes if the topological invariant is N ≠ 0 mod 8. In [16, 17, 26] it was shown that the edge zero modes of a 1D system are classified by projective representations of the symmetry group, or equivalently, the second cohomology of the symmetry group. Here the symmetries of the system are 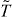 and the fermion number parity F which is always a symmetry for fermion systems.
and the fermion number parity F which is always a symmetry for fermion systems. 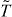 and F commutes with each other, and form the symmetry group of
and F commutes with each other, and form the symmetry group of 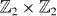 . There are eight distinct projective representations of this group which corresponds to N = 0,1,...,7 number of Majorana zero modes. Therefore from the results on 1D BDI class, one can conclude that the domain wall zero modes for N = 1,2,...,7 are stable.
. There are eight distinct projective representations of this group which corresponds to N = 0,1,...,7 number of Majorana zero modes. Therefore from the results on 1D BDI class, one can conclude that the domain wall zero modes for N = 1,2,...,7 are stable.
Figure 1. (a) Illustration of the T-breaking mass domain wall along the edge of the 2D TSC. The mass is induced by a proximity effect of the TSC with an s-wave superconductor, and the mass domain wall corresponds to a Josephson junction between two such s-wave superconductors (see text). (b) Illustration of a strip of 2D TSC with the edge states on the two edges gapped by opposite mass terms m and −m, which is topologically equivalent to a 1D TSC in the BDI class, with Majorana zero modes at the end.
Download figure:
Standard image High-resolution imageSince the 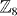 classification of such Majorana zero modes is given by the topological classification of 1D BDI class, naively it seems possible to drive a boundary phase transition which changes the number of domain wall Majorana zero modes without affecting the bulk. However, the special mass term (9) guarantees that such boundary phase transition cannot occur, so that the classification of domain wall zero modes is indeed a bulk property. To prove this statement, it is sufficient to prove that a trivial bulk state coupled to the edge mass term (9) is always topologically trivial. Since the bulk is trivial, the system is equivalent to two purely 1D wires along the upper and lower half of the edge in the D' class, with the Hamiltonians Hu(l) = Hu(l)0 ± HΔ. Here Hu(l)0 preserves T and R symmetries, and HΔ is the pairing term in equation (9) with a constant amplitude Δ(x) = Δ. This mass term has the following essential property:
classification of such Majorana zero modes is given by the topological classification of 1D BDI class, naively it seems possible to drive a boundary phase transition which changes the number of domain wall Majorana zero modes without affecting the bulk. However, the special mass term (9) guarantees that such boundary phase transition cannot occur, so that the classification of domain wall zero modes is indeed a bulk property. To prove this statement, it is sufficient to prove that a trivial bulk state coupled to the edge mass term (9) is always topologically trivial. Since the bulk is trivial, the system is equivalent to two purely 1D wires along the upper and lower half of the edge in the D' class, with the Hamiltonians Hu(l) = Hu(l)0 ± HΔ. Here Hu(l)0 preserves T and R symmetries, and HΔ is the pairing term in equation (9) with a constant amplitude Δ(x) = Δ. This mass term has the following essential property:
- For an arbitrary quadratic Hu(l)0 in D' class, the Hamiltonian Hu(l) always has a gap Eg ⩾ |Δ|.
This property is a direct consequence of the time-reversal symmetry which determines the form of HΔ. The detailed proof of this property is given in the appendix B. Since the open boundary system has a finite gap, there is no Majorana zero modes and the system must be topologically trivial. For Hu(l)0 with interaction, if the interaction strength V is much weaker than |Δ|, the gap remains robust and thus the system remains trivial. Exactly parallel discussion can be made to a topologically non-trivial bulk state. For a bulk state with gap Ebulk and interaction strength V ≪Ebulk, one can always choose the boundary mass term with V ≪|Δ| ≪ Ebulk, in which case the argument above demonstrates that no boundary phase transition can occur, and thus the domain wall Majorana zero modes are completely determined by the bulk state. In summary, we reach the conclusion that the 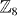 classification of 2D D' class is robust at least for weak interaction strength. In principle, it is possible to have new phases in strong interaction that is not adiabatically connected to any of the eight weak interacting states.
classification of 2D D' class is robust at least for weak interaction strength. In principle, it is possible to have new phases in strong interaction that is not adiabatically connected to any of the eight weak interacting states.
It is helpful to make more comments on the relation of the N = 8 edge state problem with the 1D BDI class. A most generic quadratic mass term allowed in the edge theory has the form of 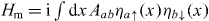 . The Hermitivity of the Hamiltonian and
. The Hermitivity of the Hamiltonian and  symmetry requires the matrix A to be real and symmetric. Such a massive Majorana fermion can be viewed as a 1D TSC in BDI class with a topological invariant N = Ind(A) defined as the number of negative eigenvalues of mass matrix A. If only quadratic mass terms Hm are considered, the topological classification would be
symmetry requires the matrix A to be real and symmetric. Such a massive Majorana fermion can be viewed as a 1D TSC in BDI class with a topological invariant N = Ind(A) defined as the number of negative eigenvalues of mass matrix A. If only quadratic mass terms Hm are considered, the topological classification would be  since some eigenvalues of Aab must vanish in order to change the index N, leading to a topological phase transition. However, the quartic mass term Hint given in equation (8) is possible for N = 8, such that it is possible to have a cross over between two Aab with index different by 8 [18]. For example, consider the mass term
since some eigenvalues of Aab must vanish in order to change the index N, leading to a topological phase transition. However, the quartic mass term Hint given in equation (8) is possible for N = 8, such that it is possible to have a cross over between two Aab with index different by 8 [18]. For example, consider the mass term 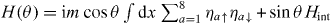 . For m > 0, the Hamiltonian at θ = 0,π has index 0 and 8, respectively. By adding the interaction term Hint, one obtains an interpolation between H(0) and H(π) without closing the gap. On the edge of 2D D' class TSC, the additional R symmetry requires the quadratic mass term Aab to vanish, so that the edge theory can be viewed as the topological phase transition theory between different topological states in the (1 + 1)-D BDI class. At presence of the quartic mass term Hint, there are only eight distinct phases in (1 + 1)-D BDI class. Thus there are eight distinct phase transition theories at presence of the R symmetry, which becomes the robust topological edge states in the (2 + 1)-D case classified by
. For m > 0, the Hamiltonian at θ = 0,π has index 0 and 8, respectively. By adding the interaction term Hint, one obtains an interpolation between H(0) and H(π) without closing the gap. On the edge of 2D D' class TSC, the additional R symmetry requires the quadratic mass term Aab to vanish, so that the edge theory can be viewed as the topological phase transition theory between different topological states in the (1 + 1)-D BDI class. At presence of the quartic mass term Hint, there are only eight distinct phases in (1 + 1)-D BDI class. Thus there are eight distinct phase transition theories at presence of the R symmetry, which becomes the robust topological edge states in the (2 + 1)-D case classified by 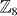 .
.
At the end of this section, we would like to further clarify why we have not studied mass terms other than the s-wave pairing term (9). Other mass terms can certainly be written down which also gap the edge states. For example, for the edge theory we can write 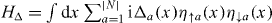 with different pairing term Δa for different flavors a. However, it has been shown explicitly in the last section that the edge state of N = 8 system can be gapped without breaking T and R symmetries, so that the system can be adiabatically deform to the N = 0 trivial state. Consequently, the only two possibilities left are (i) the topological classification is Z8; and (ii) the topological classification is some quotient group of Z8, if some of the N = 1,2,...,7 phases are actually trivial. Therefore as long as we can find a suitable mass term that proves the stability of the eight phases—which is what has been demonstrated above using the pairing term (9)—it is sufficient to conclude that the topological classification is Z8. This is why we did not discuss other mass terms. If we choose other mass terms, we may get a weaker condition, which is not contradictory with the conclusion above, but does not provide the complete topological classification. For example if we consider the even topological classes N = 2n, and give the flavors a = 1,2,...,n pairing Δ(x) and the rest a = n + 1,n + 2,...,2n opposite pairing −Δ(x), and Δ(x) has the same configuration as is shown in figure 1, the corresponding 1D superconductor is in BDI class but with topological invariant 0 (due to cancelation of the two groups with opposite sign of pairing). Therefore we are not able to conclude whether the N = 2n classes are trivial or non-trivial.
with different pairing term Δa for different flavors a. However, it has been shown explicitly in the last section that the edge state of N = 8 system can be gapped without breaking T and R symmetries, so that the system can be adiabatically deform to the N = 0 trivial state. Consequently, the only two possibilities left are (i) the topological classification is Z8; and (ii) the topological classification is some quotient group of Z8, if some of the N = 1,2,...,7 phases are actually trivial. Therefore as long as we can find a suitable mass term that proves the stability of the eight phases—which is what has been demonstrated above using the pairing term (9)—it is sufficient to conclude that the topological classification is Z8. This is why we did not discuss other mass terms. If we choose other mass terms, we may get a weaker condition, which is not contradictory with the conclusion above, but does not provide the complete topological classification. For example if we consider the even topological classes N = 2n, and give the flavors a = 1,2,...,n pairing Δ(x) and the rest a = n + 1,n + 2,...,2n opposite pairing −Δ(x), and Δ(x) has the same configuration as is shown in figure 1, the corresponding 1D superconductor is in BDI class but with topological invariant 0 (due to cancelation of the two groups with opposite sign of pairing). Therefore we are not able to conclude whether the N = 2n classes are trivial or non-trivial.
5. Conclusion and discussions
In summary we have defined a new class D' of TSC defined by two discrete symmetries T and R satisfying the conditions in equation (3). We demonstrate that TSC in D' class has a topological classification of Z8. The (2 + 1)-D D' TSC is related to the (1 + 1)-D BDI class of TSC with symmetry 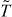 by adding one spatial direction and one additional discrete symmetry T. Such a relation between TSM in different dimensions applies to more generic cases. In non-interacting fermion systems, the single-particle Hamiltonian and anti-unitary symmetry generators anti-commute with each other and form a Clifford algebra, which determines the topological classification [8]. For eight of the ten symmetry classes that correspond to real Clifford algebras, the topological classification stays the same when the spatial dimension is increased by 1 and a new anti-unitary symmetry satisfying T2 = −1 is added to the system, which anti-commutes with all existing generators of the Clifford algebra. With interaction the single-particle Hamiltonian and Clifford algebra approach do not apply, but our result shows that the relation between TSM in different dimensions with different symmetries can be generalized by considering the domain wall geometry illustrated in figure 1(b). Consider a (d + 1)-dimensional system with one of the dimensions (the vertical direction in figure 1(b)) small compared to other dimensions. When the added symmetry (T in the case of D' class) in the d + 1 dimensional system is broken on the boundary but preserved in the bulk, generically the surface states are gapped and such a (d + 1)-dimensional system can be viewed as a d-dimensional TSM in the known symmetry class. However there are always two ways to gap the surface states, which corresponds to doing a T transformation to the boundary symmetry breaking terms. A domain wall forms between the two regions with opposite symmetry breaking mass terms, as is shown in figure 1(b). If the d-dimensional TSM obtained in this way is topological non-trivial, the domain wall must carry gapless modes which are topologically equivalent to the boundary states of the d-dimensional TSM. Following the same reasoning as we did for 2D D' class, for weak interacting states the domain wall gapless modes are completely determined by the bulk and can be used to characterize the bulk topological invariant.
by adding one spatial direction and one additional discrete symmetry T. Such a relation between TSM in different dimensions applies to more generic cases. In non-interacting fermion systems, the single-particle Hamiltonian and anti-unitary symmetry generators anti-commute with each other and form a Clifford algebra, which determines the topological classification [8]. For eight of the ten symmetry classes that correspond to real Clifford algebras, the topological classification stays the same when the spatial dimension is increased by 1 and a new anti-unitary symmetry satisfying T2 = −1 is added to the system, which anti-commutes with all existing generators of the Clifford algebra. With interaction the single-particle Hamiltonian and Clifford algebra approach do not apply, but our result shows that the relation between TSM in different dimensions with different symmetries can be generalized by considering the domain wall geometry illustrated in figure 1(b). Consider a (d + 1)-dimensional system with one of the dimensions (the vertical direction in figure 1(b)) small compared to other dimensions. When the added symmetry (T in the case of D' class) in the d + 1 dimensional system is broken on the boundary but preserved in the bulk, generically the surface states are gapped and such a (d + 1)-dimensional system can be viewed as a d-dimensional TSM in the known symmetry class. However there are always two ways to gap the surface states, which corresponds to doing a T transformation to the boundary symmetry breaking terms. A domain wall forms between the two regions with opposite symmetry breaking mass terms, as is shown in figure 1(b). If the d-dimensional TSM obtained in this way is topological non-trivial, the domain wall must carry gapless modes which are topologically equivalent to the boundary states of the d-dimensional TSM. Following the same reasoning as we did for 2D D' class, for weak interacting states the domain wall gapless modes are completely determined by the bulk and can be used to characterize the bulk topological invariant.
We would like to emphasize an important difference between the cases of interacting and non-interacting systems. For non-interacting TSM, the D class with no symmetry and the D' class with T,R symmetries are completely equivalent, but they are distinct in interacting systems. This is consistent with the fact that the edge domain wall construction only works when a proper discrete symmetry is added, rather than removed. More systematical discussion on this dimensional reduction approach to TSM is reserved for future works.
A natural question is how to realize the D' class in real materials. One possible class of systems is inversion symmetric 2D films. The inversion symmetry suppresses the spin-flip terms such as the Rashba term, leading to an approximate realization of the D' class. More detailed study to this problem will be left for future work.
Acknowledgments
I acknowledge helpful discussions with Lukas Fidkowski and Alexei Kitaev. This work is supported by the Packard Foundation. Recently I became aware of several independent approaches to similar 2D TSM classified by 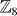 [27–29].
[27–29].
Appendix A.: Further analysis on the interaction Hamiltonian (8)
In this appendix we provide an explicit explanation on the symmetry property of the interaction term (8). The analysis is already presented in [18], but we would like to provide an alternative illustration that is hopefully simpler and more explicit.
To see the symmetry breaking induced by the interaction term (8), we introduce the Clifford algebra Cliff(8,0) with the generators Γa,a = 1,2,...,8 satisfying

Γa can be represented by Hermitian matrices. If we do not require the representation of Clifford algebra to be real, the minimal dimension of faithful representation for the algebra Cliff(2n,0) is 2n. If we require the representation to be real Γa = Γ*a, usually the minimal dimension is larger than 2n. The special property of Cliff(8,0) is that the faithful representation with minimal dimension 24 = 16 is also real. To obtain an explicit understanding, one can consider the following matrix representation of Γa:

Here νi,σi,τi,μi are matrices in four independent 2 × 2 spaces, which are defined as the Pauli matrices for i = x,y,z, and 2 × 2 identity matrices for i = 0. The multiplication in the equation above shall be understood as direct product, so that Γa are 16 matrices. It can be directly verified that this representation of Γa is real, and satisfies the Clifford algebra defined in equation (A.1).
We define the generators Tab of vector representation of SO(8) as

A generic 8 × 8 orthogonal matrix is written as ![$O=\exp [\mathrm {i}\,T_{ab}\theta ^{ab}]$](https://content.cld.iop.org/journals/1367-2630/15/6/065002/revision1/nj465428ieqn48.gif) . The spinor representation of SO(8) is generated by the commutators Γab = [Γa,Γb]/4 i. The elements of the spinor representation are
. The spinor representation of SO(8) is generated by the commutators Γab = [Γa,Γb]/4 i. The elements of the spinor representation are ![$U=\exp [\mathrm {i}\,\Gamma _{ab}\theta ^{ab}]$](https://content.cld.iop.org/journals/1367-2630/15/6/065002/revision1/nj465428ieqn49.gif) . Γa carries the vector representation of SO(8) under the similarity transformation defined by Γa → U−1ΓaU ≡ OabΓb. In the choice of representation (A.2), all Γab have the form of Γab = ν0... or Γab = νz.... Consequently, all Γab are block diagonal with two 8 × 8 blocks. In other words, the spinor representation is reducible. The two 8 × 8 blocks are the spinor representation and the conjugate spinor representation of SO(8). Moreover, because Γa is real, Γab is purely imaginary and the rotation in the spinor representation U is real. If we denote
. Γa carries the vector representation of SO(8) under the similarity transformation defined by Γa → U−1ΓaU ≡ OabΓb. In the choice of representation (A.2), all Γab have the form of Γab = ν0... or Γab = νz.... Consequently, all Γab are block diagonal with two 8 × 8 blocks. In other words, the spinor representation is reducible. The two 8 × 8 blocks are the spinor representation and the conjugate spinor representation of SO(8). Moreover, because Γa is real, Γab is purely imaginary and the rotation in the spinor representation U is real. If we denote

one can define the mappings from vector representation to the spinor representations
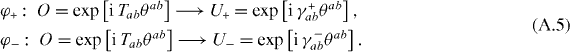
Because U± are also real orthogonal matrices, the two maps φ± are isomorphisms between the vector representation and the spinor representations. This is the so-called triality property of SO(8).
Now we consider eight Majorana fermion operators ηa. The Hilbert space of such as system is 16 dimensional, the same as that of four complex fermions. Since ηa satisfies the Clifford algebra in equation (A.1), we can take a basis in the Hilbert space so that the matrix representation of operators ηa is Γa. The time-reversal symmetry 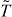 acts on ηa as
acts on ηa as  . Therefore in the representation given in equation (A.2), one can take the time-reversal symmetry to be
. Therefore in the representation given in equation (A.2), one can take the time-reversal symmetry to be 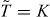 which is the complex conjugation. Now we want to define a time-reversal invariant Hamiltonian in this Hilbert space with a unique ground state. The simplest choice is a projection operator
which is the complex conjugation. Now we want to define a time-reversal invariant Hamiltonian in this Hilbert space with a unique ground state. The simplest choice is a projection operator

which has all entries vanishing except the lower right corner. Such a projector Hamiltonian breaks the SO(8) of the lower 8 × 8 block to SO(7). However, this SO(7) is the SO(7) which rotates the first seven columns of the lower 8 × 8 block. This is not the usual SO(7) subgroup of SO(8) which preserves a given vector. Instead, it is the subgroup that preserves a given spinor (0,0,...,1).
We would like to express such a Hamiltonian in the Majorana fermion operators ηa, i.e. Γa in this representation. In general, a complete basis of 16 × 16 real matrices can be obtained by multiplying different Γa. The set of {1,Γa,ΓaΓb,ΓaΓbΓc,...,Γ1Γ2....Γ8} (with all a,b,c... in each term different from each other) contains exactly
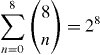
independent real matrices. Because Γa are all off-diagonal, the multiplication of even Γa is non-vanishing in the diagonal 8 × 8 blocks and those of odd Γa is non-vanishing in the off-diagonal 8 × 8 blocks. In this set, the matrices with non-zero overlap with Hproj are those which are both symmetric and block-diagonal. Besides the identity 1, there are only two set matrices satisfying these two conditions: ΓaΓbΓcΓd and F = Γ1Γ2...Γ8. In the representation (A.2) F = −νz. Physically, F is the fermion number parity. Since the Hamiltonian (A.6) vanishes in the upper 8 × 8 block, we can focus on the basis of the lower 8 × 8 block obtained by the projection

The antisymmetric tensor  abcdefgh is introduced to extract only the components of ΓaΓbΓcΓd with a,b,c,d all different from each other. γabcd satisfies the orthogonality condition
abcdefgh is introduced to extract only the components of ΓaΓbΓcΓd with a,b,c,d all different from each other. γabcd satisfies the orthogonality condition
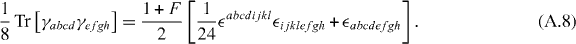
For example 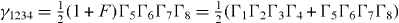 , which is orthogonal to other γabcd except γ5678 = γ1234. The number of independent γabcd is therefore
, which is orthogonal to other γabcd except γ5678 = γ1234. The number of independent γabcd is therefore  which is consistent with the number of symmetric traceless 8 × 8 matrices
which is consistent with the number of symmetric traceless 8 × 8 matrices 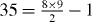 . Using the orthogonality condition one can expand the Hamiltonian to
. Using the orthogonality condition one can expand the Hamiltonian to
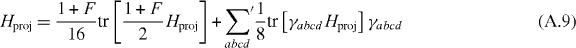
with the first term taking care of the trace part and the second term an expansion of the traceless part in γabcd. Here the sum  stands for the sum over the 35 independent groups of abcd. For the particular Hamiltonian Hproj, we have
stands for the sum over the 35 independent groups of abcd. For the particular Hamiltonian Hproj, we have

which is the last diagonal component of γabcd. In the representation given by equation (A.2), γabcd is also a direct product of Pauli matrices or identity. Consequently, the 16,16 component is only non-zero if γabcd = νiσjτkμl with all i,j,k,l = 0 or z. Therefore, there are only 7 = 23 − 1 terms with non-zero contributions. They can be explicitly found as
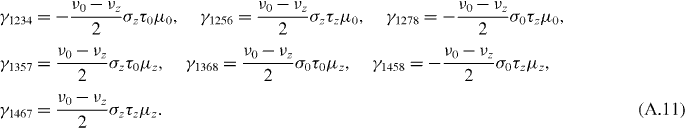
Therefore, we obtain
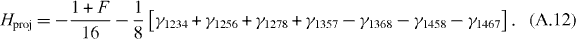
γabcd can be written in the product of Γa, which in the operator form are ηa. For example 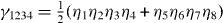 . Compare equation (A.12) with equation (8) one finds that except for a trivial constant term, they are identical if we only take the zero modes ηa,k=0↑(↓) in equation (8). Consequently, we have demonstrated that the Hamiltonian (8) leads to a unique ground state in the Hilbert space of the eight Majorana zero modes.
. Compare equation (A.12) with equation (8) one finds that except for a trivial constant term, they are identical if we only take the zero modes ηa,k=0↑(↓) in equation (8). Consequently, we have demonstrated that the Hamiltonian (8) leads to a unique ground state in the Hilbert space of the eight Majorana zero modes.
Appendix B.: More details on the gap induced by the mass term in equation (9)
In this section we will prove the essential property given in section 4:
- For an arbitrary quadratic Hu0 in D' class, the Hamiltonian Hu = Hu0 + HΔ always has a gap Eg ⩾ |Δ|.
To discuss the generic situation we write down the most generic lattice model form of Hu0. If the system is non-interacting, Hu0 can be generically written in the Majorana basis as

with i,j labeling all lattice sites and all internal band indices. The symmetry operations T and R act on the Majorana operators ηi as

The matrices 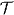 and
and 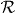 satisfy
satisfy
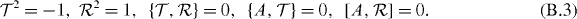
The mass term HΔ is defined by
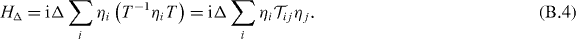
Therefore, the total Hamiltonian is
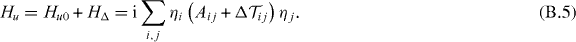
Since 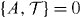 , the single-particle Hamiltonian
, the single-particle Hamiltonian 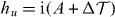 satisfies
satisfies

Therefore h2u − Δ2 is semi-positive definite for any A, and thus all eigenvalues En of hu satisfy |En| ⩾ |Δ|. The derivation above proves that any quadratic Hamiltonian Hu which is a sum of an arbitrary T, R invariant Hamiltonian Hu0 and the special mass term HΔ is guaranteed to have a finite gap |Δ|. Therefore Hu as a chain with open boundary can never have any topological edge states. In other words, we have proved that any Hu with the form of Hu = Hu0 + HΔ is topological trivial. The same proof applies to Hl. Therefore, we reach the conclusion that in non-interacting systems in  class with the boundary mass term HΔ, there is no purely boundary contribution to the domain wall Majorana zero modes, and the number of Majorana zero mode is uniquely determined by the topological invariant N of the bulk.
class with the boundary mass term HΔ, there is no purely boundary contribution to the domain wall Majorana zero modes, and the number of Majorana zero mode is uniquely determined by the topological invariant N of the bulk.
Footnotes
- 1
- 2
For similar discussions in the edge state of topological insulators, see [22].
- 3
I acknowledge a private communication with Alexei Kitaev who explained this proof of bulk–boundary relation for generic symmetry protected topological states.