Abstract
We propose a method to infer the single-particle entropy of bosonic atoms in an optical lattice and to study the local evolution of entropy, spin squeezing and entropic inequalities for entanglement detection in such systems. This method is based on experimentally feasible measurements of non-nearest-neighbour coherences. We study a specific example of dynamically controlling atom tunnelling between selected sites and show that this could potentially also improve the metrologically relevant spin squeezing.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
The quest for novel cooling schemes to control the entropy of ultracold atoms in optical lattices is attracting considerable interest because thermal and quantum fluctuations limit the use of these systems for quantum simulation or quantum metrology. For example, the experimental observation of magnetic ordering, a milestone for the quantum simulation of spin systems, is hindered by finite entropy in the system [1–4]. In metrology, finite entropy limits the amount of achievable spin squeezing, a useful resource for quantum-enhanced high precision measurements [5–9]. Not only controlling the entropy is challenging; it is also difficult to measure on a microscopic level. Only in the low atomic filling regime of the Mott-insulating phase a mapping of observable on-site atom number fluctuations to single-particle entropy has been achieved [10], stimulating interest in entanglement detection by entropy measurements [11, 12]. Recent experiments show that individual atoms can now be manipulated on a single-spin level at individual lattice sites [13] and, in principle, the entropy can be locally engineered in order to effectively cool the system [14].
We propose techniques for accurate local detection and control of a single-particle entropy of a bosonic atomic gas in an optical lattice in the large filling regime, opening up novel avenues for estimating entropy-based quantities and engineering entropy. In the case of non-negligible tunnelling of atoms between adjacent sites, access to the inter-site coherence is crucial for the determination of the entropy. An essential ingredient of our proposed entropy measurement is a technique for a spatially resolved measurement of long-range coherence of the lattice system based on a matter-wave homodyne measurement with respect to a reference condensate. Using this method we theoretically show how the entropy and entropic inequalities of entanglement detection can be accurately estimated in experimentally realistic cases [9, 15] by the atom number in individual sites and the relative phase coherence between the atoms in different sites. The proposed coherence measurement may also lead to improved detection of spin squeezing of atoms between different sites, with potential applications to high-precision measurements. It also allows the detection of spin squeezing between non-nearest-neighbour sites and other spatially separated regions. Moreover, we study a specific example of controlling entropy by locally tailoring the trapping potential. We show how the coupling between the high-entropy regions and the rest of the system is adjusted by suddenly applying laser barriers between the central and outermost sites, altering the entropy distribution and affecting spin squeezing in the system. An illustration of the proposed scheme is shown in figure 1 together with the variation of the entropy and the on-site atom number fluctuations in the initial state: the barriers suppress the interactions between the atoms in the central sites and the outer-well atoms that exhibit stronger thermal and quantum fluctuations. We present example simulations in which injecting the laser barriers leads to reduced spin fluctuations and improved spin squeezing. We also find spin squeezing between atoms occupying spatially distant sites.
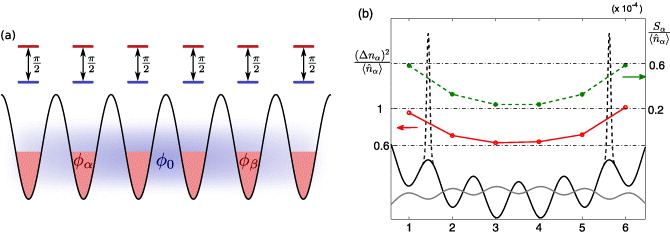
Figure 1. (a) A schematic illustration of the relative phase measurement scheme. (b) Entropy engineering in the optical lattice where the tunnelling of the atoms from the outermost sites to the rest of the system is suppressed, e.g. by applying symmetrically positioned, tightly focused, blue-detuned laser beams. We show the combined lattice potential and the optical barriers (black solid and dashed lines), the initial atom density before the sites are decoupled (solid grey line), the single-particle entropy 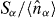 per atom in site α (green dashed line with stars), and the normalized on-site atom number fluctuations
per atom in site α (green dashed line with stars), and the normalized on-site atom number fluctuations  (red solid line with circles) in the initial state for each lattice site. The initial temperature in the numerics is 4 nK.
(red solid line with circles) in the initial state for each lattice site. The initial temperature in the numerics is 4 nK.
Download figure:
Standard image High-resolution imageWe consider Bose-condensed atoms confined in an elongated trap in which we neglect density fluctuations in the radial direction. In the axial direction the atoms experience a combined harmonic and optical lattice potential of a few sites, forming an array of weakly linked Bose–Einstein condensates (BECs). As the lattice height is increased the atom number fluctuations in each site are reduced and the system can exhibit metrologically relevant spin squeezing between the atoms in adjacent sites [9]. Each lattice site occupies a multi-mode BEC and the atom number statistics in such a system is influenced by interactions between several modes in each site [15] (in the simulations we calculate the fluctuations by including nine vibrational modes in each site). By numerically solving for the amplitudes of the wavefunctions |φαj〉, determined by the lattice sites α and vibrational levels j, we can construct the atom number fluctuations, phase coherence and the entire density matrix of the system,

This can then be used to evaluate the single-particle von Neumann entropy

The density matrix elements pαj,βl are determined by the mode populations and their relative phase coherence (see appendix A).
Experimentally, it is challenging to measure populations of the individual vibrational levels or the relative phase coherence between them. In order to circumvent the need to gather such detailed information, we will show that in experimentally realistic situations the single-particle entropy may be estimated by the atom number and the relative phase coherence between the atoms in different sites that are obtained by averaging over the vibrational level structure in each site.
In the experiments [9, 15] a high-precision optical absorption imaging provided site-resolved detection by integration of the imaged atom density. Moreover, local interference measurements were performed after a short condensate expansion time allowing only the atoms from adjacent sites to overlap. The relative phase coherence of the atoms between the adjacent sites was then inferred from the phase variance of the interference pattern. In order to detect the long-range phase coherence in the lattice and extract sufficiently accurate information of the entropy, we propose a matter-wave homodyne measurement scheme for the atoms: we consider a system where the bosonic atoms in the lattice are surrounded by a BEC in a different internal state, e.g. a different hyperfine level for alkali-metal atoms or a metastable triplet state for alkaline-earth or rare-earth metal atoms (figure 1). The atoms in this second internal state are assumed to experience a much weaker lattice potential or weaker interactions, so that their phase coherence is well preserved over the entire lattice length. Experimentally, inter-species interaction might be controlled by a Feshbach resonance or by adjusting the spatial overlap between the two species, e.g. with superlattices [16, 17]. The surrounding BEC serves as a common phase reference in analogy to local oscillators in quantum optical homodyne measurements. The phase coherence of the atoms in each lattice site can be locally determined by interfering the atoms with the reference condensate, e.g. by Raman transitions between the hyperfine levels [18]. Due to negligible phase fluctuations in the reference condensate, local interference measurements of the lattice atoms with the reference condensate provide information about the relative phase fluctuations between the atoms in distant sites. The proposed scheme has the advantage of precise coherence readout by particle counting as experimentally problematic shot-to-shot fluctuations of the magnetic field (which lead to excess phase fluctuations) do not disturb such measurements as long as they are spatially homogeneous. The measurement method could also be suitable for two-dimensional lattice systems when combined with recently developed high-resolution imaging techniques [10, 19].
In order to demonstrate how the long-range coherence and atom number detection can be used to infer locally a single-particle entropy and spin squeezing in an experimentally realistic system we study a specific example of dynamically adjusting the atom tunnelling between central and outermost sites (see figure 1). We assume that the atoms are initially confined in a thermal equilibrium state in a shallow lattice. We then simulate the resulting dynamics when the coupling of the outermost sites to the rest of the system is suppressed by a rapid injection of laser barriers, followed by a slow ramp up of the lattice potential. The increase in the lattice depth results in reduced atom number fluctuations and stronger spin squeezing between atoms in adjacent sites. The laser barriers alter the entropy distribution in the system, as the initial thermal fluctuations in the trap are not uniform (figure 1). Our numerical simulations are based on the truncated Wigner approximation (TWA) [20–27], using an approach similar to the one introduced in [15]. Here thermal and quantum fluctuations of the atoms in the stochastic initial state are calculated by self-consistently solving the ground-state and excited-state populations within the Hartree–Fock–Bogoliubov approximation [28, 29]. During the time dynamics the field amplitudes in the wavefunction basis |φαj〉 are obtained by projecting from the numerically calculated stochastic Wigner field (see appendix A).
We take the experimental parameters that were used to observe spin squeezing between the atoms in adjacent sites [9] in which case N = 5300 atoms were confined in a combined one-dimensional (1D) lattice potential, with the spacing d ≃ 5.7 μm, and an elongated harmonic trap with the frequencies ω ≃ 2π × 21 Hz and ω⊥ ≃ 2π × 427 Hz (ω ≪ ω⊥), so that about 95% of the atoms occupied the six central sites. In [15] the 1D TWA model provided a good qualitative agreement with the experimental findings of the on-site and the relative atom number fluctuations. Here we use the same approach with the potential

The initial lattice height of 24ER (with the recoil energy ER = ℏ2π2/2md2) is slowly turned up to 72ER. We study two different ramping speeds 15.6 and 17.2 Hz ms−1. The strength of the nonlinear atom–atom interaction is given by g1DN = 487ℏωl, where g1D = 2ℏω⊥a, a is the s-wave scattering length and l = (ℏ/mω)1/2. We consider the selection of the four central sites by injecting narrow, blue-detuned laser beams, or a scissors potential, before the ramping up of the lattice. The laser potential can be modelled by two symmetric Gaussian intensity distributions centered at ±xb
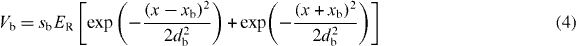
with the waist 2db = 600 nm (1/e2 intensity radius) that can be achieved by diffraction-limited focusing of a laser with wavelength in the visible light region. We vary the barrier height sb and the cutting is fast compared to any other time scale so that the system has no time to relax during the process.
We evaluate the entropy per atom SI in the central four wells and compare this to the entropy per atom ST in the full system. The effect of different strengths of the scissors potential is shown in figure 2 by displaying the entropy in different cases at the end of the lattice ramping. The simulation results of the barrier injection provide an example that demonstrates how a single-particle entropy can be engineered in a non-equilibrium process by laser barriers. Without scissors SI < ST, since in a combined optical lattice and harmonic trap thermal phonon excitations and entropy are mostly concentrated on the outermost sites. Decoupling those sites from the rest of the system therefore reduces the effect of higher excitation modes. For weak scissors (sb ≲ 60), the entropy does not notably increase and SI remains lower than the value of ST without the potential barriers. In the insets in figure 2 we display the ratio SI/ST. We find an increasing total entropy (but decreasing SI/ST) for strong scissor potentials owing to excitations induced by injected barriers. A detailed investigation of these excitations and resulting entropy waves, which is beyond the scope of the present work, could in itself provide an interesting further study of entropy phenomena in a coupled multi-mode BEC system.
Figure 2. Estimates (dashed lines) derived from (5) and exact results (solid lines) for the total entropy per atom ST (lines with crosses) and internal entropy per atom SI (lines with circles) for different strengths of the scissors. Top row: initial temperature T = 4 nK for the ramping speeds (from left to right) 15.6 and 17.2 Hz ms−1. Bottom row: the same for T = 0. The curve for the total entropy per atom is shown together with the sampling error calculated numerically over 800 individual stochastic realizations (see appendix A.1). The insets show the ratio SI/ST (exact results) for each case.
Download figure:
Standard image High-resolution imageAs it is not practical to measure the entropy by detecting all the vibrational mode amplitudes, we propose an entropy estimate based on the lattice site occupation numbers and the long-range coherence values. In figure 2 we compare the entropy calculated from the 6 × 6 density matrix estimate pest(α,β) that is built by measuring separately only the average well populations and the relative phases between the atoms in the six different sites
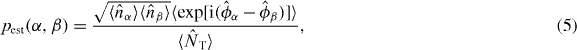
where 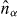 and
and 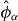 denote the atom number and phase operators in the site α, respectively, and
denote the atom number and phase operators in the site α, respectively, and 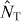 represents the total atom number in the six sites (for calculating these quantities in the numerics, see appendix A). The good agreement between the estimated entropy and the one based on the full basis state representation can be explained by negligible atom number pair correlations between different lattice sites
represents the total atom number in the six sites (for calculating these quantities in the numerics, see appendix A). The good agreement between the estimated entropy and the one based on the full basis state representation can be explained by negligible atom number pair correlations between different lattice sites  and correlations between the phases and atom numbers
and correlations between the phases and atom numbers ![$\langle \sqrt { \hat n_\alpha \hat n_\beta } \exp [\mathrm {i}(\hat \phi _\alpha -\hat \phi _\beta )]\rangle \simeq \langle \sqrt { \hat n_\alpha \hat n_\beta } \rangle \langle \exp [\mathrm {i}(\hat \phi _\alpha -\hat \phi _\beta )]\rangle $](https://content.cld.iop.org/journals/1367-2630/15/6/063035/revision1/nj463978ieqn7.gif) . Similar correlations between the atoms in vibrational states within the same site only weakly affect the entropy. In addition, the loss of phase coherence between the vibrational levels k,l within the same site is small
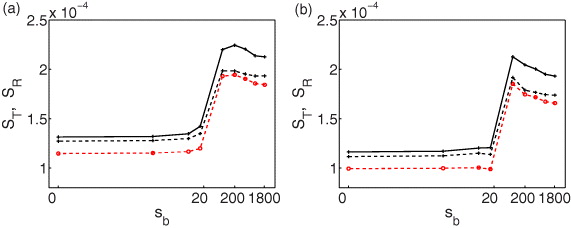
. Similar correlations between the atoms in vibrational states within the same site only weakly affect the entropy. In addition, the loss of phase coherence between the vibrational levels k,l within the same site is small ![$\langle \exp [\mathrm {i}(\hat \phi _{\alpha k}-\hat \phi _{\alpha l})]\rangle \gtrsim 0.99$](https://content.cld.iop.org/journals/1367-2630/15/6/063035/revision1/nj463978ieqn8.gif) . The entropy approximation (5) is better at low temperatures owing to the weaker effect of thermal fluctuations on intra-site correlations between the atoms in different vibrational states. Analogously, stronger quantum fluctuations at stronger nonlinearities can lead to larger deviations from the exact result. Well-known estimates of von Neumann entropy are based on combinations of Rényi entropies [30] (see appendix B). It is therefore interesting to compare our estimate to the Rényi entropy estimates. We show in figure 3 how our entropy estimate based on experimental observables provides for this system a more accurate approximation of the entropy than the estimate SR based on the Rényi entropies.
. The entropy approximation (5) is better at low temperatures owing to the weaker effect of thermal fluctuations on intra-site correlations between the atoms in different vibrational states. Analogously, stronger quantum fluctuations at stronger nonlinearities can lead to larger deviations from the exact result. Well-known estimates of von Neumann entropy are based on combinations of Rényi entropies [30] (see appendix B). It is therefore interesting to compare our estimate to the Rényi entropy estimates. We show in figure 3 how our entropy estimate based on experimental observables provides for this system a more accurate approximation of the entropy than the estimate SR based on the Rényi entropies.
Figure 3. Exact results for the total entropy ST (solid lines) and its estimates (dashed lines) for different strengths of the barrier. The dashed black lines with crosses show the estimate derived from our approximate expression of the density matrix based on direct experimental observables (5); the red lines with circles show the estimate SR from equation (B.4) based on the Rényi entropies. Initial temperature T = 4 nK for the ramping speeds (from left to right) 15.6 and 17.2 Hz ms−1.
Download figure:
Standard image High-resolution imageInjecting laser barriers affects the achievable spin squeezing between the central sites after turning up of the lattice. We define the relative atom number squeezing between the atoms in sites α and β by
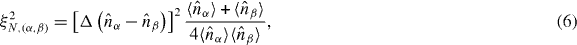
where  denotes the relative atom number fluctuations. The spin squeezing of the atoms
denotes the relative atom number fluctuations. The spin squeezing of the atoms

not only depends on ξ2N,(α,β), but also on the relative phase coherence 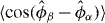 between the atoms. The proposed long-range phase coherence measurement scheme allows the detection of spin squeezing also between non-nearest-neighbour sites and other spatially separated regions. In quantum-enhanced metrology a high-precision quantum interferometer can overcome the standard quantum limit of classical interferometers, provided that ξS,(α,β) < 1 [5–9]. The same condition also implies quantum many-body entanglement in the system [31].
between the atoms. The proposed long-range phase coherence measurement scheme allows the detection of spin squeezing also between non-nearest-neighbour sites and other spatially separated regions. In quantum-enhanced metrology a high-precision quantum interferometer can overcome the standard quantum limit of classical interferometers, provided that ξS,(α,β) < 1 [5–9]. The same condition also implies quantum many-body entanglement in the system [31].
Results for the spin squeezing between the atoms in the two adjacent central wells (sites 3 and 4 of figure 1) at the end of the ramping for two different ramping speeds are shown in figures 4(a) and (b) at the experimentally relevant initial temperature T = 4 nK [15]5. At intermediate scissor strengths sb, when the non-adiabatic injection does not significantly perturb the system (cf figure 2(a)), we find slightly stronger spin (as well as the relative atom number) squeezing than in the system where no laser potential was applied. The spin squeezing between the atoms in non-nearest-neighbour sites (sites 2 and 5 of figure 1) is shown in figures 4(c) and (d). The system exhibits spin squeezing and quantum many-body entanglement between spatially separated regions specified by the distant sites. Weak excitations of the system due to lattice and barrier ramping affect the squeezing as can be seen from the differences between the two ramping speed cases. At stronger scissor strengths the barriers perturb the system, resulting in notably stronger dynamics of the squeezing. We also find that in the region of improved spin squeezing the relative phase coherence is not notably affected. Our analysis provides a proof-of-principle demonstration that adjusting the coupling between the inner and outermost sites could potentially lead to technologies for improving atomic spin squeezing.
Figure 4. Top row: spin squeezing ξ2S between the atoms in the two central lattice sites (sites 3 and 4 in figure 1) for different strengths of the scissors potential, with the ramping speeds (from left to right) 15.6 and 17.2 Hz ms−1. Bottom row: spin squeezing between the atoms in non-nearest-neighbour sites (sites 2 and 5 in figure 1), with the ramping speeds (from left to right) 15.6 and 17.2 Hz ms−1. The dashed line shows the value obtained with no laser beam potential and the grey shaded area represents its uncertainty. The lattice is slowly ramped up to 72ER after the barriers are rapidly introduced in thermal equilibrium at the lattice height 24ER and T = 4 nK.
Download figure:
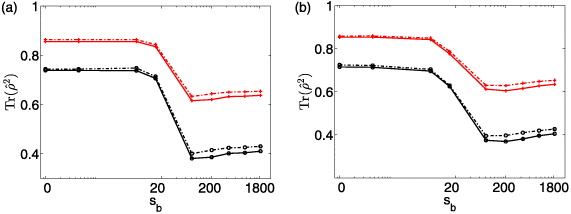
Standard image High-resolution imageSpin squeezing flags the presence of entanglement in the system. As an alternative signature of entanglement one can use entropic inequalities in a bipartitite system [32–34]. The purity Tr(ρ2l(r)) of the reduced density matrices of the left (right) part of the system, compared to the purity of the combined system Tr[(ρl⊗ρr)2], signals entanglement if Tr(ρ2l(r)) < Tr[(ρl⊗ρr)2]. Even though we find spin squeezing in our system, the purity based entanglement inequality is not violated (see appendix C). Remarkably, however, the purity estimates derived from (5) agree well (figure C.1) with the exact results (within 1% for sb ≲ 20 and within 6% for all values of sb), thus potentially providing a direct experimental detection method for the presence of entanglement.
In conclusion, we have shown how the single-particle entropy can be measured and engineered in an optical lattice in the large filling limit. The measurement can be achieved by matter-wave homodyne detection of long-range phase coherence using a reference condensate. The proposed scheme provides a good approximation of the density matrix such that it might be used to detect entanglement via entropic inequalities. We provided a proof-of-principle demonstration that controlling tunnelling in selected locations of the lattice may find quantum technological applications in manipulating metrologically important spin squeezing. Improvement in spin squeezing has practical implications since in the experiments it is typically limited by thermal fluctuations [9]. We may also envisage a procedure where the atomic spin squeezing is improved during every injection cycle of the laser barriers that is followed by an adiabatic adjustment of the trapping potential. Iterating the process could then potentially lead to progressively stronger spin squeezing.
Acknowledgments
We acknowledge discussions with A D Martin and financial support by the Leverhulme Trust.
Appendix A.: Stochastic phase-space method
A.1. Dynamics
In order to simulate the experimental conditions, quantum and thermal fluctuations are included via a classical stochastic field description based on TWA [20–27]. TWA has provided a useful methodology for analysing relative atom number correlations between different lattice sites [15] and, e.g. between different solitons in interferometric applications [35]. The dynamics is unraveled into stochastic trajectories where the initial state of the quantum operator  is represented by an ensemble of classical fields ψW(x,t = 0), sampled according to its Wigner distribution that is determined by the temperature, the atom statistics and the multimode nature of the system. The initial state
is represented by an ensemble of classical fields ψW(x,t = 0), sampled according to its Wigner distribution that is determined by the temperature, the atom statistics and the multimode nature of the system. The initial state 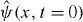 is expanded in terms of the BEC ground state and the excited states as
is expanded in terms of the BEC ground state and the excited states as
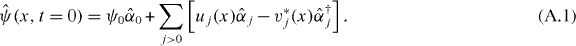
Here 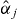 represent the quasiparticle annihilation operators and the quasiparticle mode functions uj(x),vj(x) are calculated by solving self-consistently the coupled Hartree–Fock–Bogoliubov equations [28, 29] for the condensate and non-condensate populations. Owing to large depleted atom number population in the studied system even at zero temperature, the Bogoliubov approximation alone is inaccurate. In addition, several modes in each well contribute to atom statistics, as demonstrated in [15], where the relative atom number fluctuations as a function of the number of initial Hartree–Fock–Bogoliubov modes were calculated.
represent the quasiparticle annihilation operators and the quasiparticle mode functions uj(x),vj(x) are calculated by solving self-consistently the coupled Hartree–Fock–Bogoliubov equations [28, 29] for the condensate and non-condensate populations. Owing to large depleted atom number population in the studied system even at zero temperature, the Bogoliubov approximation alone is inaccurate. In addition, several modes in each well contribute to atom statistics, as demonstrated in [15], where the relative atom number fluctuations as a function of the number of initial Hartree–Fock–Bogoliubov modes were calculated.
The quasiparticle operators are than replaced by stochastic complex variables αj,α*j, obtained by sampling the corresponding Wigner distribution. Each individual stochastic realization is dynamically evolved according to the Gross–Pitaevskii equation and represents a possible outcome of an individual experimental run. Ensemble averages calculated from the TWA numerical results give a statistical description of the dynamics of the system.
A.2. Analysis of correlations
The multi-mode nature of the system and phonon–phonon interactions were shown to be important for the evaluation of the atom number fluctuations even at T = 0 [15]. Multi-mode effects are included by projecting the full stochastic field ψW after the simulations onto a mode function basis formed by energy eigenfunctions of the lattice sites for a given number of energy bands. In the coupled BEC system considered here, we found that the atom number fluctuations of the stochastic field ψW were accurately represented when we included at least nine vibrational mode functions in each well at both T = 0 and 4 nK. This further emphasizes the multi-band nature of the present lattice system.
The projection technique allows to transform the symmetrically ordered expectation values of stochastic representations of quantum operators in the Wigner distribution to normally ordered expectation values [15, 23, 36, 37]. The projected quantities are used in calculation of the atom number statistics and the phase coherence of the system. This also provides a model for the single-particle entropy, evaluated from the single-particle density matrix in the same mode function basis.
We define an eigenmode basis for each site given by the mode functions φη,j(x) with η = 1,...,Nw,j = 1,...,Nm. Here the first index runs over all the sites, with Nw = 6 in our case, and the second index runs over all the vibrational state mode functions in individual sites. We denote the stochastic amplitude for the atoms in the jth vibrational mode of site η as aη,j which can be numerically obtained from the projection of the stochastic field ψW(x,t) as

The macroscopic phase for the atoms in each site may be calculated by averaging over the vibrational states
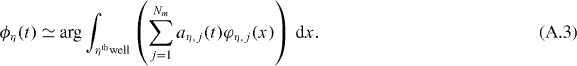
The relative phase coherence between the atoms in the sites η and μ can then be obtained from

where the subscript W denotes the Wigner expectation value over many realizations. The projected amplitudes may be used to calculate the various normally ordered quantum expectation values. The site populations read
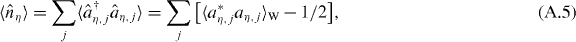
where the summation is over all the vibrational modes in the site η. The contribution −1/2 in the last term is a result of the symmetrical ordering of Wigner expectation values. The on-site atom number fluctuations for site η are similarly given by
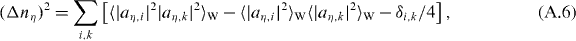
whereas the relative atom number fluctuations between two sites η and μ are obtained from
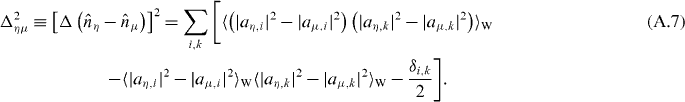
The single-particle density matrix  can be evaluated from the projected amplitudes and it is given by the ensemble average of the stochastic realizations
can be evaluated from the projected amplitudes and it is given by the ensemble average of the stochastic realizations  where
where

The matrix elements p(k)αj,βl are given by

Here  denotes the atom number in the studied six central sites. The diagonal elements are determined by the mode populations and the off-diagonal elements contain information on the phase coherence.
denotes the atom number in the studied six central sites. The diagonal elements are determined by the mode populations and the off-diagonal elements contain information on the phase coherence.
Appendix B.: Entropy
We first calculate the single-particle (generalized von Neumann [38]) entropy S of equation (2) numerically in the projected single-particle basis and then propose an estimate of the entropy based only on direct experimental observables [9, 15]. After injecting the barriers the entropy per atom SI can be evaluated in the new reduced lattice system of the four central sites:

where the prime in the sum indicates a summation over the wells that are inside the scissors and S(x) the entropy density. We compare this with the entropy per atom ST of the full system

where the summation is now over all the sites.
For comparison we also calculate an estimate of the von Neumann entropy provided by a combination of the Rényi entropies. The Rényi entropy of order n is given by [39]

In the limit n → 1, it coincides with the von Neumann entropy. The Rényi entropy can be used to approximate the von Neumann entropy [40]. Specifically, an estimate SR of the von Neumann entropy in terms of the Rényi entropy can be given as

where Su,Sd23,Sd12 are appropriately defined functions of S2 and S3 (see equation (32) in [30]). We find that our entropy estimate that is based on experimental observables provides a more accurate approximation of the entropy than the one based on the Rényi entropies, as shown in figure 3.
Appendix C.: Entanglement
Constructing the density matrix has useful applications, e.g. for identifying bipartite entanglement in the system [32, 34]. A simple test can be done by comparing the purity of the full system described by  to that of a subsystem (described by the reduced density matrix
to that of a subsystem (described by the reduced density matrix 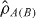 ). Separability of the two subsystems requires Tr
). Separability of the two subsystems requires Tr  . Since there are only a few experimentally accessible tests for entanglement in many body systems (see e.g. [41]), it is interesting to compare the purities obtained from the proposed estimate of the density matrix to the exact results. As an example, we define the left half of the lattice system as subsystem A, the right half as subsystem B. We calculate the purity of the reduced density matrix of the left-half subsystem A and compare it to the purity of the combined bipartite system. As shown in figure C.1 this test does not detect entanglement, but remarkably the results calculated from our density matrix estimate (5) based on experimental observables provides a good approximation of the exact result. The purities agree within 1% for low barrier heights (below sb = 20) and within 6 % for all values of sb.
. Since there are only a few experimentally accessible tests for entanglement in many body systems (see e.g. [41]), it is interesting to compare the purities obtained from the proposed estimate of the density matrix to the exact results. As an example, we define the left half of the lattice system as subsystem A, the right half as subsystem B. We calculate the purity of the reduced density matrix of the left-half subsystem A and compare it to the purity of the combined bipartite system. As shown in figure C.1 this test does not detect entanglement, but remarkably the results calculated from our density matrix estimate (5) based on experimental observables provides a good approximation of the exact result. The purities agree within 1% for low barrier heights (below sb = 20) and within 6 % for all values of sb.
Figure C.1. Exact results (solid lines) and estimates (dashed lines) for the purity of system A ( , red lines with crosses) and of the combined bipartite system C (
, red lines with crosses) and of the combined bipartite system C ( , black lines with circles) for different strengths of the barrier for the ramping speeds (from left to right) 15.6 and 17.2 Hz ms−1. The dashed lines show the estimates derived from our approximate expression of the density matrix based on direct experimental observables (5). Initial temperature T = 4 nK. The relative sampling errors for the exact results are smaller than those shown in figure 2.
, black lines with circles) for different strengths of the barrier for the ramping speeds (from left to right) 15.6 and 17.2 Hz ms−1. The dashed lines show the estimates derived from our approximate expression of the density matrix based on direct experimental observables (5). Initial temperature T = 4 nK. The relative sampling errors for the exact results are smaller than those shown in figure 2.
Download figure:
Standard image High-resolution imageFootnotes
- 5
Note that the actual experimental temperature in three-dimensional trap may be higher than the one corresponding to experimental findings in 1D simulations.