Abstract
The dual symmetry between electric and magnetic fields is an important intrinsic property of Maxwell equations in free space. This symmetry underlies the conservation of optical helicity and, as we show here, is closely related to the separation of spin and orbital degrees of freedom of light (the helicity flux coincides with the spin angular momentum). However, in the standard field-theory formulation of electromagnetism, the field Lagrangian is not dual symmetric. This leads to problematic dual-asymmetric forms of the canonical energy–momentum, spin and orbital angular-momentum tensors. Moreover, we show that the components of these tensors conflict with the helicity and energy conservation laws. To resolve this discrepancy between the symmetries of the Lagrangian and Maxwell equations, we put forward a dual-symmetric Lagrangian formulation of classical electromagnetism. This dual electromagnetism preserves the form of Maxwell equations, yields meaningful canonical energy–momentum and angular-momentum tensors, and ensures a self-consistent separation of the spin and orbital degrees of freedom. This provides a rigorous derivation of the results suggested in other recent approaches. We make the Noether analysis of the dual symmetry and all the Poincaré symmetries, examine both local and integral conserved quantities and show that only the dual electromagnetism naturally produces a complete self-consistent set of conservation laws. We also discuss the observability of physical quantities distinguishing the standard and dual theories, as well as relations to quantum weak measurements and various optical experiments.
Export citation and abstract BibTeX RIS
Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
GENERAL SCIENTIFIC SUMMARY Introduction and background. The dual symmetry between electric and magnetic fields is an intrinsic property of Maxwell equations in free space. This symmetry underlies the conservation of optical helicity, which is associated with the photon's spin component along its direction of propagation. Therefore, the dual symmetry and helicity conservation are intimately related to the separation of spin and orbital degrees of freedom of light (albeit this was not fully appreciated previously). However, in the standard formulation of classical electromagnetism, the field Lagrangian is not dual symmetric. This leads to problematic dual-asymmetric forms of the canonical energy–momentum, spin and orbital angular momentum tensors. Moreover, we show that the components of these tensors conflict with the helicity and energy conservation laws.
Main results. To resolve this discrepancy between the symmetries of the Lagrangian and Maxwell equations, we put forward a dual-symmetric Lagrangian formulation of classical electromagnetism. This dual electromagnetism preserves the form of Maxwell equations, yields meaningful canonical energy–momentum and angular momentum tensors, and ensures a self-consistent separation of the spin and orbital degrees of freedom of light. We make the Noether analysis of the dual and Poincaré symmetries, examine both local and integral conserved quantities, and show that only the dual electromagnetism naturally produces a complete self-consistent set of conservation laws (see figure). We also discuss the observability of physical quantities distinguishing the standard and dual theories, as well as relations to quantum weak measurements and recent optical experiments.
Wider implications. Our results have implications in numerous optical problems involving mechanical properties of light and light–matter interactions. We hope that this work will also motivate the analysis of quantum aspects of dual electromagnetism.
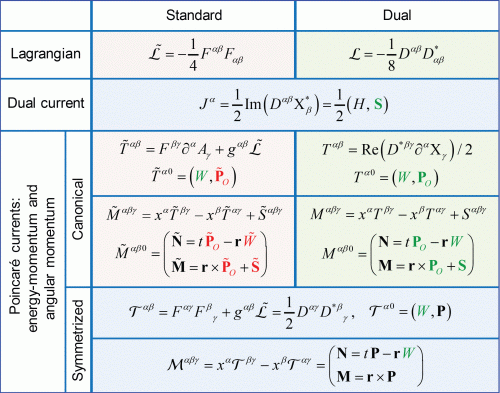 Figure. Summary of the conserved Noether currents which appear in the standard and dual versions of electromagnetism. The helicity current Jα and symmetrized Poincaré currents (energy–momentum and angular momentum tensors, Tαβ and Mαβγ) are common and dual-symmetric. At the same time, the canonical energy–momentum and angular momentum tensors, Tαβ and Mαβγ, conflict with the helicity and energy conservation laws in the standard electromagnetic theory. These discrepancies disappear in the dual electromagnetism. Inconsistent quantities are shown in red, as opposed to the consistent ones, shown in green. The fields are characterized by the magnetic four-potential Aα, field tensor Fαβ, their dual counterparts: electric four-potential Cα and dual field tensor Gαβ, and combined complex quantities Xα = Aα + iCα and Dαβ = Fαβ + iGαβ.
Figure. Summary of the conserved Noether currents which appear in the standard and dual versions of electromagnetism. The helicity current Jα and symmetrized Poincaré currents (energy–momentum and angular momentum tensors, Tαβ and Mαβγ) are common and dual-symmetric. At the same time, the canonical energy–momentum and angular momentum tensors, Tαβ and Mαβγ, conflict with the helicity and energy conservation laws in the standard electromagnetic theory. These discrepancies disappear in the dual electromagnetism. Inconsistent quantities are shown in red, as opposed to the consistent ones, shown in green. The fields are characterized by the magnetic four-potential Aα, field tensor Fαβ, their dual counterparts: electric four-potential Cα and dual field tensor Gαβ, and combined complex quantities Xα = Aα + iCα and Dαβ = Fαβ + iGαβ.
1. Introduction
The symmetry between electric and magnetic fields in Maxwell's electromagnetism has attracted considerable attention since the end of the 19th century [1, 2]. It was then noticed that Maxwell equations in free space are symmetric with respect to the following exchange of the electric and magnetic fields:

This discrete symmetry is a particular case of the continuous dual symmetry with respect to the electric–magnetic rotation:

where θ is an arbitrary pseudo-scalar. One of the manifestations of this symmetry is that all fundamental properties of free electromagnetic field (such as energy, momentum, angular momentum, etc) are symmetric with respect to the transformation (1.2), which is referred to by Berry as 'electric–magnetic democracy' [3].
Interest in the symmetry between the electric and magnetic properties of nature caught its second wind after seminal papers by Dirac that examined the possibility of the existence of magnetic charges (monopoles) [4]. Starting from the 1960s, this stimulated a series of works discussing the dual-symmetric formulation of electromagnetism and light–matter interactions [5–21]. Simultaneously, in 1964 Lipkin discovered a series of novel conservation laws (sometimes called 'Lipkin's zilches') in Maxwell equations, which were remarkably symmetric with respect to the electric and magnetic fields [22]. The Lipkin zilches include a pseudo-scalar, a pseudo-vector and higher-rank tensors. Analysis of these conserved quantities revealed that the pseudo-scalar integrated over space is related to the difference between the numbers of right-hand and left-hand circularly polarized photons, i.e. the optical helicity [23–28]. It was pointed out by Zwanziger [8] and also considered by Deser and Teitelboim [12] that it is the symmetry (1.2) that leads to the conservation of the helicity of light. However, in most other works the dual symmetry and helicity conservation were considered within different contexts.
Recently, the interest in helicity conservation arose again in connection with optical chirality, i.e. interaction of light with chiral structures [29–32]. Tang and Cohen [29, 30] argued that Lipkin's pseudo-scalar and pseudo-vector characterize the optical chirality density and its flux unrelated to the polarization of light. However, it was soon recovered in [33, 34] that for monochromatic fields these quantities should be associated with the helicity density and its flux. Moreover, it was shown that the helicity flux represents the dual-symmetric spin angular momentum of light [33]. Thus, importantly, the dual symmetry and conservation of helicity are closely related to the definition of the spin density in the electromagnetic field—a long-standing problem in itself. Finally, this year, the fundamental relations between the dual symmetry, helicity conservation law, spin and Lipkin's zilches were examined in detail in papers by Cameron et al [35]. Furthermore, Fernandez-Corbaton et al [36] first considered the electric–magnetic symmetry and helicity conservation as a practical tool describing a number of experimentally observed features in light–matter interactions.
Despite such extensive discussions about the dual symmetry (1.2) and helicity conservation, the standard electromagnetic field theory still has a significant drawback. Namely, the Lagrangian of the electromagnetic field, 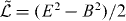 , is not dual-invariant with respect to (1.2). This results in dual-asymmetric Noether currents and conservation laws [37, 38]. In particular, the canonical energy–momentum and angular-momentum tensors are dual-asymmetric [37], which results in the known asymmetric definition of the spin and orbital angular momenta for the electromagnetic field [39]. (The usual symmetric energy–momentum tensor is obtained via an additional Belinfante symmetrization procedure, which is related to the separation of the spin and orbital degrees of freedom of the field [37, 40].) Therefore, the helicity and spin densities become inconsistent with each other in the standard Lagrangian electromagnetic theory: the helicity flux does not coincide with the spin. Sometimes, this evokes a false dual-asymmetric helicity (a partner of the asymmetric spin), which is not conserved in Maxwell equations [25, 27, 28, 34] (see also [20, section 1.6]). Thus, there is a fundamental discrepancy in the symmetries of the free-space Lagrangian and field equations, which manifests itself in inconsistent definitions of the helicity, spin and orbital angular-momentum densities. Deser and Teitelboim [12] showed that even for the asymmetric Lagrangian, the integral action is dual-invariant, and the proper conserved helicity can be derived from it. However, this does not resolve the dual asymmetry of the spin and orbital quantities, and below we argue that the symmetry of the Lagrangian and the corresponding canonical Noether currents still makes an important difference. It is worth noting that there were several attempts to restore the dual symmetry in the field Lagrangian [13–19] but all these have difficulties and do not result in a clear, manifestly dual-symmetric formulation of electromagnetism.
, is not dual-invariant with respect to (1.2). This results in dual-asymmetric Noether currents and conservation laws [37, 38]. In particular, the canonical energy–momentum and angular-momentum tensors are dual-asymmetric [37], which results in the known asymmetric definition of the spin and orbital angular momenta for the electromagnetic field [39]. (The usual symmetric energy–momentum tensor is obtained via an additional Belinfante symmetrization procedure, which is related to the separation of the spin and orbital degrees of freedom of the field [37, 40].) Therefore, the helicity and spin densities become inconsistent with each other in the standard Lagrangian electromagnetic theory: the helicity flux does not coincide with the spin. Sometimes, this evokes a false dual-asymmetric helicity (a partner of the asymmetric spin), which is not conserved in Maxwell equations [25, 27, 28, 34] (see also [20, section 1.6]). Thus, there is a fundamental discrepancy in the symmetries of the free-space Lagrangian and field equations, which manifests itself in inconsistent definitions of the helicity, spin and orbital angular-momentum densities. Deser and Teitelboim [12] showed that even for the asymmetric Lagrangian, the integral action is dual-invariant, and the proper conserved helicity can be derived from it. However, this does not resolve the dual asymmetry of the spin and orbital quantities, and below we argue that the symmetry of the Lagrangian and the corresponding canonical Noether currents still makes an important difference. It is worth noting that there were several attempts to restore the dual symmetry in the field Lagrangian [13–19] but all these have difficulties and do not result in a clear, manifestly dual-symmetric formulation of electromagnetism.
In this paper we put forward a dual-symmetric modification of the free-space classical Maxwell electromagnetism. Our theory is based on a dual-symmetric Lagrangian which is invariant with respect to the transformation (1.2). Therefore, the straightforward application of the Noether theorem to this Lagrangian immediately yields the proper helicity conservation law. The field equations, the symmetric energy–momentum tensor and the corresponding angular-momentum tensor remain the same as in standard electromagnetic theory. At the same time, the canonical versions of these tensors (which directly follow from the Noether theorem but are usually considered as auxiliary quantities [37, 38]) become meaningful physical quantities in our approach. They provide a dual-symmetric separation of the spin and orbital degrees of freedom, i.e. the spin and orbital parts of the momentum density (the Poynting vector) and the corresponding spin and orbital angular momenta of light. We show that only the dual-symmetric Lagrangian results in the canonical Noether currents—momentum, spin and orbital angular momenta, and boost momentum—fully consistent with each other and with the helicity conservation law. Thus, all the discrepancies present in the standard electromagnetism are removed in our dual-symmetric theory. Note that the separation of spin and orbital parts of the angular momentum of light is a long-standing and controversial problem; it was recently re-examined by several authors [41–44]. In particular, the importance of the electric–magnetic symmetry was emphasized in [3, 42, 43]. Remarkably, the spin and orbital characteristics of the electromagnetic field, which were suggested in [3, 42–44] using various arguments, now become intrinsic in the dual formulation of electromagnetism, and are derived in a rigorous way.
This paper is organized as follows. In section 2 we summarize the standard Lagrangian formulation of classical electromagnetism, emphasizing its inherent difficulties related to its lack of duality. We present a complete Noether analysis of the dual symmetry and all Poincaré symmetries, and examine both local and integral conserved quantities. Afterwards, in section 3 we formulate the dual-symmetric modification of electromagnetic field theory, with its step-by-step comparison with section 2 and other relevant results. To facilitate the comparison of the Noether currents in the standard and dual theories, we summarize them in figure 1. Section 3.3 also contains a quantum-like operator representation of the conserved physical characteristics for monochromatic fields [3, 42, 44]; such a self-consistent representation is impossible within standard electromagnetism. In section 4 we discuss the issues of observability of spin and orbital angular momenta and local currents, which distinguish standard and dual theories. A number of known results and experiments are discussed from the viewpoint of dual symmetry. We argue that the suggested optical experiments are related to the concept of quantum weak measurements and unavoidably involve light–matter interactions. The remarks in section 5 conclude the paper.
Figure 1. Summary of the main Noether currents which appear in the standard (section 2) and dual (section 3) versions of electromagnetism. The helicity current and symmetrized Poincaré currents (energy–momentum and angular momentum tensors, 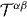 and
and 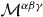 ) are common and dual-symmetric. At the same time the canonical energy–momentum and angular-momentum tensors, Tαβ and Mαβγ, conflict with the helicity and energy conservation laws in the standard electromagnetic theory. These discrepancies disappear in the dual electromagnetism. Inconsistent quantities are shown in red, as opposed to the consistent ones, shown in green. The fields are characterized by the magnetic four-potential Aα, field tensor Fαβ, their dual counterparts: electric four-potential Cα and dual field tensor Gαβ, and combined complex quantities Xα = Aα + i Cα and Dα
β
= Fα
β
+ i Gα
β
.
) are common and dual-symmetric. At the same time the canonical energy–momentum and angular-momentum tensors, Tαβ and Mαβγ, conflict with the helicity and energy conservation laws in the standard electromagnetic theory. These discrepancies disappear in the dual electromagnetism. Inconsistent quantities are shown in red, as opposed to the consistent ones, shown in green. The fields are characterized by the magnetic four-potential Aα, field tensor Fαβ, their dual counterparts: electric four-potential Cα and dual field tensor Gαβ, and combined complex quantities Xα = Aα + i Cα and Dα
β
= Fα
β
+ i Gα
β
.
Download figure:
Standard image2. Standard electromagnetism
2.1. Field Lagrangian, Maxwell equations and basic currents
The electromagnetic field is described by the four-potential Aα (rα ) = (A0 ,A) and antisymmetric field tensor

Here and in what follows, we use the Minkowski space–time rα = (t,r) with signature ( - ,+,+,+) and assume natural units ε0 = μ0 = c = 1 . We will adopt the transverse Coulomb gauge, A0 = 0 , ∇ ⋅ A = 0 (A = A⊥ ), because it is the transverse part of the potential which is gauge-invariant and can determine physically meaningful quantities for the transverse radiation fields [39, 41, 43]. Also, all fields are assumed to be decaying sufficiently fast when 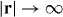 , to make all spatial integrals converging.
, to make all spatial integrals converging.
The standard Lagrangian of the free electromagnetic field is

Here and in what follows, emphasizing the dual asymmetry of some important quantities, we will mark them with a tilde; their dual-symmetric counterparts will be marked by the same letters without a tilde. The field Hamiltonian, following from (2.2), is known to be [39] 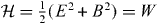 , where W is the dual-symmetric energy density of the electromagnetic field.
, where W is the dual-symmetric energy density of the electromagnetic field.
The free-space Maxwell equations can be written as

or
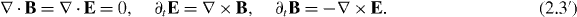
Here we introduced the dual field tensor:

where εα β γ δ is the Levi–Civita symbol. Note that only the first Maxwell equation in (2.3) represents the Euler–Lagrange equation of motion when varying the Lagrangian (2.2) with respect to Aα . At the same time, the second equation in (2.3) is the Bianchi identity, which follows automatically from the form of the field tensor (2.1).
As compared to the field tensor (2.1), the dual field tensor (2.4) consists of the electric and magnetic fields E and B exchanged with each other via (1.1). Evidently, the Maxwell equations (2.3) are symmetric with respect to the dual exchange (1.1) 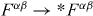 , because
, because  . It is easy to show that equations (2.3') are also invariant with respect to the continuous dual transformations (1.2).
. It is easy to show that equations (2.3') are also invariant with respect to the continuous dual transformations (1.2).
Note that the coupling with matter (which consists of electric charges and currents) breaks the dual symmetry of the free field. The Lagrangian (2.2) acquires the coupling part 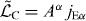 , where jEα is the electric four-current, and the first equation of motion (2.3) becomes ∂ β
Fα
β
= jEα . It is seen from this that the presence of both electric and magnetic charges is problematic in this picture, because it requires a modification of the second equation (2.3) with the magnetic current jMα :
, where jEα is the electric four-current, and the first equation of motion (2.3) becomes ∂ β
Fα
β
= jEα . It is seen from this that the presence of both electric and magnetic charges is problematic in this picture, because it requires a modification of the second equation (2.3) with the magnetic current jMα : 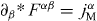 [4–20]. However, this would contradict the Bianchi identity for the field tensor (2.1), and the relation between the field and potential should be modified.
[4–20]. However, this would contradict the Bianchi identity for the field tensor (2.1), and the relation between the field and potential should be modified.
In contrast to Maxwell equations, the field Lagrangian (2.2) is not invariant with respect to the duality transformations (1.1) and (1.2). To illustrate its transformation properties, we introduce the complex Riemann–Silberstein vector D = E + iB [45]. The Lorentz transformations represent complex-angle rotations of this vector [38], and its square, D⋅ D = (E2 - B2 ) + 2 i E⋅ B ≡ I1 + i I2 , provides the two Lorentz invariants of the electromagnetic field:

In terms of the Riemann–Silberstein vector, the dual transformation (1.2) becomes the U(1) gauge transformation 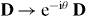 , whereas the field Lagrangian (2.2) takes the form
, whereas the field Lagrangian (2.2) takes the form 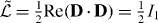 . From these equations, we immediately see that the dual transformation (1.2) induces a rotation of the field invariants
. From these equations, we immediately see that the dual transformation (1.2) induces a rotation of the field invariants

and the Lagrangian is transformed as
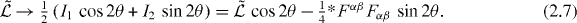
The transformation (2.7) changes the Lagrangian, but does not affect the Maxwell equations of motion. Indeed, 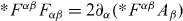 (we can use here
(we can use here  , because this is the Bianchi identity rather than the equation of motion), and the transformation (2.7) adds a total divergence alongside with a multiplication by the constant cos 2θ .
, because this is the Bianchi identity rather than the equation of motion), and the transformation (2.7) adds a total divergence alongside with a multiplication by the constant cos 2θ .
Considering an infinitesimal version of (2.7) with  , we have
, we have

From here it is speculated in [20, section 1.6] that the dual symmetry of Maxwell equations implies the conservation of the dual current

The components of the current (2.9) are often considered as the helicity density
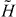 and the spin angular momentum density
and the spin angular momentum density 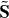 (coinciding here with the helicity flux density) of the field [25, 34, 39, 41]. However, this is not the case, and this false helicity is not conserved [25–28]:
(coinciding here with the helicity flux density) of the field [25, 34, 39, 41]. However, this is not the case, and this false helicity is not conserved [25–28]:
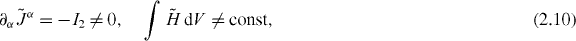
where dV ≡ d3 r and 'const' denotes constancy in time. It was shown in a number of works [27, 28, 35, 43] that the dual-asymmetric definitions for the helicity and spin densities (2.9) are not satisfactory in the general case. Instead, the dual-symmetric modifications of equations (2.9) and (2.10) form the true helicity–spin current providing the helicity conservation [8, 12, 16, 27, 28, 35]:
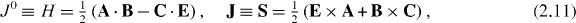

Here A and C are the magnetic and electric vector-potentials: ∇ × C = - E and ∇ × A = B (see equations (3.6)). The second quantity in (2.11) was recently identified as the physically meaningful spin angular-momentum density [42–44].
Let us make one more observation, the meaning of which will be clarified below. Akin to the infinitesimal dual transformation, we consider an infinitesimal time-translation transformation 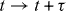 ,
, 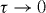 . In a way similar to equation (2.8), using the Maxwell equation ∂ α
Fα
β
= 0 , one can show that the value of the Lagrangian (2.2) on the minimal-action trajectories is transformed as
. In a way similar to equation (2.8), using the Maxwell equation ∂ α
Fα
β
= 0 , one can show that the value of the Lagrangian (2.2) on the minimal-action trajectories is transformed as

Then, akin to equations (2.9) and (2.10), this evokes a false energy–momentum current:
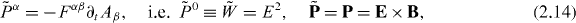
where the energy is not conserved:
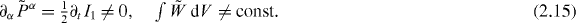
The current (2.14) and (2.15) contains the proper Poynting vector (=energy flux density =momentum density) P = E × B, but also contains the dual-asymmetric energy density 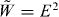 , which would appear if the energy were concentrated solely in the electric field. Of course, the true conserved energy–momentum current, associated with the time-translation invariance, is dual-symmetric and reads
, which would appear if the energy were concentrated solely in the electric field. Of course, the true conserved energy–momentum current, associated with the time-translation invariance, is dual-symmetric and reads


The proper energy conservation (2.16) and (2.17) follows from the Noether-theorem analysis, which is considered in section 2.2. Also, Deser and Teitelboim [12] showed that the proper helicity conservation (2.11) and (2.12) can be obtained from the dual-asymmetric Lagrangian (2.2). However, we will also see that the false spin density (2.9) 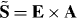 and the false energy density (2.14)
and the false energy density (2.14) 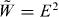 appear in the components of the canonical angular-momentum tensor following from the Lagrangian (2.2). This is an important discrepancy of the standard dual-asymmetric Lagrangian formulation of electromagnetism which fails to produce conservation laws consistent with each other.
appear in the components of the canonical angular-momentum tensor following from the Lagrangian (2.2). This is an important discrepancy of the standard dual-asymmetric Lagrangian formulation of electromagnetism which fails to produce conservation laws consistent with each other.
2.2. Energy–momentum and angular-momentum tensors
In this section we summarize the main conservation laws for the free electromagnetic field, which are associated with the Poincaré group of symmetries, i.e. translations and rotations of the Minkowski space–time. We will obtain the corresponding conserved quantities by applying the Noether theorem to the Lagrangian (2.2), and will emphasize their specific features which are important for our theory. This section mostly follows the standard textbook approach [37, 38].
2.2.1. Canonical tensors
The invariance with respect to translations in space and time generates the conservation of momentum and energy. The application of the Noether theorem [46] yields the following dual-asymmetric but conserved energy–momentum tensor from the Lagrangian (2.2):
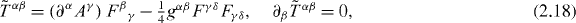
where gα
β
is the metric tensor. Tensor (2.18) is non-symmetric, 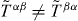 , and is known as the canonical energy–momentum tensor. The corresponding four-momentum density of the field is given by
, and is known as the canonical energy–momentum tensor. The corresponding four-momentum density of the field is given by 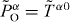 (the indices 'O' and 'S' indicate 'orbital' and 'spin' quantities, see below). Its temporal component (in the chosen Coulomb gauge) reads
(the indices 'O' and 'S' indicate 'orbital' and 'spin' quantities, see below). Its temporal component (in the chosen Coulomb gauge) reads
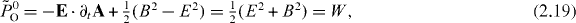
which is the proper dual-symmetric energy density (2.16). At the same time, the spatial components of the canonical momentum density form the dual-asymmetric vector

(Here and in what follows, we use the notations of Berry [3], for which the scalar product links the vectors E and A, whereas the gradient is external:  ; the Latin indices i,j,k take on values 1, 2, 3.) As we will see, the canonical momentum density
; the Latin indices i,j,k take on values 1, 2, 3.) As we will see, the canonical momentum density  represents the orbital part of the energy flux density. The total energy flux density (Poynting vector) P is given by the spatial components of
represents the orbital part of the energy flux density. The total energy flux density (Poynting vector) P is given by the spatial components of  , which form the proper conserved energy–momentum current (2.16) in the chosen Coulomb gauge.
, which form the proper conserved energy–momentum current (2.16) in the chosen Coulomb gauge.
Next, the symmetry with respect to Lorentz transformations (rotations of the Minkowski space–time) results in the conservation of the relativistic angular momentum. Recall that the angular momentum is described in relativistic field theory by a rank-3 tensor Mα
β
γ
, where the anti-symmetric rank-2 tensor Mα
β 0 can be represented by a pair of three-vectors:  . Here the pseudo-vector
. Here the pseudo-vector 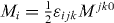 is the usual angular momentum, which has the form of M = r × P for point particles and is related to the symmetry with respect to spatial rotations. At the same time, the vector Ni = M0i0 could be referred to as the boost momentum. It is related to the symmetry with respect to Lorentz boosts and has the form N = t P- r W for point particles. Conservation of the boost momentum ensures the rectilinear motion of the energy centroid in free space [38, 47]. The application of the Noether theorem to the Lagrangian (2.2) results in the following dual-asymmetric but conserved canonical angular-momentum tensor:
is the usual angular momentum, which has the form of M = r × P for point particles and is related to the symmetry with respect to spatial rotations. At the same time, the vector Ni = M0i0 could be referred to as the boost momentum. It is related to the symmetry with respect to Lorentz boosts and has the form N = t P- r W for point particles. Conservation of the boost momentum ensures the rectilinear motion of the energy centroid in free space [38, 47]. The application of the Noether theorem to the Lagrangian (2.2) results in the following dual-asymmetric but conserved canonical angular-momentum tensor:
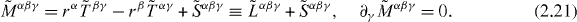
Here 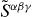 is the spin tensor, which has the form
is the spin tensor, which has the form
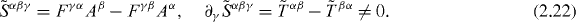
Importantly, the canonical angular-momentum tensor (2.21) suggests a natural separation into orbital and spin parts, 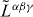 and
and 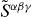 . Calculating the angular-momentum vector
. Calculating the angular-momentum vector 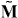 from equations (2.18)–(2.22), we arrive at
from equations (2.18)–(2.22), we arrive at

Equation (2.23) describes the canonical angular-momentum density, where the orbital angular momentum can be written in 'mechanical' form  , consistent with the canonical momentum density (2.20). At the same time, the expression for the spin angular-momentum density
, consistent with the canonical momentum density (2.20). At the same time, the expression for the spin angular-momentum density 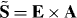 here coincides with the false (non-conserved) dual-asymmetric helicity flux density (2.9) rather than with the proper (conserved) dual-symmetric quantity (2.11) S! This is the first important discrepancy in the standard Lagrangian formulation of electromagnetism.
here coincides with the false (non-conserved) dual-asymmetric helicity flux density (2.9) rather than with the proper (conserved) dual-symmetric quantity (2.11) S! This is the first important discrepancy in the standard Lagrangian formulation of electromagnetism.
Next, the canonical boost momentum density 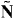 derived from tensor (2.21) can also be separated into orbital and spin parts, which yields
derived from tensor (2.21) can also be separated into orbital and spin parts, which yields
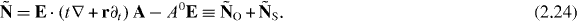
In the chosen Coulomb gauge, this results in

Thus, the spin part of the boost momentum vanishes [43] (apparently, this reflects the truly intrinsic nature of spin, which does not involve energy transport [42, 48–53]). At the same time, the orbital boost momentum 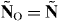 takes a clear mechanical-like form in (2.25). It involves the canonical momentum density (2.20)
takes a clear mechanical-like form in (2.25). It involves the canonical momentum density (2.20) 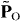 and false (non-conserved) dual-asymmetric energy density (2.14)
and false (non-conserved) dual-asymmetric energy density (2.14) 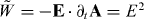 rather than the proper conserved quantity (2.16) and (2.19) W ! And this is the second important discrepancy in the standard Lagrangian formulation of electromagnetism.
rather than the proper conserved quantity (2.16) and (2.19) W ! And this is the second important discrepancy in the standard Lagrangian formulation of electromagnetism.
2.2.2. Symmetrized tensors
Although the canonical energy–momentum tensor (2.18) and momentum density (2.20) directly follow from the Noether theorem and Lagrangian (2.2), they are usually considered as auxiliary quantities. Instead the symmetric energy–momentum tensor  is obtained via the Belinfante symmetrization procedure [40], i.e. the addition of a suitable total divergence to the canonical energy–momentum tensor. As applied to the tensor
is obtained via the Belinfante symmetrization procedure [40], i.e. the addition of a suitable total divergence to the canonical energy–momentum tensor. As applied to the tensor 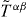 , this procedure results in
, this procedure results in
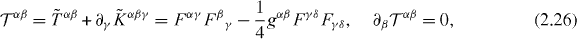
where the tensor 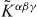 is constructed from the spin tensor (2.22):
is constructed from the spin tensor (2.22):
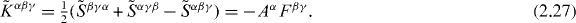
When integrated over the whole space, both tensors (2.18) and (2.26) yield the same momentum of the field (see section 2.2.3). The symmetric tensor (2.26) is manifestly gauge-invariant, and its components contain: the proper energy density W , the momentum density coincident with the total energy flux (Poynting vector) P and also the Maxwell stress tensor σij for the electromagnetic field:
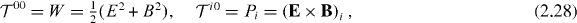
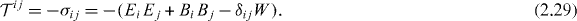
Importantly, the quantities (2.26), (2.28) and (2.29) are dual-invariant with respect to the transformation (1.2), in contrast to the canonical quantities (2.18) and (2.20).
The symmetrization procedure (2.26) has an important physical meaning [37, 48–51]. Let us consider the tensor 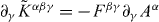 , which is added to the canonical energy–momentum tensor. Its contribution to the field momentum is
, which is added to the canonical energy–momentum tensor. Its contribution to the field momentum is 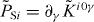 :
:

This is the spin current, i.e. the spin part of the energy flux density. Indeed, the Poynting vector (2.28) is the sum of the orbital part (2.20) and the spin part (2.30):

Although the spin current makes no contribution to the integral momentum of the field,

circulations of the orbital and spin energy fluxes produce, respectively, orbital and spin angular momenta (2.23):
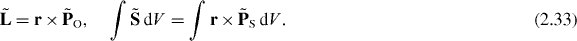
Here the second equation is obtained using integration by parts with ∇ ⋅ E = 0 , and it displays a 'non-local' action of the spin current. (This peculiar current does not transport energy and flows along the boundary resembling the magnetization current or topological quantum-Hall states in condensed-matter systems.) A detailed description and analysis of the spin and orbital energy fluxes can be found in [3, 37, 42, 48–53]. Note also that an analogue of the second equation (2.33) for the spin part of the boost momentum 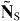 reads
reads 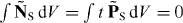 , and does not give new information.
, and does not give new information.
A symmetrized angular-momentum tensor can be constructed from the symmetric energy–momentum tensor (2.26). Since the latter includes both orbital and spin parts of the momentum density, the angular-momentum tensor becomes
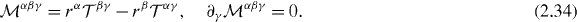
This tensor is dual symmetric, and differs from the canonical angular-momentum tensor (2.21): 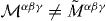 . Nonetheless, when integrated over space, both tensors
. Nonetheless, when integrated over space, both tensors 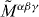 and
and 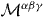 yield the same total angular momentum of the field [37] (see section 2.2.3). The angular momentum and boost momentum densities following from the tensor (2.34) are expressed through the symmetrized energy–momentum components (2.28) (cf equations (2.23)–(2.25)):
yield the same total angular momentum of the field [37] (see section 2.2.3). The angular momentum and boost momentum densities following from the tensor (2.34) are expressed through the symmetrized energy–momentum components (2.28) (cf equations (2.23)–(2.25)):

We emphasize that  describes the total angular-momentum density of the field, without separation of the orbital and spin parts.
describes the total angular-momentum density of the field, without separation of the orbital and spin parts.
Thus, the symmetrized energy–momentum and angular-momentum tensors (2.26) and (2.34) are convenient characteristics for the calculations of the integral (non-local) dynamical properties of the field. However, it is impossible to separate spin and orbital angular-momentum degrees of freedom in 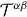 and
and 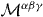 without involving the canonical tensors.
without involving the canonical tensors.
2.2.3. Integral conserved quantities
Above we considered local conservation laws associated with the dual and Poincaré symmetries. It is also interesting to discuss the corresponding conserved integral (i.e. non-local) quantities.
First, equations (2.9)–(2.12) and (2.14)–(2.17) involving true and false helicity, spin and energy densities can be formulated in the following integral form:
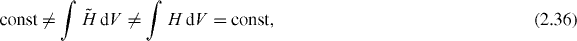
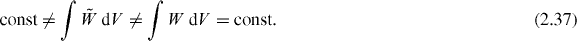
Next, from equations (2.18) and (2.26), the integral energy–momentum following from the canonical and symmetric energy–momentum tensors are both conserved in time and equal to each other:

i.e.
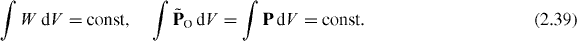
The second equality here is consistent with the vanishing of the integral spin momentum, equations (2.31) and (2.32).
Similar equalities take place for the angular momenta following from canonical and symmetrized angular-momentum tensors (2.21) and (2.34):

In components, this yields
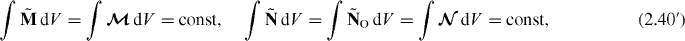
i.e.
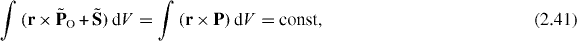
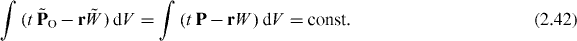
An interesting new equality follows from equations (2.42) and (2.39):
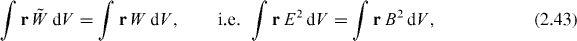
although  and
and  .
.
Equation (2.42) results in the equation of the rectilinear motion of the centroid of the energy density W . Indeed, using 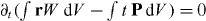 and the energy–momentum conservation (2.39), we obtain
and the energy–momentum conservation (2.39), we obtain
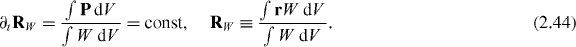
At the same time, we note that the centroid of the false energy density 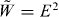 entering the canonical boost-momentum density
entering the canonical boost-momentum density  does not move rectilinearly, because
does not move rectilinearly, because  is not conserved, equation (2.37):
is not conserved, equation (2.37):
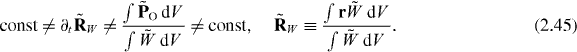
Thus, the equation of motion of the energy centroid does not follow from the form of the canonical boost momentum (2.24) and (2.25)  in standard electromagnetism.
in standard electromagnetism.
Equations (2.36)–(2.44) summarize all non-local conserved quantities following from the differential conservation laws. In addition, there are also important integral conserved quantities which have no differential counterparts. Namely, despite the fact that the spin and orbital parts of the angular-momentum density (2.21) do not form conserved Noether currents, see equation (2.22), their integral values are conserved in time [41]:
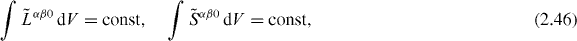
i.e.

This can be verified by substituting here the spin and orbital angular-momentum densities (2.23) and performing differentiation with respect to time. Equations (2.46') agree with the approach of modern optics, where the spin and orbital angular momenta of light are regarded as separately observable and conserved (in free space) quantities [41, 54] (for reviews, see [55]). Note, however, that the integral values of the spin and orbital angular momenta 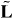 and
and 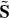 are not dual-symmetric. Moreover, their dual-symmetric versions are also conserved quantities. For instance, the dual-symmetric spin S, entering the proper helicity conservation (2.11) and (2.12), also obeys
are not dual-symmetric. Moreover, their dual-symmetric versions are also conserved quantities. For instance, the dual-symmetric spin S, entering the proper helicity conservation (2.11) and (2.12), also obeys
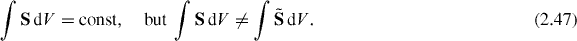
Equations (2.36), (2.37), (2.45) and (2.47) demonstrate that the spin and orbital angular momenta following from the canonical angular-momentum tensor (2.21) and standard Lagrangian (2.2) conflict with the helicity and energy conservations not only locally but also in their integral values.
2.2.4. Summary of the problems
The above picture shows that the canonical energy–momentum and angular-momentum tensors are intimately related to the separation of the spin and orbital degrees of freedom of the electromagnetic field. In turn, the properly defined spin is a crucial part of the helicity conservation (2.11) and (2.12). Therefore, it is important that these canonical tensors 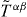 and
and 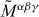 should be physically meaningful and consistent with each other and the helicity conservation. However, in the standard formulation, they lack the dual invariance with respect to the transformation (1.2). As a result of this, the Lagrangian (2.2) leads to the false spin density (2.9)
should be physically meaningful and consistent with each other and the helicity conservation. However, in the standard formulation, they lack the dual invariance with respect to the transformation (1.2). As a result of this, the Lagrangian (2.2) leads to the false spin density (2.9) 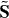 and false energy density (2.14)
and false energy density (2.14) 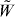 , which appear in the components of
, which appear in the components of 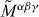 ; while the proper dual-symmetric spin and energy densities, S and W , are given by equations (2.11) and (2.16) or (2.28). In turn, the definition of the spin is closely related to the definitions of other quantities: orbital angular-momentum density
; while the proper dual-symmetric spin and energy densities, S and W , are given by equations (2.11) and (2.16) or (2.28). In turn, the definition of the spin is closely related to the definitions of other quantities: orbital angular-momentum density 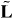 , spin and orbital parts of the energy flux (momentum) density,
, spin and orbital parts of the energy flux (momentum) density,  and
and  . Recent investigations suggested that all these dual-asymmetric quantities should be substituted by their dual-symmetric modifications [3, 42–44, 51, 53]. Thus, we observe a number of inconsistencies in the canonical conservation laws of standard electromagnetic theory; these are all summarized in figure 1. We have also shown that the discrepancies between the dual-symmetric and asymmetric versions of the helicity, energy, spin and orbital angular momenta appear in both local and integral values of these quantities.
. Recent investigations suggested that all these dual-asymmetric quantities should be substituted by their dual-symmetric modifications [3, 42–44, 51, 53]. Thus, we observe a number of inconsistencies in the canonical conservation laws of standard electromagnetic theory; these are all summarized in figure 1. We have also shown that the discrepancies between the dual-symmetric and asymmetric versions of the helicity, energy, spin and orbital angular momenta appear in both local and integral values of these quantities.
It should be emphasized that the above discrepancies involve measurable quantities. There are no doubts that the integral helicity and energy are observable. Modern optics regards the spin and orbital parts of the angular momentum as separately measurable quantities [41, 54, 55]. Remarkably, even local densities of energy, spin and orbital energy flow can be retrieved from optical experiments [51, 54, 56]. We further discuss the observability issues in section 4.
3. Dual electromagnetism
3.1. Dual-symmetric Lagrangian and basic currents
To construct the Lagrangian formalism which would contain the dual symmetry (1.2), we first consider the field tensor Fα
β
and its dual pseudo-tensor  as independent quantities based on two different four-potentials Aα and Cα :
as independent quantities based on two different four-potentials Aα and Cα :
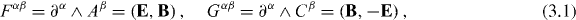
Such a two-potential representation is extensively used in studies on magnetic monopoles and optical helicity [5–21, 23–28, 35]. Next, we suggest a dual-symmetric Lagrangian, which is the symmetrization of the standard Lagrangian (2.2) with respect to Fα β and Gα β :

Here the two fields are considered independently, but since they actually describe the same electromagnetic field, we should impose an additional duality constraint:
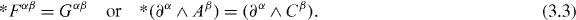
The value of the Lagrangian vanishes with this constraint: 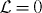 . Nonetheless, by varying the Lagrangian (3.2) with respect to the potentials Aα and Cα independently, we obtain two Euler–Lagrange equations of motion:
. Nonetheless, by varying the Lagrangian (3.2) with respect to the potentials Aα and Cα independently, we obtain two Euler–Lagrange equations of motion:

At the same time, the Bianchi identity for the fields (3.1) yields

Applying now the constraint (3.3), we see that the two pairs of equations (3.4) and (3.5) result in the same pair of free-space Maxwell equations (2.3). This derivation of the equations of motion is equivalent to the use of a Lagrange multiplier with the constraint (3.3) in the Lagrangian.
Thus, the Maxwell equations are recovered from the symmetrized Lagrangian (3.2). It should be noted, however, that this formalism describes only free radiation transverse fields. As was pointed out in section 2.1, a coupling with matter brings about currents in the right-hand side of equations (3.4), which would contradict equations (3.5). In this case, one has to modify the relation (3.1) between the potentials and fields to include the longitudinal parts of the fields [4–20].
As in section 2, we now consider only the transverse radiation fields, and adopt the transverse Coulomb gauge for the potentials: A0 = C0 = 0 and ∇ ⋅ A = ∇ ⋅ C = 0 (A = A⊥ , C = C⊥ ) [35, 43]. Note that the Coulomb gauge and constraint (3.3) are equivalent to 'Maxwell equations' for the vector-potentials [35]:
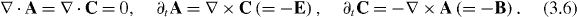
Therefore, the duality rotation (1.2) generates the same rotation of the vector-potentials [8, 10, 13, 17, 18, 35]:

The dual-symmetric formalism acquires a particularly laconic form if we introduce the complex Riemann–Silberstein-like four-potential Xα and the corresponding field tensor Dα β :
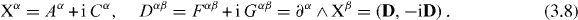
In this manner, the Lagrangian (3.2) becomes

whereas the duality constraint (3.3) is

The Euler–Lagrange equations for the Lagrangian (3.9) with respect to Xα or X*α , or the Bianchi identity for the field (3.8), yield the Maxwell equations reduced now, by virtue of (3.10), to a single equation:

The proper Hamiltonian of the field is readily recovered from the Lagrangian (3.9) using the Lagrangian formalism for complex fields (see [39, section II.A.2]) and also the connection between the potentials and fields (3.6): ∂ t
X = - i∇ × X = - D. This yields  .
.
The dual transformations (1.2) and (3.7) become a simple U(1) gauge transformation in this complex formalism:

The Lagrangian (3.9) is obviously invariant with respect to (3.12). The corresponding conserved Noether current is easily obtained and equals

This conservation law represents the true helicity conservation in Maxwell equations and coincides with equations (2.11) and (2.12) including the proper helicity and spin densities:
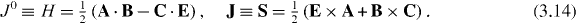
The same expressions for the helicity and spin densities were obtained in [8, 12, 16, 27, 28, 35, 43]. In the case of monochromatic fields, they are proportional to the components of Lipkin's zilch current [22, 23, 29, 33, 35] and coincide with spin angular momentum in [42, 44] (see section 3.3). It is worth emphasizing that the derivation of the helicity current (3.13) and (3.14) from the standard Lagrangian (2.2) requires a sophisticated procedure described by Deser and Teitelboim [12], while with the dual-symmetric Lagrangian (3.2) or (3.9) it arises in a straightforward manner.
Furthermore, considering an infinitesimal time-translation transformation, 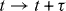 ,
,
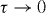 , in a manner similar to (2.13)–(2.17), one can show that the Lagrangian (3.2) and (3.9) is transformed on the minimal-action trajectories (without taking into account the duality constraint) as
, in a manner similar to (2.13)–(2.17), one can show that the Lagrangian (3.2) and (3.9) is transformed on the minimal-action trajectories (without taking into account the duality constraint) as

In contrast to (2.13)–(2.15), this immediately evokes the true conserved energy–momentum current (2.16) and (2.17):


Thus, our dual-symmetric Lagrangian formalism generates the same Maxwell equations, but also naturally reveals the proper helicity and energy conserved currents, containing the physically meaningful dual-symmetric helicity, spin and energy densities. Below, we provide a complete Noether analysis of conservation laws associated with the Poincaré symmetries and show that the choice of dual-symmetric Lagrangian (3.2) or (3.9) makes an important difference in the canonical form of the conservation laws.
3.2. Energy–momentum and angular-momentum tensors
In this section, we follow the plan of section 2.2, but now using the dual-symmetric Lagrangian (3.2) and its representation (3.9) via the complex Riemann–Silberstein fields Xα = Aα + i Cα and Dα β = Fα β + i Gα β . We will consider canonical and symmetrized energy–momentum and angular-momentum Noether currents and compare them with their counterparts obtained previously within standard electromagnetism.
3.2.1. Canonical tensors
Firstly, the canonical energy–momentum tensor following from Lagrangian (3.9) is
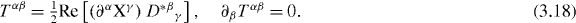
This tensor is non-symmetric, 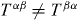 , and the corresponding four-momentum density is given by
, and the corresponding four-momentum density is given by ![$P_{\rm{O}}^\alpha = T^{\alpha 0} = \frac{1}{2}{\rm Re}\left[ {{\bf{R}}^* \cdot \left( {\partial ^\alpha } \right){\bf{{X}}}} \right]$](https://content.cld.iop.org/journals/1367-2630/15/3/033026/revision1/nj448360ieqn75.gif) . This yields the proper energy density
. This yields the proper energy density 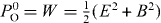 , and also the following orbital energy flux density, the dual-symmetric modification of (2.20):
, and also the following orbital energy flux density, the dual-symmetric modification of (2.20):

In turn, the total energy flux density is given by 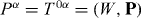 , in agreement with (3.16) and (3.17).
, in agreement with (3.16) and (3.17).
Secondly, akin to equation (2.21), the canonical angular-momentum tensor takes on the form
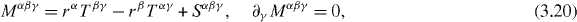
where the spin tensor is
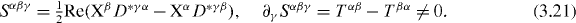
Calculating the pseudo-vector of the angular-momentum density,  , we arrive at the following orbital and spin parts, M = L + S (cf (2.23)):
, we arrive at the following orbital and spin parts, M = L + S (cf (2.23)):
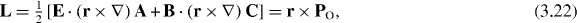

In turn, the boost-momentum components in the tensor (3.20), Ni = M0i0 , yield (cf (2.24) and (2.25))
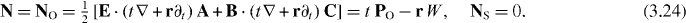
Thus, the components (3.19), (3.22)–(3.24) of the canonical energy–momentum and angular-momentum tensors contain now the proper conserved energy density W , spin density S coinciding with the conserved helicity flux density (2.11) or (3.14), and the corresponding orbital momentum density PO . Therefore, the dual electromagnetism fixes all the discrepancies in the canonical Noether currents of the standard electromagnetic theory. This approach naturally contains a meaningful dual-symmetric separation of the spin and orbital degrees of freedom [3, 42, 43], consistent with the helicity and energy conservation laws (see also figure 1).
3.2.2. Symmetrized tensors
Belinfante's symmetrization procedure can be applied to the canonical energy–momentum tensor (3.18), which results in the same symmetric energy–momentum tensor 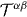 as in equations (2.26) (but now simplified in the dual-complex form):
as in equations (2.26) (but now simplified in the dual-complex form):

where 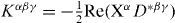 . The components of
. The components of 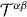 are displayed in equations (2.28) and (2.29). The spin current is obtained as PS i = ∂ γ
Ki0γ
, which yields the dual-symmetric version of equation (2.30):
are displayed in equations (2.28) and (2.29). The spin current is obtained as PS i = ∂ γ
Ki0γ
, which yields the dual-symmetric version of equation (2.30):

Akin to equations (2.31)–(2.33), the Poynting vector is the sum of the orbital and spin energy flux densities (3.19) and (3.26):

where the spin current makes no contribution to the integral momentum:

The circulations of the orbital and spin currents produce, respectively, the orbital and spin angular momenta (3.22) and (3.23):
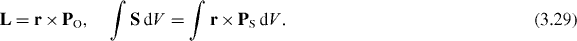
The dual-symmetric spin and orbital parts of the energy flux density (3.19) and (3.26) coincide with those suggested recently in [3, 42, 51].
Evidently, the symmetrized angular-momentum tensor also coincides in the standard- and dual-electromagnetism approaches:

Its components are described by equations (2.35). This suggests that the symmetrized energy–momentum and angular-momentum tensors are independent of the choice of the Lagrangian. The price of this independence is the impossibility to separate the spin and orbital degrees of freedom and to trace the connection with the helicity conservation.
3.2.3. Integral conserved quantities
As usual, differential conservation laws can be written in the form of integral conserved quantities. In dual electromagnetism, they are similar to their standard counterparts and, furthermore, a number of them coincide in the two formalisms. In a way entirely analogous to the derivation of equations (2.38)–(2.42), we obtain
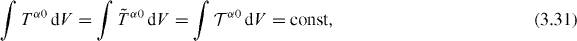
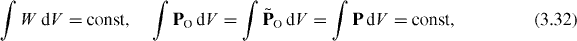
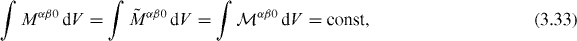
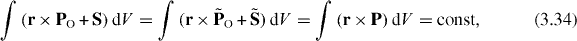
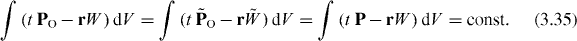
Note that equation (2.44) for the rectilinear motion of the energy centroid immediately follows from the canonical dual-symmetric boost momentum (3.24) N and equation (3.32), in contrast to the canonical (2.25)  in the standard approach.
in the standard approach.
At the same time, the integral spin and orbital angular momenta are different in the standard and dual approaches, although they are all conserved quantities (see (2.46) and (2.47)):
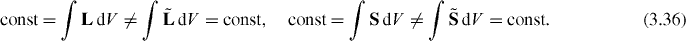
And, again, for the sake of completeness, we repeat here equations (2.36) and (2.37) involving integral forms of the true and false helicity and energy that appear in the standard and dual formalisms:
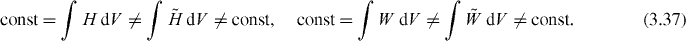
From a complete set of equations (3.31)–(3.37), augmented by relations (2.31), (2.33), (3.27) and (3.29), one can see that the integral conserved quantities of the dual electromagnetism (i.e. those without 'tilde') form a perfectly consistent system, as opposed to those of the standard electromagnetic theory. In section 3.3 we show that the dual-symmetric approach is also in agreement with the quantum-like operator formalism [3, 42, 44].
3.3. Monochromatic fields and operator representation
In a vast majority of optical problems, monochromatic electromagnetic fields and their time-averaged characteristics are considered. In this case, all linear field characteristics (O = A,C,E,B) have the form ![${\bf{O}}\left( {{\bf{r}},t} \right) = {\rm Re}[ {\boldsymbol{\sf O}\left( {\bf{r}} \right){\rm{e}}^{ - {\rm{i}}\omega t} } ]$](https://content.cld.iop.org/journals/1367-2630/15/3/033026/revision1/nj448360ieqn83.gif) , where ω is the frequency and
, where ω is the frequency and  is the complex field amplitude. Substituting this into equations (3.6), we find that the complex amplitudes of the potentials and fields become proportional to each other:
is the complex field amplitude. Substituting this into equations (3.6), we find that the complex amplitudes of the potentials and fields become proportional to each other:

Next, the time average (over one period of oscillations) of any real quadratic field form  becomes
becomes

The dynamical characteristics of the field (helicity, energy, momentum, etc) considered in previous sections represent quadratic forms with respect to the fields and potentials. Then, applying the time averaging (3.39) with relations (3.38) to the densities of energy–momentum (2.28), helicity (2.11) or (3.14), spin and orbital momenta (3.19), (3.26) and angular momenta (3.22), (3.23) and boost momentum (3.24), we obtain
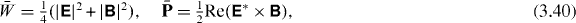



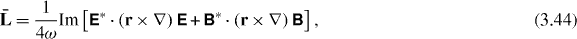

When deriving (3.43) we used Maxwell equations  . Note that the time-averaged boost momentum
. Note that the time-averaged boost momentum 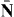 does not give a meaningful result for the monochromatic field, because N in equation (3.24) explicitly contains time t . In addition, a monochromatic field cannot be localized in three dimensions, and the energy centroid (related to the boost-momentum conservation) becomes ill-defined. At the same time, the averaged total angular-momentum density (2.35) from the symmetrized angular-momentum tensor
does not give a meaningful result for the monochromatic field, because N in equation (3.24) explicitly contains time t . In addition, a monochromatic field cannot be localized in three dimensions, and the energy centroid (related to the boost-momentum conservation) becomes ill-defined. At the same time, the averaged total angular-momentum density (2.35) from the symmetrized angular-momentum tensor  is naturally expressed via the energy and momentum (3.40):
is naturally expressed via the energy and momentum (3.40):

The dual-symmetric and gauge-invariant expressions (3.40)–(3.45) coincide with results obtained in different contexts in recent works [3, 33, 42, 44, 51, 53]. In particular, equations (3.41) and (3.45) demonstrate the proportionality of the helicity and spin densities to Lipkin's zilch pseudo-scalar and pseudo-vector [33–35]. Remarkably, for a monochromatic field, the time averages of the dual-asymmetric helicity (2.9) and the true helicity (2.11) or (3.14) coincide with each other:

At the same time, all other quantities—energy, spin and orbital energy fluxes and angular momenta—remain essentially different in their dual-symmetric and asymmetric 'tilded' versions:
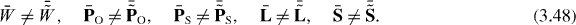
Equation (3.47) explains why the false dual-asymmetric helicity  is associated with the dual-symmetric conserved Lipkin's zilch in [34]: monochromatic fields and integral quantities are considered there. Rigorously speaking, the integral characteristics diverge for monochromatic fields, as it cannot be localized and contains an infinite number of photons. Note also that the spin energy flux density (3.43) represents the curl of the spin density (3.45):
is associated with the dual-symmetric conserved Lipkin's zilch in [34]: monochromatic fields and integral quantities are considered there. Rigorously speaking, the integral characteristics diverge for monochromatic fields, as it cannot be localized and contains an infinite number of photons. Note also that the spin energy flux density (3.43) represents the curl of the spin density (3.45):  . This reveals the divergence-less character of the spin current. According to (3.28) and (3.29) this current makes no contribution to the integral momentum of the field, and only generates a purely intrinsic spin angular momentum [42, 48–53]. An entirely similar spin current generates the spin of the relativistic quantum electron [48–50, 57].
. This reveals the divergence-less character of the spin current. According to (3.28) and (3.29) this current makes no contribution to the integral momentum of the field, and only generates a purely intrinsic spin angular momentum [42, 48–53]. An entirely similar spin current generates the spin of the relativistic quantum electron [48–50, 57].
Importantly, equations (3.40)–(3.45) reveal profound quantum-mechanical analogies and can be reduced to the following simple forms:






Here we used the dual-symmetric state vector
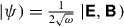 , the inner product assumes the real part of the scalar product (without volume integration, since here we calculate local densities), whereas the operators are
, the inner product assumes the real part of the scalar product (without volume integration, since here we calculate local densities), whereas the operators are
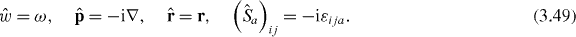
The spin-1 matrix operator 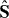 acts as
acts as ![${{\boldsymbol{\sf O}}^* \cdot ( {{\hat{\bf S}}} ){\boldsymbol{\sf O}}} = {\rm Im}\left[ {{\boldsymbol{\sf O}}^* \times {\boldsymbol{\sf O}}} \right]$](https://content.cld.iop.org/journals/1367-2630/15/3/033026/revision1/nj448360ieqn93.gif) , and we also used Maxwell equations and the dispersion relation p2 = ω2 . Importantly, within the standard electromagnetism of section 2, the dual-asymmetric 'tilded' quantities (3.40')–(3.45') would be given by the same equations, with the same operators, but with the dual-asymmetric state vector
, and we also used Maxwell equations and the dispersion relation p2 = ω2 . Importantly, within the standard electromagnetism of section 2, the dual-asymmetric 'tilded' quantities (3.40')–(3.45') would be given by the same equations, with the same operators, but with the dual-asymmetric state vector
 . But some of these quantities (e.g. the false energy
. But some of these quantities (e.g. the false energy 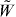 ) are not conserved, and even the standard electromagnetism operates with the proper energy W which requires the use of the dual-symmetric state vector
) are not conserved, and even the standard electromagnetism operates with the proper energy W which requires the use of the dual-symmetric state vector 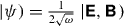 (see, e.g., [44, 45], where the Riemann–Silberstein vector is considered as a natural choice for the photon wave function). Therefore, within the standard electromagnetism, it is impossible to write all the characteristics of the field in a consistent quantum-like operator form (3.40')–(3.45'). Here we do not consider quantization of the fields, but even the first-quantization formalism for classical fields shows that only the dual-symmetric formulation of electromagnetism yields meaningful and mutually consistent expectation values of quantum spin and orbital operators with a suitable state vector.
(see, e.g., [44, 45], where the Riemann–Silberstein vector is considered as a natural choice for the photon wave function). Therefore, within the standard electromagnetism, it is impossible to write all the characteristics of the field in a consistent quantum-like operator form (3.40')–(3.45'). Here we do not consider quantization of the fields, but even the first-quantization formalism for classical fields shows that only the dual-symmetric formulation of electromagnetism yields meaningful and mutually consistent expectation values of quantum spin and orbital operators with a suitable state vector.
Equations (3.40')–(3.45') allow a straightforward transition to the Fourier (momentum) representation [23, 27, 28, 33, 42, 44, 51, 52]:  . In doing so, one merely has to change the momentum and coordinate operators (3.49) as
. In doing so, one merely has to change the momentum and coordinate operators (3.49) as 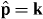 and
and 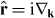 . In the Fourier representation, it becomes clear that the helicity represents the difference in number of the right-hand and left-hand circularly polarized plane waves [23, 27, 28, 33–35]. If the field has a well-defined quantum helicity σ = ± 1 (i.e. the Fourier spectrum of the field contains only plane waves with one circular polarization σ ), then the complex electric and magnetic amplitudes are related as
. In the Fourier representation, it becomes clear that the helicity represents the difference in number of the right-hand and left-hand circularly polarized plane waves [23, 27, 28, 33–35]. If the field has a well-defined quantum helicity σ = ± 1 (i.e. the Fourier spectrum of the field contains only plane waves with one circular polarization σ ), then the complex electric and magnetic amplitudes are related as  . In this case, the helicity (3.41), spin (3.45), energy and momentum (3.40) become simply related as
. In this case, the helicity (3.41), spin (3.45), energy and momentum (3.40) become simply related as

Then, the helicity conservation (2.11), (2.12) or (3.13), (3.14) becomes equivalent to the energy conservation (Poynting theorem) (2.16), (2.17) or (3.16), (3.17) [33]. Furthermore, in such a pure helicity state, the electric and magnetic contributions are equal in all quantities (3.40)–(3.46), so that the standard calculations of section 2 and the dual-symmetric formalism are equivalent. However, for a generic field containing different helicity states in the Fourier spectrum, the helicity conservation represents a truly independent conservation law, whereas the dual-symmetric quantities (3.40), (3.42)–(3.45) differ from their 'tilded' counterparts obtained within the standard approach.
4. Observability and relation to quantum weak measurements
Here, we briefly discuss observable consequences of the dual symmetry and quantities that make a difference between the standard and dual formulations of electromagnetism. It is important to emphasize that although we discuss the properties of the free electromagnetic field, they are experimentally observed only via various light–matter interactions (any detector involves matter).
Firstly, we note that the dual symmetry and conservation of helicity
H are not abstract properties, but they have immediately observable consequences. In particular, it follows that any perturbation which does not break the electric–magnetic symmetry will keep the electromagnetic helicity as an exact invariant of the problem. This explains the conservation of the helicity of photons in an arbitrary gravitational field [45]. Furthermore, the helicity turns out to be exactly conserved in any optical scattering on macroscopic objects with equal electric and magnetic constants ε = μ [36, 45, 58], which is usually interpreted as matching of optical impedances 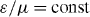 . At the same time, any coupling with matter having asymmetric electric and magnetic properties will in general produce a conversion between the two helicity states of photons. As the helicity conservation involves the spin angular momentum, the conversion of the helicity is usually accompanied by a conversion between the spin and orbital angular momenta [36, 59], although the opposite is not generally true. Thus, the dual symmetry and helicity conservation offer an additional integral of motion which can be used in the analysis of various optical interactions.
. At the same time, any coupling with matter having asymmetric electric and magnetic properties will in general produce a conversion between the two helicity states of photons. As the helicity conservation involves the spin angular momentum, the conversion of the helicity is usually accompanied by a conversion between the spin and orbital angular momenta [36, 59], although the opposite is not generally true. Thus, the dual symmetry and helicity conservation offer an additional integral of motion which can be used in the analysis of various optical interactions.
Secondly, let us consider physical quantities which appear to be essentially different in the standard and dual versions of electromagnetism—the spin and orbital angular momenta of light, S and L. Although quantum electrodynamics sometimes concerns the separation of the spin and orbital parts of the photon angular momentum as physically meaningless, modern optics points to the independent observability of these quantities [41, 54, 55]. Indeed, locally the orbital and spin parts of the angular momenta of light cause qualitatively different motions (orbiting and spinning) of probe particles immersed in the field [54]. In quantum electrodynamics, the photon interaction with an atom also causes changes in the extrinsic and intrinsic angular momentum of the atom, quite similar to the orbital and spinning motion of the classical probe particle [41]. In addition, the integral value of the intrinsic orbital angular momentum is closely related to the spatial distribution of the field intensity and its localizability [42, 60]. Thus, if we regard the spin and orbital angular momenta of the electromagnetic field as separately measurable quantities (either in their local or integral values), this allows us to discriminate between the standard and dual electromagnetic theories.
The spin and orbital angular momenta of the field are generated, respectively, by spin and orbital energy fluxes PS and PO [3, 37, 42, 48–53], see equations (2.33) and (3.29), which together form the Poynting vector P = PO + PS . These local quantities are different in the standard and dual theories. Remarkably, although the Poynting vector P is usually considered as a physically meaningful quantity, it turns out that the local orbital energy flux PO (i.e. the canonical momentum density) can be measured more easily and in a more straightforward way via the motion of a probe particle [51, 54, 56]. Indeed, it is the orbital energy flux that transports energy, represents the local expectation value of the momentum operator (see equations (3.42) and (3.42')), and can be associated with the standard quantum-mechanical probability current [3, 48–50]. (In contrast, the spin energy flux, PS , is sometimes regarded as a virtual divergence-less current which cannot be observed per se [48–50].) Thus, measuring the canonical momentum density PO , one can also discriminate between the standard and dual theories.
The observability of the local densities and currents is an important problem by itself. In standard field theories, all local densities are usually interpreted as unobservable auxiliary quantities, whereas only the integral energy, momentum and angular momentum of the field make physical sense. However, classical optics naturally regard the local energy density W , momentum density P and other currents as meaningful and observable characteristics of the field [3, 51]. Moreover, it seems that quantum measurements also allow the detection of local currents [3, 61]. This is related to the concept of quantum weak measurements [62–64]. Both classical-optics and quantum weak-measurement approaches are based here on a natural idea: a straightforward way to measure a current of any flow is to place a small probe particle in the flow and to trace its motion.
In classical optical fields, a small particle experiences the action of the radiation pressure force and moves proportional to the local momentum density of the field [54, 56]. For small Rayleigh particles this force is proportional to the canonical (orbital) momentum density PO rather than to the Poynting vector P [3, 56]. Furthermore, the particle spins proportionally to the local spin density of the field [54]. Thus, by measuring the velocity of the linear motion of the particle and the angular velocity of its spinning motion, one can determine the local momentum density PO (hence, also the orbital angular-momentum density L = r × PO ) and the spin density S.
The same experiments can be interpreted within the quantum weak-measurement picture [3, 61–64]. Let us represent the field distribution as a quantum photon state  with indeterminate coordinate (i.e. the spread is much larger than the size of the probe particle). If this photon interacts with the particle located at r = r0 , this fixes the coordinate of the photon, i.e. the particle post-selects the photon in the state with well-defined coordinate,
with indeterminate coordinate (i.e. the spread is much larger than the size of the probe particle). If this photon interacts with the particle located at r = r0 , this fixes the coordinate of the photon, i.e. the particle post-selects the photon in the state with well-defined coordinate, 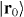 . Although the photon–particle interaction has a very low probability
. Although the photon–particle interaction has a very low probability  , averaging over many events (as happens with classical multi-photon fields) provides simultaneous information about the position of the photon and its local momentum (current). This is expressed via the following quantum weak-measurement equation [3, 61]:
, averaging over many events (as happens with classical multi-photon fields) provides simultaneous information about the position of the photon and its local momentum (current). This is expressed via the following quantum weak-measurement equation [3, 61]:
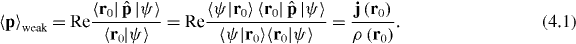
Here 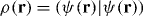 and
and 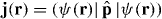 are the local probability density and current in the field. As described in section 3.3, we have
are the local probability density and current in the field. As described in section 3.3, we have 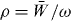 and
and 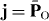 for a monochromatic electromagnetic field, so that the quantum weak measurement of the field momentum is essentially the local measurements of the orbital current PO . Recently, the same weak-measurement scheme (4.1) (but employing another, non-particle, detector) was successfully used to detect the local photon 'trajectories' in the double-slit experiment [65]. These Bohmian trajectories are nothing but the streamlines of the orbital energy flux PO. Furthermore, the momentum exchange in the resonant interaction between a moving atom and an electromagnetic wave also reveals the local value of the canonical momentum. This is seen, e.g., in the Doppler-shift experiments with evanescent waves, where
for a monochromatic electromagnetic field, so that the quantum weak measurement of the field momentum is essentially the local measurements of the orbital current PO . Recently, the same weak-measurement scheme (4.1) (but employing another, non-particle, detector) was successfully used to detect the local photon 'trajectories' in the double-slit experiment [65]. These Bohmian trajectories are nothing but the streamlines of the orbital energy flux PO. Furthermore, the momentum exchange in the resonant interaction between a moving atom and an electromagnetic wave also reveals the local value of the canonical momentum. This is seen, e.g., in the Doppler-shift experiments with evanescent waves, where 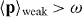 [66], in agreement with a superluminal character of the orbital energy flux discussed in [53]. For the local measurements of the spin angular-momentum density via a spinning particle, one can write a weak-measurement equation similar to (4.1):
[66], in agreement with a superluminal character of the orbital energy flux discussed in [53]. For the local measurements of the spin angular-momentum density via a spinning particle, one can write a weak-measurement equation similar to (4.1):
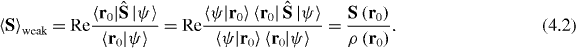
It might seem that the above local measurements of optical currents and angular momenta solve the problem and result in unambiguous and objective determination of the field properties. However, this is not so. The problem is that the results of the measurements based on a probe particle (i.e. involving light–matter interaction) crucially depend on the properties of the particle. For instance, the light scattering on a small dielectric particle can be considered in the electric-dipole (Rayleigh) approximation, and then it turns out that the radiation force that pushes the particle is proportional to the electric orbital momentum density [3, 56] (cf equation (3.42)):

This is clearly a dual-asymmetric expression consistent with the standard electromagnetism and momentum density 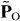 defined in equation (2.20). However, if the same measurement is made by a small magnetic particle [56, 67] and the interaction has a magnetic-dipole character, the radiation force will be proportional to a similar magnetic expression for the orbital momentum density:
defined in equation (2.20). However, if the same measurement is made by a small magnetic particle [56, 67] and the interaction has a magnetic-dipole character, the radiation force will be proportional to a similar magnetic expression for the orbital momentum density:

Finally, only a particle with equivalent electric and magnetic properties will measure the dual-symmetric orbital momentum density PO , equations (3.19) and (3.42):
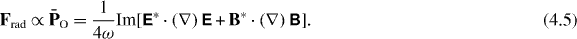
Similar observations can be made for measurements of the spin and orbital angular momenta. For instance, in the paper [41] the authors point to the separate observability of the spin and orbital angular momenta of light, and analyze the photon interaction with an atom. This interaction is approximated by the electric-dipole coupling, and, due to this, the changes in the atomic states would measure the dual-asymmetric angular momenta 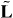 and
and 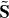 following from the standard approach.
following from the standard approach.
Hence, the results of measurements of the dynamical characteristics of the electromagnetic field depend critically on the properties of the measuring device. They can naturally be dual-asymmetric as a consequence of the electric–magnetic asymmetry in matter (the absence of magnetic charges). However, this does not mean that we should ascribe dual-asymmetric features to the free electromagnetic field. Indeed, in practice, it is difficult even to measure the energy density  or the Poynting vector
or the Poynting vector 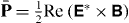 , which are natural dual-symmetric conserved characteristics of the field. Typically, only the electric energy density, i.e.
, which are natural dual-symmetric conserved characteristics of the field. Typically, only the electric energy density, i.e. 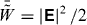 , can be measured. Obviously, such an asymmetry of measuring interactions does not suggest that we should associate the non-conserved dual-asymmetric quantity
, can be measured. Obviously, such an asymmetry of measuring interactions does not suggest that we should associate the non-conserved dual-asymmetric quantity 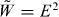 with the energy density of the electromagnetic field! Thus, in spite of such difficulties with measurements, if we would like to ascribe fundamental dynamical characteristics to the electromagnetic field per se, we have to maintain the electric–magnetic symmetry which is inherent in the free field. Naturally, only the dual electromagnetic theory suggested here provides such characteristics of the fields. Formally, they can be thought of as a result of measurements made by an electromagnetically neutral (e.g. gravitational or macroscopic with ε = μ ) detector.
with the energy density of the electromagnetic field! Thus, in spite of such difficulties with measurements, if we would like to ascribe fundamental dynamical characteristics to the electromagnetic field per se, we have to maintain the electric–magnetic symmetry which is inherent in the free field. Naturally, only the dual electromagnetic theory suggested here provides such characteristics of the fields. Formally, they can be thought of as a result of measurements made by an electromagnetically neutral (e.g. gravitational or macroscopic with ε = μ ) detector.
To conclude this section and support our arguments, let us mention two recent examples where an improper dual-asymmetric interpretation of the field and measurement properties brought about confusing results.
Firstly, Tang and Cohen [29, 30] introduced a novel concept of 'superchiral light', i.e. light that shows optical chirality (helicity) higher than that of a circularly polarized plane wave. They observed that the so-called dissymmetry factor in local light interaction with a chiral particle can be anomalously large in such 'superchiral' field configurations. In fact, it was shown in [33, 34] that this enhanced chiral response arises not from extraordinary properties of the optical chirality or helicity density—it can never exceed the limit 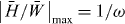 of a circularly polarized plane wave. Instead, this is a property of the particle involving the electric-dipole interaction which is sensitive only to the electric energy density, i.e.
of a circularly polarized plane wave. Instead, this is a property of the particle involving the electric-dipole interaction which is sensitive only to the electric energy density, i.e.  . This electric energy density appears in the denominator of the dissymmetry factor and causes its enhancement in the vicinity of the electric-field nodes. If a magnetic-dipole coupling of equal strength were also present, the dissymmetry factor would have never been larger than that of a circularly polarized plane wave [68].
. This electric energy density appears in the denominator of the dissymmetry factor and causes its enhancement in the vicinity of the electric-field nodes. If a magnetic-dipole coupling of equal strength were also present, the dissymmetry factor would have never been larger than that of a circularly polarized plane wave [68].
Secondly, some of us described an unusual transverse spin angular momentum of linearly polarized evanescent (e.g. surface plasmon–polariton) electromagnetic waves [53]. This was followed by the paper [69] which claims that such a spin is present only in transverse-magnetic modes and absent in transverse-electric waves, and even that 'the rotation of the magnetic field cannot generate spin'. Such misleading conclusions appeared because of the use of the dual-asymmetric definition of the spin density  ,
,  , appearing in standard electromagnetism. Obviously, the presence of the angular momentum of the free field should not be attributed solely to the electric rather than magnetic field. The use of the proper dual-symmetric spin density S and equation (3.45) removes this problem, so that both transverse-electric and transverse-magnetic evanescent modes carry the same spin angular momentum [53].
, appearing in standard electromagnetism. Obviously, the presence of the angular momentum of the free field should not be attributed solely to the electric rather than magnetic field. The use of the proper dual-symmetric spin density S and equation (3.45) removes this problem, so that both transverse-electric and transverse-magnetic evanescent modes carry the same spin angular momentum [53].
5. Concluding remarks
To summarize, we have constructed a classical Lagrangian electromagnetism possessing dual symmetry with respect to the electric and magnetic fields. This symmetry is a fundamental property of Maxwell equations which corresponds to the helicity conservation law, where the helicity flux density coincides with the spin angular-momentum density. Therefore, we conclude that the dual symmetry is also closely related to the separation of the spin and orbital degrees of freedom in the electromagnetic field. It is important to note that such a separation can only be made using canonical Noether currents corresponding to the Poincaré symmetries (i.e. canonical energy–momentum and angular-momentum tensors).
The standard Lagrangian formulation of electromagnetism lacks the dual symmetry, and the helicity conservation is derived in a non-trivial way [12]. Components of the canonical energy–momentum and angular-momentum tensors also lack dual symmetry and contain important discrepancies. In particular, spin density differs from the helicity flux density, a false (non-conserved) energy density appears in the boost momentum, etc. In addition, both local and integral values of the spin and orbital angular momenta are not dual symmetric, which is bizarre for the free electromagnetic field.
In contrast, the dual electromagnetism suggested in this paper is free of all these drawbacks. The helicity conservation naturally appears here as the basic current from the 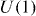 gauge transformation. The canonical energy–momentum and angular-momentum tensors provide a meaningful and dual-symmetric separation of the spin and orbital degrees of freedom of the field. In particular, the spin density coincides with the helicity flux density, the true energy density appears in the boost momentum, and so on. The spin and orbital momentum and angular-momentum densities following from the dual electromagnetism are in agreement with the expressions suggested recently within several other approaches [3, 42–44]. Thus, the dual electromagnetic theory inherently contains straightforward and physically meaningful descriptions of the helicity, spin and orbital characteristics of light. A comparative summary of the main conserved quantities in the standard and dual electromagnetic theories is shown in figure 1.
gauge transformation. The canonical energy–momentum and angular-momentum tensors provide a meaningful and dual-symmetric separation of the spin and orbital degrees of freedom of the field. In particular, the spin density coincides with the helicity flux density, the true energy density appears in the boost momentum, and so on. The spin and orbital momentum and angular-momentum densities following from the dual electromagnetism are in agreement with the expressions suggested recently within several other approaches [3, 42–44]. Thus, the dual electromagnetic theory inherently contains straightforward and physically meaningful descriptions of the helicity, spin and orbital characteristics of light. A comparative summary of the main conserved quantities in the standard and dual electromagnetic theories is shown in figure 1.
In addition to the formal consideration of the characteristics of the free electromagnetic field, we have discussed their measurability and possible observable consequences of the two theories. It should be taken into account that any measurement of the field characteristics involves light–matter interactions and can critically depend on the properties of the measuring device. Therefore, the dual symmetry can be broken by the measuring device, which is typically sensitive to the electric rather than magnetic parts of the optical fields. Understanding the inherent dual symmetry of the free field and asymmetry of matter offers a powerful tool for the analysis of light–matter interactions and suggests clarifications and deeper interpretations of a number of experimental and theoretical results [29, 30, 36, 41, 53–56, 58, 59, 67–69]. At the same time, the dual asymmetry of measuring devices does not mean that one should ascribe dual-asymmetric non-conserved characteristics (e.g. the false energy density 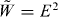 ) to the electromagnetic field. Therefore, all fundamental characteristics of the free field must be dual-symmetric, as they appear only within the dual electromagnetism.
) to the electromagnetic field. Therefore, all fundamental characteristics of the free field must be dual-symmetric, as they appear only within the dual electromagnetism.
Importantly, the spin and orbital angular momenta and local energy fluxes are regarded as separably observable quantities in optics. Probe particles move and spin, experiencing the local action of orbital and spin degrees of freedom of the field. If such particles have equivalent electric and magnetic properties, their evolution corresponds to the spin density and orbital energy flux which appear in the dual electromagnetism. Furthermore, the spatial distribution of the field energy density (including both electric and magnetic parts) is directly related to the orbital angular momentum of the field [42, 60]. This distribution is consistent with the dual-symmetric orbital angular momentum obtained in our theory rather than with that following from the standard electromagnetic theory.
Thus, it seems that there are grounds to discriminate between the two formulations of electromagnetism in favor of the dual version. This raises a provocative question on classical field theory: can we discriminate between different field Lagrangians leading to the same equations of motion? The usually assumed answer is 'no'. However, from our consideration it follows that if the spin and orbital angular momenta and local currents are measurable, then the answer is 'yes'. (Different Lagrangians yield different Noether currents and different spin and orbital angular momenta.) A similar question was considered in a recent paper [61], discussing non-relativistic quantum mechanics and ways to discriminate between different possible definitions of the local probability current. It is argued there that quantum weak measurements of the field momentum allow measurements of the local current and enable the singling out one particular definition of the current. Indeed, this was experimentally implemented for an electromagnetic field in [65]. Thus, it seems that modern concepts of quantum measurements and classical field theories are in contradiction with each other. The probable resolution of this contradiction lies in the separation of the 'measured' and 'measuring' systems. Light and matter are considered as a single macro-system in field theory, while 'matter measures light' in the quantum weak-measurement approach. Apparently, both points of view make physical sense in their corresponding areas of validity.
Finally, we have considered only classical electromagnetism. Field quantization and possible manifestations of the dual electromagnetism in quantum electrodynamics raise intriguing and non-trivial questions. Interaction with matter must be included in such a theory even if it only appears via virtual particles. Should the matter include magnetic monopoles or should there be a dual-symmetry breaking mechanism? Will this affect observable quantities in quantum electrodynamics, such as atomic-level shifts, particle-scattering cross-section, etc? We hope that this paper motivates the analysis of quantum aspects of dual electromagnetism.
Acknowledgments
We are grateful to Stanley Deser and Yakov Shnir for fruitful and critical correspondence, to Ioannis Bakas, Michael Berry, Yuri Bliokh, Mark Dennis, and Abraham Kofman for helpful discussions and to Igor Ivanov for bringing [20] to our attention. This work was partially supported by the European Commission (Marie Curie Action), Army Research Office, JSPS-RFBR contract no. 12-02-92100, Grant-in-Aid for Scientific Research (S) from MEXT Kakenhi on quantum cybernetics and the Japan Society for the Promotion of Science via its FIRST program.
After posting the first version of this paper in arXiv, another paper by Cameron and Barnett discussing dual-symmetric electromagnetism based on the Lagrangian (3.2) was submitted to the New J. Phys. [70]. This also brought some previous relevant works [71–73] to our attention. Papers [70–73] examine a number of additional conservation laws: Lipkin's zilches and those corresponding to special conformal symmetries. However, they do not treat canonical Noether currents corresponding to the Poincaré symmetries, which provide a separation of the spin and orbital degrees of freedom. Therefore, while Cameron and Barnett consider the dual-symmetric formalism as 'an alternative rather than a replacement' to the standard approach, we argue that the choice of the Lagrangian makes a difference and has important physical consequences. Note also that our complex Riemann–Silberstein-like formalism sheds light on the appearance of the 'trivial partners' in the conservation laws discussed in [70]. Using the complex potential Xα = Aα + i Cα , one can see that the partner conformal transformations (6.18) in [70] represent regular conformal transformations (6.11) but with imaginary parameters. In particular, this explains the partner relations between the spin rotation and boost symmetries—a Lorentz boost is a rotation of the Riemann–Silberstein vector by an imaginary angle [38]. Correspondingly, the partner Noether currents are given by the real and imaginary parts of the same complex tensors in our formalism.



