Abstract
The Affleck–Dine mechanism is an attractive scenario for generating the observed baryon asymmetry of the universe utilizing flat directions in the scalar potential of supersymmetric theories. In this mini review, we describe this mechanism in its original version, its explicit realization within the minimal supersymmetric standard model and its variants. We discuss the formation of a condensate along the flat directions in the inflationary era, its post-inflationary evolution leading to baryogenesis and its fate. In some cases the condensate may fragment into non-topological solitons, known as Q-balls, during its evolution. In models of gravity-mediated supersymmetry breaking, the Q-balls can be long-lived, in which case their decay will be the source of all baryons and dark matter in the form of the lightest supersymmetric particle. In models of gauge-mediated supersymmetry breaking, the Q-balls can be absolutely stable and form dark matter that can be searched for directly.
Export citation and abstract BibTeX RIS
Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
During primordial inflation [1], all scalar fields with a shallow potential can acquire non-zero vacuum expectation values (VEVs). Supersymmetric extensions of the standard model (SM) include plenty of such scalar fields, called flat directions, along which the scalar potential identically vanishes in the limit of exact supersymmetry (SUSY). An important example is flat directions of the minimal supersymmetric standard model (MSSM), which comprise the scalar partners of quarks and leptons, called squark and slepton, and Higgs fields.
Affleck and Dine proposed a novel scenario for generating baryon asymmetry of the universe that utilizes supersymmetric flat directions [2]. According to this scenario, a condensate forms along the flat direction during the inflationary epoch. The non-zero VEV of the condensate spontaneously breaks C and CP. As a result, during the post-inflationary evolution, baryon number violating operators (which are induced by new physics at a high scale) result in a rotating trajectory for the VEV. If the flat direction has a non-zero baryon number B, the rotating condensate carries a baryon asymmetry. This asymmetry is transferred to ordinary particles when the condensate decays to fermions.
In this mini review, we present a brief description of the Affleck–Dine (AD) mechanism. A detailed treatment of the supersymmetric flat directions and their cosmological consequences can be found in the extensive reviews that exist in the literature [3, 4]. In this paper, we highlight the essential features of this mechanism including some of the more recent developments related to it.
This paper is organized as follows. In section 2, we describe the AD scenario within MSSM. In section 3, we discuss the role of thermal effects in the flat direction dynamics and vice versa. We briefly mention variants of the AD scenario in various contexts in section 4. In section 5, we discuss a possible fragmentation of the flat direction oscillations into Q-balls and its consequences. The conclusions are presented in section 6.
2. Affleck–Dine (AD) baryogenesis within the minimal supersymmetric standard model (MSSM)
2.1. MSSM flat directions
The superpotential for MSSM is given by [5]
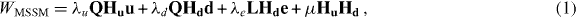
where Hu,Hd,Q,L,u,d,e are chiral superfields representing the two Higgs fields (and their Higgsino partners), left-handed (LH) (s)quark doublets, right-handed (RH) up- and down-type (s)quarks, LH (s)lepton, doublets and RH (s)leptons respectively. The dimensionless Yukawa couplings λu,λd,λe are 3 × 3 matrices in the flavor space, and we have omitted the gauge and flavor indices. The last term is the μ term, which is a supersymmetric version of the SM Higgs boson mass.
The field space of supersymmetric theories contains many directions along which the D-term contributions to the scalar potential identically vanish. The scalar potential along these 'flat' directions arises from F-terms and SUSY breaking contributions. A very interesting class of flat directions is those made up of SUSY partners of the SM fermions, namely the squarks and sleptons, and the Higgs fields. The D-flat directions in MSSM are parameterized by gauge invariant monomials of the chiral superfields [6, 7]. Many of these directions are also F-flat in the sense that their potential does not receive any contribution from the MSSM superpotential (1). There are nearly 300 such directions [7].
MSSM flat directions are lifted by SUSY breaking terms and higher order terms in the superpotential. The latter arise from the effect of new physics above a high scale M (typically Planck or string scale), which appears as non-renormalizable superpotential terms (n ⩾ 4) of the form

where Φ is the superfield comprising the flat direction ϕ and its fermionic partner, and 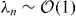 . MSSM flat directions typically carry a baryon and /or lepton number. For example, consider the cases when ϕ represents the LLe, udd and HuL flat directions, respectively. Then the baryon number B and lepton number L carried by ϕ are B = 0 and L = + 1, B = −1 and L = 0, B = 0 and L = + 1, respectively. The superpotential terms that lift ϕ are W ∼ (LLe)2, (udd)2 and (HuL)2, respectively.
. MSSM flat directions typically carry a baryon and /or lepton number. For example, consider the cases when ϕ represents the LLe, udd and HuL flat directions, respectively. Then the baryon number B and lepton number L carried by ϕ are B = 0 and L = + 1, B = −1 and L = 0, B = 0 and L = + 1, respectively. The superpotential terms that lift ϕ are W ∼ (LLe)2, (udd)2 and (HuL)2, respectively.
Low-energy SUSY breaking results in soft terms in the scalar potential. In addition, SUSY breaking by the non-zero energy density of the universe contributes to the flat direction potential. The scalar potential along a flat direction can then be written as [6]
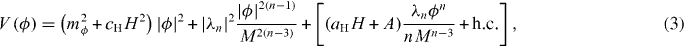
where n ⩾ 4. The three terms on the right-hand side of this equation represent, respectively, the sum of low-energy and Hubble-induced soft mass terms, the contribution of the non-renormalizable superpotential term and the sum of low-energy and Hubble-induced A-terms. In the above equation, H is the Hubble expansion rate and  .
.
2.2. Flat direction dynamics and generation of baryon asymmetry
The role of flat directions in the early universe crucially depends on cH, see equation (3). If cH ≳ 1, the flat direction mass exceeds the Hubble expansion rate during inflation HI. Then, due to fast rolling, the condensate would settle down to the origin of its potential during inflation, and would remain there at all times. Therefore the flat direction will have no interesting consequences in this case. Note, however, that it is possible to find a local minimum for a very large, aH, such that a2H > 4(n − 1)λ2nc2H. In this case, the condensate can play an interesting role similar to what happens when cH < 0 [8] (which will be discussed shortly).
If 0 < cH ≪ 1, quantum fluctuations are accumulated along the flat direction according to a random walk giving rise to a coherent state. The flat direction VEV is in this way displaced from the origin and its variance follows 〈ϕ2〉1/2 ∼ H2I/mϕ. This, however, assumes that other fields that are coupled to the flat direction are not excited in this fashion. If one considers the growth of quantum fluctuation along all independent fields, the maximum VEV that the flat direction can reach will be much smaller [9].
The case with cH < 0 is more interesting. A negative cH can arise at the tree level [6] or as a result of radiative correction [10, 11]. The flat direction VEV is in this case driven away from the origin and quickly settles at a large value 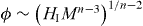 .
.
After inflation, the flat direction VEV slides down to an instantaneous value: 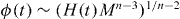 . Once H(t) ≃ mϕ, the soft SUSY breaking mass term in the potential takes over and the flat direction starts oscillating around its origin with an initial amplitude
. Once H(t) ≃ mϕ, the soft SUSY breaking mass term in the potential takes over and the flat direction starts oscillating around its origin with an initial amplitude

If M = MP, we will have ϕ0 ∼ 1010 GeV for n = 4, and ϕ0 ∼ 1016 GeV for n = 9. The mismatch between the phases of A-terms from low-energy and Hubble-induced SUSY breaking yields a torque and gives rise to rotational motion of the flat direction VEV [6]. If the flat direction has a non-zero baryon and/or lepton number, the rotating condensate will carry a baryon and/or lepton asymmetry [2, 6].
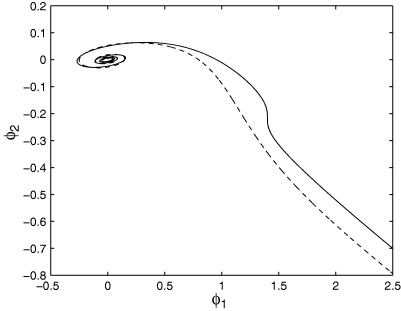
The dynamics of the AD condensate is non-trivial as shown in figure 1. The baryon/lepton number density is given by 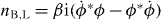 , where β is the corresponding baryon/lepton charge of the AD field. The time evolution of nB,L follows
, where β is the corresponding baryon/lepton charge of the AD field. The time evolution of nB,L follows
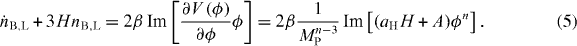
The comoving density of the baryon/lepton number is given by
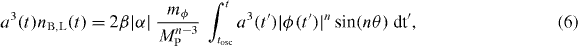
where a(t) is the scale factor of the universe, and tosc ∼ m−1ϕ is the time at the onset of ϕ oscillations. 'α' denotes the CP-violating phase that arises because of the mismatch between the phases of the low-energy and Hubble-induced A-terms, and can be parameterized by sin δ.
Figure 1. The trajectory of the AD condensate ϕ = ϕ1 + iϕ2 for a gravity-mediated case with an initial CP-violating phase θi = −π/10 [3]. The potential is lifted by non-renormalizable terms of order n = 4 (solid) and n = 6 (dashed), see equation (3). The units of ϕ1 and ϕ2 are arbitrary, but the relative scales correspond to the initial condition.
Download figure:
Standard imageNote that in the above equation the integrand falls off very quickly since the amplitude of oscillations is redshifted according to |ϕ(t)|n∝a−n(t) (recall that n > 3). As a result, the generated asymmetry will reach its final value after a few oscillations, which is given by [6]
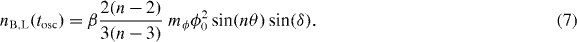
After using equation (4), with M = MP, and for  , we find that
, we find that
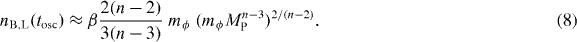
2.3. Flat direction decay and the baryon-to-entropy ratio
The baryon and/or lepton asymmetry carried by the AD field will be eventually transferred to fermions when it decays. The rotating condensate induces a large mass ∼y|ϕ| for the fields coupled to it (y being a gauge or Yukawa coupling). The one-particle decay will be kinematically forbidden as long as y|ϕ| ≳ mϕ. Therefore the condensate VEV will only be subject to redshift by Hubble expansion initially. The AD field eventually decays, yielding a net baryon/lepton-to-entropy ratio that is given by [3]
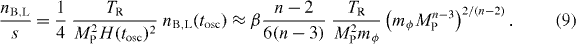
Here s = (2π2/45)g*T3R is the entropy density of the universe when transition from inflation to a radiation-dominated universe is complete, with g* being the number of relativistic degrees of freedom and TR being the reheat temperature of the universe. We have used H(tosc) ≈ mϕ and equation (8) to obtain the final result. For n = 4, we have
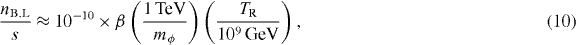
and for n = 6
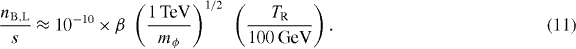
This ratio remains frozen during the subsequent evolution of the universe unless there is additional entropy production at a later time.
We note that any lepton asymmetry is partially converted by electroweak sphalerons into a baryon asymmetry according to nB = (8/23)nB−L [12]. Therefore, all that is actually needed is that the AD field carries a non-zero B − L so that the generated asymmetry survives washout by the sphalerons. An interesting scenario is AD leptogenesis driven by the HuL flat direction for which B = 0 and L = + 1 [13]. As mentioned above, the non-renormalizable superpotential term that lifts the flat direction is (HuL)2, which also contributes to the light neutrino masses. It is therefore a rather predictive scenario for obtaining the observed baryon asymmetry, yielding [14]
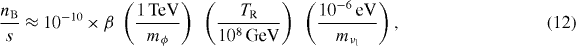
where mνl denotes the lightest neutrino mass.
We close this subsection by making a comment on the decay of the AD field. It has been shown that a rotating condensate can give rise to non-perturbative particle production [15]. Although efficient, this however does not lead to a fast decay of the AD field [16]. The momenta of particles thus produced are of the order of mϕ, which implies that they quickly become non-relativistic due to the Hubble redshift. These particles will decay perturbatively at late times, as mentioned above. Therefore non-perturbative effects do not alter the picture presented here in a significant way. This is very different from non-perturbative particle production after inflation, which typically results in a very rapid decay of the inflaton oscillations [17]. The difference can be understood based on the trajectory of the scalar field motion in the two cases. Oscillations of the inflaton field can result in the production of quanta whose momenta are much higher than the frequency of oscillations. On the other hand, a rotating AD condensate carries a baryon/lepton number whose conservation along with the conservation of energy inhibits populating high-momentum modes and thus a fast decay, via non-perturbative effects [16].
3. Flat directions and thermal effects
3.1. Thermal effects on AD baryogenesis
In the above estimation of baryon asymmetry, we have ignored the finite-temperature corrections to the flat direction potential. As a source of SUSY breaking, they can have important effects on the dynamics of flat directions and hence must be included. Thermal corrections are inevitable if the inflaton decays dominantly into the visible sector fields and produces MSSM degrees of freedom, as required by observations. Since the AD condensate is made up of MSSM scalars, the finite-temperature corrections would only involve those degrees of freedom that are coupled, directly or via loops, to these scalars. The VEV of the AD condensate naturally induces a mass ∼y|ϕ| to the coupled fields, where y is an SM gauge or Yukawa coupling between the fields. Depending on whether y|ϕ| ≲ T or y|ϕ| ≫ T, with T being the temperature of the thermal bath, different situations can arise.
Thermal effects from light fields. If y|ϕ| ≲ T, the fields that are coupled to the AD field have a mass smaller than temperature and hence reach thermal equilibrium with the thermal bath. The backreaction from these fields then results in a thermal correction to the flat direction mass

where typically yT ≫ mϕ. The flat direction ϕ starts oscillating once mϕ,]eff ≃ H. Therefore, if y|ϕ| ≲ T and yT > H are both satisfied when 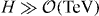 , thermal effects trigger early oscillations of the flat direction [18]. This requires that y be not too large (so that yϕ ≲ T) nor too small (so that yT > H). It turns out that for y ∼ 10−4–10−2, thermal effects can lead to early oscillations of flat directions that are lifted by superpotential terms of order 4 ⩽ n ⩽ 6 [18].
, thermal effects trigger early oscillations of the flat direction [18]. This requires that y be not too large (so that yϕ ≲ T) nor too small (so that yT > H). It turns out that for y ∼ 10−4–10−2, thermal effects can lead to early oscillations of flat directions that are lifted by superpotential terms of order 4 ⩽ n ⩽ 6 [18].
When early oscillations start at 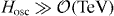 , the flat direction is in the minimum of its potential along the angular direction set by the Hubble-induced A-term, see equation (3). Rotational motion, which is a prerequisite for the generation of baryon asymmetry, can occur if a new A-term with a different phase from that of the Hubble-induced A-term appears at this time. Thermal effects [18, 19] and supergravity effects [19] can give rise to such new
A-terms:
, the flat direction is in the minimum of its potential along the angular direction set by the Hubble-induced A-term, see equation (3). Rotational motion, which is a prerequisite for the generation of baryon asymmetry, can occur if a new A-term with a different phase from that of the Hubble-induced A-term appears at this time. Thermal effects [18, 19] and supergravity effects [19] can give rise to such new
A-terms:
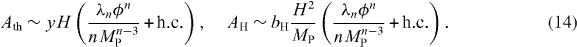
However, A-terms do not receive an enhancement similar to the flat direction mass. As a result, in the cases when thermal masses lead to early oscillations of the flat direction, the generated baryon asymmetry is typically suppressed compared to that at zero temperature [18, 19].
Thermal effects from heavy fields. If y|ϕ| ≫ T, the fields that are coupled to the AD field have a mass larger than temperature and will decouple from the thermal bath. For the same reason, they are also decoupled from the running of gauge coupling constants at finite temperature. The leading effect can then be determined by considering the free energy as a function of the coupling constant g:

Decoupling of the heavy fields from the running of g(T) amounts to a logarithmic correction to the flat direction potential [19]:

where V (ϕ) is given by the expression in equation (3) and α(T) is the gauge fine structure constant at temperature T. The prefactor a can either be positive or negative depending on whether the gauge/gaugino or the scalar/fermion fields are decoupled from the thermal bath. A positive logarithmic correction triggers early oscillations of the AD field.
To elucidate, let us consider the HuL flat direction. This flat direction VEV breaks the electroweak symmetry down to a U(1), but does not touch the strong interactions. It also induces a large mass to the top (s)quarks, thus making them heavy, through the large top Yukawa coupling. Gluon/gluino fields and those (s)quarks that are not heavy give rise to a contribution to the free energy as in equation (15), with gS(T) being the strong coupling constant at temperature T. The decoupling of top (s)quarks from the running of gS(T) results in a positive logarithmic correction to the flat direction potential:

which leads to early oscillations of the flat direction.
In summary, the exact effect of thermal corrections depends on the nature of the AD condensate. In general, however, they must be taken into account for a precise calculation of the baryon asymmetry via the AD mechanism.
3.2. The effect of flat directions on the thermal history of the universe
Our discussion of thermal effects has been based on the existence of a thermal plasma from inflaton decay at arbitrarily early times. This implicitly assumes that particles produced from decay of the inflaton immediately reach thermal equilibrium. However, it is known that reheating after inflation can be a very complicated process involving various perturbative and non-perturbative phenomena [17]. Particles produced from inflaton decay, typically, have a non-thermal distribution, and the time scale of their equilibration is model dependent. Assignment of a temperature T to the reheat plasma is only justified after full thermal equilibrium is achieved.
When in thermal equilibrium, the number density n and the energy density ρ of a relativistic species are given by n∝T3 and ρ∝T4, with T being the temperature of the thermal bath. A thermal distribution is therefore characterized by the relation n ∼ ρ3/4. Right after inflaton decay, we typically have n ≪ ρ3/4 or n ≫ ρ3/4 [17]. If inflaton decay products thermalize immediately, reheat temperature of the universe will be given by TR ∼ (ΓdMP)1/2, where Γd is the inflaton decay rate. However, thermalization may take a much longer time.
Let us consider the situation after perturbative inflaton decay, for which n ≪ ρ3/4. This implies that the number density of particles is smaller than that of a thermalized distribution, while the average energy of particles is larger than the thermal value. In order to reach full thermal equilibrium, one therefore needs inelastic reactions that increase the number of particles as well as elastic reactions that redistribute the energy among particles. It has been shown that the dominant processes for thermalization are 2 → 2 and 2 → 3 scattering processes with gauge boson exchange in the t-channel [20, 21]. Thermal equilibrium is established when these processes are efficient, i.e. their rates Γ2→2 and Γ2→3 are larger than the Hubble rate H.
Since the AD condensate is made up of fields that carry gauge quantum numbers, its VEV spontaneously breaks gauge symmetries. This induces a large mass ∼g|ϕ| to the gauge fields via the Higgs mechanism, thereby suppressing the rate of processes relevant for thermalization. If the entire SM gauge group is broken, thermalization can be delayed substantially [22]. This can happen, for example, when the udd and LLe flat directions independently acquire large VEVs. In fact, flat directions that are lifted by superpotential terms of order n ⩾ 6, see equation (3), can result in reheat temperatures well below the naive estimate TR ∼ (ΓdMP)1/2, perhaps as low as  [22]. Moreover, the inflaton decay itself may be delayed as a result of kinematic blocking due to the large masses induced by the flat direction VEV [23].
[22]. Moreover, the inflaton decay itself may be delayed as a result of kinematic blocking due to the large masses induced by the flat direction VEV [23].
Therefore flat directions can affect the thermal history of the universe significantly, which has interesting and important cosmological consequences [22].
4. Variants of the AD scenario
To discuss various variants of the AD scenario, we first briefly recount its highlights. The first of the three Sakharov's conditions [24], namely baryon number violation, is provided by the higher-order superpotential term and its corresponding A-term. The second condition, C and CP violation, is provided by the VEV of a complex scalar field and its deviation from the minimum of the potential in the angular direction. The third condition, out of thermal equilibrium, is evident due to the presence of a condensate. Upon satisfying the three conditions, the baryon number violating interactions create a baryon (and/or lepton) asymmetry in the condensate, which will be eventually transferred to matter via baryon number conserving decays.
SUSY provides a natural framework to implement this scenario. In the above, we discussed explicit realization of AD baryo/leptogenesis in MSSM. Note, however, that the mechanism does not hinge upon having a low-scale SUSY. In fact, it can also work if the scale of SUSY is much higher than TeV, for example in split SUSY [25].
Moreover, one can consider variants of AD scenario that work along the same line with or without SUSY. We note that any complex scalar field ϕ carries a U(1) global number, which we denote by U(1)ϕ. In the case of squarks/sleptons, the U(1) charge is readily identified with baryon/lepton number. Satisfying the three Sakharov's conditions, one can therefore generate an asymmetry associated with the U(1)ϕ number stored in a rotating ϕ condensate. This asymmetry can be transformed into a baryon asymmetry through baryon number violating decays of the condensate.
In the context of SUSY, a simple possibility is to have a superpotential term 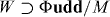 that violates baryon number by one unit ΔB = −1. This case has been studied when ϕ is a modulus field [26]. ϕ and ϕ* quanta decay to anti-baryons and baryons, respectively. Therefore a baryon asymmetry nB = nϕ is generated upon the decay of ϕ condensate, where nϕ is the asymmetry associated with U(1)ϕ.
that violates baryon number by one unit ΔB = −1. This case has been studied when ϕ is a modulus field [26]. ϕ and ϕ* quanta decay to anti-baryons and baryons, respectively. Therefore a baryon asymmetry nB = nϕ is generated upon the decay of ϕ condensate, where nϕ is the asymmetry associated with U(1)ϕ.
A similar scenario has been proposed in a non-supersymmetric context to explain baryogenesis in models with large extra dimensions [27]. In this case, ϕ is a complex scalar field in the bulk, which is coupled to fermions through an interaction term in the Lagrangian 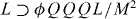 . This term violates baryon and lepton numbers by one unit ΔB = ΔL = + 1. As a result, ϕ and ϕ* quanta decay to baryons/leptons and anti-baryons/anti-leptons, respectively. Note that although B − L = 0 upon the decay of ϕ condensate, the baryon asymmetry will survive the washout by sphalerons since baryogenesis occurs at very low temperatures (i.e. well below the electroweak phase transition) at which sphalerons are not active.
. This term violates baryon and lepton numbers by one unit ΔB = ΔL = + 1. As a result, ϕ and ϕ* quanta decay to baryons/leptons and anti-baryons/anti-leptons, respectively. Note that although B − L = 0 upon the decay of ϕ condensate, the baryon asymmetry will survive the washout by sphalerons since baryogenesis occurs at very low temperatures (i.e. well below the electroweak phase transition) at which sphalerons are not active.
Finally, it is possible that the scalar ϕ carries baryon/lepton number and its couplings to matter also violate baryon/lepton number. This case requires some care in order for baryon/lepton number violating decays to not erase the asymmetry stored in the rotating condensate. An explicit example of this variant of the AD scenario is leptogenesis from the RH sneutrino [28]. In this case, a lepton asymmetry is first generated in a rotating condensate of the RH sneutrino field 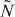 . The condensate then decays to LH leptons and sleptons via
. The condensate then decays to LH leptons and sleptons via 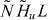 and
and  interaction terms, respectively, with the corresponding lepton number violations ΔL = + 2 and ΔL = 0, respectively. If the two channels have the same decay rate, as is the case at zero temperature, there will be no net lepton asymmetry after the condensate decays. However, the two decay channels have different rates at finite temperature owing to different statistics for bosons and fermions. Therefore a net lepton asymmetry can be generated in this model, which will be partially converted to baryon asymmetry via sphalerons.
interaction terms, respectively, with the corresponding lepton number violations ΔL = + 2 and ΔL = 0, respectively. If the two channels have the same decay rate, as is the case at zero temperature, there will be no net lepton asymmetry after the condensate decays. However, the two decay channels have different rates at finite temperature owing to different statistics for bosons and fermions. Therefore a net lepton asymmetry can be generated in this model, which will be partially converted to baryon asymmetry via sphalerons.
5. Fragmentation of AD condensate
In our discussion we have so far assumed that coherent oscillations of the AD field ϕ last very long until the condensate decays. The stability of oscillations under small perturbations, which are inevitably introduced by quantum fluctuations of the field, depends on the shape of the potential. In this section, we analyze the stability of oscillations of the AD field and discuss its consequences.
5.1. Q-balls
The ground state of the AD condensate is determined by the coherent oscillations in a potential V (ϕ) with a frequency that is large compared to the Hubble expansion rate. In our case the motion of the condensate is not simply oscillatory; instead, similar to the case of a rotating trajectory with a phase, one obtains an elliptical orbit. For a sufficiently small amplitude, the trajectory follows a simple potential:

The equation of state for such an oscillatory trajectory is given by γ ≡ p/ρ = (1 + x)/(1 + x/2), p = x/(2 + x). This gives rise to a negative pressure whenever x < 0. This is a sign of an instability of the scalar field oscillations under arbitrarily small perturbations. When the effective mass of the scalar field is much larger than the Hubble rate, the quantum fluctuations in the condensate grow according to

If K = 2x < 0, quantum fluctuations of the condensate at the scale, λ = 2π/|k|, will grow exponentially in time:

In reality, the onset of nonlinearity sets the scale at which the spatial coherence of the field can no longer be maintained and the condensate fragments. The initial fluctuations in the condensate are set by perturbations of the AD field generated during the inflationary era.
If the condensate carries a global charge, the energy-to-charge ratio changes as the condensate fragments. This is what happens in the case of MSSM flat directions [29–33]. The AD condensate responsible for generating the baryon asymmetry at the first instance could fragment into non-topological solitons with a fixed charge, called the Q-ball [34, 35]. Typically, fragmentation of the AD condensate is a violent process, and can generate observable gravitational waves as shown in [36].
5.2. Q-balls and dark matter
The stability of Q-balls produced from fragmentation of the AD condensate depends on their energy-to-charge ratio. The crucial point is the presence of a global U(1) charge carried by the Q-ball, which is denoted by Q. The configuration that has the lowest energy-to-charge ratio will then be the stable one.
For a sufficiently large Q, the Q-ball energy is given by E = |νQ| [34, 35, 37]. Therefore, if |νQ| < mϕ|Q|, the Q-ball will not decay into plane waves corresponding to ϕ quanta. The stable configuration will instead be a soliton whose profile is given by  , where
, where 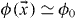 inside and
inside and 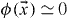 outside the soliton. Note that the global U(1) symmetry is broken inside the soliton by the non-zero value of ϕ0, but remains unbroken outside the soliton.
outside the soliton. Note that the global U(1) symmetry is broken inside the soliton by the non-zero value of ϕ0, but remains unbroken outside the soliton.
In models of gauge-mediated SUSY breaking the Q-balls can be absolutely stable, and hence a candidate for cold dark matter (CDM) [38]. In these models the potential for the AD field takes the form  , where
, where 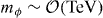 represents the soft mass of sparticles. The profile of a Q-ball follows
represents the soft mass of sparticles. The profile of a Q-ball follows  , and its energy E in terms of the charge Q is given by [38]
, and its energy E in terms of the charge Q is given by [38]

Typically, Q represents the baryon number B carried by the Q-ball. This allows for the existence of some entirely stable B-balls, provided that B is sufficiently large. Indeed, the energy per baryon number, given by ∼(1 TeV) × B−1/4, is less than 1 GeV for B > 1012. Such large B-balls cannot decay into protons and neutrons and are entirely stable. If they were produced in the early universe, they would exist at present as a form of dark matter [38]. The astrophysical and terrestrial constraints [39, 40], as well as bounds from direct searches for Q-balls [41], place a lower limit of |B| > 1022 on the size of B-balls.
In models of gravity-mediated SUSY breaking, the B-balls are not stable. In these models the potential for the AD field has the form V (ϕ) = m2ϕ|ϕ|2(1 + Kln(ϕ2/μ2)) [30]. K can be calculated for a given flat direction, and the potential is flatter than |ϕ|2 when K < 0. Due to the smallness of K, the B-balls are not stable in this case regardless of how large |B| is. Instead they decay via surface evaporation. The VEV of ϕ near the surface is low enough, and so are particles that are coupled to the ϕ, to kinematically allow the B-ball decay to the latter.
When a B-ball decays, for each unit of baryon number (corresponding to the decay of three squarks to quarks), at least three lightest supersymmetric particle (LSP) are produced. Depending on the nature of the cascade produced by the squark decay, and the LSP mass, more LSPs could be produced. The baryon-to-dark matter ratio right after the decay is given by

where mn and mLSP are the nucleon and LSP mass, respectively, NLSP ⩾ 3 is the number of LSPs produced per baryon number, and fB is the fraction of the total baryon asymmetry contained in the B-ball. It is therefore rather natural to obtain rB < 1 from the decay of B-balls.
The subsequent evolution of the LSPs thus produced depends on their nature. If the LSP is a neutralino, the produced quanta will annihilate with a thermally averaged rate 〈σv〉 = a + b(T/mLSP), where a and b depend on the identity of the neutralino and annihilation final states [42]. Moreover, the neutralinos collide with the SM particles in the background, which keeps them in kinetic equilibrium with the thermal bath down to a temperature 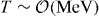 [43]. As a result, the LSPs produced in B-ball decays will spread out by a random walk with a rate ν determined by the collision frequency divided by a thermal velocity vth ≈ (T/mLSP)1/2. Since the decay is spherically symmetric, it is very likely that the LSPs have a Gaussian distribution. Assuming an efficient LSP production, so that fB ≈ 1, the dark matter abundance in terms of the density parameter can be written as [44]
[43]. As a result, the LSPs produced in B-ball decays will spread out by a random walk with a rate ν determined by the collision frequency divided by a thermal velocity vth ≈ (T/mLSP)1/2. Since the decay is spherically symmetric, it is very likely that the LSPs have a Gaussian distribution. Assuming an efficient LSP production, so that fB ≈ 1, the dark matter abundance in terms of the density parameter can be written as [44]
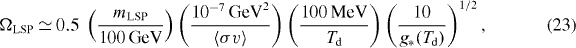
where Td is the decay temperature of the B-ball given by
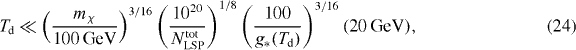
with g*(Td) being the effective number of relativistic degrees of freedom at Td. Sufficiently large B-balls decay below the freeze-out temperature such that Td ≪ Tf ∼ mLSP/20.
A similar analysis can be performed when gravitino is the LSP. The annihilation of gravitinos with each other and their collision with the SM particles are negligible as they proceed through interactions of gravitational strength. In this case the dark matter abundance from the decay of B-balls is given by [45]

which is valid for reheating temperatures below 107 GeV. A similar expression can be derived for the abundance of axino dark matter from decaying B-balls [46].
We note that dark matter connection to stable or unstable B-balls occurs in a non-thermal fashion, i.e. dark matter relic abundance is not set by thermal freeze-out of its annihilation. Therefore a possibility arises for explaining the dark matter–baryon coincidence puzzle [47] in the context of the AD mechanism. Hidden sector scenarios of addressing this coincidence problem via the AD mechanism have recently been proposed [48]. These scenarios, however, involve more uncertainties as they rely on assumptions about the hidden sector.
6. Conclusion
The AD mechanism is an attractive scenario for baryogenesis within SUSY. It utilizes flat directions in the scalar potential of supersymmetric models, notably MSSM. Displacement of the flat direction field from the origin during the inflationary epoch results in the formation of a condensate. The initial field value is typically set by Hubble-induced terms that break SUSY. Spontaneous violation of C and CP by the condensate, combined with baryon/lepton number violating interactions induced by new physics at a high scale, gives rise to a rotating trajectory for the condensate in the post-inflationary era. A non-zero baryon/lepton number carried by the flat direction leads to a baryon/lepton asymmetry stored in the condensate. The created asymmetry is eventually transferred to ordinary particles after the condensate decays.
In some cases, the condensate fragments into non-topological solitons called Q-balls. Depending on the mechanism for transmission of SUSY breaking to the visible sector, these Q-balls can be long lived or even absolutely stable. In models of gravity mediation, one can have long-lived Q-balls that decay into fermions below thermal freeze-out of dark matter. Q-balls can in this case be the source of baryons and non-thermal dark matter in the universe. In models of gauge mediation, one can have sufficiently large Q-balls that are stable. These Q-balls will themselves be the dark matter candidate.
Inflationary reheating can affect the flat direction dynamics and vice versa. Thermal effects from reheat plasma can trigger early oscillations of the flat direction field, thus altering the generated baryon asymmetry. On the other hand, spontaneous breakdown of gauge symmetries by the flat direction condensate can induce large masses for the particles in the reheat plasma, thereby delaying their production and/or thermalization. This can change the thermal history of the universe in a significant way, leading to important cosmological consequences.
The AD scenario was originally introduced in the context of low-energy SUSY. However, this is not requisite for its success and it can work well in models of high-energy SUSY. The scenario has various variants where an asymmetry in a global U(1) charge, carried by a rotating condensate of a complex scalar field, is transformed into a baryon asymmetry upon the condensate decay.
Acknowledgments
The work of AM is funded by STFC grant no. ST/J000418/1.