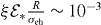Abstract
We propose a framework for inducing strong optomechanical effects in a suspended carbon nanotube based on deformation potential (DP) exciton–phonon coupling. The excitons are confined using an inhomogeneous axial electric field which generates optically active quantum dots with a level spacing in the milli-electronvolt range and a characteristic size in the 10 nm range. A transverse field induces a tunable parametric coupling between the quantum dot and the flexural modes of the nanotube mediated by electron–phonon interactions. We derive the corresponding excitonic DPs and show that this interaction enables efficient optical ground-state cooling of the fundamental mode and could allow us to realize the strong and ultra-strong coupling regimes of the Jaynes–Cummings and Rabi models.
Export citation and abstract BibTeX RIS
Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The realization of the quantum regime of a macroscopic mechanical degree of freedom [1, 2] has emerged as a natural goal from considering the fundamental limits for the measurement of small forces and displacements [3–7]. This achievement could provide a versatile alternative for the exploration of the quantum-to-classical transition and the development of quantum technologies. Recent progress in the implementation of optomechanical [4–7] and electromechanical [3] microsystems and nanosystems has already enabled access to this regime [8–12]. Some critical requirements in this respect are: (i) quantum limited measurement of the transduced output, (ii) sufficiently low effective masses and (iii) sufficiently low mechanical dissipation. Optomechanical schemes are ideally suited to meet (i) given the availability of shot-noise limited photodetection. In turn, suspended single-walled carbon nanotubes (CNTs) [13] are emerging as unique candidates to meet criteria (ii) and (iii) [14, 15]. Indeed, recent transport experiments in these systems have demonstrated a strong coupling of charge to vibrational resonances [16–18] and mechanical quality-factors (Q) exceeding 105 for resonant frequencies approaching 1 GHz [19]. Thus, implementing optomechanical systems based on suspended CNTs would represent a significant milestone.
The standard paradigm in optomechanics is based on an optical cavity whose frequency is modulated by the motion of one of its mirrors or of a dielectric object inside it via radiation pressure effects [4–6]. Although this approach has recently been successfully carried over to nanoresonators with subwavelength dimensions [20–22], it becomes inefficient for high-frequency resonators (≳1 GHz) with low polarizabilities such as sub-micron CNTs. Here, we propose a promising alternative based on a way of inducing coherent optomechanical transduction that exploits the unique properties of excitons in CNTs [23–26]. The role of the optical cavity is played by an excitonic resonance of the CNT that couples parametrically to the flexural motion via deformation potential (DP) electron–phonon interactions [27, 28]. Homodyne detection of the in-phase component of the output field of the resonantly driven two-level emitter afforded by the excitonic resonance allows then to carry out a continuous measurement of the mechanical displacement. This procedure, which could be implemented using the differential transmission technique [29], is akin to ion-trap measurements [30] and is analogous to cavity-assisted schemes [31]. However, a two-level emitter is a highly nonlinear system, in stark contrast to an optical cavity mode, and this feature provides an additional motivation for our proposal given the potential it offers for the demonstration of non-classical motional states of the CNT. In fact, a major advantage of this particular mechanical resonator–exciton system with respect to prior scenarios [32] is the possibility of realizing a mechanical analogue of the strong-coupling regime of cavity-QED [33, 34] with a vacuum Rabi splitting in the 100 MHz range.
As shown in figure 1, we envisage a suspended neutral semiconducting CNT where the centre of mass (CM) of the exciton is localized via the spatial modulation of the Stark shift induced by a static inhomogeneous electric field. We analyse a tip-electrode configuration that effectively engineers a pair of tunable optically active nanotube quantum dots (NTQDs) with excitonic level spacing in the meV range implying a confinement length below 10 nm. The quantum confinement is induced by the inhomogeneity in the field component along the CNT axis E∥. In turn, the normal component E⊥ breaks the axial symmetry inducing a tunable parametric coupling between the exciton and the in-plane flexural motion of the CNT. This allows for optical ground-state cooling [11, 32, 35, 36] of the fundamental mode at an ambient temperature in the Kelvin range.
Figure 1. (a) The perpendicular field E⊥(z), the effective confining potential V(00)eff(z) and the resulting exciton CM probability distribution (a.u.) in the harmonic approximation for V1 = −0.75 V and V2 = 1.75 V—the tailored confinement generates a double well with minima at |z| = z0 (E∥(z0) = 9.6 Vμm−1 and the inter-well tunnelling is negligible). (b) Schematic view of the device (both the tip electrodes and the CNT are suspended). Here we consider the restrictions imposed on the fields by the need to avoid sizable static deflections (cf section 3.2), field emission (the maximum field at the tip electrodes is approximately 200 Vμm−1) and dielectric breakdown, and assume for simplicity cylindrical symmetry around the tips' axis.
Download figure:
Standard imageAnother aspect of the CNT systems proposed here is their relevance in the broader context of quantum photonics applications. The optical manipulation of single carriers trapped at well-defined and repeatedly addressable locations has proved invaluable to probe the foundations of quantum mechanics and constitutes a key resource for enabling quantum technologies. In this respect, solid state zero-dimensional optical emitters offer a promising alternative to realizations based on trapped atoms. Examples of such systems are semiconductor quantum dots [37], rare-earth-doped crystals [38, 39], NV colour centres in diamond [40, 41] and, more recently, the system considered here, i.e. excitons in semiconducting CNTs [24]. For the latter, photon antibunching has already been observed and there is indirect evidence that exciton localization arises spontaneously [24], probably as a result of charged defects in the surrounding matrix or disorder in the CNT. Naturally, in view of the aforementioned quantum applications it would be desirable to artificially tailor exciton confinement in a controlled fashion in an ultra-clean suspended CNT. However, the band-gap engineering approach deployed for this purpose in more standard semiconductor materials is hardly viable for CNTs. Suspension is motivated by the need to (i) avoid substrate-induced fluorescence quenching and (ii) control the enhanced phonon-induced optical dephasing that results from the one-dimensional (1D) nature of this system.
We will first present in section 2 a suitable model for the CNT excitons that will be used to analyse both their quantum confinement generating the NTQD and their interaction with CNT low-frequency phonons, as modified by the applied electrostatic fields. Subsequently, in section 3, we will consider the axial phonon confinement induced by the finite CNT suspended length and derive an effective model for the fundamental in-plane flexural-phonon mode coupled to the NTQD. Finally, also in section 3, this effective model will be used to describe optomechanical effects induced when the NTQD is driven by a laser—e.g. the possibility of efficient laser cooling of the fundamental mode close to its motional quantum ground state.
2. The exciton effective model
The electronic structure of a CNT can be understood in terms of graphene rolled into a seamless cylinder. In graphene, the conduction and valence bands cross at two inequivalent 'Dirac points' in the reciprocal lattice [42] (K and K'). The corresponding effective (k·p) Dirac Hamiltonian reads

where 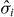 (
(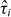 ) are Pauli matrices in sublattice (A–B) space (valley (K–K') space) and
vF ≈ 106 m s−1 is the Fermi velocity. Here, we follow the representation used by Ando [43] in which the Dirac spinor is expressed in terms of Bloch amplitudes as (ψKA,ψKB,ψK'A,−ψK'B). A rotation by the CNT's chiral angle θ is performed to align
) are Pauli matrices in sublattice (A–B) space (valley (K–K') space) and
vF ≈ 106 m s−1 is the Fermi velocity. Here, we follow the representation used by Ando [43] in which the Dirac spinor is expressed in terms of Bloch amplitudes as (ψKA,ψKB,ψK'A,−ψK'B). A rotation by the CNT's chiral angle θ is performed to align 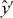 with the nanotube axis (
with the nanotube axis (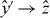 )—henceforth, we adopt cylindrical coordinates. Thus, the unit vectors in sublattice and valley space correspond to graphene two-dimensional (2D) Bloch functions with wavevector K [K']: (1,0,0,0) [(0,0,1,0)] is constructed from pz orbitals centred at the A sites with phase e−iθ/2 [eiθ/2] at the central site, whereas (0,1,0,0) [(0,0,0,1)] has the pz orbitals centred at the B sites with phase eiθ/2 [ − e−iθ/2] at the central site [42]. After folding, the resulting periodic boundary conditions imply that a wide-gap semiconducting nanotube is obtained when the nanotube indices satisfy mod(2n' + m',3) ≠ 0. The associated subband electronic 1D Bloch functions for kz = 0 are given by
)—henceforth, we adopt cylindrical coordinates. Thus, the unit vectors in sublattice and valley space correspond to graphene two-dimensional (2D) Bloch functions with wavevector K [K']: (1,0,0,0) [(0,0,1,0)] is constructed from pz orbitals centred at the A sites with phase e−iθ/2 [eiθ/2] at the central site, whereas (0,1,0,0) [(0,0,0,1)] has the pz orbitals centred at the B sites with phase eiθ/2 [ − e−iθ/2] at the central site [42]. After folding, the resulting periodic boundary conditions imply that a wide-gap semiconducting nanotube is obtained when the nanotube indices satisfy mod(2n' + m',3) ≠ 0. The associated subband electronic 1D Bloch functions for kz = 0 are given by

with single-particle eigenenergies
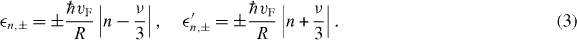
Here + and − label, respectively, the conduction and valence bands, the index n corresponds to the quantization of the single-particle azimuthal momenta (n = 0,±1,±2,...), ν = 2 mod(2n' + m',3) − 3 = ± 1 denotes the type of semiconducting CNT [44], R is the CNT radius and φ is the azimuthal angular coordinate (figure 1).
The K − K' degeneracy, implied by equations (2) and (3), and the electron spin yield for the lowest-energy exciton manifold a sixteenfold degeneracy in the lowest order k·p approximation provided by equation (1). This degeneracy is partially split by inter-valley mixing and exchange effects [43]. In the absence of a magnetic field, there is a single bright level5: the singlet bonding direct exciton 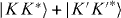 which typically has the highest energy [45] (here the conjugated wavefunctions correspond to the hole). Threading through the cross-section a small Aharonov–Bohm flux ϕAB renders the antibonding state
which typically has the highest energy [45] (here the conjugated wavefunctions correspond to the hole). Threading through the cross-section a small Aharonov–Bohm flux ϕAB renders the antibonding state  weakly allowed [43] so that its spontaneous emission rate can be tuned by varying the magnetic field. Note that the zero field splitting between the states
weakly allowed [43] so that its spontaneous emission rate can be tuned by varying the magnetic field. Note that the zero field splitting between the states 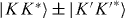 has been observed to be in the 1 meV range [26].
has been observed to be in the 1 meV range [26].
Henceforth, we will mainly focus on the E11 excitons  and consider their DP coupling to the low-frequency acoustic phonons of the CNT in the presence of weak static electric fields. There are four phonon branches whose frequency vanishes with the wavevector, namely: compressional (stretching), torsional and two flexural (bending) branches. However, relevant exciton–phonon interactions will only affect the compressional branch and the flexural branch polarized along
and consider their DP coupling to the low-frequency acoustic phonons of the CNT in the presence of weak static electric fields. There are four phonon branches whose frequency vanishes with the wavevector, namely: compressional (stretching), torsional and two flexural (bending) branches. However, relevant exciton–phonon interactions will only affect the compressional branch and the flexural branch polarized along  . Indeed, the excitonic wavefunctions of interest are non-degenerate and, in the absence of a magnetic field (i.e. for ϕAB = 0), the field configuration in figure 1 has reflection symmetry with respect to the xz plane. Thus, the torsional branch and the flexural branch polarized along
. Indeed, the excitonic wavefunctions of interest are non-degenerate and, in the absence of a magnetic field (i.e. for ϕAB = 0), the field configuration in figure 1 has reflection symmetry with respect to the xz plane. Thus, the torsional branch and the flexural branch polarized along  , which are antisymmetric with respect to this reflection operation, are decoupled.
, which are antisymmetric with respect to this reflection operation, are decoupled.
To obtain a tractable model for the excitonic wavefunction suitable for analysing the CM confinement of the exciton and its coupling to acoustic phonons, we adopt a phenomenological approach based on: (i) the aforementioned k·p graphene zone-folded scheme following Ando [43, 46] but neglecting inter-subband transitions [47, 48], and (ii) an envelope function approximation within each subband with the parametrization developed in [44, 48] (based on a comparison of tight binding and ab initio approaches) but the Bloch function at K, K' as determined by (i) and assuming electron–hole symmetry. In line with this last assumption, we take for the effective mass associated with a given subband the average of the electron and hole effective masses obtained in [44]. This framework neglects the impact of curvature effects on the Bloch functions but allows us to incorporate realistic values for the effective masses of electrons and holes [44] and for the exciton Bohr radius [48]—here the Bloch functions mainly play a role in determining the selection rules. In the absence of external fields, this leads to the following singlet direct exciton wavefunctions:
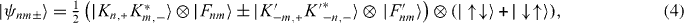
where the envelope functions |Fnm〉, |F'nm〉 satisfy Fnm(ze,zh) = F'nm(zh,ze). Here, we use that the single-particle eigenenergies  n,+ (
n,+ ( n,−) and
n,−) and  '−n,+ (
'−n,+ ( '−n,−) are degenerate and inter-valley mixing preserves the total orbital momentum and angular momentum along
'−n,−) are degenerate and inter-valley mixing preserves the total orbital momentum and angular momentum along  . One should note that, in general, equation (4) implies entanglement between the valley and orbital degrees of freedom, but for axially symmetric excitons such that n = m, the envelope functions differ at most by a π-phase so that they factor out and the axial degrees of freedom become disentangled (n = m = 0 for E11 excitons).
. One should note that, in general, equation (4) implies entanglement between the valley and orbital degrees of freedom, but for axially symmetric excitons such that n = m, the envelope functions differ at most by a π-phase so that they factor out and the axial degrees of freedom become disentangled (n = m = 0 for E11 excitons).
2.1. Exciton confinement
We now turn to the analysis of the quantum confinement of the exciton's CM motion induced by an applied inhomogeneous electrostatic field. The symmetric tip electrode configuration sketched in figure 1 with voltages V1 and V2 allows independent tuning of E⊥ and E∥, as the reflection symmetries imply that their magnitudes are determined, respectively, by (V2 − V1)/2 and (V2 + V1)/2. In order to generate a Stark-shift-induced excitonic quantum dot, we consider parameters such that the length scale over which E⊥ and E∥ vary appreciably is much larger than the CNT radius R (i.e. they can be regarded as constant across the CNT's cross-section) and larger than the excitonic Bohr radius. It follows that for sufficiently weak magnitudes (see below): (i) the effect of E∥ is dominated by intrasubband virtual transitions whose effect on the CM motion can be treated adiabatically, while (ii) E⊥ leads to a perturbation ∝e±iφ that only induces intersubband virtual transitions.
More precisely, the effect of the external fields on the exciton can be described by the following interaction Hamiltonian:

with

and

Here U(x,z) is the external electrostatic potential (in the plane y = 0), so that  and
and 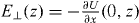 , and
, and  ⊥ ≈ 1.6 denotes the intrinsic relative permittivity normal to this axis [49]. Given that the depolarization effect only affects the perpendicular field and the fact that the typical level spacing between the relevant excitonic states arising from a given pair of subbands n, m is smaller than the intersubband energy spacing, we can assume that the Stark-shift-induced CM confinement will be dominated by
⊥ ≈ 1.6 denotes the intrinsic relative permittivity normal to this axis [49]. Given that the depolarization effect only affects the perpendicular field and the fact that the typical level spacing between the relevant excitonic states arising from a given pair of subbands n, m is smaller than the intersubband energy spacing, we can assume that the Stark-shift-induced CM confinement will be dominated by 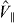 and neglect
and neglect 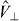 in this subsection6. Then, for each pair of subbands n, m, we perform the substitution
in this subsection6. Then, for each pair of subbands n, m, we perform the substitution

with inverse
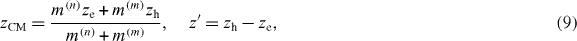
where m(n) (m(m)) is the effective mass of subband n (m) and μ = m(n)m(m)/(m(n) + m(m)) is the excitonic reduced mass. Here the indices n, m refer to the K point and the corresponding envelope function is enough to determine the wavefunction (cf equation (4))—note that an analogous substitution can be performed for the K' point and 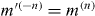 . The aforementioned smoothness of the fields implies that
. The aforementioned smoothness of the fields implies that 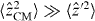 so that substituting equation (8) into (6) and Taylor expanding we obtain a linear potential
so that substituting equation (8) into (6) and Taylor expanding we obtain a linear potential

We now consider E∥(z) much smaller than the critical field to ionize the exciton so that the relevant intrasubband matrix elements of 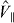 are much smaller than the binding energy. The latter warrants for the ground state manifold of the excitonic hydrogenic series [50] associated with n, m, a description in terms of an effective Hamiltonian by adiabatic elimination of the corresponding excited manifolds. Naturally, the corresponding states have well-defined parity. Thus, this effective Hamiltonian for the CM motion has a potential part whose leading contribution is second order in
are much smaller than the binding energy. The latter warrants for the ground state manifold of the excitonic hydrogenic series [50] associated with n, m, a description in terms of an effective Hamiltonian by adiabatic elimination of the corresponding excited manifolds. Naturally, the corresponding states have well-defined parity. Thus, this effective Hamiltonian for the CM motion has a potential part whose leading contribution is second order in 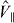 . From equation (10), we obtain for this effective confining potential
. From equation (10), we obtain for this effective confining potential

where

is the corresponding excitonic polarizability. Here we have introduced the wavefunctions {|f(nm)eh,l〉} on the relative coordinate z' for the hydrogenic series l = 0,1,... arising from n, m. In a classical picture, the field polarizes the exciton that thus experiences a force proportional to the gradient of the squared field. If one considers the characteristic level spacings

and the order of the relevant matrix elements ∼σ(nm)eh (where σ(nm)eh is the exciton Bohr radius and  n−m(q) an appropriate dielectric function [43]), it follows from equation (12) that the excitonic polarizability is of order
n−m(q) an appropriate dielectric function [43]), it follows from equation (12) that the excitonic polarizability is of order

Here  0(0) =
0(0) =  ∥ ≈ 7 corresponds to the intrinsic relative permittivity along the CNT axis [49].
∥ ≈ 7 corresponds to the intrinsic relative permittivity along the CNT axis [49].
We focus now on E11 excitons so that n = m = 0. To determine the electrostatic potential generated by the aforementioned symmetric tip electrode configuration, we have performed finite element method (FEM) calculations with COMSOL multiphysics for relevant parameters (section 3.1). We assume for simplicity cylindrical symmetry around the tips' axis so that the ground electrode corresponds to a cylindrical shell with diameter approximately equal to the CNT length L (figure 1). To model this configuration with electrodes of length LT ≫ L, we consider Neumann boundary conditions at |x| = L* with L* smaller but comparable to LT (i.e. Ex = 0 for |x| = L* ∼ 1 μ). The effective confining potential Veff is then estimated from equations (11) and (14). As expected it vanishes at the origin and is given by a double well with minima at |z| = z0, comparable to the distance between the tip electrodes (i.e. the tailored confinement generates a QD molecule). For typical parameters, it is permissible to neglect inter-well tunnelling and use in our estimates the harmonic approximation for the ground state of each well. We consider as a representative example a (9,4) CNT, E∥(z0) = 9.6 Vμm−1 and z0 = 21 nm (figure 1). This results in an excitonic CM zero point motion σ(00)CM ∼ 9 nm (corresponding to σ(00)eh ≈ 1.5 nm [48] and mCM = 0.2me [44], with me the electron mass in vacuum) and a level spacing ΔE ∼ 2 meV—where 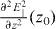 is taken from the FEM calculation. Alternatively, heuristic considerations imply that the curvature at the well minima is of order |V(nm)eff(z0)|/z20 which, together with equations (11) and (14), yields
is taken from the FEM calculation. Alternatively, heuristic considerations imply that the curvature at the well minima is of order |V(nm)eff(z0)|/z20 which, together with equations (11) and (14), yields

and

where we have omitted the subband superscripts. Given the subwavelength separation between the wells, for each doublet only the symmetric state is bright so that the degeneracy is irrelevant. Thus, the wavefunctions for relevant E∥ are well approximated by the form given in equation (4) with a suitable envelope function
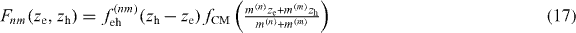
(cf equation (9)), and for the ground state of the E11 bonding (antibonding) manifold, henceforth denoted by |ψ00+〉 (|ψ00−〉), we take both functions fCM and feh to be Gaussian [48].
Finally, more precise criteria to warrant the above adiabatic treatment are given by
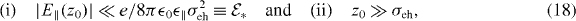
which follow, respectively, from requiring that the relevant matrix elements of  be much smaller than the corresponding unperturbed energy differences (equation (13)) and that the variation of the fields be smooth enough7. This second condition (ii) is necessary, together with (i), to ensure that
be much smaller than the corresponding unperturbed energy differences (equation (13)) and that the variation of the fields be smooth enough7. This second condition (ii) is necessary, together with (i), to ensure that
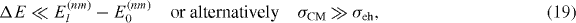
which justifies the Taylor expansion leading to equation (10), and can be obtained using equations (11), (13)–(16) together with the assumptions σeh ∼ 4π 0
0 ∥ℏ2/μe2 and μ ∼ mCM.
∥ℏ2/μe2 and μ ∼ mCM.
2.2. Field-induced exciton–phonon coupling
In what follows, we will first consider the influence of the transverse field E⊥ on the ground state of the E11 axially polarized exciton, which will amount to a slight hybridization with the cross-polarized excitonic states, and then proceed to derive the corresponding excitonic DPs in the presence of the applied fields.
To this end, we treat the effect of 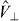 on |ψ00±〉 to lowest order in perturbation theory. In principle, the linear correction |ψ(1)00±〉 involves contributions from all four excitonic manifolds for which |n| = 1, m = 0 or n = 0, |m| = 1, namely E12, E21, E13 and E31. It is straightforward to determine the necessary single-particle matrix elements of
on |ψ00±〉 to lowest order in perturbation theory. In principle, the linear correction |ψ(1)00±〉 involves contributions from all four excitonic manifolds for which |n| = 1, m = 0 or n = 0, |m| = 1, namely E12, E21, E13 and E31. It is straightforward to determine the necessary single-particle matrix elements of  within our model for the excitonic wavefunctions, provided that the 2D 'lattice contributions' (on the folded graphene sheet) are first reduced to momentum matrix elements which can be read out from the k·p Hamiltonian (1). To this effect, one can first consider the CNT as a 1D lattice so that there is only a 'lattice contribution' to the matrix elements. Given that the operators
within our model for the excitonic wavefunctions, provided that the 2D 'lattice contributions' (on the folded graphene sheet) are first reduced to momentum matrix elements which can be read out from the k·p Hamiltonian (1). To this effect, one can first consider the CNT as a 1D lattice so that there is only a 'lattice contribution' to the matrix elements. Given that the operators  and
and  are well behaved on the corresponding Bloch functions (which have finite range in the transverse directions) we can apply the standard relation between their matrix elements
are well behaved on the corresponding Bloch functions (which have finite range in the transverse directions) we can apply the standard relation between their matrix elements

reducing the problem to the evaluation of matrix elements of 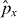 8—analogous relations hold for states at K'. We now use: (i)
8—analogous relations hold for states at K'. We now use: (i) 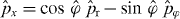 , (ii) that Π-orbitals have reflection symmetry with respect to the graphene sheet so that they do not carry
, (ii) that Π-orbitals have reflection symmetry with respect to the graphene sheet so that they do not carry 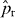 and (iii) that for Bloch functions near the Dirac points
and (iii) that for Bloch functions near the Dirac points 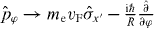 . These, together with equations (3) and (20), imply
. These, together with equations (3) and (20), imply
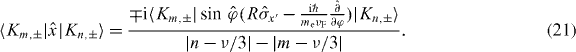
Subsequently, from equations (2), (3) and (21), and using that ν = ± 1 implies

and that
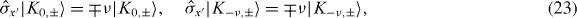
we obtain
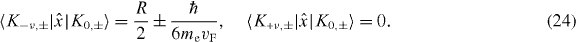
In turn, equations (2) and (3) imply that the substitution ν → − ν yields, for the states |K'n,±〉 and |K'm,±〉, expressions analogous to equations (21)–(24) so that
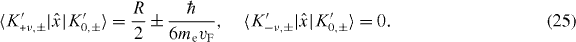
Finally, from equations (4), (7), (24) and (25) and using that  is invariant under time reversal, it is straightforward to obtain
is invariant under time reversal, it is straightforward to obtain
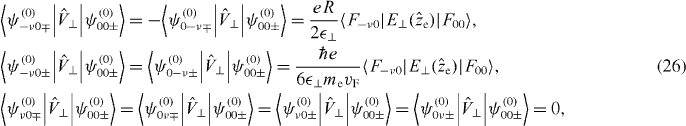
where we have used

and that for a suitable choice of phases (equation (17))

Thus, the contribution from |ψ(0)ν0±〉 (|ψ(0)0ν±〉) corresponding to E12 (E21) vanishes identically and, to first order in perturbation theory, we obtain for the admixture of cross-polarized excitons to the states |ψ00±〉 induced by E⊥
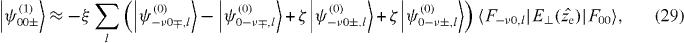
where ξ ≡ eR/2 ⊥(E13 − E11), ζ ≡ ℏ/3mevFR and l labels a complete set of envelope functions for the E13 and E31 manifolds. Here, we have assumed for the latter that those having appreciable overlap with |F00〉 correspond to excitons with energies well approximated by the lowest one (E13 = E31) and have neglected the splitting between the bonding and antibonding manifolds. Note that these manifolds are likely to consist of delocalized electron–hole pair-like states as is the case with the E33 band, so that the analysis in section 2.1 may not apply [51]. However, our treatment of E⊥ relies only on the validity of equations (4) and (28) irrespective of the specific form of the envelope functions F−ν0,l, and on satisfying the weakness criterion |ξE⊥(z0)|2 ≪ 1.
⊥(E13 − E11), ζ ≡ ℏ/3mevFR and l labels a complete set of envelope functions for the E13 and E31 manifolds. Here, we have assumed for the latter that those having appreciable overlap with |F00〉 correspond to excitons with energies well approximated by the lowest one (E13 = E31) and have neglected the splitting between the bonding and antibonding manifolds. Note that these manifolds are likely to consist of delocalized electron–hole pair-like states as is the case with the E33 band, so that the analysis in section 2.1 may not apply [51]. However, our treatment of E⊥ relies only on the validity of equations (4) and (28) irrespective of the specific form of the envelope functions F−ν0,l, and on satisfying the weakness criterion |ξE⊥(z0)|2 ≪ 1.
The Hamiltonian describing the interaction between electrons and low-frequency phonons has two distinct terms: (i) a DP contribution diagonal in sublattice space corresponding to an energy shift of the Dirac point,

and (ii) a bond-length change contribution off-diagonal in sublattice space [27, 28] that in the Dirac picture emulates a gauge field,
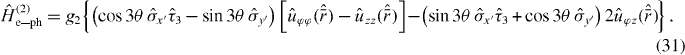
Here g1 ≈ 30 eV is the DP constant, g2 ≈ 1.5 eV the off-diagonal electron–phonon coupling constant [27, 28], and  only act on the 'orbital' part of the 1D Bloch functions (equation (2)). The single-particle Hamiltonians (30) and (31) naturally lead to the following excitonic two-particle Hamiltonian9:
only act on the 'orbital' part of the 1D Bloch functions (equation (2)). The single-particle Hamiltonians (30) and (31) naturally lead to the following excitonic two-particle Hamiltonian9:
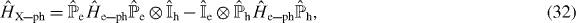
where  and
and 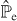 (
(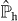 ) denotes the projector on the conduction (valence) band.
) denotes the projector on the conduction (valence) band.
Given that the relevant phonon modes have wavelengths, 2π/q, that are much larger than the CNT radius, R, one can describe them using a continuum shell model [27, 52], with 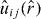 the corresponding Lagrangian strain operator, and keeping only the lowest orders in qR [27, 52], which amounts to the use of thin rod elasticity (TRE) [53]. Within this approximation, both compressional and flexural deformations have the structure of a local stretching so that the strain components satisfy uφz = 0, uφφ = −σuzz with the latter given, respectively, by
the corresponding Lagrangian strain operator, and keeping only the lowest orders in qR [27, 52], which amounts to the use of thin rod elasticity (TRE) [53]. Within this approximation, both compressional and flexural deformations have the structure of a local stretching so that the strain components satisfy uφz = 0, uφφ = −σuzz with the latter given, respectively, by
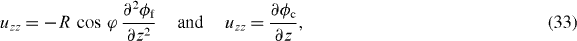
where ϕf(z) [ϕc(z)] is the flexural (compressional) 1D field [53] that satisfies the Euler–Bernoulli (classical-wave) equation and σ = 0.2 is a Poisson ratio for the CNT [52]. Finally, we consider the lowest-order contributions in the external field (zeroth order in ϕAB) to the interaction between the lowest bright exciton states |ψ00±〉 ≈ |ψ(0)00±〉 + |ψ(1)00±〉 of the NTQD and low-frequency phonons, i.e.
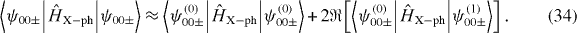
Naturally, the axial angular momentum is preserved by coupling to compressional phonons and modified by interactions with flexural phonons, so that only the first or the second term on the rhs of equation (34) contributes, respectively, to the corresponding NTQD DPs (equations (30)–(33)). Then, equations (2), (4), (22), (23), (27)–(34) and
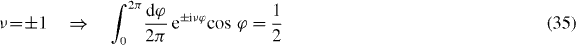
allow us to obtain

which is independent of the excitonic wavefunction's symmetry (bonding versus antibonding). Here, we have exploited the completeness of the basis {|F−ν0,l〉}. The 'off-diagonal' coupling to flexural phonons, i.e. the term proportional to ζ, constitutes a negligible correction given that ζ = αFcaB/3vFR ≲ 0.1 (for stable CNT radii [52]) and g2/g1 ≈ 0.05.
To recapitulate, in the present section we have used an envelope function approximation based on the graphene zone-folded description to analyse how weak inhomogeneous electrostatic fields affect the axially polarized direct excitons of a wide-gap semiconducting CNT. We have shown that such perturbative fields can induce quantum confinement of the CM motion dominated by the axial component and characterized by a level spacing in the milli-electronvolt range, and have derived the effective DP for the lowest-energy direct-exciton states of the resulting optically active quantum dot (NTQD). This approximation for the excitonic DP in the presence of applied electrostatic fields, given by equation (36), constitutes a central result of this paper. It relies on: (i) the aforementioned envelope function approximation, (ii) the existence of a weakly confined Wannier-exciton state |ψ00〉—which requires the adiabatic conditions on E∥(z) detailed in equation (18), (iii) neglecting the dispersion of the relevant cross-polarized excitonic manifold and (iv) the weakness criterion on the transverse field |ξE⊥(z0)|2 ≪ 1.10 This effective excitonic DP involves coupling to both compressional (i.e. stretching) and flexural phonons. The latter is linear in the transverse field E⊥, which induces a hybridization with the cross-polarized excitons. Interestingly, within our envelope function approximation (i), the 1D subband Bloch functions alternate between the two orthogonal eigenstates of the sublattice pseudospin  as the corresponding eigenenergy is increased—cf equations (2) and (3). This leads to the selection rules embodied in equations (24) and (25), which imply that the contribution from the E12 and E21 excitons vanishes.
as the corresponding eigenenergy is increased—cf equations (2) and (3). This leads to the selection rules embodied in equations (24) and (25), which imply that the contribution from the E12 and E21 excitons vanishes.
3. Exciton-assisted optomechanics
In this section, we consider the scenario relevant to optomechanics where axial phonon confinement due to the finite suspended length of the CNT plays a leading role. Whence the flexural and compressional phonon branches of the CNT are characterized by sharp resonances with a free spectral range comparable to the optical linewidth of the zero phonon line (ZPL) of the transition associated with the state |ψ00−〉 (analogous considerations apply to |ψ00+〉). We focus on laser excitation of the latter near-resonant with the ensuing lowest-frequency flexural phonon sidebands. More precisely, we consider a bridge geometry (figure 1) with a length (L ∼ 100 nm) short enough that the relative strength of these phonon sidebands is weak, but long enough that phonon-radiation losses (i.e. clamping losses) are negligible [53]. Hereafter, we follow [32] in which an analogous scenario was analysed in a semiconductor heterostructure.
To this effect we use the formalism developed in [53] and adopt a resonator-bath representation with the resonator mode (annihilation operator b0, angular frequency ω0 and quality factor Q) corresponding to the fundamental in-plane flexural resonance (that we intend to manipulate and laser cool to the ground state) and the bath including the other nanotube vibrational resonances coupled to the three-dimensional (3D) substrate that supports the CNT. Thus, we use for the effective field operators 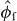 ,
,  in equation (36) the following resonator-bath mode decomposition:
in equation (36) the following resonator-bath mode decomposition:
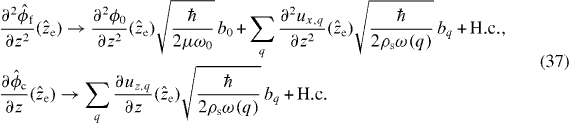
Here ϕ0(z) is the normalized resonator 1D eigenmode and μ is the linear mass density of the CNT; whereas ux,q(z) [uz,q(z)] with z∈ CNT is the x [z] component of the CM displacement of the CNT cross-section at z (figure 1) for the bath mode (annihilation operator bq) corresponding to the scattering eigenmode q [53], and ρs is the mass density of the substrate. Subsequently, substituting equation (37) into (36), we obtain
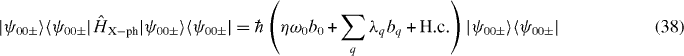
with
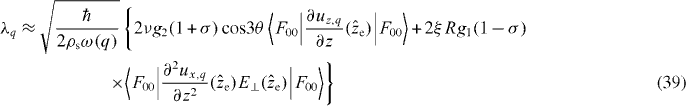
and

where we have introduced the effective field 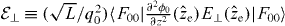 , set ζ → 0 and used
, set ζ → 0 and used  . Here, q0 ≈ 4.73/L is the fundamental mode's Euler–Bernoulli wavevector for clamped–clamped boundary conditions, and EG = 340 N m−1 and σG = 7.6 × 10−7 kg m−2 are, respectively, the 2D Young modulus [54] and mass density of graphene (a = 0.246 nm [50]). The parameter η is the 'modulation parameter' associated with the phonon sidebands that characterizes the strength of the exciton–resonator coupling, with e−η2/2 corresponding to the Franck–Condon factor (η2 is also known as the Huang–Rhys parameter). We will focus mainly on regimes such that η ≪ 1. Note that the perturbative nature of E⊥ underpinning equation (40) implies that
. Here, q0 ≈ 4.73/L is the fundamental mode's Euler–Bernoulli wavevector for clamped–clamped boundary conditions, and EG = 340 N m−1 and σG = 7.6 × 10−7 kg m−2 are, respectively, the 2D Young modulus [54] and mass density of graphene (a = 0.246 nm [50]). The parameter η is the 'modulation parameter' associated with the phonon sidebands that characterizes the strength of the exciton–resonator coupling, with e−η2/2 corresponding to the Franck–Condon factor (η2 is also known as the Huang–Rhys parameter). We will focus mainly on regimes such that η ≪ 1. Note that the perturbative nature of E⊥ underpinning equation (40) implies that 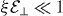 .
.
Then, from equation (38), adopting Pauli matrix notation for the optical pseudospin (σz = 1 corresponds to |ψ00−〉 and σz = −1 corresponds to the empty neutral NTQD) and a frame rotating at the laser frequency ωL, and applying the shift
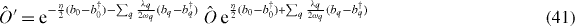
to the phonon modes, we obtain the following Hamiltonian for the laser-driven NTQD coupled to the resonator mode (ℏ = 1):
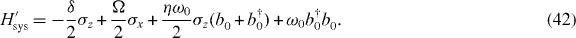
Here δ is the laser detuning from the ZPL and Ω the Rabi frequency.
To analyse the dynamics that arises from the interplay between H'sys and the couplings to the phonon bath and to the radiation field (annihilation operators ak and couplings gk), we perform the following canonical transformation [32],

to a 'polaronic' representation. The resulting complete Hamiltonian consists of three contributions, H = Hsys + Hint + HB, given by (ℏ = 1)
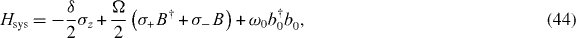
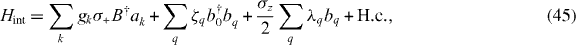
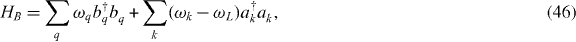
where B ≡ eη(b0−b†0). The couplings ζq and λq to the phonon bath lead, respectively, to the resonator mode's phonon-radiation losses and to pure dephasing of the NTQD induced by the DP (equations (38) and (39)). To assess their role we note that (i) qR ≪ 1 and (ii) the reflection symmetry of the whole structure with respect to the y–z plane imply that the q can be effectively identified with the low-frequency CNT phonon branches so that the couplings ζq involve only modes with a flexural character [53]. The RWA for the latter is justified given that Q ≫ 1 and η ≪ 1. These conditions and the anharmonicity of the flexural spectrum also imply that the effects of the λq associated with the flexural branch can be neglected [55].
In turn, the pure dephasing induced by the compressional (stretching) phonons is determined by the low-frequency behaviour of the spectral density

with q∈ the compressional branch. The latter can be obtained from equation (39), building upon the scattering formalism developed previously (see equation (34) of [53]) by incorporating now the leading correction in qR to the zeroth-order 1D–3D reflection amplitude at a single junction between the resonator and the support (clamping point) and considering the 'single-support' case in which both clamping points connect to the same elastic half-space so that interference effects are crucial—as relevant to our scenario where the gap below the CNT satisfies ≲L (see figure 1). This procedure, which will be detailed elsewhere, yields a superohmic phonon spectral density [56],

with

where

is the clamping-loss limited Q-value of the fundamental compressional mode for the 'double-support' case [53] (Qc ∼ 50 for L ∼ 100 nm), and α is the dimensionless dissipation parameter [56] for the corresponding Ohmic (1D continuum) result (note that the size of the QD molecule generated by the tip electrodes is set by z0)

which is valid in the limit L → ∞ (keeping ω fixed). Here cSAW and Es are, respectively, the phase velocity of surface acoustic waves and the Young modulus of the substrate which is assumed to have a Poisson ratio νs = 1/3.
The dissipation parameter α plays a crucial role in determining the different phases of the corresponding spin-boson model (equations (44)–(46) with η = gk = ζq = 0), in particular whether excitonic Rabi oscillations are possible for Γ ≪ Ω < ωU [56]. Using the results of section 2.2 it is straightforward to obtain

which has a marked dependence on the chirality angle θ. We note that for stable CNT radii, equation (52) always yields α < 0.02. In turn, a straightforward analysis of the linear absorption spectrum (i.e. for Ω ≪ Γ) that results from this weak-coupling continuum Ohmic model [56] (in the relevant low-temperature regime kBT/ℏ ≪ ωU) implies a pure-dephasing contribution to the linewidth given by γph = 2παkBT/ℏ and an asymmetric power law tail ∼δ2α−1, which is only observable for 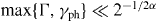 . The confined scenario embodied by equation (48) leads to a favourable suppression of this phonon-induced decoherence, which would otherwise preclude achieving the desired resolved-sideband condition for realistic parameters (cf section 3.1). Thus, this feature constitutes a cornerstone of the scheme proposed here. More precisely, the superohmic behaviour with n ⩾ 3 and αcon ≪ 1 implies that for relevant values of the ratios Γ/ω0 and Ω ≲ ω0 (cf section 3.1), the impact of these 'background modes' on optomechanical effects involving the resonator mode is completely negligible [55]—henceforth we take λq → 0.
. The confined scenario embodied by equation (48) leads to a favourable suppression of this phonon-induced decoherence, which would otherwise preclude achieving the desired resolved-sideband condition for realistic parameters (cf section 3.1). Thus, this feature constitutes a cornerstone of the scheme proposed here. More precisely, the superohmic behaviour with n ⩾ 3 and αcon ≪ 1 implies that for relevant values of the ratios Γ/ω0 and Ω ≲ ω0 (cf section 3.1), the impact of these 'background modes' on optomechanical effects involving the resonator mode is completely negligible [55]—henceforth we take λq → 0.
In the following subsections, we show how the resulting optomechanical system can be used for ground-state cooling of the fundamental mode (section 3.1), consider the main practical limits to the strength of the optomechanical coupling that can be achieved (section 3.2) and discuss the prospects for reaching the corresponding strong and ultra-strong coupling regimes (section 3.3).
3.1. Laser cooling
To analyse the laser cooling of the resonator mode, we derive first a reduced master equation for the NTQD–resonator system and subsequently a rate equation for its populations. For the relevant regimes, all environmental couplings can be treated within the Born–Markov approximation and, after eliminating the bath phonon modes and the radiation field, the Liouvillian of the driven NTQD coupled to the resonator mode reads
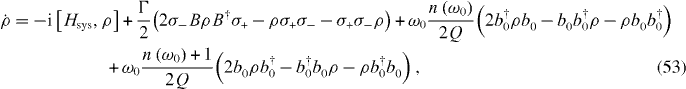
where n(ω0) is the thermal equilibrium occupancy at the ambient temperature,
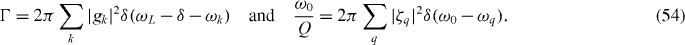
Other relevant sources of dissipation beyond those considered in the Hamiltonian given by equations (44)–(46), namely internal losses of the CNT resonator and nonradiative recombination of the exciton [24], can be incorporated, respectively, by simply adopting modified values of Q and Γ. We note that the nonradiative recombination rate for an ultra-clean CNT dark exciton has not been measured so far.
In analogy with the Lamb–Dicke limit (LD approximation), we expand up to second order the translation operators B and adiabatically eliminate the NTQD to obtain a rate equation for the populations of the resonator mode's Fock states [57]. The latter reads [32]
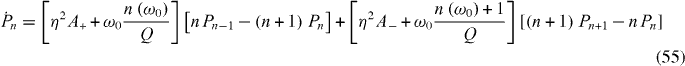
with the cooling (η2A−) and heating (η2A+) transition rates per quanta determined by A∓ = Γ[(δ ∓ ω0)2 + Γ2/4](ω20 + Γ2 + Ω2/2)Ω2/D, where
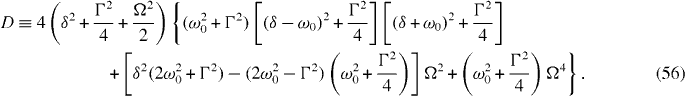
We note that in this system, in stark contrast with atomic laser cooling, A∓ → 0 in the limit Ω → ∞—in the polaronic representation this is associated with quantum interference effects between multiple paths [32]. Thus the steady-state occupancy for Q → ∞, i.e. the quantum backaction limit, reduces to

Remarkably, this result is independent of the Rabi frequency and coincides with the expression valid for the optomechanical cavity-assisted backaction cooling [58, 59] (equation (6) of [58]) with the cavity decay rate 1/τ replaced by the spontaneous emission rate, which for the optimal detuning 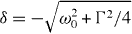 yields the fundamental limit
yields the fundamental limit 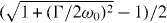 . This coincidence can be better understood by performing the adiabatic elimination in the 'original' representation corresponding to equation (42)—a thorough analysis using this representation has been performed by Jaehne et al [60].
. This coincidence can be better understood by performing the adiabatic elimination in the 'original' representation corresponding to equation (42)—a thorough analysis using this representation has been performed by Jaehne et al [60].
Figure 2 shows the resulting temperature dependence of the optimal steady-state occupancy (nf) that follows from equation (55), i.e.

minimized with respect to the laser detuning δ and the Rabi frequency Ω, for typical parameters. These correspond, for instance, to Γ = ω0/2, Q = 1.5 × 105 and η = 0.086. The latter can be realized, for example, with a (9,4) nanotube (equation (40))11 (R = 0.45 nm) of length L = 120 nm (ω0/2π = 1.67 GHz) and a transverse effective field 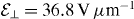 (corresponding to the field configuration in figure 1). For this case, an ambient temperature T = 4.2 K [n(ω0) = 52] allows cooling to a final (steady state) occupancy nf = 0.10. In the high-temperature regime (II), the cooling factor is constant and straightforward arguments imply that its optimum is approximately bounded by η2Q ≲ n(ω0)/nf ≲ ηQ [32, 60]. We note that for the parameters considered here (figure 1) in this linear regime, the initial effective modulation parameter is no longer small, i.e. η2[n(ω0) + 1] ≳ 1, and we find for the optimum A−|opt ∼ (A− − A+)|opt ∼ ω0, so that initially η2[〈b†0b0〉 + 1]A− ≳ Γ and equation (56) fails to describe the complete cooling process which will suffer a slowing down. Nonetheless, for these parameters η2[nf + 1]A−|opt/Γ < 0.03 for all n(ω0) < 103, and the LD approximation remains valid for the steady state—these aspects have been analysed in detail by Rabl [62].
(corresponding to the field configuration in figure 1). For this case, an ambient temperature T = 4.2 K [n(ω0) = 52] allows cooling to a final (steady state) occupancy nf = 0.10. In the high-temperature regime (II), the cooling factor is constant and straightforward arguments imply that its optimum is approximately bounded by η2Q ≲ n(ω0)/nf ≲ ηQ [32, 60]. We note that for the parameters considered here (figure 1) in this linear regime, the initial effective modulation parameter is no longer small, i.e. η2[n(ω0) + 1] ≳ 1, and we find for the optimum A−|opt ∼ (A− − A+)|opt ∼ ω0, so that initially η2[〈b†0b0〉 + 1]A− ≳ Γ and equation (56) fails to describe the complete cooling process which will suffer a slowing down. Nonetheless, for these parameters η2[nf + 1]A−|opt/Γ < 0.03 for all n(ω0) < 103, and the LD approximation remains valid for the steady state—these aspects have been analysed in detail by Rabl [62].
Figure 2. (a) Optimal steady-state (final) occupancy (nf) versus equilibrium (thermal) occupancy n(ω0) for Γ/ω0 = 1/2 and η2Q = 1.1 × 103. The optimum results of minimizing nf with respect to the laser parameters. For 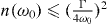 laser cooling is not operational. For
laser cooling is not operational. For  there are two regimes (dotted line): (I) when
there are two regimes (dotted line): (I) when 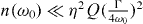 , nf is determined by the quantum backaction limit
, nf is determined by the quantum backaction limit 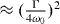 and (II) when n(ω0) is large [
and (II) when n(ω0) is large [ 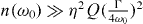 ] thermal noise dominates and the optimum becomes linear in the ambient temperature. (b) Rabi frequency (grey) and laser detuning (black) for which nf is minimized (in units of ω0).
] thermal noise dominates and the optimum becomes linear in the ambient temperature. (b) Rabi frequency (grey) and laser detuning (black) for which nf is minimized (in units of ω0).
Download figure:
Standard image3.2. Implementation
The choice of parameters in section 3.1 takes into account the restrictions imposed on the applied electric fields by the need to avoid: deleterious static deflections due to gradient forces [63], field emission and dielectric breakdown (figure 1). For the nanotube the latter is taken care of by the aforementioned restrictions imposed on the fields E⊥(z0) ∼ E⊥(0) and E∥(z0) so as to avoid dissociation of the E11 exciton (section 2), while the suspended tip geometry of the electrodes (figure 1) allows for a strong suppression of the field at the dielectric substrate with respect to the maximum field. In fact, static deflections pose the most stringent limitation when trying to maximize the exciton–resonator coupling η, given that they scale as

—here the prefactor is of order unity provided that the transverse dimension of the electrodes is comparable to or smaller than z0 < L, and we have used the reflection symmetries, which imply that the total electrostatic force on the nanotube scales as 2(α∥ + α⊥)E⊥(0)E∥(z0). Note that due to the Duffing geometric nonlinearity associated with a bridge geometry, this static deflection would mainly result in an effective stiffening of the resonator for Δx ≳ R. For the parameters considered in section 3.1, a detailed calculation based on the FEM electric fields (cf section 2.1), the Euler–Bernoulli theory for the CNT flexural response and static polarizabilities [α⊥ = 13(4π 0Å2), α∥ = 75(4π
0Å2), α∥ = 75(4π 0Å2)] estimated from [64, 65] yields Δx = 0.013 nm (note that R = 0.45 nm). Under these conditions we find that the modification of the resonator's frequency
0Å2)] estimated from [64, 65] yields Δx = 0.013 nm (note that R = 0.45 nm). Under these conditions we find that the modification of the resonator's frequency 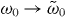 induced by the electric fields and the effect of the Duffing geometric nonlinearity (which lead, respectively, to softening and stiffening) is completely negligible (∼0.1%). In general, this modification also results in a correction to the NTQD modulation parameter given by
induced by the electric fields and the effect of the Duffing geometric nonlinearity (which lead, respectively, to softening and stiffening) is completely negligible (∼0.1%). In general, this modification also results in a correction to the NTQD modulation parameter given by 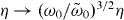 .
.
The proposed device is compatible with a confocal setup but places stringent requirements on the nanotube positioning needed to enforce the desired reflection symmetries. We note that the latter are not essential for our scheme but just a convenient means of enabling a wider parameter range. If they are relaxed, while it is still possible to tune independently ΔE and η via the two voltages V1 and V2, |V2 − V1| ≫ |V2 + V1| can now result in regions where E⊥ ∼ E∥, which reduces the maximum feasible E⊥ given that E∥ should not exceed the critical field for the breakdown of an E11 exciton. Nonetheless, relevant couplings could still be achieved (equation (40)). In turn, for such an asymmetric arrangement the NTQD may also couple to the out-of-plane flexural resonances, but this has no impact on the validity of our effective model (equations (44)–(46) with λq = 0 for q∈ flexural branch) given that the electrostatic fields and the mechanical coupling to the substrate break the degeneracy between the two flexural branches. A variant of this asymmetric scenario, albeit relinquishing the independent tunability of ΔE and η, is to use a single voltage configuration in which the fields are applied with an STM tip. Another interesting option is to effect the optical excitation of the nanotube using the evanescent field of a tapered fibre, which could allow one for instance to cancel the static deflection by using the optical gradient forces induced by an additional off-resonant laser, thereby lifting the restriction imposed on the length by equation (59) [66].
As the required fields are relatively large (∼10 Vμm−1) and inhomogeneous, it seems natural to also analyse the impact of voltage fluctuations arising from the Johnson–Nyquist noise of the electrodes and/or of the voltage sources used. These induce a fluctuation of the effective potential defining the NTQD (equation (11))
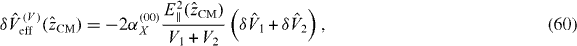
which, given kBT < ΔE, only affects the exciton as a pure dephasing contribution described by the interaction Hamiltonian  with
with 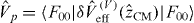 . Here the white noise variables
. Here the white noise variables 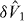 and
and 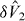 are uncorrelated and determined by
are uncorrelated and determined by 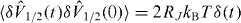 , where RJ and T are the relevant resistance and temperature—for estimating an upper bound we assume without loss of generality that the noise is symmetric and dominated either by the electrodes or the unfiltered sources. Then within the Markov approximation, these voltage fluctuations result in an excess linewidth (full-width at half-maximum (FWHM))
, where RJ and T are the relevant resistance and temperature—for estimating an upper bound we assume without loss of generality that the noise is symmetric and dominated either by the electrodes or the unfiltered sources. Then within the Markov approximation, these voltage fluctuations result in an excess linewidth (full-width at half-maximum (FWHM)) 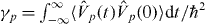 . The latter can be estimated using equations (60), (14) and
. The latter can be estimated using equations (60), (14) and 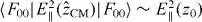 , leading to
, leading to

Finally, for the envisaged parameters (section 2.1 and figure 1), 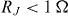 and T < 300 K, equation (61) yields γp/2π ≲ 200 kHz, which is negligible compared to the values for Γ ≳ 100 MHz considered here (sections 3.1 and 3.3). In principle, this voltage noise will also induce a fluctuation of the gradient forces exerted on the CNT (equation (59)), resulting in additional dissipation of the resonator mode. However, this effect is completely negligible for relevant parameters12.
and T < 300 K, equation (61) yields γp/2π ≲ 200 kHz, which is negligible compared to the values for Γ ≳ 100 MHz considered here (sections 3.1 and 3.3). In principle, this voltage noise will also induce a fluctuation of the gradient forces exerted on the CNT (equation (59)), resulting in additional dissipation of the resonator mode. However, this effect is completely negligible for relevant parameters12.
Another potential source of exciton dephasing is the Brownian motion of the suspended portion of the electrodes, which entails a limit to the suspended length, beyond which performance would be degraded. The convenience of electrode suspension, beyond that imposed by fabrication constraints, resides in the suppression it can induce of the maximum electric field at the neighbouring dielectric free surfaces (Ed−f) with respect to the maximum field. Assuming a cantilever geometry for the suspended portion of the electrode and an electrode–substrate gap size comparable to the suspended length Le, the suppression factor will scale as (he/2Le)2—where he is the transverse dimension of the electrode. For the envisaged device (figure 1), he = 30 nm and Le = 100 nm would already lead to Ed–f ≲ 5 V μm−1. If we assume some generic misalignment of the CNT, both the Brownian motion of the electrode's flexural (in-plane and/or out-of-plane) and compressional modes will contribute a term linear in the relevant displacement Xe to the corresponding fluctuation of the effective confining potential 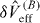 . The latter will play a role completely analogous to
. The latter will play a role completely analogous to 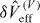 but with
but with 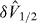 replaced by the {Xe}. In all cases, the relevant fluctuation of the electric field satisfies
replaced by the {Xe}. In all cases, the relevant fluctuation of the electric field satisfies

and a suitable model to estimate an upper bound for the corresponding excess linewidth (FWHM) γB is afforded by considering only the contributions from the fundamental resonances of each relevant branch (resonant frequency ωe) which can be treated separately—we assume in what follows that the Brownian motions of different electrodes are uncorrelated. These contributions can be analysed using the exact solution of the ensuing independent-boson model [55]. If we assume Au electrodes with the aforementioned cantilever dimensions, we have for the fundamental flexural mode ωe ∼ 1 GHz so that Γ ≲ ωe (cf sections 3.1 and 3.3). There are then two distinct effects of the electrodes' Brownian motion on the optical response of the exciton that could potentially interfere with our scheme: (i) generation of a sideband spectrum and (ii) pure dephasing leading to an excess linewidth of the corresponding ZPL. A critical parameter is the relative weight of the single-phonon sidebands (S) which for each branch, in the relevant regime kBT ≫ ℏωe and using equations (11) and (62), can be bounded by

where me is the corresponding effective mass. If we consider the envisaged device parameters (cf section 2.1 and figure 1), the aforementioned 'electrode' cantilever dimensions, the material properties of Au and T = 4.2 K, we obtain from equation (63) adding over all relevant branches of both electrodes: S ≲ 0.07—the ratio of the corresponding polaron shift to the one associated with the CNT resonator (η2ω0) is ≲0.03 (cf section 3.1). Thus, the influence of (i) on the proposed optomechanical manipulations would be minimal.
In turn, the pure dephasing (ii) is determined by the weak dissipation of these resonances induced by the 3D substrate and is characterized by an Ohmic environmental spectral density. The conditions S ≪ 1 and kBT ≫ ℏωe are sufficient to ensure that the dephasing is Markovian and amenable to a treatment similar to the one we have followed for the voltage fluctuations. Each of the relevant fundamental resonances coupled to the substrate satisfies [53]
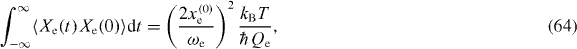
where x(0)e and Qe are, respectively, the corresponding zero-point motion and Q-value. Then, following a procedure analogous to the one used for estimating γp, we obtain from equations (11), (62) and (64)

Here, we have also assumed that given the low aspect ratio, the {Qe} are limited by clamping losses; used the results of [53] (table 1) which imply that 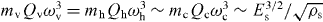 ; and added the bounds for all three relevant branches of both electrodes—here v, h and c denote, respectively, the flexural vertical, flexural horizontal and compressional fundamental resonances of the 'electrode' cantilever and the dimensionless prefactors are functions of νs. Strikingly, once a cantilever geometry is assumed, the dimensionless prefactor close to unity in equation (65) is independent of any other property of the electrode as it depends only on the Poisson ratio of the substrate. Thus, the magnitude of the suspended length Le would only begin to play a role in exciton dephasing if it became large enough to ensure that the mechanical dissipation were dominated by internal losses. Finally, we find that for the proposed parameters (cf section 2.1 and figure 1) and typical substrate properties determined by ρs = 2 g cm−3 and Es = 100 GPa, equation (65) yields a completely negligible excess linewidth γB/2π ≲ 20 kHz ≪ Γ.
; and added the bounds for all three relevant branches of both electrodes—here v, h and c denote, respectively, the flexural vertical, flexural horizontal and compressional fundamental resonances of the 'electrode' cantilever and the dimensionless prefactors are functions of νs. Strikingly, once a cantilever geometry is assumed, the dimensionless prefactor close to unity in equation (65) is independent of any other property of the electrode as it depends only on the Poisson ratio of the substrate. Thus, the magnitude of the suspended length Le would only begin to play a role in exciton dephasing if it became large enough to ensure that the mechanical dissipation were dominated by internal losses. Finally, we find that for the proposed parameters (cf section 2.1 and figure 1) and typical substrate properties determined by ρs = 2 g cm−3 and Es = 100 GPa, equation (65) yields a completely negligible excess linewidth γB/2π ≲ 20 kHz ≪ Γ.
Lastly, we have estimated radiation pressure effects and found that the corresponding static deflection and shot noise heating rate are also completely negligible, with typical parameters implying a launched power for a diffraction-limited spot size below 1 nW.
3.3. Strong coupling
Beyond optical transduction and cooling, the platform introduced here could allow us to realize a mechanical analogue of the strong and ultra-strong coupling regimes of cavity QED. If the driving laser is tuned exactly on resonance, i.e. δ = 0 in equation (42), after a π/2 rotation of the pseudospin around 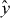 (σz → σx, σx → − σz), the system Hamiltonian reduces to the Rabi model [67] (H'sys → H''sys)
(σz → σx, σx → − σz), the system Hamiltonian reduces to the Rabi model [67] (H'sys → H''sys)
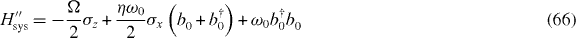
with the spin degree of freedom afforded by the NTQD states dressed by the laser field, i.e.
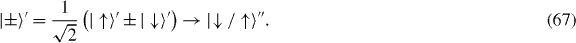
Here |↑〉' ≡ |ψ00−〉 corresponds to the relevant single-exciton state and |↓〉' to the empty NTQD. The spin-oscillator coupling and resonance condition are given, respectively, by ηω0/2 and Ω = ω0. Thus, given 1/Q ≪ η ≪ 1, reaching the strong coupling regime of the Jaynes–Cummings model (i.e. the Rabi model neglecting counter-rotating terms) depends on satisfying ηω0 ≳ Γ, which for the aforementioned parameters would require Γ/2π ≲ 100 MHz. Here the precise threshold will differ from the more usual one, ηω0 = Γ/2, given that the dissipation of the pseudospin induced by the radiation will no longer correspond to a simple relaxation channel. As discussed in section 2 the radiative contribution to Γ can be tuned with the axial magnetic field. We note that as the bright–dark exciton splitting lies in the 100 GHz range (cf section 2) and the radiative decay rate of the bright exciton is in the 10 GHz range [23], Γ ∼ 100 MHz with Ω ∼ ω0 ∼ 1 GHz is compatible with keeping the excitation of the bright exciton off-resonant.
The strong coupling regime discussed here is akin to the ion-trap realizations of the Jaynes–Cummings model and the parametric normal mode splitting in cavity optomechanics [68] in that the large energy-scale discrepancy between the optical and mechanical domains is bridged by the driving laser, which entails an advantageous frequency upconversion of the output. It offers a wide range of possibilities for the demonstration of quantum signatures in the motion. In particular, a judicious modulation of η locked to pulsed laser excitation could allow us to emulate the adiabatic passage scheme used in [34] for carrying out QND measurements of the oscillator's energy. This would enable observation of motional quantum jumps.
Furthermore, from the analysis in section 3.2 it follows that higher transverse fields 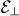 could be applied without disrupting the scheme. Then, a tenfold increase in
could be applied without disrupting the scheme. Then, a tenfold increase in 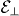 would result in η ∼ 1, allowing us to crossover to the ultra-strong coupling regime of the Rabi model, which has not been realized so far [67]. In this regime where the coupling becomes comparable with or larger than the resonator's level spacing, the ground state is characterized by an appreciable mean phonon occupancy and presents substantial entanglement between the excitonic quantum dot and the resonator [69]. To gain insight into this regime it is instructive to consider the limit η ≫ 1, which is simple to analyse in the 'polaronic' representation by treating the second term in the lhs of equation (44) perturbatively. Thus, one obtains for the ground state of the coupled system
would result in η ∼ 1, allowing us to crossover to the ultra-strong coupling regime of the Rabi model, which has not been realized so far [67]. In this regime where the coupling becomes comparable with or larger than the resonator's level spacing, the ground state is characterized by an appreciable mean phonon occupancy and presents substantial entanglement between the excitonic quantum dot and the resonator [69]. To gain insight into this regime it is instructive to consider the limit η ≫ 1, which is simple to analyse in the 'polaronic' representation by treating the second term in the lhs of equation (44) perturbatively. Thus, one obtains for the ground state of the coupled system
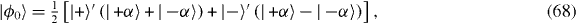
where 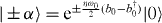 . This corresponds to a maximally entangled state for which measurements of σx yield orthogonal Schrödinger cat states of the resonator.
. This corresponds to a maximally entangled state for which measurements of σx yield orthogonal Schrödinger cat states of the resonator.
4. Conclusions and outlook
In conclusion, we set forth a scheme for inducing strong optomechanical effects in suspended CNTs via the DP exciton–phonon coupling. This provides an alternative to radiation–pressure-based schemes [4–6] for an ultra-low-mass and high-frequency nanoscale resonator leading to large backaction-cooling factors and opening a direct route to the quantum behaviour of a 'macroscopic' mechanical degree of freedom as it affords a mechanical analogue of cavity-QED. Most importantly, these breakthroughs rely on a lifetime-limited ZPL much narrower than the smallest CNT linewidths reported so far [23]. Indeed, the envisaged NTQDs will allow us to suppress the two most likely linewidth-broadening mechanisms, namely: inhomogeneous broadening and phonon-induced dephasing [70], by providing a controlled electrostatic environment and strong confinement of low-frequency phonons. Beyond nanomechanical applications, a doped version of these NTQDs will enable a tunable spin–photon interface [71]. Our technique could apply also to other high-quality 1D semiconductors such as prismatic nanowires [72]. Lastly, the simple approximation (equation (36)) we have derived for the DP of a confined E11 direct exciton subjected to a transverse electric field will further the understanding of electron–phonon interactions in these CNT systems.
Acknowledgment
IWR acknowledges helpful discussions with Naser Qureshi, Adrian Bachtold and Peter Rabl and financial support from the Nanosystems Initiative Munich and the DFG (grant no. WI-3859/1-1).
Footnotes
- 5
Note, however, that manipulating the indirect excitons may also be viable [25].
- 6
- 7
We note that
 is comparable to the axial critical field for exciton dissociation and yields ∼50 V μm−1 for relevant CNT parameters (cf section 3.1).
is comparable to the axial critical field for exciton dissociation and yields ∼50 V μm−1 for relevant CNT parameters (cf section 3.1). - 8
Note that the validity of equation (20) hinges on the fact that homogeneous boundary conditions are satisfied for x,y → ± ∞, and this relation between matrix elements breaks down for periodic boundary conditions as those satisfied along z.
- 9
As in equation (29), here we assume that only the contributions involving virtual transitions to single exciton states are relevant.
- 10
Note that 1/|ξ| is comparable to the transverse critical field for exciton dissociation—1/|ξ| ∼ 104 Vμm−1 for relevant nanotube parameters (section 3.1).
- 11
Since, to our knowledge, the optical transition energy E13 has not been determined so far, we take as a rough estimate of the energy difference in ξ, E13 − E11 ∼ E12 + 2ℏvF/3R, which corresponds to assuming that the correlation energy for E13 is the same as that for the cross-polarized excitons E12, and use for the latter the value reported in [61]—this procedure yields 1.3 eV.
- 12
A straightforward derivation using that the susceptibility associated with the voltage noise is determined by ℑ{χ(ω)} = RJω yields for the corresponding contribution to the mechanical linewidth
 , which for
, which for  implies that γm/2π ≲ 50 μ Hz.
implies that γm/2π ≲ 50 μ Hz.