Abstract
Active matter systems, which convert internal chemical energy or energy from the environment into directed motion, are ubiquitous in nature and exhibit a range of emerging non-equilibrium behaviors. However, most of the current works on active matter have been devoted to particles, and the study of active polymers has only recently come into the spotlight due to their prevalence within living organisms. The intricate interplay between activity and conformational degrees of freedom gives rise to novel structural and dynamical behaviors of active polymers. Research in active polymers remarkably broadens diverse concepts of polymer physics, such as molecular architecture, dynamics, scaling and so on, which is of significant importance for the development of new polymer materials with unique performance. Furthermore, active polymers are often found in strongly interacting and crowded systems and in complex environments, so that the understanding of this behavior is essential for future developments of novel polymer-based biomaterials. This review thereby focuses on the study of active polymers in complex and crowded environments, and aims to provide insights into the fundamental physics underlying the adaptive and collective behaviors far from equilibrium, as well as the open challenges that the field is currently facing.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Recommended by Dr Mark Geoghegan
1. Introduction
Active matter refers to systems in which the individual components either transform internal chemical energy into directed motion, or utilize energy from the environment [1, 2]. Prototypes are omnipresent in nature, ranging from the sub-cellular scale of the cytoskeleton in living cells [3–6], over self-propelled algae, sperm, and bacteria on the single cell level [7], to the macroscopic scale of flocks of birds, school of fish, and mammalian herds [8]. Due to the continuous flow of energy, active matter exhibits a wealth of emerging non-equilibrium behaviors, including, for example, swarming and the emergence of other collective properties [9]. Research in this field holds great promise for discovering new properties and innovative strategies for designing intelligent devices.
To date, the majority of research on active matter has been devoted to point-like particles, which lack shape-induced alignment interactions [10–15]. However, biological systems are abundant in polymeric and filamentous structures, which are heavily involved in various non-equilibrium processes. For instance, DNA is duplicated by DNA-polymerase actively displacing on it [16]; ribosomes synthesize proteins by actively sliding along RNA strands [17]. In recent years, active polymers [18, 19] have come under the spotlight of physical and biophysical research communities due to the crucial role it plays in numerous fundamental biological processes, such as cell mitosis and migration [20, 21]. In vitro experiments showed that, from motility assays, microtubules can self-organize into a lattice of nematic vortices [3, 22] and microfilaments can self-assemble into clusters, swirls and bands [4]. Besides the bio-polymeric active matter, chains of synthetic self-propelled colloidal particles have already been realized in experiments [23–25], which may potentially serve as a more flexible and controllable model system for studying the collective behaviors of active polymers. Nevertheless, we are still far from understanding the interplay between out-of-equilibrium fluctuations, corresponding polymer conformations, and emerging activity-driven self-organized structures of polymers and filaments.
Moreover, many existing studies have focused on understanding how living and inanimate active matter systems develop social and tunable collective behaviors that are not attainable by their counterparts at thermal equilibrium. However, real-life environments (e.g. in living tissues and porous soils) are strongly interacting and crowded systems [2]. Investigating the behavior of active polymers in complex environments is of great importance for our future understanding of transport processes in biological systems. This review thereby addresses the distinctive conformational and dynamic properties of active polymers in complex and crowded environments. In this review, we use the term 'active polymer' to refer to a chain-like structure of which the segments exhibit active motion, i.e. individual self-propelled monomers. The dynamic behaviors of self-propelled rods, which represent a special form of polymer chains with near-infinite rigidity, closely resemble those of active polymers and are also addressed in this review.
2. The physics of active polymers
Before proceeding to analyze the behavior of active polymers in complex and crowded environments, we first introduce the physics of active polymers in homogeneous environments.
2.1. Active Brownian particle
A generic model of a self-propelled particle is the well-known active Brownian particle, of which the overdamped equations of motion are given by [19]
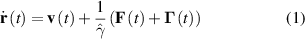

where v= v0
e is the propulsion velocity, F a force exerted on the particle, Γ and 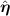 are the translational and rotational noise, satisfying
are the translational and rotational noise, satisfying
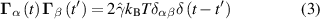
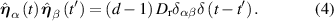
Here, kB is the Boltzmann constant, T the temperature, 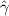 the translational friction coefficient, which is related to the translational diffusion coefficient Dt via
the translational friction coefficient, which is related to the translational diffusion coefficient Dt via 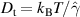 , Dr is the rotational diffusion coefficient, d is the spatial dimension, and
, Dr is the rotational diffusion coefficient, d is the spatial dimension, and 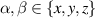 . For a particle in a viscous fluid in three dimensions,
. For a particle in a viscous fluid in three dimensions,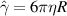 , with η the viscosity and R the particle radius, hence, Dr and Dt are related according to Dt
/Dr
R2
= 4/3. The rotational motion is independent of the translational motion. As a particular result, the correlation function
, with η the viscosity and R the particle radius, hence, Dr and Dt are related according to Dt
/Dr
R2
= 4/3. The rotational motion is independent of the translational motion. As a particular result, the correlation function  is obtained.
is obtained.
In two dimensions, the theoretical mean-square displacement (MSD) of an active Brownian particle is given by [26–28]
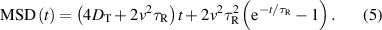
At short times, this expression becomes 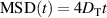 so that the motion is diffusive. At intermediate times,
so that the motion is diffusive. At intermediate times, 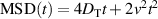 and the motion is super-diffusive. At long time scales,
and the motion is super-diffusive. At long time scales,  and diffusive motion is recovered, with a substantial enhancement of the effective diffusion coefficient, corresponding to
and diffusive motion is recovered, with a substantial enhancement of the effective diffusion coefficient, corresponding to  .
.
2.2. Active Brownian polymers
Active Brownian polymers refer to chains comprised of active Brownian particles connected by linear springs, of which the structural and dynamical properties are typically studied analytically by the well-known Rouse model. In this case, every monomer changes its propulsion direction independently in a diffusive manner, as schemed in figure 1(a). Systems of active Brownian polymers can be realized when passive polymers are embedded in a bath of active Brownian particles, as illustrated in figure 1(b). The structural properties of a linear active Brownian polymers are characterized by the mean square end-to-end distance 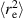 , as illustrated in figure 1(c) [29]. In the case of flexible polymers, where the persistence length lp is much smaller than the contour length L,
, as illustrated in figure 1(c) [29]. In the case of flexible polymers, where the persistence length lp is much smaller than the contour length L, 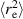 increases monotonically with the Péclet number (Pe). This is because active forces acting on the monomers push them in different directions, thereby stretching the polymer chain and leading to swelling. In such cases, the activity is typically treated as an effective temperature when mapping the polymers onto corresponding passive chains. However, in the case of semiflexible polymers, where lp is comparable to or larger than L, the behavior is more intricate. Specifically, at low Pe, the activity enhances fluctuations transverse to the polymer contour, resulting in a zig-zag configuration of the chain, resulting in an initial shrinkage. At higher Pe, the tension in the polymer contour, which increases with activity, dominates over the energetic contribution of bending, making the latter negligible. As a result, a semiflexible polymer behaves like a flexible one at high Pe.
increases monotonically with the Péclet number (Pe). This is because active forces acting on the monomers push them in different directions, thereby stretching the polymer chain and leading to swelling. In such cases, the activity is typically treated as an effective temperature when mapping the polymers onto corresponding passive chains. However, in the case of semiflexible polymers, where lp is comparable to or larger than L, the behavior is more intricate. Specifically, at low Pe, the activity enhances fluctuations transverse to the polymer contour, resulting in a zig-zag configuration of the chain, resulting in an initial shrinkage. At higher Pe, the tension in the polymer contour, which increases with activity, dominates over the energetic contribution of bending, making the latter negligible. As a result, a semiflexible polymer behaves like a flexible one at high Pe.
Figure 1. Conformational and dynamical properties of active Brownian polymers. (a) Illustration of an active Brownian polymer comprised of active monomers in a solution of passive particles. (b) Illustration of a passive polymer in an active bath. (c) Mean-square end-to-end distances as a function of the Péclet number. p is related to the persistence length as p = 1/2lp. The dashed line is a flexible polymer limit. (d) Mean-square displacements of a flexible active polymer with pL = 103. The dashed lines are the mean-square displacements in the polymer center-of-mass reference frame. Reproduced from [29]. CC BY 4.0.
Download figure:
Standard image High-resolution imageAnother crucial parameter used to assess the dimensions of a polymer coil is the radius of gyration (RG). According to the Flory scaling law, RG of a real chain has a power-law dependence on the number of monomers N, RG ∼ Nν with ν = 3/(d + 2), where d is the dimension of the embedding space [30]. For active Brownian polymers, the scaling is proven to hold in two-dimensional (2D) space [31], that is, the exponent ν = 3/4 is not affected by self-propulsion of the monomers.
The dynamical properties are characterized by the contour-length averaged MSD [32], as shown in figure 1(d). Obviously, the diffusive motion is significantly enhanced by activity. At short time scales, a quadratic scaling for the ballistic motion is observed for Pe ≳ 20. The well-known Rouse-dependence (t1/2) is observed at intermediate time scales, originating from the internal polymer dynamics, see the dashed lines in figure 1(d). At long time scales, the MSDs turn to be linear with time t, which are dominated by the center-of-mass motion. Furthermore, the relaxation process is accelerated by activity and the relaxation times become shorter with increasing Pe [29]. At low Pe, the well-known mode-number dependence 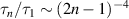 is valid for semi-flexible polymers [33]. At high Pe, a semiflexible polymer exhibits behavior similar to that of a flexible polymer, as previously stated. Consequently, relaxation times exhibit the dependence
is valid for semi-flexible polymers [33]. At high Pe, a semiflexible polymer exhibits behavior similar to that of a flexible polymer, as previously stated. Consequently, relaxation times exhibit the dependence 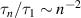 of flexible polymers.
of flexible polymers.
2.3. Tangentially driven filament
The activity of monomers is not always randomly oriented, such as the motor-induced sliding of aligned microtubules and the wriggling of worms where they are considered to be propelled tangentially to their contour, as illustrated in figure 2(a). In contrast to the swelling of active Brownian polymers, Bianco et al [34] found that the gyration radius of tangentially driven filaments is monotonically reduced with increasing activity, as shown in figure 2(b). The activity-induced collapse is attributed to a coil-to-globulelike transition of the filament, highlighted by a marked change of the scaling exponent of the gyration radius, as shown in figure 2(c). Note that Philipps et al [36] has argued that the conformational properties of tangentially driven polymers are independent of propulsion if the active force is applied along the bond vector instead of the vector connecting the first neighbors of monomer. The center-of-mass MSDs can also be divided into three different regimes. At short time scales, a passive diffusive regime 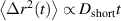 with Dshort = D0
/N takes place, where N is the number of monomers. At intermediate time scales, a typical super-diffusive regime of active systems is observed. At long time scales, the diffusive regime is recovered, characterized by an enhanced diffusion coefficient Dlong
> Dshort, as shown in figure 2(d). The normalized diffusion coefficient as a function of N and Pe is given in figure 2(e). At small Pe, Dlong decreases with the polymer size (blue region), while Dlong is almost independent of N for larger values of Pe (red region) since thermal contribution can be disregarded. Tangentially driven filament exists across scales ranging from motor-driven biofilaments to polymer-like worms. In macroscopic active filaments, inertial effects on their motion cannot be ignored. Combining simulations and analytical theory, Fazelzadeh et al [37] found that inertial collisions of monomers can cause extended conformations and result in enhanced diffusion of tangentially driven filaments. These findings are expected to enrich our comprehension of macroscopic active systems, such as worms [38] and snakes [39].
with Dshort = D0
/N takes place, where N is the number of monomers. At intermediate time scales, a typical super-diffusive regime of active systems is observed. At long time scales, the diffusive regime is recovered, characterized by an enhanced diffusion coefficient Dlong
> Dshort, as shown in figure 2(d). The normalized diffusion coefficient as a function of N and Pe is given in figure 2(e). At small Pe, Dlong decreases with the polymer size (blue region), while Dlong is almost independent of N for larger values of Pe (red region) since thermal contribution can be disregarded. Tangentially driven filament exists across scales ranging from motor-driven biofilaments to polymer-like worms. In macroscopic active filaments, inertial effects on their motion cannot be ignored. Combining simulations and analytical theory, Fazelzadeh et al [37] found that inertial collisions of monomers can cause extended conformations and result in enhanced diffusion of tangentially driven filaments. These findings are expected to enrich our comprehension of macroscopic active systems, such as worms [38] and snakes [39].
Figure 2. Conformational and dynamical properties of tangentially driven filament. (a) Illustration of a tangentially driven filament. (b) RG as a function of the Péclet number. (c) Exponent ν of RG for different values of Pe. (d) Mean-square displacements. (e) Normalized diffusion coefficient Dlong (N, Pe)/Dlong (40, Pe) as a function of N and Pe. Reprinted (figure) with permission from [34], Copyright (2018) by the American Physical Society. (f) RG as function of N, for active self-avoiding rings and active ghost rings. (g) Monomer velocity distributions. (h) Position of the minimum of the bond correlation. (i) Dynamic phase diagram for active rings. Collapsed rings are reported as blue squares, inflated rings as red circles, passive-like rings as green diamonds, and systems showing a more complex behavior as gray crosses. Reprinted (figure) with permission from [35], Copyright (2021) by the American Physical Society.
Download figure:
Standard image High-resolution imageThe structural and dynamical properties of active Brownian ring polymers are in general similar to that of linear chains [40]. For example, flexible rings monotonically swell with increasing activity, whereas semiflexible rings shrink at moderate activities and swell again at large Péclet numbers. However, the properties of tangentially driven polymer rings are significantly different from that of linear chains [35]. In contrast to the monotonous behavior of tangentially driven linear chains, a nonmonotonic dependence of the gyration radius on the polymer size and Pe is observed for tangentially driven polymer rings. At sufficiently high activity, short rings ( ) swell, whereas long rings (
) swell, whereas long rings ( ) collapse, as shown in figure 2(f). For
) collapse, as shown in figure 2(f). For 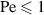 , the scaling exponent ν = 0.588 for passive polymers is recovered for all values of N. For
, the scaling exponent ν = 0.588 for passive polymers is recovered for all values of N. For  , two distinct regimes are identified with different scaling exponents. More precisely,
, two distinct regimes are identified with different scaling exponents. More precisely,  for short chains, similar to the behavior of fully rigid polymers. Hence, the activity induces an effective bending rigidity, which is in contrast to activity-induced softening of active Brownian rings. For long chains,
for short chains, similar to the behavior of fully rigid polymers. Hence, the activity induces an effective bending rigidity, which is in contrast to activity-induced softening of active Brownian rings. For long chains, 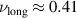 indicates a very compact conformation, but not exactly the one expected in bad solvent conditions
indicates a very compact conformation, but not exactly the one expected in bad solvent conditions 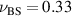 . Indeed, the collapsed structure is very complex, being comprised of a compact self-wrapped core and a few dangling sections fluttering on its surface, as shown in the snapshot in figure 2(f). The dangling sections lead to the larger value of
. Indeed, the collapsed structure is very complex, being comprised of a compact self-wrapped core and a few dangling sections fluttering on its surface, as shown in the snapshot in figure 2(f). The dangling sections lead to the larger value of 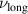 as compared to
as compared to  , which is also verified by the velocity distributions of the monomers of the collapsed state. As shown in figure 2(g), the distributions exhibit two peaks at sufficient high Pe, at
, which is also verified by the velocity distributions of the monomers of the collapsed state. As shown in figure 2(g), the distributions exhibit two peaks at sufficient high Pe, at 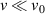 for monomers trapped in the collapsed section and
for monomers trapped in the collapsed section and  for monomers in the dangling sections. The formation of the inflated and collapsed states is attributed to steric interactions of the monomers and topology conservation of the rings. When two loops meet, they merge and give rise to a larger loop for short rings, as indicated by the minimum of bond spatial correlation function
for monomers in the dangling sections. The formation of the inflated and collapsed states is attributed to steric interactions of the monomers and topology conservation of the rings. When two loops meet, they merge and give rise to a larger loop for short rings, as indicated by the minimum of bond spatial correlation function  , where
, where  , as shown in figure 2(h). For long rings, they will thread one into another, trapping the monomers and inducing the collapse of the entire chain. Finally, a phase diagram for active rings is given in figure 2(i), showing a complex behavior of the system. At small Pe, active rings retain their equilibrium scaling for all values of N. At high Pe, the scaling of Rg with N depends on the active ring size. At intermediate Pe, the dependence of Rg on N is more complex and the active rings can be either jumping in between fairly compact and fairly open conformation or quasi-collapsed but not arrested conformations. Note that Philipps et al [41] has also argued that the conformational and dynamical properties of tangentially driven polymer rings are independent of the active force if an alternative discretization is employed.
, as shown in figure 2(h). For long rings, they will thread one into another, trapping the monomers and inducing the collapse of the entire chain. Finally, a phase diagram for active rings is given in figure 2(i), showing a complex behavior of the system. At small Pe, active rings retain their equilibrium scaling for all values of N. At high Pe, the scaling of Rg with N depends on the active ring size. At intermediate Pe, the dependence of Rg on N is more complex and the active rings can be either jumping in between fairly compact and fairly open conformation or quasi-collapsed but not arrested conformations. Note that Philipps et al [41] has also argued that the conformational and dynamical properties of tangentially driven polymer rings are independent of the active force if an alternative discretization is employed.
3. Complex environments
So far, complex behaviors of active polymers have been discovered even in homogeneous environments without any physical boundaries. In this section, we will focus on the studies of active polymers in complex environments and the role of physical obstacles in the structural and dynamic properties of active polymers.
3.1. Anchored at one end
Oscillatory beating of eukaryotic cilia and flagella is known to play a crucial role in driving processes such as directed cell migration [42], embryogenesis [43], and mucus clearance [44]. Sanchez et al [45] described a minimal model system, which is composed of microtubules and molecular motors and exhibits similar oscillatory beating patterns, as shown in figures 3(a)–(d). Taxol-stabilized microtubules and biotin-labeled kinesin motors, which are bound into clusters through multimeric streptavidin, spontaneously self-assemble into bundles through the depletion attractions induced by polyethylene glycol. The kinesin clusters actively bind and walk on adjacent microtubules and the sliding motion is transformed into local bending with the attachment at the base, leading to large-scale beating patterns. Note that the buckling instability, which essentially yields the periodic motions, is available only when the microtubules are attached to a fixed boundary. The primary factor that determines the beating frequency is the length of the bundle, with longer bundles exhibiting longer beating periods. Combining simulations and theory, Chelakkot et al [46] suggested a simple proposal to mimic the beating of eukaryotic cilia. Rather than having motors walk along two neighboring filaments, similar beating patterns can be generated by using connected self-propelled particles. Moreover, the mode of oscillation is dramatically changed by the boundary condition at the anchored end. When the filament is clamped at one end, regular flagella-like beating can be observed, whereas a pivoted end allows the filament to form spiral shapes and rotate freely if the propulsion forces are tightly parallel to the local tangent, as shown in top and middle images in figures 3(e) and (f). For a wide range of active forces, the frequencies of the beating and rotation as a function of propulsion force fp follow the same power law ω ∼ fp 4/3 to balance the active energy input into the system owing to the self-propulsion and the energy dissipated viscously. On the other hand, if the coupling between directions of the chemical linkage and the propulsion force is reduced, the systems turn to exhibit erratic motions instead of periodic oscillations, as shown in bottom images in figures 3(e) and (f), providing an independent and experimentally accessible parameter to tune the filament behavior. At the macroscopic scale, Zheng et al [47] has achieved such filamentous robots that exhibit flagellar motion when pinned at one end, thus providing a powerful tool to investigate the collective self-oscillation of active polymers.
Figure 3. (a)–(d) A minimal experimental system of microtubules, molecular motors, and depleting polymers assembles into actively beating microtubule bundles. From [45]. Reprinted with permission from AAAS. (e) Dynamical shapes observed in simulations for a filament clamped at one end. (f) Spiral shapes for a filament with one free end and one end that can pivot. Reproduced from [46] with permission from the Royal Society of Chemistry.
Download figure:
Standard image High-resolution image3.2. Pushing a load
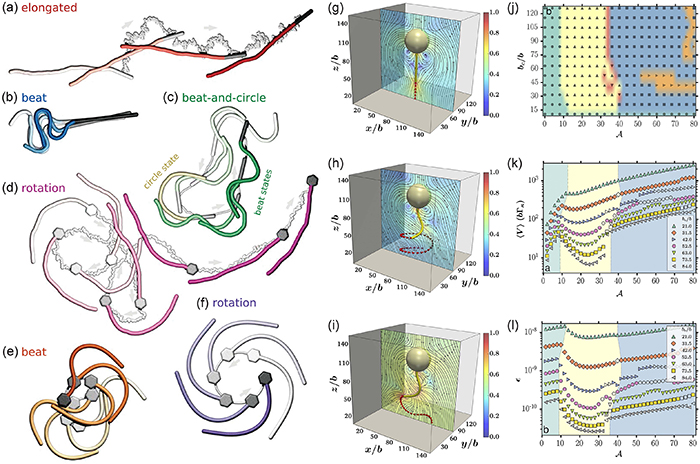
Between the two extremes of pivoted or clamped filaments, which do not have translational degrees of freedom, and freely swimming filaments, Isele-Holder et al [48] studied the motion of a self-propelled filament pushing a load in a viscous fluid. The hydrodynamic friction of the load and propulsive force cause a compression in the filament that results in a buckling instability and versatile motion. As shown in figures 4(a)–(f), four characteristic types of motion of the filament can be identified, depending on the strength of propulsion and shape of the load (a rod or a hexagon). For low propulsion strengths, an elongated phase is observed where the filament is almost straight (figure 4(a)). As the propulsion force is increased, the filament buckles under the compressive load, exhibiting a sperm-like beating pattern (figure 4(b)). At large thermal noise, the beating motion is interrupted by a short-lived circular swimming motion (figure 4(c)). When attached to hexagonal heads, the filaments swim in a circle (figure 4(d)), as previously observed for asymmetric rigid bodies [49, 50]. Under strong propulsion, beat motion is recovered (figure 4(e)) and the rotational motion is more evident at lower temperatures (figure 4(f)).
Figure 4. (a)–(f) Sequence of filament snapshots showing different filament motion. Time increases from transparent to opaque. The gray lines are the trajectories of the load. Reproduced from [48]. CC BY 3.0. (g)–(i) Snapshots of different dynamical states of the filament-colloid assembly with increasing activity. Linear state (g), helical state (h), and planar state (i). (j) Phase diagram as a function of the size of colloid and activity. Linear state (circle), helical state (triangle up), helical beating with periodic switching of sign (triangle down), planar (square), and sculling like beating (triangle right). (k)–(l) The average speed and efficiency of transport as a function of activity for different colloid radius. Reprinted from [51], with the permission of AIP Publishing.
Download figure:
Standard image High-resolution imageBy clamping an active filament to the surface of a spherical colloid, Manna et al [51] studied the dynamics of the colloid-filament assembly. As shown in figures 4(g)–(i), three typical states of motion are identified with increasing activity. At low activity, the transport of the colloid occurs without any deformation of the filament (figure 4(g)). At moderate activity, the filament moves in a non-planar corkscrew-like motion as it transports the colloid (figure 4(h)). At high activity, a planar beating motion of the filament is observed when transporting the colloid (figure 4(i)). Phase diagram as a function of the size of colloid and activity is shown in figure 4(j), the majority of which is occupied by the abovementioned three states. Due to the variation in modes of the motion, the transport speed varies non-monotonically with activity, especially for large colloids, as shown in figure 4(k). The greatest transport speed of colloid occurs at the highest activity, but it does not necessarily result in the most efficient transport, as shown in figure 4(l). These findings hold significant importance in optimizing the design parameters of such assemblies for potential biomimetic applications.
3.3. Translocation through a pore
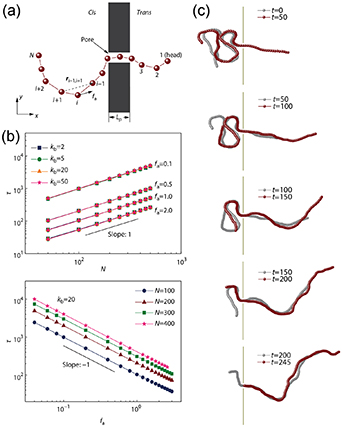
The translocation of polymer chains through small pores is universal in biological processes, such as transportation of biological polymers (proteins, RNA, DNA) through protein pores in biological membranes [52–54]. Using coarse-grained simulations, Wang et al [55] studied the translocation of tangentially driven filament through a pore (figure 5(a)). In contrast to the translocation of passive polymers where the translocation time τ increases monotonously with chain stiffness, the translocation time is independent of the rigidity of the polymer (figure 5(b)). Moreover, the translocation time can be expressed by a scaling relation 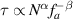 with
with  and
and  . The value of
. The value of  is much smaller than 1 + 2 v (=2.5 for 2D) for the unforced translocation and 1 + v (=1.75 for 2D) for the forced translocation of passive flexible polymers through small pores. Observation of the details of the translocation process demonstrates that active polymers show a railway motion (figure 5(c)), resulting in the dependence of τ on N and fa.
is much smaller than 1 + 2 v (=2.5 for 2D) for the unforced translocation and 1 + v (=1.75 for 2D) for the forced translocation of passive flexible polymers through small pores. Observation of the details of the translocation process demonstrates that active polymers show a railway motion (figure 5(c)), resulting in the dependence of τ on N and fa.
Figure 5. (a) Schematic of translocation of tangentially driven filament through a pore. (b) The dependence of translocation time τ on polymer size N and propulsive force fa. (c) Snapshots of a tangentially driven filament at different times during the translocation process. Reproduced from [55], with permission from Springer Nature.
Download figure:
Standard image High-resolution image3.4. Within cavities
The interplay between confinement and the entropic, elastic, and out-of-equilibrium properties of filament plays a significant role in determining their activity, conformation, and structure [56–58]. Of particular interest is the spherical confinement, which represents the simplest model from which one can understand the stacking of chromatin in the cell nucleus [59], DNA packaging inside virus capsids [60, 61], and self-organization of actin filaments inside the cell [62]. Saintillan et al [59] developed a coarse-grained active polymer model where chromatin is represented as a long flexible Brownian polymer chain acted upon by stochastically activated dipolar forces. Different from the propulsion forces of active Brownian polymers or tangentially driven filaments, the active dipoles occur on the scale of one link, representing the action of ATP-powered enzymes, as shown in figure 6(a). In the absence of active motors, a roughly uniform density is observed due to the balance of steric and fluctuation forces. The macroscopic dynamics of the passive chain is extremely slow as its motion is strongly hindered by confinement and its self-entanglement. The results of contractile dipoles are comparable to that of the passive chain, with little evidence of long-range ordering. However, the dynamics is very different when extensile motors are active. The system rapidly reorganizes itself as the chromatin fiber is stretched into long and mutually aligned segments, as shown in figure 6(b). As a result, large regions with high nematic order in fiber orientation appear (figure 6(c)). Moreover, extensile systems exhibit coherent chain motions on large length and time scales, produced by the motor-induced nucleoplasmic flows, emphasizing the interplay between hydrodynamic interactions mediated by the embedding fluid and connectivity of dipoles in a chain (figure 6(d)).
Figure 6. (a)–(d) Simulations of chromatin inside the nucleus. (a) Active dipoles (extensile or contractile) bind stochastically to individual link. (b) Filament configurations at different times. (c) The nematic structure on the surface of the confining sphere. (d) Chromatin displacement map. Reproduced with permission from [59]. (e)–(h) Snapshots of different configurations acquired by an active filament inside a spherical cavity for different Péclet numbers. Reprinted from [63], with the permission of AIP Publishing.
Download figure:
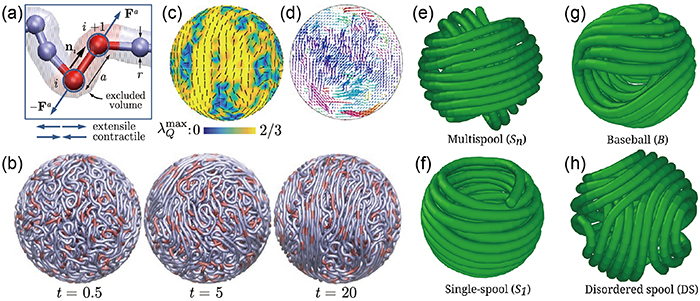
Standard image High-resolution imageFor a tangentially driven filament, Das and Cacciuto [63] performed numerical simulations inside a rigid spherical cavity and discovered novel configurations that are not observed for the passive counterpart, depending on the strength of the active forces. For passive semiflexible filament, multispool-like morphologies (Sn
) are acquired, which has been widely observed in simulations [64–66], as shown in figure 6(e). However, a single-spool conformation (S1) characterized by two polar opposite holes (two + 1 defects) is more dominant even for very small amounts of activity ( ), as shown in figure 6(f). The S1 configuration is unwrapped from the Sn
state by pushing the inner spools toward the cavity and orienting them parallel to each other. Once the activity is removed from the S1 state, the filament can easily reach Sn
configuration. As the Péclet number is further increased, a baseball-like (B) conformation with four opposite holes (four + 1/2 defects) is also attainable from the S1 conformation, as shown in figure 6(g). Due to the large bending energy barriers, the filament tends to retain the B state when the activity is removed despite the high bending energy cost. However, a slight amount of activity is again able to drive a system from B state back to S1 state. The intermediate states during these transitions can be generically described as disordered spools, as shown in figure 6(h). The highly dynamic behavior is one of the most interesting features of the active filaments when they are confined within a spherical cavity, which, however, is far from well understood.
), as shown in figure 6(f). The S1 configuration is unwrapped from the Sn
state by pushing the inner spools toward the cavity and orienting them parallel to each other. Once the activity is removed from the S1 state, the filament can easily reach Sn
configuration. As the Péclet number is further increased, a baseball-like (B) conformation with four opposite holes (four + 1/2 defects) is also attainable from the S1 conformation, as shown in figure 6(g). Due to the large bending energy barriers, the filament tends to retain the B state when the activity is removed despite the high bending energy cost. However, a slight amount of activity is again able to drive a system from B state back to S1 state. The intermediate states during these transitions can be generically described as disordered spools, as shown in figure 6(h). The highly dynamic behavior is one of the most interesting features of the active filaments when they are confined within a spherical cavity, which, however, is far from well understood.
Theoretically, Das and Cacciuto [67] delved into the behavior of active flexible polymers within more complex cavities. Recent numerical simulations, as mentioned in section 2, have demonstrated that the equilibrium size scaling for the radius of gyration of a self-avoiding polymer also holds for active polymers in 2D space [31]. However, the commonly accepted theory, which is effective in explaining the behavior of passive polymers in various environments, fails to accurately describe active polymers under confinement. In particular, the free energy to confine a passive self-avoiding polymer between two parallel plates at a distance 2R from each other or within an infinitely long cylindrical channel of radius R scales as  . If this holds for an active polymer, the force it exerts on the constraining walls or cylinder should scale as
. If this holds for an active polymer, the force it exerts on the constraining walls or cylinder should scale as 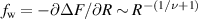 . As illustrated in figure 7(a), the active polymer behaves consistently with the expected behavior of a passive polymer between two plates (2D) when
. As illustrated in figure 7(a), the active polymer behaves consistently with the expected behavior of a passive polymer between two plates (2D) when 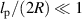 , where lp is the characteristic persistence length of the active path (lp = vp
/Dr). However, when
, where lp is the characteristic persistence length of the active path (lp = vp
/Dr). However, when 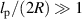 , the associated exponent α becomes systematically smaller, and this also decays with increasing Pe. A similar dependence of the force exerted by an active polymer is obtained when confined within a cylinder (three-dimensional), as shown in figure 7(b). When
, the associated exponent α becomes systematically smaller, and this also decays with increasing Pe. A similar dependence of the force exerted by an active polymer is obtained when confined within a cylinder (three-dimensional), as shown in figure 7(b). When 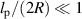 , the polymer is not strongly affected by the active force and behaves effectively as a passive polymer at a higher temperature (figure 7(c)). However, when
, the polymer is not strongly affected by the active force and behaves effectively as a passive polymer at a higher temperature (figure 7(c)). However, when  , the polymer adopts conformations that can be described as a mixture of collapsed configurations followed by fully stretched segments (figure 7(d)). Such highly dynamic heterogeneous conformations cannot be treated with the standard blob scaling representation, resulting in the large deviations of the associated exponent α.
, the polymer adopts conformations that can be described as a mixture of collapsed configurations followed by fully stretched segments (figure 7(d)). Such highly dynamic heterogeneous conformations cannot be treated with the standard blob scaling representation, resulting in the large deviations of the associated exponent α.
Figure 7. (a), (b) Force exerted by an active polymer within cavities for different Pe. Between two parallel walls (d= 2) at a distance 2R from each other (a) and within a cylinder (d= 3) of radius R (b). The dashed lines show the expected dependence for the passive system 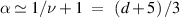 . (c), (d) Typical configurations for active polymers confined between two walls at a distance 2 R. Pe = 2 (c) and Pe = 80 (d). Reprinted (figure) with permission from [67], Copyright (2019) by the American Physical Society.
. (c), (d) Typical configurations for active polymers confined between two walls at a distance 2 R. Pe = 2 (c) and Pe = 80 (d). Reprinted (figure) with permission from [67], Copyright (2019) by the American Physical Society.
Download figure:
Standard image High-resolution image3.5. Interaction with obstacles
Usually, the application environments of active polymers are complex and the basic question resides in their interaction with one single obstacle. Shen et al [68] studied the structure and dynamics of a tangentially driven active polymer absorbed on a cylindrical obstacle with a smooth surface in a three-dimensional space (figure 8(a)) and found three typical conformations of the active polymer, depending on the chain length, cylinder radius, and primarily chain stiffness. At low rigidity, the polymer is easy to bend and the spiral configuration is favored (figure 8(b)). At intermediate rigidity, the polymer wraps around the cylinder and a helix-like state appears. At high rigidity, the bending of chain is suppressed, thus entering a straight state. In the absence of active force, the polymer cannot spontaneously wind up due to the entropy effect, which resists spiral formation. The phase boundary between helix-like state and straight state shifts toward the low rigidity region for passive polymers, indicating that active force can reduce the stiffness of the semi-flexible chain, which is consistent with that observed in a free environment [34]. Interestingly, a small radius of curvature (high surface curvature) hinders the formation of spiral due to the high penalty of bending energy. Dynamically, in the spiral state, the polymer exhibits rotational motion (figure 8(c)) that follows a power-law relation with the form 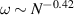 , which is consistent with the torque-balance theory of general Archimedean spirals. In the helix-like state, the polymer displays a snake-like motion with stochastic turning back (figure 8(d)), while in the straight state, it exhibits translational motion at a constant speed along the axial direction.
, which is consistent with the torque-balance theory of general Archimedean spirals. In the helix-like state, the polymer displays a snake-like motion with stochastic turning back (figure 8(d)), while in the straight state, it exhibits translational motion at a constant speed along the axial direction.
Figure 8. (a) Schematic of the system showing a polymer absorbed on a cylinder. (b) Phase diagram as a function of chain rigidity and radius of the cylinder. The dark square, red circle, and blue triangle represent the spiral state, helix-like state, and straight state, respectively. The light-blue and light-cyan colors, represent helix-like and straight states without active force, respectively, in the background. (c) Schematic diagram of the rotational angle in the spiral state. (d) Typical snapshots of forward and turning back of the polymer. Reproduced from [68] with permission from the Royal Society of Chemistry. (e) Phase diagram of active chains as a function of Pe and  with colored background representing radius of gyration and representative snapshots of the different states. Reproduced from [69] with permission from the Royal Society of Chemistry.
with colored background representing radius of gyration and representative snapshots of the different states. Reproduced from [69] with permission from the Royal Society of Chemistry.
Download figure:
Standard image High-resolution imageWhen the number of obstacles in the system becomes multiple, Wu et al [69] found more interesting dynamical and conformational states in a 2D space. As illustrated in figure 8(e), active polymers can exist in different states, including the diffusive expanded or collapsed state, as well as the localized state, which is determined by the activity strength and rigidity of the chain. In the diffusive expanded state, the active polymer undergoes a railway motion, which has been depicted in figure 5(c), while in the diffusive collapsed state the chain behaves like a deformable droplet that can move freely through the gaps between obstacles. Due to obstacle constraints and self-trapping, active polymers at high activity tend to remain in a localized state and exhibit a vortex-like configuration. Contrary to intuition, it has been observed that the diffusion of active chains is actually enhanced in crowded environments, as compared to obstacle-free environments, which is attributed to a structural reason that the obstacles prevent active chains from collapsing. Importantly, this finding has been found to hold true across different levels of crowdedness and obstacle packing fractions, indicating its robustness. These findings may provide insights into the design of novel drug delivery systems.
3.6. In porous media
As the density of obstacles increases, the environment turns to be porous. Understanding the motion of biological agents in such porous media is essential for a wide range of biological, medical, and industrial processes. Mokhtari and Zippelius [70] found that the motion of active filaments in a porous medium depends critically on chain length, activity, and flexibility. As expected, flexible polymers form spirals as observed in unobstructed environment and are localized around the obstacles because they cannot pass through the narrow channels. However, stiff polymers tend to bend only slightly to pass around an obstacle (figure 9(a)). As shown in figure 9(b), the MSD curves can be divided into three regions: ballistic at small t, diffusive at intermediate t, and saturated at large t. Typical trajectories of stiff and flexible filaments are depicted in figure 9(c). When Pe is increased, the gyration radius of tangentially driven filament is monotonically reduced (figure 2(b)), implying a stronger tendency to spiraling and localization. At extremely high activity, directed motion in the extended state is favored and the diffusive motion of filament is recovered (figure 9(d)). Flexible polymers have to unwind before passing the narrow channels, after which they immediately spiral again (figure 9(c)). Therefore, the motion of flexible polymers can be well described by the continuous-time random walk model with unspiraling events corresponding to the renewal process, allowing the polymer to make a displacement. By calculating the waiting time distribution 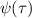 , a heavy tail with an algebraic decay approximately like t−
1.3 is observed (figure 9(e)), implying a sub-diffusive behavior MSD ∼ t0.3.
, a heavy tail with an algebraic decay approximately like t−
1.3 is observed (figure 9(e)), implying a sub-diffusive behavior MSD ∼ t0.3.
Figure 9. (a) Flexible (left) and stiff (right) polymers in a porous medium. (b) Mean-square displacement of active filament for different values of stiffness. (c) Center-of-mass trajectories of stiff (left) and flexible (right) polymers. (d) Phase diagram with various stiffness and activity. Triangles, localized phase; circle, diffusive regime. (e) Waiting time distribution of the CTRW model. Reprinted (figure) with permission from [70], Copyright (2019) by the American Physical Society.
Download figure:
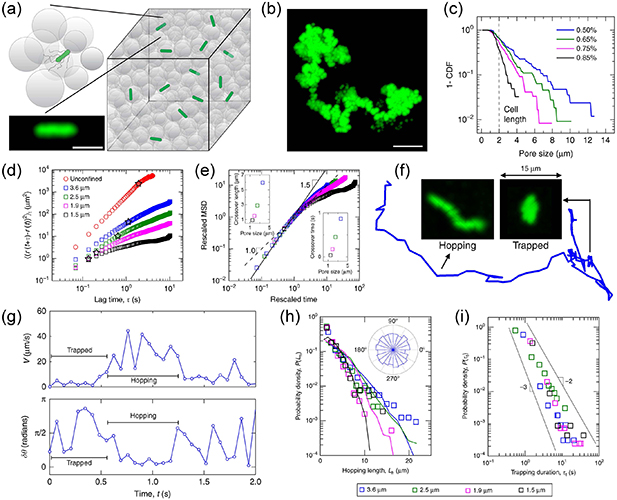
Standard image High-resolution imageDue to their elongated shape, bacteria are often modeled as active filaments. By confining jammed packings of hydrogel particles as solid matrices that bacteria can swim through (figure 10(a)), Bhattacharjee and Datta [71] provided a direct visualization of bacterial motility in porous media (figure 10(b)). By tuning the packing density of hydrogel particles, the pore size distribution can be controlled, which essentially determines the motion of bacteria in porous media (figure 10(c)). As expected, bacteria swim slower in porous media than in unconfined liquid (figure 10(d)). What is striking is that the MSDs vary as τ1.5 instead of τ2 at short time scales and a sub-diffusive behavior is observed at long time scales, as indicated in figure 10(e). These results indicate that the run-and-tumble (RT) motility may not persist in a porous medium. Inspection of individual trajectories shows that bacteria move via intermittent hopping and trapping (figure 10(f)). By calculating the instantaneous speed of bacteria when they pass through the porous medium, one can clearly observe the switching between hopping and trapping, as shown in figure 10(g). When a bacterium is trapped, it constantly reorients its body until it can escape from the trap, characterized by small velocity and large reorientation angle. During a cell hopping, a bacterium moves in a directed path until it is trapped again, characterized by large velocity and small reorientation angle. Therefore, the hop length is determined by the length of straight chord that can fit within the pore space, as shown in figure 10(h). As the modeling of large polymers during their thermal diffusion, each trap can be thought as an entropic trap. The difference between the numbers of possible ways that a cell can configure itself in the pore and at an outlet of a trap determines the free energy cost of a hopping and the trapping durations. Therefore, the probability density of trapping durations is given by 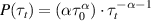 , where τ0 is the characteristic time of swimming and α measures the competition between activity and confinement. Increasing confinement leads to reduced α, as verified by the weak decrease of α in figure 10(i).
, where τ0 is the characteristic time of swimming and α measures the competition between activity and confinement. Increasing confinement leads to reduced α, as verified by the weak decrease of α in figure 10(i).
Figure 10. (a) Schematic of three-dimensional porous media made by jammed packings of hydrogel particles. (b) Time-projection of tracer particle. (c) Complementary cumulative distribution function of the smallest confining pore size for four different packing densities of hydrogel particles. (d) Mean-square displacements for bacteria in unconfined liquid and in porous media. (e) Mean-square displacements rescaled by the crossover length and time scales, as indicated by the stars in (d). (f) Representative single-cell trajectory. (g) Instantaneous speed and reorientation angle of a representative cell. (h) Probability density of hopping lengths; curves show distribution of chord lengths. (i) Probability density of trapping durations. Reproduced from [71]. CC BY 4.0.
Download figure:
Standard image High-resolution imageBesides locomotion, reorientation of microorganisms generated by intrinsic biophysical mechanisms is also indispensable for their efficient search for nutrients or escape from poisonous environments. Upon introducing a reversal mechanism (figure 11(a)), Kurzthaler et al [72] demonstrated that the dispersion of stiff active polymers through porous media is amplified by more than two orders in magnitude (figure 11(b)). At short time scales, all the MSDs of active polymers with different reversal rates collapse, indicating a passive diffusive motion. At intermediate time scales, the run-reversal polymers exhibit a super-diffusive motion while rarely reversing polymers display a sub-diffusive behavior. At long time scales, a diffusive regime with a linear increase is recovered. Importantly, for a broad range of Pe, the long-time effective diffusivities of run-reverse polymers display a nonmonotonic behavior with respect to the reversal rate, as characterized by the trade-off between the maximal pore length of the medium and the run length of the polymer (figure 11(c)). More importantly, the effective diffusivities for all Pe display a prominent maximum, where Lc,max /ℓrun ≈1. When Lc,max exceeds ℓrun, reversal events happen too often for direct movement in porous media, whereas if Lc,max is less than ℓrun, reversal events are infrequent after active polymers encounter obstacles. For porous media with fewer obstacles, the non-monotonic behavior becomes weaker until it approaches the monotonic behavior in unconfined environment (figure 11(d)). Furthermore, the geometric criterion remains valid when the reorientation mechanism is a RT motion where the swimming direction after the tumbling event is random instead of reversing (figure 11(e)). In dilute environments (N = 1000), RT polymers are found to spread faster than run-reverse polymers. However, the spreading in dense environments (N = 1200) is independent of reorientation mechanisms and fully determined by the geometry, as indicated by the collapsed curves in figure 11(e). It further demonstrates the validation of the geometric criterion that the longest pore length of the environment is the characteristic length that dictates the transport behavior of active polymers in porous media.
Figure 11. (a) Schematic of run-reverse mechanism of the active polymer and simulation snapshot of active polymers in a porous medium. (b) Mean-square displacements with different reversal rates. (c) Effective diffusivities of active polymers as a function of scaled path length for different Péclet numbers. (d) Effective diffusivities as a function of reversal rate for porous media with different numbers of obstacles N. (e) Rescaled effective diffusivities of run-reversal (RR) and run-and-tumble (RT) active polymers for different N. Reproduced from [72]. CC BY 4.0.
Download figure:
Standard image High-resolution imageTo further explore the most efficient strategy for active polymers to spread in porous media, Irani et al [73] suggested a local adaptation mechanism of the dynamics. As illustrated in figure 12(a), the local density φlocal is defined for each bacterium by a concentric area centered around the head of a bacterium. In contrast to the standard RT dynamics with constant reorientation rate, bacteria are endowed with the ability to sense the local density. For the reorientation probability of a sigmoidal form (figure 12(b)), the bacterium reorients with a high probability in a locally dense region and a very low probability in a locally dilute region. As shown in the inset in figure 12(c), a non-monotonic behavior of the diffusion constant with respect to the reorientation time is obtained as previously observed for constant reorientation rate (inset of figure 12(c)). For very long orientation times, both models show the same diffusion behavior because orientation event is so rare that collision events dominate the dynamics. However, a strong boost of the dynamics is observed for density-sensing bacteria for small orientation times and the diffusion coefficient is larger by almost two orders of magnitude than bacteria with constant reorientation rate. For dense systems, the dynamics is accelerated by reducing the trapping times due to the high probability of reorientation. In dilute environments, the diffusion is also enhanced due to an uninterrupted ballistic motion as a result of the low probability of reorientation.
Figure 12. (a) The local area fraction φlocal defined by the overlap of the hypothetical disk with neighboring obstacles. (b) Uniform and sigmoidal form for the reorientation probability. (c) Mean-square displacements with different reorientation times. Full lines and dashed lines represent reorientation probability of a sigmoidal form and constant reorientation rate, respectively. Reprinted (figure) with permission from [73], Copyright (2022) by the American Physical Society.
Download figure:
Standard image High-resolution image3.7. Through periodic spaces
In contrast to trapped motion in porous media formed from high-density random obstacles, active polymers are not localized in spaces filled with periodic arrays of pillars. Using Tubifex tubifex worms as a model system, Heeremans et al [74] investigated the transport of active polymers through a channel filled with a hexagonal pillar array. Actually, Tubifex tubifex has recently emerged as a promising experimental model for studying active polymers [75, 76] because the anatomy of the worm consists of many segments, similar to how polymers are composed of multiple repeating units. Moreover, by changing the temperature of the water in the experimental setup, the activity of the worms can be tuned continuously. As shown in figure 13(a), the difference between the two levels of activity is clearly visible. Further analysis shows that the elution time is approximately linearly dependent with the relaxation time and the contour length of the worm (figure 13(b)). Actually, activity dominates the elution time by shaping the conformations of worms while transported in the pillar array. In addition to the conventional 'trapping', 'gliding', and 'vaulting' modes of transport for passive polymers [77], highly active worms exhibit 'curling' and 'knotting' conformations that help them circumvent the pillars (figure 13(c)). The size-dependent elution time is reminiscent of slalom chromatography where the most efficient traveling of polymers occurs when the polymer size is comparable to the pillar spacing [78]. As the worms are basically larger than the pillar spacing, the larger the worms, the more difficult for them to turn around the obstacles, leading to longer elution time through the pillar arrays. Since conventional polymer mixtures are separated based on their size, the question remains whether active polymer mixtures can be separated according to their activity level. As shown in figure 13(d), the mixture is injected at the entrance of the channel, where low-activity worms are prepared by exposing them to a solution of 5% ethanol before injection, and the elution times are recorded by a camera. High-activity worms are found to reach the outlet of the channel about 50 s after injection, followed by low-activity worms with a time delay Δt ≈ 40 s. The distribution of elution times is given in figure 13(e), demonstrating the potential of sorting mixtures of active polymers based on their activity level.
Figure 13. (a) Trajectories in the channel for the same worms at two different temperatures. (b) Activity and contour length dependence of the elution time of the active worms. (c) Typical polymer conformations and conformation statistics in the channel for two different levels of activity. (d) Separation of low- and high-activity worm mixture. (e) Distribution of elution times. Reproduced from [74]. CC BY 4.0.
Download figure:
Standard image High-resolution image4. Crowded environments
In the preceding section, we have discussed the structural and dynamical properties of a single active polymer in complex environments. In the dilute regime, the role of steric interactions is limited, and it is possible to gain insights by studying individual filaments or hydrodynamic equations derived from microscopic models. However, in dense systems, it is no longer justifiable to neglect excluded-volume interactions, as their combination with self-propulsion may lead to distinctive phases and dynamics. For instance, counterintuitive behavior such as 'crowded is faster' has been observed in swimming bacteria within macromolecular polymer solutions [79], as well as in self-propelled stiff filaments within strongly interacting crowded systems [80]. In this section, we will turn our attention to the emergent behavior of active polymers in crowded environments.
4.1. Collective behaviors
Using Langevin dynamics simulations, Prathyusha et al [81] studied the dynamical behavior of a dense planar layer of tangentially driven filaments and found four distinctive non-equilibrium phases, as shown in figures 14(a)–(d). At low activity, flowing melt with ±1/2 topological defects is observed (figure 14(a)), which is commonly observed in experiments [5, 82–88]. For semi-flexible filaments, increasing activity leads to a swirling state, where the dynamics is dominated by large fluctuations of filament shapes (figure 14(b)). For stiff filaments, increase in activity gives rise to a phase-segregated state, in which the filaments align and flow as a coherent bundle (figure 14(c)), similar to motility-induced phase separation of self-propelled particles [15, 89, 90]. At extremely high activity, filaments curl into long-lived spirals (figure 14(d)), of which the centers move diffusively.
Figure 14. (a)–(d) Snapshots of simulations in four non-equilibrium phases. (a) Flowing melt. (b) Swirl. (c) Segregated phase. (d) Spirals. Arrows in (a) point to examples of + 1/2 (red) and −1/2 (yellow) topological defects. Reprinted (figure) with permission from [81], Copyright (2018) by the American Physical Society. (e)–(g) Snapshots of high-density phases for various Pe. (e) Jamming. (f) Laning. (g) Active turbulence. Reproduced from [91] with permission from the Royal Society of Chemistry. (h)–(k) Snapshots of the time evolution of an initially nematic system. (h) Polarity-sorted bands. (i) Bending of bands. (j) Breaking of bands. (k) Long-time disordered structure. From [92]. © The Authors, some rights reserved; exclusive licensee AAAS. Distributed under a CC BY-NC 4.0 license http://creativecommons.org/licenses/by-nc/4.0/. Reprinted with permission from AAAS.
Download figure:
Standard image High-resolution imageAt higher densities, the movement of filaments become progressively more obstructed. Duman et al [91] found that filaments get jammed at low activity due to the high energy barriers associated with structural rearrangements (figure 14(e)). As activity increases, filaments are able to overcome energy barriers and reorganize into a steady-state nematic lane regime (figure 14(f)). However, because the propulsion forces decrease the effective persistence length, nematic lanes break up and an active turbulence phase comes into being at high activity (figure 14(g)).
By adding motors to an initially globally nematic suspension of filaments with random left–right filament orientation, Vliegenthart et al [92] investigated the buckling of the polar bands. The polar bands remain stable when either the activity is insufficient or the filaments are excessively rigid. However, the polar bands become unstable and buckle at a particular wavelength λ for sufficiently large active forces, as shown in figures 14(h)–(k). Initially, the system exhibits bands that are sorted by polarity, followed by a gradual process of bending and eventually breaking of these bands. The wavelength of the instability displays a square root dependence on the filament persistence length,  , suggesting an Euler buckling-type instability [93].
, suggesting an Euler buckling-type instability [93].
In a broader sense, active nematics refer to active systems that are characterized by self-driven units with elongated shape. The emergent collective behaviors of active nematics, such as phase transitions, pattern formation, and dynamic instabilities, are remarkably similar to that of active polymers. However, the main difference lies in the conformational freedom of active polymers, which leads to more diverse forms of motion and the lack of orientational order.
4.2. Crowding-mediated single-filament motion
In crowded environments, the motion of individual filaments is influenced by the surrounding filaments, and thus exhibits unique dynamic behaviors. Bacterial swarming is an example of dynamic self-assembly in microbiology in which the collective interaction of a population of bacterial cells leads to emergent behavior [94–96]. Auer et al [97] found that swarmer cells display remarkable flexibility and a shape that is dynamically altered by adjacent cell motion and collisions. As shown in figure 15(a), cells can undergo large conformational changes from rod-like to strongly bend structures while moving collectively in a film with other cells. By adjusting their stiffness based on the density of the surrounding environment, the swarmer cells facilitate cooperative movement. Further theoretical investigations are required to elucidate the mechanisms underlying the intricate stimuli-responsive behaviors exhibited by living active polymers within crowded environments.
Figure 15. (a) Time series of Proteus mirabilis swarmer cells in a colony actively moving across the surface of an agarose gel. Reproduced from [97]. CC BY 4.0. (b), (c) Self-propelled stiff filament suspended in filament solutions. (b) Mean-square displacements at different number densities. (c) Orientational relaxation times at different number densities for several Pe. Inset: rescaled effective diffusivities. Reprinted (figure) with permission from [80], Copyright (2020) by the American Physical Society.
Download figure:
Standard image High-resolution imageFor stiff filaments, Mandal et al [80] found a remarkable increase of their effective diffusivity by more than one order of magnitude upon increasing the filament number density (n*). As shown in figure 15(b), the diffusive behavior at short times is not affected by crowding. At intermediate times, the ballistic behavior is dominated by the directed motion and the directed regime is extended with increasing density. At long times, the terminal diffusive regime is recovered. Most prominently, the long-time diffusion increases drastically as the number density increases, indicating an enhanced effective diffusion due to crowding. To rationalize the counterintuitive behavior, the effective tube model introduced by Doi and Edwards [98] for passive crowded systems is adopted for the active crowded solution. With increasing density, the active filaments are forced to move within an effective tube formed by their neighboring filaments, leading to an increased rotational relaxation time. As a result, the directed motion is extended and the long-time diffusion is enhanced. Moreover, a scaling theory for the effective diffusivity is given as  , providing a theoretical prediction for the nontrivial spatiotemporal dynamics over the entire range of length and timescales (figure 15(c)).
, providing a theoretical prediction for the nontrivial spatiotemporal dynamics over the entire range of length and timescales (figure 15(c)).
4.3. Nucleation and growth
Nucleation and growth are of utmost importance in the process of crystallization, as they ultimately determine the structure, shape, and properties of a crystal. For passive polymers, due to the entropy barrier for crystal nucleation of polymer chains, thermal density fluctuations [99–101] are known to play a crucial role in the early stages of crystallization. This raises the question how polymers nucleate under active motion. By investigating mixed bacterial swarms with different aspect ratios, Peled et al [102] found that it is possible to significantly influence the behavior of a swarm by introducing a small number of cells with a distinct aspect ratio compared to the majority. Through the cooperative action of numerous short cells, in conjunction with a minority of longer cells, more ordered swarming patterns are attained (figures 16(a) and (b)). Moreover, a small number of long cells helps to organize the dynamics of the bacterial colony, with long cells acting as nucleation cites around which aggregates of short, rapidly moving cells can form (figures 16(c) and (d)). For homogeneous active polymers, Wang et al [103] found that their assembly is a two-state system in the presence of a big single obstacle (figures 16(e)–(m)), that is, all filaments either disperse freely in space or gather almost completely together into a giant jammed aggregate attached to the surface of the obstacle. In the absence of the obstacle, an active polymer chain is known to bend and form spiral configuration at low rigidity or strong propulsion [81]. When an obstacle is put into the system, such dynamics and structures do not change significantly as the spirals only swirl under propulsion and their translational motion is not affected by the driving force. However, in the situation that active polymers form clusters, their motion is greatly disturbed by the obstacle. Under certain conditions, the active polymers pack tightly on the surface of the obstacle and form a stable giant jammed aggregate. Unlike the trapping of self-propelled rods at a wedge [104, 105], the giant jammed aggregate spontaneously forms on a smooth convex surface instead of a concave one. Moreover, the process of the formation of a giant jammed aggregate is reminiscent of the nucleation of hard spheres near a spherical seed [57, 106], with some active polymers forming a hedgehog-like nucleus on the surface of the obstacle first, based on which then the whole giant jammed aggregate grows. In figures 16(e)–(m), we can see that there are three distinct types of nucleation processes. The first type occurs when a single drifting active polymer cluster collides directly with the obstacle, resulting in the formation of a hedgehog-like nucleus as shown in figures 16(e)–(g). The second type involves several small active polymer clusters colliding with the obstacle in close proximity and merging to form a nucleus, as depicted in figures 16(h)–(j). The third type is characterized by large active polymer clusters colliding with and sliding chaotically on the surface of the obstacle, leading to the accidental formation of a jammed hedgehog-like nucleus, as seen in figures 16(k)–(m). At present, the sophisticated assembly structures and highly dynamic behavior exhibited by active polymers during crystallization on the obstacle surface and in free space are far from well understood, presenting a critical issue requiring attention.
Figure 16. (a), (b) Microscopic images of a mixed swarming colony at different magnifications. The wild-type cells in red and the elongated cells in green. (c), (d) Two consecutive snapshots showing two elongated cells, each surrounded by a group of wild-type cells (0.3 s apart). Reprinted (figure) with permission from [102], Copyright (2021) by the American Physical Society. (e)–(m) Crystallization of active semiflexible filaments on the surface of an obstacle. Reproduced from [103] with permission from the Royal Society of Chemistry.
Download figure:
Standard image High-resolution image4.4. Phase separation
Phase separation, exhibited by polymer mixtures, is a central concept for passive polymers [108, 109]. By investigating the spontaneous aggregation of randomly dispersed active worms, Deblais et al [75] studied the phase separation of active polymers. As shown in figures 17(a)–(c), the worms aggregate spontaneously into highly entangled 'blobs' when randomly distributed over a volume of water, similar to polymer phase separation. Unlike the entropy-driven separation of passive polymers [110, 111], the biological function of this aggregation is to minimize exposure to dissolved oxygen, high levels of which are poisonous to the worms [112]. Interestingly, the phase separation of the active worms does not seem to occur through Ostwald ripening, where the aggregation is driven by the combined effect of surface tension of the aggregates and diffusion of the aggregating particles. Moreover, the growth of the blobs exhibits a power-law behavior with 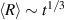 , independent of the initial worm concentration. To shed more light on the power-law growth kinetics, additional simulations of the coalescence of diffusing droplets are performed. If the effective diffusion constant of the blobs Dblob is assumed to depend on its radius R as the Brownian random motion, Dblob = R−
1, a power-law growth of the average blob size
, independent of the initial worm concentration. To shed more light on the power-law growth kinetics, additional simulations of the coalescence of diffusing droplets are performed. If the effective diffusion constant of the blobs Dblob is assumed to depend on its radius R as the Brownian random motion, Dblob = R−
1, a power-law growth of the average blob size 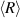 is obtained with an exponent of ∼0.20. However, if Dblob is assumed to be size-independent, a growth exponent of ∼0.30 is obtained, in good agreement with the experimentally observed value (figure 17(d)). Such a phenomenon can be explained from the fact that the active random motion arises from the worms at the surface of the blob, resulting in a steady-state speed that is independent of the blob size.
is obtained with an exponent of ∼0.20. However, if Dblob is assumed to be size-independent, a growth exponent of ∼0.30 is obtained, in good agreement with the experimentally observed value (figure 17(d)). Such a phenomenon can be explained from the fact that the active random motion arises from the worms at the surface of the blob, resulting in a steady-state speed that is independent of the blob size.
Figure 17. (a)–(c) Snapshots of active-worm aggregation. (d) Average blob radius as a function of time obtained from simulations. Reprinted (figure) with permission from [75], Copyright (2020) by the American Physical Society. (e) Order parameter as a function of Th and N. (f) Entropy production per hot particle in the steady state as function of χ and N. Insets: velocity distributions of the hot and cold particles in the separated state. Two steady-state snapshots are shown mixed (top) and phase separated (bottom) with hot chains (black) and cold chains (yellow). Reprinted (figure) with permission from [107], Copyright (2017) by the American Physical Society.
Download figure:
Standard image High-resolution imageFor passive polymers, a commonly accepted fact in the context of equilibrium phase separation of polymer mixtures is that the critical Flory interaction parameter, which describes the degree of interaction asymmetry between the two polymer species and governs their segregation, is inversely related to the length of the polymers N [113]. For spherical colloidal particles, it is found that mixtures containing their active and passive components undergo phase separation, but only at extremely high activity ratios [114, 115]. This leads to an analogous question whether small activity difference can lead to phase separation for long active polymers, which bears great importance for our understanding of the behavior of biopolymers such as DNA [116]. Using standard bead spring model for polymer melt systems, Smrek and Kremer [107] found that longer chains lead to lower transition temperatures for both semi-flexible and fully flexible polymers, as shown in figure 17(e). The thermalization of particles is much faster than their local environments and the effective temperatures of the active and passive polymers can be extracted from their fits of the Maxwellian velocity distributions, as shown in the inset in figure 17(f). Accordingly, the asymmetry of the effective temperatures  can be seen as an analog of the Folry–Huggins interaction parameter. To determine more accurately the dependence of the critical temperature asymmetry on N, the entropy production of the system is taken into consideration, which is given by
can be seen as an analog of the Folry–Huggins interaction parameter. To determine more accurately the dependence of the critical temperature asymmetry on N, the entropy production of the system is taken into consideration, which is given by  in the steady state. As shown in figure 17(f), the entropy production rises with
in the steady state. As shown in figure 17(f), the entropy production rises with  as the heat flux increases, until a critical activity ratio
as the heat flux increases, until a critical activity ratio 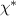 is reached. Beyond this point, the entropy production plateaus due to the development of the interface between the phases. Through phase separation, the hot chains are able to maintain a higher effective temperature by avoiding contact with the cold chains, thereby reducing the overall entropy production.
is reached. Beyond this point, the entropy production plateaus due to the development of the interface between the phases. Through phase separation, the hot chains are able to maintain a higher effective temperature by avoiding contact with the cold chains, thereby reducing the overall entropy production.
4.5. Rheology
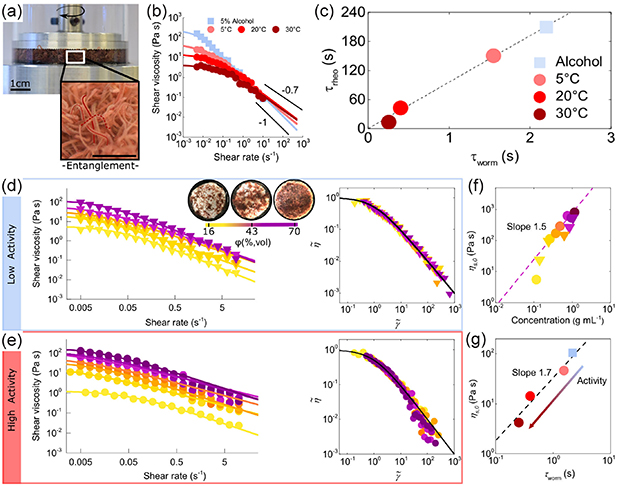
Polymers are a type of complex fluid whose rheology is well-understood, particularly in regards to predicting phenomena like shear-thinning and behavior in various flow situations [117]. However, this understanding becomes inadequate when studying active polymers [76], where the interplay between conformations, hydrodynamic interactions, and filament activity results in a wide range of novel structural and dynamic characteristics that were previously unknown [118, 119]. Using living worms as an entangled polymer-like system, Deblais et al [76] experimentally studied the rheology of active polymers (figure 18(a)). Similar to passive polymers, a shear-thinning phenomenon is observed, as shown in figure 18(b). However, the results are quantitatively different from that of regular polymers, as evidenced by the increased slope of the shear-thinning curves in the high-shear rate region, which changes from approximately −1 to approximately −0.7. Shear thinning is a reflection of the orientation of chain segments. Using the continuous Gaussian semiflexible polymer model, Martín-Gómez et al [120] demonstrated that the activity-induced preference in alignment leads to an enhanced shear thinning of highly active Brownian polymers. The increase of the shear-thinning exponent for the polymer-like worms might stem from the activity-induced shrinkage of tangentially driven filaments. Moreover, all these flow curves are well described by a classical polymer rheological model (solid lines in figure 18(b)) based on the cross equation 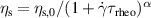 [121]. Active polymers show a lower value of the zero-shear viscosity and a higher value of the characteristic shear rate for the onset of shear-thinning, as indicated by the linear relation between τrheo and τworm (figure 18(c)), where τworm is the characteristic time determined from the half-decay time of the autocorrelation function. An increase in concentration leads to a higher zero-shear viscosity plateau, a lower onset shear rate for shear thinning, and a more pronounced shear-thinning effect (figures 18(d) and (e)). What is unexpected is the deviations from the simple cross model at high shear rates (inset in figure 18(e)) as a result of the complicated interaction between active polymers and the flow. Furthermore, the zero-shear viscosity shows a much weaker dependence on concentration, with a power-law exponent around 1.5 (figure 18(f)), compared to the exponent around 3 for conventional polymers. Essentially, shear thinning is a reflection of the orientation of chain segments. Therefore, the zero-shear viscosity is also strongly influenced by polymer activity, suggesting a power-law relation between ηs,
0 and τworm (figure 18(g)).
[121]. Active polymers show a lower value of the zero-shear viscosity and a higher value of the characteristic shear rate for the onset of shear-thinning, as indicated by the linear relation between τrheo and τworm (figure 18(c)), where τworm is the characteristic time determined from the half-decay time of the autocorrelation function. An increase in concentration leads to a higher zero-shear viscosity plateau, a lower onset shear rate for shear thinning, and a more pronounced shear-thinning effect (figures 18(d) and (e)). What is unexpected is the deviations from the simple cross model at high shear rates (inset in figure 18(e)) as a result of the complicated interaction between active polymers and the flow. Furthermore, the zero-shear viscosity shows a much weaker dependence on concentration, with a power-law exponent around 1.5 (figure 18(f)), compared to the exponent around 3 for conventional polymers. Essentially, shear thinning is a reflection of the orientation of chain segments. Therefore, the zero-shear viscosity is also strongly influenced by polymer activity, suggesting a power-law relation between ηs,
0 and τworm (figure 18(g)).
Figure 18. (a) Picture of the custom-designed rheology cell. The enlargement emphasizes the entangled state of the worms. (b) Shear viscosity as a function of shear rate at different levels of activity. Colored solid lines are fits to the cross model. (c) Relation between characteristic times τrheo and τworm. (d), (e) Shear viscosity as a function of the shear rate for different concentrations of worms at a low (d) and high (e) level of activity. Insets: normalized rheology curves by the fitting parameters of the cross model. (f) Zero-shear viscosity as a function of concentration at a high level of activity. (g) Zero-shear viscosity as a function of activity. Reprinted (figure) with permission from [76], Copyright (2020) by the American Physical Society.
Download figure:
Standard image High-resolution image5. Summary and future perspectives
Active polymers represent a captivating and rapidly growing field of study within the realm of active matter. As we continue to explore the behavior of these polymers in complex and crowded environments, we are presented with exciting opportunities for future research. This includes the development of new theoretical models and experimental systems, as well as potential applications in biomedicine and soft robotics. With these advancements, we will undoubtedly gain deeper insights into the fundamental physical principles underlying behaviors of active polymers and their ability to adapt and function far from equilibrium. As such, it is clear that the study of active polymers in complex and crowded environments is an area of research that will continue to evolve and flourish for many years to come. Concretely, a series of so far unexplored research directions can be identified as follows:
5.1. Soft robotics
For traditional centrally controlled and algorithm-based swarm robotics, each individual robot is equipped with costly and sophisticated sensors, which is subject to many limitations including design complexity, low fault tolerance, and scalability problems. To overcome these limitations, stochastic local interactions between individual robots can be utilized to perform collective tasks in a decentralized way. Through physical entanglement, active worms have been designed to display emergent locomotion [38] and to reliably grasp, lift, and move objects [122]. Study on entangled active polymers, which self-organize and dynamically respond to changing environmental conditions, could provide a promising way to achieve this goal and might inspire new classes of synthetic super-materials and soft robotics that perform tasks in complex natural environments [123].
5.2. Topological defects
Topological defects are typically observed in the self-assembly of active filaments. These defects arise due to the competition between the ordering tendency of the filaments and the inherent stochasticity in their motion. In passive nematics, defects gradually disappear through annealing unless they become trapped by imperfections or boundaries. However, the presence of activity can trigger the spontaneous generation of topological defects, leading to the breakdown of long-range nematic order and the emergence of chaotic features. These motile topological defects can significantly affect the collective behavior of the filaments and lead to the emergence of novel physical properties, such as non-equilibrium dynamics and pattern formation. Moreover, topological defects can also serve as building blocks [124] for creating functional materials with unique properties, including enhanced mechanical stability and responsiveness to external stimuli, thereby providing an exciting way to synthesize smart materials and design future robots. Therefore, understanding and controlling the formation and dynamics of topological defects in the self-assembly of active filaments is of great importance for developing new materials and advancing our understanding of the physics of living systems.
5.3. Time-varying environments
In previous studies, the complex environments in which active polymers reside have often been considered as temporally constant. However, real-world systems are subject to biological activity and external disturbance, resulting in time-varying environments. For instance, the twin-pore translocase complex in the inner membrane of mitochondria [125] and the nuclear pore complex [126] exhibit periodic changes in channel width during the translocation process. In the realm of biological respiration, the environments hosting active polymers often undergo periodic fluctuations. The temporal variability of these environments, encompassing frequency and amplitude, is expected to exert significant influences on the dynamic behaviors of active polymers. Exploring the behavior of active polymers in such time-varying environments offers an exciting avenue for future research, both fundamental and applied.
5.4. Stimuli-responsive behavior
In biological systems, organisms often recognize their surrounding environment and respond accordingly to search for nutrients more effectively, such as Lévy flights adopted by birds and run-reverse behavior exhibited by bacteria. To adapt to environmental changes, Proteus mirabilis and Vibrio parahaemolyticus, which are known human pathogens, could alter their cell morphology to facilitate cooperative movement [98]. Investigating the responsive behavior of active polymers, including variations in chain stiffness, activity, and even chain length, in complex and crowded environments will significantly enhance our understanding of the intricate behavior of real-world filamentous organisms and polymer-like worms.
5.5. Confinement and deformable boundaries
In natural environments, active polymers frequently encounter confined spaces, such as bacterial motility within porous soil, DNA accumulation within cell nuclei, and the movement of actin proteins on cell membranes. The interplay between confinement, conformational freedom, and activity gives rise to distinctive structural and dynamic behaviors of active polymers, which however still lack in-depth investigation. For instance, due to the inherent Gaussian curvature, spherical surfaces lead to topological defects that cannot be eliminated [127]. How these topologic defects interact and react with those induced by activity remains an open question to be answered. Moreover, the boundaries can be deformable, such as cell membranes and vesicle walls, which allow for active polymers to undergo more intricate shape changes and deformations. Understanding and manipulating confinement and deformable boundaries is crucial for the design and development of novel active polymer materials with specific properties and functions, including drug delivery, sensing, and actuation [128].
5.6. Active–passive copolymers
Block copolymers that are passive in nature can spontaneously organize themselves into a variety of ordered structures with adjustable properties, such as spherical, cylindrical, gyroid, and lamellar morphologies, depending on the composition and combination parameter [129, 130]. Copolymers consisting of monomers with varying levels of activity exhibit an even broader range of dynamic and phase behavior, providing further opportunities for regulating the formation of structures and transportation. These copolymers may even serve as intelligent materials, which sense and respond autonomously to other units and show swarm-intelligent behavior as schools of fish or flocks of birds [131, 132]. Given that biological macromolecules tend to be intrinsically disordered rather than homogeneous, research into active copolymer systems is crucial for enhancing our comprehension of structure formation in biological cells and for designing future smart biomaterials.
5.7. Crystallization
The crystallization of active matters is significantly different from their passive counterpart. For instance, passive colloidal particles in a dilute suspension do not naturally aggregate unless there are intense attractive forces, whereas active particles in a suspension can still form clusters even in the presence of exclusively repulsive interactions [133]. As it is well known, crystallization of polymers is a process associated with partial alignment of their molecular chains, upon cooling from melting, mechanical stretching or solvent evaporation. However, some polymers retain a disordered structure upon freezing and readily convert into amorphous solids. Moreover, such alignment is hindered by the entanglement although it would be energetically favorable for the polymer chains to align parallel. Under self-propulsion, how the rapid relaxation of active polymers affects their crystallization dynamics and to what extent the crystalline structures are regulated by activity are critical issues to be addressed.
Acknowledgments
We acknowledge support from National Natural Science Foundation of China (Grant Nos. 22025302, 22303029 and 21873053) and the Fundamental Research Funds for the Central Universities. L-T Y acknowledges financial support from Ministry of Science and Technology of China (Grant No. 2022YFA1203203) and State Key Laboratory of Chemical Engineering (No. SKL-ChE-23T01).
Data availability statement
No new data were created or analyzed in this study.
Notes
The authors declare no competing financial interests.