Abstract
Objective. Electrical impedance tomography (EIT) is a noninvasive imaging method whereby electrical measurements on the periphery of a heterogeneous conductor are inverted to map its internal conductivity. The EIT method proposed here aims to improve computational speed and noise tolerance by introducing sensitivity volume as a figure-of-merit for comparing EIT measurement protocols. Approach. Each measurement is shown to correspond to a sensitivity vector in model space, such that the set of measurements, in turn, corresponds to a set of vectors that subtend a sensitivity volume in model space. A maximal sensitivity volume identifies the measurement protocol with the greatest sensitivity and greatest mutual orthogonality. A distinguishability criterion is generalized to quantify the increased noise tolerance of high sensitivity measurements. Main result. The sensitivity volume method allows the model space dimension to be minimized to match that of the data space, and the data importance to be increased within an expanded space of measurements defined by an increased number of contacts. Significance. The reduction in model space dimension is shown to increase computational efficiency, accelerating tomographic inversion by several orders of magnitude, while the enhanced sensitivity tolerates higher noise levels up to several orders of magnitude larger than standard methods.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Electrical impedance tomography (EIT) of conducting volumes holds great promise, particularly in the field of medicine as an alternative or a complement to x-ray computed tomography (CT), magnetic resonance imaging (MRI), and sonograms, with further applications in sensors (Liu et al 2020), engineering (Jordana et al 2001, Tapp et al 2003), and geoscience (Ducut et al 2022). Although its images may have lower resolution than some of these competing methods, the disadvantage of EIT's diffuse nature can be compensated by the advantages of being radiation-free, easily portable, wearable for extended periods, and low-cost. Two longstanding challenges have prevented wider adoption of EIT in potential applications. First, the computational time of existing algorithms increases exponentially with the dimension of the model space (Boyle et al 2012). The ill-posed nature of the inverse problem under standard algorithms employs a dense mesh of upwards of 10 000 model elements, necessitating computationally costly regularization with no benefit in resolution. The second challenge is that present-day EIT relies on data spaces which include low sensitivity measurements whose data are vulnerable to experimental noise. Error in these low sensitivity measurements will impair the fidelity of the inverse problem, further reducing the resolution of the inverted model. In this work, we reframe the EIT problem by introducing a sensitivity volume figure-of-merit into a modified EIT method in order to create a model space of reduced dimensionality that achieves rapid computational refresh rates, while acquiring only data of high importance, thereby accelerating data collection and enhancing robustness against experimental noise.
The remainder of this paper is structured as follows. Section 2 reviews standard EIT concepts in anticipation of section 3, which summarizes the overall strategy of the sensitivity volume method. Section 4 demonstrates this sensitivity volume method with example simulations resulting in orders-of-magnitude accelerated computational time or orders-of-magnitude enhanced noise tolerance, compared to state-of-the-art EIT inverse solvers. Finally, for comparison section 5 contextualizes other strategies in the literature for optimization of the EIT inverse problem.
2. Standard EIT
The essential components of an EIT method are reviewed here with notation drawn from Tarantola (2005). The description of the EIT problem begins with a model m representing a conductivity map of a sample. The generalized forward EIT problem
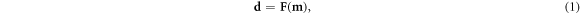
relates this model m to a dataset d representing four-point (Van der Pauw 1958) or 'tetrapolar' (Ragheb et al 1992) resistance measurements that are taken according to a measurement protocol of electrical contacts around the sample edges (Holder 2005). A popular example is the empirical 'Adjacent–Adjacent' or 'Sheffield' protocol, which uses pairs of neighboring current injection contacts in combination with pairs of neighboring voltage measurement contacts (Brown and Seagar 1987, Kauppinen et al 2006). Only half of these are independent (Buttiker 1988), and form what will henceforth be referred to as the adjacent measurement protocol.
Typically, the forward problem can be directly solved using Maxwell's equations in the form of Laplace's equation with various boundary conditions to determine the dataset from the model, as described, for example, by Holder (2005). We will define an inverse problem method as the selection of the model space, the data space, and the inverse algorithm by which the data space is mapped back to the model space.
The mixed-determined EIT inverse problem can be solved to linear order with consideration of noisy, non-ideal data dobs and the selection of a reference model mref. The experimentally observed data dobs from the forward problem in the presence of measurement noise n can be written as (Braun et al 2017):

For a subset of models lying within linear perturbation Δm = m − mref of a common reference model mref (Grychtol and Adler 2013), the forward problem can be approximated to linear order as a deviation Δd = dobs − dref from the inverted reference data dref = F(mref):
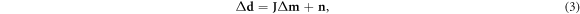
where the linearized forward operation is now represented by the Jacobian matrix J, also referred to as the sensitivity matrix, (Polydorides and Lionheart 2002, Gómez-Laberge and Adler 2008) with elements:
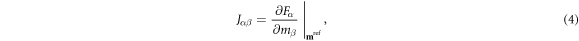
where α ∈ {1, ⋯ D} indexes the dataset elements from 1 to the dimension D of the data space  , and β ∈ {1, ⋯ M} indexes the model elements from 1 to the dimension M of the model space
, and β ∈ {1, ⋯ M} indexes the model elements from 1 to the dimension M of the model space  and the derivatives are evaluated at the reference model coordinates mref. Each Jacobian element Jα
β
quantifies the sensitivity of the αth data space measurement to perturbations in the βth model space component with respect to the reference model. For simplicity, in the remainder of this text d and m will refer to the linearized difference coordinates Δd and Δm relative to dref and mref, respectively, in the context of the linearized problem. This work considers a homogeneous reference mref, throughout. In general, prior knowledge can be utilized to produce more meaningful case-specific references (Grychtol and Adler 2013). The EIT inverse problem, therefore consists of mapping from an observed dataset dobs to some model m. In the linearized inverse problem, this is written as m = J−g
dobs, where J−g
is the generalized inverse of the Jacobian matrix J.
and the derivatives are evaluated at the reference model coordinates mref. Each Jacobian element Jα
β
quantifies the sensitivity of the αth data space measurement to perturbations in the βth model space component with respect to the reference model. For simplicity, in the remainder of this text d and m will refer to the linearized difference coordinates Δd and Δm relative to dref and mref, respectively, in the context of the linearized problem. This work considers a homogeneous reference mref, throughout. In general, prior knowledge can be utilized to produce more meaningful case-specific references (Grychtol and Adler 2013). The EIT inverse problem, therefore consists of mapping from an observed dataset dobs to some model m. In the linearized inverse problem, this is written as m = J−g
dobs, where J−g
is the generalized inverse of the Jacobian matrix J.
Singular value decomposition (SVD) of the Jacobian is a frequently used tool for analyzing and solving the EIT inverse problem (Holder 2005). SVD decomposes the Jacobian into two unitary matrices (U, V) whose respective columns are left and right singular vectors of J, and a diagonal matrix ( S ) of singular values that are ordered from largest to smallest. This decomposition is written as
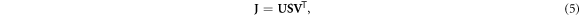
where the number of non-zero singular values in S is equivalent to the rank of the Jacobian (Press et al 2007). When J is square, SVD can be used to form the following inverse of J:
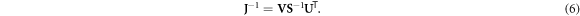
When J is not square, a portion of either the data or the model space is not accessed. And depending on the measurement protocol and model parameterization, some diagonal elements of S may be zero or small, requiring the formation of a generalized inverse. In this case, the reciprocals of those zero and small singular values should be replaced with zeros in the inverse of S. This replacement is referred to as truncated SVD ((T)SVD). In (T)SVD a truncation point of k < rank(S) replaces the reciprocals of small singular values to suppress the influence of noise in the inverse problem (Hansen 1990b). The Picard condition is one proposed method of selecting the truncation point k using a known data noise level (Hansen 1990a). The result is the following inverse solution in the presence of noise:
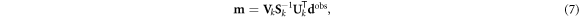
where m is the best possible model reconstruction from the noisy data dobs,  is the generalized inverse of J, and the subscript k indicates truncation. This (T)SVD solution represents a fast and efficient way to solve the linearized inverse problem using standard methods.
is the generalized inverse of J, and the subscript k indicates truncation. This (T)SVD solution represents a fast and efficient way to solve the linearized inverse problem using standard methods.
3. Components of sensitivity volume method
The strategy behind the proposed sensitivity volume method as a solution to the EIT inverse problem is presented below. This method is designed to minimize susceptibility to experimental noise and maximize computational efficiency, while also being agnostic to the geometry and dimension of the EIT problem. The description of this method is broken down according to the component elements of the EIT problem, namely model space and data space selection, contact number selection, and finally the choice of solver for the linearized inverse problem. In the course of this description, the concept of a sensitivity vector is introduced to represent the fidelity of a given measurement to a weighted sum of model basis elements; a sensitivity volume figure of merit is proposed to optimize measurement protocols for targeted features; and a distinguishability criterion is generalized to assess fidelity in resolving these features.
3.1. Model space selection: 
Consider the full model space  of the EIT problem with dimension M0. Typical EIT inverse methods parameterize this full model space as a mesh defined over the volume of interest, with one independent model coordinate per mesh piece. Our strategy will be instead to choose a much smaller model subspace
of the EIT problem with dimension M0. Typical EIT inverse methods parameterize this full model space as a mesh defined over the volume of interest, with one independent model coordinate per mesh piece. Our strategy will be instead to choose a much smaller model subspace  with dimension M ≪ M0 spanned by orthogonal basis functions comprised of linear combinations of these mesh pieces and designed to target the features of interest. Prior knowledge of the system can be used either to identify the most important features, for example, with proper orthogonal decomposition (POD) (Lipponen 2013), or, alternatively, to provide balanced resolution throughout, for example, with a harmonic polynomial series appropriate to the geometry of interest, such as Legendre polynomials, Zernike polynomials, or Fourier decomposition.
with dimension M ≪ M0 spanned by orthogonal basis functions comprised of linear combinations of these mesh pieces and designed to target the features of interest. Prior knowledge of the system can be used either to identify the most important features, for example, with proper orthogonal decomposition (POD) (Lipponen 2013), or, alternatively, to provide balanced resolution throughout, for example, with a harmonic polynomial series appropriate to the geometry of interest, such as Legendre polynomials, Zernike polynomials, or Fourier decomposition.
3.2. Contact number selection: C
Whereas standard EIT methods use the number of contacts C to fix the dimension D of the data space  , here an increased contact number C0 will be used to define a larger data space
, here an increased contact number C0 will be used to define a larger data space  of dimension D0 greater than strictly necessary. Inside this expanded data space, an optimal subspace
of dimension D0 greater than strictly necessary. Inside this expanded data space, an optimal subspace
 of dimension D < D0 can be found, according to the steps in the following section. Note that under this method, contacts do not have to be equally spaced around the periphery, but can be placed arbitrarily, for example with higher density near features of interest, though for most common applications the need for uniform resolution dictates equal spacing of contacts.
of dimension D < D0 can be found, according to the steps in the following section. Note that under this method, contacts do not have to be equally spaced around the periphery, but can be placed arbitrarily, for example with higher density near features of interest, though for most common applications the need for uniform resolution dictates equal spacing of contacts.
Consider the dimensionality D of a desired data space and the corresponding minimum number of contacts C that spans that data space (Brown and Seagar 1987),
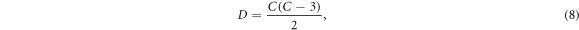
which can be inverted to yield the equivalent relation,
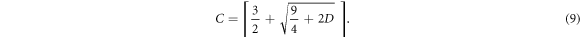
Here the ceiling function ⌈ · ⌉ ensures an integer number of contacts.
Since advantages of the sensitivity volume method come from increasing the dimensionality of the data space and therefore increasing the contact number, it is important to quantify what increase in contact number corresponds to what increase in data space dimension. If the data space is expanded to dimension D0 by a data space inflation factor rD ,
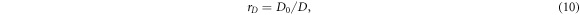
the number of contacts must increase to C0.
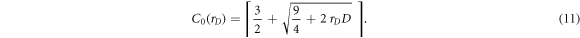
This increase can be represented with a contact number inflation factor rC ≃ C0/C, which can be determined from the above equations:
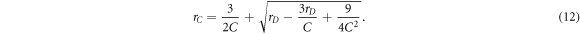
Note that with a large number of contacts, the relation between rD
and rC
simplifies to  meaning that the data space inflates roughly quadratically with the contact number.
meaning that the data space inflates roughly quadratically with the contact number.
The larger the data space inflation factor rD
, the likelier the inflated data space of dimension D0 = rD
D can contain a subspace of desired dimension D that includes only the most independent and noise-robust measurements. Note that the total number of possible four-point measurements Dmax that can be made with arbitrarily chosen contacts is of order  :
:
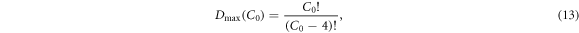
thus the search space for optimization increases geometrically with the contact number. We will refer to the list of all Dmax possible four-point data measurements as the measurement library, from which D measurements will be chosen to form the candidate protocols.
3.3. Sensitivity vectors: μ
Having identified the model space  , the contact number and placement, and the full data space
, the contact number and placement, and the full data space  with total number of possible measurements Dmax, the Jacobian can now be calculated from the forward problem. Let each row of the Jacobian matrix J represent a sensitivity vector
μ
a
in model space, composed of the sensitivity coefficients defined in equation (4),
with total number of possible measurements Dmax, the Jacobian can now be calculated from the forward problem. Let each row of the Jacobian matrix J represent a sensitivity vector
μ
a
in model space, composed of the sensitivity coefficients defined in equation (4),
As illustrated in figure 1, each sensitivity vector represents the overall sensitivity of the ath data measurement  to the set of β = {1... M} orthonormal basis functions of the chosen model space. The overall sensitivity of a given measurement is thus proportional to the magnitude of its sensitivity vector.
to the set of β = {1... M} orthonormal basis functions of the chosen model space. The overall sensitivity of a given measurement is thus proportional to the magnitude of its sensitivity vector.
Figure 1. Sensitivity-vectors and sensitivity volumes. (a) Data measurements dα of circular sample on left overlaid with mesh show current injection (arrows) and voltage measurement (+/−) electrodes associated with Dmax different measurement configurations. (b) In a 2D model space, the top choice of sensitivity vectors { μ 1, μ 2} subtends a larger 2D sensitivity volume S(2) than the bottom { μ 1, μ 3}. (c) In the 3D case, the top sensitivity vectors { μ 1, μ 2, μ 4} subtend a larger 3D volume S(3) than the bottom { μ 1, μ 3, μ 4}.
Download figure:
Standard image High-resolution image3.4. Sensitivity volume: S(D)
The sensitivity volume is the key figure-of-merit introduced here in order to compare and optimize choice of candidate measurement protocols. The sensitivity of a set of D independent measurements selected from the library of Dmax available measurements can be quantified as the D-dimensional volume S(D) of a parallelotope subtended by the chosen α = 1 ... D sensitivity vector rows of the Jacobian matrix:

as illustrated in figure 1. Conceptually, the sensitivity volume can be thought of as the product
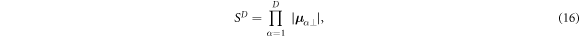
where μ α⊥ is the perpendicular component of sensitivity vector α with respect to all other vectors in the set. This result is also identical to the product of the α = {1 ... D} singular values sα of the SVD decomposition:
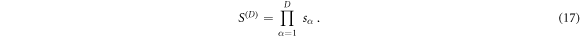
The geometric mean S of the singular values sα is then the average sensitivity per measurement in the data space, or the Dth root of the D-dimensional sensitivity volume, henceforth referred to as the specific sensitivity or in appropriate context simply the sensitivity of that measurement protocol:
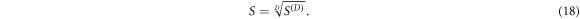
3.5. Data space selection: 
The data space  will be chosen to have dimension D that matches that of the model space D = M, setting up an exactly determined inverse problem. The underdetermined case D < M would leave some of the desired model space features undefined, and the overdetermined case D > M would measure redundant information at the cost of computational efficiency and measurement duration. With the sensitivity volume figure-of-merit defined above, the strategy will then be to search for a data subspace
will be chosen to have dimension D that matches that of the model space D = M, setting up an exactly determined inverse problem. The underdetermined case D < M would leave some of the desired model space features undefined, and the overdetermined case D > M would measure redundant information at the cost of computational efficiency and measurement duration. With the sensitivity volume figure-of-merit defined above, the strategy will then be to search for a data subspace
 with dimension D = M whose measurement protocol is selected from the measurement library to have maximal sensitivity volume S(D) according to the chosen basis functions of our model space
with dimension D = M whose measurement protocol is selected from the measurement library to have maximal sensitivity volume S(D) according to the chosen basis functions of our model space  .
.
3.6. Inverse solve selection: J−1
In the exact determined linearized inverse problem considered here D = M, the Jacobian J is square and invertible such that J−g = J−1. This makes the inverse solve in the absence of data noise computationally efficient by eliminating the need for regularization, such as Tikhonov regularization, gradient damping, or total variation regularization (Holder 2005, Menke 2012). Because of the increase in sensitivity S under the sensitivity volume method, it is less likely that truncation of singular values will be required under SVD analysis, making direct matrix inversion adequate in many cases. But in the presence of noise that exceeds the Picard condition, a simple regularization procedure, such as truncated (T)SVD, can still remove the influence of small singular values overcome by noise (Hansen 1990a). And with the dimensionality of J greatly reduced, there remain significant improvements in computational efficiency over T(SVD) of a standard Jacobian.
3.7. Distinguishability: z, and noise threshold: ηt
To differentiate between two model cases under increasing data noise, we generalize the distinguishability criterion z proposed by Adler et al (2011), Yasin et al (2011) and also define a noise threshold for distinguishability ηt . Consider the noiseless inverse models {ma, mb} corresponding to two different model cases to be distinguished under noise. In the linear regime, noisy inverse solves will fall in a neighborhood around these models, described by the posterior model covariance matrix Cm :

where the data covariance matrix Cd
= η2
I represents, in this case, uncorrelated Gaussian experimental noise with standard deviation η, and I is the identity matrix. Whereas Adler et al identified a spatial cross-section of interest for statistical analysis, here the analysis will be conducted along a segment in model space that connects two model cases to be distinguished. A unit vector  can be defined along this segment connecting the two noise-free models:
can be defined along this segment connecting the two noise-free models:

and the component of each model's covariance Cm projected along this direction is:
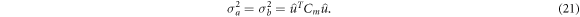
Following Adler et al, the standard deviation of the model difference σm becomes
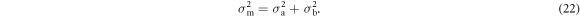
The result is a generalization of Adler et al's distingushability z in model space:
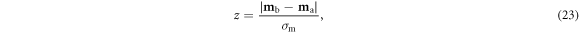
where z = 1 represents the threshold for distinguishability, and statistical significance is defined as z > 2 per mathematical convention (Cowan 1998).
A noise threshold ηt for distinguishability in the case of uncorrelated Gaussian noise can be determined by solving equations (19)–(23) according to the condition z = 1:
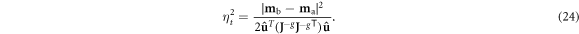
Noise exceeding this threshold renders cases {ma} and {mb} indistinguishable, i.e. within a standard deviation of noise of each other, and noise below half ηt means the two cases can be discerned with statistical significance.
4. The sensitivity volume method: demonstration
In the following, the sensitivity volume method will be demonstrated in two simulated scenarios, a biomedical one and an engineering one, with varying degrees of data noise to simulate experimental conditions. To illustrate the advantage of the sensitivity volume method in both cases, the inverse problem will be solved using two measurement protocols with the same number of measurements: one being the standard adjacent measurement protocol and the other being the sensitivity volume maximized measurement protocol.
The first demonstration is a simplified biomedical scenario representing interior chest imaging, which may aid in cardiac measurements of stroke volume and ejection fraction that can diagnose dangerous cardiac conditions such as heart failure and coronary syndrome (Zlochiver et al 2006, Proenca et al 2014, Rao et al 2018, Putensen et al 2019). The second demonstration is a structural engineering example since maintenance inspections of historical structures or enforcement of building codes may require identifying the number of reinforcement rods present in a concrete pillar. Various individual steps of the simulation employed the EIDORS EIT package (Adler and Lionheart 2006), including mesh building and plotting. The results of the biomedical and engineering demonstrations are shown in figures 3 and 4, respectively.
4.1. Model space selection: demonstration
According to the sensitivity volume method, one first chooses a reduced model space (M < M0) that will have sufficient feature resolution. Given the circular symmetry of this test problem, the results of POD from Allers and Santosa (Allers and Santosa 1991) and from Lipponen et al (2013) suggest that Zernike polynomials shown in figure 2 defined over a mesh will provide an excellent empirical basis for model space parameterization. The orthonormal Zernike polynomial functions are defined on a unit disk in terms of polar coordinates  , with increasing radial order n = {0, ... N} and angular order h = { − n, − n + 2, ... n − 2, n} representing increasing resolution where N is the highest polynomial order of the Zernike polynomials used (Lakshminarayanan and Fleck 2011):
, with increasing radial order n = {0, ... N} and angular order h = { − n, − n + 2, ... n − 2, n} representing increasing resolution where N is the highest polynomial order of the Zernike polynomials used (Lakshminarayanan and Fleck 2011):
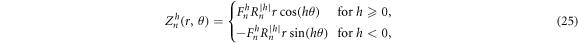
where  is defined as
is defined as
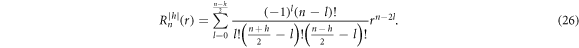
The normalization prefactor Fn h is
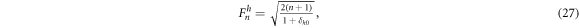
where δh0 is the Kronecker delta function (Lakshminarayanan and Fleck 2011). Using this polynomial basis, any conductivity map can be represented as a linear combination of Zernike polynomials:
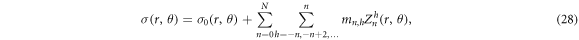
where σ0(r, θ) is the reference, chosen here to be homogeneous.
Figure 2. Zernike polynomials. Defined in equation (25), these form a basis for a reduced dimensional model space of polynomials MP, ranked from low to high resolution of radial order n and angular order h plotted with EIDORS (Adler and Lionheart 2006).
Download figure:
Standard image High-resolution imageFor a given polynomial order N, the dimension MP of the polynomial model space up to and including that order is:
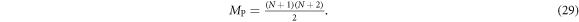
In practice, the order N of the polynomial will be chosen large enough that MP ≥ M, and the specific M polynomials for the model space basis are chosen to suit prior knowledge of electrode symmetries and the desired resolution of the problem at hand. Thus, the model conductivity m is represented here as a vector of length M describing the set of weights for each polynomial mn,h .
To deploy these continuous basis functions in a finite element solver, Zernike polynomials (Fricker 2023) were projected onto a fine mesh generated in EIDORS with Netgen (Adler and Lionheart 2006). An M0 × M-dimensional mapping matrix Z transforms the M-dimensional model vector m in the polynomial basis into a M0-dimensional vector mmesh on a finite element mesh,
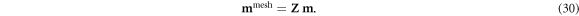
The same mapping matrix Z maps a D × M0-dimensional Jacobian Jmesh derived on a finite element mesh into a D × M-dimensional Jacobian J:
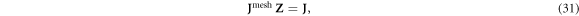
where each of M columns of Z corresponds to the mesh-element parameterization of each continuous Zernike polynomial. As a result, the forward problem can be written as:
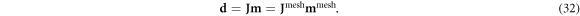
For the biomedical example of a 'normal' versus 'enlarged heart,' M = 27 independent standard Zernike polynomials of increasing resolution were chosen up through order N = 6. This uniform resolution model space is represented by all the polynomials plotted in figure 2 except for the bottom center n = 6; h = 0. For the engineering example comparing 3 versus 6 reinforcement rods, prior knowledge that the system of interest had either 3-fold or 6-fold rotational symmetry allowed the M = 27-dimensional model space to be constrained, accordingly. Here, this model space is represented by the first M = 27 standard Zernike polynomial functions that satisfy the 3- and 6-fold symmetry requirements, requiring the sampling of polynomials up to order N = 12. In both cases, a homogeneous constant background was used as a reference, and the higher conductivity test features were given a 20% enhancement in the conductivity.
4.2. Contact number selection: demonstration
For both examples, the contacts are equally spaced at the circumference with the number of contacts set according to equation (11). In order to have D = M = 27 measurements, we find for the adjacent measurement protocol that an uninflated rD = 1 data space (and uninflated contact number rC = 1) requires C0 = C = 9 contacts. For the sensitivity volume measurement protocol, an inflated data space with rD = 12 gives overall dimension D0 = rD D = 324 which requires C0 = 3C = 27 contacts per equation (11). It is observed that when using Zernike polynomials as the model space basis, an odd number of contacts C0 is preferred to minimize the null space at the maximum radial order n = N.
4.3. Sensitivity vectors: demonstration
For the inflated data space with C0 = 27 contacts, sensitivity vectors for both the biomedical and engineering examples were calculated per equation (14) for all  possible measurements. These calculations used the default EIDORS forward solver with the adjoint Jacobian (Vauhkonen et al
2001, Adler and Lionheart 2006) on a homogeneous reference, along with appropriate mapping matrices Z per equation (30) for each scenario's model space. The resulting libraries of Dmax sensitivity vectors formed measurement search spaces for the two respective cases.
possible measurements. These calculations used the default EIDORS forward solver with the adjoint Jacobian (Vauhkonen et al
2001, Adler and Lionheart 2006) on a homogeneous reference, along with appropriate mapping matrices Z per equation (30) for each scenario's model space. The resulting libraries of Dmax sensitivity vectors formed measurement search spaces for the two respective cases.
4.4. Sensitivity volume: demonstration
Sensitivity volumes were determined for each case per equation (17) for various measurement protocols with D = M = 27 sensitivity vectors chosen from the library of Dmax available. The sensitivity volumes are then compared to find which D out of Dmax specific vectors maximizes the sensitivity volume figure-of-merit S(D). Various search algorithms can be implemented such as a greedy search (Williamson and Shmoys 2011), genetic search (Press et al 2007), or simulated annealing (Press et al 2007) to find this measurement protocol with maximum sensitivity volume. In the examples below, a modified greedy search was implemented.
4.5. Data space selection: demonstration
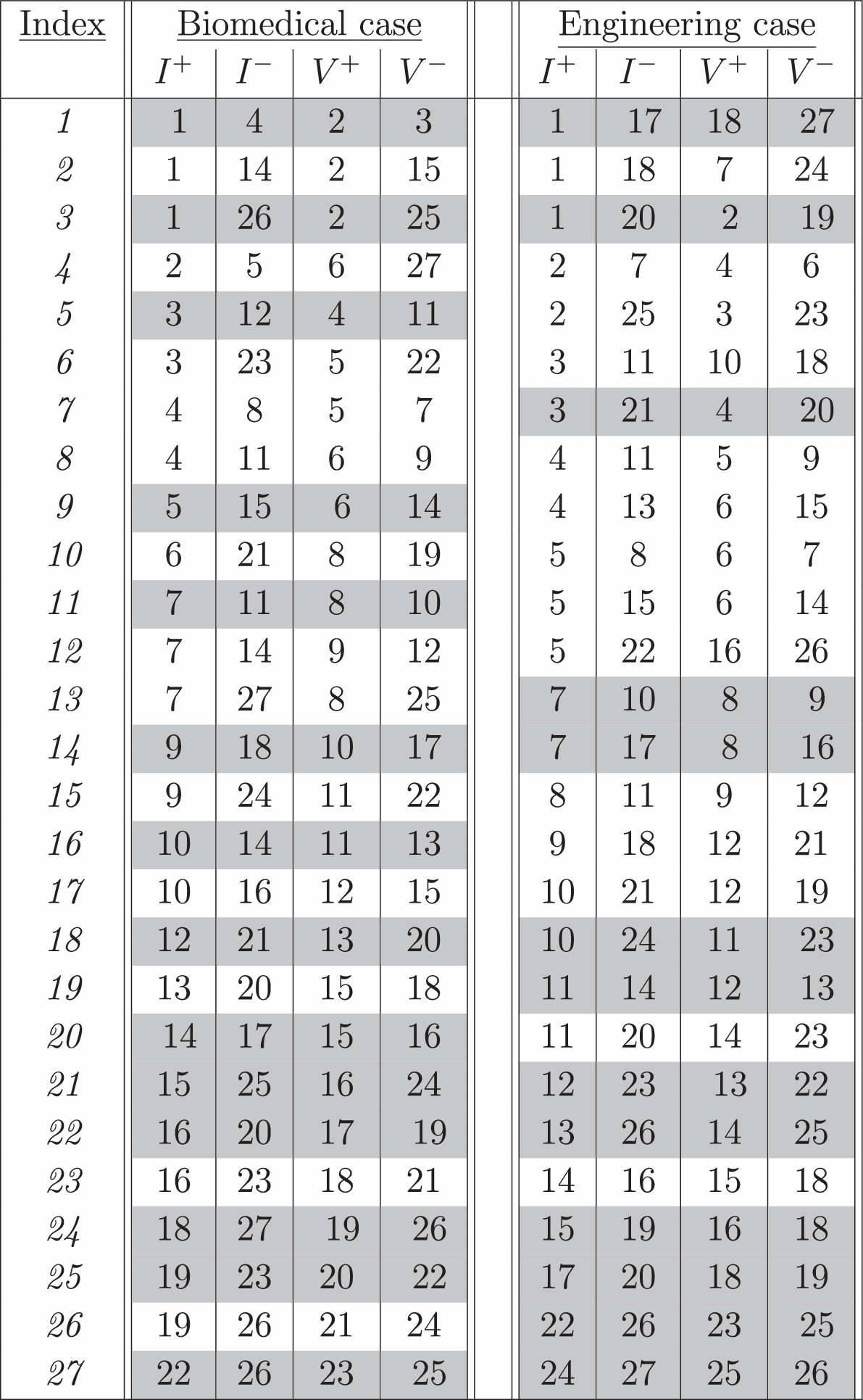
Table 1 shows the sensitivity volume optimized protocol for data space measurements for the biological and engineering scenarios, respectively. Just over half of these measurements (highlighted) have a similar configuration whereby the current injection electrode I+ neighbors the positive voltage V+ electrode, the current sink I− neighbors the negative voltage V−, and the inner/outer pairs are of the same type, either current or voltage. Because the contacts of this frequent configuration are the same as an adjacent configuration but functionally rotated analogous to a Van der Pauw conjugate measurement (Van der Pauw 1958), this contact configuration will be referred to as the 'adjacent–conjugate' configuration. But it should be pointed out that the resulting measurements in the protocols do not follow a rotational symmetry like the adjacent or skip measurement protocols and could not have been empirically guessed in advance. Furthermore, the biological problem with its uniform resolution model results in a rather different measurement protocol than the engineering problem with its 3/6-fold constrained symmetry, illustrating the dependence of the measurement protocol on the model structure.
Table 1. Measurement protocols for the biomedical and engineering examples, with current injection between I+ and I− electrodes and voltage measurement across electrodes V+ and V−. More than half the measurements (highlighted in grey) are of a similar configuration which we define to as 'adjacent–conjugate,' whereby each voltage electrode neighbors a current electrode, and the inner/outer pairs are current/voltage electrodes.
 |
We reiterate that once an optimal measurement protocol is determined, there is no need to repeat the sensitivity volume optimization. Because the computationally intensive steps of sections 4.3 through 4.5 are performed in advance to generate the Jacobian for the optimized data space, the inverse solve can now be extremely rapid, as fast as a simple matrix multiplication.
4.6. Inverse solver selection: demonstration
To complete the sensitivity volume method, one must solve the resultant exact determined inverse problem (M = D). A Matlab code was written to use (truncated) singular value decomposition (T)SVD to solve the linearized, non-iterative inverse problem for orthogonal polynomial model spaces per equation (7). Data was simulated using EIDORS' default forward solver and a finite element mesh. Gaussian noise with standard deviation η was added to the simulated data to emulate realistic experimental conditions.
4.7. Distinguishability and noise threshold: demonstration
In the biomedical example, our SVD solver was used with no truncation of singular values. Figure 3(a) shows the 'input' conductivity maps in the forward problem for the 'normal' heart (top) and the 'enlarged' heart (bottom) using an EIDORS derived mesh. Reconstructed conductivity maps of the noiseless (η = 0) normal and enlarged heart are shown in color in the left of panel (b) for the standard adjacent measurement protocol, and the left of panel (c) for the sensitivity volume maximized measurement protocol. The polynomial model space in section 4.1 and the inverse solver described in section 4.6 were used to produce reconstructed images from simulated datasets using both measurement protocols. In the absence of noise, all reconstructions show similar resolution, with the exception that the enlarged case for the adjacent measurement protocol shows artifacts with residual oscillations at the periphery.
Figure 3. Biological example: noise advantage of sensitivity volume method using the M = 27 Zernike polynomial model space. Reconstruction quality of a 'normal heart' and 'enlarged heart' in a simplified 2D model of a chest cavity are compared. (a) From input conductivity maps on a mesh (black and white), mean inverse maps following the color scheme (far right) are shown with increasing input noise level η from left to right from both (b) adjacent measurements C = 9, D = 27 and (c) sensitivity maximized measurements C = 27, D = 27. Calculations of distinguishability z show that the sensitivity volume method can withstand (z > 1, green) over an order of magnitude higher noise than the adjacent measurements before becoming indistinguishable (z < 1, red). On the conductivity color scale on the right 10 represents the homogeneous reference. Images plotted using EIDORS (Adler and Lionheart 2006).
Download figure:
Standard image High-resolution imageTo investigate noise tolerance, the mean results of 1000 simulated SVD inversions of normal and enlarged hearts were generated with increased data noise η. As noise increases to the right in figure 3, the standard adjacent measurements in the top rows generate average inverse maps that deviate further from the noiseless reconstructions, and eventually become overwhelmed by the noise. By contrast, reconstructions using sensitivity volume derived measurements in the bottom rows can withstand over an order of magnitude more noise than the adjacent measurements.
The results can be quantified using the distinguishability and noise tolerance metrics of Subsection 3.7. The distinguishability z was calculated at each noise level η for reconstruction of both adjacent and sensitivity maximized measurement protocols. The distinguishability threshold is defined as z = 1, whereupon the normal and enlarged cases become statistically indistinguishable, and ηt is the corresponding noise level threshold. For z > 1, the average inverse maps begin to show differences from the noise-free scenario, and z = 2 represents the threshold for statistically significant distinguishability (Cowan 1998). The noise threshold ηt for both cases is listed in table 2 and shows that the sensitivity volume maximized dataset tolerates a factor of 25 × more noise than the adjacent measurement protocol, with the same number of measurements. Table 2 also lists the increase in relative sensitivity S/S0 of the sensitivity volume measurement protocol from equation (18) relative to that of the adjacent measurement protocol.
Table 2. Noise tolerance of sensitivity volume measurement protocol compared to adjacent measurement protocol. Although the protocols differ in contact number C, they have the same number of data space measurements D and model space dimensions M. Nonetheless, the sensitivity volume protocol shows significantly larger noise thresholds ηt and significantly larger sensitivity S/S0 normalized relative to the adjacent case, exceeding an order of magnitude for the biomedical case (figure 3) and two orders of magnitude for the engineering case (figure 4).
| Measurement protocol | Biomedical case | Engineering case | |||||
|---|---|---|---|---|---|---|---|
| C | D | M | ηt | S/S0 | ηt | S/S0 | |
| Adjacent | 9 | 27 | 27 | 0.13 × 10−6 | 1 | 0.011 × 10−6 | 1 |
| Sensitivity | 27 | 27 | 27 | 3.2 × 10−6 | 10.8 | 14 × 10−6 | 236 |
In the engineering example, our (T)SVD solver was used for both measurement protocols with a truncation point of k = 18 singular values, as necessitated by smaller amplitudes of the singular values from the Jacobian matrices. Figure 4(a) shows the forward problem input maps of 3 rods (top) and 6 rods (bottom). Reconstructed conductivity maps of the noiseless (η = 0) cases are shown in color in the left of panel (b) for the standard adjacent measurement protocol, and the left of panel (c) for the sensitivity volume maximized measurement protocol. Datasets generated using both measurement protocols were reconstructed using the 3- and 6-fold symmetric polynomial model space described in section 4.1. Once again, the mean results of 1000 (T)SVD inverse solves are generated with increasing noise η from left to right. In the reconstructions from adjacent measurements in panel (b), small singular values in the (T)SVD inversion cause the noise to rapidly overtake any meaningful model features. In contrast, sensitivity volume maximized measurements in panel (c), can withstand three orders of magnitude more noise before such model obfuscation occurs, with the respective ηt values again listed in table 2.
Figure 4. Engineering example: noise advantage of sensitivity volume method using the feature targeted, 3- and 6-fold symmetric M = 27 polynomial model space. Reconstruction quality of 3 versus 6 reinforcement rods in the cross-sectional model of a concrete pillar are compared. (a) From input conductivity maps on a mesh (black and white), mean inverse maps following the color scheme (far right) are shown with increasing input noise level η from left to right from both (b) adjacent C = 9, D = 27 and (c) sensitivity maximized measurements C = 27, D = 27. Calculations of distinguishability z show that the sensitivity volume method can withstand (z > 1, green) more than two orders of magnitude higher noise than the adjacent measurements before becoming indistinguishable (z < 1, red). On the conductivity color scale on the right 10 represents the homogeneous reference. Images plotted using EIDORS (Adler and Lionheart 2006).
Download figure:
Standard image High-resolution image4.8. Iterative versus non-iterative solvers: optimizing computational speed
The final advantage of the sensitivity volume method is to leverage the gain in sensitivity to achieve faster computational time. A rapid refresh rate for tomographic mapping is important in applications where the system under study is dynamically varying, such as a beating heart or a structural element under imminent failure. But when solving inverse problems in the presence of data noise, it is typically necessary to rely on an iterative solver which can slow down the inversion algorithm.
Here, a standard iterative solver is challenged against the non-iterative sensitivity volume method with the same distinguishability problem for the biomedical and engineering cases, above. The noise threshold, and its computation times were compared to the computation times of our non-iterative sensitivity volume method under the same noise level. The iterative solver to be compared is the publicly available EIDORS iterative Gauss Newton inverse solver (Adler and Lionheart 2006), which can conduct inverse solves in 100 or fewer iterations with the regularizing hyperparameter set to 1 × 10−7. For calculations of the EIDORS noise threshold, the model covariance was estimated from ensembles of 100 different inverse solves for different noise amplitudes η, and the resulting noise thresholds are listed in table 3. The noise threshold of the iterative EIDORS regularized inversion with the adjacent data space, is always of the same order of magnitude and slightly less than the noise tolerated by the non-iterative (T)SVD inversion with the sensitivity volume method. Table 3 shows the significant speed advantage of inverting with the non-iterative sensitivity volume method over inverting with a regularized, iterative solver by comparing their computation times tc for the examples shown previously. The sensitivity volume method produces results in approximately 1/600 000th the computation time of the EIDORS inverse solver.
Table 3. Computational advantage of sensitivity volume method over default EIDORS inverse solvers. Comparisons of computation times tc and noise thresholds ηt show the sensitivity volume method can produce comparable noise-tolerance to EIDORS but 600 000× faster.
| Inverse Solver | Biomedical case | Engineering case | ||
|---|---|---|---|---|
| tc | ηt | tc | ηt | |
| EIDORS | 69 s | 1.7 × 10−6 | 67 s | 3.1 × 10−6 |
| Sensitivity | 110 μs | 3.2 × 10−6 | 110 μs | 14 × 10−6 |
4.9. Inflated versus uninflated data spaces
In the sensitivity volume method, inflating the data space comes at a cost of adding more contacts. Thus, it is important to quantify the degree to which an inflation of the data space leads to an improvement in the overall sensitivity. A computational study of the sensitivity for a 2D circle was undertaken for various data space inflation factors rD = 1, 3, 5, and 10 with equally spaced circumferential contacts, a homogeneous reference, and a Zernike polynomial model space, and the corresponding factor of increase in contact number rC was compared.
In figure 5, the initial number of contacts C listed on the bottom axis will set the baseline data space dimension D per equation (8). Then this data space will be increased by the factor rD
to the value D0, requiring that the contact number also be correspondingly increased to C0(rD
) listed along the top axis of figure 5 per equation (9). The inset of figure 5 compares the exact value by which the contact number is inflated C0(rD
)/C (filled circles) along with the analytical expression for rC
from equation (12) (solid lines), showing good agreement. In particular, equation (12) predicts that the rC
factor saturates at  for large contact number (dashed horizontal lines), with this saturation evident already for C > 10.
for large contact number (dashed horizontal lines), with this saturation evident already for C > 10.
Figure 5. Normalized sensitivity improvement S/S0 versus contact number C for different data space inflation factors rD
. The bottom horizontal axis sets the baseline number of contacts C with no inflation of the data space, rD
= 1. When the data space is inflated by the factors rD
= 3 (green), 5 (red), and 10 (blue), respectively, the number of contacts C0 required to generate these larger data spaces are listed in the colored horizontal axes above the plot for each value of C. The increase in sensitivity relative to the uninflated data space S/S0 is plotted on the vertical axis. Power law curves according to equation (33) are overlaid as guides to the eye. Inset: Inflation factor for the contact number C0/C (dots) and rC
from equation (12) (line) are plotted versus baseline contact number C for the same data space inflation factors rD
showing good agreement. rC
asymptotically approaches  in the limit of large C (horizontal dashed lines).
in the limit of large C (horizontal dashed lines).
Download figure:
Standard image High-resolution imageThe sensitivity improvement S is then plotted on the vertical axis of figure 5 relative to the adjacent measurement protocol S0. The behavior reveals significant increase in the sensitivity ratio S/S0 by one-and-a-half orders of magnitude as the data space D0 expands by increasing factors of rD , and this enhanced sensitivity is most dramatic with the largest number of contacts. For convenience, the following empirical expression for the sensitivity enhancement can serve as a guide to the eye, plotted as continuous curves in figure 5
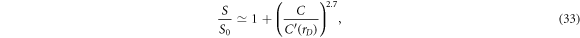
with the empirical parameter  of the plots of figure 5 found to be
of the plots of figure 5 found to be  ,
,  , and
, and  . Equation (33) can be inverted to determine roughly how many contacts would be needed to achieve a desired increase in sensitivity S/S0 over the adjacent protocol
. Equation (33) can be inverted to determine roughly how many contacts would be needed to achieve a desired increase in sensitivity S/S0 over the adjacent protocol
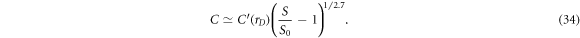
Note that large gains in sensitivity can be achieved with only a modest inflation factor. As shown in the inset for the case of rD = 3 and assuming an initial C = 11 contacts, the number of contacts only needs to be increased by 65% to C0 = 18 contacts to result in more than an order of magnitude improvement in sensitivity S/S0. As another example, for an initial C = 16 contacts common in EIT systems, an increase in contact number to C0 = 27 will increase the signal-to-noise by a factor of ×25. The sensitivity can be further increased with an increase in the data space scaling factor to rD = 5 or rD = 10 corresponding to approximately twice (rC = 2) or triple (rC = 3) the number of contacts.
As an aside, we note that without increasing the number of contacts (rD = rC = 1), the sensitivity volume method does not show significant improvement over the adjacent or skip (Adler et al 2011) data sets in this general case of a homogeneous disc, achieving at most a 20% improvement in S/S0. Such gains show why the adjacent data space has stood the test of time as a popular empirical rule for choosing a 2D data space. But in the case of an inhomogeneous reference, a restricted model space such as the engineering example of figure 4, or irregular geometries, the sensitivity volume method is expected to show performance advantages.
5. Alternate optimization strategies
Alternative EIT method optimization efforts are categorized below according to the optimization parameter of interest, and contextualized relative to the sensitivity volume method introduced above for comparison.
5.1. Model space selection: method comparison
The strategic choice of a model space in the sensitivity volume method was informed by prior work within the EIT literature, wherein this choice has also been referred to as selection of the 'model' (Lipponen et al 2013), choice of 'conductivity basis functions' (Tang et al 2002), or the 'parameterization of the domain' (Boyle et al 2012). Reduced dimensionality model spaces can be constructed using prior knowledge (Vauhkonen et al 1997, Tang et al 2002) to significantly decrease computation time (Gómez-Laberge and Adler 2008, Boyle et al 2012). For example, Lipponen et al (2013) used POD to produce orthonormal functions that strongly resembled Zernike polynomials, a known set of orthonormal polynomial functions used by Allers and Santosa as a model space basis for a 2D circular sample (Allers and Santosa 1991). In keeping with the spirit of the above examples, the sensitivity volume method, leverages the advantage of a reduced model space.
5.2. Contact selection: method comparison
Other EIT literature has sought to increase contact number (Coxson et al 2022) and vary contact placement (Yan et al 2006, Smyl and Liu 2020, Karimi et al 2021) to optimize results. Additional works have used two-point measurements or electrode segmentation schemes to select contacts (Polydorides and McCann 2002, Kantartzis et al 2013, Zhang et al 2016, Ma et al 2020) that may have some strict mathematical advantage, but are disadvantageous for use in biomedical applications (Putensen et al 2019) or with existing EIT hardware. Although these works have considered the effect of contacts on the EIT problem, the proposed sensitivity volume method offers a specific figure of merit to optimize contact number and placement.
5.3. Sensitivity and EIT: method comparison
The use of the term 'sensitivity' in relation to EIT is borrowed from the common alias of the Jacobian as the 'sensitivity matrix' (Holder 2005). The sensitivities of different prescribed measurement protocols have been compared by examining the matrices derived from singular value decomposition (Polydorides and McCann 2002, Tang et al
2002, Graham and Adler 2007, Kantartzis et al
2013). Other sensitivity-based figures of merit are limited to model spaces comprised of the full finite element mesh  (Grychtol et al
2019, Coxson et al
2022) or require subjective visual judgements (Kauppinen et al
2006, Paldanius et al
2022). The sensitivity volume parameter proposed here, by contrast, is a mathematically precise, objective scalar representing the overall sensitivity of a set of measurements.
(Grychtol et al
2019, Coxson et al
2022) or require subjective visual judgements (Kauppinen et al
2006, Paldanius et al
2022). The sensitivity volume parameter proposed here, by contrast, is a mathematically precise, objective scalar representing the overall sensitivity of a set of measurements.
5.4. Figures of merit for optimization: method comparison
In the optimization of EIT methods, it becomes necessary to develop figures of merit for quantitative comparisons. A wide variety of metrics have been proposed within the EIT literature that are often case specific (Graham and Adler 2006, 2007, Adler et al 2009, 2011, Yasin et al 2011, Grychtol et al 2016, Wagenaar and Adler 2016, Thürk et al 2019) or cannot be applied until after an inverse solve is completed (Yorkey et al 1987, Tang et al 2002, Coxson et al 2022). In comparison, the sensitivity volume figure-of-merit is unique, unambiguous, consistent, and broadly applicable.
5.5. Data space selection: method comparison
Data space selection has been referred to as an 'electrode selection algorithm' (Coxson et al 2022), a measurement 'protocol' (Holder 2005), an 'electrode stimulation and measurement configuration' (Grychtol et al 2016), or an 'electrode placement configuration' (Graham and Adler 2007). These prior works often take trial and error approaches (Adler et al 2011), are limited to highly specific cases (Ma et al 2020), or require optimization of multi-step machine learning algorithms (Coxson et al 2022). In addition to the adjacent measurement protocol mentioned in the introduction, skip measurements have grown in popularity as a data space standard based on an empirical extrapolation of adjacent data space (Adler et al 2011, de Castro Martins et al 2019, Adler and Zhao 2023). In the sensitivity volume method, by contrast, increased data importance is achieved by selecting current and voltage contacts not empirically, but according to a maximized figure-of-merit.
5.6. Inverse solver: method comparison
The EIT literature seeks to maximize computational efficiency in solving the inverse problem. To this end, small model space dimensions have been recommended to reduce the ill-posed nature of the problem and decrease computation time (Vauhkonen et al 1997, Tang et al 2002), despite the continued prevalence of large model spaces with M ≫ D. In contrast, by solving an exact-determined problem M = D, the sensitivity volume method quickly solves EIT with less regularization. A comparison computational efficiency (Yorkey et al 1987, Gómez-Laberge and Adler 2008, Boyle et al 2012, Lipponen et al 2013) is shown in section 4 to demonstrate this advantage.
The ill-posedness and inherently nonlinear nature of the EIT problem often necessitates iterative solutions, such as those available in the popular open source Matlab package EIDORS (Vauhkonen et al 2001, Adler and Lionheart 2006, Graham and Adler 2006). Whereas the treatment in this manuscript has focused on the linearized problem, we note that the a priori calculations in the sensitivity volume method can also be implemented prior to solving the nonlinear problem and provide the same advantages in noise robustness. It should be noted that one does not need to use the reduced basis model space for inversion. One may merely use the sensitivity volume method to generate a measurement protocol with high sensitivity, and then use any favored EIT inverse solver to convert those highly sensitive data measurements to an image reconstruction.
5.7. Distinguishability and noise tolerance metrics: method comparison
In addition to the metric proposed by Adler et al (2011), Yasin et al (2011), Adler and Zhao (2023) and generalized in section 3.7, other measures of distinguishability have been proposed in the EIT literature (Vauhkonen et al 1997, Graham and Adler 2007, Adler et al 2009, Braun et al 2017). For example, Isaacson (1986), Gisser et al (1988) defined distinguishability in terms of current patterns using all electrodes. But hardware capabilities, current limits, and the inconvenience of optimization during measurement limited use of these maximal distinguishability patterns (Holder 2005). In contrast, the sensitivity volume method uses pair drive current patterns and a priori calculations to optimize measurements for existing EIT systems and achieve improvements in signal to noise.
6. Conclusions
This manuscript details a sensitivity volume method for optimizing the EIT inverse-problem for increased noise robustness of measurements and improved computational efficiency. The above analysis demonstrates the benefit of targeted selection of model space, data space, and inverse solver for increased data importance by leveraging prior information and introducing the sensitivity volume figure of merit. The sensitivity volume method chooses a model space of targeted features in which to optimize and solve the EIT problem, identifies an appropriate contact number to inflate the available data space, selects the data subspace with the largest sensitivity volume, and finally, solves an exact-determined inverse problem. In the simulated examples presented to illustrate our methods, we observed a factor of over two orders of magnitude improvement in noise tolerance compared to a standard EIT model space, data space, and inverse solver choice, or ×600 000 improvement in computation time over iterative solvers with comparable fidelity. The proposed sensitivity volume method makes important steps towards the goal of rapid-refresh, noise-robust, high-resolution EIT inversion.
Acknowledgments
This work was supported in part by Northwestern University and NSF grants ECCS-1912694, DMR-1720139, and support from Leslie and Mac McQuown.
Data availability statement
The data in this study are most easily reproduced using the simple step by step models described in the manuscript. The code for generating the data is likewise described step by step in the manuscript. The specific code that we have implemented and the specific 18 000 element meshes are nonetheless available upon request. The data that support the findings of this study are available upon reasonable request from the authors.