Abstract
Rate-induced tipping (R-tipping) occurs when time-variation of input parameters of a dynamical system interacts with system timescales to give genuine nonautonomous instabilities. Such instabilities appear as the input varies at some critical rates and cannot, in general, be understood in terms of autonomous bifurcations in the frozen system with a fixed-in-time input. This paper develops an accessible mathematical framework for R-tipping in multidimensional nonautonomous dynamical systems with an autonomous future limit. We focus on R-tipping via loss of tracking of base attractors that are equilibria in the frozen system, due to crossing what we call regular R-tipping thresholds. These thresholds are anchored at infinity by regular R-tipping edge states: compact normally hyperbolic invariant sets of the autonomous future limit system that have one unstable direction, orientable stable manifold, and lie on a basin boundary. We define R-tipping and critical rates for the nonautonomous system in terms of special solutions that limit to a compact invariant set of the autonomous future limit system that is not an attractor. We focus on the case when the limit set is a regular edge state, introduce the concept of edge tails, and rigorously classify R-tipping into reversible, irreversible, and degenerate cases. The central idea is to use the autonomous dynamics of the future limit system to analyse R-tipping in the nonautonomous system. We compactify the original nonautonomous system to include the limiting autonomous dynamics. Considering regular R-tipping edge states that are equilibria allows us to prove two results. First, we give sufficient conditions for the occurrence of R-tipping in terms of easily testable properties of the frozen system and input variation. Second, we give necessary and sufficient conditions for the occurrence of reversible and irreversible R-tipping in terms of computationally verifiable (heteroclinic) connections to regular R-tipping edge states in the autonomous compactified system.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Recommended by Dr Hinke M Osinga
Footnotes
- 4
Dangerous bifurcations have a discontinuity in the parametrised family (or branch) of attractors at the bifurcation point and include, for example, saddle-node and subcritical Hopf bifurcations [125].
- 5
Often referred to as an 'alternative stable state'.
- 6
We give non-degeneracy conditions for connecting orbits in remark 7.3.
- 7
Note that if t is in units second and r is in units inverse second then τ is dimensionless.
- 8
This is the flow
 written as a process [64] with the r dependence explicitly shown. Given a solution
written as a process [64] with the r dependence explicitly shown. Given a solution ![$x^{[r]}(\tau,x_0,\tau_0)$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) to system (3), one can easily obtain the corresponding solution to system (2) by setting
to system (3), one can easily obtain the corresponding solution to system (2) by setting  and
and  . However, it is important to note that, for different r > 0, a fixed initial state
. However, it is important to note that, for different r > 0, a fixed initial state  in system (3) corresponds to a fixed value of the external input
in system (3) corresponds to a fixed value of the external input  , but different initial states
, but different initial states  in system (2).
in system (2). - 9
The smallest closed subset of
 containing S.
containing S. - 10
See appendix A.4 for the definition of an attractor.
- 11
Notions of convergence to invariant sets η are discussed in appendix A.1.
- 12
Note that
 is contained in its stable manifold, that is
is contained in its stable manifold, that is  .
. - 13
We recall some notions used in discussion of differentiable manifolds in appendix A.2.
- 14
Note that the stable invariant manifold of η contains η.
- 15
See appendix A.4 for the definition of an attractor.
- 16
Not to be confused with the 'static' notion of 'basin stability' introduced in [81] as a measure related to the volume of the basin of attraction.
- 17
Equivalently, a moving sink
 is 'forward basin stable' if, at each point in time, the basin of attraction of
is 'forward basin stable' if, at each point in time, the basin of attraction of  contains all the previous positions of
contains all the previous positions of  .
. - 18
The signed distance
 is discussed in appendix A.3.
is discussed in appendix A.3. - 19
Note that
 is not necessarily a regular edge state from definition 4.4(c); it may be a saddle with more than one unstable direction, or even a repeller of codimension-two or higher, and/or not necessarily hyperbolic.
is not necessarily a regular edge state from definition 4.4(c); it may be a saddle with more than one unstable direction, or even a repeller of codimension-two or higher, and/or not necessarily hyperbolic. - 20
In the one dimensional case, recall that the moving regular threshold and edge state are one and the same.
- 21
We say a moving sink
 on I is forward threshold stable if there are no
on I is forward threshold stable if there are no  and finite
and finite  that can satisfy condition (15).
that can satisfy condition (15). - 22
Recall the notation introduced in section 2.4.
- 23
Here, we define

- 24
See appendix A.4 for the definition of an attractor.
- 25
By abuse of notation, we use τ to denote both the independent variable and the additional dependent variable.
- 26
 is denoted
is denoted  in [132].
in [132]. - 27
For example, when
 as
as  .
. - 28
The notion of Hausdorff distance dH is discussed in appendix A.1.
- 29
- 30
Note that
 passes through λa
before λb
, though it may pass through either or both of these values several times.
passes through λa
before λb
, though it may pass through either or both of these values several times. - 31
Note that the subscript in τα is not related to the compactification parameter α.
- 32
The notion of Hausdorff distance dH is discussed in appendix A.1.
- 33
The notion of signed distance ds is discussed in appendix A.3.



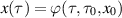
![$x^{[r]}(\tau,x_0,\tau_0)$](https://content.cld.iop.org/journals/0951-7715/36/6/3238/revision2/nonaccb37ieqn33.gif)

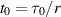
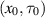
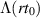

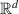
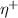
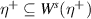
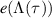

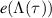




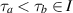
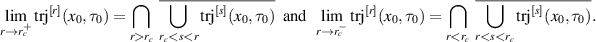

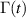


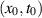
![$(x_0,s_0^{[r]})$](https://content.cld.iop.org/journals/0951-7715/36/6/3238/revision2/nonaccb37ieqn985.gif)
