Abstract
It has been highly desired to provide an accurate and reliable method to calculate core electron binding energies (CEBEs) of crystals and to understand the final state screening effect on a core hole in high resolution x-ray photoelectron spectroscopy (XPS), because the ΔSCF method cannot be simply used for bulk systems. We propose to use the quasiparticle calculation based on many-body perturbation theory for this problem. In this study, CEBEs of band-gapped crystals, silicon, diamond, β-SiC, BN, and AlP, are investigated by means of the GW approximation (GWA) using the full ω integration and compared with the preexisting XPS data. The screening effect on a deep core hole is also investigated in detail by evaluating the relaxation energy (RE) from the core and valence contributions separately. Calculated results show that not only the valence electrons but also the core electrons have an important contribution to the RE, and the GWA have a tendency to underestimate CEBEs due to the excess RE. This underestimation can be improved by introducing the self-screening correction to the GWA. The resulting C1s, B1s, N1s, Si2p, and Al2p CEBEs are in excellent agreement with the experiments within 1 eV absolute error range. The present self-screening corrected GW approach has the capability to achieve the highly accurate prediction of CEBEs without any empirical parameter for band-gapped crystals, and provide a more reliable theoretical approach than the conventional ΔSCF-DFT method.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Since the invention of high resolution x-ray photoelectron spectroscopy (XPS) by Siegbahn et al [1–4], XPS has been widely used as a method to investigate the valence nature and chemical properties of atoms in variety of materials [5]. A significantly increasing number of papers related to XPS have been published so far [6]. The core electron binding energy (CEBE) certainly reflects the nature of chemical bonds and local electronic structures involving the ionic valence and so on. However, since these environmental effects are difficult to characterize quantitatively, a comparison with reliable reference data is always required [7], and the development of an accurate first-principles method to calculate CEBEs has been highly desired [2, 3, 7]. The most important point here is that, the binding energies (BEs) measured in XPS are directly related to the quasiparticle (QP) energies, which are defined as the difference between the total energy of the N-electron ground (initial) state, 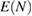 , and the total energy of the (N − 1)-electron excited (final) state,
, and the total energy of the (N − 1)-electron excited (final) state, 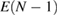 [8].
[8].
Historically, in initial-state theory, thanks to Koopman's theorem, the Hartree–Fock (HF) energy eigenvalue 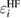 of a core level was simply used for the CEBE by changing sign under the fixed wave functions. However, the results were not good at all even if chemical shifts, i.e. relative values of CEBEs were concerned [3, 9]. Since then, it has been well recognized that final-state theory, which includes the relaxation effects of the final state, is essential to obtain accurate CEBEs [10, 11]. One successful approach in this theory is to use the delta self-consistent field (ΔSCF) method using quantum chemistry approaches (beyond HF) for isolated systems [10–12]. This is the direct approach calculating the total energy of the system before and after introducing a core hole in the electronic configuration. However, such quantum chemistry approaches cannot be simply applied to crystalline systems. On the other hand, the application of density functional theory (DFT) [13, 14] to the final state calculation is not guaranteed because DFT is basically the ground state theory and cannot be simply applied to the excited state having a core hole. In addition, the practical final state calculation in the ΔSCF method requires the charge compensation to keep the charge neutrality of a supercell under a periodic boundary condition. For the latter problem, recent reports argued that this charge compensation may be inadequate particularly in band-gapped materials [15]. To obtain absolute CEBEs with the ΔSCF-DFT, Walter et al [16] had to introduce the offset parameter
of a core level was simply used for the CEBE by changing sign under the fixed wave functions. However, the results were not good at all even if chemical shifts, i.e. relative values of CEBEs were concerned [3, 9]. Since then, it has been well recognized that final-state theory, which includes the relaxation effects of the final state, is essential to obtain accurate CEBEs [10, 11]. One successful approach in this theory is to use the delta self-consistent field (ΔSCF) method using quantum chemistry approaches (beyond HF) for isolated systems [10–12]. This is the direct approach calculating the total energy of the system before and after introducing a core hole in the electronic configuration. However, such quantum chemistry approaches cannot be simply applied to crystalline systems. On the other hand, the application of density functional theory (DFT) [13, 14] to the final state calculation is not guaranteed because DFT is basically the ground state theory and cannot be simply applied to the excited state having a core hole. In addition, the practical final state calculation in the ΔSCF method requires the charge compensation to keep the charge neutrality of a supercell under a periodic boundary condition. For the latter problem, recent reports argued that this charge compensation may be inadequate particularly in band-gapped materials [15]. To obtain absolute CEBEs with the ΔSCF-DFT, Walter et al [16] had to introduce the offset parameter 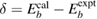 , although there is no clear physical explanation. In addition, recent studies [15–18] use the frozen core orbital approximation in the final state calculation, although the all-electron calculation is essential to estimate the full relaxation energies (REs) in the CEBEs.
, although there is no clear physical explanation. In addition, recent studies [15–18] use the frozen core orbital approximation in the final state calculation, although the all-electron calculation is essential to estimate the full relaxation energies (REs) in the CEBEs.
In the ΔSCF method, it is difficult to discuss the relationship between CEBEs and the quantitatively defined relaxation effects, namely, the REs. Hedin and Johansson [19] and Bechstedt [20] discussed the relationship between the HF energy eigenvalue, 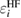 , and the RE, Ri, which is originally called the polarization potential [19], as
, and the RE, Ri, which is originally called the polarization potential [19], as

Because 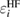 does not take account of any relaxation effect of the wave function, the RE, Ri, includes the full relaxation effects in the final state, which can be calculated by the above-mentioned quantum chemistry approaches for isolated systems. For bulk systems, Bechstedt [20] demonstrated the necessity of using the Green's function in many-body perturbation theory (MBPT) for this purpose, although he did not perform any explicit calculation of real materials. The systematic perturbation expansion of the self-energy in the Green's function enables us to extract the RE and the CEBE as the QP energy. In this approach, one can directly express the RE as the expectation value of the correlation part of the self-energy
does not take account of any relaxation effect of the wave function, the RE, Ri, includes the full relaxation effects in the final state, which can be calculated by the above-mentioned quantum chemistry approaches for isolated systems. For bulk systems, Bechstedt [20] demonstrated the necessity of using the Green's function in many-body perturbation theory (MBPT) for this purpose, although he did not perform any explicit calculation of real materials. The systematic perturbation expansion of the self-energy in the Green's function enables us to extract the RE and the CEBE as the QP energy. In this approach, one can directly express the RE as the expectation value of the correlation part of the self-energy 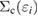 for ith orbital,
for ith orbital,
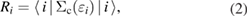
where 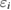 and
and ![$ \newcommand{\ket}[1]{\,\vert\,{#1}\,\rangle} \ket{i}$](https://content.cld.iop.org/journals/0953-8984/30/21/21LT01/revision2/cmaabdfeieqn009.gif) are the QP energy and the QP wave function (for precise notation
are the QP energy and the QP wave function (for precise notation ![$ \newcommand{\bra}[1]{\langle\,{#1}\,\vert\,} \newcommand{\braket}[2]{\langle\,{#1}\,\vert\,{#2}\,\rangle} \braket{{\boldsymbol r}}{i}$](https://content.cld.iop.org/journals/0953-8984/30/21/21LT01/revision2/cmaabdfeieqn010.gif) ) of the core hole level i. In this sense, the first-principles Green's function method in MBPT is the most suitable approach for the CEBE calculations for crystalline systems if the effect of lattice relaxation can be ignored as in typical semiconductors. One merit of this method is that the poles of the Green's function directly represent the QP energies. Another merit of this method is that it does not require supercell calculations.
) of the core hole level i. In this sense, the first-principles Green's function method in MBPT is the most suitable approach for the CEBE calculations for crystalline systems if the effect of lattice relaxation can be ignored as in typical semiconductors. One merit of this method is that the poles of the Green's function directly represent the QP energies. Another merit of this method is that it does not require supercell calculations.
Here, it should be emphasized that equation (2) represents the full relaxation effects on the core state i without explicitly introducing the core hole. In ordinary perturbation theory starting from the ground state, one might expect that the electrons far apart from the Fermi level cannot contribute to the screening effects. In terms of the RE, Ri, the previous studies [21, 22] assume that the valence electrons have a dominant role in CEBEs implicitly. However, such a naive expectation is very questionable, because, in the existence of a core hole, the core wave functions must be significantly deformed as well as the valence wave functions. All these effects are included in equation (2) although one needs not explicitly introduce a core hole in the calculation. This is a very important advantage of this method.
In order to exploit these merits, we have to use the Green's function method. Nowadays, the so-called GW approximation (GWA) [22–25], which describes the dynamical screening effect within the random phase approximation (RPA), has been successfully used for calculating the QP energies of valence and conduction states. However, to the best of our knowledge, the GWA has not been applied to the calculation of the CEBE except for a previous calculation [26] using the generalized plasmon pole (GPP) model [27].
There are some problems in the GWA when applied to the CEBE and RE calculations. First of all, the evaluation of the GW self-energy requires the numerical frequency (ω) integration. However, the numerical ω integration has been often avoided by using the GPP model due to the computational cost. The GPP model deals with the dielectric property from the collective excitation at a plasmon oscillation only and ignores the individual excitation contributions. Therefore the validity of the GPP model is very questionable [28–30]. Second, it is known that the RPA polarization function of the GWA contains the unphysical self-screening error [31]. The formulation of the self-screening corrected GWA has already been given by several authors and tested on some models [32, 33], although there is no report on the corresponding first-principles results. Therefore, it is desirable to perform the self-screening corrected GWA in the core hole problem. Third, most of the previous GW calculations have been focused on valence and conduction electron properties only and relied on pseudopotentials in the frozen core approximation. However, the amount of the core electron contribution to CEBEs is still unclear and the systematic investigation using the all-electron GW calculation is highly required. An important question here is how much the core contribution exists in the RE, Ri. To answer this question, it is important to investigate the RE of core and valence electron contributions to the CEBEs within the GWA.
The purpose of this paper is to demonstrate that the self-screening corrected GWA with the full ω integration has enough capability to estimate accurate CEBEs in band-gapped crystalline systems. Needless to say, this is the first report on this issue using such a GWA.
2. Methods
In this paper, we consistently adopt the (one-shot) GWA [27] as a Green's function approach in an all-electron formalism. One important merit of the Green's function method is that it can directly deduce the RE as explained in the Introduction. As usual, the QP energies and wave functions required in the intermediate steps are replaced by the Kohn–Sham (KS) energy eigenvalues and wave functions (denoted by  and
and ![$ \newcommand{\bk}{{\boldsymbol k}} \newcommand{\ket}[1]{\,\vert\,{#1}\,\rangle} \ket{n, \bk}$](https://content.cld.iop.org/journals/0953-8984/30/21/21LT01/revision2/cmaabdfeieqn012.gif) , respectively), and the QP equation is solved to first order with respect to the difference between the exchange-correlation part of the self-energy
, respectively), and the QP equation is solved to first order with respect to the difference between the exchange-correlation part of the self-energy 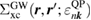 and the KS exchange-correlation (XC) function
and the KS exchange-correlation (XC) function 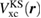 ,
,
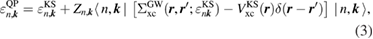
where the renormalization factor 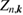 is defined as
is defined as
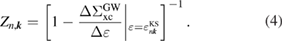
The correlation part 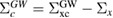 of the GW self-energy corresponds to the RE in equation (2). The matrix element of the correlation part is expressed as
of the GW self-energy corresponds to the RE in equation (2). The matrix element of the correlation part is expressed as

with
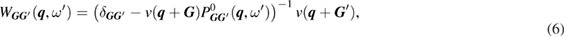

and

In order to explore the contributions of the relaxation effect from the core electrons, we separate the contribution to the polarization function 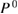 into the core contribution,
into the core contribution, 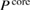 , and the valence contribution,
, and the valence contribution, 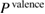 , as
, as
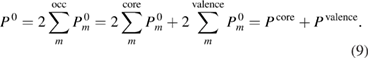
Then we define the core and valence contributions to the RE as 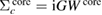 and
and 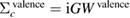 with
with  (
( core and valence). The corresponding
core and valence). The corresponding 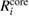 and
and 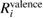 are obtained via equation (2). The core contribution,
are obtained via equation (2). The core contribution, 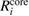 , represents the screening effect on a core hole orbital i caused by the core polarization.
, represents the screening effect on a core hole orbital i caused by the core polarization.
In addition to the standard GWA, we introduce the self-screening corrected GWA. The problem of the self-screening effect occurs in the final state relaxation process. This process can be considered as follows. For example, after a core hole is created in the 1s state, there is one occupied orbital and one empty orbital in the 1s state; only the other core electron can contribute to the screening of the 1s core hole. In view of this concern, the polarization function in the GWA gives an excess contribution to the RE. Therefore, we estimate the amount of the self-screening effect coming from, for example, i = C1s orbital itself. For this purpose, we introduce the self-screening corrected (SSC) porlarization function of the GWA as [32]

in place of 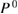 , where
, where 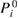 is given by equation (8). This polarization function constitutes the self-screening corrected GW self-energy
is given by equation (8). This polarization function constitutes the self-screening corrected GW self-energy 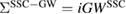 .
.
In this study, we used the all-electron mixed basis program, TOMBO, in which both plane waves (PWs) and numerical atomic orbitals (AOs) are used as basis functions [34, 35], although lattice constants were determined by the structure optimization within the LDA using CASTEP code [36, 37]. We selected silicon, diamond, β-SiC, BN, and AlP as target materials. All our one-shot GW calculations begin with the local-density approximation (LDA) calculation. We used the Perdew–Zunger's XC functional [38]. The KS wave functions and energy eigenvalues were substituted for the QP wave functions and energies of the GWA. All our calculations included semi-relativistic effects in the LDA level. The lattice constants, AOs, cutoff energies for PWs, 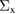 , and
, and 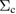 (
( ), the number of levels, calculated
), the number of levels, calculated 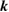 points, special
points, special 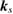 points and
points and 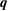 points in the irreducible zone are listed in table 1.
points in the irreducible zone are listed in table 1.
Table 1. Optimized lattice parameters, atomic orbitals (AOs), cutoff energies for plane waves (PWs), exchange ( ) and correlation (
) and correlation (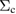 and
and 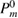 ), number of levels, and
), number of levels, and 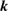 -points used in the GW calculations.
-points used in the GW calculations.
| Material | Structure | Lattice parameter (Å) | AO | 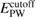 PW (eV) PW (eV) |
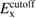 exchange (eV) exchange (eV) |
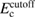 correlation (eV) correlation (eV) |
Number of levels | 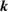 points, points, 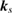 points, points, 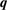 points points |
|---|---|---|---|---|---|---|---|---|
| Silicon | Diamond | a = b = c = 3.840 | Si1s2s2p | 2204 | 13 223 | 1469 | 520 | 8, 10, 8 |
| Diamond | Diamond | a = b = c = 2.500 | C1s | 2913 | 16 275 | 1180 | 360 | 8, 10, 8 |
| β-SiC | Zinc blend | a = b = c = 3.063 | Si1s2s2p, C1s | 3607 | 18 529 | 2308 | 560 | 8, 10, 8 |
| BN | Hexagonal | a = b = 2.491, c = 6.687 | (B,N)1s | 4750 | 18 998 | 2932 | 350 | 18, 9, 12 |
| AlP | Zinc blend | a = b = c = 3.863 | (Al,P)1s2s2p | 2579 | 16 125 | 1703 | 750 | 8, 10, 8 |
3. Results and discussion
3.1. Reference level problem
In order to make an accurate comparison with experimental XPS data, we should first consider the reference level problem [7] and redefine the CEBEs in non-metallic systems. In XPS experiments of crystalline systems, the BEs are commonly measured from the Fermi level 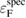 of the spectrometer and defined as
of the spectrometer and defined as 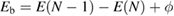 , where ϕ is the work function given by
, where ϕ is the work function given by  . (Here
. (Here 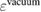 is the vacuum level.) For metals, the reference value ϕ of the standard sample can be directly used to deduce the experimental CEBEs, because the Fermi level is automatically adjusted; therefore, there is no ambiguity in the experimental CEBE values. However, in the case of insulators, there is the so-called reference level problem [7], which is the uncertainty of the ϕ value, because the Fermi level is not always the same between the insulator sample and the experimental device. Indeed, for the CEBEs,
is the vacuum level.) For metals, the reference value ϕ of the standard sample can be directly used to deduce the experimental CEBEs, because the Fermi level is automatically adjusted; therefore, there is no ambiguity in the experimental CEBE values. However, in the case of insulators, there is the so-called reference level problem [7], which is the uncertainty of the ϕ value, because the Fermi level is not always the same between the insulator sample and the experimental device. Indeed, for the CEBEs, 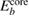 , there are many scattered values reported experimentally as shown by Walter et al [16] and the comparison with experimental values may not be so simple.
, there are many scattered values reported experimentally as shown by Walter et al [16] and the comparison with experimental values may not be so simple.
To avoid this problem, one should notice that the work function of the spectrometer is a constant value during measurements [2]. Hence, the valence band maximum (VBM), 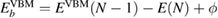 , can be used as a reference level instead of ϕ itself. The point is that
, can be used as a reference level instead of ϕ itself. The point is that 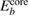 and
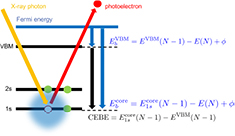
and 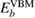 has the same work function ϕ and their difference does not contain ϕ, and a firm definition of the CEBEs is possible by using this difference as shown in figure 1. This valence band offset technique has often been used in XPS experiments to determine the band-gap discontinuity at semiconductor–semiconductor interfaces [39, 40].
has the same work function ϕ and their difference does not contain ϕ, and a firm definition of the CEBEs is possible by using this difference as shown in figure 1. This valence band offset technique has often been used in XPS experiments to determine the band-gap discontinuity at semiconductor–semiconductor interfaces [39, 40].
Figure 1. A schematic energy diagram of XPS. Shaded area illustrates the charge redistribution around a 1s core-hole orbital in the final state.
Download figure:
Standard image High-resolution image3.2. Standard GWA
Here, we compare the result of the GPP model (GPP) to that of the numerical integration (NI) in the CEBE. The CEBE(GPP) and CEBE(NI) using the polarization function 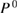 (see equation (9) above) are listed in table 2 together with the corresponding experimental values. The difference between the calculated CEBE(Cal) (Cal is either GPP, NI, or SSC; for SSC, see below) and experimental CEBE(Expt) are shown also in figure 2.
(see equation (9) above) are listed in table 2 together with the corresponding experimental values. The difference between the calculated CEBE(Cal) (Cal is either GPP, NI, or SSC; for SSC, see below) and experimental CEBE(Expt) are shown also in figure 2.
Table 2. Calculated relaxation energeis, Ri, and core electron binding energies, CEBEs, together with the experimental values of CEBEs, CEBE(Expt), in units of eV. The GPP and NI mean the result in the standard GWA using the generalized plasmon pole model and the numerical integration respectively. The SSC means the result in the self-screening corrected GWA using the numerical integration.
| Material | Orbital | Ri | CEBE (eV) | |||||
|---|---|---|---|---|---|---|---|---|
| (GPP) | (NI) | (SSC) | (GPP) | (NI) | (SSC) | (Expt) | ||
| Silicon | Si2p | 10.5 | 11.2 | 11.0 | 99.7 | 98.8 | 98.8 | 98.95 |
| Diamond | C1s | 12.5 | 14.0 | 13.4 | 288.7 | 283.7 | 284.1 | 284.44 |
| β-SiC | Si2p | 9.9 | 10.7 | 10.2 | 100.6 | 99.6 | 100.2 | 99.3 ± 0.1 |
| C1s | 15.0 | 15.5 | 14.2 | 282.4 | 280.4 | 281.3 | 281.45 |
|
| BN | N1s | 16.7 | 17.3 | 16.9 | 395.6 | 393.1 | 393.4 | 394.4 |
| B1s | 12.0 | 12.7 | 12.0 | 187.2 | 185.2 | 185.7 | 186.7 |
|
| AlP | Al2p | 8.7 | 9.6 | 9.2 | 73.2 | 72.2 | 72.5 | 72.43 ± 0.03 |
aReference [41], bReference [42], cReference [39], dReference [43], eReference [40].
Figure 2. Deviation of CEBE(GPP), CEBE(NI) and CEBE(SSC) from experimental values CEBE(Expt) for silicon, diamond, SiC, BN, and AlP, in units of eV.
Download figure:
Standard image High-resolution imageThe difference between the CEBE(GPP) and the CEBE(NI), i.e. CEBE(GPP) − CEBE(NI), is 0.9, 5.0, 1.0, 2.0, 2.5, 2.0, and 1.0 eV for Si2p (silicon), C1s (diamond), Si2p (β-SiC), C1s (β-SiC), N1s (BN), B1s (BN), and Al2p (AlP). This difference is not negligible at all. The GPP model assumes that the collective excitation at the plasma frequency plays a dominant role for the screening. However, the GPP model cannot be used to accurately estimate the dielectric function, due to the multi-peak structure of the energy loss function in the frequency domain. Our results clearly show that the GPP model is not appropriate to reproduce the numerical integration in the correlation part of the GW self-energy in the CEBE calculation. In what follows, the CEBEs and REs are evaluated by the numerical integration method only.
Next, we compare CEBEs(NI) with CEBEs(Expt). The difference between CEBE(NI) and CEBE(Expt), i.e. CEBE(NI) − CEBE(Expt), is −0.2 eV for Si2p of silicon; −0.7 eV for C1s of diamond; −1.1 eV and 0.3 eV for C1s and Si2p of β-SiC; −1.5 eV and −1.3 eV for B1s and N1s of BN; and −0.2 eV for Al2p of AlP. From these results, the GW calculation with the numerical integration has a general tendency to underestimate the experimental CEBEs except for Si2p of β-SiC. On the other hand, the GPP model overestimates the experimental CEBEs. The REs obtained with the numerical integration, R(NI), are larger than those obtained with the GPP model, R(GPP). The numerical integration contains the contributions from both the collective excitations and the individual ones. Consequently, the numerical integration makes the screening effect larger and the CEBEs shallower. The difference between CEBE(NI) and CEBE(Expt) is slightly larger than 1eV in C1s(SiC), B1s(BN), and N1s(BN), which means the underestimation of the CEBE within the standard GWA.
3.3. Core and valence contributions
The calculated REs of valence, core, and all-electron contributions are listed in table 3 and figure 3. From these results, we find the systematic tendency that 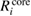 (NI) is smaller than
(NI) is smaller than 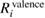 (NI) for 1s of second row elements, while
(NI) for 1s of second row elements, while 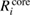 (NI) is comparable to or more than
(NI) is comparable to or more than 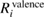 (NI) for 2s/2p of third row elements, Si and Al. This fact indicates that the relaxation effect accounted from only valence electrons such as in the frozen core orbital approximation is not enough and the all-electron calculation is inevitable for the CEBEs and the REs. In particular, for third row elements, the core electron contributions to the REs are very large. For core electron excitations, the final state is a highly excited state and can be screened even from core states. The important fact is that this tendency is obviously related to the number of core orbitals and can be easily understood as follows: third row elements have 1s, 2s and 2p core orbitals that can polarize, while second row elements have 1s core orbitals only. Both valence and core electrons play an important role in the RE and the all-electron calculation is required to obtain the reliable CEBEs.
(NI) for 2s/2p of third row elements, Si and Al. This fact indicates that the relaxation effect accounted from only valence electrons such as in the frozen core orbital approximation is not enough and the all-electron calculation is inevitable for the CEBEs and the REs. In particular, for third row elements, the core electron contributions to the REs are very large. For core electron excitations, the final state is a highly excited state and can be screened even from core states. The important fact is that this tendency is obviously related to the number of core orbitals and can be easily understood as follows: third row elements have 1s, 2s and 2p core orbitals that can polarize, while second row elements have 1s core orbitals only. Both valence and core electrons play an important role in the RE and the all-electron calculation is required to obtain the reliable CEBEs.
Figure 3. Calculated relaxation energies (REs) of valence (magenta colour), core (cyan colour), and all electron (yellow colour) contributions in units of eV.
Download figure:
Standard image High-resolution imageTable 3. Calculated results of the relaxation energy (RE), Ri, together with its core and valence contributions in the standard GWA with the numerical integration, 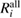 ,
, 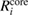 , and
, and 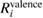 , in units of eV.
, in units of eV.
 |
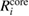 |
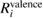 |
||
|---|---|---|---|---|
| (NI) | (NI) | (NI) | ||
| Silicon | Si2p | 11.2 | 6.6 | 7.7 |
| Si2s | 12.4 | 7.3 | 6.9 | |
| Diamond | C1s | 14.0 | 2.2 | 12.4 |
| β-SiC | Si2p | 10.7 | 6.2 | 6.6 |
| Si2s | 12.3 | 8.1 | 6.2 | |
| C1s | 15.5 | 2.5 | 13.8 | |
| BN | N1s | 17.3 | 2.0 | 16.1 |
| B1s | 12.7 | 3.1 | 10.5 | |
| AlP | Al2p | 9.6 | 5.6 | 5.7 |
3.4. Self-screening corrected GWA
As the reason of the underestimation of the CEBE in the GWA, it should be noted that the GWA does not rigorously satisfy Pauli's exclusion principle [31–33]. This problem is called the self-screening interaction. The unphysical contribution to the REs from the self-screening interaction may cause the underestimation of CEBE(NI). In order to discuss how much the self-screening interaction affects the CEBEs and the REs in XPS, we have carried out the self-screening corrected GW calculations in addition to the standard GWA.
The CEBEs evaluated with the numerical integration using either the self-screening corrected GWA or the standard GWA are listed in table 2. The self-screening corrected (SSC) CEBE, CEBE(SSC), of C1s for diamond and SiC, and of N1s and B1s for BN is much closer to the experimental CEBE(Expt) than the original CEBE(NI) is. In particular, CEBE(SSC) and CEBE(Expt) of C1s for SiC agree with each other within 0.1 eV. The difference between the calculated CEBE(Cal) and experimental CEBE(Expt) is shown in figure 2 also. Moreover, the RE, i.e. the correlation part of the self-energy, with the self-screening correction, Ri(SSC), is also listed in table 2. Compared with the RE, Ri(NI), in the standard GWA, the self-screening corrected RE, Ri(SSC), reduces the excess screening contribution, resulting in Ri(SSC) < Ri(NI). As seen in figure 2, the underestimation of CEBEs(NI) is improved by removing this excess RE. For the third row elements (Si2p and Al2p), slight changes by 0.2–0.5 eV are obtained by the self-screening correction. Although 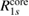 (NI) is smaller for the second row elements as seen in table 2, relatively larger changes by 0.4–1.3 eV appear in R1s by introducing the self-screening correction to the 1s core hole. This indicates the particular importance of the self-screening correction for the 1s orbital of the second row elements.
(NI) is smaller for the second row elements as seen in table 2, relatively larger changes by 0.4–1.3 eV appear in R1s by introducing the self-screening correction to the 1s core hole. This indicates the particular importance of the self-screening correction for the 1s orbital of the second row elements.
Consequently, the CEBEs evaluated in the SSC-GWA coincide with the experimental values within the absolute error range 1 eV. The accuracy of XPS measurements within 1eV was first achieved by Siegbahn [1], and since then the chemical shift analysis has been used by many researchers. The present study using the self-screening corrected GW approach also achieved the same accuracy for band-gapped crystals. As demonstrated in the Introduction, our Green's function method in MBPT is obviously more preferable than the conventional ΔSCF-DFT method. The accomplishment of the method to obtain such high accurate CEBEs from the quasiparticle approach is truly significant.
Finally, we will briefly discuss the reason why the GWA and SSC-GWA give a good result for CEBEs without introducing a explicit core hole like ΔSCF approaches. According to Hedin and Johannson [19], the ΔSCF-HF method corresponds to the second-order perturbation approximation with the HF approximation. Without doubt, this correspondence can be established for DFT also. To preserve only the direct term 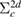 in second-order perturbation theory [19] is of course an approximation based on linear response theory. However, there is no guarantee that such a linear response calculation presents a good result for the CEBEs. From the total energy formulation of Galitskii–Migdal [44], the matrix element
in second-order perturbation theory [19] is of course an approximation based on linear response theory. However, there is no guarantee that such a linear response calculation presents a good result for the CEBEs. From the total energy formulation of Galitskii–Migdal [44], the matrix element ![$ \newcommand{\bra}[1]{\langle\,{#1}\,\vert\,} \newcommand{\ket}[1]{\,\vert\,{#1}\,\rangle} \bra{1s}\Sigma_{\rm xc}\ket{1s}$](https://content.cld.iop.org/journals/0953-8984/30/21/21LT01/revision2/cmaabdfeieqn067.gif) clearly means the expectation value of the electron–electron Coulomb interaction for the 1s orbital apart from the Hartree term. This expression guarantees that the 1s QP energy gives the total energy difference between the ground state and the excited state with the 1s core-hole orbital. Therefore, the matrix element
clearly means the expectation value of the electron–electron Coulomb interaction for the 1s orbital apart from the Hartree term. This expression guarantees that the 1s QP energy gives the total energy difference between the ground state and the excited state with the 1s core-hole orbital. Therefore, the matrix element ![$ \newcommand{\bra}[1]{\langle\,{#1}\,\vert\,} \newcommand{\ket}[1]{\,\vert\,{#1}\,\rangle} \bra{1s}\Sigma^{\rm GW}_{\rm xc}-\Sigma^{\rm 2d}-V_{\rm xc}^{\rm LDA}\ket{1s}$](https://content.cld.iop.org/journals/0953-8984/30/21/21LT01/revision2/cmaabdfeieqn068.gif) in the GWA represents the remaining electron-electron interaction, including the Fock exchange term and the higher-order direct terms beyond the second-order perturbation approximation. That is, our method includes the higher-order screening contributions beyond the second-order perturbation approximation, which enables us to obtain the excellent results.
in the GWA represents the remaining electron-electron interaction, including the Fock exchange term and the higher-order direct terms beyond the second-order perturbation approximation. That is, our method includes the higher-order screening contributions beyond the second-order perturbation approximation, which enables us to obtain the excellent results.
4. Conclusion
As a conclusion, we have calculated the core electron binding energies (CEBEs) and the core-hole relaxation energies (REs) in XPS using the standard or the self-screening corrected GW approaches as first-principles methods. Our investigation of the core and valence contributions to the RE in CEBEs showed that the core electron plays an important role in the RE as well as valence electrons, and the all-electron calculation is required to obtain the reliable CEBEs. It should be emphasized that the all-electron GW method using the full ω integration has the capability for the highly accurate prediction of XPS core electron binding energies without any empirical parameter. Compared to the experimental CEBEs, the CEBEs obtained by the numerical integration method, CEBEs(NI), have a tendency to slightly underestimate CEBEs(Expt) because of the overestimated REs. Therefore, we explored the self-screening effect on XPS core electron binding energies by introducing the self-screening corrected GW approximation. In general, the self-screening correction improves excess REs of the GWA, and the resulting CEBEs(SSC) are more accurate compared with the CEBEs of the standard GWA. We succeeded in obtaining CEBEs(SSC) which are different from CEBEs(Expt) by at most 1 eV (0.5 eV in average) without resort on any empirical parameter.
Although both the GWA and the ΔSCF methods are based on the definition of CEBEs and include the relaxation effects in the final state, there are significant differences between these frameworks at a theoretical level. Our approach based on the GWA includes not only the second-order direct term but also the exact Fock term and the higher-order contributions to the RE and the CEBE. Therefore, the relaxation effects are fully included in the electronic correlations in both the GWA and the SSC-GWA.
Acknowledgments
This work was supported by the HPCI promoted by MEXT for the use of the supercomputing systems at Hokkaido University, at IMR, Tohoku University, and at ISSP, the University of Tokyo (Project IDs. hp160072, hp160234, hp170268, and hp170190).