Abstract
Introduction of a gain medium in lossy plasmonic metamaterials reduces and compensates losses or even amplifies an incident light often with nonlinear optical effect. Here, optical gain in a pump-probe experimental setup is effectively calculated in the frequency-domain by approximating a gain material as an inhomogeneous medium. Spatially varying local field amplitudes of the pump and probe beams are included in the model to reproduce the inhomogeneous gain effect, in which population inversion occurs most strongly near the surface and decays along the propagation direction. We demonstrate that transmission spectra calculated by this method agree well with finite-difference time-domain simulation results. This simplified approach of gain modelling offers an easy and reliable way to analyze wave propagation in a gain medium without nonlinear time-domain calculation.
Export citation and abstract BibTeX RIS
1. Introduction
Research on artificially structured materials with exotic optical behavior, called metamaterials, has made immense progress for several decades enabling negative refractive index [1, 2], huge artificial magnetism [3] and super-resolution imaging [4, 5]. Being composed of subwavelength dimensions, metamaterials are usually described as a homogeneous medium with effective optical parameters such as effective permittivity and permeability despite the spatially non-uniform artificial nanostructures [6]. However, resonances are generally accompanied in their optical responses by extraordinary optical parameters such as negative or extremely high refractive index, which results in high optical losses. Since the losses hinder realization and practical application of metamaterials, a new mechanism to overcome the intrinsic limitations are in demand. Gain materials, including fluorescent dye and semiconductors, which absorb incident light and emit light with lower energy, have been reported to provide field amplification to compensate the losses [7]. The inclusion of such gain materials reduces the optical losses of metamaterials or even enables metamaterials with negative losses, in other words, amplification [8–10].
Gain materials are usually modelled as a four-level system [10–13], or they can be simply described as a homogeneous medium with effective gain permittivity [14, 15]. However, since the excitation of ground-level electrons to a higher level by the photon absorption occurs locally rather than globally, the gain effect is inherently not uniform throughout the whole gain medium. Instead, the attenuation of pump beam leads to a spatially non-uniform gain effect which makes the gain stronger near the front surface and degraded as the beam propagates. In this paper, we propose a new modelling approach of gain medium where an inhomogeneous gain effect is taken into account. Refractive index as a function of propagation distance and transfer matrix method (TMM) of electromagnetic fields in a multilayer system are combined to offer frequency-domain calculations of the gain in a four-level system. Our model consists of two steps. First, the interaction between a gain medium and the pump beam generates spatially non-uniform population difference. Then, for the given population difference profile, absorption and stimulated emission caused by the propagation of probe are simulated. Electric field amplitudes, population inversions and transmission spectra for a finite-thickness slab of an artificial gain material will be calculated and compared using (i) standard nonlinear four-level one-electron system, (ii) homogeneous gain and (iii) inhomogeneous gain approach. This approach will enable a simplified but relatively accurate calculation of wave propagation in gain materials.
2. Effective pump-probe experiment in a frequency-domain
In this paper, we will focus on pump-probe experiments where a high-intensity pump beam with narrow bandwidth excites the gain medium first, and then relatively weak and broadband probe beam is used to detect the nonlinear effects with a time delay  after the pump beam has been turned off. In the visible wavelength range, for example, the pump and the probe beam correspond to picosecond laser and white light source with femtosecond scale pulse length respectively, and the
after the pump beam has been turned off. In the visible wavelength range, for example, the pump and the probe beam correspond to picosecond laser and white light source with femtosecond scale pulse length respectively, and the  is on the order of tens of picosecond. To model the gain effect, we consider a four-level one-electron system (figure 1(a)) as it successfully describes gain effect in dye materials. Especially, Rhodamine 800 (refractive index
is on the order of tens of picosecond. To model the gain effect, we consider a four-level one-electron system (figure 1(a)) as it successfully describes gain effect in dye materials. Especially, Rhodamine 800 (refractive index  , total carrier density
, total carrier density  ) with an area
) with an area  is pumped by 4 picosecond pulse laser (
is pumped by 4 picosecond pulse laser ( ) with an amplitude of
) with an amplitude of  .
.
Figure 1. (a) Gain mechanism of a four-level system and (b) schematics of homogeneous gain assumption (top) and inhomogeneous gain assumption (bottom).  and
and  are the population inversion and effective permittivity due to the gain.
are the population inversion and effective permittivity due to the gain.
Download figure:
Standard image High-resolution image2.1. Local field effect in a gain medium
For a slab of a single uniform gain medium, the inhomogeneous gain effect originates from two factors, the attenuation of pump beam along the propagation direction and the oscillatory field intensity due to the interference between the forward and backward waves. The former results in non-uniform gain feature in a scale longer than the pump wavelength and the latter in the order of a half of the pump wavelength. Firstly, to ensure the optical pump generates inhomogeneous population inversion without reaching the saturation regime, the pump energy should be comparable to the maximum absorbable energy. Here, the maximum absorbable energy is the photon energy required to excite all electrons in the lower level ( ) to the higher level (
) to the higher level ( ) during propagation of one wavelength:
) during propagation of one wavelength:  , where
, where  and
and  are the absorption wavelength and the absorption angular frequency respectively. The pump beam energy is the incident power multiplied by the pulse length:
are the absorption wavelength and the absorption angular frequency respectively. The pump beam energy is the incident power multiplied by the pulse length:  where
where  is the vacuum permittivity and
is the vacuum permittivity and  is the light speed in free space. For the parameters chosen for our pump-probe experiment (see above), the maximum absorbable energy
is the light speed in free space. For the parameters chosen for our pump-probe experiment (see above), the maximum absorbable energy  is not negligible compared with the pump energy
is not negligible compared with the pump energy  . It implies that the pump loses a considerable amount of its energy by exciting the lower level electrons to the higher states when it enters the slab and the attenuated pump beam excites fewer electrons as it propagates through the slab. In addition, since the electric field at a given point is the sum of forward and backward travelling waves, it will show an oscillatory spatial profile rather than a modest change in amplitude. Therefore, a slab of gain material should be described as an inhomogeneous medium with spatially varying gain parameters as shown in figure 1(b) instead of a uniform effective medium with constant population inversion
. It implies that the pump loses a considerable amount of its energy by exciting the lower level electrons to the higher states when it enters the slab and the attenuated pump beam excites fewer electrons as it propagates through the slab. In addition, since the electric field at a given point is the sum of forward and backward travelling waves, it will show an oscillatory spatial profile rather than a modest change in amplitude. Therefore, a slab of gain material should be described as an inhomogeneous medium with spatially varying gain parameters as shown in figure 1(b) instead of a uniform effective medium with constant population inversion  and gain permittivity
and gain permittivity  .
.
2.2. Relation between the electric field and effective gain permittivity
Our four-level system is assumed to have only two optical transitions: absorption (transition  ) and stimulated emission (transition
) and stimulated emission (transition  ). Three non-radiative decay processes to the right below each level are added to describe temporal dynamics of carrier densities. Time evolution of carrier densities in four-level systems follows these coupled equations [11]:
). Three non-radiative decay processes to the right below each level are added to describe temporal dynamics of carrier densities. Time evolution of carrier densities in four-level systems follows these coupled equations [11]:
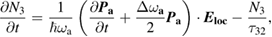
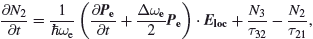

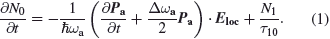
Here, the subscript a and e indicate absorption and emission respectively.  and
and  are the resonance angular frequencies,
are the resonance angular frequencies,  and
and  are the full bandwidths,
are the full bandwidths,  and
and  are the polarization densities for absorption and emission respectively.
are the polarization densities for absorption and emission respectively.  is carrier density in the
is carrier density in the  th level (
th level ( ) and the total carrier density
) and the total carrier density  is given by
is given by  .
.  is the lifetime of carriers for the non-radiative decay transition from
is the lifetime of carriers for the non-radiative decay transition from  to
to  . Other non-radiative terms such as successive decays are assumed to be negligible.
. Other non-radiative terms such as successive decays are assumed to be negligible.  is a local electric field given by
is a local electric field given by ![$[\left( \varepsilon +2 \right)/3]\boldsymbol{E}$](https://content.cld.iop.org/journals/0953-8984/30/6/064003/revision2/cmaaa473ieqn039.gif) from the Lorentz approximation, not the average electric field [16].
from the Lorentz approximation, not the average electric field [16].
In equation (1), the terms that contain the polarization densities  and local electric field
and local electric field  correspond to excitation of the ground-level electrons and stimulated emission for
correspond to excitation of the ground-level electrons and stimulated emission for  and
and  respectively while the other terms represent non-radiative relaxation processes. Gain materials such as dyes or semiconductors which are good candidates to be implemented in metamaterials have long
respectively while the other terms represent non-radiative relaxation processes. Gain materials such as dyes or semiconductors which are good candidates to be implemented in metamaterials have long  compared to
compared to  and
and  [17], so that electrons in the third and first level rapidly decay to the lower level, but stay in the second level. The second level is sometimes called as a metastable level for its relatively long lifetime [12]. In other words, electrons in the first and the third level relax fast whereas they stay in the second level longer compared to the time delay (
[17], so that electrons in the third and first level rapidly decay to the lower level, but stay in the second level. The second level is sometimes called as a metastable level for its relatively long lifetime [12]. In other words, electrons in the first and the third level relax fast whereas they stay in the second level longer compared to the time delay ( ). Therefore, a probe beam experiences the gain materials in which the electrons relaxed from the highest level stay in the metastable level giving rise to a population inversion.
). Therefore, a probe beam experiences the gain materials in which the electrons relaxed from the highest level stay in the metastable level giving rise to a population inversion.
To calculate the absorption and gain effect, population difference of two optical transitions  and
and  should be known. In the remaining part of this section, we will find a formula of the spatial-dependent population difference and then show that effective permittivity for the pump and the probe beam can be expressed in terms of electric field.
should be known. In the remaining part of this section, we will find a formula of the spatial-dependent population difference and then show that effective permittivity for the pump and the probe beam can be expressed in terms of electric field.
For a ground state before the excitation, the initial condition is given by  . As a pulse of the pump beam propagates in the gain medium, the carrier densities vary in time and then after the pump is turned off and before the probe is turned on, they reach a state which is different from the initial state. Since the carrier densities in all level vary slowly due to the scale mismatch of the lifetime and time delay between the pump and the probe, we approximate this state as a stationary state. In the absence of the probe beam, the carrier density in each level at the stationary state can be obtained by applying
. As a pulse of the pump beam propagates in the gain medium, the carrier densities vary in time and then after the pump is turned off and before the probe is turned on, they reach a state which is different from the initial state. Since the carrier densities in all level vary slowly due to the scale mismatch of the lifetime and time delay between the pump and the probe, we approximate this state as a stationary state. In the absence of the probe beam, the carrier density in each level at the stationary state can be obtained by applying  to the second and third equations of (1). Then the carrier densities for
to the second and third equations of (1). Then the carrier densities for  at the stationary state follow
at the stationary state follow

Additionally, the time evolution of  can be also expressed as a simplified form in terms of stimulated transition probability
can be also expressed as a simplified form in terms of stimulated transition probability  [12].
[12].
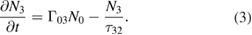
We will now derive the expression for the spatial-dependent  starting from a formula
starting from a formula  [14] where
[14] where  is a local intensity and
is a local intensity and  is the absorption cross section. The Lorentzian term in the absorption cross section in [14] can be neglected by assuming the narrow bandwidth of the pump beam. The radiative decay rate
is the absorption cross section. The Lorentzian term in the absorption cross section in [14] can be neglected by assuming the narrow bandwidth of the pump beam. The radiative decay rate  is given by Fermi's golden rule [18]:
is given by Fermi's golden rule [18]:  . Here,
. Here,  is dipole length when the dipole is oriented parallel to the incident polarization. Note that
is dipole length when the dipole is oriented parallel to the incident polarization. Note that  and
and  are the permittivity and the speed of light in the medium, both of which depend on the propagation distance
are the permittivity and the speed of light in the medium, both of which depend on the propagation distance  . In other words, the absorption cross section and the intensity are both functions of propagation distance. However,
. In other words, the absorption cross section and the intensity are both functions of propagation distance. However,  is dependent only on the field amplitude, but not on refractive index as
is dependent only on the field amplitude, but not on refractive index as  are cancelled out. Therefore, spatially varying population difference is explicitly determined by the local field amplitude. Note that the population difference is only dependent on the wave propagation direction but uniform with respect to the wavefront plane due to plane symmetry.
are cancelled out. Therefore, spatially varying population difference is explicitly determined by the local field amplitude. Note that the population difference is only dependent on the wave propagation direction but uniform with respect to the wavefront plane due to plane symmetry.
We introduce a time-independent variable  to effectively describe the stimulated transition probability in the frequency domain using slowly varying envelope approximation. The electric field of pump has the Gaussian envelope with an oscillating term of its angular frequency:
to effectively describe the stimulated transition probability in the frequency domain using slowly varying envelope approximation. The electric field of pump has the Gaussian envelope with an oscillating term of its angular frequency:  where
where  is center of the Gaussian envelope and
is center of the Gaussian envelope and  . First, ignoring the fast oscillating term
. First, ignoring the fast oscillating term  , a crude approximation will be taking average of the Gaussian envelope in time, which leads to effective electric field amplitude as
, a crude approximation will be taking average of the Gaussian envelope in time, which leads to effective electric field amplitude as 
 . Then, we can obtain
. Then, we can obtain  by substituting
by substituting  instead of
instead of  into
into  and multiplying additional
and multiplying additional  to take into account the square term of
to take into account the square term of  . To sum up,
. To sum up,  is used instead of
is used instead of  to remove time dependence. Finally, by incorporating equation (2) with (3), we obtained the expression for the population difference of both absorption and emission which are defined as
to remove time dependence. Finally, by incorporating equation (2) with (3), we obtained the expression for the population difference of both absorption and emission which are defined as  and
and  :
:
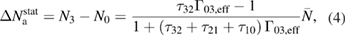
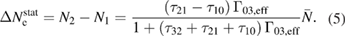
Meanwhile, the population densities are governed by the following equations of motion for  and
and  [14].
[14].
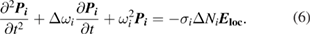
The coupling constant  of
of  to the local electric field is provided by
to the local electric field is provided by  . The coupling constant and the population difference determine the strength of the coupling between the induced polarization density and the local electric field and thereby effective gain permittivity. Given that pump beam usually has a picosecond scale pulse length for a narrow bandwidth and the relatively broadband probe is in tens of femtoseconds scale for visible range, both pump and probe beams can be considered as continuous waves for their relatively long pulse lengths compared to the wavelength. Therefore, we can simplify the partial differential equations to get effective permittivity using the time-harmonic assumption.
. The coupling constant and the population difference determine the strength of the coupling between the induced polarization density and the local electric field and thereby effective gain permittivity. Given that pump beam usually has a picosecond scale pulse length for a narrow bandwidth and the relatively broadband probe is in tens of femtoseconds scale for visible range, both pump and probe beams can be considered as continuous waves for their relatively long pulse lengths compared to the wavelength. Therefore, we can simplify the partial differential equations to get effective permittivity using the time-harmonic assumption.
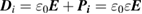
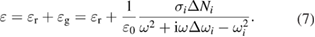
The total relative permittivity  is a sum of relative permittivity
is a sum of relative permittivity  of the gain material itself and effective gain permittivity
of the gain material itself and effective gain permittivity  with Lorentzian line shape.
with Lorentzian line shape.
To calculate the changes of the population difference and permittivity in the gain medium, let us consider the propagation of the pump beam which corresponds to absorption process by exciting electrons in the lowest level to the higher levels. Strictly speaking, the excitation of electrons by the pump is a transient process, which requires nonlinear time-domain simulation. In other words, the effective gain permittivity is a function of both time and propagation distance. To remove the time dependence, we used population difference for absorption by averaging the population difference of the initial state ( ) and that of the stationary state (
) and that of the stationary state ( ). Then, we can effectively describe the interaction between the pump and the gain slab as a wave propagation in an inhomogeneous medium with the following effective gain permittivity.
). Then, we can effectively describe the interaction between the pump and the gain slab as a wave propagation in an inhomogeneous medium with the following effective gain permittivity.

Here, the negative sign of the population difference indicates a loss. Note that the contribution of optical transition  can be disregarded here as the pump beam does not overlap with emission wavelength. On the other hand, the propagation of probe beam is a more complicated process which involves both absorption and stimulated emission. The probe beam usually has broad wavelength range centered at the emission wavelength. In other words, the probe contains waves with absorption wavelength as well as those with emission wavelength. The wave with absorption wavelength works as if it is another pump during the propagation of the gain medium. It excites the electrons in
can be disregarded here as the pump beam does not overlap with emission wavelength. On the other hand, the propagation of probe beam is a more complicated process which involves both absorption and stimulated emission. The probe beam usually has broad wavelength range centered at the emission wavelength. In other words, the probe contains waves with absorption wavelength as well as those with emission wavelength. The wave with absorption wavelength works as if it is another pump during the propagation of the gain medium. It excites the electrons in  level to
level to  level and decays. In contrast, the wave with emission wavelength induces radiative emission of electrons in
level and decays. In contrast, the wave with emission wavelength induces radiative emission of electrons in  level to
level to  level. Therefore, the probe beam experiences a medium with two Lorentzian permittivities, one is positive (loss from absorption) and the other is negative (gain from stimulated emission).
level. Therefore, the probe beam experiences a medium with two Lorentzian permittivities, one is positive (loss from absorption) and the other is negative (gain from stimulated emission).
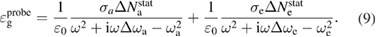
Here, the spatially non-uniform parameters in effective gain permittivity of both pump and probe are population difference  and
and  , which can be easily obtained by the local field amplitude as stated earlier. All the other parameters are constant. Therefore, we can get effective permittivity if the field amplitude is known. Importantly, the change of the carrier densities caused by the probe can be neglected as the intensity of the probe beam is several orders of magnitude smaller than that of the pump beam.
, which can be easily obtained by the local field amplitude as stated earlier. All the other parameters are constant. Therefore, we can get effective permittivity if the field amplitude is known. Importantly, the change of the carrier densities caused by the probe can be neglected as the intensity of the probe beam is several orders of magnitude smaller than that of the pump beam.
So far, a frequency-domain approach has been introduced for an effective modelling of the gain medium in a pump-probe experiment with narrowband laser pump and broadband probe beams. Based on stationary state assumption, time-harmonic assumption and slowly varying envelope approximation, we proposed an approach to calculate effective gain permittivity in frequency-domain. In the next section, we will discuss how to describe the propagation of the pump and probe beams through the spatially varying effective medium.
2.3. Transfer matrix method for an inhomogeneous medium
To calculate the electromagnetic fields in the inhomogeneous medium, we employ the transfer matrix method for a dielectric multilayer film [19, 20]. Wave propagation in a medium with spatially varying permittivity can be readily calculated by taking a limit of thickness to zero in the dielectric multilayer problem. Suppose a dielectric multilayer slab is placed between two semi-infinite media labelled as  and
and  (figure 2). We assume that the dielectric media are non-magnetic (
(figure 2). We assume that the dielectric media are non-magnetic ( ). The slab is composed of
). The slab is composed of  layers (
layers ( ), where
), where  th layer has refractive index
th layer has refractive index  , impedance
, impedance  and thickness
and thickness  , and the total gain slab has thickness
, and the total gain slab has thickness  . Then the electric and magnetic fields at the layer
. Then the electric and magnetic fields at the layer  and the layer
and the layer  are related by transfer matrix
are related by transfer matrix  according to continuity equation [20]:
according to continuity equation [20]:
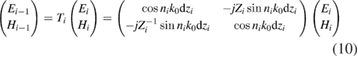
for  with
with  and the initial condition
and the initial condition  . Taking a limit of
. Taking a limit of  for
for  gives the first order differential equation with zero diagonal terms. It is solvable for a constant or simple form of refractive index. However, since the refractive index of each layer is dependent on the electric field amplitude as described in the previous section, wave propagation in the inhomogeneous gain medium requires a TMM calculation with an infinitesimal thickness. If
gives the first order differential equation with zero diagonal terms. It is solvable for a constant or simple form of refractive index. However, since the refractive index of each layer is dependent on the electric field amplitude as described in the previous section, wave propagation in the inhomogeneous gain medium requires a TMM calculation with an infinitesimal thickness. If  is known,
is known,  can be calculated by the equations (8) and (9) for pump and probe beams respectively. Then
can be calculated by the equations (8) and (9) for pump and probe beams respectively. Then  can be obtained from the equation (10). Consequently, the electromagnetic fields in the layer
can be obtained from the equation (10). Consequently, the electromagnetic fields in the layer  is given by
is given by
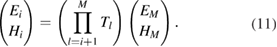
Figure 2. Wave propagation in a medium of spatially varying optical parameters.
Download figure:
Standard image High-resolution imageCombined with equations (8) and (9), the equation (11) fully determines the electromagnetic fields at every dielectric layer. Furthermore, we can get transmission and reflection spectra by  and
and  respectively.
respectively.
2.4. Numerical simulations and comparison
We performed a numerical pump-probe experiment with a gain slab using (i) nonlinear calculation in time-domain, (ii) homogeneous gain and (iii) inhomogeneous gain approach. Rhodamine 800 of thickness  , which corresponds to ten times of the pump wavelength, is used and modelled as 500 layers with an equal thickness. Since the overall thickness is comparable to the wavelength, the slab acts as a Fabry–Perot resonator with oscillatory transmission spectrum. Therefore, the thickness is determined to have a unity transmission at the emission wavelength to exclude the effect from multiple reflections. We also assume the gain material to have zero imaginary part of the refractive index in the absence of pump to distinguish gain effect from the attenuation from inherent losses.
, which corresponds to ten times of the pump wavelength, is used and modelled as 500 layers with an equal thickness. Since the overall thickness is comparable to the wavelength, the slab acts as a Fabry–Perot resonator with oscillatory transmission spectrum. Therefore, the thickness is determined to have a unity transmission at the emission wavelength to exclude the effect from multiple reflections. We also assume the gain material to have zero imaginary part of the refractive index in the absence of pump to distinguish gain effect from the attenuation from inherent losses.
The simulation parameters are chosen as follows [11]: 

 and
and  . The incident pump amplitude is set as
. The incident pump amplitude is set as  . For time-domain calculations, we used Lumerical finite-difference time-domain (FDTD) solution [21] with an additional plugin. In the FDTD simulation, the pulse lengths of pump and probe beams are set to
. For time-domain calculations, we used Lumerical finite-difference time-domain (FDTD) solution [21] with an additional plugin. In the FDTD simulation, the pulse lengths of pump and probe beams are set to  and
and  respectively with
respectively with  delay between the pump and probe.
delay between the pump and probe.
Electric fields calculated by the homogeneous gain analysis, inhomogeneous gain approach and the FDTD are shown in figures 3(a)–(c) respectively. In the homogeneous assumption, the field amplitude of pump exhibits standing wave-like amplitude originated from the interference of waves propagating forward (transmitting) and backward (reflecting) direction as shown in figure 3(a). Instead of the oscillatory amplitude, incident field amplitude is used to calculate population inversion, which leads to constant population inversion which is overestimated throughout the slab (figure 3(d)). On the contrary, local field effect included in inhomogeneous gain analysis gives rise to distinct characteristics. The pump attenuates as well as oscillates during the propagation as shown in figure 3(b). Affected by the local field amplitude, the population inversion also decays with oscillations during the propagation which agrees well with the FDTD calculation results (figure 3(f)).
Figure 3. (a)–(c) Pump amplitude and (d)–(f) population inversion  normalized by the total carrier density, calculated by homogeneous gain approach (left column), inhomogeneous gain approach (middle column) and FDTD (right column), respectively.
normalized by the total carrier density, calculated by homogeneous gain approach (left column), inhomogeneous gain approach (middle column) and FDTD (right column), respectively.
Download figure:
Standard image High-resolution imageDue to the modulated population inversion, real and imaginary part of the refractive index ( ) at emission wavelength varies in space for the inhomogeneous gain model and FDTD whereas the refractive index is constant for the homogeneous gain model (figures 4(a)–(c)). Since the amplitude of the incident probe is much smaller than that of the pump, we simulated two cases where the absorption of probe, which corresponds to the first term in the right-hand side of equation (9), is neglected (middle column) and included (right column). In both cases, the imaginary part of the refractive index increases implying the diminished gain effect during the propagation. When the absorption is not included, the imaginary part of the refractive index is negative over the entire slab meaning that the probe beam will experience only the gain effect. Accordingly, the electric field amplifies gradually despite the negative gradient. On the other hand, if the absorption is included, the imaginary part of the refractive index becomes positive after some point and the electric field starts to decay. It means that even at the emission wavelength, absorption occurs and even exceeds the stimulated emission after several wavelengths.
) at emission wavelength varies in space for the inhomogeneous gain model and FDTD whereas the refractive index is constant for the homogeneous gain model (figures 4(a)–(c)). Since the amplitude of the incident probe is much smaller than that of the pump, we simulated two cases where the absorption of probe, which corresponds to the first term in the right-hand side of equation (9), is neglected (middle column) and included (right column). In both cases, the imaginary part of the refractive index increases implying the diminished gain effect during the propagation. When the absorption is not included, the imaginary part of the refractive index is negative over the entire slab meaning that the probe beam will experience only the gain effect. Accordingly, the electric field amplifies gradually despite the negative gradient. On the other hand, if the absorption is included, the imaginary part of the refractive index becomes positive after some point and the electric field starts to decay. It means that even at the emission wavelength, absorption occurs and even exceeds the stimulated emission after several wavelengths.
Figure 4. (a)–(c) Refractive index at emission wavelength where  and
and  are the real and imaginary part, and (d)–(f) the probe amplitude, calculated by homogeneous gain approach (left column), by inhomogeneous gain approach while neglecting (middle column) and including (right column) the absorption of the probe beam, respectively.
are the real and imaginary part, and (d)–(f) the probe amplitude, calculated by homogeneous gain approach (left column), by inhomogeneous gain approach while neglecting (middle column) and including (right column) the absorption of the probe beam, respectively.
Download figure:
Standard image High-resolution imageTo check the functionality of our inhomogeneous gain approach, the transmission spectra of the probe beam are calculated with the homogeneous gain analysis, inhomogeneous gain approach and the FDTD for three different slab thickness:  ,
,  and
and  (figure 5). These thicknesses are chosen to give unity transmission without gain, but the scheme is not limited to this condition and applicable for an arbitrary thickness. Transmission spectra obtained from homogeneous gain approach is indicated by lines with asterisk marks with an oscillating feature due to the multiple reflections. Here, the gain effect is overestimated especially when the slab is several orders thicker than the pump wavelength. Although the inhomogeneous gain approach with neglected probe absorption shows reduced gain (dotted lines), which is similar to FDTD calculation (solid lines), it fails to explain low transmission near the absorption wavelength originating from the excitation of electrons by the probe beam. However, if the probe absorption is included (dashed lines), the calculated transmission contains both the gain at emission wavelength and the loss at absorption wavelength. A notable feature here is that the inhomogeneous gain calculated in frequency-domain perfectly reproduces transmission spectra simulated by nonlinear time-domain calculation. A numerical pump-probe experiment which has been regarded to be available at only time-domain can be performed in the frequency-domain either for this simple slab geometry.
(figure 5). These thicknesses are chosen to give unity transmission without gain, but the scheme is not limited to this condition and applicable for an arbitrary thickness. Transmission spectra obtained from homogeneous gain approach is indicated by lines with asterisk marks with an oscillating feature due to the multiple reflections. Here, the gain effect is overestimated especially when the slab is several orders thicker than the pump wavelength. Although the inhomogeneous gain approach with neglected probe absorption shows reduced gain (dotted lines), which is similar to FDTD calculation (solid lines), it fails to explain low transmission near the absorption wavelength originating from the excitation of electrons by the probe beam. However, if the probe absorption is included (dashed lines), the calculated transmission contains both the gain at emission wavelength and the loss at absorption wavelength. A notable feature here is that the inhomogeneous gain calculated in frequency-domain perfectly reproduces transmission spectra simulated by nonlinear time-domain calculation. A numerical pump-probe experiment which has been regarded to be available at only time-domain can be performed in the frequency-domain either for this simple slab geometry.
Figure 5. Transmission spectra calculated by homogeneous gain approach (lines with asterisk), inhomogeneous gain approach by neglecting the probe absorption (dotted lines), inhomogeneous gain approach by considering the probe absorption (dashed lines) and FDTD (solid lines), respectively. The thickness of the slab is (a)  , (b)
, (b)  and (c)
and (c)  .
.
Download figure:
Standard image High-resolution image3. Conclusion
In conclusion, optical gain in a pump-probe experiment is calculated on the basis of an inhomogeneous gain approach and compared with an FDTD analysis and the usual approach assuming a spatially homogeneous gain distribution. By considering absorption of the incident photons' energy, we include the local field distribution into the effective gain approach, allowing us to relax the constant field assumption. Successful reproduction of the oscillatory and decaying shape of the pump and probe beam is presented. We also demonstrate that the inhomogeneous gain approach can be readily used to calculate transmission spectra of a probe beam for a slab with a finite thickness, which shows excellent agreement with the FDTD results. The current study can generally be applied to complex 3D gain geometries, but for comparison with the transmission matrix method is here restricted to 1D slabs. We anticipate that the simplified analysis for gain materials can also be performed for loss-compensated metamaterials for real applications, providing speedy and accurate modelling of gain materials such as dyes or semiconductors.
Acknowledgments
This work is financially supported by the National Research Foundation grants (NRF-2017R1E1A1A03070501, NRF-2015R 1A5A1037668, CAMM-2014M3A6B3063708) funded by the Ministry of Science, ICT and Future Planning (MSIP) of the Korean government and part-funded by the European Regional Development Fund through the Welsh Government. MK acknowledges Global PhD Fellowships (NRF-2017H1A2A1043204) from NRF-MSIP of Korean government.






