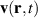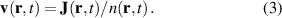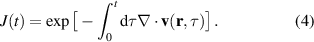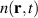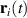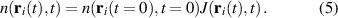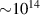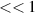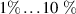Abstract
Imaging the microscopic world in real space and real time is a grand challenge of science. In the landscape of time-resolved imaging techniques, laser-induced electron diffraction (LIED) has recently shown to be a promising candidate to push the frontiers of ultrafast molecular imaging. In this work, we review the main achievements of LIED research in terms of experimental results and advanced modelling. We also envision interesting perspectives toward the future advancement of time-resolved LIED imaging.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction: watching the microscopic world
Advancing our capabilities of imaging matter is one of the most compelling challenges of science. This general statement is true for mostly any discipline, and represents the main goal of many branches of research today, ranging from astronomy to microscopy. In the latter case, imaging the microscopic world predominantly aims at solving molecular structures at the atomic level [1, 2]. By doing so, indeed, we can disclose those fundamental interactions between neighbouring atoms that govern, for example, chemical reactions or the functionality of materials [3, 4]. This general context naturally translates into a technical requirement: since the typical bond lengths are in the order of picometers (1 pm m), microscopic imaging calls for a spatial resolution of 1 or few pm to accurately solve even small variations of inter-atomic distances.
However, spatial resolution is normally not sufficient to provide a comprehensive picture of the microscopic world. Indeed, matter continuously undergoes dynamical processes on a vast range of timescales, and—for this reason—temporal resolution is another highly desirable ingredient of imaging spectroscopy. In particular, while macrostructural dynamics such as protein folding can take milliseconds (1 ms s) to occur, the dynamics of individual molecular bonds can be extremely faster. For example, light diatomic molecules such as H2 can rotate in space on sub-picosecond time scales, while interatomic distances—even in large polyatomic molecules—typically vibrate on femtosecond time scales (1 fs s) [5]. The electrons surrounding atoms move on even faster time scales, typically between few femtoseconds and attoseconds (1 as s) [6]. Watching atoms and electrons in real-time is promising to understand—and potentially control—a plethora of phenomena occurring in nature. Building upon these considerations, advanced imaging of the microscopic world ultimately aims at solving molecular dynamics with attosecond and picometer resolution simultaneously.
In the last decades, several methods have been developed or advanced in this direction. Ultrafast electron diffraction (UED), for example, employs a combination of ultrashort laser pulses and multi-KeV electron pulses to initiate the dynamics in the sample and to probe the following structural change, respectively [1, 7–11]. UED can be employed on a vast range of targets, ranging from gas-phase molecules to biological systems and materials. While providing atomic spatial resolution with sub-picometer accuracy, the temporal resolution is typically in the order of hundreds of fs, being fundamentally determined, and limited, by energy spread, group velocity mismatch (between electrons and photons) and space charge effects. However, such hindrances can be circumvented with single-electron pulses [12] or optical wavefront tilt methods [13], allowing for temporal resolutions down to few fs or even a.s. Analogous results have been obtained by electron microscopy and electron crystallography [1]. Outstanding results have been also obtained with UED in the MeV energy regime [14, 15]. As an alternative to electron pulses, ultrafast x-ray diffraction and serial femtosecond crystallography (SFC), instead, employ ultrashort and high-photon-energy light pulses, typically from synchrotron radiation or x-ray free-electron lasers (XFEL) [16]. In particular, SFC is emerging as an excellent tool to image three-dimensional macro-molecular structures [16], providing a temporal resolution that is mostly limited by the duration of the XFEL pulses, i.e. few tens of fs, and a typical picometer spatial resolution. However, scattering cross sections for x-rays are orders of magnitude lower than for electrons, thus requiring large photon fluxes (normally photons/pulse).
In the landscape of ultrafast imaging methods, x-ray photoelectron diffraction (XPD) has produced remarkable results [17–19]. In XPD, an electron is extracted upon x-ray absorption from a localised inner-shell orbital in the vicinity of an emitter atom. Before reaching the detector, the electron can be scattered by the surrounding atoms, thus carrying a diffractive signature of the molecular structure. In particular, the diffraction pattern consists in the interference between unscattered and scattered portions of the detected electron wavepacket. In this way, transient molecular structures can be studied in a pump-probe scheme, for example, upon excitation by an optical laser pulse [20]. We note that intense, femtosecond x-ray pulses were also employed for Coulomb explosion imaging of aromatic heterocyclic organic compounds [21].
Recently, lightwave-driven scanning tunnelling microscopy pushed the frontiers of advanced imaging, showing the possibility of controlling structural dynamics in single-molecule switches [22]. With this method, well-established tunnelling probe techniques are combined to the near-field action of a single-cycle THz laser pulse in order to apply ultrafast atomic-scale forces to the target. By doing so, imaging with picometer and femtosecond resolution was achieved, promoting lightwave scanning tunnelling microscopy as one of the most promising tools to interrogate and coherently control quantum systems at their natural time scale.
In addition to the above-mentioned imaging methods, laser-induced electron diffraction (LIED) has shown the be a promising candidate to push the frontiers of ultrafast molecular imaging [23–28]. The seminal concept of LIED falls into the field of strong-field physics, i.e. the discipline addressing the interaction of matter with ultra-intense lasers [29]. In the last two decades, such a branch of research has demonstrated the capability to investigate dynamical processes in atoms, molecules, and condensed-phase targets, with unprecedented spatiotemporal resolution. Figure 1 shows the prototypical three-step interaction between a strong-field laser (peak intensity W cm−2) and an atom. The electric field of the laser is strong enough to bend the atomic coulomb potential and to extract a valence electron through tunnel ionisation (step 1). Then, the free electron is accelerated by the vector potential of the laser in vacuum (step 2) and eventually driven back to the parent ion due to the sign change of the driving electric field (step 3). Such three-step dynamics occur within a fraction of the optical cycle of the driving laser, i.e. on a time of scale of a few fs for near infrared wavelengths. The recollision with the parent ion predominantly results in radiative recombination or electron rescattering [30]. We note that both recombination and rescattering are low-probability events, with cross sections that are typically several orders of magnitude lower than the probability of strong-field ionisation. The rescattering process, for example, can be quantitatively described by the scattering cross-section and the spread of the electron wavepacket after ionisation [31]. The radiative recombination generates high-order harmonics (HHG) of the driving laser frequency, in the typical form of weak, extreme ultraviolet, attosecond light bursts. As an alternative to recombination, a portion of the photoelectron wavepacket can be rescattered during recollision and further accelerated by the value of the vector potential at recollision, and a coherent diffraction pattern of the ion is encoded in the rescattered electrons (green waveform in figure 1) [32, 33]. Such a self-diffraction process, namely LIED, presents several peculiarities with respect to UED. First, the photoelectron wavepacket produced in a strong-field photo-interaction typically has sub-fs duration. Consequently, extremely large current densities are obtained at recollision, with values close to 1011 A cm−2. The spatial resolution, instead, is closely related to the de Broglie wavelength of the photoelectrons at recollision, , with the maximum photoelectron kinetic energy Ek depending on the ponderomotive potential of the driving field as . In this context, mid-infrared ultraintense lasers can accelerate the photoelectrons to hundreds-eV energy, allowing LIED experiments to be performed with spatial resolution of few tens of pm and accuracy down to 5 pm [24].
Figure 1. Pictorial sketch of the prototypical three-step strong-field photo-interaction. The intense laser field bends the potential of the target and initiates tunnelling ionisation (step 1). The photoelectron is then accelerated by the external laser field (step 2) and eventually brought back to the parent ion (step 3). The rescattering event occurring at recollision encodes a coherent diffraction pattern of the parent ion in the detected photoelectron wave packet. The three-step dynamics occurs for every half optical cycle of the laser field.
Download figure:
Standard image High-resolution imageSuch electron energies are several orders of magnitude lower than in UED, making LIED particularly suitable for imaging light atoms. For example, at these low impact energies hydrogen presents higher values of scattering cross section with respect to those at the high energies employed in UED [34]. However, we note that remarkable results have been recently obtained in locating hydrogens in crystals and liquids with high-energy electron diffraction [14, 35].
In this context, LIED has the potential to accomplish the above-mentioned goal of imaging the microscopic world with attosecond and picometer resolution. However, the LIED approach also presents several limitations. First, with this method only ions, and not neutral molecules, can be imaged. Second, the use of ultraintense lasers is potentially disruptive and invasive for the target. Third, while increasing the driving wavelength allows for accelerating the photoelectrons to higher kinetic energies and thus achieving better spatial resolution, the rescattering cross section rapidly decreases with the driving wavelength () [36], typically resulting in very weak high-spatial-resolution LIED patterns to be analysed. Furthermore, competing processes such as double ionisation or electron impact ionisation can contaminate the LIED signal, thus requiring the experiments to be performed with coincidence detection to be mostly background free [37]. As a consequence of the above-mentioned limitations, the use of LIED as been confined so far to small gas-phase molecules, while the extension to more complex targets appears to be intrinsically challenging.
In this work, we will review the most important achievements of LIED and envision the main future perspectives. In the first section, we will present the main experimental results that were obtained in the last years. The second section will focus on the most recent theoretical models that are employed in LIED and the main challenges related to them. In the last part of the paper, we will outline new research directions that promise to overcome the above-mentioned limitations of LIED and further advance this imaging method.
2. Experimental achievements of LIED
In 1996, Zuo, Brandauk, and Corkum investigated strong-field-driven rescattering as a tool to image molecular structures with femtosecond temporal resolution [38]. In this context, they simulated the above-threshold-ionisation (ATI) patterns of photoelectrons produced in molecular hydrogen. They observed that the two-dimensional ATI pattern produced in atomic H upon photo-ionisation by an intense (I W cm−2) visible-light femtosecond pulse differed from the same pattern produced in H2. Furthermore, the interference fringes emerging in the ATI from the molecular target appeared to be sensitive to the internuclear distance. This was a clear demonstration that the ATI photoelectrons carried a signature of the molecular structure similarly to a coherent diffraction pattern. Furthermore, given the ultrafast nature of the laser-driven process, it was also clear that such an approach was promising to image molecules with high temporal resolution. Building upon these observations, Zuo and coworkers dubbed the method LIED.
Following the work by Zuo et al intense research focused on the possibility of using the returning electron wavepacket in a strong-field interaction to image atoms and molecules. Morishita et al demonstrated that the differential scattering cross sections from a variety of atomic ions can be identified in the photoelectron angular distribution, in what they called 'back-rescattering ridges' [39]. This concept was experimentally proved by Ray and coworkers [40]. In their work, they employed few-fs 800 nm-wavelength laser pulses with peak intensity up to W cm−2 to photoionise rare gas atoms (Xe, Kr, Ar) in the above-threshold ionisation regime. Then, the angle-resolved momentum distribution of the photoelectrons was collected in a double-side time-of-flight spectrometer. In the classical picture of the ATI physics, the photoelectrons are driven by the intense laser after ionisation, and their final kinetic energy is a function of ponderomotive energy U of the laser field. In particular, a portion of the photoelectron wavepacket can be driven back to the parent ion, rescatter on it, and be further accelerated by the external field up to 10 U kinetic energy [41]. The 10 U cutoff consists of electrons that are back-rescattered from the ion, thus constituting the ridges described in [39]. By analysing the angular features in this high-energy portion of the photoelectron spectrum, Ray et al were able to retrieve the differential scattering cross sections for the rare gas atoms under study, setting an important benchmark for the development of self-diffraction imaging. However, it was the advent of table-top optical parametric amplifiers (OPA) that promoted LIED as a concrete tool for molecular structure retrieval. Indeed, OPA-based down-conversion sources can produce intense mid-infrared laser light that—as mentioned in the introduction—is key to accelerate photoelectrons up to hundreds of eV in a strong-field interaction. The high-energy electrons accelerated by mid-infrared lasers deeply penetrate into the target and rescatter against the core-lying electron states of the parent ion. On the one hand, the diffraction pattern imprinted in such rescattered electrons is not (or only very weakly) affected by the valence electron distribution. On the other hand, the de Broglie wavelength of the rescattered electrons is small enough to image molecular bonds with atomic spatial accuracy. In 2012, Blaga and coworkers employed a tunable OPA source for the strong-field photoionsation of molecular nitrogen and molecular oxygen [24]. In particular, by exposing the molecules to 2.3 µm-wavelength laser pulses with peak intensity W cm−2, the photoelectron achieved eV kinetic energy upon recollision, with a corresponding de Broglie wavelength of pm. In this condition, the bond lengths were imaged at the recollision instant with an uncertainty of around 5 pm. In addition, a time-resolved interrogation of the molecular structure was achieved by exploiting the spectral tunability of the driving laser. The concept is sketched in figure 2. At constant rescattering photoelectron momentum, the time interval between ionisation and rescattering is proportional to the optical cycle and thus to the wavelength of the driving laser. By focusing on back-rescattered electrons and tuning the wavelength from 1700 nm to 2300 nm, for example, the bond length of the ion is probed at fs and fs, respectively. By doing so, a large change in the O–O equilibrium distance was imaged in oxygen with respect to the smaller variation of the N–N in nitrogen, as a clear signature of the anti-bonding highest occupied molecular orbital (HOMO) of O2 in contrast with the bonding HOMO of N2. This result was the first example of time-resolved molecular imaging with 5 pm and 2 fs spatiotemporal resolution.
Figure 2. Sketch of time-resolved LIED with variable driving wavelength as implemented in [24]. The time interval between ionisation and rescattering is proportional to the optical cycle and thus to the wavelength of the driving laser. By tuning the wavelength, the parent ion is revisited and interrogated in a time-resolved fashion. The maximum photoelectron kinetic energy at recollision ranged from 125 eV to 230 eV in the wavelength region between 1700 and 2300 nm.
Download figure:
Standard image High-resolution imageFollowing the pioneering achievement by Blaga et al many efforts have been done in the last years to extend the capabilities of LIED-based imaging. For example, a polyatomic molecule was imaged for the first time by Pullen et al by probing the C–H and C–C bonds in acetylene [37]. In this work, the strong-field photo-interaction was driven by an optical-parametric chirp-pulsed-amplifier source with 3.1 µm wavelength and 160 KHz repetition rate. The molecules were weakly aligned in the laboratory frame by employing an auxiliary 1.7 µm laser, and the photoelectrons were measured in coincidence with the corresponding ionic fragments. As mentioned in the introduction, the detection in coincidence allows for the selection of only those photoelectrons that are correlated with the parent ion, thus discarding the spurious contribution of competing processes such as double ionisation and electron impact ionisation. Furthermore, the combination of this detection with molecular alignment is key to studying the self-diffraction imaging in the molecular frame. i.e. with a well-defined position of the molecular coordinates with respect to the laboratory frame. Exploiting such an approach, the authors selectively probed the molecular structure with the molecular axis parallel or perpendicular with respect to the polarization axis of the laser field, showing a potential attosecond and picometer spatiotemporal resolution.
Following the same experimental protocol as in [37], Wolter and coworkers employed LIED to image a prototypical chemical reaction, i.e. the dissociation of the acetylene dication C2H into H+ and C2H+ [42]. This reaction is known to represent one of the fastest expected proton motions and can occur through different pathways. It is interesting to note that the authors analysed the CH bond dynamics for the molecule aligned perpendicularly or parallel to the ionising laser field, and observed that a much larger, and asymmetric, elongation occurs for parallel alignment with respect to perpendicular alignment, as a clear signature of the strong laser pulling apart the molecule for the parallel case. In the latter case, indeed, the molecular potential energy surfaces are dressed by the strong field, while for perpendicular alignment a quasi-field-free condition is obtained. This analysis leads to important considerations: on the one hand, molecular-frame LIED allows for circumventing—at least partially—the disruptive action of the external laser field by selecting the molecular orientation for which the dressing of the molecular states is minimised; On the other hand, it also allows—at least at a certain extent—for controlling the molecular dissociation.
Building upon the above mentioned promising results, many works recently investigated the possibility of extending the capabilities of LIED. For example, the molecular structure of polyatomic molecules was imaged [43], and non-adiabatic dynamics such as the Renner–Teller effect in small gas-phase molecules were interrogated with attosecond and picometer resolution [44]. LIED has been also used to image the structural deformation of the fullerene C60 in the presence of an intense mid-infrared laser [45]. Besides the increasing target complexity, intense research has also been pursued in order to refine the molecular structure retrieval from the angle-resolved photoelectron momentum distribution that is detected in a LIED measurement. Typically, experimental differential scattering cross sections (DCS) are extracted from LIED data for a range of scattering angles with respect to the laser polarisation at a given scattering electron energy [32]. Then, the molecular structure is retrieved by minimising the difference between the experimental DCS and theoretical DCS calculated from the independent atom model ((IAM), see next section for details). The Fourier-transform LIED (FT-LIED) method [46], instead, demonstrated that the DCS can be also retrieved along the backward scattering direction at a range of scattering electron energies, and the Fourier transform of the DCS directly corresponds to the bond length distribution. Recently, Sanchez et al discussed the advantage of extracting two-dimensional DCS from LIED data, as a way to increase the accuracy and simplicity of the structure retrieval [47].
While the above-mentioned studies are promoting LIED as a highly competitive scheme in the landscape of time-resolved molecular imaging, we note that important works have recently investigated the fundamental concept of photoelectron-driven self-diffraction, in particular addressing the following query: at which extent does the photoionisation dynamics influence the following rescattering and, thus, the diffractive pattern imprinted in the detected photoelectron spectra? In the conventional picture of LIED, the electron wavepacket that is revisiting the parent ion can be well approximated to a distribution of plane waves, on which the scattering phase is then imprinted through recollision. This concept paved the way for quantitative rescattering theory (QRS) [33] and allows the measured photoelectron momentum distribution to be easily mapped into DCS. However, it is also known that the ionised molecular orbital can shape the rescattered portion of the photoelectron wave packet [48]. Starting from the above-mentioned query, Schell and coworkers recently investigated the strong-field electron rescattering in aligned 1,3-butadiene molecules [49]. In particular, the molecule was photo-ionised through two different continuum channels corresponding to different, characteristic nodal structures. Then, the channel-resolved photoelectron momentum distributions were measured with a particular attention on the rescattering tail. The authors observed that the electron return probability is dependent on the molecular frame and carries a clear signature of the structure of the ionised molecular orbital. The findings by Schell et al unambiguously demonstrated that the rescattering dynamics depends on the ionisation channel and on the angle between the molecular frame and the polarisation axis of the driving laser field. Furthermore, the result is not limited to any peculiar feature of butadiene, indeed any molecule showing nodal planes in the ionised orbitals is expected to trigger the same qualitative photoelectron dynamics.
In the framework of investigating the impact of the ionisation step on the self-diffraction dynamics, the strong-field rescattering in aligned carbonyl sulphide (OCS) molecules was investigated by Trabattoni et al [50]. In the experiment, an ensemble of OCS molecules was adiabatically aligned in the laboratory frame within a narrow angular confinement, i.e. , by using a linearly polarised, 500 ps laser pulse, centred at 800 nm. The molecules were aligned in two different configurations, shown in figure 3(a), with the molecular axis along the Y and Z axes, named parallel and perpendicular alignment, respectively. A second 1300 nm laser pulse was employed to singly ionise the OCS molecules. The produced molecular-frame angle-resolved photoelectron spectra were recorded in a velocity map imaging spectrometer with its detector parallel to the XY plane for the two molecular alignments. In order to better analyse the rescattering tails at high momentum, the photoelectron momentum distributions were angularly integrated within a cone of with respect to the Y axis and converted to an energy scale in units of the ponderomotive energy of the ionising laser. The obtained curves are shown for parallel (blue) and perpendicular (red) alignment in figure 3(b), where the distribution between 2 U and 10 U is known to be dominated by rescattered electrons [41]. We note that in this region the perpendicular/parallel ratio of the two area-normalised spectra (green) shows a predominance of yield for perpendicular alignment up to the cutoff. In order to quantitatively evaluate the cutoffs, the authors used the turning-point of the signal drop, i.e. the minimum of the first derivative, at large longitudinal momenta, as shown figure 3(c). The first minimum represents the drop of direct electrons and it was around 2 U for both alignments. The second minimum, instead, behaves differently for the two alignments. While it is located around 10 U for perpendicular alignment, as expected from the classical theory, the cutoff is shifted down to a value around 8.5 U for parallel alignment. This experimental observation was supported and confirmed by time-dependent density-functional theory (TDDFT) calculations. As a main result of the work, the authors assigned the reduced cutoff to the contribution of the molecular potential onto the electron emission and the propagation until recollision. To do so, semiclassical trajectory simulations based on the Ammosov–Delone–Kraǐnov (ADK) tunnelling theory [51] in combination with a simple man propagation [52] were performed to track the molecular-frame electron dynamics during the strong-field interaction. The result of the trajectory computations is reported in figure 4, where the final absolute momentum acquired by the electron after photoionisation is plotted as a function of the recollision phase for perpendicular (figure 4(a)) and parallel (figure 4(b)) alignment. The broad peaks appearing every half cycle of the electric field at phases close to , correspond to the recollision events (also called revisits) of the electron with the molecular cation when the laser field's vector potential is maximum. The conventional analysis of LIED experiments approximates the photoelectron rescattering to occur only at the first revisit, for which the electron acquires the largest momentum [41]. Looking at figure 4, it is evident that such an assumption is only valid for perpendicular alignment. In this case, indeed, the large momentum is reached at the first rescattering event, corresponding to an asymptotic kinetic energy around 10 U as observed in the experiment. We note that the yield of the first peak is anyway attenuated by the nodal plane of the HOMO orbital perpendicular to the molecular axis. For parallel alignment, instead, the first rescattering event is strongly suppressed and most of the large-momentum electrons come from the third revisit at a phase of . Therefore, the maximum achievable momentum is smaller, corresponding to a final kinetic energy of ∼9 U , in agreement with the experimentally observed reduced cutoff for parallel alignment. In this framework, the reduction of the cutoff is mainly driven by the molecular potential: first, the node of the HOMO along the laser polarisation imprints an angle on the electron emission; then, this angle not only reduces the total rescattering cross section [48], but in particular prevents the electron from rescattering at the first revisit; however, the Coulomb attraction of the ionised molecule forces the electron to stay in the interaction region and to recollide at later revisits (see the sketched trajectory in figure 4(b) with respect to the simpler case of perpendicular alignment in figure 4(a)). On the one hand, this result demonstrates that the rescattered photoelectron wavepacket carries a clear signature of the electronic structure at ionisation. On the other hand, it points out that the molecular frame photo-electron cutoff carries crucial time information. As reported in figure 4, the most probable rescattering event, and thus the time lapse between ionisation and recollision, is strongly dependent on the angle between the molecular axis and the polarisation axis of the driving laser, as well as the final kinetic energy of the photoelectron. The work by Trabattoni et al [50] highlighted that the molecular potential sets a complex time-energy encoding in the electron dynamics.
Figure 3. (a) Parallel and perpendicular alignments of OCS molecules and (b) corresponding energy distributions. In (a), the charge distribution of the HOMO of neutral OCS is reported for the two alignments. The electric field of the ionising laser is depicted as E and it is polarised along the Y axis of the laboratory frame. (c) Time derivative of the energy distributions to evaluate the cutoff. Reproduced from [50]. CC BY 4.0.
Download figure:
Standard image High-resolution imageFigure 4. Final absolute photoelectron momentum as a function of the recollision phase (bottom) and revisit order (top) for (a) perpendicular and (b) parallel alignment, calculated with ADK-SM. The colour scale maps the electron counts at every momentum-phase point. The dashed black circles highlight the largest-momentum electrons at the most probable revisit order for the two alignments. The solid black line depicts the external electric field. The insets give pictorial representations of molecular-frame electron trajectories, where the cardinals represent the revisit order. For parallel alignment, the yield of the first revisit is strongly depleted due to the initial angle imprinted in the photoelectron trajectory by the HOMO. Indeed, due this angle the electron is far way from the molecule at the time of the first revisit. Reproduced from [50]. CC BY 4.0.
Download figure:
Standard image High-resolution imageWe want to emphasise that the studies of strong-field electron rescattering presented in [49, 50] were obtained at lower wavelength ( nm) and smaller U than what is considered an optimal 'LIED regime'. Indeed, LIED is typically performed in the regime of deep tunnelling, i.e. Keldysh parameter , and core recollision, i.e. returning electron kinetic energy eV. These conditions are usually obtained for wavelengths µm and U values of at least a few tens of eV [53]. Thus, one may wonder about the relevance of the results of [49, 50] for LIED. Therefore, we note that a similar effect as the one discussed by Trabattoni et al [50] was also observed by some of us for experiments with a 2 µm driving laser wavelength [54], with experimental parameters that fully put the experiment into the regime of 'diffraction' [24]. Indeed, the same conditions were employed to accurately characterise the molecular structure of OCS, yielding bond-lengths with a precision and accuracy of better than ±5 pm [43]. For these reasons, we can conclude that the aspects discussed in [49, 50] are completely relevant not only in the framework of strong-field electron rescattering but also for the interpretation of time-resolved LIED experiments. Thus they can also be exploited to develop a new generation of attosecond LIED spectroscopy, in which single recollision events are selected and controlled.
3. Modelling and interpreting LIED data
From the stand point of LIED theory, the approaches employed in the literature are largely based on the concepts developed to study strong-field phenomena. Models and approximations employed by the community since the nineties, such as, the scattering theory based on the three-step model [30] in the single active electron approximation (SAE) and the strong field approximation (SFA) [55], are the principal tenets for the analysis and the interpretation of the data.
One of the most notable theory based on these ideas is the QRS [33] where the analogy of LIED with conventional electron diffraction is carried out in the presence of the external field. According to QRS theory, for a molecule oriented in space with angles denoted with θ, the photoelectron distribution, , in the rescattering energy region (2U ) can be factorised as the product of the momentum distribution of the returning electrons, , and the field-free elastic differential cross-section of the molecular cation, :
In this theory the connection between the final electron momentum, k, measured in the laboratory frame and the rescattered one, kr , in the laser polarization frame is estimated classically observing that an electron rescattering in the presence of the field acquires an additional momentum from the vector potential A of the laser field at the return time , i.e. . This is the mechanism at the origin of the characteristic displaced rings observed in the high-energy photoelectron angular distribution. QRS theory offers a way to retrieve the elastic DCS directly from the high-energy photoelectron spectra under the assumption that, in LIED, the momentum distribution of the returning electrons have a weak energy dependence and that the angle distribution can be accurately estimated from ADK tunnelling theory . DCS obtained with this approach appear in good agreement with theoretical predictions especially for atoms. Calculating DCS for molecules is, in general, a much more complicated matter. This task can, however, be greatly simplified in the IAM where the potential seen by the incident electron is approximated by the sum of the potentials from the individual atoms. This approximation is justified for high-energy electrons because scattering occurs only near the centre of each atom in the molecule and thus the molecule can be approximated by a collection of independent atoms. Within the IAM the molecular DCS is obtained as the square modulus of the total scattering amplitude as
where N is the number of atoms in the molecule, fα is the scattering amplitude of the αth atom located at , and q it the momentum transferred in the scattering process. From the formula, the total scattering amplitude clearly depends on the internuclear distance. The simple IAM formula for the DCS in conjunction with the cheap computational cost needed to obtain the photoelectron distribution thanks to the QRS theory factorisation makes apparent how, with the appropriate inversion algorithm, it is in principle possible to retrieve molecular bond lengths from LIED [56, 57].
One should note that QRS theory is formulated in the energy domain, and therefore it is not suitable to access spatial and temporal informations such as, for instance, the distribution of the rescattering wavepacket or the number of revisits before recollision. Semiclassical approaches are more suited to deal with this kind of problems. This is because, to a large extent, these informations rely on a classical picture of the electron motion in the continuum and the fact that its whereabouts can be decomposed into classical trajectories which, once acquired and carefully analysed, can be used to gain understanding on the intricate details of the rescattering events. Broadly speaking, semiclassical methods rely on the combination of quantum-mechanical and classical pictures. Typically, they proceed with the generation of a number of initial conditions determining positions and velocities of the electrons based on tunnelling theory, followed by the propagation of electrons along trajectories determined by the field. Reconstruction of the final momentum distribution is obtained by collecting the contribution of all the trajectories weighted by a phase accounting for quantum-mechanical interference. In this class of models, the two most important approaches employed to describe the electron's phase in the vacuum are the so-called Coulomb-corrected SFA [58] and the semiclassical approximation to the quantum propagator [59]. These methods have successfully been employed in the literature to explain many strong-field experiments in atoms [60–62]. In the vast majority of cases, however, electrons in the vacuum are propagated in the presence of the electrostatic force field of a cation approximated by a single point charge which is not enough to capture the features of typical LIED experiments aimed at molecular geometry retrieval. This trend has changed in recent works, notably from some of the authors, where the motion of the electrons in the electrostatic potential of the cation molecule was fully included in the classical evolution to investigate LIED in indole [63] and OCS [50] molecules—results from this last one are reported in figure 4.
To catch up with the current trend of performing LIED experiments on increasingly large and complex polyatomic molecules requires the use of models capable to capture the interplay between the interaction of the electrons with the external field and with each other. Even the assumption that the ionisation takes place from the single HOMO invoked in the SAE may be questioned already in relatively small molecules, for instance where many occupied orbitals have nearly degenerate binding energies. Strong-field ionisation of polyatomic molecules often involves ionisation from different orbitals as shown, for instance, in HHG experiments on aligned CO2 [64] and strong-field ionisation experiments performed in hydrocarbons [65].
These are some of the reasons why ab-initio approaches, i.e. with no free parameters, based on theories such as TDDFT have been attracting the interest of the community. The appeal of TDDFT is that it reformulates the many-electrons time-dependent Shrödinger equation (TDSE) into a set of manageable, albeit non-linear, single-particle propagation equations for each electron in the system, represented by the so-called Kohn–Sham (KS) orbitals , that interact with each other via an exchange and correlation potential, , which is a functional of the total time-dependent density, [66, 67]. It is an exact reformulation of the time-dependent many-body problem that, to perform calculations, requires approximations for of which the exact functional form is unknown. In practice, employing the adiabatic approximation for vxc , i.e. making it dependent only on the instantaneous density, opens the door to the use of all the approximations that have been developed over the last few decades for time-independent DFT [68]. Strictly speaking, KS orbitals are mere mathematical objects serving the purpose of calculating the density which is the only quantity that is guaranteed to have physical meaning. However, more often then not occupied KS orbitals in DFT likewise in TDDFT can be considered as physically meaningful objects based on the track record of their positive comparison with molecular orbitals obtained from more sophisticated quantum chemistry approaches. Similar considerations hold for quantities that are calculated as a function of time-dependent KS orbitals like the photoelectron probability distribution [69], which can be obtained as a straightforward multi-orbital extension of the time-dependent surface flux (t-SURFF) method derived for the TDSE of a single electron [70]. With this technique it was shown in a LIED experiment on CF3I and explained with TDDFT that the photoelectron angular distribution results from the contribution of multiple orbitals [71]. A clear picture of such multi-orbital contribution is presented in figure 5 where one can appreciate how the orbital contributions is modulated by the relative orientation of the molecular axis and the field polarisation. In particular in the aligned geometry one can see that there is a substantial portion of the spectrum, in the high energy region, that is dominated by the HOMO-1 orbital–cfr. figures 5(b) and (d). One should note that ab-initio simulations of LIED experiments in polyatomic molecules are computationally quite heavy because one of the main advantages of TDDFT, that the computational cost scales linearly with the number of atoms, is counteracted by the fact that the largest computational burden of the simulation is spent to describe electrons' dynamics in the vacuum surrounding the system where they sit before rescattering. In addition, having to deal with polyatomic molecules means that little or no spatial symmetry is available to exploit and therefore the problem has to be faced fully in three-dimensions. On a more technical note, this means that state-of-the-art open boundary conditions such as infinite range complex scaling [73], already difficult to implement in spherical or spheroidal coordinates, can become too cumbersome and one has to fold back to simpler absorbers [74] or develop alternative strategies [75]. All considering, fully three-dimensional simulations of strong-field ionisation dynamics can be carried out without too much effort on molecules as large as C60 [76].
Figure 5. Simulation of multi orbital contribution in LIED from CF3I molecules. From the figure it is evident how in the configuration where the field and the molecule are aligned, (b), the spectrum is a combination of the HOMO and HOMO-1 orbitals, panels (c) and (d), whereas in the anti-aligned configuration, panels (g) and (h), the contribution from the HOMO is dominant. Adapted from [72] with permission from the Royal Society of Chemistry.
Download figure:
Standard image High-resolution image4. Future perspectives of time-resolved LIED
The experimental and theoretical work described in the previous two sections highlighted the unique capabilities of LIED to image matter with extremely high spatiotemporal resolution. However, LIED has been so far benchmarked only in small gas-phase molecules, and its competitiveness in the landscape of molecular imaging is still questionable. Novel approaches are required to overcome the intrinsic limitations of strong-field-driven self-diffraction and intense research is currently pursued towards this aim. In this context, we dedicate the last section of this review to envision a few interesting perspectives towards the advancement of LIED-based imaging and the theoretical approaches employed to model it.
4.1. Exact trajectories
Purely quantum-mechanical approaches like TDSE in the SAE and full TDDFT are powerful tools to study LIED, however what they provide in accuracy they lack in simplicity of interpretation, since crucial informations that are naturally accessible in trajectory-based approaches are not easily extracted from the time dependence of a sloshing wavefunction. There is however, in principle, the possibility to keep the best of both worlds by deriving trajectories from the time-dependent wavefunction with Bohmian mechanics [77]. Bohmian mechanics is an exact reformulation of time-dependent quantum mechanics where the wave function dynamics is substituted with particle trajectories, the Bohmian trajectories, from which every quantum-mechanical observable can be, in principle, calculated [78, 79]. The trajectories can be generated by tracer particles following a velocity field, , obtained from the probability current density according to the guidance equation
Compared with classical trajectories, Bohmian trajectories have naturally built-in quantum-mechanical effects such as wavefunction interference and non-local effects. This last ones in particular are responsible for the peculiar feature that trajectories are not allowed to cross one another and therefore constitute a univocal map, deterministically connecting different spatial portions of the density at all times. Quantum-mechanical interference is recovered by co-propagating along each trajectory the volume element whose inflation and deflation dynamics is determined by the gradient of the velocity field with the equation (J stands for Jacobian):
As an example in figure 6(a) we show the Bohmian trajectories underlying the time evolution of the charge density of a one-dimensional hydrogen model system under the effect of an ultrashort and strong pulse. From the figure it is apparent how the trajectories give a nice picture of the scattering event and how they avoid crossings. Quite crucially, the density can be reconstructed from the trajectory picture, as shown in figure 6(b), combining the value of sampled on the trajectory, , at time zero with the co-propagated time-dependent volume element according to the equation
Figure 6. Trajectory-based description of the time evolution of quantum mechanical states based on Bohmian mechanics. (a) Time evolution of the probability density for a soft-core one-dimensional hydrogen model is represented as a density plot together with a selection of trajectories (green lines), , calculated propagating the guidance equation obtained from the time-dependent wavefunction. (b) Snapshot of the time dependent density (orange) at 100 a.u.—dashed line in panel (a)—and the density reconstructed on the trajectories (green).
Download figure:
Standard image High-resolution imageFrom the figure, one can also appreciate how the quantum-mechanical interference of reflected and transmitted waves resulting in a strong oscillation of the density is perfectly captured by the trajectory picture. It must be noted that the numerical integration of the guidance equations, needed to obtain the trajectories, can become challenging in the region of space where the density vanishes and the velocity field diverges: this is especially relevant for scattering processes, like the case illustrated in figure 6(b), where quantum-mechanical interference of transmitted and reflected wavepackets give rise to strong modulation of the density. In spite of the challenges, over the years there have been a number of applications of Bohmian mechanics on the strong-field physics of atoms, for instance, to investigate: the role of quantum potentials in above threshold ionisation [80], the contribution of long and short trajectories in HHG [81, 82], the tunnelling time and exit in ionisation processes [83] and Coulomb effects in attoclock measurements [84]. Perhaps because of the numerical challenges mentioned above, applications of Bohmian trajectories to LIED are still missing, but considering the advantage that a quantum-mechanically exact trajectory picture could contribute to the field we believe it would be well worth the effort.
4.2. Increasing target complexity
One of the main challenges for LIED is to image complex systems, and intense research has been recently performed in this direction [63, 85]. In this context, one of the main obstacles comes from the intrinsic nature of strong-field photo-interactions that are invasive and potentially destructive. Indeed, under the action of such intense electric fields the energy states of the target are bent through Stark-shift effects [86], and consequently the structure, as well as the electronic dynamics, are altered. In general, the dynamical response of the target is modified by the external laser [42]. While such an invasive interaction may be acceptable for specific observables in robust systems such as a single atom or a small molecule, it could jeopardize the study of large biological molecules or the real-time investigation and control of the electronics in a complex system. In these systems, indeed, the interaction with strong laser fields typically leads to high probability for multiple ionisation and fragmentation, making the use of LIED for imaging the parent ion really challenging or even impossible. Furthermore, the typical laser intensity employed in LIED experiments, i.e. W cm−2, exceeds the damage threshold of most of solid targets, preventing the use of self-diffraction to investigate, for example, ultrafast surface phenomena. In principle, such a problem can be partially circumvented by increasing the wavelength of the driving field. Indeed, longer wavelengths allows lower intensities to be employed without decreasing the ponderomotive energy and, consequently, the spatial resolution of the LIED measurement. However, also this approach presents severe constraints. First, larger driving wavelengths correspond to lower rescattering cross sections, as described in the introduction. Second, the laser intensity–in any case–needs to be sufficiently high to trigger tunnelling ionisation. As an alternative to simply decrease the laser intensity, two-colour schemes can be used. In this context, a large literature exists about two-colour strong-field driven high-harmonic generation [87–91], while two-colour LIED is mostly unexplored. A possible implementation of this concept is depicted in figure 7. An ultrashort UV laser pulse [92] photoionises the target at threshold, i.e. promoting an electron in the continuum with extremely low kinetic energy ( eV). Then, a synchronised IR laser is used to accelerate the photoelectron until recollision and rescattering. Such a scheme replaces the strong-field tunnelling ionisation with a one- or two-photon transition, depending on the ionisation potential of the target and the photon energy of the UV pulse. The duration of the UV pulse should be much shorter than the optical cycle of the IR laser, but this requirement is compatible with currently available UV sources [92]. Furthermore, the properties of the IR laser (such as wavelength and intensity) can be tuned with much more flexibility with respect to the scheme of figure 1. The use of this scheme is promising to circumvent the above-mentioned problem of imaging large molecules with low ionisation potential. Indeed, if the strong-field ionisation is replaced by a one- or two-photon transition, such a ionisation step minimises multiple ionisation and fragmentation. Then, the acceleration and recollision can be driven by an IR laser at moderate intensity and long wavelength to preserve a large ponderomotive energy while, again, minimising multiple ionisation and fragmentation. This approach can enable the use LIED on complex molecules with sufficiently large cation signals. With respect to the conventional LIED approach, one has to consider that one- or two-photon threshold ionisation processes have a lower cross section than tunnelling ionisation. However, typically ionisation by UV absorption allows to excite of the molecules in a sample. Once the photoelectron is created the IR pulse can drive it really efficiently in the continuum, since no further photon absorption is required. In this framework, the rescattering rate for such a two-colour scheme can be expected to be one or two orders of magnitude lower than conventional one-colour LIED (for the same wavelength of the IR field). However, the expected low fragmentation rate for the two-colour approach would allow experiments to be performed without coincidence imaging, thus allowing to acquire tens of electrons/shot instead of the typical 0.1 event/shot rate required by coincidence; and this can even still be performed at very high repetition rates [93]. Furthermore, the two-colour scheme would open the path to self-diffraction experiments on extended systems such as, e.g. a solid lattice, in which the rescattering rate may be much larger than in the single atom/molecule case.
Figure 7. Two-colour three-step dynamics to be compared with the conventional one-colour strong-field scheme depicted in figure 1. The short UV pulse is employed to assist the first step and replace the tunnelling ionisation. To be compared with figure 1.
Download figure:
Standard image High-resolution imageBesides the limitations due to the strong-field interaction, the applicability of LIED to complex systems is also hindered by the way LIED data are conventionally analysed and interpreted. Indeed, while the QRS theory enables the extraction of field-free elastic electron scattering cross-sections and the retrieval of the molecular structure from the photoelectron momentum distribution, in the presence of multiple bond lengths the QRS retrieval quickly becomes inaccurate due to the difficulty in identifying a unique solution in the multi-dimensional solution space. Although FT-LIED promised to overcome this limitation, a multi-peak fitting procedure is required anyway to retrieve the bond lengths and it becomes ambiguous when the structure of the distribution function is too rich. Furthermore, all the currently available methods are based on the comparison of LIED data with a precalculated structure. This is accompanied by the need of computing a large set of molecular configurations in different orientations and with high resolution.
In order to overcome this limitation, it has been recently proposed to employ a machine learning (ML) algorithm to analyse LIED data [57]. In this work, the authors demonstrated the capability of accurately extracting the three-dimensional molecular structure of large molecules such as fenchone (C10H16O) with sub-picometer resolution. The ML approach avoids the use of fitting procedures or ab-initio calculations and only relies on the interpolation and learning capabilities of ML. Such a method significantly reduces the required molecular configurations to train the system for a much larger solution space, and it is a promising advancement towards the imaging of complex molecules with LIED.
4.3. Control over recollision events
As discussed in the previous sections, the dynamics of strong-field-driven electron rescattering in molecules can be remarkably influenced by later revisits of the photoelectron at the parent ion. This phenomenon is governed by the interplay between the molecular potential and the external laser field, and sets a complex temporal structure in the photoelectron energy distribution. Such a structure can jeopardise the interpretation of time-resolved LIED especially if photoelectron energies below the 10-U cutoff are considered, as discussed in [50]. For this reason, time-resolved molecular-frame LIED calls for a knob of control over recollision events and secondary revisits. In the field of attosecond science, many methods have been developed in the last two decades in order to control the photoelectron recombination in the framework of high-harmonic generation. In particular, intense research has been pursued to select a single recombination event—and thus a single high-harmonic burst—from a multi-cycle driving field, as a key prerequisite to generate isolated attosecond pulses [94]. The polarisation gating technique, for example, relies on the fact that the strong-field driven photoelectron trajectories are highly dependent on the ellipticity of the external field. In particular, recollision with subsequent rescattering or recombination is dramatically suppressed if the polarisation is not linear. In this context, the transient polarisation of a few-cycle strong-field laser can be manipulated by employing two birefringent plates, i.e. a first thick plate and a zero-order quarter waveplate. The linearly-polarised incoming pulse is split into two delayed cross-polarised components by the first plate, where the delay is proportional to the plate thickness. As the consequence, the pulse acquires a time-dependent polarization, that is circular at its centre where the two components overlap and linear in the wings. After crossing the quarter waveplate, a narrow gate of linear polarisation is obtained, as depicted in figure 8. If this concept is applied to LIED, a single rescattering event can be selected and, thus, later revisits can be suppressed. We note that the use of polarisation-gated pulses, in the case of few-cycle driving fields, is expected to reduce the rate of rescattering electrons by one order of magnitude, similar to the corresponding drop in photon flux of isolated attosecond pulses generated in the same way. However, the selection of a single revisit would allow to evaluate and utilise rescattered electrons at much lower energy than 10 U , thus with a much higher count rate of the LIED process, as the problematic influence of electrons from later revisits is suppressed [50]. Furthermore, the transient polarisation of the driving laser can be adjusted in order to compensate for the transverse momentum imposed by specific molecular orbitals to the ejected electron. In general, controlling the polarisation of the strong-field laser is promising to control the electron trajectory and further increase the temporal resolution and the information that can be extracted from time-resolved LIED.
Figure 8. Pictorial representation of polarisation-gated photoelectron rescattering, as a way to trigger a single rescattering event.
Download figure:
Standard image High-resolution image4.4. Approaching femtochemistry with two-colour pump-probe LIED
It has long been a dream in the molecular sciences to observe and unravel ultrafast chemical-reaction dynamics with ultimate spatiotemporal resolution, i.e., atomic spatial and (sub)femtosecond to picosecond temporal resolution, as described in the introduction. Tremendous progress has been made in the time-resolved observation of chemical dynamics in the gas-phase, such as detailed measurements of the temporal evolution of isolated chemical systems using, for instance, time-resolved photoelectron spectroscopy or time-resolved x-ray and electron scattering measurements [5, 95, 96]. In these pump-probe approaches the dynamics are triggered through photoexcitation using a very short laser pulse, which typically results in ultrafast dynamics due to the excited non-equilibrium geometries and nonadiabatic couplings between different electronic states. Merged with quantum-theoretical support, this has been very successful in following ultrafast photo-chemical dynamics.
While some experiments following this 'femtochemistry' approach are only indirectly related to structural dynamics and accompanying quantum-chemistry simulations are employed to transfer the experimental time-resolved measurements into computed 'molecular movies' [97, 98], other studies directly imaged dynamical structures, for example employing high-energy electron or x-ray diffraction [15, 99–101]. Developing LIED to an experimental tool to unravel the structural dynamics of gas-phase molecular systems following a laser-pump pulse [102] will provide direct access to the structural domain, as already envisioned by the late Ahmed Zewail for the alternative approach of conventional electron diffraction [1].
LIED offers important and significant advantages regarding the cross section of the diffraction experiment and thus allows to perform the experiment on well-defined samples in the gas phase. Furthermore, LIED could provide significant better temporal resolution [24] where needed. However, at the same time it is unclear in how far the molecules under investigation traversing multiple electronic states will complicate the issue.
One highly interesting proof-of-principle investigation of such dynamics is the UV-induced dissociation dynamics of the triatomic OCS molecule, which bends in the electronically excited states, resulting in highly rotationally excited CO molecules from the dissociation that were characterised in quantum-state resolved spectroscopic measurements and analysed in terms of quantum-chemical computations [103, 104]. In collaboration with Arnaud Rouzée at MBI Berlin, some of us have set up a research program [102] and performed several experiments toward the disentangling of the actual structural dynamics of this bending and dissociation process. We've computed the expected wavepacket dynamics on the electronically-excited-state surfaces and experimentally recorded time-dependent transients of the dynamics using ion imaging [105]. These data show a clear and interesting discrepancy between the time-dependent yield of the photofragments and the computations and earlier spectroscopic results, which needs further investigation and could surely be resolved by a direct structural probe, such as LIED.
Furthermore, we have demonstrated the determination of the bond length of intact OCS with an accuracy of 5 pm [43]. In our attempts to resolve the mentioned structural dynamics we have implemented very-strong laser alignment of OCS [106] and utilised these samples to record molecular-frame (MF) LIED data for many alignment directions [54] of the molecule in order to maximise the information content of the obtained diffraction volume. The recording of MF-LIED data for the UV-induced dynamics is ongoing in the laboratory in Berlin. These concepts and approaches could clearly be transferred to a wide variety of classical femtochemistry studies of photochemical dynamics, where LIED could then provide direct structural information in addition to the existing photoelectron-spectroscopy-based transients.
Importantly, we propose that LIED is very well suited to investigate electronic ground-state structural processes, which are abundant in chemical dynamics and pose extremely challenging and important questions that ask for the recording of structural dynamics. These including simple bond-breaking processes and solvation-dynamics processes, e.g. the breaking of hydrogen bonds in microsolvated clusters [107–109] as well as isomerisation reactions, e.g. in the molecular building blocks of life [110–112].
For instance, for the example of the prototypical microsolvation system indole-water one finds that UV excitation of the indole chromophore leads to the traversing of multiple conical intersections and electronic state in the first 10 ps, resulting in a vibrationally-hot electronic ground-state system after these 10 ps (see figure 9(a)). The latter dissociates into indole and water fragments on a timescale of 100 ps. Resolving the structural rearrangements, and the distribution thereof, during the initial phase of this photochemical reaction is challenging due to the repeated change of electronic states/character and thus Ei . However, UV-pump LIED-probe experiments (as sketched in figure 9(b)) could proceed by following the parallelism with excited-state HHG [113]. For the longer-time, picosecond dissociation dynamics in the electronic ground state, instead, standard LIED can be directly applied, as the vertical ionisation energy will be largely unaffected by the vibrational excitation. Thus, it is directly in line with the described experiments on complex molecules, vide supra.
Figure 9. Probing structural dynamics of molecules depicted for the example of the UV-induced dynamics of indole-water. (a) The temporal evolution of the UV excited indole-water system, depicted on the left, into separated indole and water moieties, depicted on the right, proceeds on femto- and picosecond timescales [109]. (b) Performing pump-probe experiments with two time delayed short laser pulses, a first one triggering dynamics e.g. through single-UV-photon absorption, and a second IR pulse probing the structure after different times.
Download figure:
Standard image High-resolution imageFurther important chemical reactions are structural rearrangements of molecules at much lower excitation energies, such as the folding of biological macromolecules. Gas-phase experiments on the isomerisation of amino acids directly mimicking these processes were performed, yielding statistical results on the terminal products [110–112]. However, performing infrared-pump LIED-probe experiments would allow one to directly follow the underlying femto- and picosecond structural rearrangements in the electronic ground state in real time and with full atomic resolution [114].
Thus, the extension of LIED to femtochemistry-inspired pump-probe experiments will yield important structural information on a wide variety of (photo)chemical processes using table-top-laser experiments.
5. Conclusions
LIED promises to advance our capability of imaging the microscopic world in real-time and space. We reviewed the main experimental and theoretical achievements on LIED, discussing its great potential and current limitations. Building upon the results obtained with LIED in the last years, we outlined a set of challenges, future perspectives, and possible advancements for LIED research. In particular, we identified the control over recollision events and two-colour-driven self-diffraction as two important, and promising, directions to be explored in order to overcome intrinsic limitations of LIED. Furthermore, we proposed a class of two-colour pump-probe LIED experiments to attack a family of femtochemistry-related questions, toward a new generation of LIED studies on complex molecular systems.
Acknowledgment
A T acknowledges support from the Helmholtz association under the Helmholtz Young Investigator Group VH-NG-1603. We acknowledge financial support by Deutsches Elektronen-Synchrotron DESY, a member of the Helmholtz Association (HGF). This work was supported by the Cluster of Excellence 'Advanced Imaging of Matter' (AIM, EXC 2056, ID 39 071 5994) of the Deutsche Forschungsgemeinschaft (DFG). U D G acknowledges support from NextGenerationEU funds MUR D.M. 737/2021 "Materials Manipulation with Light".
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Conflict of interest
The authors declare no competing interests.


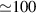
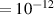

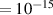
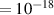
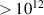
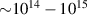


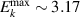


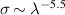
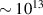
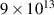



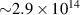

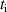
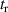



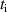


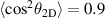






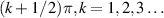








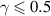
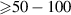



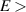


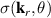
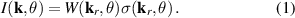

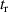
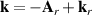
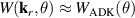
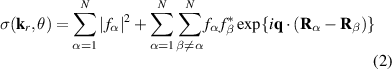
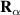
$](https://content.cld.iop.org/journals/0953-4075/56/5/054002/revision2/bacb872ieqn58.gif)
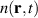
$](https://content.cld.iop.org/journals/0953-4075/56/5/054002/revision2/bacb872ieqn60.gif)