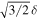Abstract
We present a theoretical study of the bichromatic force exerted on magnesium monofluoride (MgF), in which we have considered the complex vibrational and rotational levels and the effects of small internal splittings and degeneracies, including fine and hyperfine structures and the magnetic quantum numbers. We calculate some parameters used in the MgF molecular transitions between X2Σ+, A2Π and B2Σ+ states. It is the first time that the radiative lifetimes of B2Σ+ → X2Σ+ and B2Σ+ → A2Π have been derived by ab initio calculations. The detailed numerical modeling of bichromatic forces by direct numerical solution for the time-dependent density matrix is presented. Here, we propose a simplified numerical model to study the dynamic process of MgF slowing by neglecting the effect of the high vibrational levels, in which a skewed magnetic field is applied to destabilize the dark state. We deduce the relation between per-bichromatic-component irradiance I and the total Rabi frequency amplitude. We also compare our proposed simplified model with two other theoretical ones (Aldridge et al 2016 Phys. Rev. A 93 013419). Monte Carlo simulations show that a buffer-gas-cooled MgF beam with a forward velocity of 120 m s−1 can be decelerated nearly to several m/s within a distance of ∼0.5 cm. Comparing with the B → X transition, we find that the A → X transition in MgF is more suitable for the bichromatic force cooling and slowing.
Export citation and abstract BibTeX RIS
1. Introduction
Laser cooling has been demonstrated with monochromatic light using both radiative and dipole forces, during which spontaneous emission is needed for energy and entropy removal [1, 2]. Recently, the controversial notion of laser cooling in the absence of spontaneous emission was demonstrated, and it was achieved by using bichromatic force (BF) on a He atomic transition with a relatively long excited state lifetime and a relatively short cooling time [3, 4]. The potential for the BF to cool should allow the extension of laser cooling to systems without closed cycling transitions, such as molecules. The BF arises from the coherent control of the momentum exchange between the atom (or molecule) and the laser fields associated with a long sequence of rapid absorption-stimulated emission cycles. BF experiments and numerical simulations based on optical Bloch equations have been demonstrated in several atom species for two-level systems [5–12]. In multilevel systems, we cannot directly utilize the theory in a two-level system to describe the BF exerted on molecules with internal degeneracies. In a molecule with internal splittings and degeneracies, each transition has different frequency and line strength, so the same laser irradiance cannot optimally drive each transition. In 2011 Eyler and coworkers examined the prospects for utilizing the optical BF to greatly enhance the radiative force on molecules [13]. In our 2015 paper we analyzed the BF on a MgF molecule, in which the analysis of the BF was based on two-level calculations combined with statistical arguments, including a weighted degeneracy factor arising from the dark ground-state levels and a 'force reduction factor' due to variations in frequency shifts and line strength from level to level [14]. Nevertheless, these treatments are phenomenological and cannot account for multilevel coherent effects. In 2016 a quantitative treatment for BF in multilevel systems by direct numerical solution for the time-dependent density matrix in the rotating-wave approximation was proposed by Eyler [15]; they compared a full 16-level simulation for the CaF B → X system with a weighted subsystem-based numerical model and with a semiquantitative estimate based on two-level systems and they showed that a cryogenic buffer-gas-cooled beam of CaF with a forward velocity of 60 m s−1 could be decelerated nearly to rest without a repumping laser.
The development of a molecular magneto-optical trap (MOT) should really mirror the huge historical success achieved by the atomic MOT [16, 17]. Additional slowing is required to load molecules into an MOT from beam source, due to the low capture velocity of a molecular MOT (<10 m s−1). Many electro-optic modulator (EOM) sidebands (eight or so) were used to extend the SrF capture range of the slowing lasers, 6% of the initial flux at velocity <50 m s−1 were detected [18]. The longitudinal velocity of a YO beam was also decelerated to below 10 m s−1 by a mixing technique of a frequency modulated and chirped continuous-wave laser [19]. Frequency-broadened white-light slowing on CaF was demonstrated, and they observed approximately 6 × 104 CaF molecules with velocities near 10 m s−1 [20]. Chirping the frequency of the light slowed the forward velocity of the CaF molecular beam [21, 22], a cryogenic pulsed beam was slowed to 15 m s−1 and the flux was ∼8 × 105 molecules per cm2 per pulse. In order to produce a diverse set of dense, ultracold diatomic molecular species, it would be interesting and worthwhile to explore how to deliver much larger numbers of slow molecules for loading into an MOT; nowadays bichromatic light force slowing is also a promising path.
We have selected MgF as a prototype molecule for laser cooling, concentrating primarily on its two lowermost electronic states, ground state X2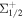 and excited state A2Π1/2 [14, 23, 24]. With just two lasers, one addressing the v = 0 branch at 359.3 nm and the other repumping the v = 1 branch at 368.7 nm, each molecule will scatter an average of 104 photons before decaying to a higher vibrational state. In addition, it has simple and specific hyperfine splitting due to electron spin (S = 1/2), nuclear rotation and nuclear spin (I = 1/2) interactions for the rotational N = 1 energy level of the electronic ground state of MgF.
and excited state A2Π1/2 [14, 23, 24]. With just two lasers, one addressing the v = 0 branch at 359.3 nm and the other repumping the v = 1 branch at 368.7 nm, each molecule will scatter an average of 104 photons before decaying to a higher vibrational state. In addition, it has simple and specific hyperfine splitting due to electron spin (S = 1/2), nuclear rotation and nuclear spin (I = 1/2) interactions for the rotational N = 1 energy level of the electronic ground state of MgF.
In this paper we theoretically investigate the BF exerted on MgF using three models based on direct numerical solution for the time-dependent density matrix. In a real molecular transition, to accurately describe the interaction between molecules and lasers, high vibrational levels should be considered. For near-cycling transitions, we propose a simplified numerical model by neglecting the high vibrational levels which yields results very similar to the exact treatment in most cases. Our proposed model is also compared with a numerical model based on several lambda-type subsystems. We calculate the radiative lifetimes of the B → X and B → A, the electric dipole matrix elements, and branching ratios for the A → X and B → X in MgF, in which we have noted that the eigenstates of F = N = 1 states in X2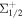 are of mixed and not pure J. We also deduce the relation between the Rabi frequency amplitude of each two-level transition and the defined quadrature sum of several Rabi frequency amplitudes, and the relation between per-bichromatic-component irradiance I and the total Rabi frequency amplitude. Monte Carlo simulations show that a cryogenic beam of MgF with a center velocity of 120 m s−1 can be decelerated nearly to rest. Our study also shows that the A → X transition in MgF is more suitable for BF cooling and slowing, comparing to the B → X transition.
are of mixed and not pure J. We also deduce the relation between the Rabi frequency amplitude of each two-level transition and the defined quadrature sum of several Rabi frequency amplitudes, and the relation between per-bichromatic-component irradiance I and the total Rabi frequency amplitude. Monte Carlo simulations show that a cryogenic beam of MgF with a center velocity of 120 m s−1 can be decelerated nearly to rest. Our study also shows that the A → X transition in MgF is more suitable for BF cooling and slowing, comparing to the B → X transition.
2. Magnesium monofluoride
The structure of the A2Π → X2Σ+ (0-0) Q12(0.5)/P11(1.5) branch is depicted in figure 1, including the fine and hyperfine sublevels. This transition has λ = 359.3 nm, τ = 7.2 ns and the Franck–Condon factor f00 for this transition has been calculated to be 0.9978 [23]. Since S = 1/2 and I = 1/2, in the X state N = 1 manifold there are four levels characterized by the hyperfine quantum number F = 2, 1+, 1−, 0 and J is a poor quantum number due to mixing of two F = N = 1 levels. In the X state N = 1 manifold, the eigenfunctions and the eigenvalues for the hyperfine sublevels are calculated using the method in [25] and the details of the calculations are in the
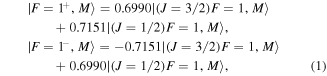
Equation (1) will be applied to the calculations of the electric-dipole matrix elements, branching ratios and magnetic-field Hamiltonian for MgF.
Figure 1. (a) A quasicycling transition for laser cooling of MgF. Solid upward lines indicate laser-driven transitions at the wavelength λvv'. Solid wavy lines indicate spontaneous decays from the A2Π1/2 state with FCFs fv'v as shown. (b) The structure of the A2Π → X2Σ+ (0-0) Q12(0.5)/P11(1.5) branch in MgF. The arrows indicate the allowed transitions for π-polarized light.
Download figure:
Standard image High-resolution imageThe electric-dipole matrix elements and branching ratios are calculated. The A2Π1/2 state is Hund's case (a) while the X2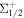 state is Hund's case (b). The calculation is done in Hund's case (a) basis
state is Hund's case (b). The calculation is done in Hund's case (a) basis 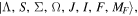 so all ground states should be converted to the Hund's case (a) basis. The excited state is one of positive parity and written in terms of basis states of signed Ω using equation (6.234) in [27]. Omitting the quantum numbers beyond J, this state is
so all ground states should be converted to the Hund's case (a) basis. The excited state is one of positive parity and written in terms of basis states of signed Ω using equation (6.234) in [27]. Omitting the quantum numbers beyond J, this state is
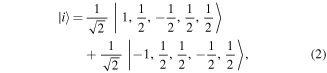
In X2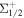 state, the expansion of the ground states in Hund's case (a) basis uses equation (6.149) in [27].
state, the expansion of the ground states in Hund's case (a) basis uses equation (6.149) in [27].
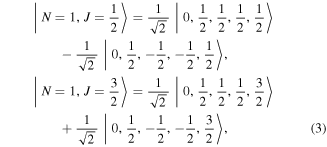
The electric-dipole operator is written in spherical tensor notation as T(1)(d). The electric dipole matrix elements can be calculated as below
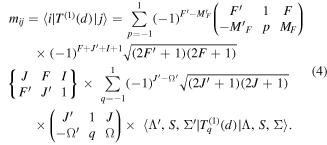
The factor  in equation (4) is common to all the branches, so we can define a relative electric-dipole transition matrix element between states
in equation (4) is common to all the branches, so we can define a relative electric-dipole transition matrix element between states  and
and  as
as
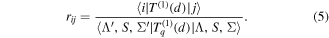
Taking into account that J is a poor quantum number due to mixing of two F = N = 1 levels, the obtained relative dipole transition matrix elements between the eigenfunctions are shown in table 1. The relative electric-dipole matrix elements for the B2Σ+ → X2Σ+PQ12(0.5)/P11(1.5) branch in MgF are also calculated using the similar method as shown in table 2. This transition has λ = 268.9 nm and τ = 8.8 ns, the Franck–Condon factor f00 for this transition has been calculated to be 0.9972, and the radiative lifetimes of B2Σ+ → A2Π is 0.82 s4 . The branching ratios are a measure of how the total intensity of a transition is distributed among the various rotational/spin-rotational/hyperfine decay paths. Using the relation Γij = 16π3dij2/(3hλ3ε0), we can get the branching ratios for the entire set of decay channels which are the square of the relative electric dipole transition matrix elements.
Table 1. Electric dipole matrix elements for the A2Π → X2Σ+ Q12(0.5)/P11(1.5) branch in MgF, in units of the total A2Π → X2Σ+ (0-0) band dipole transition moment.
| F' = 0 | F' = 1 | |||||
|---|---|---|---|---|---|---|
| J | F | mF | m'F = 0 | m'F = −1 | m'F = 0 | m'F = 1 |
| 3/2 | 2 | −2 | 0 | 0.4082 | 0 | 0 |
| −1 | 0 | −0.2887 | 0.2887 | 0 | ||
| 0 | 0 | 0.1667 | −0.3333 | 0.1667 | ||
| 1 | 0 | 0 | 0.2887 | −0.2887 | ||
| 2 | 0 | 0 | 0 | 0.4082 | ||
| 3/2 | 1 | −1 | −0.1041 | −0.4536 | −0.4536 | 0 |
| 0 | 0.1041 | 0.4536 | 0 | −0.4536 | ||
| 1 | −0.1041 | 0 | 0.4536 | 0.4536 | ||
| 1/2 | 1 | −1 | −0.5679 | −0.2103 | −0.2103 | 0 |
| 0 | 0.5679 | 0.2103 | 0 | −0.2103 | ||
| 1 | −0.5679 | 0 | 0.2103 | 0.2103 | ||
| 1/2 | 0 | 0 | 0 | 0.4714 | 0.4714 | 0.4714 |
Table 2. Electric dipole matrix elements for the B2Σ+ → X2Σ+ PQ12(0.5)/P11(1.5) branch in MgF, in units of the total B2Σ+ → X2Σ+ (0-0) band dipole transition moment.
| F' = 0 | F' = 1 | |||||
|---|---|---|---|---|---|---|
| J | F | mF | m'F = 0 | m'F = −1 | m'F = 0 | m'F = 1 |
| 3/2 | 2 | −2 | 0 | −0.5774 | 0 | 0 |
| −1 | 0 | 0.4082 | −0.4082 | 0 | ||
| 0 | 0 | −0.2357 | 0.4714 | −0.2357 | ||
| 1 | 0 | 0 | −0.4082 | 0.4082 | ||
| 2 | 0 | 0 | 0 | −0.5774 | ||
| 3/2 | 1 | −1 | −0.5679 | −0.0736 | −0.0736 | 0 |
| 0 | 0.5679 | 0.0736 | 0 | −0.0736 | ||
| 1 | −0.5679 | 0 | 0.0736 | 0.0736 | ||
| 1/2 | 1 | −1 | 0.1041 | −0.4016 | −0.4016 | 0 |
| 0 | −0.1041 | 0.4016 | 0 | −0.4016 | ||
| 1 | 0.1041 | 0 | 0.4016 | 0.4016 | ||
| 1/2 | 0 | 0 | 0 | 0.3333 | 0.3333 | 0.3333 |
3. BF and magnetic-field Hamiltonian
In realistic multilevel systems, such as a molecule with internal splittings and degeneracies, each transition has different frequency and line strength, so the same laser irradiance cannot optimally drive each transition. In order to account for multilevel coherent effects, in 2016 a quantitative treatment for BF in multilevel systems by direct numerical solution for the time-dependent density matrix in the rotating-wave approximation was proposed by Eyler [15]. Based on a similar theoretical method, we study the theory of the BF on MgF in realistic multilevel systems. The relation between per-bichromatic-component irradiance I and the total Rabi frequency amplitude is deduced. The dark states remixing is also studied by applying a magnetic field with magnitude B0 at an angle θB relative to the laser polarization.
3.1. Theory for BF in realistic multilevel systems
In the bichromatic field, assuming that a pair of monochromatic beams is symmetrically detuned from a carrier frequency ω by δ and both frequency components have the same amplitude E0, the electric field from the counter propagating beams aligned along the z-axis can be given by

Where k = 2π/λ = ω/c and Δk = δ/c. Grouping terms, we can rewrite equation (6) as
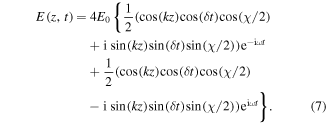
Where χ = 2Δkz = 2δz/c is the phase difference between the electric fields of the counterpropagating beat notes. If the slowing length satisfies the condition of 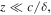 the χ remains approximately constant. Each transition shown in table 1 is associated with a Rabi frequency defined by
the χ remains approximately constant. Each transition shown in table 1 is associated with a Rabi frequency defined by

Where dij is the electric-dipole transition matrix element between states 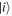 and
and 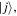 and d is the total A2Π → X2Σ+ (or B2Σ+ → X2Σ+) dipole transition moment,
and d is the total A2Π → X2Σ+ (or B2Σ+ → X2Σ+) dipole transition moment, 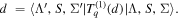 We can find that the same optical field can simultaneously drive multiple transitions at different Rabi frequencies with reference to table 1. The Rabi frequency
We can find that the same optical field can simultaneously drive multiple transitions at different Rabi frequencies with reference to table 1. The Rabi frequency 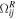 can be written into two terms:
can be written into two terms:
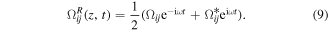
Combining equations (7) and (8) we can find that
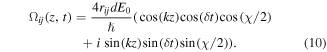
In which we define Rabi frequency amplitude 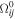 as
as
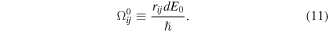
The Hamiltonian for the multilevel system in the bichromatic field consists of the zero-field energies and the interaction energies between the system and the light field. This Hamiltonian is given by
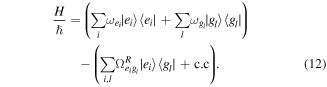
Here 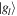 is the ground state and
is the ground state and 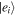 is the excited state.
is the excited state.
The equations of motion of the density matrix, including the contribution from spontaneous emission, are given by
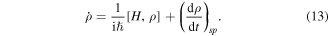
In the rotating-wave approximation, the full set of equations of motion of density matrix of a multilevel system with an upper-state manifold of Ne levels and a lower-state manifold of Ng levels are given by
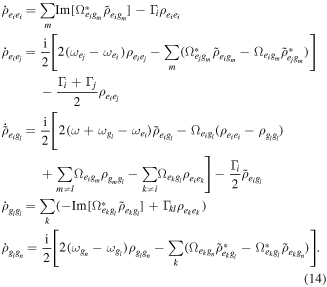
Where 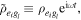
 is the total decay rate of the excited state
is the total decay rate of the excited state  and
and  is a specific channel decay rate. Here we should know the sums over an excited state index (i, j, k) from 1 to Ne and a ground state index (l, m, n) from 1 to Ng. Numerical solutions to this set of equations are computed using the built-in numerical differential equation solver in MatLab. The average force on the multilevel system is given by
is a specific channel decay rate. Here we should know the sums over an excited state index (i, j, k) from 1 to Ne and a ground state index (l, m, n) from 1 to Ng. Numerical solutions to this set of equations are computed using the built-in numerical differential equation solver in MatLab. The average force on the multilevel system is given by
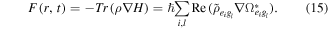
3.2. Rabi frequency and laser intensity in multilevel systems
In the two-level systems, the optimal Rabi frequency amplitude is 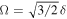 and the corresponding laser irradiance for each traveling wave is given by
and the corresponding laser irradiance for each traveling wave is given by
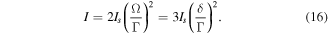
Where Is = πhcΓ/(3λ3) is the saturation irradiance and Γ is the upper-level decay rate. Whereas in the multilevel systems each of the lower states can have a different electric dipole coupling to a given upper level as shown in table 1. So the same optical field can simultaneously drive multiple transitions at different Rabi frequencies. For the given bichromatic detunings δ, to find the optimal laser irradiance, we need to utilize a total Rabi frequency amplitude Ωtot to describe our system. The Ωtot is defined as the quadrature sum of the each Rabi amplitude,
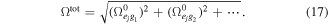
From equations (11) and (17) we can express each Rabi amplitude as

Here, the index m denotes all possible Rabi oscillations for the excited state 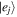 for π-polarized light in our work.
for π-polarized light in our work.
Using the relations 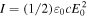 and
and

we can obtain
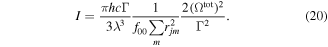
Here, Γ is the spontaneous decay rate of the upper level, ωjp is the resonance frequency between the excited state 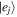 and the ground state
and the ground state 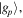 the index p denotes all possible final states in the decay of the excited state. We have made the approximation that ωjp = 2πc/λ for all final states. In the numerical simulations we can find the optimal Ωtot to determine the required laser irradiance I.
the index p denotes all possible final states in the decay of the excited state. We have made the approximation that ωjp = 2πc/λ for all final states. In the numerical simulations we can find the optimal Ωtot to determine the required laser irradiance I.
3.3. Magnetic-field Hamiltonian
From figure 1 and table 1 we can find that the dark states exist in the ground state X2 (v = 0, N = 1), in which F = 2, m = ±2 these two states are dark states for π-polarized light. In the absence of a remixing mechanism, population will accumulate in these dark states and cycling will cease, which causes the BF to rapidly diminish to zeros. Here, we apply a magnetic field with magnitude B0 at an angle θB relative to the laser polarization to remix dark states.
(v = 0, N = 1), in which F = 2, m = ±2 these two states are dark states for π-polarized light. In the absence of a remixing mechanism, population will accumulate in these dark states and cycling will cease, which causes the BF to rapidly diminish to zeros. Here, we apply a magnetic field with magnitude B0 at an angle θB relative to the laser polarization to remix dark states.
In the presence of an external magnetic field B, the Zeeman Hamiltonian is well approximated by, in the space-fixed axis system,
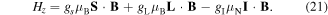
Here the electron g-factor is 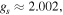 the electron orbital g-factor is
the electron orbital g-factor is  and the nuclear g-factor is
and the nuclear g-factor is 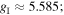
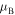 is the Bohr magneton, and
is the Bohr magneton, and  is the nuclear magneton. Since
is the nuclear magneton. Since 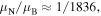 the last term can be neglected and the Zeeman Hamiltonian can be expressed as
the last term can be neglected and the Zeeman Hamiltonian can be expressed as
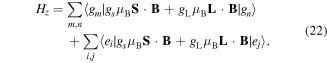
Here magnetic coupling between ground states and excited states is neglected because this coupling is small compared with optical coupling. For the A2Π → X2Σ+ transition, mixing caused by magnetic fields in the excited state is negligible since the A2Π1/2 state lacks a magnetic moment. The magnetic Hamiltonian in equation (22) can be evaluated using equations (A4) and (A5) in the  are of mixed and not pure J. The applied skewed magnetic field will cause Larmor precession of the ground-state Zeeman sublevels. This precession will act to mix the bright states with the dark states so that the dark state destabilization is realized.
are of mixed and not pure J. The applied skewed magnetic field will cause Larmor precession of the ground-state Zeeman sublevels. This precession will act to mix the bright states with the dark states so that the dark state destabilization is realized.
4. Numerical calculations and Monte Carlo simulations
A simplified numerical model is proposed to study the dynamic process of MgF slowing by neglecting the effect of the high vibrational levels, in which a skewed magnetic field is applied to destabilize dark state. We compare our proposed model (a) with two other theoretical ones (b) and (c) in [15]. The method (a) can estimate the BF for near-cycling transition which has the same accuracy as method (b), and it is not only simpler, but also the computational time needed in method (a) is much less than that in method (b).
4.1. Model (a): a full 16-level simulation
We firstly use the simplified modeling without considering the high vibrational levels but the effects of small internal splittings and degeneracies are considered, including fine structure and hyperfine structure as well as the magnetic quantum numbers, as shown in figure 1. In the modeling, a full 16-level simulation of the system is carried out (for X2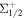 (v = 0, N = 1), 12 magnetic sublevels; for A2Π1/2 (v' = 0, J' = 1/2), four magnetic sublevels). To obtain the optimum BF, we first should investigate the influences of the main parameters on force.
(v = 0, N = 1), 12 magnetic sublevels; for A2Π1/2 (v' = 0, J' = 1/2), four magnetic sublevels). To obtain the optimum BF, we first should investigate the influences of the main parameters on force.
From table 1 and figure 2, we can find that for each of the four sublevels in the excited state, the factor  in equation (20) is 1/3 for π-polarized light, so the same laser irradiance can drive all transitions with the same Ωtot. Using the optimal χ from the two-level systems and the optimal Ωtot referred to [15], which has been verified in our work, the remaining parameters, including the magnitude and angle of the magnetic field and carrier frequency detuning from the transition center of mass of the system (CM), are surveyed within several velocities near zeros, in order to find optimal parameters. Our simulation results show that the optimal magnitude and angle of the magnetic field are not unique. Using those optimal parameter values at each of δ = 15Γ, 25Γ, 50Γ, simulations across the full velocity range are carried out as shown in figure 3, in which the Γ/k = 7.9 m s−1 for the A → X transition in MgF. The velocity capture range and the velocity-averaged force near zero are summarized in table 3 in the columns labeled as method (a).
in equation (20) is 1/3 for π-polarized light, so the same laser irradiance can drive all transitions with the same Ωtot. Using the optimal χ from the two-level systems and the optimal Ωtot referred to [15], which has been verified in our work, the remaining parameters, including the magnitude and angle of the magnetic field and carrier frequency detuning from the transition center of mass of the system (CM), are surveyed within several velocities near zeros, in order to find optimal parameters. Our simulation results show that the optimal magnitude and angle of the magnetic field are not unique. Using those optimal parameter values at each of δ = 15Γ, 25Γ, 50Γ, simulations across the full velocity range are carried out as shown in figure 3, in which the Γ/k = 7.9 m s−1 for the A → X transition in MgF. The velocity capture range and the velocity-averaged force near zero are summarized in table 3 in the columns labeled as method (a).
Figure 2. The Rabi oscillations of the A2Π → X2Σ+ (0-0) Q12(0.5)/P11(1.5) branch in MgF for π-polarized light. Relative dipole transition matrix elements are indicated for each transition.
Download figure:
Standard image High-resolution imageFigure 3. Simulations of the BF for the 16-level A2Π → X2Σ+ (0-0) Q12(0.5)/P11(1.5) branch in MgF for π-polarized light. The magnitude and velocity range of the force increase with larger bichromatic detuning.
Download figure:
Standard image High-resolution imageTable 3. A summary of results for three different methods of estimating the BF for π-polarized light in the 16-level A2Π → X2Σ+ Q12(0.5)/P11(1.5) system in MgF. The methods are (a) a full 16-level simulation without considering the high vibrational levels, including dark state destabilization by a dc magnetic field, (b) a 16-level simulation adding a high vibrational level, including dark state destabilization by a DC magnetic field and a repumping laser, and (c) a weighted subsystem-based multilevel simulations.
| δ = 15Γ | δ = 25Γ | δ = 50Γ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (a) | (b) | (c) | (a) | (b) | (c) | |
| Irradiance (W cm−2) | 127 | 127 | 127 | 351 | 351 | 351 | 1405 | 1405 | 1405 |
| Carrier detuning from CM (MHz) | 20 | 20 | 80 | 20 | 20 | 80 | −10 | −10 | 70 |
| Magnetic field magnitude (Guass) | 25 | 25 | — | 30 | 30 | — | 60 | 60 | — |
| Magnetic field angle (°) | 65 | 65 | — | 65 | 65 | — | 60 | 60 | — |
| Force near zero velocity (hkΓ/4π) | 1.97 | 1.87 | 1.35 | 3.46 | 3.31 | 2.66 | 6.65 | 6.34 | 4.66 |
| Velocity range (m s−1) | 150 | 150 | 140 | 230 | 230 | 220 | 360 | 360 | 320 |
| Average excited fraction | 0.14 | 0.13 | 0.10 | 0.12 | 0.12 | 0.09 | 0.12 | 0.12 | 0.08 |
| Time to slow by 120 m s−1 (ms) | 1.09 | 1.08 | 1.01 | 0.55 | 0.57 | 0.67 | 0.38 | 0.38 | 0.87 |
| Slowing length (cm) | 0.5 | 0.5 | 0.5 | 0.35 | 0.35 | 0.4 | 0.22 | 0.22 | 0.55 |
| Fully-slowed population fraction (%) | 6.04 | 6.23 | 6.22 | 12.1 | 11.9 | 11.3 | 15.6 | 15.5 | 12.2 |
4.2. Method (b): a 16-level simulation adding a high vibrational level
In a real molecular transition, the high vibrational levels should be taken into account because in the actual optical cycles the molecule will be lost into some inaccessible high vibrational levels. For the A → X transition, the Franck–Condon factor f00 of 0.9978 means that the molecules will be lost to out-of-system in hundreds of spontaneous decay cycles without the repumping lasers. Therefore, a 16-level simulation adding a high vibrational level should be carried out and this model evaluating the BF on molecule is more accurate [15]. Clearly the available interaction time is constrained by out-of-system radiative decays, hence a continuous repumping laser field should be used to transfer population from the dark state to the same excited state used by the cycling BF transition. Using the optimal parameter values from the simplified model at each bichromatic detuning, the BF as a function of repumping laser Rabi frequency is surveyed. For each of the several detunings δ in the figure 4, there is an optimum value for the repumping laser irradiance and the optimum repumping Rabi frequency is about 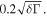 Here the integral time of computation of the time-dependence of the density matrix is about 10 μs, with longer integral time the amplitude of the BF will be to zero without repumping laser but it will be almost unchanged under the repumping laser irradiance. Taking into account that it will take too much time to complete the computation for longer integral time, the integral time is set to a suitable value of 10 μs. Then, using those parameters, simulations across the full velocity range are carried out and the calculated results are summarized in table 3 in the columns labeled as method (b).
Here the integral time of computation of the time-dependence of the density matrix is about 10 μs, with longer integral time the amplitude of the BF will be to zero without repumping laser but it will be almost unchanged under the repumping laser irradiance. Taking into account that it will take too much time to complete the computation for longer integral time, the integral time is set to a suitable value of 10 μs. Then, using those parameters, simulations across the full velocity range are carried out and the calculated results are summarized in table 3 in the columns labeled as method (b).
Figure 4. The BF as a function of the repumping laser Rabi frequency.
Download figure:
Standard image High-resolution image4.3. Method (c): a weighted subsystem-based multilevel simulations
In this paper, another more simplified modeling method to evaluate the BF on the MgF is carried out. Using this modeling method, the computation of the time-dependence of the density matrix requires much less time compared with the other two modelings without giving up a great deal of accuracy. As shown in figure 2, no ground-state sublevel is laser-coupled to more than one excited-state sublevel, so that the entire system can be viewed as two three-level and two four-level lambda-type subsystems [15]. In this modeling, we think these four subsystems are independent by neglecting the radiative coupling between them and proportionally increase the decay rates within each subsystem to compensate for the neglected decays. Using the optimal Ωtot and χ at each of δ = 10Γ, 15Γ, 25Γ and 50Γ, each of the four subsystems is independently simulated for a range of BF carrier frequencies. Then the results from each subsystem are combined together with a weighting given by the fraction of the ground state sublevels included in each subsystem. Figure 5 shows the calculated averaged force with near-zero velocities as a function of the BF carrier frequencies and indicates there is an optimum in the carrier frequencies for each of the detunings δ. As shown in figure 5, the averaged force peaks at a carrier frequency detuned from the hyperfine center of mass, at a location near the F = 0. This carrier frequency is compromise between two three-level subsystems and two four-level subsystems. Because transitions from F = 1− are the strongest transitions in the three-level subsystems but in the four-level subsystems transitions from F = 1+ are the strongest transitions. Using the optimal carrier frequencies, simulations across the full velocity range are carried out and the calculated results are summarized in table 3 in the columns labeled as method (c).
Figure 5. A weighted average of the force on isolated subsystems of the (0-0) Q12(0.5)/P11(1.5) branch in MgF for π-polarized light. It indicates the optimal carrier frequency detuning at each of δ.
Download figure:
Standard image High-resolution imageComparing the results for three different methods estimating the BF in the 16-level A2Π → X2Σ+ Q12(0.5)/P11(1.5) system in MgF, as shown in table 3, we can find that the calculated results using methods (a) and (b) are almost consistent in the velocity range and force as well as average excited state fraction. However, the calculations using method (a) are not only simpler, but the computational time needed in method (a) is much less than that in method (b). It is also clear that the subsystem approach consistently underestimates the force and velocity range as well as average excited state fraction.
Without the repumping laser, the molecules will be lost to out-of-system in hundreds of spontaneous decay cycles in MgF. The characteristic out-of-system decay time can be evaluated by
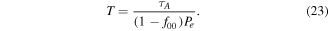
Where τA is the radiative decay lifetime of the A state, Pe is the average excited state fraction. The Pe can be attained by averaging the calculated excited state fraction over the velocity range in which the force is large. The result is Pe ≈ 1/8 and we can estimate an out-of-system decay time of about 25 μs. Actually, in our calculations we find the out-of-system decay time is about 100 μs. Because when the integral time is set to 100 μs, at last, the BF will be to zero without a repumping laser.
4.4. Slowing of the MgF molecular beam
The source of MgF in our simulations is a cryogenic buffer gas cell [28], the final output diameter of molecular beam is 1.5 mm and the transverse velocity is ±1 m s−1 after two times collimation [29]. Five cm after the collimating aperture, the beam enters the bichromatic-force slowing and cooling region. We assume that the MgF in the beam has a forward velocity of v∣∣ = 120 m s−1 with a spread of Δv∣∣ ≈ 40 m s−1. In the longitudinal slowing of MgF molecular beam, the bichromatic laser beams are tightly focused to waists with a top-hat diameter of 1 mm to provide the required irradiance. Using the BF with a detuning of δ = 15Γ, a cryogenic buffer-gas-cooled beam of MgF can be decelerated nearly to 4 m s−1 within a longitudinal distance of about 0.5 cm and the efficiency is about 6.23% with respect to the source of MgF, taking into account that the molecular beam flies free for a distance of 5 cm before it is illuminated by bichromatic lasers. Under this condition using equation (20), the laser irradiance for each traveling wave is 127 W cm−2 and the corresponding laser power is 0.994 W. The time to slow is about 1.08 ms but the out-of-system decay time is about 100 μs, so the repumping laser should be added. Using these three different methods at each of δ = 15Γ, 25Γ and 50Γ, estimated values for the key properties relevant to longitudinal slowing of MgF molecular beam are summarized in table 3. When the laser irradiances for each traveling wave are 351 W cm−2 and 1405 W cm−2, respectively, the corresponding laser powers is 2.757 W and 11.035 W. With the limitation of the laser technique, nowadays the required powers for the δ of 25Γ and 50Γ cannot be realized. But these results indicate that as long as the required laser irradiance is available, the BF can provide larger force and much better slowing results.
4.5. Comparison of A → X system and B → X system in MgF
We also compare the results of the A → X system and the B → X system in MgF at detuning δ of 10Γ, as shown in table 4. For each of the systems, Γ is the spontaneous decay rate of the upper level. The saturation irradiance of B → X system is almost twice as much as that of A → X system, so laser irradiance for each traveling wave of B → X system is almost twice that of the A → X system. In addition, we find that the velocity range in A → X system is larger than that in B → X system because the velocity range is proportional to δ/k. However, in the A → X system Γ/k = 7.9 m s−1, but in the B → X system Γ/k = 4.9 m s−1. The deceleration efficiency in the A → X system is also twice that of the A → X system when the MgF molecular beam is slowed by 60 m s−1. From these results, we can find that the A → X transition in MgF is more suitable for the BF cooling and slowing.
Table 4. The comparison of results in the sixteen-level A2Π → X2Σ+ Q12(0.5)/P11(1.5) system and B2Σ+ → X2Σ+ PQ12(0.5)/P11(1.5) system in MgF at detuning δ of 10Γ. For each of the systems, Γ is the spontaneous decay rate of the upper level, respectively.
| δ = 10Γ | A2Π → X2Σ+ | B2Σ+ → X2Σ+ | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (a) | (b) | (c) | |
| Irradiance (W cm−2) | 56.2 | 56.2 | 56.2 | 109.8 | 109.8 | 109.8 |
| Carrier detuning from CM (MHz) | 50 | 50 | 60 | −10 | −10 | −70 |
| Magnetic field magnitude (Guass) | 15 | 15 | — | 20 | 20 | — |
| Magnetic field angle (o) | 65 | 65 | — | 50 | 50 | — |
| Force near zero velocity (hkΓ/4π) | 1.28 | 1.21 | 0.88 | 0.92 | 0.86 | 1.06 |
| Velocity range (m s−1) | 115 | 115 | 100 | 63 | 66 | 75 |
| Average excited fraction | 0.152 | 0.145 | 0.11 | 0.18 | 0.17 | 0.14 |
| Time to slow by 60 m s−1 (ms) | 0.71 | 0.71 | 0.63 | 0.83 | 0.82 | 1.19 |
| Slowing length(cm) | 0.35 | 0.35 | 0.3 | 0.4 | 0.4 | 0.6 |
| Fully-slowed population fraction | 6.87% | 6.89% | 6.65% | 3.32% | 3.75% | 3.16% |
5. Summary and conclusions
We have examined the possibility using optical BF to decelerate a MgF molecular beam in realistic multilevel systems. In conclusion:
- (1)We have demonstrated that it is feasible to evaluate the BF by direct numerical solution for the density matrix. We show that a repumping laser and a small skewed magnetic field can be effective to realize a substantial longitudinal slowing. We find the relation between the per-bichromatic-component irradiance I and the quadrature sum of the Rabi frequency amplitudes of the addressed transitions which should be equal to
 .
. - (2)In this paper the A2Π → X2Σ+ system in MgF has been studied in detail, in which we have treated the system as three different theoretical models. From the comparison of methods (a) and (b), we can find that the repumping laser is effective to repopulate the cycling system from the dark state and method (a) can estimate the BF for near-cycling transition which has the same accuracy as method (b). Our method (a) is not only simpler, but the computational time needed in method (a) is much less than that in method (b). The results show that the required laser power is attainable and the magnitude of the force is larger than the radiative force. A cryogenic MgF molecular beam can be decelerated nearly to 4 m s−1, which can be captured by molecular MOT.
- (3)We also calculate the BF for the B2Σ+ → X2Σ+ system in MgF. With the limitation of the saturation irradiance Is and the value of Γ/k, we find that the A → X transition in MgF is more suitable for BF cooling and slowing. It indicates to us that an atomic or molecular system with larger Γ/k and smaller πhcΓ/(3λ3) is more appropriate to be a candidate for BF slowing.
Optical BF may be an effective tool to rapidly slow and cool the molecules and complex atoms in the future as long as the required laser irradiance is available to drive the BF with large detunings. It also paves the way for optical slowing and loading of a diverse set of dense, ultracold diatomic species into a molecular MOT [21, 30–32].
Acknowledgments
We acknowledge support from the National Natural Science Foundation of China under grants 11374100, 11504256, 91536218, 11274114, and the outstanding doctoral dissertation cultivation plan of action of ECNU under Grant No. PY2015026.
Appendix
In Hund's case (b) basis  the states in the ground state X2Σ+ can be abbreviated to
the states in the ground state X2Σ+ can be abbreviated to  For the F = 2, 0 state, the eigenfunctions and eigenvalues can be simply given. For the remaining two states F = N = 1, the eigenfunctions are given by
For the F = 2, 0 state, the eigenfunctions and eigenvalues can be simply given. For the remaining two states F = N = 1, the eigenfunctions are given by

In which the coefficients  and
and  have the relationship as below
have the relationship as below

In which the eigenvalues are

where γ is the spin-rotation constant, b is the hyperfine constant, c is the dipole-dipole constant and C is the nuclear spin-rotation constant. The constant C is negligibly small for our purposes but is included for completeness.Taking into account that the X2 state is Hund's case (b), the Zeeman Hamiltonian can be written in a Hund's case (b) basis (
state is Hund's case (b), the Zeeman Hamiltonian can be written in a Hund's case (b) basis (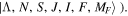 The matrix elements of the two terms in equation (22) in a Hund's case (b) basis are as follows,
The matrix elements of the two terms in equation (22) in a Hund's case (b) basis are as follows,
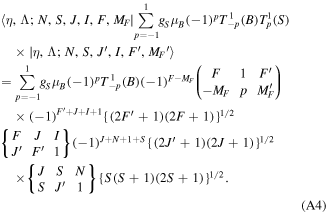
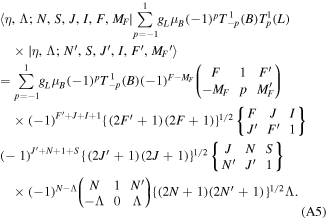
Here the magnetic field B and electronic orbital angular momentum N and electron spin S are written in the first-rank spherical tensor.
Footnotes
- 4
The ab initio calculations are performed by Molpro2012 package, and the ro-vibrational levels are acquired by LEVEL 8.0 program through solving the ro-vibrational Schrödinger equation. Furthermore, radiative lifetimes of A2Π → X2Σ+ (6.9 ns), B2Σ+ → X2Σ+ (8.8 ns) and B2Σ+ → A2Π (0.82 s) are calculated using LEVEL 8.0 program as well.