Adiabatic and thermally insulated: should they have the same meaning?

Conceptual difficulties in thermodynamics are often enhanced by the fact that some definitions and concepts are not consistently or clearly stated in the literature, their understanding becoming thus conditioned by our intuition and previous knowledge.

One such concept is that of adiabatic process, which in turn is closely related to the concept of adiabatic wall. The former is of utmost importance in thermodynamics because not only does it appear, for instance, in Caratheodory's statement of the second law [1], but it is also studied in its theoretical and practical aspects. Essentially, a process is adiabatic if the system is enclosed by adiabatic walls, i.e. walls that inhibit any flow of energy through them that would result from a temperature difference between system and surroundings. There are however other situations where, although the walls are not adiabatic, the process can still be considered adiabatic provided it is sufficiently quick to inhibit such energy flow [2, 3].

On the other hand, the term thermally insulated is often used as an alternative to adiabatic depending on the author, a situation which is evident from the references cited in [4], which use either the term adiabatic or thermally insulated indifferently. If the two terms mean the same, which is the idea tacitly assumed, there is no problem in opting for one or the other, as long as consistency is maintained when discussing topics where the concept is present.

However, our proposal is different: to continue to use the already existing terms of adiabatic and thermally insulated, but to give them different meanings. As we shall see, although in many cases the advantage in doing so is minimal, there are others where distinguishing between such terms brings added value to their understanding as it helps clarify the underlying concepts. For instance, in the case of the adiabatic piston problem, our proposal enables the adiabatic piston to be described by a process which is adiabatic but not thermally insulated, a distinction which is decisive to overcome important conceptual issues raised in the literature, see e.g. [5], with regard to this problem.

Finally, this study provides a good example of the use of symmetry as a powerful tool to clarify concepts and definitions, thereby being relevant also from a didactical and pedagogical perspective.

For the sake of intuitiveness, consider PVT systems. A system-surroundings interaction constitutes a thermodynamic process, which is assumed here to be quasistatic (reversible or irreversible) [6], meaning that the system develops through a sequence of equilibrium states, such assumption not implying loss of conceptual generality, because if the actual process is non-quasistatic, we use the concept of identical process [7], to consider in its place a quasistatic process identical to it as detailed in [8].

Given that throughout a quasistatic process all thermodynamic variables, of both system and surroundings, are defined [6], we can envisage a system-surroundings interchange and define as process-invariant an equation or quantity that remains unchanged under such interchange. In other words, a process-invariant exhibits full symmetry and does not depend on which is labelled as system or as surroundings. If subscript 'e' (for external) is used for surroundings variables, a system-surroundings interchange is a conceptual operation which corresponds solely to removing subscript 'e' from surroundings variables and assigning it to system variables. If when doing so we obtain a formally identical expression, i.e. indistinguishable from the starting one, we are faced with a process-invariant. Process-invariants are physically very relevant because they express properties of a process, which are independent of what is labelled as system or as surroundings.

Using the fundamental relation [6] and the conservation of energy, a thermodynamic process is described by the process-invariant

$$\begin{eqnarray}&&T\,{\rm{d}}S-P\,{\rm{d}}V=-{T}_{{\rm{e}}}\,{\rm{d}}{S}_{{\rm{e}}}+{P}_{{\rm{e}}}\,{\rm{d}}{V}_{{\rm{e}}},\end{eqnarray} \tag{ 1 }$$

where T, S, P and V are, respectively, temperature, entropy, pressure and volume.

Another process-invariant is the entropy generation ${\rm{d}}{S}_{{\rm{GEN}}},$ which satisfies the relation

$$\begin{eqnarray}&&{\rm{d}}{S}_{{\rm{GEN}}}={\rm{d}}S+{\rm{d}}{S}_{{\rm{e}}}\geqslant 0,\end{eqnarray} \tag{ 2 }$$

constituting a concise statement of the second law of thermodynamics. Unlike energy, which is always conserved, entropy is generated in irreversible processes, which constitutes an additional difficulty in grasping this concept. One possible interpretation of entropy is that it is generated whenever work is lost, i.e. work that is dissipated and can no longer be used as such. More precisely, entropy generation can be defined as the ratio of lost work $\delta {W}_{{\rm{Lost}}}$ by the temperature at which it was dissipated, i.e.

$$\begin{eqnarray}&&{\rm{d}}{S}_{{\rm{GEN}}}=\displaystyle \frac{\delta {W}_{{\rm{Lost}}}}{{\rm{T}}{\rm{e}}{\rm{m}}{\rm{p}}{\rm{e}}{\rm{r}}{\rm{a}}{\rm{t}}{\rm{u}}{\rm{r}}{\rm{e}}}.\end{eqnarray} \tag{ 3 }$$

A system-surroundings interchange fully preserves the boundary properties, in particular whether or not heat can flow through it. If not, the wall is called adiabatic, and therefore the property of a wall being adiabatic is process-invariant. For a non-adiabatic wall, heat crossing the wall due to the difference between the system and surroundings temperatures is anti-symmetric under a system-surroundings interchange, meaning that heat changes its sign under such an interchange (i.e. it is a flux). As this heat is closely related to differences in temperature we qualify it as calorimetric and denote it by $\delta {Q}_{{\rm{C}}}.$ In the light of lost work, how can $\delta {Q}_{{\rm{C}}}$ generate entropy?

To clarify this issue, let us compare the process shown in figure 1(a) to the one in figure 1(b). In figure 1(a), the system at temperature T is put in thermal contact with surroundings at temperature ${T}_{{\rm{e}}}\gt T$ and calorimetric heat $\delta {Q}_{{\rm{C}}}$ flows from surroundings to system, being $\delta {Q}_{{\rm{C}}}\gt 0$ since we take energy (i.e. heat and/or work) entering the system as positive (and negative otherwise). It is well-known (see e.g. [6]) that the entropy generated by such process is

$$\begin{eqnarray}&&{\rm{d}}{S}_{{\rm{GEN}}}^{{Q}_{{\rm{C}}}}=\left(\displaystyle \frac{1}{T}-\displaystyle \frac{1}{{T}_{{\rm{e}}}}\right)\,\delta {Q}_{{\rm{C}}},\end{eqnarray} \tag{ 4 }$$

but it being a pure heat interaction, how was there lost work and where was it dissipated?

Zoom In Zoom Out Reset image size

To answer this, imagine a Carnot engine (CE) working between surroundings and system, see figure 1(b). With ${T}_{{\rm{e}}}\gt T,$ we can adjust CE to remove from surroundings the same heat $\delta {Q}_{{\rm{C}}}$ that was exchanged by direct contact, producing work which is given by the well-known expression (e.g. [6])

$$\begin{eqnarray}&&{\rm{\delta }}{W}_{{\rm{L}}}^{* }=\left(1-\displaystyle \frac{T}{{T}_{{\rm{e}}}}\right)\,\delta {Q}_{{\rm{C}}},\end{eqnarray} \tag{ 5 }$$

and rejecting to the system the heat $\delta {Q}_{{\rm{C}}}^{* }\lt \delta {Q}_{{\rm{C}}}.$ Clearly, the CE being reversible and cyclic, neither $\delta {Q}_{{\rm{C}}}$ nor $\delta {Q}_{{\rm{C}}}^{* }$ contribute here to entropy generation. Therefore, in figure 1(b), only $\delta {W}_{{\rm{L}}}^{* }$ is eligible to generate entropy, from (3) such generation occurring only if there is some dissipation of $\delta {W}_{{\rm{L}}}^{* }.$ If $\delta {W}_{{\rm{L}}}^{* }$ is completely dissipated in the system, which is at temperature T, then the entropy generated is, according to (3), $\delta {W}_{{\rm{L}}}^{* }/T$ which combined with (5) gives an entropy generation expression identical to (4), thereby showing that the process that includes the system, surroundings and the CE in figure 1(b) is indistinguishable from the direct heat exchange process in figure 1(a). Such indistinguishability means that entropy generation in the direct heat exchange process can be interpreted as resulting from the work $\delta {W}_{{\rm{L}}}^{* },$ this work being designated here as lost work because it is entirely dissipated in the system.

Figure 1(c) illustrates a system-surroundings interchange where the new calorimetric heat of figure 1(a) is denoted with a prime. Lost work is now denoted by $\delta {W}_{{\rm{L}}}^{* * },$ but bearing in mind the anti-symmetry of calorimetric heat, i.e. $\delta {Q}_{{\rm{C}}}^{{\prime} }=-\delta {Q}_{{\rm{C}}},$ it is readily shown to be formally given also by (5), i.e.

$$\begin{eqnarray}&&\delta {W}_{{\rm{L}}}^{* * }=\left(1-\displaystyle \frac{T}{{T}_{{\rm{e}}}}\right)\,\delta {Q}_{{\rm{C}}}\end{eqnarray} \tag{ 6 }$$

and, if such work is completely dissipated in the system, the entropy generation is $\delta {W}_{{\rm{L}}}^{* * }/T,$ which with (6) again results in an entropy generation expression identical to (4).

Even though the above conclusion was obtained assuming ${T}_{e}\gt T$, the same result for ${\rm{d}}{S}_{{\rm{GEN}}}^{{Q}_{{\rm{C}}}}$ would have been obtained, as required by symmetry, if the other remaining possibility had been considered, i.e. keeping the choice of the system and surroundings but choosing ${T}_{{\rm{e}}}\lt T.$ Since calorimetric heat is anti-symmetric, i.e. $\delta {Q}_{{\rm{C}}}^{{\prime} }+\delta {Q}_{{\rm{C}}}=0,$ the generation of entropy given by (4) is also process-invariant.

Carefully note, however, that calorimetric heat $\delta {Q}_{{\rm{C}}}$ is not the only way to generate entropy, since work can also be lost by direct mechanical dissipation. In thermodynamics, work $\delta W$ is defined in terms of surroundings variables only [6] by

$$\begin{eqnarray}&&\delta W={P}_{{\rm{e}}}{\rm{d}}{V}_{{\rm{e}}},\end{eqnarray} \tag{ 7 }$$

unlike configuration work $\delta {W}_{{\rm{C}}}$ which is defined in terms of system variables only by

$$\begin{eqnarray}&&\delta {W}_{{\rm{C}}}=-P\,{\rm{d}}V.\end{eqnarray} \tag{ 8 }$$

While $\delta W$ is the work that surroundings exchange with the system, $\delta {W}_{{\rm{C}}}$ is the part of it that is used to configure the system. Therefore, the difference between ${P}_{{\rm{e}}}\,{\rm{d}}{V}_{{\rm{e}}}$ and $-P\,{\rm{d}}V$ is a positive (or zero) quantity that can be appropriately taken as the dissipative work $\delta {W}_{{\rm{D}}},$ i.e. [9]

$$\begin{eqnarray}&&\delta {W}_{{\rm{D}}}={P}_{{\rm{e}}}\,{\rm{d}}{V}_{{\rm{e}}}+P\,{\rm{d}}V\geqslant 0,\end{eqnarray} \tag{ 9a }$$

which, from (1), can also be written as

$$\begin{eqnarray}&&\delta {W}_{{\rm{D}}}=T\,{\rm{d}}S+{T}_{{\rm{e}}}\,{\rm{d}}{S}_{{\rm{e}}}\geqslant 0.\end{eqnarray} \tag{ 9b }$$

Dissipative work $\delta {W}_{{\rm{D}}},$ given above, is thus always positive or zero and is work that was not spent for system configuration but converted into internal energy of system and/or surroundings and, therefore, can no longer be recovered as work. In other words, ${\rm{\delta }}{W}_{{\rm{D}}}$ is also lost work that, in line with (3), generates entropy. A direct inspection of (9) shows that dissipative work is a process-invariant. Of course, since $\delta W={P}_{{\rm{e}}}{\rm{d}}{V}_{{\rm{e}}},$ first law $T\,{\rm{d}}S-P\,{\rm{d}}V=\delta Q+\delta W$ with (1) requires that heat $\delta Q$ be given by

$$\begin{eqnarray}&&\delta Q=-{T}_{{\rm{e}}}\,{\rm{d}}{S}_{{\rm{e}}}.\end{eqnarray} \tag{ 10 }$$

From the above analysis, if $\delta {W}_{{\rm{D}}}=0,$ by (7), (9) and (10), $\delta W={P}_{{\rm{e}}}\,{\rm{d}}{V}_{{\rm{e}}}=-P\,{\rm{d}}V$ and $\delta Q=-{T}_{{\rm{e}}}\,{\rm{d}}{S}_{{\rm{e}}}=T\,{\rm{d}}S,$ i.e. work and heat change sign under a system-surroundings interchange and are therefore anti-symmetric quantities (i.e. are fluxes). Moreover, since in this case ${\rm{d}}S=\delta Q/T$ and ${\rm{d}}{S}_{{\rm{e}}}=-\delta Q/{T}_{{\rm{e}}},$ the total generated entropy (2) becomes

$$\begin{eqnarray}&&{\rm{d}}{S}_{{\rm{GEN}}}=\left(\displaystyle \frac{1}{T}-\displaystyle \frac{1}{{T}_{{\rm{e}}}}\right)\,\delta Q,\end{eqnarray} \tag{ 11 }$$

which has to be equal to (4) because no entropy is generated from dissipative work if $\delta {W}_{{\rm{D}}}=0.$ Therefore, if $\delta {W}_{{\rm{D}}}=0$ we get that $\delta Q=\delta {Q}_{{\rm{C}}}.$

However, if $\delta {W}_{{\rm{D}}}\gt 0,$ the above relations ${P}_{{\rm{e}}}\,{\rm{d}}{V}_{{\rm{e}}}=-P\,{\rm{d}}V$ and $-{T}_{{\rm{e}}}\,{\rm{d}}{S}_{{\rm{e}}}=T\,{\rm{d}}S$ are no longer valid and, therefore, the anti-symmetry of the terms in (1) is broken, resulting in some conceptual difficulties, namely the somewhat counterintuitive fact that work and heat are no longer fluxes. In other words, for $\delta {W}_{{\rm{D}}}\gt 0,$ under a system-surroundings interchange not only the signs of heat and work change but also their absolute values. Evidently, the calorimetric heat $\delta {Q}_{{\rm{C}}}$ should remain a flux and can no longer be identified with $\delta Q.$ Thus, the heat $\delta Q=-{T}_{{\rm{e}}}\,{\rm{d}}{S}_{{\rm{e}}}$ must now contain a non anti-symmetric component, which is denoted here by $\delta {Q}_{{\rm{D}}}$ as it is a consequence of the existence of $\delta {W}_{{\rm{D}}},$ i.e.

$$\begin{eqnarray}&&\delta Q=\delta {Q}_{{\rm{C}}}+\delta {Q}_{{\rm{D}}},\end{eqnarray} \tag{ 12 }$$

which, from (9b) and (10), can also be written as

$$\begin{eqnarray}&&\delta Q=T\,{\rm{d}}S-\delta {W}_{{\rm{D}}}\end{eqnarray} \tag{ 13 }$$

showing that, since $\delta {W}_{{\rm{D}}}\geqslant 0,$ we get that $T\,{\rm{d}}S\geqslant \delta Q,$ a well-known [10] thermodynamics expression where the equality sign corresponds to processes for which $\delta {W}_{{\rm{D}}}=0$ and the inequality one to those for which $\delta {W}_{{\rm{D}}}\gt 0,$ by contrast to the Clausius relation ${T}_{{\rm{e}}}\,{\rm{d}}S\geqslant \delta Q$ where the former sign corresponds to reversible processes and the latter to irreversible ones [10].

Figure 2 illustrates the work interaction, and the fact that work is defined by (7) as $\delta W={P}_{{\rm{e}}}\,{\rm{d}}{V}_{{\rm{e}}}$ means that the sum of all work-related arrow-lines connecting to surroundings (or to system) should be ${P}_{{\rm{e}}}\,{\rm{d}}{V}_{{\rm{e}}},$ implying that there can be no other work-related arrow-line connected to surroundings. So, the reading of the figure 2 is that surroundings interact with the system through work $\delta W,$ part of it, $\delta {W}_{{\rm{C}}},$ being used for system configuration and the other part, ${\rm{\delta }}{W}_{{\rm{D}}},$ being entirely lost by dissipation into the system. However, this conclusion is paradoxical: since $\delta {W}_{{\rm{D}}}$ is process-invariant, i.e. it exhibits total symmetry, the fact that it can only influence the system breaks this symmetry, resulting in a contradiction. Such contradiction is all the more evident if we consider a system-surroundings interchange, because the dissipation of work now occurs where, before the interchange, was surroundings, and physics cannot depend on which is chosen as system or as surroundings.

Zoom In Zoom Out Reset image size

An attempt to solve this contradiction is to understand the effect of $\delta {W}_{{\rm{D}}}$ on surroundings as heat, the natural choice being the heat component $\delta {Q}_{{\rm{D}}}$ that appears in (12) as a consequence of the existence of $\delta {W}_{{\rm{D}}}.$ But how can heat be involved in a pure work interaction such as that shown in figure 2? And even if it were, if ${T}_{{\rm{e}}}\gt T$ how can heat flow from system to surroundings?

If ${T}_{{\rm{e}}}\gt T,$ we may consider that instead of all ${\rm{\delta }}{W}_{{\rm{D}}}$ being dissipated in the system, part of it, say $\delta {W}^{* },$ feeds a Carnot refrigerator (CR) that removes the heat $\delta {Q}^{* }$ from the system and supplies the heat $\delta {Q}_{{\rm{D}}}$ to surroundings, as shown in figure 3(a). On the other hand, if ${T}_{{\rm{e}}}\lt T$ the heat removed from the system and the one supplied to surroundings are accomplished through a CE, producing the work $\delta {W}^{* }$ which we choose to be dissipated in the system, so that the net work dissipated in the system is $\delta {W}_{{\rm{D}}}+\delta {W}^{* },$ as shown in figure 3(b). Since $\delta {Q}_{{\rm{D}}}$ is an attempt to explain the effect of $\delta {W}_{{\rm{D}}}$ in surroundings, it must be negative and satisfy

$$\begin{eqnarray}&&0\leqslant -\delta {Q}_{{\rm{D}}}\leqslant \delta {W}_{{\rm{D}}}\end{eqnarray} \tag{ 14 }$$

or, equivalently,

$$\begin{eqnarray}&&\delta {Q}_{{\rm{D}}}=-{\alpha }_{{\rm{e}}}\delta {W}_{{\rm{D}}},\,{\rm{with}}\,0\leqslant {\alpha }_{{\rm{e}}}\leqslant 1.\end{eqnarray} \tag{ 15 }$$

Zoom In Zoom Out Reset image size

Adopting the sign convention that $\delta {W}^{* }\lt 0$ for the CR and $\delta {W}^{* }\gt 0$ for the CE, as shown in figure 3, in both cases the lost work by dissipation in the system is given by $\delta {W}_{{\rm{D}}}+{\rm{\delta }}{W}^{* },$ which, using (3), gives

$$\begin{eqnarray}&&{\rm{d}}{S}_{{\rm{GEN}}}^{{W}_{{\rm{D}}}}=\displaystyle \frac{\delta {W}_{{\rm{D}}}+\delta {W}^{* }}{T}.\end{eqnarray} \tag{ 16 }$$

The work supplied to CR or produced by CE is given by (5) with $\delta {Q}_{{\rm{D}}}$ instead of $\delta {Q}_{{\rm{C}}},$ i.e.

$$\begin{eqnarray}&&\delta {W}^{* }=\left(1-\displaystyle \frac{T}{{T}_{{\rm{e}}}}\right)\,\delta {Q}_{{\rm{D}}}.\end{eqnarray} \tag{ 17 }$$

So, inserting (17) into (16) and using (15), we get

$$\begin{eqnarray}&&{\rm{d}}{S}_{{\rm{GEN}}}^{{W}_{{\rm{D}}}}=\left(\displaystyle \frac{\alpha }{T}+\displaystyle \frac{{\alpha }_{{\rm{e}}}}{{T}_{{\rm{e}}}}\right)\,\delta {W}_{{\rm{D}}},\end{eqnarray} \tag{ 18 }$$

where $\alpha$ and ${\alpha }_{{\rm{e}}}$ are related by

$$\begin{eqnarray}&&\alpha +{\alpha }_{{\rm{e}}}=1.\end{eqnarray} \tag{ 19 }$$

Performing a system-surroundings interchange and remembering that after the interchange the new quantities are denoted with a prime, $\delta {W}_{{\rm{D}}}$ being process-invariant, (15) becomes

$$\begin{eqnarray}&&\delta {Q}_{{\rm{D}}}^{{\prime} }=-\alpha \,\delta {W}_{{\rm{D}}},\,{\rm{with}}\,0\leqslant \alpha \leqslant 1,\end{eqnarray} \tag{ 20 }$$

which with (15) gives

$$\begin{eqnarray}&&\delta {Q}_{{\rm{D}}}+\delta {Q}_{{\rm{D}}}^{{\prime} }=-\delta {W}_{{\rm{D}}},\end{eqnarray} \tag{ 21 }$$

showing that under a system-surroundings interchange, dissipative heat $\delta {Q}_{{\rm{D}}}$ is not anti-symmetric, because $\delta {Q}_{{\rm{D}}}+\delta {Q}_{{\rm{D}}}^{{\prime} }\ne 0,$ unlike calorimetric heat $\delta {Q}_{{\rm{C}}}$ which satisfies

$$\begin{eqnarray}&&\delta {Q}_{{\rm{C}}}+\delta {Q}_{{\rm{C}}}^{{\prime} }=0.\end{eqnarray} \tag{ 22 }$$

Figure 4(a) is a unified version of figure 3, showing quantities that model the work interaction. Figure 4(b) shows how quantities in figure 4(a) change under a system-surroundings interchange.

Zoom In Zoom Out Reset image size

Adding (4) with (18), the total generated entropy is given by

$$\begin{eqnarray}&&{\rm{d}}{S}_{{\rm{GEN}}}=\left(\displaystyle \frac{1}{T}-\displaystyle \frac{1}{{T}_{{\rm{e}}}}\right)\,\delta {Q}_{{\rm{C}}}+\left(\displaystyle \frac{\alpha }{T}+\displaystyle \frac{{\alpha }_{{\rm{e}}}}{{T}_{{\rm{e}}}}\right)\,\delta {W}_{{\rm{D}}},\end{eqnarray} \tag{ 23 }$$

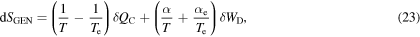
an equation that, as it should, shows that the total generated entropy ${\rm{d}}{S}_{{\rm{GEN}}}$ is a process-invariant, i.e. applying the transformation $\{T\leftrightarrow {T}_{{\rm{e}}};\,\alpha \leftrightarrow {\alpha }_{{\rm{e}}};\,\delta {Q}_{{\rm{C}}}\leftrightarrow -\delta {Q}_{{\rm{C}}};\,\delta {W}_{{\rm{D}}}\leftrightarrow \delta {W}_{{\rm{D}}}\}$ (23) remains unchanged. It is important to note that to fully characterize the process it is necessary to introduce the new parameters $\alpha$ and ${\alpha }_{{\rm{e}}},$ which satisfy $\alpha +{\alpha }_{{\rm{e}}}=1$ and whose meanings were already explained. Finally, being the entropy generation always determined by (3) and since the lost work, given by $\delta {W}_{{\rm{L}}}^{* }$ or $\delta {W}_{{\rm{L}}}^{* * }$ for the heat interaction in figure 1 and by $\delta {W}_{{\rm{D}}}+{\rm{\delta }}{W}^{* }$ for the work interaction in figure 3, is always dissipated in the system, the answer to the question of where entropy is generated is that it always is in the system, in line with Prigogine (see p 16 of [11]). Consequently, no entropy generation occurs in surroundings, being this the fundamental characteristic underlying the reservoir concept.

As far as known to us, a distinction between $\delta Q$ and $\delta {Q}_{{\rm{C}}}$ is virtually absent from textbooks, which propitiates confusion between them, or the assumption of their equivalence. Moreover, such distinction also suggests a distinction between the concepts of adiabatic and thermally insulated, which is the main purpose of this study. Given that before a system-surroundings interchange, see (12), $\delta Q=\delta {Q}_{{\rm{C}}}+\delta {Q}_{{\rm{D}}}$ and after such interchange $\delta Q^{\prime} =\delta {Q}_{{\rm{C}}}^{{\prime} }+\delta {Q}_{{\rm{D}}}^{{\prime} },$ from (21) and (22), we get $\delta Q+\delta Q^{\prime} =-\delta {W}_{{\rm{D}}}$ meaning that, if $\delta Q=0,$ $\delta Q^{\prime}$ is not necessarily zero which contradicts the definition of adiabatic process as one for which $\delta Q=0,$ since such definition does not exhibit invariance under a system-surroundings interchange, i.e. the adiabatic concept should not depend on which is labelled as system or surroundings. Therefore, we propose defining adiabatic process as one for which $\delta {Q}_{{\rm{C}}}=0$ and not one for which $\delta Q=0.$ Moreover, as mentioned earlier, since wall properties exhibit the same symmetry as $\delta {Q}_{{\rm{C}}}$ under a system-surroundings interchange, and the adiabatic wall definition has to be compatible with that of adiabatic process, an adiabatic wall should be defined as one that inhibits $\delta {Q}_{{\rm{C}}}$ and not one that inhibits $\delta Q.$ On the other hand, we propose that $\delta Q=0$ be the defining condition for a thermally insulated process. Except when $\delta Q=\delta {Q}_{{\rm{C}}}$ (i.e. $\delta {Q}_{{\rm{D}}}=0$ which happens, from (15) with (19), when $\delta {W}_{{\rm{D}}}=0$ or $\alpha =1$), with these new definitions, the terms 'adiabatic' and 'thermally insulated' take on different meanings, even though they have up to now been used indifferently in the literature (see [4] and references therein).

Before concluding it is worth underlining some implications of the definitions proposed in this study. One of them is that defining calorimetric heat in terms of its symmetry property using (22) dispels apparent difficulties in reconciling the concept of calorimetric heat with that of temperature difference in the case of a reversible process, and with wall properties in the case of the adiabatic piston's second process [5]. Firstly, consider the reversible process. If the definition of $\delta {Q}_{{\rm{C}}}$ is made to depend on temperature difference between the system and surroundings, in reversible processes $\delta {Q}_{{\rm{C}}}$ has to be zero because for such ideal processes $T={T}_{{\rm{e}}},$ an apparent contradiction which is usually addressed by considering a reversible process as the limit of a succession of irreversible processes with a constant $\delta {Q}_{{\rm{C}}}\ne 0$ for which $| \,T-{T}_{{\rm{e}}}|$ of each succession term becomes arbitrarily small. However, by using the symmetry of (22), $\delta {Q}_{{\rm{C}}}$ is defined even though $T={T}_{{\rm{e}}}.$ Secondly, consider the case of the so-called adiabatic piston, which is another example where $\delta {Q}_{{\rm{C}}}$ is better defined using (22) rather than resorting to wall thermal properties. In fact, after mechanical equilibrium is reached ($P={P}_{{\rm{e}}}$ but $T\ne {T}_{{\rm{e}}}$), the piston undergoes a second process, which lasts until thermalization is reached ($T={T}_{{\rm{e}}}$) [5]. Therefore, even though the piston has zero thermal conductivity, the piston has to be considered non-adiabatic, because thermalization requires heat flow through it [5]. As dissipative work is absent during this process such heat has to be calorimetric, i.e. it satisfies (22), and thus there is no conflict with the zero thermal conductivity of the piston, since (22) applies regardless of wall thermal properties.

Furthermore, using (13), system entropy variation dS can be expressed as

$$\begin{eqnarray}&&{\rm{d}}S=\displaystyle \frac{\delta Q}{T}+\displaystyle \frac{\delta {W}_{{\rm{D}}}}{T},\end{eqnarray} \tag{ 24a }$$

or equivalently, inserting (12) and (21) in (24a), and using (20),

$$\begin{eqnarray}&&{\rm{d}}S=\displaystyle \frac{\delta {Q}_{{\rm{C}}}}{T}+\displaystyle \frac{\alpha \,\delta {W}_{{\rm{D}}}}{T},\end{eqnarray} \tag{ 24b }$$

meaning that both for $\delta Q=0$ and $\delta {Q}_{{\rm{C}}}=0$ we have ${\rm{d}}S\geqslant 0,$ i.e. the principle of entropy increase, which was commented in [4], can now be formulated as follows: both for thermally insulated ($\delta Q=0$) and for adiabatic ($\delta {Q}_{{\rm{C}}}=0$) processes the system entropy cannot decrease. However, an important difference exists between the two: while for a thermally insulated process system entropy increases or remains unchanged depending on whether the process is irreversible or reversible, respectively, for an adiabatic process system entropy remains unchanged, not only for reversible processes, but also for those irreversible processes where $\alpha =0,$ i.e. those for which $\delta {Q}_{{\rm{D}}}=-\delta {W}_{{\rm{D}}},$ see (15) with (19). Moreover, since the second rhs term in (24b) is always positive or zero, the decrease in entropy of a system can only be achieved by means of calorimetric heat, that is, the process cannot be adiabatic.

Finally, let us note that our proposal is compatible with the Caratheodory statement of the second law, which states [1]: in the neighbourhood (however close) of any equilibrium state of a system of any number of independent coordinates, there exist other equilibrium states which are inaccessible by means of reversible adiabatic processes. In the case of the above statement, the process being reversible, one has $\delta {W}_{{\rm{D}}}=0$ and the concepts of adiabatic and thermally insulated coincide, i.e. $\delta {Q}_{{\rm{C}}}=\delta Q=0,$ and thus our proposal is peaceful.

The concepts of process-invariant and of lost work, defined, respectively, as an equation or quantity that remains invariant under a system-surroundings interchange and work that becomes unusable as such, were applied in the context of entropy generation being interpreted as the ratio of lost work by the temperature at which it is dissipated. It was found that entropy generation always occurs in the system, i.e. no entropy is generated in surroundings, the latter being the fundamental characteristic underlying the reservoir concept. Is was also shown that the effect dissipative work has on surroundings is equivalent to a heat interaction, leading to distinguish between calorimetric heat $(\delta {Q}_{{\rm{C}}})$ and heat $(\delta Q)$ which in turn propitiated a distinction between adiabatic and thermally insulated processes, the former being now defined as one for which $\delta {Q}_{{\rm{C}}}=0$ and the latter as one for which $\delta Q=0.$ The proposed distinction between adiabatic and thermally insulated dispelled apparent difficulties in reconciling the concept of calorimetric heat with that of temperature difference in the case of a reversible process, and with wall properties in the case of the adiabatic piston's second process. Lastly, although for both thermally insulated $(\delta Q=0)$ and adiabatic $(\delta {Q}_{{\rm{C}}}=0)$ processes system entropy cannot decrease, an important difference exists between the two: while for thermally insulated process the system entropy increases or remains unchanged depending, respectively, on whether the process is irreversible or reversible, for an adiabatic process system entropy remains unchanged not only for reversible processes, but also for those irreversible processes where dissipative work is entirely converted into dissipative heat $\delta {Q}_{{\rm{D}}},$ the latter being defined as $\delta {Q}_{{\rm{D}}}=\delta Q-\delta {Q}_{{\rm{C}}}.$