Abstract
We point out that the anomalous threshold effect in one dimension occurs when the reflection probability at zero energy R(0) has some other value than unity, rather than  or
or  as implied by Ahmed et al in their paper entitled 'The paradoxical zero reflection at zero energy' (2017 Eur. J. Phys. 38 025401).
as implied by Ahmed et al in their paper entitled 'The paradoxical zero reflection at zero energy' (2017 Eur. J. Phys. 38 025401).
Export citation and abstract BibTeX RIS
We have read with interest the article by Ahmed et al [1] dealing with the anomalous threshold effect in the one-dimensional scattering problem. The authors discuss the reflection probability  , which normally is unity at zero energy, i.e.,
, which normally is unity at zero energy, i.e.,  . However the exception, or anomaly, occurs when the interaction, which the scattering particle is subject to, supports a zero-energy bound state, in particular a half-bound state, i.e., a non-normalizable zero-energy bound state. The authors consider the cases when
. However the exception, or anomaly, occurs when the interaction, which the scattering particle is subject to, supports a zero-energy bound state, in particular a half-bound state, i.e., a non-normalizable zero-energy bound state. The authors consider the cases when  or
or 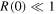 . We would like to supplement the authors' conclusions by pointing out that the anomaly includes the range of values for the reflection coefficient
. We would like to supplement the authors' conclusions by pointing out that the anomaly includes the range of values for the reflection coefficient 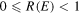 when there is a half-bound state and E is zero or very small.
when there is a half-bound state and E is zero or very small.
In the original discussion of the threshold anomaly in one-dimension, Senn [2] already pointed out that R(0) can have any value between 0 and 1. See, for example, Senn's figure 1 [2]. Nogami and Ross [3] considered two classes of anomaly due to half-bound states: class I has 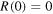 for symmetric potentials, and class II with
for symmetric potentials, and class II with 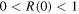 for asymmetric potentials. Kiers and van Dijk [4] reached the same conclusions from the analysis of N-channel one-dimensional systems with general symmetric and asymmetric interactions. de Bianchi also discussed the threshold behaviour [5].
for asymmetric potentials. Kiers and van Dijk [4] reached the same conclusions from the analysis of N-channel one-dimensional systems with general symmetric and asymmetric interactions. de Bianchi also discussed the threshold behaviour [5].
Figure 1. The reflection amplitude when E = 0 as a function of λ when the potential supports a half-bound state.
Download figure:
Standard image High-resolution imageTo illustrate these features, which are true in general3 , we use the well-known example of a two-delta function potential,
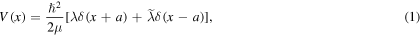
where μ is the (reduced) mass of the particle(s) and 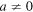 . In the formulation below we use results, reduced to the single channel case, from section III.B.2 of [4]. The wave function has asymptotic form
. In the formulation below we use results, reduced to the single channel case, from section III.B.2 of [4]. The wave function has asymptotic form
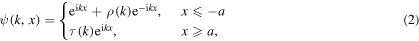
where 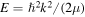 , and
, and 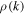 and
and 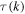 are the reflection and transmission amplitudes, respectively. The reflection amplitude is
are the reflection and transmission amplitudes, respectively. The reflection amplitude is
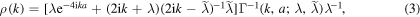
where
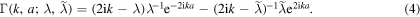
The reflection probability is 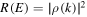 . It can be shown that the bound-state energies occur at the pure imaginary poles of reflection amplitude, so that the condition for these energies is
. It can be shown that the bound-state energies occur at the pure imaginary poles of reflection amplitude, so that the condition for these energies is

where 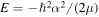 . By setting
. By setting 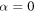 in (5), we have the condition on
in (5), we have the condition on 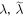 and a such that the system presents a half-bound state. The condition is the simple relation
and a such that the system presents a half-bound state. The condition is the simple relation
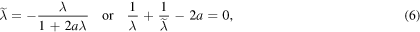
which is equivalent to equation (6.16) of [3].
Let us first consider the reflection amplitude at zero energy which is a real quantity. For graphing purposes we choose units so that the basic unit of length is a and of energy is  . In other words, both quantities are set to unity. In figure 1 we plot
. In other words, both quantities are set to unity. In figure 1 we plot  as a function λ when relation (6) is satisfied, so that for each value of λ the potential supports a half-bound state. Since
as a function λ when relation (6) is satisfied, so that for each value of λ the potential supports a half-bound state. Since  is complex when
is complex when  , we plot
, we plot 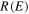 as a function of λ for the half-bound cases for two energies, E = 0 and 0.25, in figure 2. Different (small) values of E yield similar curves. It should be noted that
as a function of λ for the half-bound cases for two energies, E = 0 and 0.25, in figure 2. Different (small) values of E yield similar curves. It should be noted that 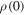 is a discontinuous function of the potential strength when it passes through the critical point at which
is a discontinuous function of the potential strength when it passes through the critical point at which 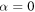 [6].
[6].
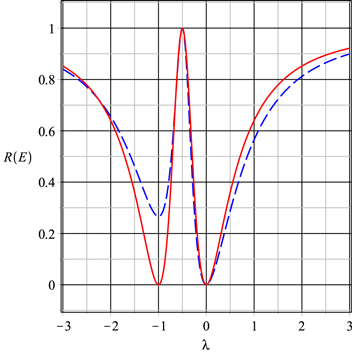
Figure 2. The reflection probability at E = 0 (solid red line) and at 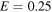 (dashed blue line) as a function of λ when the potential supports a half-bound state.
(dashed blue line) as a function of λ when the potential supports a half-bound state.
Download figure:
Standard image High-resolution imageFrom both figures it is clear that when there is a half-bound state, the reflection probability at threshold has a range 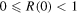 . At
. At  ,
, 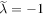 , and the symmetric potential obtains, and
, and the symmetric potential obtains, and  . When
. When  the potential is zero, and
the potential is zero, and 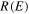 vanishes. When
vanishes. When 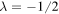 ,
,  and the potential is an infinite barrier. Then R(0) has the normal value of unity. From (6) it is clear that the antisymmetric potential, i.e.,
and the potential is an infinite barrier. Then R(0) has the normal value of unity. From (6) it is clear that the antisymmetric potential, i.e., 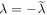 , occurs only when
, occurs only when  . For all other λ the potential is asymmetric and
. For all other λ the potential is asymmetric and 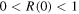 . In conclusion it is appropriate to speak of a threshold anomaly when
. In conclusion it is appropriate to speak of a threshold anomaly when 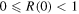 , rather than just
, rather than just 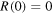 or
or 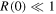 .
.
Footnotes
- 3
The anomalous threshold effect in one-dimension was examined in a general framework in [3]. In that reference no explicit form of the potential was assumed.