Abstract
First-principles calculations are used to characterize the bulk elastic properties of cubic and tetragonal phase metal dihydrides, 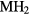 {
{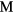 = Sc, Y, Ti, Zr, Hf, lanthanides} to gain insight into the mechanical properties that govern the aging behavior of rare-earth di-tritides as the constituent 3H, tritium, decays into 3He. As tritium decays, helium is inserted in the lattice, the helium migrates and collects into bubbles, that then can ultimately create sufficient internal pressure to rupture the material. The elastic properties of the materials are needed to construct effective mesoscale models of the process of bubble growth and fracture. Dihydrides of the scandium column and most of the rare-earths crystalize into a cubic phase, while dihydrides from the next column, Ti, Zr, and Hf, distort instead into the tetragonal phase, indicating incipient instabilities in the phase and potentially significant changes in elastic properties. We report the computed elastic properties of these dihydrides, and also investigate the off-stoichiometric phases as He or vacancies accumulate. As helium builds up in the cubic phase, the shear moduli greatly soften, converting to the tetragonal phase. Conversely, the tetragonal phases convert very quickly to cubic with the removal of H from the lattice, while the cubic phases show little change with removal of H. The source and magnitude of the numerical and physical uncertainties in the modeling are analyzed and quantified to establish the level of confidence that can be placed in the computational results, and this quantified confidence is used to justify using the results to augment and even supplant experimental measurements.
= Sc, Y, Ti, Zr, Hf, lanthanides} to gain insight into the mechanical properties that govern the aging behavior of rare-earth di-tritides as the constituent 3H, tritium, decays into 3He. As tritium decays, helium is inserted in the lattice, the helium migrates and collects into bubbles, that then can ultimately create sufficient internal pressure to rupture the material. The elastic properties of the materials are needed to construct effective mesoscale models of the process of bubble growth and fracture. Dihydrides of the scandium column and most of the rare-earths crystalize into a cubic phase, while dihydrides from the next column, Ti, Zr, and Hf, distort instead into the tetragonal phase, indicating incipient instabilities in the phase and potentially significant changes in elastic properties. We report the computed elastic properties of these dihydrides, and also investigate the off-stoichiometric phases as He or vacancies accumulate. As helium builds up in the cubic phase, the shear moduli greatly soften, converting to the tetragonal phase. Conversely, the tetragonal phases convert very quickly to cubic with the removal of H from the lattice, while the cubic phases show little change with removal of H. The source and magnitude of the numerical and physical uncertainties in the modeling are analyzed and quantified to establish the level of confidence that can be placed in the computational results, and this quantified confidence is used to justify using the results to augment and even supplant experimental measurements.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
I. Introduction
Rare earth metals (lanthanides) and many transition metals readily form hydrides, making them useful for storage of hydrogen and its isotopes. The rare-earth metal hydrides are particularly suitable materials for long term storage of tritium. Erbium tritide has been frequently studied [1–4] as a prominent example of such a material, with the goal to gain insight into the aging process as the tritium decays. The decay of tritium into helium introduces a complication not present in conventional studies of hydride chemistry, as the composition of the material changes via radioactive decay of the constituent tritium, 3H. The consequent build-up of helium, 3He, in the material ultimately leads to formation of high-pressure He bubbles [2]. This pressure can eventually rupture the material, the release of helium leading to failure of devices dependent upon the integrity of the material.
Fundamental understanding is lacking in each step of this degradation process—nucleation of bubbles, migration of He through the lattice to the bubbles, bubble growth, coalescence of bubbles, and finally fracture and release—and integrating these individual physical scales into an useful and actionable comprehensive understanding is an ongoing challenge for effective modeling and simulation to quantify aging effects in tritides. Some progress has been made in microstructural-scale models of tritide aging and helium bubble growth and resultant fracture [5–9], which examine the evolution of bubbles and quantify the structural integrity of the material before fracture. These models are dependent upon empirical parameters such as the initial bubble nucleation density and, the focus of this study, the elastic properties of the target tritide [10–12]. It is not the purpose of this paper to assess the relative merits of these models, but rather speak to the requirements of quantified mechanical properties of the materials that are common to all of them. These data are difficult to obtain experimentally. Rare-earth hydrides samples are exceedingly brittle, partly because of a 10–15% lattice expansion upon hydriding. While thin film samples can be manufactured that lack the brittleness of their bulk counterparts, these films are not amenable to standard techniques used to measure bulk elastic properties. First-principles calculations are particularly well-suited for this purpose and, furthermore, also can provide insight into the causes of the changes in mechanical behavior. While the energetics and electronic properties of these hydrides have been frequently studied [13–15], these crucial elastic properties have received much less attention.
Our investigation centers around ErH2. ErH2 has been the subject of several first-principles studies looking at the defects and impurities, seeking to identify and quantify the atomic processes that govern the material chemical evolution [16–18]. Stoichiometric ErH2, just as most of its rare earth (RE) brethren, crystallizes into a CaF2 structure (Fm m, #225), a cubic (fcc) form illustrated in figure 1. Almost all the rare earth dihydrides (including the dihydrides of all the Group IIIB metals, Sc, Y, and La,), also form a bulk ground state in the CaF2 structure. Shifting one column to the right in the Periodic table, the Group-IVB TiH2, ZrH2, and HfH2 instead form a tetragonally distorted fluorite structure (I4/mmm, #139), where the cube in figure 1 is compressed along one axis.
m, #225), a cubic (fcc) form illustrated in figure 1. Almost all the rare earth dihydrides (including the dihydrides of all the Group IIIB metals, Sc, Y, and La,), also form a bulk ground state in the CaF2 structure. Shifting one column to the right in the Periodic table, the Group-IVB TiH2, ZrH2, and HfH2 instead form a tetragonally distorted fluorite structure (I4/mmm, #139), where the cube in figure 1 is compressed along one axis.
Figure 1. CaF2 fcc crystal structure of 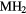 . The large grey spheres represent the metal
. The large grey spheres represent the metal 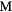 atoms and the small white spheres represent the hydrogen atoms.
atoms and the small white spheres represent the hydrogen atoms.
Download figure:
Standard image High-resolution imageThe analysis of the energies of this structural distortion has been often studied [15, 19–22]. The consensus for the cause of the distortion of the crystal into the tetragonal form has coalesced around the high density of states (DOS) at the Fermi level for the Group IVB dihydrides. This high DOS has been associated with a John-Teller-like instability, that drives this distortion, although that interpretation has recently been disputed [22]. The band structure of these materials bear great similarity to one another, demonstrated in many of these studies [15, 19–22]. A rigid band picture of occupation has been proposed to rationalize the properties [15], with the changes being determined by the position of the Fermi level—the number of valence electrons—in a mostly similar band structure. This indicates that there will be a strong dependence of the elastic properties upon the stoichiometry. This dependence might need to be incorporated in any microstructural model to obtain accurate description of the material aging.
The stoichiometry of the material is initially determined by the manufacturing, and then modified by entropic effects, which can create vacancies in the H lattice and create H interstitials. In addition, in the tritide, the aging process also modifies the stoichiometry over time. As the 3H decays, 3He is generated in the lattice. The modest nuclear recoil energy in this decay, ∼1 eV, is insufficient to cause atomic displacement, leaving the daughter helium atom initially near the same location as its tritium parent. To dislodge a 3He from a tetrahedral site into the lattice requires an activation energy of 1.31 eV [16] in Er2.
In a rigid band picture, this transmutation of hydrogen into helium fills more of the band structure, shifting it toward a band filling and Fermi level that favors a tetragonal distortion. In the aging material, however, the He is observed not to stay in place long enough for sufficient buildup of He to cause a distortion. Instead, the He migrates away to join bubbles, leaving behind a H vacancy and substoichiometric hydride. We investigate the importance of these stoichiometry changes on the elastic properties of the material through an atom-potential averaging method. Changing the nuclear charge on the H atom, increasing its charge toward He to model an average population of He substituting for H, decreasing its charge to model partial vacancy population on the H site, we probe the elastic properties of the resultant off-stoichiometric material. First-principles results of the energetics of these dihydrides, particularly in the tetragonal distortions of the Group-IVB dihydrides, have not given consistent results [15, 19, 22], and calculations of elastic constants in metals are particularly prone to numerical problems [23, 24]. In this work, we apply particularly careful attention to the numerical aspects of the modeling that inject uncertainties into the computation of structure and elastic constants. Examination of the convergence behavior provides numerical uncertainties that quantify the level of confidence in the simulations, and key results are verified through comparison of different means of computation and through comparisons to experiments.
II. Computational details
We used the generalized gradient approximation with the Perdew, Burke, Ernzerhof (PBE) functional [25] for all the density functional theory (DFT) calculations. The rationale for using PBE and not the local density approximation (LDA) [26] had been discussed previously [16]: the LDA is unable to describe the ground state structure of the Er bulk metal correctly, disqualifying it for the longer-term goals of the study. Additional details for the Er-H calculations can also be found in this previous work [16], salient details are summarized here.
The DFT calculations for Er, Group-IIIB and Group-IVB hydrides were done with SeqQuest [27], using Hamann-type generalized norm-conserving pseudopotentials [28], and well-optimized, valence double-ζ plus polarization, contracted Gaussian basis sets. The metal atoms all included their respective semi-core p-shell in the valence, and then added a non-linear core correction [29] to treat the non-linear exchange-correlation effects of the valence electrons interacting with the core, using a cutoff radius that was tested to be converged to an asymptotic full-core limit. The hydrogen atom pseudopotential was generated using a new method by Hamann [30] (verified to give equivalent results to the standard Hamann pseudopotentials [31]). To represent non-integral charge off-hydrogen atoms Hz, 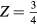 ,
,  , and
, and  atoms, standard Hamann pseudopotentials [28] were developed. All the hydrogen and off-hydrogen atoms used triple-ζ- s plus single-ζ- p polarization basis sets. The triple-ζ- s results are almost identical to results using the double-ζ- s results for the metal hydrides.
atoms, standard Hamann pseudopotentials [28] were developed. All the hydrogen and off-hydrogen atoms used triple-ζ- s plus single-ζ- p polarization basis sets. The triple-ζ- s results are almost identical to results using the double-ζ- s results for the metal hydrides.
All the SeqQuest DFT calculations were done in the 3-atom primitive cells using a 243 real space grid: the fcc rhombohedral unit cell for the cubic phase and the corresponding distorted cell for the tetragonal phase.
The transition metal dihydrides considered here are non-magnetic. For the Er and other rare-earth dihydrides, any magnetism is confined to the f-electrons. The lanthanide series fills the first shell of f-electrons, electrons localized very close to the metal core and only weakly interacting with valence electrons. These only very minimally affect the bonding in the hydrides. For computational convenience, the f-electrons (and, hence, all magnetism) have been place in the core of the pseudopotential. Spin effects in the hydrides are ignored throughout this work.
These dihydrides are all metallic, requiring an artificial electronic temperature to converge. We use a simple Fermi function with an effective electronic temperature of ∼41 meV. While artificial electron temperatures can skew results, particularly causing discrepancies between stress- and energy-derived quantities [24], the consistency checks below indicate that this modest electronic temperature is small enough to be converged to the 0 K limit, well within the other numerical uncertainties in the calculation.
Calculations of elastic constants, particularly shear moduli, can be very sensitive to k-point sampling [23, 24] and other computational model parameters, so extra diligence was exercised to converge and verify these results. The calculations (see below) sampled the Brillouin Zone with regular grids ranging from 83 through 203 (in some cases, to 243) centered at 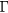 . Zone samples less than 123 were typically poorly converged, those denser than 123 exhibited random scatter about a single value. We adopt the (unweighted) average of results from samples with k-point samples 133 and larger as the 'k-limit' converged bulk value, and the range of scatter about that k-limit value to represent the uncertainty. The optimal lattice constant converges relatively quickly with k-point sampling, hence, all elastic constants (for every k-sample) were computed at the k-limit lattice constant.
. Zone samples less than 123 were typically poorly converged, those denser than 123 exhibited random scatter about a single value. We adopt the (unweighted) average of results from samples with k-point samples 133 and larger as the 'k-limit' converged bulk value, and the range of scatter about that k-limit value to represent the uncertainty. The optimal lattice constant converges relatively quickly with k-point sampling, hence, all elastic constants (for every k-sample) were computed at the k-limit lattice constant.
The elastic constants were computed from linear fits to the strain derivatives of the appropriate component of the computed stress tensor, obtained as finite differences between stress calculations for strains of 0.001 to 0.008, in increments of 0.001 (0.1%). For the cubic crystals, two strains, a compression along the z-axis and the xz-shear, were sufficient to obtain the three unique elastic constants. For the tetragonal crystal, an x-axis compression and yz-axis shear were added to obtain the additional unique elastic constants. The real-space integral cutoffs were extended to converge the stress tensor calculations sufficiently to extract numerically meaningful stress derivatives from the small incremental strain calculations. In the sheared crystals, it is necessary to relax the (hydrogen) atoms in order to get the ground state of the relaxed crystals, the need to resolve accurate stress derivatives from stress differences for such small strains required that atomic configurations be much more finely converged than for typical configuration relaxations, to forces less than 0.26 meV 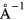 .
.
As a verification of the stress-derived results, the bulk modulus was also computed from fits to the potential energy surface. For the cubic crystal, fixed point DFT calculations were performed for 13–15 regularly spaced lattice parameters (0.02 Bohr increments, to ∼±1.5%) about the equilibrium lattice constant, and fit with a Birch–Murnaghan equation of state, using a third order polynomial [32–34]. Previous experience indicates that the uncertainties in the computed bulk modulus—from the number and selection of the sample points, form of the equation of state, etc—are about 1 GPa, and this experience is reflected in the results presented later. For the tetragonal crystals, the sampling points for the equation of state calculations were obtained from a series of cell-optimization calculations with applied pressures. Cells were optimized with applied pressures ranging from +12 GPa to −12 GPa, in increments of 1 GPa. The resulting cell volumes and energies, like the cubic crystals, were fit with a Birch–Murnaghan equation of state, again using a third order polynomial. As seen later, these potential energy fits for the tetragonal crystal also have an apparent accuracy of ∼1 GPa.
Additional density functional theory calculations, to compute the elastic constants of cubic rare earth hydrides, were performed with the Vienna ab initio simulation package (VASP) [35], using the projector augmented wave (PAW) method. The PAW pseudopotentials were taken from the VASP database [36]. These calculations were all performed in the conventional 12-atom cubic cell (four formula units), rather than the 3-atom fcc primitive unit cells used for the SeqQuest calculations. First, we performed systematic tests on ErH2 to determine parameters sufficient to numerical converge the computed properties. The convergence testing and computation of elastic constants were done in the integrated MedeA computational environment [37]. The total energy was converged to less than 0.0001 eV atom−1 with a plane wave energy cutoff of 562.5 eV and with a 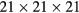 sampling of the Brillouin Zone (centered at the
sampling of the Brillouin Zone (centered at the  point), and these converged settings were subsequently used for all VASP calculations for cubic rare earth dihydrides. The elastic constants computed with VASP were calculated using a 'stress-strain' approach [38], using a strain of 0.5% from the equilibrium lattice structure.
point), and these converged settings were subsequently used for all VASP calculations for cubic rare earth dihydrides. The elastic constants computed with VASP were calculated using a 'stress-strain' approach [38], using a strain of 0.5% from the equilibrium lattice structure.
III. Results
III.A. Numerical uncertainties
The dihydrides considered in this study are all metals, observed in the current calculations, and illustrated in the band structures presented in many previous computational studies of metal dihydrides[13–15, 22]. In metallic systems, the calculations of elastic constants can be profoundly sensitive to the Brillouin Zone sampling and the effective electronic temperature [23, 24]. In bcc-Ta, the equilibrium lattice parameter and total energy converged relatively quickly with k-point density, but the elastic constants, and particularly the shear moduli, C44 and Cs, defined as

showed large dependence with k-sampling (5 GPa variability) out to k-points samples as large as 403 [24]. Hence, while converged calculations of the ground state lattice constant, total energy, and bulk modulus are relatively straightforward to obtain, computation of elastic constants might have much greater uncertainties and need to be approached more skeptically.
Figure 2 illustrates the k-sampling dependence of the bulk modulus and the elastic constants computed for cubic ErH2, from a 83 through a 243 k-sampling of the full Brillouin Zone for the 3-atom primitive cell. In all cases we consider, the lattice constant and total energy exhibit almost no k-point dependence, i.e. they have converged to within 0.001 Å and 2 meV/formula-unit (f.u.) over the range of k-point samples investigated. The bulk modulus also converges very well (to within 0.1–0.2 GPa) and relatively quickly. The other elastic constants exhibit much greater variability, as seen in earlier analyses of elastic constant computations in metals [23, 24]. Once the sampling gets denser than 123, the computed constants appear to converge around an average value, and there is little apparent diminution in the scatter of the computed values about this average out to the largest k-point sampling we consider. This variability with k-sampling dominates the uncertainties associated with computation of elastic constants and is the principal factor in the numerical precision with which the elastic constants can be predicted. The typical numerical uncertainties due to k-sampling for computation of shear moduli in the cubic dihydrides are 2–3 GPa, but are as large as 5–6 GPa in some cases.
Figure 2. The computed elastic constants of cubic ErH2 are plotted as a function of the k-point sampling. The stress-derived bulk modulus converges very quickly (to within 0.1 GPa), but the other elastic constants converge much more slowly, becoming unreliable at a k-sampling smaller than 123. The true DFT value would be the k-converged value, which is estimated as a k-limit average with an uncertainty due to the large-k scatter (see text), e.g. the shear constant C44 varies by ∼3 GPa around an average value of 39 GPa.
Download figure:
Standard image High-resolution imageIt is pointless to attempt to numerically refine these elastic constants any further. First, the apparent rate of convergence, narrowing of the width of the scatter, is very slow with number of k-points but, more importantly, this k-dependent scatter has become smaller than the expected accuracy of the DFT. The B computed with semi-local functionals such as PBE can typically only predict experimental results for a bulk modulus to within 10–20%. The rapidly increasing computational cost of using denser k-sampling does not improve the total quality of the numerical predictions, i.e. the increased computational cost is not recouped in increased fidelity when these physical uncertainties are also considered.
This variability does not indict the quality of the calculation of C11 and C12 at each k-sampling density (from which the elastic modulus Cs is constructed). The bulk modulus in a cubic system, is also constructed from these same elastic constants:

The stress-derived B({Cij}) show very small variability (typically ∼0.1 GPa) with k-point sampling. As seen in figure 2, C11 and C12 suffer significant variations with k-point sample out to the largest sampling we consider, but these values are very closely correlated, leading to an almost constant bulk modulus. An independent calculation of the bulk modulus, B(E) from a fit to a third-order Birch–Murnaghan equation of state of the total energies at different lattice parameters, yields the same result for the bulk modulus as the stress-derived calculation, to within ∼1 GPa, verifying this evaluation of B({Cij}) from the elastic constants. Moreover, the lattice constant and B from the stress-derived calculation and from the total energy Birch–Murnaghan equation of state closely match, indicating the (artificial) electronic temperature used to facilitate self-consistency in these metallic calculations gives a close approximation to a 0 K limit. This isolates the k-dependence as responsible for the variation in evaluated Cij, and not numerical artifacts from other aspects of the computational model.
Figure 3 illustrates the convergence of the elastic constants with k-sampling for the tetragonal structure HfH2. In tetragonal dihydrides, the k-dependence of bulk properties becomes more severe, and spreads to the assessment of the lattice parameters. This can be attributed to a sensitivity of the structure and energy to occupation of states at the Fermi level. The associated computational challenge is to resolve the larger DOS at the Fermi level in the tetragonal dihydrides [15]. As in the cubic structure, the shear elastic constants are particularly sensitive. While the lattice constants a0 and c0 (not plotted) show greater variability, the equilibrium volume converges better with k-point sampling, converging as well as the volume (and lattice constant) had for the cubic crystal.
Figure 3. The computed elastic constants of tetragonal HfH2 are plotted as a function of the k-point sampling index (sampling is a regular k3 grid). The stress-derived bulk modulus converges quickly, only slightly less well than for a cubic structure (to within 0.2 GPa), but the other elastic constants converge much more slowly, becoming unreliable at a k-sampling smaller than 123, and only becoming converged to within ∼2–3 GPa after k-sampling larger than 163 (the C66 shear constant only to within 5 GPa).
Download figure:
Standard image High-resolution imageThe bulk modulus can be evaluated in terms of the elastic constants as
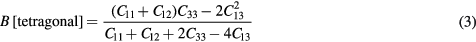
in a tetragonal crystal [39]. This stress-derived B({Cij}) also shows more rapid convergence with k-sampling, although not quite as fast nor quite as tight as for the cubic structure.
The bulk modulus can alternatively be computed from the equation of state. The B(E) can be obtained from analytic derivatives of a Birch–Murnaghan fit to the total energies of a sequence of pressure-optimized tetragonal cells. The energy-fit B(E) match very well the stress-derived B({Cij}), to within the same ∼1 GPa that was observed for the cubic crystal, verifying that the calculation of elastic constants using strain-derivatives of the stress is consistent with the total energy calculations for the tetragonal structure. This verifies the form and evaluation of equation (3), and verifies the computation of the elastic constants within the formula given in equation (3).
III.B. Cubic structure metal hydrides
The results for the structure and elastic constants for the cubic structure of ErH2 and the Group-IIIB and Group-IVB dihydrides are presented in table 1. The k-limit values are the full converged prediction of the DFT simulations. The quoted uncertainties in the k-limit values reflect numerical uncertainty in the converged average value, taken as the magnitude of the scatter from the average as the k-point sampling is increased. The value using a 123 k-sampling is also presented, a representative of the value one obtains with just a single k-point sample, at the threshold at which the simulations appear to converge to a k-limit asymptotic average. The 123 k-sample results in table 1 are at the boundary of the asymptotic range, i.e. converged within the uncertainties of the k-limit values. The formation energy and lattice constants are fully k-sampling converged, to the precision quoted in table 1.
Table 1. Structural properties and elastic constants computed for cubic metal dihydrides.
 (eV) (eV) |
a0 (Å) | C11 (GPa) | C12 (GPa) | C44 (GPa) | Cs (GPa) | B({Cij}) (GPa) | B(E) (GPa) | |
|---|---|---|---|---|---|---|---|---|
| ErH2 | 2.281 |
5.126 |
||||||
| k-limit | — | a0(expt.) | 137(5) | 61(3) | 76.8(0.5) | 38(5) | 86.5(.1) | — |
| k-limit | 2.071 | 5.113 | 140(4) | 63(2) | 77.8(0.5) | 39(3) | 89.1(.1) | 88.3(.1) |
| k = 123 | 2.075 | 5.113 | 145.4 | 61.1 | 78.5 | 42.2 | 89.2 | 88.4 |
| ScH2 | 2.073 |
4.783 |
||||||
| k-limit | 1.990 | 4.766 | 166(5) | 63(2) | 80(1) | 51(4) | 97.4(.2) | 97.3(.1) |
| k = 123 | 1.992 | 4.766 | 168.8 | 61.7 | 76.9 | 53.6 | 97.5 | 97.4 |
| YH2 | 2.346 |
5.195 |
||||||
| k-limit | 2.091 | 5.206 | 132(3) | 58(2) | 73(1) | 37(3) | 82.8(.1) | 82.9(.1) |
| k = 123 | 2.095 | 5.205 | 132.6 | 56.2 | 73.6 | 38.2 | 82.8 | 82.9 |
| LaH2 | 2.151 |
5.663 |
||||||
| k-limit | 1.697 | 5.710 | 95(2) | 48(1) | 53(1) | 23(1) | 63.5(.1) | 63.8(.1) |
| k = 123 | 1.698 | 5.710 | 95.7 | 47.5 | 54.1 | 24.1 | 63.6 | 63.9 |
| TiH2 | 1.283 |
4.475 |
||||||
| k-limit | 1.434 | 4.417 | 119(1) | 155(1) | −21(4) | −18(1) | 143.1(.1) | 140.2(.1) |
| k = 123 | 1.435 | 4.417 | 120.5 | 154.3 | −21 | −17 | 143.0 | 140.3 |
| ZrH2 | 1.687 |
4.794 |
||||||
| k-limit | 1.614 | 4.811 | 88(2) | 157(1) | −30(4) | −34(2) | 133.9(.1) | 134.4(.1) |
| k = 123 | 1.615 | 4.810 | 89.0 | 156.3 | −30 | −33.7 | 133.9 | 134.5 |
| HfH2 | 1.375 |
4.713 |
||||||
| k-limit | 1.376 | 4.713 | 88(3) | 179(2) | −42(3) | −45(3) | 148.5(.1) | 149.7(.1) |
| k = 123 | 1.376 | 4.713 | 81.5 | 182.1 | −49 | −50.3 | 148.6 | 149.6 |
aExperimental result from Beavis [40]. b[41]. c[42]. dAt 0 K, [43]. eAt 300 K [44] (N.B., ground state is tetragonal below 300 K [45]). fExtrapolated to TiT2, from sub-stoichiometric data using linear relationship in [46]. gExtrapolated to ZrH2 from sub-stoichiometric data using linear relationship in [47]. hFor HfH1.7, from [48]. Note: The value in the parentheses for the k-limit values reflects its k-sampling uncertainty, variation with respect to k-sampling in the large k-sampling limit.
The elastic properties are not much changed for ErH2 if computed at the experimental lattice parameter rather than the computed a0. Usually the PBE functional significantly overestimates the lattice constant and therefore strongly underestimates the resulting computed bulk modulus, and elastic properties computed at the experimental lattice parameter improve the accuracy of the calculations. For the rare earth dihydrides, the bare PBE lattice constant, absent zero-point effects and magnetism, yields exceptionally good agreement with experiment, PBE only <0.3% different and smaller. This fortuitously good agreement in a0 means the predictions lack a bias from a mistaken volume. Nonetheless, that the small 0.3% change in a0 leads to almost a 3 GPa change in the computed bulk modulus serves as a cautionary result, slight changes in the structure could result in significant changes in dependent properties such as the bulk modulus, injecting another source of error into the analysis.
The formation energy  for a dihydride of metal
for a dihydride of metal 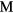 is obtained from the computed total energy of
is obtained from the computed total energy of 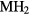 , and of the ground state of the bulk metal and hydrogen molecule,
, and of the ground state of the bulk metal and hydrogen molecule, 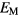 and
and 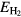 :
:

Thermal effects are neglected in equation (4), they are minor on the scale of errors in the physical approximation of the DFT. Zero-point effects are also ignored. The largest zero-point correction to the formation energy reduces the formation energy by the zero-point vibration of the hydrogen molecule [49]. This molecular constant is partially counterbalanced by the zero-point vibrational energy of the hydrogen atom in each metal lattice. The H2 ZPE gives a sense of the magnitude of the remaining errors in Ef and could be trivially added to the computed values for improved comparison to experiment. The ZPE had been computed in the PBE simulation context to be 0.224 eV [49] for this ZPE, but we note that it would be a more accurate and appropriate physical comparison to use the 'exact' ZPE for H2, 0.270 eV/H2 [50] in any such adjustment. The agreement of our computed formation energy, ΔEf in table 1, with experimental heats of formation, as given by Beavis [40], is surprisingly good for ErH2 and ScH2 and still reasonable for the other hydrides, despite neglecting thermal and quantum nuclear effects. The ΔEf calculated here for ErH2 matches a VASP-calculated value to within 3 meV [49].
The computed lattice constant for β-ErH2, 5.113 Å, agrees well with experiment [41], 5.126 Å. Our VASP calculation gives a0 = 5.129 Å, consistent with this result. This agreement between the two codes, with very different pseudopotentials and basis sets, provides additional verification of the computational methods. Our results also agree with previous VASP calculations [49], who quote a0 = 5.128 Å. The computed lattice parameters for the other dihydrides presented table 1 agree well with experiment [42–48] and with previous calculations [18, 21, 22, 51–55]. The stoichiometric group-IVB dihydrides are known to be tetragonal, and adopt the cubic phase for a small range of substoichiometric H. The TiH2 transforms into a fcc-CaF2 phase above 310 K [45], but adopts the tetragonal structure at lower temperatures. In table 1, the first quoted experimental lattice parameter for TiH2 is for this observed high-temperature cubic phase [44]. The substoichiometric hydrides show only a small dependence of lattice parameter on the H content over the range of H content where the cubic phase is stable, and the relationship between H content and lattice constant is roughly linear. The second quoted 'experimental' lattice parameter for TiT2 is obtained by extrapolating to the stoichiometric ditritide using the relationship developed [46] over the range of substoichiometric tritide where the fcc phase is stable (1.5 < T/Ti < 1.8). This extrapolated a0 in TiT2 is slightly smaller, partially attributable to an isotope effect, the hydrogen vibrations causing a larger expansion in the lattice than the tritium.
Unlike for TiH2, no cubic form of the stoichiometric ZrH2 has been observed, but, similarly, a linear relationship was developed for the substoichiometric ZrH2−x system [47], which we use to extrapolate to obtain the 'experimental' value of a0 = 4.794 Å quoted in table 1 for the dihydride. The lattice constant measured for HfH1.7 is used as the experimental value here for the dihydride; we were unable to find the experimental data to perform a comparable extrapolation from substoichiometric data for HfH2. The agreement of the calculated a0 with these inferred 'experimental' lattice constants for the cubic structure of group-IVB dihydrides is very good.
The C11, C12, and C44 elastic constants are computed from the strain-derivatives of the stress, the shear modulus Cs and B({Cij}) are evaluated from these using the analytical relationships in equations (1) and (2). The alternate energy-fit calculation of B(E) agrees with B({Cij}) across this set of dihydrides, verifying the computation of B. The computed bulk modulus for TiH2 is less good, the difference is slightly larger, 3 GPa. This signals a potential numerical issue in the calculation, and upon investigation we discovered that this larger discrepancy was due to inaccuracy in the real space integration in the total energy evaluation. A finer real space grid, increased from 243 to 323 (or more) brought the B(E) verification into the same agreement as for the other dihydrides, and had minimal effect on the elastic constants computed from the stress-strain relations. This exercise illustrates how seemingly redundant verification checks, with meaningful estimates of expected and actual uncertainties, can identify potential inaccuracies in the calculation, and thereby add greater confidence to the computational results.
Quijano, et al [22] had done a notably careful study of the structural properties of the group-IVB dihydrides, examining stability of the fcc versus the fct phase, additionally examining the importance of relativistic effects. Their results for fcc phase TiH2, ZrH2, and HfH2 lattice parameters of cubic (4.428, 4.817, and 4.727 Å, respectively) and the bulk modulus (144, 136, 148 GPa) are closely mimicked in the current results. We find that these group-IVB cubic dihydrides all have negative shear moduli, both the C44 and the tetragonal shear Cs, indicating that the cubic structure is unstable to a distortion. Given that these are all known to take tetragonal ground states, this is not surprising, but the result indicates that the cubic phase does not even have a locally stable region, and, further, suggests that these shear elastic constants might be used computationally to detect the instability of the cubic phase, a notion we examine later. This structural instability leads to numerical instabilities in the assessment of the stresses in the calculation of the C44. The computed stresses are negative, and not cleanly linear, so the numerical evaluations of C44 from the stress-strain results are much more uncertain at each k-point.
III.C. Rare earth cubic dihydrides
We now shift to erbium's immediate neighbors, to examine the mechanical properties of cubic dihydrides in the rare earths (RE). A search was performed on the Pearson database [56] of crystals to identify all the RE dihydrides that formed a cubic (Fm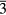 m) dihydride ground state. The cubic structure is the stable ground state across almost the entire lanthanide series. The ground state crystal structure of PmH2 is not known. Promethium has no stable isotope and only trace amounts are found in naturally occurring ores (it has never been made). The dihydrides of Eu and Yb instead crystallize into an orthorhombic structure (Pnma, #62), rather than the cubic structure of ErH2 and the other RE dihydrides. This could be anticipated, as Eu and Yb do not always exhibit the same [+3] oxidation state that characterizes the other rare earths, but instead can also adopt a [+2] oxidation state, i.e. with respect to the other RE atoms, they will have one fewer valence electron.
m) dihydride ground state. The cubic structure is the stable ground state across almost the entire lanthanide series. The ground state crystal structure of PmH2 is not known. Promethium has no stable isotope and only trace amounts are found in naturally occurring ores (it has never been made). The dihydrides of Eu and Yb instead crystallize into an orthorhombic structure (Pnma, #62), rather than the cubic structure of ErH2 and the other RE dihydrides. This could be anticipated, as Eu and Yb do not always exhibit the same [+3] oxidation state that characterizes the other rare earths, but instead can also adopt a [+2] oxidation state, i.e. with respect to the other RE atoms, they will have one fewer valence electron.
Table 2 presents the DFT results for the lattice parameter and elastic constants computed for the RE dihydrides in the fcc CaF2 structure. Results are presented both from SeqQuest calculations using a linear combination of atomic orbitals (lcao) basis set (using the 3-atom primitive cell and a 203 k-point sampling), and also from calculations using VASP with a plane wave (pw) basis. In these results, to examine the trends across the RE series, the lcao calculations for EuH2 and YbH2 use pseudpotentials with a [+3] oxidation state (rather than the [+2] oxidation state pseudpotential), and in the cubic (fcc) structure rather than the Pnma orthorhombic structure observed in nature.
Table 2. Lattice parameters a0 (Å), elastic constants (GPa), and computed Debye temperature (K) for cubic RE dihydrides.
| Hydride | a0(Exp.) |
a0(DFT) | C11 | C12 | C44 | B({Cij}) | Cs | 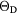 (DFT) (DFT) |
|
|---|---|---|---|---|---|---|---|---|---|
| LaH2 | lcao | 5.667 | 5.710 | 93.5 | 48.5 | 53.7 | 63.5 | 22.5 | 364 |
| pw | 5.658 | 89.3 | 48.5 | 47.3 | 62.1 | 20.4 | 343 | ||
| CeH2 | lcao | 5.581 | 5.622 | 98.6 | 50.6 | 56.2 | 66.6 | 24.0 | 369 |
| pw | 5.437 | 90.7 | 55.7 | 46.7 | 67.4 | 17.5 | 324 | ||
| PrH2 | lcao | 5.518 | 5.552 | 102.2 | 51.6 | 58.4 | 68.5 | 25.3 | 374 |
| pw | 5.555 | 102.0 | 52.1 | 53.1 | 68.7 | 25.0 | 363 | ||
| NdH2 | lcao | 5.464 | 5.487 | 106.3 | 52.8 | 60.6 | 70.7 | 26.7 | 376 |
| pw | 5.490 | 107.4 | 54.0 | 55.5 | 71.8 | 26.7 | 366 | ||
| PmH2 | lcao | 5.428 | 111.8 | 54.5 | 63.1 | 73.6 | 28.7 | 382 | |
| pw | 5.431 | 111.6 | 55.6 | 58.3 | 74.3 | 28.0 | 372 | ||
| SmH2 | lcao | 5.374 | 5.375 | 116.8 | 55.5 | 65.5 | 75.9 | 30.6 | 383 |
| pw | 5.385 | 115.8 | 56.3 | 60.2 | 76.1 | 29.8 | 372 | ||
| EuH2 | lcao | 5.325 | 121.8 | 56.4 | 67.8 | 78.2 | 32.7 | 388 | |
| GdH2 | lcao | 5.303 | 5.279 | 126.8 | 57.5 | 70.4 | 80.6 | 34.7 | 388 |
| pw | 5.285 | 122.3 | 58.7 | 65.4 | 79.9 | 31.8 | 374 | ||
| TbH2 | lcao | 5.246 | 5.234 | 130.9 | 58.2 | 72.4 | 82.4 | 36.3 | 391 |
| pw | 5.237 | 127.0 | 59.5 | 68.1 | 82.0 | 33.8 | 379 | ||
| DyH2 | lcao | 5.201 | 5.191 | 135.4 | 59.5 | 74.3 | 84.8 | 37.9 | 392 |
| pw | 5.200 | 131.7 | 62.0 | 68.7 | 85.2 | 34.8 | 377 | ||
| HoH2 | lcao | 5.165 | 5.151 | 139.5 | 60.2 | 76.8 | 86.6 | 39.7 | 395 |
| pw | 5.160 | 133.7 | 62.6 | 73.5 | 86.3 | 35.6 | 382 | ||
| ErH2 | lcao | 5.123 | 5.113 | 144.4 | 61.3 | 78.2 | 89.0 | 41.6 | 396 |
| pw | 5.122 | 137.5 | 63.7 | 74.6 | 88.3 | 36.9 | 382 | ||
| TmH2 | lcao | 5.090 | 5.074 | 147.5 | 62.4 | 81.2 | 90.8 | 42.5 | 399 |
| pw | 5.090 | 140.1 | 66.0 | 75.4 | 90.7 | 37.1 | 381 | ||
| YbH2 | lcao | 5.039 | 150.3 | 63.3 | 82.7 | 92.3 | 43.5 | 397 | |
| LuH2 | lcao | 5.033 | 5.004 | 153.7 | 64.5 | 84.4 | 94.2 | 44.6 | 398 |
| pw | 5.020 | 145.7 | 66.6 | 78.5 | 93.0 | 40.0 | 381 |
aExperimental lattice parameter for LaH2 and CeH2 from [57]; PrH2 through LuH2 from [58], except GdH2 from [59]. bPmH2 has never been made. cComputed result shown is for a pseudopotential with the [3+] oxidation state. dComputed from elastic constants using relation from [60].
The agreement between the lcao and pw calculations for each RE dihydride is very good across the series. The differences in elastic constants between the pw and lcao results are consistent with the numerical uncertainties with respect to k-sampling reported in table 1. The bulk modulus, as illustrated in figure 2 for ErH2 and analyzed in table 1 for several dihydrides, exhibits much finer convergence with k-point sampling, so that the total uncertainty in this quantity is dominated by the form of the equation of state, estimated above to be ∼1 GPa, rather than k-sampling dependence. The differences between the lcao and pw results for B in the RE series are typically ∼1 GPa, consistent with the estimated uncertainty in the model form used to extract the elastic properties. Because the k-point sampling used in computing the elastic constants for the RE series are well within the asymptotic range used for computing the k-limit result, the uncertainties (with respect to the k-limit value) due to k-sampling in the values quoted in table 2 will be the same as those presented for the stable cubic dibidrides in table 1, i.e. ∼4 GPa for C11 and Cs, ∼2 GPa for C12, ∼3 GPa for C44. The values in table 2 are quoted to tenths of GPa only to facilitate finer comparisons between the lcao and pw calculations, and also to analyze trends across the series, this finer precision is otherwise physically meaningless. That the results using very different pseudopotentials and basis sets, using different methods for extracting elastic constants for the results, and using different cells and k-point sampling, are in good agreement lends greater confidence to the numerical predictions. The different approaches give chemically and numerically consistent results.
The computed properties of the RE dihydrides are similar to one another and follow a monotonic trend from one end of the lanthanide series to the other. The small exception is the plane wave result for C12 (and the Cs derived from it) for CeH2. Ce is another rare earth that often adopts an oxidation state different from [+3]: it can promote its f-electron into the valence electrons to access a [+4] oxidation state. The lcao result uses a pseudopotential leaving exactly one f-electron in the core, imposing the [+3] oxidation state that is consistent with its neighbors, while the PAW pseudopotential of the PW calculation does not make this constraint on the oxidation state.
The lattice parameter steadily shrinks across the series, the effective size of the RE atom getting smaller as the nuclear charge increases. The computed a0 are in very good agreement with experiment [43, 58, 59]. The PBE calculation gives a0 slightly larger than experiment early in the series and then trends to become slightly smaller than experiment at the end of the series.
All the computed shear moduli are positive, indicating that the RE dihydrides are (at least locally) stable in the cubic phase, consistent with the experimental observations [56]. The elastic constants all steadily become stiffer, as would be expected as the lattice parameter decreases for a given structure. This supports the notion that the bonding and electronic structure are very similar across the RE dihydrides, the dominant difference being the shrinking in size in the RE atom across the series. Overall, DFT with the PBE functional appears to give a very good description of the mechanical properties of cubic dihydrides. Using the relations developed by Deligoz et al [60], an estimate for the Debye temperature can be obtained directly from the elastic constants. The computed results are presented in the last entry in table 2. Unremarkably, the variation across the lanthanides is small.
III.D. Group IVB tetragonal dihydrides
The negative shear elastic constants for the group-IVB dihydrides presented in table 1 signal that the cubic phase is unstable to a distortion for these materials. Table 3 summarizes the structural properties of the tetragonal (fct) ground state group-IVB dihydrides. In agreement with experiment[61–63], and recent theory [21, 22], the tetragonal form with c/a <1 is the ground state for all of these, favored over the c/a > 1 form. The preference for the c/a < 1 is weak, only 4 meV f.u.−1 in TiH2 and 12 meV f.u.−1 in both ZrH2 and HfH2, but meaningful within the numerical uncertainties present in these calculations. These lattice parameters and energy preferences match well with the relative structural distortion energies computed by Quijano, et al [22].
Table 3. Structural properties for tetragonal metal dihydrides.
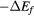 (eV) (eV) |
a0 (Å) | c0 (Å) | c/a | V(fct) (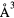 ) ) |
V(fcc) (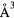 ) ) |
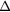 E(fcc) (meV f.u.−1) E(fcc) (meV f.u.−1) |
||
|---|---|---|---|---|---|---|---|---|
| TiH2 | Exp. |
4.528 | 4.279 | .945 | ||||
| c/a < 1 | k-limit | 1.445 | 4.531(2) | 4.184(4) | 0.924(1) | 21.47 | 21.54 | −11 |
| k = 123 | 1.445 | 4.524 | 4.198 | 0.928 | 21.48 | 21.54 | −10 | |
| c/a > 1 | k-limit | 1.441 | 4.329(1) | 4.591(2) | 1.061(1) | 21.51 | 21.54 | −7 |
| k = 123 | 1.440 | 4.331 | 4.587 | 1.059 | 21.51 | 21.54 | −5 | |
| ZrH2 | Exp. |
4.9825(9) | 4.4488(9) | 0.8929(8) | ||||
| Exp. |
4.975(3) | 4.447(3) | 0.894(1) | |||||
| c/a < 1 | k-limit | 1.646 | 5.011(3) | 4.400(6) | 0.878(1) | 27.62 | 27.82 | −32 |
| k = 123 | 1.646 | 5.018 | 4.385 | 0.874 | 27.61 | 27.83 | −31 | |
| c/a > 1 | k-limit | 1.634 | 4.647(1) | 5.135(3) | 1.105(1) | 27.73 | 27.82 | −20 |
| k = 123 | 1.634 | 4.644 | 5.142 | 1.107 | 27.73 | 27.83 | −19 | |
| HfH2 | Exp. |
4.919 | 4.363 | 0.886 | ||||
| c/a < 1 | k-limit | 1.418 | 4.935(3) | 4.267(5) | 0.865(2) | 25.98 | 26.17 | −42 |
| k = 123 | 1.418 | 4.942 | 4.254 | 0.861 | 25.98 | 26.17 | −42 | |
| c/a > 1 | k-limit | 1.406 | 4.525(2) | 5.094(3) | 1.126(2) | 26.08 | 26.17 | −30 |
| k = 123 | 1.405 | 4.520 | 5.107 | 1.130 | 26.08 | 26.17 | −32 |
We performed additional calculations in the LDA, and obtained the same structural preference for TiH2 and ZrH2, of roughly the same magnitudes as with the PBE functional. The result by Ackland favoring c/a > 1 for ZrH2 [19] is probably attributable to an inadequate k-point sampling (the quoted k-sampling [19], a sampling less than the 123 asymptotic threshold for reliable results determined in this study). The result favoring c/a > 1 for TiH2 by Wolf and Herzig [15], using an all-electron method, is more mysterious. But the energy preference in TiH2 involved is so small, 3–4 meV f.u.−1, and may not be physically significant; this is perhaps within the numerical accuracy that can reasonably be expected of older computational DFT methods.
Negative shear elastic constants signal the instability of the cubic structure to a distortion, but do not predict the form that this distortion will take. Given that both the planar shear and tetragonal shear constant presented in table 1 for the group IVB fcc dihydrides are negative, any candidate distortion is plausible. A negative Cs alone would be suggestive of a tetragonal distortion, but that a negative C44 accompanies it indicates other distortions would also be energy-lowering. We investigated rhombohedral crystal distortions, compressing and expanding the cubic structure along the (1 1 1)-axis, for both TiH2 and ZrH2. Both compression and expansion lead to energy-lowering distortions, and these hexagonally strained structures are favored over the fcc structure just as both tetragonally-strained fct structures are favored over the fcc structure.
The ZrH2 favors the (1 1 1)-compressed rhombohedral structure over the fcc structure by 7 meV, and the (1 1 1)-expanded structure is favored by 5 meV, somewhat smaller than energy-lowering obtained with the tetragonally distorted structures. The TiH2 also favors the (1 1 1)-compressed hexagonal structure over (1 1 1)-expanded structure, at 6 and 1 meV f.u.−1 below the cubic structure. We note that the compressed hexagonal structure is actually more stable than the c/a > 1 tetragonal distortion. These results suggest that the cubic fcc structure is a local maximum in the structure, surrounded by a valley of lower energy distortions in all directions. This would more readily facilitate the fct → fcc transition observed at 310 K [45] for TiH2, the barrier to a homogeneous distortion would be lower than a barrier represented by a transition through the cubic structure.
The lattice parameters for the fct structures show slightly more variability than for the cubic structure with k-point sampling. Whereas the cubic structures converged to less than 0.001 Å at a 123 k-sample, the k-sampling variability in the optimized a0 and c0 for the fct structure can be as much as 0.2%, a numerical uncertainty that is as large or larger than the uncertainties in the experimental measurements. However, this variation in the computed lattice parameters a0 and c0 is tightly correlated. The total cell volume is converged to better than 0.01 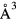 already at 123, indicating that the details of the sampling of the electronic states at the Fermi level have a more significant effect on the shape of the structure, the c/a ratio, than its volume.
already at 123, indicating that the details of the sampling of the electronic states at the Fermi level have a more significant effect on the shape of the structure, the c/a ratio, than its volume.
Table 4 presents the computed elastic constants of the ground state (c/a < 1) tetragonal metal dihydrides. The uncertainties in the evaluated elastic constants due to k-sampling are comparable, if slightly larger than for the cubic structure presented in table 1 (leaving aside the pathologies that manifest in the calculation of C44 due to the instability of the cubic structure). The tetragonal crystal has a lowered symmetry from the cubic crystal, there are more independent elastic constants to compute than for the fcc structure, and the calculations are more computationally demanding, making it more challenging to verify the results. A couple of the consistency checks we performed are presented in table 4.
Table 4. Computed elastic properties (in GPa) for tetragonal metal dihydrides.
| C11 | C12 | C13 | C31 | C33 | C44 | C66 | B({Cij}) | B(E) | |
|---|---|---|---|---|---|---|---|---|---|
| TiH2 | |||||||||
| k-limit | 178(2) | 149(2) | 119(2) | 120(2) | 159(2) | 17(1) | 59(2) | 140.2(.1) | — |
| k = 123 | 178.1 | 146.2 | 120.9 | 122.1 | 155.5 | 18.7 | 57.7 | 140.0 | 139.8 |
| ZrH2 | |||||||||
| k-limit | 177(2) | 143(2) | 106(2) | 107(1) | 151(3) | 40(2) | 74(4) | 130.7(.2) | — |
| k = 123 | 181.0 | 138.7 | 106.9 | 106.9 | 149.4 | 35.4 | 65.6 | 130.5 | 131.1 |
| PBE(k = 123) |
165.6 | 140.9 | 106.8 | — | 145.5 | 30.5 | 60.6 | 130 | — |
| PBE(k = 203) |
166 | 149 | 109 | — | 149 | 26.5 | 55.8 | 133 | — |
| HfH2 | |||||||||
| k-limit | 190(2) | 159(2) | 118(2) | 118(2) | 175(4) | 49(2) | 76(6) | 146.3(.2) | — |
| k = 123 | 195.6 | 154.8 | 117.4 | 117.4 | 175.3 | 44.0 | 66(3) | 146.3 | 147.0 |
First, we computed C13 and C31 independently. To obtain C11, an axial strain along the c-axis is used, and the C13 can be obtained from the derivative of the off-axis stress within the same strain. To obtain C33, it is necessary to perform a strain along the a-axis. The C31 can be obtained from a stress-derivative along a different axis than this strain. By symmetry, C13 and C31 should be identical, but numerically will differ due to different real-space grid spacing and reciprocal space grid spacing along the direction of the strain. This difference can be used as a consistency check, to assess how well the elastic constant calculation is numerically converged with respect to the integration grids. The difference between C13 and C31 is ∼1 GPa or less for all the tetragonal dihydride calculations, less than the expected k-sampling uncertainty for any individual elastic constant.
A second consistency check involved independent calculations of the bulk modulus. The bulk modulus for these tetragonal crystals was first obtained from the computed elastic constants using the analytic relationship of equation (3). For the 123 k-sample, we also obtained the energy-fit bulk modulus B(E) from an analytic derivative of a Birch–Murnaghan equation of state, fit to a series of optimized cells under a series of compressive and tensile pressures. This more holistic test assesses both the consistency of the energy and stress calculations and also the efficacy and proper application of the relationship between the elastic constants and the bulk modulus for a tetragonal crystal given in equation (3). The agreement between the stress-derived and the energy-fit bulk modulus is better than 1 GPa, once more within the expected accuracy of the elastic constant calculations, and also matches the known uncertainty in the numerical fit to the equation of state.
For ZrH2, there are two earlier sets of results for the elastic constants using PBE [52, 54], that are reasonably well-converged and compatible with the current study. Our computed elastic constants match the previous results of Zhang et al [54], and Olsson, et al [52] reasonably well. Our calculations were derived from stress-strain relationships, and these authors instead used a series of energy-fits to obtain their elastic constants, which might explain the modest differences between the different sets of results. All the IVB dihydrides pass the stability tests for the tetragonal structure, and, despite differences in an individual elastic constant as large as 10 GPa (in C11), the resultant bulk modulus still agrees well between these different DFT calculations.
III.E. Off-stoichiometry stability
These metals tend to form hydrides over a wide range of H stoichiometry; for instance, erbium and the other RE elements can be readily hydrided to form up to a trihydride [40]. The stability of the different erbium hydrides, ErH, ErH2, and ErH3, was investigated with first-principles calculations [49]. The interest in erbium for tritium storage is in the cubic structure. The single phase cubic form is stable for Er:H ratios ranging from 1.9 to 2.1 [40]. In the tritide, the stoichiometry of the initial manufactured sample will change with aging, as tritium decays into helium and modify the mechanical properties of the material. Helium replaces hydrogen in the lattice, and then the helium diffuses away and coalesces into bubbles, leaving behind a substoichiometric tritide. These compositional changes can potentially affect the elastic properties (and the stability of the cubic phase) and therefore are important for modeling the mechanical behavior of aging tritides.
To examine the trends of the elastic properties with a change in stoichiometry, we adopt an averaged-atom approach, where every hydrogen H in the lattice is replaced with a hydrogen atom Hz with a modified nuclear charge z. The advantage of this averaged-atom approach is that it preserves the full symmetry of the crystal in the small primitive cell while exploring off-stoichiometry effects. For 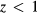 , this approach mimics the average population of x = 2(1 − z) vacancies on the H site in the structure, i.e. a random ErH2−x structure, while for
, this approach mimics the average population of x = 2(1 − z) vacancies on the H site in the structure, i.e. a random ErH2−x structure, while for  , this approach mimics a random ErH2−xHex structure where x = 2(z − 1). The results for the elastic properties of ErHz are presented in table 5 for z = 0.75 to z = 1.50, using the theoretical lattice constant appropriate to each Hz.
, this approach mimics a random ErH2−xHex structure where x = 2(z − 1). The results for the elastic properties of ErHz are presented in table 5 for z = 0.75 to z = 1.50, using the theoretical lattice constant appropriate to each Hz.
Table 5. Computed structural and elastic properties (in GPa) for cubic ErH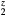 (k = 203).
(k = 203).
| a0(Å) | C11 | C12 | C44 | Cs | B({Cij}) | |
|---|---|---|---|---|---|---|
ErH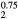 |
5.226 | 124.1 | 49.0 | 58.8 | 37.5 | 74.0 |
ErH |
5.113 | 144.4 | 61.3 | 78.2 | 41.6 | 89.0 |
ErH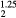 |
5.060 | 117.9 | 80.3 | 73.1 | 18.8 | 92.9 |
ErH |
5.088 | 82.6 | 105.5 | −39.1 | −34.3 | 82.6 |
| ErHHe | 5.238 |
The averaged-atom results indicate that C11 decreases and C12 increases with replacement of H with He in the lattice, culminating with 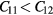 for ErH
for ErH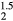 , indicating a structural instability. The shear moduli C44 and Cs decrease and then sharply drop at z = 1.5. The optimized tetragonal structure for ErH
, indicating a structural instability. The shear moduli C44 and Cs decrease and then sharply drop at z = 1.5. The optimized tetragonal structure for ErH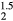 is more stable by 57 meV f.u.−1 than the cubic crystal. Given that ErH1.5 is isovalent—the same number of valence electrons—with HfH2, this is not surprising. The lattice parameter first decreases and then turns slightly larger with increasing He concentration. The bulk modulus does not change much across this composition change; only the shear moduli exhibit strong changes.
is more stable by 57 meV f.u.−1 than the cubic crystal. Given that ErH1.5 is isovalent—the same number of valence electrons—with HfH2, this is not surprising. The lattice parameter first decreases and then turns slightly larger with increasing He concentration. The bulk modulus does not change much across this composition change; only the shear moduli exhibit strong changes.
The numerical results for the averaged-atom structures should not be taken too literally. An ErHHe fcc structure (where every second H atom in ErH2 is replaced by a He atom), isovalent with the ErH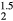 , has a significantly larger lattice constant than ErH
, has a significantly larger lattice constant than ErH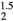 . This cubic ErHHe model, nonetheless, exhibits the same structural instability as ErH
. This cubic ErHHe model, nonetheless, exhibits the same structural instability as ErH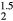 , although with a larger margin, 157 meV, favoring the tetragonal distortion.
, although with a larger margin, 157 meV, favoring the tetragonal distortion.
The effects of transmutation of H into He in the lattice have been studied previously [64] using an explicit-atom approach. Using a larger supercell (96 atoms), between one and six H atoms in a larger 96 atom ErH2 supercell were replaced with He atoms, probing a gradation in He composition much finer than considered here. For small x, those results show C12 decreases rather than increases, and the bulk modulus decreases significantly, and over a much smaller gradation of He composition. This indicates that effects for small concentrations of clustered He on H lattice sites the mechanical properties will be different than for dispersed concentrations of He.
Results for dispersed He should be taken as illustrative of trends rather than as physically predictive. The tritides are not observed to sustain even small concentrations of He located on H sites, but rather the He generated from decayed tritium diffuses away and segregates into bubbles almost immediately [9]. The macroscopically observed changes in mechanical properties of the aging material are dominated by microstructural effects: the bubble density, shape, and size, the pressures within the He bubble interacting with the elastic properties of the remaining tritide matrix, and the dislocations and mesoscale features this interaction generates [3]. The components that go into such an analysis include the elastic properties of the matrix, but that matrix will retain minimal residual He concentrations. The computational results are more useful, indicative of incipient local structural instabilities, if a few He atoms, before they diffuse into bubbles, are found within close proximity of each other. This instability to local distortions due to heterogeneity of local He concentrations could perhaps facilitate increased diffusion of He, and, more speculatively, the statistical likelihood of a near approach of several He might be a contributor to the initial nucleation of bubbles. Tuning ErH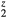 to z = 1.5 creates a system isovalent with HfH2. If several H are replaced by He in a local region, this might favor local distortions and strains.
to z = 1.5 creates a system isovalent with HfH2. If several H are replaced by He in a local region, this might favor local distortions and strains.
Simulations of the substoichiometric tritide, on the other hand, should provide more realistic models of reality, either for a tritide that was less than fully loaded, or because He segregation in the aging tritide leaves behind a substoichiometric matrix. The results in table 5 indicate that with an average of 1/4 H vacancies, the lattice becomes slightly (2%) larger and all the elastic constants get slightly softer (∼20%)—relatively small changes considering the large composition change. XRD studies of aging ErT2 show a linear anisotropic increase in lattice constant of ∼1% when 1/83H have converted to 3He [65], consistent with this result. For use in a macroscopic model of the mechanical response of the aging material, this kind of variability in the elastic properties in the matrix could be readily incorporated, or even, given the modest and isotropic change in the elastic properties with (sub)stoichiometry, might be safely ignored.
The examination of the structural phase stability with this stoichiometry yields insight into the nature of the bonding that determines the structure. Consider again the group IVB metals: all crystallize in the tetragonal phase for the dihydride, but all adopt the cubic phase over a range of substoichiometric hydrogen. The single-phase cubic structure, the δ-phase, is present for a 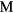 :H ratio of 1.5 to 1.8 for Ti [46], ranging from 1.5 to 1.7 for Zr [47], and appears below ∼1.7 for Hf [48]. Above this δ-phase, the lattice converts to the ε-phase (fct structure), below this range it becomes a mixed α(hexagonal)-δ phase, essentially hydrogen dissolved in the pure-metal lattice. This trend of conversion to the cubic phases is consistent with a rigid band picture [19], where the band structure of these different hydrides are very similar to one another, and the principle difference is the number of valence electrons that fill that band structure. The
:H ratio of 1.5 to 1.8 for Ti [46], ranging from 1.5 to 1.7 for Zr [47], and appears below ∼1.7 for Hf [48]. Above this δ-phase, the lattice converts to the ε-phase (fct structure), below this range it becomes a mixed α(hexagonal)-δ phase, essentially hydrogen dissolved in the pure-metal lattice. This trend of conversion to the cubic phases is consistent with a rigid band picture [19], where the band structure of these different hydrides are very similar to one another, and the principle difference is the number of valence electrons that fill that band structure. The 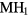 (or
(or  ) would be isoelectronic with the RE cubic dihydrides (the RE atoms having three valence electrons, the IVB atoms four). Within an average-atom picture, the effective substoichiometric HfH
) would be isoelectronic with the RE cubic dihydrides (the RE atoms having three valence electrons, the IVB atoms four). Within an average-atom picture, the effective substoichiometric HfH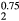 already favors the cubic structure, even before the HfH
already favors the cubic structure, even before the HfH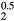 that is isovalent. As one adds electrons to the ErH2 lattice, transmuting to ErH
that is isovalent. As one adds electrons to the ErH2 lattice, transmuting to ErH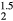 , the crystal distorts to the tetragonal form of the isovalent HfH2.
, the crystal distorts to the tetragonal form of the isovalent HfH2.
Figure 4 plots the computed shear elastic constants, C44 and Cs, as one varies Hz, to fill the valence band structure with more (H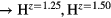 ) and fewer (H
) and fewer (H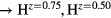 ) electrons. The elastic constants for cubic LaH
) electrons. The elastic constants for cubic LaH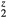 , and ErH
, and ErH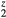 are shown, along with the HfH
are shown, along with the HfH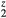 versus the number of electrons filling the valence band structure. Plotting against valence electron count, all three show similar behavior, with negative shear moduli at six valence electrons f.u.−1 signaling the instability of the cubic phase to a distortion. This supports a rigid band picture, where the filling of the band structure rather than the chemical nature of the metal determines the structure. Whether one attributes this to a Jahn–Teller-like distortion due to a high density of states at the Fermi level for the group IVB dibydrides, or disputes that interpretation otherwise through a detailed analysis of the HfH2 band structure [22], it is unambiguous from comparing these disparate dihydrides that it is the filling within the band structure with six valence electrons that triggers the instability.
versus the number of electrons filling the valence band structure. Plotting against valence electron count, all three show similar behavior, with negative shear moduli at six valence electrons f.u.−1 signaling the instability of the cubic phase to a distortion. This supports a rigid band picture, where the filling of the band structure rather than the chemical nature of the metal determines the structure. Whether one attributes this to a Jahn–Teller-like distortion due to a high density of states at the Fermi level for the group IVB dibydrides, or disputes that interpretation otherwise through a detailed analysis of the HfH2 band structure [22], it is unambiguous from comparing these disparate dihydrides that it is the filling within the band structure with six valence electrons that triggers the instability.
Figure 4. The dependence of the shear elastic constants in the cubic structure 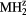 on the number of valence electrons, for
on the number of valence electrons, for  = La, Er, Hf, obtained by modifying the core charge on the H to give a non-integer total charge for Hz. The open(filled) symbols present the computed C44 (Cs) values, the (red) circles connected by solid lines are for LaH
= La, Er, Hf, obtained by modifying the core charge on the H to give a non-integer total charge for Hz. The open(filled) symbols present the computed C44 (Cs) values, the (red) circles connected by solid lines are for LaH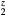 , the (blue) squares by dashed lines for ErH
, the (blue) squares by dashed lines for ErH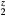 , and the (orange) diamonds by dotted line for HfH
, and the (orange) diamonds by dotted line for HfH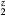 . The LaH2 and ErH2, at five valence electrons per f.u., have a positive plateau in the shear constants, but these drop precipitously at z = 1.5 and become negative, the negative shear constants indicating an instability to distortion at the electron count (6 E− f.u.−1) that makes this isovalent with fct-HfH2. Conversely, reducing the electron count in HfH
. The LaH2 and ErH2, at five valence electrons per f.u., have a positive plateau in the shear constants, but these drop precipitously at z = 1.5 and become negative, the negative shear constants indicating an instability to distortion at the electron count (6 E− f.u.−1) that makes this isovalent with fct-HfH2. Conversely, reducing the electron count in HfH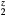 stabilizes the fcc structure, and the HfH
stabilizes the fcc structure, and the HfH exhibits the same positive plateau in the shear elastic constants as the isovalent LaH2 and ErH2 with the same number of valence electrons.
exhibits the same positive plateau in the shear elastic constants as the isovalent LaH2 and ErH2 with the same number of valence electrons.
Download figure:
Standard image High-resolution imageIII.F. Analysis and relation to experiment
The parameters crucial for modeling bubble growth and fracture in aging tritides like ErT2, such as surface energies and mechanical properties [11], are exceedingly difficult to obtain with accuracy from experimental measurements, indicating a first-principles approach as a means to obtain the materials properties [4] is needed to model the bubble evolution, growth and ultimate fracture of the material. The first-principles calculations in this paper provide detailed analysis of the mechanical properties, such as the elastic constants, paying careful attention to the numerical uncertainties that attend the DFT calculations.
The thin film materials are polycrystalline, so the quantities of interest for microstructural modeling of the materials are averaged quantities, such as the bulk shear modulus μ, and the Young's modulus E. For single crystals, these quantities can be obtained straightforwardly from the computed elastic constants [33, 39], but assessment of these quantities in a polycrystalline material adds further numerical uncertainties into the analysis. Analyses by Reuss and Voigt for the shear modulus, 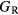 and
and 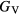 , place bounds on the bulk shear modulus in a polycrystalline material. Both of these bounds incorporate a numerical uncertainty roughly equivalent to the numerical uncertainty in computing the crystalline shear elastic constants. Conventionally, the 'predicted' bulk shear modulus
, place bounds on the bulk shear modulus in a polycrystalline material. Both of these bounds incorporate a numerical uncertainty roughly equivalent to the numerical uncertainty in computing the crystalline shear elastic constants. Conventionally, the 'predicted' bulk shear modulus 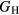 is defined as the average of these [33], but in many cases this convention injects additional numerical uncertainties into the 'predicted' shear modulus, as the difference in the
is defined as the average of these [33], but in many cases this convention injects additional numerical uncertainties into the 'predicted' shear modulus, as the difference in the 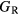 and
and 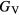 bounds can be significant, larger than 10 GPa, for the hydrides.
bounds can be significant, larger than 10 GPa, for the hydrides.
This shear modulus G, with the bulk modulus B, is used to estimate Young's modulus E:

which, being proportional to 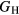 , carries roughly the same proportion of numerical uncertainty as G. The consequence is that the numerical calculations for these essential quantities, even obtained from precise DFT calculations, embody numerical uncertainties as large as the rather substantial uncertainties derived from the experimental analysis of these quantities, even discounting the physical uncertainties associated with the accuracy of the DFT approximation.
, carries roughly the same proportion of numerical uncertainty as G. The consequence is that the numerical calculations for these essential quantities, even obtained from precise DFT calculations, embody numerical uncertainties as large as the rather substantial uncertainties derived from the experimental analysis of these quantities, even discounting the physical uncertainties associated with the accuracy of the DFT approximation.
Table 6 presents the results of the DFT analysis for these bulk mechanical properties, along with their experimental counterparts. The Debye temperature can also be used as an experimental comparison as it can be computed directly from shear moduli [60]. The values in parenthesis are the numerical uncertainties in the DFT predictions. These incorporate uncertainties inherent within the Reuss 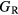 and Voigt
and Voigt 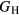 bounds from the numerical k-limit uncertainties of the underlying shear elastic constants from which these are computed, and then adds an uncertainty given estimating the shear modulus
bounds from the numerical k-limit uncertainties of the underlying shear elastic constants from which these are computed, and then adds an uncertainty given estimating the shear modulus 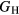 as an average midway between these bounds. It is this total uncertainty in
as an average midway between these bounds. It is this total uncertainty in 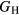 that can be compared meaningfully to the appropriate experimental quantity. Even if the DFT approximation were physically perfectly accurate, these numerical uncertainties from the averaging and k-sampling would remain. The shear modulus across these materials can only be predicted to within 10–20%, roughly half of this uncertainty due to the k-convergence in the computation of the elastic constants, and the other half in the estimation of
that can be compared meaningfully to the appropriate experimental quantity. Even if the DFT approximation were physically perfectly accurate, these numerical uncertainties from the averaging and k-sampling would remain. The shear modulus across these materials can only be predicted to within 10–20%, roughly half of this uncertainty due to the k-convergence in the computation of the elastic constants, and the other half in the estimation of 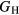 within the bounds given by
within the bounds given by  and
and 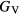 .
.
Table 6. Experimental and computed moduli (in GPa) and Debye temperatures (K).
| Young's modulus | 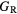 —reuss shear bound —reuss shear bound |
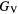 —voigt shear bound —voigt shear bound |
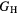 —shear Modulus —shear Modulus |
Bulk modulus | Debye |
||
|---|---|---|---|---|---|---|---|
| ErH2 | Exp. | 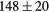 |
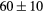 |
 |
381 | ||
| GGA-PBE | 144 (17) | 55.2 | 62.1 | 59 (7) | 89 (1) | 389.8 (6.5) | |
| YH2 | Exp. | 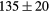 |
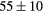 |
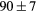 |
537 | ||
| GGA-PBE | 136 (15) | 52.5 | 58.6 | 56 (6) | 83 (1) | 521 (8) | |
| LaH2 | Exp. | 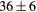 |
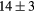 |
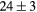 |
243 | ||
| GGA-PBE | 95 (10) | 34.6 | 41.2 | 38 (4) | 89 (1) | 365.5 (6.5) | |
| TiH2 | Exp. | 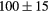 |
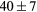 |
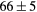 |
|||
| (fct) | GGA-PBE | 68 (14) | 20.8 | 27.1 | 24 (5) | 143 (1) | |
| ZrH2 | Exp. | 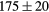 |
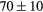 |
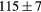 |
|||
| (fct) | GGA-PBE | 113 (24) | 35.4 | 47.7 | 42 (9) | 131 (1) |
aExperimental Debye temperature from [66].
Young's modulus E is, to lowest order, proportional to 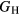 , see equation (5), and thereby inherits the same proportion of uncertainty as
, see equation (5), and thereby inherits the same proportion of uncertainty as  , which amounts to 10–24 GPa, uncertainties comparable to those seen in the experimental measurements. Once more, in the face of such numerical uncertainties, it is pointless to quote
, which amounts to 10–24 GPa, uncertainties comparable to those seen in the experimental measurements. Once more, in the face of such numerical uncertainties, it is pointless to quote 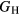 or E to finer than 1 GPa.
or E to finer than 1 GPa.
The experimental and first-principles-based results for ErH2 and YH2 exhibit very good agreement, the difference in 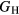 being ∼1 GPa. We reiterate that this close agreement, while gratifying, is not very meaningful; both the experimentally derived and first-priniciples computed
being ∼1 GPa. We reiterate that this close agreement, while gratifying, is not very meaningful; both the experimentally derived and first-priniciples computed 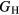 carry 10 GPa uncertainties. The bulk modulus comparison, where the PBE results are ∼10% smaller than the experimentally inferred value, is more typical of the kind of agreement that can typically be expected between DFT and experiment. These results both confirm (validate) the accuracy of the DFT for the elastic properties of the dihydrides, and lend greater confidence to the computed values of these mechanical properties, greater confidence than in the rather involved analysis to obtain these values from experiment. The 10% differences in B are expected, and the computations offer refined guidance for microstructural models.
carry 10 GPa uncertainties. The bulk modulus comparison, where the PBE results are ∼10% smaller than the experimentally inferred value, is more typical of the kind of agreement that can typically be expected between DFT and experiment. These results both confirm (validate) the accuracy of the DFT for the elastic properties of the dihydrides, and lend greater confidence to the computed values of these mechanical properties, greater confidence than in the rather involved analysis to obtain these values from experiment. The 10% differences in B are expected, and the computations offer refined guidance for microstructural models.
The comparisons between experimental and computational values for LaH2, TiH2 and ZrH2 are much worse. The results for ZrH2 are almost within agreement, strictly speaking, invoking the full combined uncertainties in both the experimentally-derived values and the DFT-derived values. However, the results for LaH2 and TiH2 are clearly well outside of the range of the uncertainties of the experimental analysis and the DFT analysis. These comparisons illustrate the value of using the experimental and computational approaches in concert for such a study. The physical uncertainties in DFT, particularly for B are known to be modest. The PBE is typically prone to be too soft, by 10–20%; this accuracy of DFT for the bulk modulus is confirmed for ErH2 and YH2. The likely explanation of the difference between the modeled cubic materials and the experimental results is the difficulty in manufacturing samples of controlled known phase. Both LaH2 and TiH2 have complex phase diagrams, and multiple phases in close proximity. Slight variations in manufacturing procedure will produce a variety of phases, possibly even mixed phases, corrupting the analysis of elastic properties of the ideal dihydride material. The problem in ZrH2 is similar but less extreme: most likely the cubic phase was also in the manufactured material. No x-ray diffraction results were taken, the specific phases or their proportion present in the LaH2 and TiH2 samples are not known. What this comparison exposes is the tremendous challenges in obtaining accurate assessment of the mechanical properties from nanoindentation experiments for dihydride films. For these materials, the DFT-derived results can be used with greater confidence in microstructural models than analyses descended from the nanoindentation experiments.
The Debye temperature estimated for ErH2 and for YH2 is in extraordinary good agreement with the measured experimental values, as is the measured 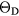 for LuH2 (361 K) [66] to the computed value in table 2. This would appear to validate the relationship between shear moduli and
for LuH2 (361 K) [66] to the computed value in table 2. This would appear to validate the relationship between shear moduli and 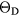 proposed by Deligoz, et al [60] The discrepancy is larger for LaH2, experiment measuring 243 K [66] while the DFT result predicts 366 K. At this point, it is not possible to state whether this is a failing in the model, or a failing in the PBE functional, or whether the experimental analysis is in some manner flawed. It would be useful to revisit the experimental measurements of
proposed by Deligoz, et al [60] The discrepancy is larger for LaH2, experiment measuring 243 K [66] while the DFT result predicts 366 K. At this point, it is not possible to state whether this is a failing in the model, or a failing in the PBE functional, or whether the experimental analysis is in some manner flawed. It would be useful to revisit the experimental measurements of 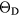 in light of the sample preparation difficulties encountered in attempting to measure elastic properties in LaH2, to resolve this discrepancy.
in light of the sample preparation difficulties encountered in attempting to measure elastic properties in LaH2, to resolve this discrepancy.
IV. Summary and conclusions
The mechanical properties of cubic and tetragonal dihydrides, focusing on the rare earths and nearby transition metals, have been analyzed using first-principles DFT methods. Specific attention was invested in elucidating the numerical accuracy of the methods used in the calculations. Directly computed quantities such as the elastic shear constants can be evaluated to no better than 3–4 GPa, and derived quantities such as the shear modulus or Young's modulus can only be predicted to no better than 10–20%, entirely distinct from the uncertainties due to the physical accuracy of the DFT approximation. The results as a function of composition explored the underlying physics in the phase change from a cubic form to a tetragonal form. The stability of the cubic structure could be probed using the stability criteria of the shear elastic constants, and is attributed to the number of electrons in the valence band structure. This supports the notion of a rigid band picture dictating the stability of the cubic and the tetragonal structure. The results for the mechanical properties of the various dihydrides considered, such as formation energies, lattice constants, and elastic constants, are shown to be in reasonably good agreement with what limited experimental data is available, and, furthermore, is able to discriminate experimental results that are suspect because of difficulties in manufacturing the materials. This accuracy suggests that the computed DFT data can be used effectively and confidently in microstructural models of tritide aging where experimental data is unavailable, with a realistic estimate of the level of quantitative confidence in the results.
Acknowledgments
Sandia is a multiprogram laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Company, for the United States Department of Energy's National Nuclear Security Administration under contract DE-AC04-94AL85000.




