Enhancement of the stability of the flow focusing technique for low-viscosity liquids

The controlled production of very small fluid entities such as drops, bubbles, emulsions and capsules has been extensively investigated over the last two decades because of its enormous relevance for a great variety of applications. Surfactants [1], electrical forces [2] or thermal gradients [3] can be used to produce fluid particles of varied morphology of micrometer or nanometer size. Extensional co-flows constitute a remarkable class of techniques in which viscous [4, 5] and/or pressure [6] forces stretch an interface until a small jet is emitted. The gas–liquid flow focusing technique working in the steady cone-jet mode uses the pressure gradient induced by an outer gas stream to 'focus' a steady liquid meniscus from whose tip a microjet is emitted. Both the liquid microjet and the co-flowing gas stream cross a discharge orifice whose diameter is much larger than that of the microjet. Gas–liquid flow focusing allows the mass production of ultrafine and monodisperse sprays, microcapsules and microparticles in a highly controlled manner.

The control achieved in the flow focusing technique fundamentally stems from the delicate balance between liquid inertia and surface tension forces appearing for Weber numbers below a few tens [6], which guarantees that the breakup of the issuing microjet is essentially caused by varicose free-surface deformations. The steady cone-jet mode is less stable as the size of the feeding capillary and/or discharge orifice increases. Specifically, for a given pressure drop applied to the gas stream, the minimum flow rate (and thus the Weber number of the emitted jet) for which the steady cone-jet mode can be obtained increases as the size of the device increases. Therefore, a certain compromise must be reached when selecting the size of the flow focusing atomizer: relatively large devices are easier to manufacture and have higher productivity, whilst smaller configurations can attain lower Weber numbers, which improves the outcome quality. One is faced with a serious design problem (e.g., in multiplexed devices consisting of a number of flow focusing tips) to meet the high productivity and quality conditions demanded in many applications. Any modification of the standard flow focusing configuration which enhances the stability of the cone-jet mode would have obvious technological implications.

Studies of the mechanisms by which the cone-jet mode destabilizes at the minimum flow rate [7–11] show that many of the experimental results obtained for low/moderate viscosity liquids cannot be explained by the well-known convective/absolute instability transition [12] of the issuing liquid jet. This occurs not only in the classical plate–orifice configuration, but also when the orifice is replaced by a converging–diverging nozzle [13, 14]. In fact, the use of converging–diverging nozzles to produce the focusing effect entails certain advantages over the classical plate–orifice configuration, but does not stabilize the meniscus in the limit of small flow rates.

The appearance of a conspicuous recirculation cell inside the tapering liquid meniscus has been unequivocally linked to the stability limit of the steady cone-jet mode for low-viscosity liquids [7, 8, 10, 11]. Thus, an immediate proposition to extend the stability limit of flow focusing is the use of some means to destroy that recirculation cell. In electrospray studies (see, e.g., [15]), the system stability was substantially enhanced by the use of a sharpened rod protruding from the mouth of the feeding capillary. In this case, the stability enhancement may be attributable to a possible charge injection mechanism at the rod tip, not necessarily to the obliteration of internal recirculation motions [16]. One can legitimately inquire whether a similar configuration would also be beneficial in flow focusing.

Figure 1 shows the flow pattern of a low-viscosity liquid in the standard flow focusing device (a) and the modified configuration (b) proposed in this work. In the first case, the liquid flows close to the meniscus free surface toward its tip dragged by the tangential viscous stresses exerted by the outer gas stream. The pressure increases in the meniscus tip because momentum accumulates in that region. This increase of pressure pumps the liquid back through the meniscus bulk, which gives rise to a recirculation pattern for small enough injected flow rates. Numerical simulations [7] and experiments [10, 11] have shown that, for sufficiently large gas pressures, there is a critical flow rate below which this flow pattern becomes unstable. In this case, the jet emission halts, and the meniscus inflates and deflates, intermittently ejecting liquid ligaments.

Zoom In Zoom Out Reset image size

The liquid motion is substantially changed by introducing a sharpened rod in the modified configuration. This rod 'arranges' the streamlines and 'directs' the flow in the meniscus tip, which prevents large recirculation cells from being formed even for very small injected flow rates and very large applied pressure drops. In this case, a new mechanism (probably associated with the surface tension) is responsible for the flow instability. In this work, the minimum flow rates attainable with the modified configuration were measured and compared with the corresponding values for the standard technique. We shall show that the use of an internal rod to destroy recirculation motions in the liquid meniscus reduces by up to five times the minimum flow rate of the standard flow focusing configuration.

2.1. Experimental method

Figure 2 shows the fluid configuration considered in our experiments. An axisymmetric meniscus is formed by injecting a liquid at a constant flow rate Q through a feeding capillary of inner radius R₁ = 100 μm. A steel calibration rod of diameter d₁ = 100 μm was positioned concentrically inside the feeding capillary. The rod end was previously sharpened to give it a conical shape characterized by the lengths h = 110 μm and d₂ = 15 μm. The feeding capillary was located at a distance H from a plate with an orifice of diameter D = 200 μm. The energy necessary to form and expel the jet comes from the pressure drop Δp applied to an air stream which co-flows with the liquid jet across the plate orifice.

Zoom In Zoom Out Reset image size

The control parameters of the experiments are the liquid flow rate Q, the applied pressure drop Δp and the capillary-to-orifice distance H. Naturally, the results can also be affected by the liquid density ρ and viscosity μ, as well as by the surface tension σ. In order to study the influence of the liquid properties on the flow stability, we considered two low-viscosity liquids with different viscosities and surface tensions: distilled water (ρ = 998 kg m⁻³, μ = 1 × 10⁻³ kg (ms)⁻¹, σ = 0.072 N m⁻¹) and hexadecane (ρ = 773 kg m⁻³, μ = 3.03 × 10⁻³ kg (ms)⁻¹, σ = 0.026 N m⁻¹). The fluid configuration analyzed in this work is the same as that studied in the earlier work [10] except for the presence of the inner rod.

Figure 3 shows the experimental setup used to determine the liquid meniscus behavior. The liquid was injected by a syringe pump (Harvard Apparatus PHD 4400) powered by a stepper motor through a capillary (A) located in front of a plate with an orifice (B). The plate covered the upper face of a cubic cell (C) in which a prescribed negative gauge pressure was applied by using a suction pump. We used two high-precision orientation systems (D) and a translation stage (E) to ensure the correct alignment of the flow focusing elements, and to set the capillary-to-orifice distance H. The liquid meniscus was formed in the open air due to the action of the air stream suctioned by the cell through the plate orifice.

Zoom In Zoom Out Reset image size

Digital images of the liquid meniscus consisting of 360 × 200 pixels were acquired at 1800 frames per second with an exposure time of 30 μs using a CMOS camera (Photonfocus MV-D1024-160) (F). The camera was equipped with optical lenses (a Mitutoyo 10× magnification zoom-objective and an Optem 70XL set of lenses with variable magnification from 0.75× to 5.25×) (G) providing a frame covering an area of about 533 × 296 μm. The magnification obtained was approximately 1.48 μm/pixel. The camera could be displaced both horizontally and vertically using a triaxial translation stage (H) to focus the liquid meniscus. The fluid configuration was illuminated from the back side by cool white light provided by an optical fiber (I) connected to a light source. We also acquired images of the liquid meniscus by using an auxiliary CCD camera (not shown in figure 3) with an optical axis perpendicular to that of the CMOS camera. The use of the two cameras allowed us to check that flow focusing was axisymmetric and that no contact between the meniscus free surface and the inner rod took place. All these elements were mounted on an optical table with a pneumatic anti-vibration isolation system (J) to damp the vibrations coming from the building.

The experimental procedure consisted of the following steps. Firstly, the capillary-to-orifice distance H was fixed. Secondly, a constant pressure drop Δp was applied to the air stream. Thirdly, the liquid was injected at a flow rate Q sufficiently high to ensure steady jetting stability. Lastly, the flow rate was reduced in steps of 0.1 ml h⁻¹ until the steady jetting became unstable. We repeated the same experimental procedure for different values of the applied pressure drop Δp and the capillary-to-orifice distance H. Images of the liquid meniscus at the minimum flow rate were recorded to measure the meniscus radius R_j just in front of the plate orifice.

2.2. Numerical method

In order to determine the influence of the inner rod on the flow topology, the streamlines were calculated with a finite volume scheme. This scheme was provided by the commercial solver Fluent v 6.3 (laminar unsteady) to resolve the mass continuity, momentum conservation and liquid volume fraction equations in the incompressible regime. The geometrical configurations analyzed were the same as those considered in the experiments. The radius of the outer boundary of the simulated fluid domain was 1 mm. The mesh was sufficiently refined to capture the strong velocity gradients experienced by the gas flow in the orifice region and to avoid numerical diffusion of the interface.

Figure 4 shows the boundary conditions used in the simulations. The velocity profile corresponding to fully developed flow with a flow rate Q was prescribed at the liquid inlet. At the gas inlet, the gauge pressure Δp was imposed, and the velocity direction was set normal to the boundary. Zero gauge pressure was prescribed at the outlet, which was located far from the jet breakup region. The nonslip boundary condition was imposed at the solid walls. The simulations started from rest by injecting a liquid flow rate Q sufficiently high to obtain steady jetting. Once the steady jetting regime was reached, Q was reduced progressively until it took the prescribed value. More details of the procedure can be found elsewhere [7].

Zoom In Zoom Out Reset image size

Figure 5 shows the minimum flow rate Q_min for a given Δp value as a function of the capillary-to-orifice distance H. The figure also shows as a reference the results obtained for the standard flow focusing configuration [10]. As can be observed, the minimum flow rates for the standard and modified flow focusing devices approximately coincide for large H values, which means that the inner rod plays no significant stabilizing role in that limit. This result was to be expected because the inner rod occupies a small portion of the meniscus volume in this case, and thus does not alter considerably the meniscus flow pattern. In contrast, the minimum flow rate for small H (H ≳ h, D/2) is greatly affected by the presence of the rod. In the standard configuration, Q_min reaches a limiting value for H ≃ D/2 [10]. The presence of the inner rod reduces this limiting value by almost five times. The stability of the modified flow focusing configuration was not explored for H ≲ h because in this case the inner rod enters the plate orifice and one is unable to observe the behavior of the entire meniscus. Hereafter, all the experimental results correspond to the capillary-to-orifice distance H which approximately led to a limiting flow rate (H = 110 and 140 μm for the standard and modified configurations, respectively).

Zoom In Zoom Out Reset image size

Figure 6 shows Q_min as a function of Δp for water and hexadecane. The figure also shows as a reference the results obtained for the standard flow focusing configuration. As can be observed, the minimum flow rate was considerably reduced over a large range of Δp by introducing the inner rod. Once the recirculation cell has been suppressed (or, at least, diminished) with the introduction of the inner rod, meniscus instability is probably caused by the surface tension retraction force, which partially explains the difference between the minimum flow rates of water and hexadecane in the modified flow focusing configuration.

Zoom In Zoom Out Reset image size

Figure 7 shows the values of the critical Reynolds and Weber numbers

$$\begin{equation} \mbox{Re}=\frac{\rho Q_{\mbox{{min}}}}{\pi R_j \mu } , \quad \mbox{We}=\frac{\rho Q_{\mbox{{min}}}^2}{\pi ^2 R_j^3\sigma }, \end{equation} \tag{ 1 }$$

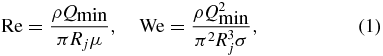
for hexadecane. We also plot in the figure the corresponding values of the standard flow focusing configuration. One can distinguish two types of stability limits. The right-hand dashed line, common to the two sets of data, corresponds to low applied pressure drops. In this case, the instability is caused by the convective/absolute instability transition [12] taking place in the emitted jet [10]. This instability mechanism is not significantly affected by the presence of the inner rod. The Weber numbers for which the convective/absolute instability transition takes place deviate significantly from the Leib and Goldstein prediction [17] because the jet's velocity profile is not uniform. Owing to the co-flowing gas stream, the jet's free surface moves with a velocity greater than that of the bulk, which naturally favors the jet to sweep growing surface waves downstream, displacing the onset of dripping to lower flow rates (Weber numbers) [18]. The left-hand dashed lines indicate the instability limits for moderate/large pressure drops. In the standard configuration, the recirculation cell appearing in the liquid meniscus for low flow rates becomes unstable. The sharpened rod introduced in the modified configuration arranges the streamlines shifting the stability limit to much lower values of the flow rate (i.e. Reynolds and Weber numbers). In this case, a new mechanism (probably associated with the surface tension) is responsible for the flow instability. Overall, considerably smaller values of the Weber number could be reached with the modified flow focusing configuration, which constitutes an important advantage in some droplet production applications.

Zoom In Zoom Out Reset image size

For not very low-viscosity liquids (e.g., hexadecane), one can easily estimate the flow rate that the air stream sets in motion by dragging the liquid layer next to the free surface. To this end, we shall assume that the free surface velocity U_s is much smaller than the velocity U_g ∼ (Δp/ρ_g)^1/2 (ρ_g is the gas density) of the gas stream (see figure 8(a)). In this case, the integral form of the momentum equation for the accelerated gas boundary layer leads to ρ_gU²_gH⁻¹ ∼ μ_gU_g/δ²_g, where μ_g is the gas viscosity, and δ_g is the characteristic boundary layer thickness. The balance of momentum on the two sides of the meniscus free surface yields μU_s/w ∼ μ_gU_g/δ_g, where w is the thickness of the Couette stream formed next to the tip of the inner rod. This thickness can be measured from the meniscus images. From the above two equations, one can estimate the free surface velocity, U_s ∼ wμ⁻¹(ρ_gμ_gU³_gH⁻¹)^1/2, and the dragged flow rate, d₂wU_s. In this way, one obtains the characteristic flow rate

$$\begin{equation} Q^*_D\equiv \frac{d_2 w^2}{\mu }\left(\rho _g^{-1/2} \mu _g \Delta p^{3/2} H^{-1}\right)^{1/2}. \end{equation} \tag{ 2 }$$

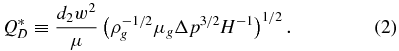
This quantity can be compared with its counterpart Q_D ≡ Dμ/ρ for the standard flow focusing configuration [7, 8, 11] (see figure 8(b)). As can be observed, the dragged flow rate in the new configuration is significantly smaller than that of the standard one, which inhibits the appearance of recirculation cells. Interestingly, the average value of Q*_D/Q_D is 0.21, similar to the ratio of minimum flow rates reached by the two configurations.

Zoom In Zoom Out Reset image size

The inner rod is an energy sink which prevents large recirculation cells from appearing for flow rates at which that pattern arises in the standard configuration. To assess the energy efficiency of this stabilizing mechanism, the radius R_j of the liquid meniscus measured just in front of the plate orifice was compared with the value

$$\begin{equation} R_0=\left(\frac{\rho Q^2}{2 \pi ^2 \Delta p}\right)^{1/4} \; . \end{equation} \tag{ 3 }$$

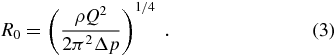
This reference value is obtained by assuming that the injected energy per unit volume, Δp, is entirely transformed into kinetic energy. Figure 9 shows the results for both the standard and modified configurations. The ratio R_j/R₀ is greater than unity in all the cases because only a part of the injected energy is transferred to the liquid between the feeding capillary end and the plate orifice. In fact, the suction caused by the gas stream continues inside the orifice, where a major amount of energy is transferred to the liquid. Similar jet sizes were obtained with the two configurations. The values of the ratio R_j/R₀ measured in the modified configuration are greater than those in the standard device due to the energy dissipated by viscous friction with the inner rod. This effect is slightly more notable for hexadecane because it is more viscous than water.

Zoom In Zoom Out Reset image size

The influence of the inner rod on the flow topology was determined from the finite volume scheme described in section 2.2. Figure 10 shows the streamlines calculated for Q = 3 ml h⁻¹ and Δp = 200 mbar. In this case, the steady jetting regime can be obtained with both the standard and modified flow focusing configurations (see figure 6). In the absence of the inner rod, two large recirculation cells appear in the liquid meniscus for both water and hexadecane. The introduction of the sharpened rod into the water meniscus greatly reduces the size of those cells, and makes them disappear in the hexadecane case. If the flow rate is lowered down to Q = 1.5 ml h⁻¹ while keeping the applied pressure drop, the standard flow focusing configuration drips (see figure 6). In contrast, the change in the flow pattern produced by the inner rod stabilizes the meniscus in the modified technique. Figure 11 shows the streamlines obtained in this case for both liquids. Small recirculation cells were produced in the water film due to its low viscosity. In the hexadecane case, the streamlines were perfectly arranged by the inner rod, and the fluid particles were smoothly directed toward the film tip. The different behaviors exhibited by water and hexadecane in the modified configuration may partially explain the difference between the minimum flow rates reached in both cases.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

To summarize, a novel flow focusing technique has been proposed and tested. This technique allowed us to steadily produce low-viscosity jets at flow rates much smaller than those reached with the standard configuration [10]. The only new element of the modified configuration is a sharpened rod located inside the liquid meniscus to eliminate the large recirculation cell appearing close to the minimum flow rate stability limit. This recirculation cell is responsible for the loss of stability of low-viscosity menisci in that limit [7, 10, 11].

The Weber numbers of the jets produced with the modified flow focusing configuration were considerably smaller than those reached with the standard technique. Therefore, one may expect that droplets with smaller kinetic/interfacial energy ratios can be obtained with the proposed configuration from the jet's breakage. This constitutes an important technological advantage in, for example, microfabrication techniques by droplet deposition on a solid substrate, where the quality of the deposition process strongly depends on the kinetic/interfacial energy ratio of the droplets.

Partial support from the Ministry of Science and Education, Junta de Extremadura and Junta de Andalucía (Spain) through grants Nos. DPI2010-21103, GR10047 and P08-TEP-04128, respectively, is gratefully acknowledged.