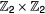Abstract
We propose using ultracold atoms trapped in a one-dimensional periodically driven optical lattice to realize the Harper–Kitaev model, where the on-site energies are periodically kicked. Such a system provides a natural platform to study both Chern insulators and Majorana fermions. Based on calculating the quasienergy spectra, we find that both Floquet Majorana modes and Hall chiral edge modes could appear at the sample boundary in the gaps between the quasienergy bands. We also study the competition of topological superconductor and Chern insulator states in the model. We calculate the 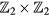 index and Floquet Chern number to characterize the above two different topological states, including the topological phase transitions in the kicked Harper–Kitaev model with the increase in the strength of the kick.
index and Floquet Chern number to characterize the above two different topological states, including the topological phase transitions in the kicked Harper–Kitaev model with the increase in the strength of the kick.
Export citation and abstract BibTeX RIS
1. Introduction
In the past years, the exploration of topological insulators and topological superconductors has attracted intense interest in condensed matter physics [1, 2]. Topological insulators are insulating in bulk and have gapless edge or surface states at their boundary. These edge sates remain to be robust even in the presence of impurities. The delicate control over these edge modes has opened a new prospect for the realization of quantum spintronic devices [3]. In topological superconductors, the edge modes are Majorana fermions. Unlike ordinary fermions, Majorana fermions are their own antiparticles and obey non-abelian exchange statistics, which could be used for topological quantum computation [4]. Significant theoretical and experimental efforts now have been devoted to search such exotic particles [5].
On the other hand, ultracold atoms trapped in optical lattices nowadays have been widely recognized as powerful simulators to study many-body problems originating from condensed matter physics [6, 7]. The cold atom systems have the advantage of clean environments and high tunability, and even some extreme physical situations unachieved in solids can be achieved with cold atoms. In particular, many great experimental progresses have been made recently in realizing artificial gauge fields and spin-orbital couplings, which turn cold atoms into a new platform for simulating topological phases. Based on engineering artificial gauge fields [8–11] and spin-orbital coupling [12–14], many theoretical proposals have been put forward to simulate topological insulators [15–20] and topological superconductors [21, 22] with cold atoms, which recently led to experimental demonstration of quantum integer Hall states and topological Chern insulators in optical lattices [23, 24].
One of recent theoretical advances in this field is Floquet topological states [25–30]. It has been shown that the introduction of time-periodic perturbations provides a practical way to manipulate the topological features of the original static system. Floquet topological states behave quite differently from static systems, which cannot be characterized by analogy to topological classification framework for static systems [25, 31, 32]. For example, Lababidi et al [33, 34] showed that a Floquet quantum Hall system exhibits some anomalous edge modes with the 'wrong' chirality, i.e. pairs of counter-propagating edge modes localized at each edge. Liu, Levchenko, and Baranger showed that unlike Majorana fermions in static systems, Floquet Majorana fermions can emerge at both quasienergy zero and quasienergy π. They are robust to perturbations and follow non-Abelian braiding statistics as their equilibrium counterparts [35]. When the optical lattices are periodically driven, cold atoms provide natural simulators for investigating Floquet topological insulators and Floquet Majorana fermions [36–41].
It is well known that the Kitaev model serves as a prototype toy model to realize Majorana fermions [50], while the Harper model provides an ideal platform to investigate topological phases both in the commensurate and incommensurate cases [42–46]. However, so far there have been no investigations on the combination of both the Kitaev model and the Harper model in one system, which may bring about new interesting phenomena. So in this paper, we propose using cold atoms trapped in a simple one-dimensional optical superlattice to achieve a hybrid Harper and Kitaev model. Different from the previous works [33, 35], this hybrid model provides a unique platform to study both Chern insulators and topological superconductors. For our purpose, we also consider periodic kick in the system and call the resulted hybrid model as the kicked Harper–Kitaev (KHK) model. It is found that the periodic kick provides an extra freedom to engineer the topological phases of the static Harper–Kitaev model. Based on calculating the quasienergy spectra and observing the band inversion, we show that the Floquet Chern insulator states and the Floquet Majorana fermions could coexist in this model. Moreover, we also study the competition of the two different kinds of topological phases with the change of the kick strength and the superconductor order parameter. Interestingly, the results show that the superconductor order could change the feature of the Hall edge states, including hybridizing the particle and hole edge states. Furthermore, we introduce the Floquet topological invariants to further characterize the above two topological phases, namely, the 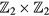 topological invariant and the Floquet Chern number.
topological invariant and the Floquet Chern number.
2. Kicked Harper–Kitaev model in optical lattice
Let us consider ultracold fermionic atoms trapped in a one-dimensional periodically optical superlattice. As shown in figure 1, the superlattice is formed with the superposition of two optical lattice potentials, given by  and
and 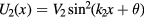 , where V1(2) are the magnitudes of the lattice potentials, and θ is the laser phase. For
, where V1(2) are the magnitudes of the lattice potentials, and θ is the laser phase. For 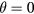 and
and 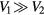 , the resulting tight binding Hamiltonian is the one that has been experimentally demonstrated for observing the Anderson localization [51]. The laser phase θ, as a tunable parameter, can simulate a second quasimomentum, such that one can find that the corresponding tight binding Hamiltonian will be the Harper model for studying quantum integer and quantum spin Hall states [52, 53].
, the resulting tight binding Hamiltonian is the one that has been experimentally demonstrated for observing the Anderson localization [51]. The laser phase θ, as a tunable parameter, can simulate a second quasimomentum, such that one can find that the corresponding tight binding Hamiltonian will be the Harper model for studying quantum integer and quantum spin Hall states [52, 53].
Figure 1. Schematic setup for the optical lattice realization of the kicked Harper–Kitaev model. The periodically varying superlattice is formed by superposition of a main lattice (solid line) and a periodically kicked lattice (dashed line).
Download figure:
Standard image High-resolution imageIn our work, the second optical lattice potential is taken to be of the time-periodic form 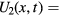
 , where
, where  is the potential strength. Such a periodically kicked optical lattice potential has been experimentally realized for simulating Anderson metal-insulator transition [54]. The resulting kicked Harper model Hamiltonian is given by
is the potential strength. Such a periodically kicked optical lattice potential has been experimentally realized for simulating Anderson metal-insulator transition [54]. The resulting kicked Harper model Hamiltonian is given by

where  , and
, and  . As will be shown below, the topological feature of this kicked Harper model is quite different from its static counterpart.
. As will be shown below, the topological feature of this kicked Harper model is quite different from its static counterpart.
Furthermore, thanks to the high tunability of a cold atom system, we can simultaneously consider the presence of p-wave superfluidity in the above kicked Harper model. In a cold atoms system, p-wave superfluid state can be prepared through the p-wave Feshbach resonance [55] or the synthetic spin-orbital coupling [56]. Here, we use the idea proposed in [57] and assume the p-wave superfluid state is prepared through s-wave interaction and the orbital degree of freedom in the lattice trap. The s-wave interaction is used for forming repulsively bound pairs, while the orbital degree of freedom is responsible for the p-wave character of these lattice bound states [57]. As a result, the Kitaev wire is naturally realized in such a system. The Hamiltonian of the resulting Kitaev model reads
where  is the p-wave superfluid order parameter. When the p-wave superfluid and the kicked optical superlattice are simultaneously considered, the total Hamiltonian of the ultracold atoms has the form
is the p-wave superfluid order parameter. When the p-wave superfluid and the kicked optical superlattice are simultaneously considered, the total Hamiltonian of the ultracold atoms has the form
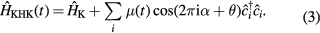
Through this KHK model, we can investigate not only the topological phases of the kicked Kitaev and kicked Harper models, but also the competitions between these phases.
3. Floquet theory and quasienergy spectrum
The above KHK model Hamiltonian 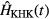 is time-periodic, i.e.
is time-periodic, i.e. 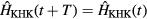 . The time evolution operator for KHK model is given by
. The time evolution operator for KHK model is given by
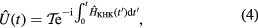
where 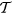 is the time-ordering operator. One can define the Floquet operator for a period of evolution as
is the time-ordering operator. One can define the Floquet operator for a period of evolution as
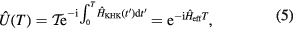
where 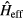 is the effective Hamiltonian. We introduce the Floquet Hamiltonian
is the effective Hamiltonian. We introduce the Floquet Hamiltonian 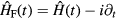 , which is also time-periodic
, which is also time-periodic  . It is easy to verify that
. It is easy to verify that  commutes with
commutes with  , and so a complete set of common eigenstates for
, and so a complete set of common eigenstates for 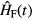 and
and 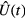 can be found. We denote them as
can be found. We denote them as 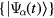 , where α is the band index. Since
, where α is the band index. Since  is unitary, its eigenvalue equation must be of the form
is unitary, its eigenvalue equation must be of the form
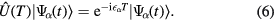
Obviously, 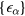 are eigenvalues of
are eigenvalues of 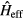 . We rewrite the eigenstates as
. We rewrite the eigenstates as
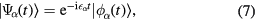
where 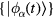 are also time-periodic. Inserting equation (7) into the Schrödinger equation
are also time-periodic. Inserting equation (7) into the Schrödinger equation 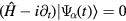 , one can find
, one can find
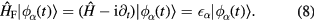
Therefore, the Floquet Hamiltonian  is equivalent to the effective Hamiltonian
is equivalent to the effective Hamiltonian 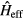 .
.
To derive the Floquet operator of the KHK model, we rewrite equation (3) in the Bogoliubov-de Gennes (BdG) form
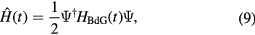
where 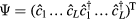 , and L is the length of the chain. The quasiparticle creation operator is taken to be
, and L is the length of the chain. The quasiparticle creation operator is taken to be
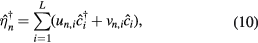
where  , and un,i and vn,i are chosen to be real. For a full period of evolution from time nT + 0− to (n + 1)T + 0−, the Floquet operator reads
, and un,i and vn,i are chosen to be real. For a full period of evolution from time nT + 0− to (n + 1)T + 0−, the Floquet operator reads
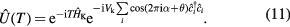
The quasienergy spectra can be obtained by numerically diagonalizing equation (11) under open boundary condition with length L. The calculated results for different kick strengths  are displayed in figure 2, where the parameters are chosen as J = t0,
are displayed in figure 2, where the parameters are chosen as J = t0, 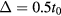 ,
, 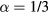 , L = 98, and
, L = 98, and  , 4t0, 6t0 and 8t0 respectively, with t0 as the energy unit. The spectral gaps around zero and ±
, 4t0, 6t0 and 8t0 respectively, with t0 as the energy unit. The spectral gaps around zero and ±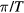 are particle-hole symmetric and will be called the BdG gaps, as figure 3 depicts. With increasing
are particle-hole symmetric and will be called the BdG gaps, as figure 3 depicts. With increasing 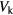 , the BdG gaps shrink. It is found that there are Floquet Majorana zero modes in the zero quasienergy bulk gap for small
, the BdG gaps shrink. It is found that there are Floquet Majorana zero modes in the zero quasienergy bulk gap for small 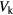 . When
. When 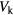 exceeds a critical value, the gaps for some θ's close and then reopen with zero modes vanishing and ±
exceeds a critical value, the gaps for some θ's close and then reopen with zero modes vanishing and ±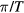 modes appearing. These zero and ±
modes appearing. These zero and ±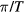 Majorana modes are protected by the particle-hole symmetry, and can be characterized by
Majorana modes are protected by the particle-hole symmetry, and can be characterized by 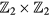 topological invariants. A detailed explanation about the relation between the Floquet Majorana modes and
topological invariants. A detailed explanation about the relation between the Floquet Majorana modes and 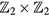 topological invariants is given in section 4.1. In cold-atom quantum wires, those FMFs can be probed using radio-frequency spectroscopy or spatially resolved rf spectroscopy [41, 47, 48].
topological invariants is given in section 4.1. In cold-atom quantum wires, those FMFs can be probed using radio-frequency spectroscopy or spatially resolved rf spectroscopy [41, 47, 48].
Figure 2. Plot of the Floquet spectra of 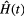 versus phase shift θ for different kick strength
versus phase shift θ for different kick strength 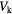 . The Floquet Majorana π mode (red line) and zero mode (blue line) are shown. The orange lines represent the chiral edge modes. The parameters are taken to be J = t0,
. The Floquet Majorana π mode (red line) and zero mode (blue line) are shown. The orange lines represent the chiral edge modes. The parameters are taken to be J = t0, 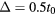 ,
, 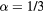 , L = 98, and (a)
, L = 98, and (a) 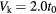 , (b)
, (b) 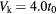 , (c)
, (c) 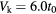 , and (d)
, and (d) 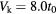 with t0 as the unit of energy.
with t0 as the unit of energy.
Download figure:
Standard image High-resolution imageFigure 3. A schematic representation of Floquet band inversions in the quasienergy gaps around 0 and 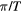 for
for 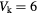 and
and 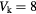 , respectively. Here we take
, respectively. Here we take 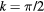 for one-dimensional cuts through the two-dimensional
for one-dimensional cuts through the two-dimensional  Brillouin zone.
Brillouin zone.
Download figure:
Standard image High-resolution imageMoreover, we can observe quantum Hall (QH) like edge modes forming within the quasienergy gaps. These QH-like edge modes are mixtures of particles and holes, and can be classified into pairs of particle-hole symmetric edge modes. Due to the artificial redundancy of the BdG formalism, a pair of such edge modes are not independent of each other, and only one of them makes contribution to the topological properties of the system. To understand the quasienergy spectra more clearly, we can map the Hamiltonian to an extended two-dimensional system, i.e. a system defined in the 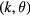 Brillouin zone. Here, θ plays a similar role to a quasimomentum ky. Therefore, we can define an unit vector
Brillouin zone. Here, θ plays a similar role to a quasimomentum ky. Therefore, we can define an unit vector 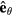 ,
,  for the direction corresponding to
for the direction corresponding to 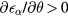
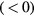 . Thus, the edge modes in the first gap above or below zero (the Chern gap, see figure 3) can be viewed as propagating along the directions ±
. Thus, the edge modes in the first gap above or below zero (the Chern gap, see figure 3) can be viewed as propagating along the directions ± . The topological properties of these QH-like edge modes can be characterized by the Floquet Chern numbers, which will be defined explicitly in section 4.2. We can also find in figure 2 that the chiral edge modes and the Floquet Majorana π mode coexist in BdG gaps because the BdG gaps are formed by the superconductivity pairing potential
. The topological properties of these QH-like edge modes can be characterized by the Floquet Chern numbers, which will be defined explicitly in section 4.2. We can also find in figure 2 that the chiral edge modes and the Floquet Majorana π mode coexist in BdG gaps because the BdG gaps are formed by the superconductivity pairing potential 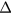 , which requires the corresponding bulk gaps closed first, under this condition, the chiral edge modes cannot exist.
, which requires the corresponding bulk gaps closed first, under this condition, the chiral edge modes cannot exist.
4. Topological phases
4.1.  invariants
invariants
The appearance of Floquet Majorana zero modes and π modes is generally attributed to the nontrivial topological properties of the bulk system. In the static Kitaev model described by equation (2), the existence of Majorana zero modes can be determined by a 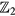 topological invariant [50]. By writing the Hamiltonian (2) in the Majorana representation in momentum space [46, 50]
topological invariant [50]. By writing the Hamiltonian (2) in the Majorana representation in momentum space [46, 50]
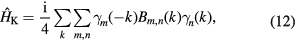
where B is a skew-symmetric matrix. The 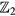 topological invariant is defined as
topological invariant is defined as
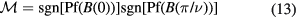
where ν is the number of atoms in an unit cell, and ![$\text{Pf}[B]$](https://content.cld.iop.org/journals/0953-8984/29/3/035601/revision1/cmaa4908ieqn068.gif) is the Pfaffian of matrix B. According to the definition,
is the Pfaffian of matrix B. According to the definition,  can have only two possible values, with
can have only two possible values, with 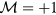 corresponding to the topological trivial phase, and
corresponding to the topological trivial phase, and 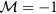 corresponding to the topological non-trivial phase. For the present Floquet system, the
corresponding to the topological non-trivial phase. For the present Floquet system, the  classification is extended to
classification is extended to 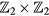 classification due to the presence of two particle-hole symmetric BdG gaps around 0 and ±
classification due to the presence of two particle-hole symmetric BdG gaps around 0 and ±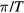 , and Majorana modes can exist in either gap. Therefore, a pair of bulk topological charges,
, and Majorana modes can exist in either gap. Therefore, a pair of bulk topological charges, 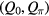 , can be defined to describe the number of Majorana modes protected by the particle-hole symmetry in the two gaps, respectively [41]. For the translationally invariant system, we can Fourier transform
, can be defined to describe the number of Majorana modes protected by the particle-hole symmetry in the two gaps, respectively [41]. For the translationally invariant system, we can Fourier transform 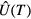 to the momentum space as
to the momentum space as 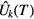 . Physically, topological charge Q0 (
. Physically, topological charge Q0 ( ) stands for the parity of times that the eigenvalues of U0(t) (
) stands for the parity of times that the eigenvalues of U0(t) (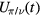 ) cross 1 (or −1) as the time variable t evolves from 0 to T.
) cross 1 (or −1) as the time variable t evolves from 0 to T.
In analogy to the static case, the mathematical expression for the topological charges has the closed form [41]
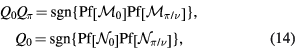
where ![${{\mathcal{M}}_{k}}=\log \left[{{U}_{k}}(T)\right]$](https://content.cld.iop.org/journals/0953-8984/29/3/035601/revision1/cmaa4908ieqn080.gif) and
and ![${{\mathcal{N}}_{k}}=\log \left[\sqrt{{{U}_{k}}(T)}\right]$](https://content.cld.iop.org/journals/0953-8984/29/3/035601/revision1/cmaa4908ieqn081.gif) are skew symmetric matrices associated with the evolution. Here,
are skew symmetric matrices associated with the evolution. Here, 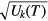 is defined by the analytic continuation from
is defined by the analytic continuation from 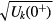 . We calculate the topological charges numerically, which are shown in figure 4. Comparing figures 4 and 2, we find that the topological charges
. We calculate the topological charges numerically, which are shown in figure 4. Comparing figures 4 and 2, we find that the topological charges 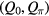 exactly reveal the existence of Floquet Majorana modes. To understand the relation between Floquet Majorana modes and kicked strength
exactly reveal the existence of Floquet Majorana modes. To understand the relation between Floquet Majorana modes and kicked strength 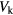 more clearly, we plot the the phase diagrams for Q0 and
more clearly, we plot the the phase diagrams for Q0 and 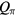 in figure 5, with the topological phase transition lines being shown in the phase diagram obviously.
in figure 5, with the topological phase transition lines being shown in the phase diagram obviously.
Figure 4. Topological charges, 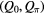 , versus the phase shift θ. (a) and (b) correspond to figures (b) and (d) in figure 2, respectively.
, versus the phase shift θ. (a) and (b) correspond to figures (b) and (d) in figure 2, respectively.
Download figure:
Standard image High-resolution imageFigure 5. Topological phase diagrams for  classification in the (
classification in the (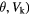 plane, with (a) Q0, (b)
plane, with (a) Q0, (b) 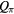 . Dark shading stands for
. Dark shading stands for 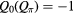 , and light shading for
, and light shading for 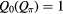 .
.
Download figure:
Standard image High-resolution image4.2. Floquet Chern numbers
To understand the topological properties of those edge modes in the Chern gaps, we first take the limit 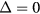 . In the basis of
. In the basis of  , the off-diagonal terms in
, the off-diagonal terms in  vanish, and the Floquet operator becomes block diagonal,
vanish, and the Floquet operator becomes block diagonal,
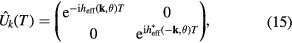
where  describes a three-band Floquet Chern insulator with
describes a three-band Floquet Chern insulator with
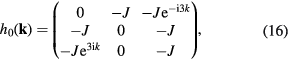
and
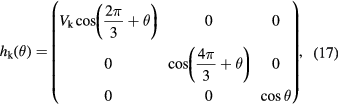
which has the same properties as Lababidi et al shows in two dimensional optical lattice [33]. If we make substitutions of 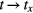 ,
,  ,
, 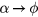 , and
, and 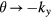 , the current one-dimensional quasiperiodic model becomes the well-known Hofstadter model [49, 58]. The Floquet Chern numbers for the system can be defined on the torus of the two variables
, the current one-dimensional quasiperiodic model becomes the well-known Hofstadter model [49, 58]. The Floquet Chern numbers for the system can be defined on the torus of the two variables 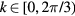 and
and 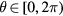 as [59]
as [59]
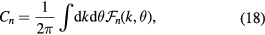
where
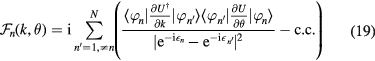
is the Berry curvature,  , n = 1, 2, 3 is the band index, and
, n = 1, 2, 3 is the band index, and 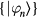 are eigenvectors of Floquet operator
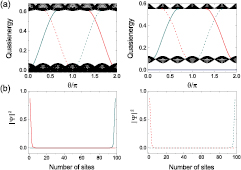
are eigenvectors of Floquet operator 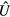 . The Floquet Chern number reveals the bulk-edge correspondence in this model. In figure 6(a), we plot the quasienergy spectra and density of states for
. The Floquet Chern number reveals the bulk-edge correspondence in this model. In figure 6(a), we plot the quasienergy spectra and density of states for 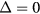 and
and 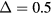 . One can find from figure 6(b) that all of these edge states are localized in the left and right edges. Consider the left edge and denote the number of edge modes at left edge propagating in the
. One can find from figure 6(b) that all of these edge states are localized in the left and right edges. Consider the left edge and denote the number of edge modes at left edge propagating in the 
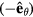 direction as
direction as 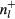
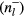 . Previous work has shown that
. Previous work has shown that 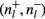 are generally related to the winding numbers rather than Chern numbers [32]. The relation between winding numbers and the number of edge modes is [32, 33]
are generally related to the winding numbers rather than Chern numbers [32]. The relation between winding numbers and the number of edge modes is [32, 33] 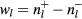 , and the relation between winding numbers and Chern numbers is
, and the relation between winding numbers and Chern numbers is 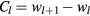 , l = 1, 2, 3. We numerically calculate the Floquet Chern numbers for
, l = 1, 2, 3. We numerically calculate the Floquet Chern numbers for 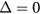 with other parameters the same as figure 2, and the results are shown in table 1. We know from the results that topological phase transition happens with increasing
with other parameters the same as figure 2, and the results are shown in table 1. We know from the results that topological phase transition happens with increasing 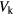 , acompanied by gap closing and reopening of the quasienergy bands, and the Chern numbers always change by multiples of 3. This can be interpreted by the Diophantine equation
, acompanied by gap closing and reopening of the quasienergy bands, and the Chern numbers always change by multiples of 3. This can be interpreted by the Diophantine equation 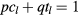 , where tl is an integer. In our model, we have chosen p = 1 and q = 3, and the Chern numbers are therefore given by
, where tl is an integer. In our model, we have chosen p = 1 and q = 3, and the Chern numbers are therefore given by 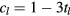 .
.
Figure 6. Plot of (a) quasienergy spectra and (b) density functions, for 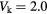 ,
, 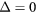 (left) and
(left) and 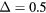 (right). The other parameters are taken to be the same as figure 2. (b) Solid line represents the u-component of
(right). The other parameters are taken to be the same as figure 2. (b) Solid line represents the u-component of 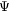 and dashed line represents the v-component.
and dashed line represents the v-component.
Download figure:
Standard image High-resolution imageTable 1. Results of numerical calculation of winding numbers wl and Chern numbers Cl for 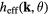 , parameters are taken the same as figure 2.
, parameters are taken the same as figure 2. 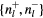 are the numbers of edge modes within the lth gap and propagating along ±
are the numbers of edge modes within the lth gap and propagating along ±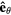 at the left edge.
at the left edge.
 |
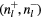 |
wl | Cl |
|---|---|---|---|
| 2 | (0, 0),(1, 0),(0, 1) | 0, 1, − 1 | 1, − 2, 1 |
| 4 | (0, 0),(1, 0),(0, 1) | 0, 1, − 1 | 1, − 2, 1 |
| 6 | (1, 1),(0, 2),(2, 0) | 0, − 2, 2 | −2, 4, − 2 |
| 8 | (1, 1),(4, 0),(0, 4) | 0, 4, − 4 | 4, − 8, 4 |
As we adiabatically turn on the 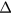 term, we find that bulk gaps remain nonzero. As a result, the Chern numbers remain to be the same, since the topological invariants cannot change values without closing the bulk gap. It is straightforward to check that the Floquet Chern numbers for the particle bands
term, we find that bulk gaps remain nonzero. As a result, the Chern numbers remain to be the same, since the topological invariants cannot change values without closing the bulk gap. It is straightforward to check that the Floquet Chern numbers for the particle bands 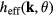 and hole bands
and hole bands 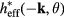 are equal, leading to the total Chern number
are equal, leading to the total Chern number 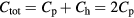 , as has previously been observed by Qi [60]. This result can account for the doubling of the edge states in the BdG formalism.
, as has previously been observed by Qi [60]. This result can account for the doubling of the edge states in the BdG formalism.
5. Conclusion
In summary, we have proposed using cold atoms trapped in a one-dimensional optical superlattice to achieve a combination of the Harper and Kitaev models. Such hybrid model allows us to simultaneously study both topological insulators and topological superconductors. We have studied the topological phases of the Harper–Kitaev model in the presence of a periodic kick. Our results show that the periodic kick provides an extra freedom to engineer the topological phases of the static Harper–Kitaev model. Based on calculating the quasienergy spectra, we show that the Floquet topological insulator states and the Floquet Majorana fermions could coexist in this model. We also have studied the competition of the two different kinds of topological phases with the change of the kick strength and the superconductor order parameter. It is found that the superconductor order could change the feature of the Hall edge states, including hybridizing the particle and hole edge states. We have also generalized our model to include an additional phase shift to investigate three-dimensional topological phases in a following work [61].
Acknowledgments
One of the authors (MNC) would like to thank Liang Jiang for helpful discussions on calculation of topological invariants. This work was supported by the State Key Program for Basic Researches of China under grants numbers 2015CB921202, 2014CB921103 (LS), the National Natural Science Foundation of China under grant numbers 11225420 (LS), and a project funded by the PAPD of Jiangsu Higher Education Institutions.