Abstract
We calculate magnetic susceptibility of paramagnetic bcc Fe-Mn and Fe-V alloys by two different approaches. The first approach employs the coherent potential approximation (CPA) combined with the dynamical mean-field theory (DMFT). The material-specific Hamiltonians in the Wannier function basis are obtained by density functional theory. In the second approach, we construct supercells modeling the binary alloys and study them using DMFT. Both approaches lead to a qualitative agreement with experimental data. In particular, the decrease of Curie temperature with Mn content and a maximum at about 10 at.% V are well described in units of the Curie temperature of pure iron. In contrast to the Mn impurities, the V ones are found to be antiferromagnetically coupled to Fe atoms. Our calculations for the two-band Anderson–Hubbard model indicate that the antiferromagnetic coupling is responsible for a maximum in the concentration dependence of Curie temperature in Fe-V alloys.
Export citation and abstract BibTeX RIS
1. Introduction
The study of substitutional alloys within the density functional theory (DFT) is usually performed by large supercells with randomly distributed atoms or by coherent potential approximation (CPA) [1]. In the CPA, the effective (coherent) potential is introduced on every site of the lattice. This potential is constructed in such way to simulate properties of the actual substitutional alloy. Obviously, the conventional single-site CPA neglects the local environment effects, which can be taken into account in the supercell approach. However, the latter introduces an artificial translational symmetry and allows one to consider only a discrete set of concentrations. To include the short-range order effects to the CPA, different extensions have been proposed (e.g. [2–4], for review see [5, 6]).
The alloys of transition metals are of great technological importance and require an accurate treatment of electron correlation effects. However, the DFT within the commonly used local density approximation (LDA) or generalized gradient approximation (GGA) usually fails to reproduce the properties of strongly correlated systems. This problem can be overcome by using, for example, a combination of the CPA with static approximation for electron correlations [7]. Another problem of DFT deals with the simulation of paramagnetic state, which cannot be described by nonmagnetic calculations. This problem is often solved by disordered local moment (DLM) model [8], which simulates the paramagnetic state by randomly distributed magnetic moments with zero net magnetization.
Both the paramagnetic state and electron correlations can be accurately captured by dynamical mean-field theory (DMFT) [9], which maps the lattice problem onto a quantum impurity embedded in a self-consistently determined bath. To date, the combination of the density functional theory and DMFT (so-called LDA+DMFT or DFT+DMFT method [10]) is one of the most effective tools for study of correlated compounds.
Since both the DMFT and CPA are mean-field approaches neglecting the spatial correlations, they can be naturally combined [11]. This combination is usually called the CPA+DMFT approach or DMFT for disordered systems. In this approach, several impurity problems are to be solved, and the local Green function of effective medium is computed as a weighted sum of impurity Green functions [11]. Using DFT for calculation of material-specific aspects, the CPA+DMFT was successfully applied to real disordered systems and alloys. In particular, the magnetic properties and thermopower of NaxCoO2 were studied in [12]. The structural fcc-hcp transition in Fe-Mn alloys was investigated in [13]. The magnetic and spectral properties of binary alloys [14–16] and Heusler alloys [17] were studied by the CPA+DMFT approach implemented within the Korringa–Kohn–Rostoker method.
In this paper, we employ the CPA+DMFT approach to calculate magnetic susceptibility of paramagnetic bcc Fe-Mn and Fe-V alloys. We also construct supercells modeling the binary alloys and study them using DMFT. Although Mn and V are close in the periodic table, these elements dissolved in bcc Fe have a different impact on the magnetic properties and phase stability. In particular, the Curie temperature of bcc Fe-Mn alloys decreases with Mn content [18, 19], while in Fe-V alloys it reaches a maximum at ∼10 at.% V [20].
The previous DFT-based studies of these bcc alloys were focused mainly on the ferromagnetic state, and the paramagnetic state was simulated only within the DLM model by Gorbatov et al [21]. In addition, the electron correlations in the previous studies were poorly treated within LDA or GGA, whereas they were shown to be significant in iron [22–24]. However, the Curie temperature of bcc Fe, which is well captured by the DLM approach [25], was substantially overestimated in previous DMFT studies. This overestimation is mainly due to neglecting non-local correlations [26] and using the approximate (density–density) form of Coulomb interaction [27]. Although different extensions and quantum impurity solvers have been proposed to overcome these difficulties, at the moment the calculations which could accurately predict the Curie temperature of Fe are prohibitively expensive. Nevertheless, previous DMFT studies of Fe showed that the magnetization and even such subtle thing as the bcc-fcc structural transition can be well described in units of Curie temperature [22, 26]. In this paper we demonstrate that the concentration dependence of Curie temperature in bcc Fe-Mn and Fe-V alloys also can be described in units of Curie temperature for pure Fe.
2. CPA+DMFT approach
The substitutional alloy can be modeled by the Anderson–Hubbard Hamiltonian
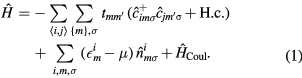
Here,  (
(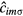 ) is the creation (annihilation) operator of an electron with spin
) is the creation (annihilation) operator of an electron with spin  at orbital m of site i,
at orbital m of site i, 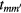 is the hopping amplitude,
is the hopping amplitude,  , μ is the chemical potential,
, μ is the chemical potential, 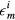 denotes the on-site energy,
denotes the on-site energy, 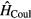 is the on-site Coulomb interaction Hamiltonian. In the case of a binary alloy A1−xBx, each lattice site is occupied by atom A with probability
is the on-site Coulomb interaction Hamiltonian. In the case of a binary alloy A1−xBx, each lattice site is occupied by atom A with probability 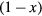 or by atom B with probability x. The single-orbital version of Hamiltonian (1) has been widely used in previous CPA+DMFT studies on the interplay between correlations and disorder [28–30].
or by atom B with probability x. The single-orbital version of Hamiltonian (1) has been widely used in previous CPA+DMFT studies on the interplay between correlations and disorder [28–30].
Calculating the kinetic contribution in Hamiltonian (1) by LDA or GGA, one obtains the following Hamiltonian
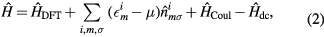
where 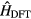 is the DFT Hamiltonian in a basis of Wannier functions or other localized orbitals,
is the DFT Hamiltonian in a basis of Wannier functions or other localized orbitals, 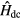 is a correction to avoid double counting of the Coulomb interaction. This correction is introduced as
is a correction to avoid double counting of the Coulomb interaction. This correction is introduced as
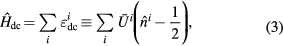
where 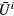 is the average Coulomb interaction in d shell,
is the average Coulomb interaction in d shell, 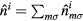 is the number of d electrons at site i. This form of the double-counting correction is widely used and corresponds to the fully localized limit.
is the number of d electrons at site i. This form of the double-counting correction is widely used and corresponds to the fully localized limit.
We will refer to atoms of type A (B) as host (impurity) atoms. In this case, the material-specific computational scheme of CPA+DMFT approach can be constructed in the following steps. First, DFT calculations within LDA or GGA are performed for the lattice containing only host (A) atoms. Second, an effective Hamiltonian 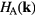 in the Wannier function basis is constructed for states near the Fermi level in the host lattice. Third, a supercell is simulated within DFT, and the disorder parameters
in the Wannier function basis is constructed for states near the Fermi level in the host lattice. Third, a supercell is simulated within DFT, and the disorder parameters 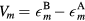 are computed as a difference between centers of gravity for local densities of states (DOS) of the impurity and the most distant host atom. In the last step, the self-consistent CPA+DMFT equations are iteratively solved. Now we proceed to these equations.
are computed as a difference between centers of gravity for local densities of states (DOS) of the impurity and the most distant host atom. In the last step, the self-consistent CPA+DMFT equations are iteratively solved. Now we proceed to these equations.
In CPA+DMFT approach, the real alloy is replaced by an effective medium with the local Green function
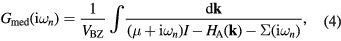
where 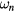 are the fermionic Matsubara frequencies, μ is the chemical potential, I is the unit matrix, VBZ is the volume of the first Brillouin zone,
are the fermionic Matsubara frequencies, μ is the chemical potential, I is the unit matrix, VBZ is the volume of the first Brillouin zone, 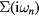 denotes the effective potential or self-energy, which contains the information about electronic correlations and disorder. The chemical potential here is to be adjusted to the average number of electrons per site in alloy. From the Dyson equation one can express the bath Green function
denotes the effective potential or self-energy, which contains the information about electronic correlations and disorder. The chemical potential here is to be adjusted to the average number of electrons per site in alloy. From the Dyson equation one can express the bath Green function
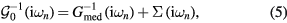
which is then used to compute the impurity Green functions 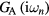 and
and 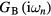 . Following the CPA approach, the local Green function of effective medium is a weighted sum of impurity Green functions:
. Following the CPA approach, the local Green function of effective medium is a weighted sum of impurity Green functions:
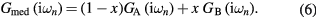
Having obtained 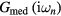 by equation (6), the new self-energy can be easily computed from the Dyson equation:
by equation (6), the new self-energy can be easily computed from the Dyson equation:
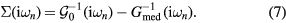
The obtained 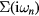 is then used to calculate
is then used to calculate 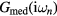 by equation (4). The equations (4)–(7) are iteratively solved until the convergence is achieved.
by equation (4). The equations (4)–(7) are iteratively solved until the convergence is achieved.
In the orbital space, the above Green functions and self-energy are matrices of the same size as 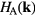 . To calculate the impurity Green functions elements in the correlated subspace (Wannier functions of d character), two single-impurity problems are to be solved by any quantum impurity solver. The effective action for these impurity problems can be expressed as
. To calculate the impurity Green functions elements in the correlated subspace (Wannier functions of d character), two single-impurity problems are to be solved by any quantum impurity solver. The effective action for these impurity problems can be expressed as
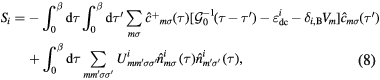
where  , β is the inverse temperature,
, β is the inverse temperature,  is the Kronecker delta,
is the Kronecker delta,  is an element of the Coulomb interaction matrix. The last term in equation (8) corresponds to the Coulomb interaction in the density–density form. In the uncorrelated subspace (Wannier functions of sp character), the impurity Green function of type A coincides with the bath Green function, while for the impurity of type B it can be expressed as
is an element of the Coulomb interaction matrix. The last term in equation (8) corresponds to the Coulomb interaction in the density–density form. In the uncorrelated subspace (Wannier functions of sp character), the impurity Green function of type A coincides with the bath Green function, while for the impurity of type B it can be expressed as
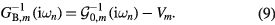
A more detailed description of the computational scheme can be found in [13].
3. Results and discussion
We performed DFT calculations using the full-potential linearized augmented-plane wave method implemented in the ELK code supplemented by the Wannier function projection procedure (exciting-plus code) [31]. The Perdew–Burke–Ernzerhof form [32] of GGA was considered. The calculations were carried out with the experimental lattice constants [18, 33]. The convergence threshold for total energy was set to 10−6 Ry.
In our calculations we employed supercells containing 8, 16 and 32 atoms. The supercells with 8 atoms were constructed by doubling all primitive vectors. For further doubling the cell volume, the new lattice vectors were built as 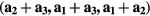 , where
, where 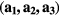 are old lattice vectors. In each of these supercells, one atom of Fe was substituted by Mn or V atom. The distances between Mn and its nearest periodic image are 4.977 Å, 5.740 Å and 8.112 Å for the supercells containing 8, 16 and 32 atoms, respectively. In the case of V impurities, these distances are equal to 4.988 Å, 5.746 Å and 8.116 Å, respectively. For the concentration of 25 at.% we used the 8-atom and 16-atom special quasirandom structures (SQS-8 and SQS-16) presented in [34]. These structures contain two (SQS-8) and four (SQS-16) impurity atoms per unit cell and are constructed to mimic the first few radial correlation functions of a perfectly random alloy [35]. The local relaxation effects were neglected, since Fe, Mn and V have close atomic radii of 1.26 Å, 1.27 Å and 1.34 Å, respectively. Integration in the reciprocal space was performed using
are old lattice vectors. In each of these supercells, one atom of Fe was substituted by Mn or V atom. The distances between Mn and its nearest periodic image are 4.977 Å, 5.740 Å and 8.112 Å for the supercells containing 8, 16 and 32 atoms, respectively. In the case of V impurities, these distances are equal to 4.988 Å, 5.746 Å and 8.116 Å, respectively. For the concentration of 25 at.% we used the 8-atom and 16-atom special quasirandom structures (SQS-8 and SQS-16) presented in [34]. These structures contain two (SQS-8) and four (SQS-16) impurity atoms per unit cell and are constructed to mimic the first few radial correlation functions of a perfectly random alloy [35]. The local relaxation effects were neglected, since Fe, Mn and V have close atomic radii of 1.26 Å, 1.27 Å and 1.34 Å, respectively. Integration in the reciprocal space was performed using 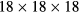
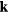 -point mesh for pure Fe, while
-point mesh for pure Fe, while 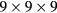 ,
, 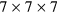 and
and 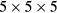 meshes were used for supercells with 8, 16 and 32 atoms, respectively.
meshes were used for supercells with 8, 16 and 32 atoms, respectively.
From converged DFT results we constructed effective Hamiltonians in the basis of Wannier functions, which were built as a projection of the original Kohn–Sham states to site-centered localized functions of spd character as described in [36]. In figure 1 we present bands of bcc Fe obtained in nonmagnetic GGA calculations in comparison with bands corresponding to the constructed effective Hamiltonians in the spd Wannier functions basis. The obtained Wannier functions are not maximally localized, that is in fact not necessary for our calculations.
Figure 1. Band structure of bcc Fe obtained in nonmagnetic GGA calculations (solid lines) in comparison with bands corresponding to the constructed spd Wannier functions (dots). The Fermi level is at zero energy.
Download figure:
Standard image High-resolution imageThe disorder parameters obtained in supercell calculations are presented in table 1. We employed 32-atoms supercells for impurity concentrations of 1.5–4.5 at.%, 16-atoms supercells for 6.25 at.% and 8-atoms supercells for all other concentrations. Since the s and p states extend beyond the region where they are well described by the constructed Wannier functions, the centers of gravity of local DOSes were calculated using an energy window of 15 eV.
Table 1. Disorder parameters for different orbital symmetries obtained in supercell calculations of Fe-Mn and Fe-V alloys.
| Alloy | x | Vs (eV) | Vp (eV) | Vd (eV) |
|---|---|---|---|---|
| Fe100−xMnx | 1.5 | 0.103 | 0.122 | 0.223 |
| 3.125 | 0.102 | 0.121 | 0.223 | |
| 4.5 | 0.101 | 0.121 | 0.223 | |
| 6.25 | 0.084 | 0.115 | 0.225 | |
| Fe100−xVx | 3.125 | 0.489 | 1.722 | 1.160 |
| 6.25 | 0.434 | 1.734 | 1.190 | |
| 9.4 | 0.480 | 1.517 | 1.058 | |
| 12.5 | 0.476 | 1.518 | 1.054 | |
| 19.0 | 0.458 | 1.514 | 1.048 | |
| 25 | 0.443 | 1.459 | 1.043 | |
We performed DMFT and CPA+DMFT calculations using the AMULET code [37]. To solve the impurity problems, we used the hybridization expansion continuous-time quantum Monte Carlo (CT-QMC) method [38]. Each iteration in the CPA+DMFT calculations contained 2 impurity problems, while 3, 5 and 7 impurity problems per iteration were solved in the DMFT calculations of supercells with 8, 16 and 32 atoms, respectively. Each iteration in the DMFT calculations of SQS-8 and SQS-16 contained 4 and 16 impurity problems, respectively. The on-site Coulomb interaction was considered in the density–density form and was parametrized via Slater integrals F0, F2 and F4 linked to the Hubbard parameter 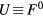 and Hund's rule coupling
and Hund's rule coupling 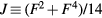 with
with 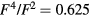 [39]. Our calculations were carried out with U from 2 to 6 eV and
[39]. Our calculations were carried out with U from 2 to 6 eV and 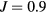 eV. These values are in agreement with U from 3 to 6 eV and
eV. These values are in agreement with U from 3 to 6 eV and 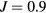 eV [13, 40] obtained for bcc Fe by constrained density functional theory (cDFT) approach and with U from 3.5 to 4.5 eV [41] obtained by constrained random-phase approximation (cRPA).
eV [13, 40] obtained for bcc Fe by constrained density functional theory (cDFT) approach and with U from 3.5 to 4.5 eV [41] obtained by constrained random-phase approximation (cRPA).
To obtain the magnetic susceptibility 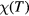 , we calculated magnetization induced by the external magnetic field. A few magnetic fields from 0.01 to 0.04 eV were used to ensure linearity of response. The temperature dependence of magnetic susceptibility in the paramagnetic region was fitted to the Curie–Weiss law
, we calculated magnetization induced by the external magnetic field. A few magnetic fields from 0.01 to 0.04 eV were used to ensure linearity of response. The temperature dependence of magnetic susceptibility in the paramagnetic region was fitted to the Curie–Weiss law 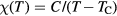 , where C is a Curie constant and TC is the paramagnetic Curie temperature.
, where C is a Curie constant and TC is the paramagnetic Curie temperature.
Our calculations for pure Fe led to the Curie temperature of 2112, 2130 and 2048 K with U equal to 2, 4 and 6 eV, respectively. These values are in agreement with the previous DFT+DMFT studies [26, 27, 42] and are much larger than the experimental value of 1043 K. As shown in [27, 42], the substantial part of the Curie temperature overestimation in Fe is due to the approximate (density–density) form of Coulomb interaction restricted to the Ising-type exchange interaction. Nevertheless, the vast majority of DFT+DMFT calculations are performed with the density–density form, since employing the full rotationally invariant form of Coulomb interaction is much more computationally expensive. To overcome this difficulty, the  structural transition in Fe upon heating was successfully described as a function of the reduced temperature
structural transition in Fe upon heating was successfully described as a function of the reduced temperature 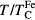 , where
, where 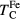 is the calculated Curie temperature of bcc Fe. Following the same way, we present the Curie temperatures of alloys in units of the Curie temperature of pure Fe.
is the calculated Curie temperature of bcc Fe. Following the same way, we present the Curie temperatures of alloys in units of the Curie temperature of pure Fe.
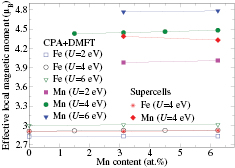
The paramagnetic state of bcc Fe-Mn alloys is observed up to about 5 at.% Mn [18], since Mn dissolved in Fe stabilizes the γ-phase with fcc lattice. In figure 2 we present the Curie temperature and Curie constant of Fe-Mn alloys as a function of Mn content. The calculated Curie temperature decreases linearly with Mn content in good agreement with the experimental data [18, 19]. The slope of this linear dependence is slightly affected by increasing U from 2 to 4 eV, and is almost not affected by further increasing U to 6 eV. The calculated Curie constant of pure Fe increases with U and for 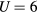 eV is about 10% less than the experimental value of 0.022 cm3 K g−1 [43]. The addition of Mn leads to a linear increase of the Curie constant for all values of U. In figure 3 we present the effective local magnetic moments obtained by fitting contributions from different constituents to the Curie–Weiss law expressed as
eV is about 10% less than the experimental value of 0.022 cm3 K g−1 [43]. The addition of Mn leads to a linear increase of the Curie constant for all values of U. In figure 3 we present the effective local magnetic moments obtained by fitting contributions from different constituents to the Curie–Weiss law expressed as 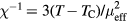 , where
, where  is the effective local magnetic moment. We found that the effective local moments are almost independent of Mn content, which results in a linear increase of the Curie constant with concentration of Mn. The supercell approach combined with DMFT and CPA+DMFT led to similar results. The most significant difference of effective local moments obtained by these two approaches is found for Mn at a content of 6.25 at.%. However, for this composition both approaches resulted in almost equal Curie temperatures.
is the effective local magnetic moment. We found that the effective local moments are almost independent of Mn content, which results in a linear increase of the Curie constant with concentration of Mn. The supercell approach combined with DMFT and CPA+DMFT led to similar results. The most significant difference of effective local moments obtained by these two approaches is found for Mn at a content of 6.25 at.%. However, for this composition both approaches resulted in almost equal Curie temperatures.
Figure 2. Curie temperature (upper panel) and Curie constant (lower panel) of bcc Fe-Mn alloys as a function of Mn content calculated by DMFT for supercell structures and by CPA+DMFT approach in comparison with the experimental data of Li et al [18], Sadron et al [19] and Sucksmith et al [43].
Download figure:
Standard image High-resolution imageFigure 3. Effective local magnetic moment in Fe-Mn alloys as a function of Mn content calculated by DMFT for supercell structures and by CPA+DMFT approach.
Download figure:
Standard image High-resolution imageSince addition of Mn results in a decrease of the bcc-fcc transition temperature, the paramagnetic phase of bcc Fe-Mn alloys exists only in a narrow temperature range which is less than 150 K (the phase diagram can be found in [44]). At the moment, there are no experimental data on magnetic susceptibility of paramagnetic Fe-Mn alloys, which can be used to extract the effective local moments. Nevertheless, the obtained effective local moments on Fe atoms (figure 3) are weakly dependent on U and are close to the experimental value of 3.13 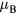 for pure bcc Fe [43].
for pure bcc Fe [43].
The obtained 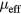 extracted from Curie–Weiss law can be linked to the effective spin peff as
extracted from Curie–Weiss law can be linked to the effective spin peff as 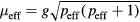 , where
, where 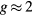 is the electron spin g-factor. According to the Rhodes–Wohlfarth criterion [45, 46], the ratio of magnetic moment
is the electron spin g-factor. According to the Rhodes–Wohlfarth criterion [45, 46], the ratio of magnetic moment 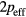 to magnetic moment in magnetically ordered state can be used to classify the systems with respect to the nature of spin fluctuations. The experimental ferromagnetic moment of bcc Fe is equal to 2.22
to magnetic moment in magnetically ordered state can be used to classify the systems with respect to the nature of spin fluctuations. The experimental ferromagnetic moment of bcc Fe is equal to 2.22 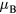 [43] resulting in Rhodes–Wohlfarth ratio of 1.05 [45]. This ratio classifies pure bcc Fe as a local-moment system. According to the experimental data, the magnetic moments on Mn atoms below the Curie temperature are very sensitive to temperature and Mn content [47, 48]. In particular, at room temperature magnetic moments from −1 to 0
[43] resulting in Rhodes–Wohlfarth ratio of 1.05 [45]. This ratio classifies pure bcc Fe as a local-moment system. According to the experimental data, the magnetic moments on Mn atoms below the Curie temperature are very sensitive to temperature and Mn content [47, 48]. In particular, at room temperature magnetic moments from −1 to 0 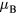 were found for less than 2 at.% Mn [48, 49], while moments from 0.5 to 1
were found for less than 2 at.% Mn [48, 49], while moments from 0.5 to 1 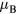 were obtained for Mn content from 2 to 9 at.% [47, 50, 51]. Similar results have been obtained in previous DFT calculations which found that states with FM and AFM couplings are close in energy [52]. Using the upper limit of 1
were obtained for Mn content from 2 to 9 at.% [47, 50, 51]. Similar results have been obtained in previous DFT calculations which found that states with FM and AFM couplings are close in energy [52]. Using the upper limit of 1 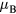 for magnetic moment on Mn below the Curie point and the calculated
for magnetic moment on Mn below the Curie point and the calculated  for Mn at
for Mn at 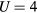 eV, one obtains the Rhodes–Wohlfarth ratio of 3.52. This indicates that the magnetism of Mn impurities is much more itinerant than that of Fe atoms.
eV, one obtains the Rhodes–Wohlfarth ratio of 3.52. This indicates that the magnetism of Mn impurities is much more itinerant than that of Fe atoms.
In contrast to Mn, the addition of V stabilizes the α-phase with bcc lattice and causes the Curie temperature to pass through a maximum at about 10 at.% V [20]. The Curie temperatures and Curie constants of Fe-V alloys are presented in figure 4. Our CPA+DMFT calculations indicate that the Curie temperature maximum shifts to higher V concentrations with increasing U. This shift is accompanied by increasing the maximum value of the Curie temperature. The best agreement with the experimental behaviour of the Curie temperature is found at  eV. Although the supercell approach combined with DMFT also gives a maximum in the Curie temperature, it results in a less satisfactory agreement with the experiment. In contrast to Fe-Mn alloys, the Curie constant of Fe-V alloys decreases with V content [20]. This decrease is well reproduced by both approaches employed (figure 4). The effective local moment of Fe also decreases with V content (figure 5) and reaches a minimum at about 19 at.% V. For 25 at.% the increase of the cell size from 8-atom SQS to 16-atom SQS is accompanied by the increase of the Curie temperature from 0.925 to 0.961
eV. Although the supercell approach combined with DMFT also gives a maximum in the Curie temperature, it results in a less satisfactory agreement with the experiment. In contrast to Fe-Mn alloys, the Curie constant of Fe-V alloys decreases with V content [20]. This decrease is well reproduced by both approaches employed (figure 4). The effective local moment of Fe also decreases with V content (figure 5) and reaches a minimum at about 19 at.% V. For 25 at.% the increase of the cell size from 8-atom SQS to 16-atom SQS is accompanied by the increase of the Curie temperature from 0.925 to 0.961  resulting in a better agreement with the CPA calculations and experimental data (figure 4). At the same time, the Curie constant obtained by SQS-8 is already close to the CPA and experimental values and is almost indistinguishable from that obtained by SQS-16. In contrast to the Mn atoms, the induced magnetization of V ones is antiparallel to that of Fe atoms, indicating that they are antiferromagnetically (AFM) coupled. This finding is in agreement with the well-known fact that the early 3d impurities couple antiferromagnetically to the host Fe atoms, while the late ones couple ferromagnetically [52].
resulting in a better agreement with the CPA calculations and experimental data (figure 4). At the same time, the Curie constant obtained by SQS-8 is already close to the CPA and experimental values and is almost indistinguishable from that obtained by SQS-16. In contrast to the Mn atoms, the induced magnetization of V ones is antiparallel to that of Fe atoms, indicating that they are antiferromagnetically (AFM) coupled. This finding is in agreement with the well-known fact that the early 3d impurities couple antiferromagnetically to the host Fe atoms, while the late ones couple ferromagnetically [52].
Figure 4. Curie temperature (upper panel) and Curie constant (lower panel) of bcc Fe-V alloys as a function of V content calculated by DMFT for supercell structures and by CPA+DMFT approach in comparison with the experimental data of Arajs et al [20]. The Curie constant for 25 at.% was obtained using SQS-16 and is almost indistinguishable from that obtained by SQS-8.
Download figure:
Standard image High-resolution imageFigure 5. Effective local magnetic moment in Fe-V alloys as a function of V content calculated by DMFT for supercell structures and by CPA+DMFT approach.
Download figure:
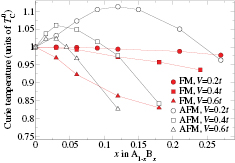
Standard image High-resolution imageTo study the origin of different Curie temperature behaviour in Fe-Mn and Fe-V alloys, we consider the degenerate two-band Anderson–Hubbard model with Hamiltonian (1) for a binary alloy A1−xBx. We aim to determine whether a maximum in the concentration dependence of Curie temperature in Fe-V alloys is due to AFM coupling or whether it is caused by disorder parameters which are significantly larger for V impurities in Fe than for Mn impurities (see table 1). We solve the Hamiltonian (1) by the CPA+DMFT approach. The noninteracting DOS of both constituents is assumed to have a semi-elliptical shape corresponding to the infinite-dimensional Bethe lattice. To obtain a similar correlation strength as in Fe-Mn and Fe-V alloys with bandwidth 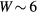 eV and
eV and 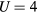 eV, we set
eV, we set  and
and 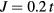 , where t is a half of the noninteracting bandwidth. The filling was fixed at
, where t is a half of the noninteracting bandwidth. The filling was fixed at  . Since our calculations of magnetic susceptibility include the spin polarization of the effective medium, the AFM coupling of impurity and host atoms was introduced by swapping the spin–up and spin–down components of bath Green function for impurity B. In the non-disordered case (
. Since our calculations of magnetic susceptibility include the spin polarization of the effective medium, the AFM coupling of impurity and host atoms was introduced by swapping the spin–up and spin–down components of bath Green function for impurity B. In the non-disordered case (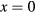 ) we obtained the Curie temperature
) we obtained the Curie temperature 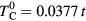 . The calculated Curie temperatures in units of
. The calculated Curie temperatures in units of 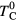 with ferromagnetic (FM) and AFM couplings are presented in figure 6. For all considered values of disorder parameter V, our calculations with AFM coupling result in a maximum in the Curie temperature curve, which shifts to lower concentrations of B atoms with increasing V. We found that this maximum cannot be obtained with FM coupling by increasing V up to
with ferromagnetic (FM) and AFM couplings are presented in figure 6. For all considered values of disorder parameter V, our calculations with AFM coupling result in a maximum in the Curie temperature curve, which shifts to lower concentrations of B atoms with increasing V. We found that this maximum cannot be obtained with FM coupling by increasing V up to 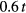 . The Curie temperature behaviour in the single-band model with FM coupling was studied by Byczuk et al [29], who found the Curie temperature enhancement caused by the band splitting for a certain range of parameters with
. The Curie temperature behaviour in the single-band model with FM coupling was studied by Byczuk et al [29], who found the Curie temperature enhancement caused by the band splitting for a certain range of parameters with 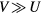 .
.
Figure 6. Curie temperature as a function of concentration obtained by CPA+DMFT for the two-band Anderson–Hubbard model with ferromagnetic (FM) and antiferromagnetic (AFM) couplings of impurity and host atoms. The calculations were performed with 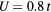 and
and 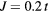 at filling
at filling 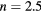 .
.
Download figure:
Standard image High-resolution image4. Conclusions
We have studied the paramagnetic properties of Fe-Mn and Fe-V alloys by CPA+DMFT and supercell approach combined with DMFT. The Curie temperatures and Curie constants of these alloys have different behaviour with concentration, which was qualitatively well described by both approaches. Although treating disorder by CPA and supercells led to similar results, the concentration dependences obtained by CPA are much smoother and agree better with the experimental data. Apparently, using larger supercells may further improve the results. However, even our DMFT calculations for supercells were quite computationally expensive and contained from 3 to 16 impurity problems per iteration, while each iteration in CPA+DMFT approach contained only 2 impurity problems. In addition, the number of DMFT iterations required to achieve the self-consistency increases with the number of impurity problems at each iteration.
Considering U from 2 to 6 eV in CPA+DMFT calculations, we found that 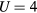 eV leads to the best agreement of the calculated Curie temperatures with the experimental values. On the other hand, the experimental Curie constants are better described with
eV leads to the best agreement of the calculated Curie temperatures with the experimental values. On the other hand, the experimental Curie constants are better described with  eV.
eV.
In contrast to the Mn impurities dissolved in bcc Fe, the V impurities are found to be AFM coupled to Fe. Our calculations for the two-band Anderson–Hubbard model indicate that the AFM coupling is responsible for a maximum in the concentration dependence of Curie temperature in Fe-V alloys. This conclusion is supported by the fact that the Cr impurities in bcc Fe are also AFM coupled and lead to a maximum of the Curie temperature at about 5 at.% Cr [53].
Acknowledgments
The authors are grateful to A Poteryaev and S Skornyakov for useful discussions. The study was supported by the grant of the Russian Scientific Foundation (project 14-22-00004).