Rare-earth pnictides and chalcogenides from first-principles

L Petit; Z Szotek; M Lüders; A Svane

doi:10.1088/0953-8984/28/22/223001

1. Introduction

The rare earth monopnictides and monochalcogenides (RX) are a very interesting class of materials due to their diverse and unusual electronic, magnetic, optical and magneto-optical properties with, among other things, potential practical applications in spintronics [1, 2], high performance computing [3], and magnetic refrigeration [4]. A variety of the interesting phenomena occuring in rare earths bearing materials take their origin from the intricate interactions between the localized rare earth 4f electrons and the itinerant spd electrons. Depending on the constituent atoms, the RX compounds show semiconducting, semimetallic, and heavy fermion properties, as well as high sensitivity to temperature, pressure and doping.

There exists a wide range of theoretical methods for studying the electronic structure of solids, most of which are based on density functional theory (DFT). In either its local (spin) density approximation (L(S)DA) or generalized gradient approximation (GGA), DFT has been instrumental in gaining current understanding of various classes of materials. However, since these approximations are based on a homogeneous electron gas, they cannot adequately treat correlated electrons and the associated electron localization. To describe the electronic structure of rare earth materials additional assumptions or parameters derived from experiment need to be invoked, diminishing the predictive power of the approach. A number of highly efficient methodologies have consequently been developed, differing in accuracy and treatment of rare earth 4 f-electrons regarding their correlated nature and degree of localization. For example, all implementations of the LDA + U approach introduce an effective Hubbard U parameter that separates the f-manifold into lower and upper Hubbard bands and removes f-degrees of freedom from the Fermi level. The self-interaction-corrected local spin density (SIC-LSD) on the other hand provides a dual picture of coexisting localized and band-like f-electrons.

Whilst exhibiting very different electronic properties, as a function of rare earth ion and/or alloying anion, the RX compounds all crystallize in the common rocksalt structure, which makes them an excellent playground for systematic testing of the predictive capabilities of the applied theoretical approaches. Conversely, by correctly reproducing the experimentally observed trends, the underlying assumptions can be validated, thereby testing the broader applicability of the methodology to rare earth materials. The main focus of this review is on the parameter-free theoretical picture of the electronic properties of the entire manifold of RX compounds (where R = Ce, Pr, Nd, Pm, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu; X = N, P, As, Sb, Bi, O, S, Se, Te, Po), based on the SIC-LSD calculations [5], with comparisons wherever possible to the other theoretical investigations, utilising different methods of calculation. Apart from LDA + U, they are respectively dynamical mean field theory (DMFT), quasiparticle self-consistent GW (QSGW), hybrid functionals, as well as empirical approaches, all of which will be briefly described in the following section. The aim is to provide the up-to-date state of this field of research and possibly identify materials of relevance for innovative technologies and the quest for renewable energies [6].

The paper is structured as follows. In the next section different theoretical methods are reviewed. The following section presents a discussion of the whole phase diagram of the electronic properties, based on the SIC-LSD results obtained for the RX compounds, stressing first the observed systematics and identifying interesting areas and classes of compounds. The most promising compounds are then analysed in individual sections. A separate section reviews the pressure behaviour of RX compounds. The last section of the article provides conclusions and outlook for future studies.

2. Methods

The correct treatment of the 4f electrons in lanthanide compounds is a great challenge for any modern theory and various methods may deal with them differently. On the one hand, when considering the spatial extent of their atomic orbitals, the 4f electrons are confined to the region close to the nuclei, i.e. they are very core-like. On the other hand, with respect to their position in energy, which is often in the vicinity of the Fermi level, they should rather be classified as valence electrons. In this section the most widely used and relevant methods for calculating the electronic structure of strongly correlated electron systems, such as the rare earth monopnictides and monochalcogenides, are overviewed.

2.1. Density functional theory

DFT relies on the proof [7] that for any non-degenerate many-electron system, there exists an energy functional E[n], where $n\left(\mathbf{r}\right)$ is the electron charge density in space-point 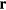$\mathbf{r}$ , which when minimized (with respect to 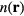$n\left(\mathbf{r}\right)$ ) provides the correct ground state energy as well as ground state electron charge density. The total energy functional,

$\begin{eqnarray}&&E\left[n\right]={{T}_{0}}\left[n\right]+U\left[n\right]+{{V}_{\text{ext}}}\left[n\right]+{{E}_{\text{xc}}}\left[n\right],\end{eqnarray} \tag{ 1 }$

consists of the kinetic energy functional, T₀[n], of a non-interacting system, the electron–electron interaction energy functional, U[n] (Hartree term), the external potential energy functional, ${{V}_{\text{ext}}}\left[n\right]$ , due to electron–ion and ion–ion interactions, and the so-called exchange-correlation energy functional, ${{E}_{\text{xc}}}\left[n\right]$ , which is unfortunately not known and therefore needs to be approximated in actual applications.

The most well known and widely used approximation to DFT is L(S)DA [8, 9], where electron correlations are treated at the level of the homogeneous electron gas, with the f-electrons described by extended Bloch states, i.e. the so-called 'f-band' approach. An improvement on the local approximation is a variety of GGAs [10, 11] which, in addition to the dependence on a homogeneous charge distribution, includes also some gradient corrections. Unfortunately, neither L(S)DA nor GGA has proved very successful for f-electron systems. For very localized f-electrons, one can also try to differentiate between the spd- and f-electrons, by restricting the variational space and including the latter into the (chemically inert) core, i.e. the so-called 'f-core' approach [12]. Generally however, the self-interaction corrected (SIC)-LSD approaches have shown to be more adequate, in particular as far as the cohesive properties are concerned [13].

2.2. SIC-LSD and hybrid functionals

A fundamental property of the exact exchange-correlation functional, ${{E}_{\text{xc}}}\left[n\right]$ , valid for any one-electron density, is that it is exactly cancelled by the Hartree energy functional. Since in the local spin density approximation ${{E}_{\text{xc}}}\left[n\right]$ is approximated ( $E_{\text{xc}}^{\text{LSD}}\left[n\right]$ ), this cancellation is no longer exact. One refers to the latter as spurious self-interactions, introduced by the approximations to the exact exchange-correlation energy functional [14]. The self-interaction problem of effective one-electron theories of solids has been realized for a long time [15, 16]. The favoured formulation of a self-interaction free functional, within the DFT framework, is due to Perdew and Zunger [17]. Their remedy to the self-interaction problem is to subtract the spurious self-interactions from the LSD functional for each occupied orbital, leading to the SIC-LSD functional of the form

$\begin{eqnarray}\begin{array}{*{35}{l}} {{E}^{\text{SIC}}} & = & {{E}^{\text{LSD}}}-\underset{\alpha}{\overset{\text{occ}.}{\sum}}\,\delta _{\alpha}^{\text{SIC}} \\ {} & = & \underset{\alpha}{\overset{\text{occ}.}{\sum}}\,\langle {{\psi}_{\alpha}}|-{{\nabla}^{2}}|{{\psi}_{\alpha}}\rangle +{{V}_{\text{ext}}}\left[n\right]+U\left[n\right]+E_{\text{xc}}^{\text{LSD}}\left[{{n}_{\uparrow}},{{n}_{\downarrow}}\right]-\underset{\alpha}{\overset{\text{occ}.}{\sum}}\,\delta _{\alpha}^{\text{SIC}}. \end{array}\end{eqnarray} \tag{ 2 }$

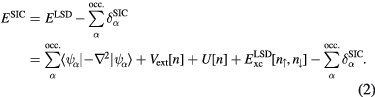
Here the sums run over all the occupied orbitals 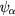${{\psi}_{\alpha}}$ , with the self-interaction corrections given by

$\begin{eqnarray}&&\delta _{\alpha}^{\text{SIC}}=U\left[{{n}_{\alpha}}\right]+E_{\text{xc}}^{\text{LSD}}\left[{{\bar{n}}_{\alpha}}\right],\end{eqnarray} \tag{ 3 }$

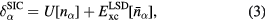
with charge density 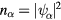${{n}_{\alpha}}=\,|{{\psi}_{\alpha}}{{|}^{2}}$ , and spin density 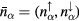${{\bar{n}}_{\alpha}}=\left(n_{\alpha}^{\uparrow},n_{\alpha}^{\downarrow}\right)$ , and α being a combined index comprising all the relevant quantum numbers of the electrons.

For itinerant states, the self-interaction 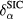$\delta _{\alpha}^{\text{SIC}}$ vanishes identically, whereas for localized (atomiclike) states, 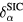$\delta _{\alpha}^{\text{SIC}}$ may be appreciable. Thus, the self-interaction correction constitutes a negative energy contribution gained by an electron upon localization, which competes with the band formation energy gained by the electron if allowed to delocalize and hybridize with the available conduction electron states. Hence, in this formulation, one distinguishes between localized and itinerant states but treats them on equal footing. The decision whether a state is to be treated as localized or extended is based on a delicate energy balance between band formation and localization. As a result, one has to explore a variety of configurations consisting of different distributions of localized and itinerant states. The minimization of the SIC-LSD total energy functional with respect to those configurations defines the global energy minimum and thus the ground state energy and valency configuration. The nominal rare earth valence is in this approach defined as the integer number of electrons available for band formation [18], namely

$\begin{eqnarray}&&{{N}_{\text{val}}}=Z-{{N}_{\text{core}}}-{{N}_{\text{SIC}}},\end{eqnarray} \tag{ 4 }$

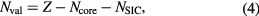
where Z is the atomic number, N_core is the total number of core (and semi-core) electrons, and N_SIC is the number of localized, SIC, states.

To ensure that the localized orbitals are indeed the most optimally localized ones, delivering the absolute energy minimum, a localization criterion [19, 20]

$\begin{eqnarray}&&\langle {{\psi}_{\alpha}}|V_{\alpha}^{SIC}-V_{{{\alpha}^{\prime}}}^{SIC}|{{\psi}_{{{\alpha}^{\prime}}}}\rangle =0\end{eqnarray} \tag{ 5 }$

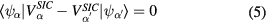
is checked at every iteration of the charge self-consistency process. The fulfilment of the above criterion is equivalent to ensuring that the energy functional is minimal with respect to the unitary rotations among the occupied orbitals. The full implementation of SIC-LSD for solids involves repeated transformations between Bloch and Wannier representations [21]. A local formulation of the self-interaction-corrected energy functionals has been proposed and tested by Lüders et al for Ce [22]. A number of other SIC schemes exist [23–28], that have however not as yet been applied to rare earth compounds.

The SIC-LSD method forms the basis of most of the work reviewed in this paper. With its focus on the total energy and valence stability aspects, this method can provide quite an accurate description of the cohesive properties throughout the lanthanide compounds. Although both LSD and SIC-LSD take into account the Hund first and third rules, with respectively the exchange interaction and spin-orbit coupling included in the total energy functional, the Hund second rule, often referred to as the tetrad effect [29], is not defined for the homogeneous electron gas underlying LSD, leading to grossly underestimated LSD orbital moments. The orbital polarization (OP) scheme by Eriksson et al [30] has improved the latter by adding to the LSD total energy functional a term accounting for the energetics of the Hund's second rule. Similarly, to account for the tetrad effect in the SIC-LSD total energy calculations of the rare earth compounds, the correction 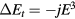$\Delta {{E}_{t}}=-j{{E}^{3}}$ is added (a posteriori) to equation (2) [5], where the parameter E³is equivalent to the Racah B-parameter [31], defined in terms of the reduced Slater integrals F_k.

Like the SIC-LSD functional, the hybrid functionals belong to the class of orbital dependent functionals. They are constructed by admixing some fraction of a non-local exchange to the local functional, thus correcting for part of the spurious self-interaction inherent in local density functionals and thereby also improving the latter. Amongst the hybrid functionals the most well known are B3LYP and PBE0 [32, 33], as well as the more recent screened-exchange variety referred to as HSE functionals which work also for metals [34, 35]. The latter are based on the short-range part of the non-local exchange only and hence are easier to calculate.

2.3. LDA + U

The LDA + U method [36] adds a quadratic term to the LSD Hamiltonian to improve the description of the correlated f manifold, namely

$\begin{eqnarray}&&{{E}^{\text{LDA}+\text{U}}}\left[n\right]={{E}^{\text{LSD}}}\left[n\right]+\underset{i}{\sum}\,{{E}^{\text{corr}}}\left({{\underset{\scriptscriptstyle-}{N}}_{i}}\right),\end{eqnarray} \tag{ 6 }$

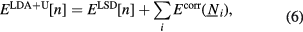
where for each site i the correlation energy term depends on the orbital occupation numbers 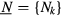$\underset{\scriptscriptstyle-}{N}=\left\{{{N}_{k}}\right\}$ . In its simplest form [36], the correlation energy term includes a Hubbard repulsion term [37] and the so-called double counting term E_dc

$\begin{eqnarray}&&{{E}^{\text{corr}}}\left(\underset{\scriptscriptstyle-}{N}\right)=\frac{1}{2}U\underset{k\ne l}{\sum}\,{{N}_{k}}{{N}_{l}}+{{E}_{\text{dc}}}.\end{eqnarray} \tag{ 7 }$

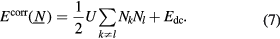
Here indices k and l run over the 14 f-orbitals on the site considered, and U is the f − f Coulomb interaction. The double counting term 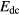${{E}_{\text{dc}}}$ is needed to correct for the fact that ${{E}^{\text{LSD}}}\left[n\right]$ already includes some Coulomb correlation contribution. A major deficiency of the LDA + U method is that E_dc is not uniquely defined, and therefore several forms of this correction have been introduced [36, 38, 39], each leading to some differences in results [40, 41]. Furthermore the appropriate value to use for U is somewhat uncertain, since it necessarily must include screening from the conduction electrons, which reduces the Coulomb interaction by a factor of 3–4 compared to the bare f − f Coulomb interaction energy. Although the U parameter used in LDA + U calculations is most commonly derived from experiment, its value may be obtained from constrained LDA calculations [42], by which the energy change due to an enforced increase of f occupancy is calculated, including effects of screening. An improvement on this scheme, based on the linear response, has been proposed by Cococcioni et al [43]. A further approach to determining the Hubbard U from first-principles is based on the so-called constrained random phase approximation [44].

The physical idea behind the LDA + U correction is like that in the OP scheme [30], namely to facilitate an orbital polarization within the f-manifold with ensuing loss in f-contribution to bonding. However, the U parameter is significantly larger, usually in the range of 6–10 eV for lanthanides, compared to the E³ parameter used in OP which is of the order of 0.1 eV in lanthanides. Therefore, LDA + U strongly favours orbital polarization and for lanthanides generally pushes the f-bands either far below or far above the Fermi level (lower and upper Hubbard bands), i.e. the occupation numbers N_k attain values of either ≈1 or ≈0. For this reason, the LDA + U scheme has not been applied to describe valence transitions. Improved descriptions include an exchange interaction parameter in the f-manifold with spin-polarisation of the conduction electrons (LSDA + U), and/or a rotationally invariant formulation [39], by which the dependence on representation (e.g. spherical versus cubic harmonics) is avoided. In full implementation this latter scheme introduces band shifts reminiscent of multiplet splittings [45, 46].

The LDA + U has been extensively used in studies of lanthanides, but a comprehensive review will not be given here. Some significant applications and reviews are reported in [45–49]. The method is almost as fast as a conventional band structure method, and when comparisons to experimental photoemission data are made, the LDA + U method provides a much improved energy position of localized bands over the L(S)DA. In addition, often the precise position of occupied f-states is not essential to describe bonding properties—rather, the crucial effect is that the f-states are moved away from the Fermi level.

2.4. Dynamical mean field theory

The dynamical mean field theory (DMFT) [50–52] is a general framework for incorporating the self-energy of a correlated atom into the solid state environment. The basic assumption is that the correlation effects are local in nature, so that as a first step the self-energy for a single atom may be computed in an otherwise uncorrelated environment, the conduction electron bath, which is described by the Green's function G_bath, i.e.

$\begin{eqnarray}&&\Sigma=\Sigma\left({{G}_{\text{bath}}}\right).\end{eqnarray} \tag{ 8 }$

This constitutes the DMFT impurity problem. Subsequently, the Green's function for the solid is constructed from

$\begin{eqnarray}&&{{G}^{-1}}=G_{0}^{-1}-\Sigma\left({{G}_{\text{bath}}}\right),\end{eqnarray} \tag{ 9 }$

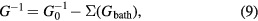
where G₀ is the Green's function of the uncorrelated solid. From G, the solid state excitations can be obtained, e.g. the spectral function (generalized density of states) 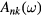${{A}_{nk}}\left(\omega \right)$ given by

$\begin{eqnarray}&&{{A}_{nk}}\left(\omega \right)=|\frac{1}{\pi}\text{Im}{{G}_{nk}}\left(\omega \right)|,\end{eqnarray} \tag{ 10 }$

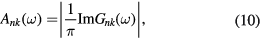
for the quasiparticle labelled by band and k-vector index nk.

Crucial to all DMFT calculations is how $\Sigma\left({{G}_{\text{bath}}}\right)$ is evaluated. There are many possibilities and the quality of the calculation depends on this. Two aspects need to be specified, namely the model adopted to describe the correlation effects of the impurity atom, and the method/approximation used to solve the impurity problem (the impurity solver), once the model has been chosen. The choice of the model requires physical insight. The Hubbard model [37] is the favoured choice in most approaches. Usually, it is necessary to reduce the number of degrees of freedom involved in the correlation problem to a minimum for computational reasons. Generally, the uncertainty of the double-counting term, haunting the LDA + U method, prevails also in the DMFT treatment. The method of solving the impurity problem can be either numerical, as in the Quantum Monte Carlo and exact diagonalization methods, or rely on approximate methods (which again require physical insight), e.g. perturbation theory. For details we refer the reader to the recent reviews of DMFT [51, 52]. Many LDA + DMFT calculations have been reported in recent years, the majority discussing 3d systems, but also several dealing with actinides. Less attention has been paid to the lanthanides, most probably because the atomic limit, i.e. the Hubbard-I approximation, is sufficient for an accurate description in most cases. In the Hubbard-I approximation, the one-electron Green's function is calculated from the Dyson equation with the self-energy approximated by the self-energy of the atomic system [53–55].

2.5. GW method

The GW method [56, 57] aims at a precise determination of the excitations of solids, which is fundamentally different from the focus on ground state properties. Its crucial quantity is the electron self-energy, 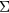$\Sigma$ , here obtained from the Green's function, G, and the screened Coulomb interaction, W. Most commonly, in realistic applications, 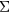$\Sigma$ is computed from LDA eigenfunctions, with W approximated by its lowest order diagram, as 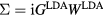$\Sigma=\text{i}{{G}^{\text{LDA}}}{{W}^{\text{LDA}}}$ . As such, GW has been most successful in weakly correlated systems, although band gaps have been underestimated even for semiconductors. The fully self-consistent GW (SCGW) method determines G self-consistently from 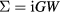$\Sigma=\text{i}GW$ , which in turn generates G. The screened Coulomb interaction is given by W =v(1 − vP)⁻¹, where v is the bare Coulomb interaction, and $P=-\text{i}G\times G$ is the irreducible polarisation function. There have been only a few applications of SCGW, but the results have been disappointing with respect to agreement with experiment. An ansatz for a different kind of SCGW has been proposed by Faleev et al [58], and shown to improve quasiparticle (QP) levels of MnO and NiO. The idea has then been successfully put forward by Kotani et al [59] and Schilfgaarde et al [60], by placing it on an underlying principle of optimising the effective one-body Hamiltonian through minimizing the perturbation to it. This approach is known as quasiparticle self-consistent GW (QSGW) and has been proposed as a universal approach to the reliable prediction of the electronic structure. It has also been applied to localized 4f systems [61]. In addition, recently it has been combined with DMFT and applied to the pnictide superconductors [62].

2.6. Other approaches

Here two less familiar approaches used in studies of RX compounds are briefly described. The first, a so-called 'combined approach', is a total energy tool successfully applied to lanthanide compounds [63]. It is based on a state-of-the-art total energy method combined with information on atomic excitation energies, which is capable to provide quite accurate valence stabilities of f-electron compounds [64].

Another approach is the 'empirical model' by Kolk et al [65] which relies on the systematic behaviour of the energy difference between the localized 4f states, the rare earth 5d conduction band and the anion p-band across the lanthanide series. By combining the relative energy trends with experimental data for some crucial compounds Rogers et al [66] were able to correctly predict a range of electrical, optical, and chemical properties of the binary lanthanide compounds, including band gaps and valencies.

3. Equilibrium properties

3.1. Introduction

The properties of rare earth monopnictides and monochalcogenides have been described in a number of reviews [67, 68]. Recent increased interest in studying these compounds is due to their potential for device applications, as well as the desire to understand the theoretical underpinnings of correlated electron systems. Apart from the electronic structure, the 4f-electrons determine both the magnetic and optical properties of the rare earth compounds. For example the large magnetic moments associated with the localized f-configuration play an important role in shape memory alloys, and the transitions from the discrete 4f-levels determine the luminescence properties of phosphors in optical displays. Although of great interest, the magnetic and optical properties are nevertheless beyond the scope of the present review. Instead in the following sections the focus will be on the underlying electronic structures as predicted from first-principles, and the electronic properties that emerge from systematically applying these methods.

3.2. SIC-LSD results: systematics and trends

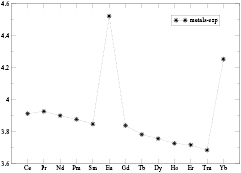
Whilst the 4f-electrons tend to be fully localized in the atomic state, in the elemental rare earth metals, shown in figure 1, the sudden increase in Wigner–Seitz (WS) radius at Eu and again at Yb indicates that a distinction needs to be made between the divalent rare earth ions R²⁺ (fⁿ), with a fully localized f-shell, and the trivalent R³⁺ (fⁿ⁻¹) ions, where one of the atomic f-electrons delocalizes and takes part in bonding. This dual character of the 4 f-electrons in the elemental rare earths gives rise to very complex electronic characteristics of the lanthanide compounds, and in particular in the rare earth monochalcogenides and monopnictides the interplay of ligand chemistry and f-electron localization/delocalization results in a rich valence and electronic phase diagram. In what follows, the corresponding results of first-principles SIC-LSD calculations are summarized. All those calculations were performed for the rocksalt structure (see figure 2) and assumed ferromagnetic arrangement of the moments. A detailed description of the study can be found in [5].

**Figure 2.** Rocksalt structured rare earth pnictide/chalcogenide. Rare earth ions are in orange, pnictide/chalcogenide ions are in blue.
Download figure:
Standard image High-resolution image

3.2.1. Total energy and valence phase diagram.

In SIC-LSD, to determine the ground state valence of a compound, the total energy differences between the relevant valence configurations have to be calculated. For a large majority of the RX compounds they are the divalent and trivalent scenarios, with their energy difference denoted by 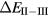$\Delta {{E}_{\text{II}-\text{III}}}$ (the main exception being the Ce compounds where the tetravalent-trivalent energy difference, 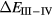$\Delta {{E}_{\text{III}-\text{IV}}}$ , is the more relevant energy scale). In the divalent configuration, one additional f-electron is treated as localized, gaining in SIC-energy, as compared to the trivalent scenario treating that one electron as itinerant, gaining in bonding energy. The competition between these two energy scales determines the sign of the total energy differences, and ultimately the ground state of the studied compound. With respect to 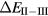$\Delta {{E}_{\text{II}-\text{III}}}$ , positive values indicate a trivalent ground state, whereas negative values imply that the divalent configuration is energetically more favourable. Mapping the calculated total energy differences onto the ground state valences, one obtains a unified picture for all the RX compounds, in terms of the valence phase diagram shown in figure 3. Here the valence scale is defined such that it runs from 3.5 for the tetravalent/trivalent degenerate compounds ( 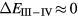$\Delta {{E}_{\text{III}-\text{IV}}}\approx 0$ ) to 2.5 for the trivalent/divalent degenerate compounds ( 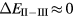$\Delta {{E}_{\text{II}-\text{III}}}\approx 0$ ). The yellow/orange areas, which dominate throughout the phase diagram, demonstrate the overall preferred trivalent ground state configuration for a large number of RX compounds. The trend towards delocalizing an additional electron is only noticeable for the CeX systems and some of the nitrides, as indicated by the correspondingly more reddish areas of the phase diagram. The trivalent-to-divalent localization transition occurs around the regions indicated in white. The blue zones represent the stable divalent configuration, which is the dominating ground state for many of the 'heavy' chalcogenides when combined with the rare earths situated in the middle and latter parts of the series. It should be noted here that Delin et al [64], using the combined approach (section 2.6), correctly reproduced the divalent-trivalent energy differences for the rare earth elements, as well as for a range of rare earth pnictides and chalcogenides, in agreement with the SIC-LSD calculations [63, 64].

From the phase diagram in figure 3, a number of trends emerge. Most noticeable is the difference between chalcogenides, where a considerable number of compounds prefer the divalent ground state, and pnictides that are mostly trivalent. In the RX compounds, the electronic structure results mainly from rare earth f- and d-orbitals on neighbouring sites overlapping with each other as well as with the p-orbitals on the ligand sites. The pnictogen atom has three unoccupied p-orbitals and in the trivalent configuration it can accommodate three electrons from the R-ion through charge transfer and hybridization, resulting in the filled p-band. The chalcogen atom, on the other hand, has one additional p-electron in its outer shell to start with, which is why the corresponding p-band can only accommodate two electrons, and as a consequence of this, in the trivalent scenario the third electron is forced to occupy the fd-conduction band. Depending on the degree of filling of the narrow f-peak, the gain in SIC-energy in connection with localization may become energetically favourable, resulting in a divalent ground state instead.

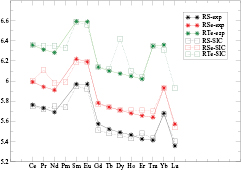
For each given compound the self-consistent calculations involve the total energy minimization as a function of lattice parameter with respect to a number of different possible localization/delocalization scenarios, and therefore the calculated global energy minimum determines the equilibrium lattice parameter as well as the ground state. In figure 4, the calculated lattice parameters for the rare earth chalcogenides, RS, RSe, and RTe are seen to decrease with increasing atomic number, and with sudden jumps around Sm/Eu and Tm/Yb. This trend, which is also observed in the rare earth metals (see WS radii in figure 1), is known as lanthanide contraction. From Ce to Yb the number of occupied f-electrons increases. The latter, being highly directional, only partially manage to screen the increasing nuclear charge, and consequently the outer electrons, including the f-electrons, tend to become more localized with increasing atomic number, resulting in smaller atomic radii, and decreasing lattice parameters. Due to the lanthanide contraction, the unoccupied f-states move towards higher binding energies, becoming gradually more occupied with the electrons charge transferring from the sd-states, and ultimately the gain in SIC-energy outweighs any eventual loss in band formation energy and localization ensues. Consequently, with less f-electrons taking part in bonding, the lattice parameter increases, resulting in the jumps around Eu and Yb. The repetitive feature of gradually increasing divalency from CeX to EuX, and again from GdX to YbX, results from combining lanthanide contraction and half-filled shell effect. A somewhat different lattice parameter behaviour applies to the rare earth pnictides as can be seen on the example of the phosphides shown in figure 5. As the pnictogen readily accepts three electrons from the rare earth ion, the ${{\text{R}}^{3+}}\to$ R²⁺ is no longer clearly observed, which makes the lanthanide contraction relatively more obvious,

**Figure 4.** Lattice parameter (in a.u.) as a function of rare earth R for RS, RSe, and RTe.
Download figure:
Standard image High-resolution image

**Figure 5.** Lattice parameter (in a.u.) as a function of rare earth of the R phosphides.
Download figure:
Standard image High-resolution image

A third trend, visible in figure 3, relates to the gradual increase in localization with anion size, i.e. from RN to RBi, as well as from RO to RPo. With increasing anion size, the distance between neighbouring rare earth ions increases, and the resulting decrease in overlap between their respective f- and d-orbitals makes the corresponding hybridization and band formation less favourable, and consequently f-localization more likely. The increase in distance between neighbouring rare earths also makes divalency more favourable in the chalcogenides compared to their elemental metals, with f-electron localization setting in already at the Sm and Tm chalcogenides. It is also important here to notice that the electronegativity decreases with increasing anion size, i.e. respectively from N to Bi and from O to Po, manifesting itself via the ligand p-bands moving up in energy, i.e. towards lower binding energies.

3.2.2. Electronic phase diagram.

The SIC-LSD electronic structure of the 140 R pnictides and chalcogenides gives rise to a rich electronic phase diagram shown in figure 6. It is based on the calculated density of states (DOS) at the Fermi energy, 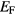${{E}_{\text{F}}}$ , with the purpose of establishing global trends in the ground state electronic structure, providing guidelines for predicting materials with specific properties. Looking at the phase diagram one distinguishes between semiconductors, semi-metals, metals, and heavy fermion-like compounds [5]. In particular, the SIC-LSD calculations predict a considerable number of compounds to be semiconductors. Specifically, the 'heavy' rare earth nitrides are found to be small gap semiconductors, with energy band gaps ranging from 0.06 eV in NdN to 0.6 eV in HoN. They arise due to the filling of the unoccupied pnictogen p-states in variance to the chalcogenide semiconductors where the, rather larger, energy gaps are brought about by localizing an additional f-electron, thus reflecting their divalent character

The dominant part of the electronic phase diagram in figure 6 consists of metallic compounds. In the pnictides, the closing of the semiconducting gap due to the onset of pnictogen p-rare earth sd overlap gives at first rise to a vanishingly small DOS, resulting in the semi-metals CeX to PrX and GdX to DyX (light blue areas). As the overlap gradually increases (due to decreasing electronegativity and/or increasing lanthanide contraction), the behaviour becomes fully metallic (dark blue areas), and eventually in the 'late' rare earths, with more and more of the f-states getting occupied, heavy fermion-like behaviour sets in (yellow-red areas). The rare earth chalcogenides display less variety in terms of metallic behaviour. Given the partially occupied conduction band the early, trivalent, rare earth compounds CeX to PmX, and GdX to ErX (apart from the polonides and a couple of tellurides) are solidly metallic, as can be seen from figure 6. Compared to the pnictides, in the late rare earth chalcogenides the f-states start filling even before moving far enough towards lower binding energies to achieve significant hybridization. Instead of forming a heavy metal, a relatively pure f-state straddles the Fermi level and the divalent semiconducting scenario correspondingly becomes energetically more favourable.

3.2.3. Summary.

The agreement between experimentally observed and SIC-LSD calculated (figure 6) properties is generally very good (apart maybe from the calculated heavy fermion monopnictides), including the accurately predicted phase transitions associated with the f-electron localization/delocalization (figure 3). This statement is well supported for example by the comparison between the experimental and theoretical lattice parameters shown in figures 4 and 5, however figure 7 provides a more complete story. Here the experimental equilibrium lattice parameters for all the studied rare earth monopnictides and monochalcogenides [71] are plotted along the x-axis, whilst the calculated SIC-LSD equilibrium counterparts are plotted along the y-axis. In this representation, the proximity of the data points to the x = y line is a measure of the agreement between theory and experiment. One can see that for the large majority of the RX compounds the calculated equilibrium lattice parameters lie within ∼1.5% of the experimental values, i.e. well below the 5% that would indicate a wrongly predicted ground state configuration. This gives confidence that the SIC-LSD calculations predict the correct ground state and valency configurations and hence are capable to make reasonable predictions for the other physical properties of these materials. However, because SIC-LSD is just an orbital dependent effective one electron theory, the resulting electronic phase diagram of figure 6, based on the calculated DOS at the Fermi energy, is likely not the complete picture of the underlying electronic properties. This is particularly true in the IV and heavy fermion-like areas, where a more adequate treatment of many-body interactions would probably introduce additional refinements into the physical trends predicted by SIC-LSD. Therefore, compounds that are situated in these areas of the phase diagram will likely benefit from further investigations by methodologies such as for example the dynamical mean field theory [72] or possibly QSGW [61]. In what follows, for some selected families of compounds of figure 6, we shall provide detailed discussion of their calculated physical properties, in comparison with experimental evidence and other theoretical studies.

**Figure 7.** Lattice parameters (in a.u.) of all the studied RX compounds: experimental (x-axis) versus theoretical (y-axis) values.
Download figure:
Standard image High-resolution image

3.3. Discussion of selected families of compounds

3.3.1. Eu and Yb compounds: the localized f-electron limit.

Experimental investigations indicate a very localized divalent character of the Eu and Yb ions in their respective chalcogenides. In particular, the study of lattice constants, providing direct information on the valency of rare earths (e.g. elemental metals in figure 1), allowed Jayaraman et al [73] to demonstrate that Eu and Yb are divalent in their sulphide, selenide and telluride compounds. Observations of the isostructural volume collapse under pressure in YbS, YbSe, and YbTe [73] are interpreted in terms of a change in the valence state from 2+ to 3+. Absorption measurements under pressure find YbS to be a divalent insulator, with an energy gap of approximately 1.2 eV between the occupied Yb 4 f-states and unoccupied Yb 5d states [74, 75]. Using x-ray photoemission and optical spectroscopies Matsunami et al [76] have determined a purely divalent character for the Yb ions in YbS, and a divalent Eu²⁺ ion has similarly been derived from x-ray absorption spectroscopy on EuS [77].

The localized nature of the Eu and Yb f-electron manifolds is confirmed by first-principles calculations. For the Yb chalcogenides, Temmerman et al [63] have shown that 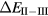$\Delta {{E}_{\text{II}-\text{III}}}$ , obtained respectively by the SIC-LSD method and the combined approach, are very similar, both finding a fully localized Yb²⁺ (f¹⁴), divalent, ground state configuration. Similarly, a divalent ground state has been established from first-principles for the Eu chalcogenides [78]. The combination of lanthanide contraction and either half-filled (Eu) or filled (Yb) f-shells results in a completely localized f-electron manifold and the divalent rare earth ion contributes only its two outer sp electrons to bonding. As noted earlier, in the chalcogenides, with two unoccupied orbitals, this results in an insulating ground state configuration.

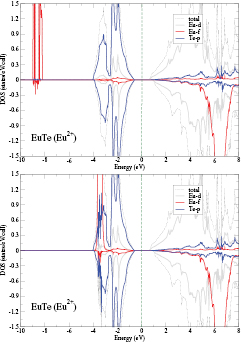
Photoemission [79] and optical absorption [73] studies have shown that the electronic structure of both Eu and Yb monochalcogenides is characterized by the localized f-state being situated in the gap between the valence and conduction bands, as seen schematically in figure 8. Although SIC-LSD calculations correctly predict the insulating ground state, they do not reproduce the character of the observed energy gaps [80, 81] and place the localized f-states at too low an energy (as can be seen from the calculated DOS for divalent EuTe in figure 9(a)). The reason being that SIC-LSD is primarily a total energy, effective one-electron, ground state theory which does not provide accurate removal energies of localized states due to an approximate treatment of electron–electron interactions (multiplet effects) [82] and the neglect of screening and relaxation effects [83]. As a consequence, in the RX compounds these occupied f-states appear as sharp resonances, unrealistically far below (∼−9 eV) the conduction band minimum. An improved estimate of the removal energies may be obtained by the Slater transition state argument [84, 85], which places the f-peak midway between its calculated SIC-LSD and LSD positions. In figure 9(b), this approach has been applied to the DOS of divalent EuTe. Compared to figure 9(a), the position of the occupied f states is improved, as they now occur at about 4 eV below the conduction band minimum, but at the bottom of the valence band rather than in the gap between the valence and conduction band states, as observed experimentally [73] (i.e. at ∼2 eV below the conduction band). Nevertheless, from here onwards, the transition state approximation will be used in all the calculations of densities of states.

**Figure 8.** Schematic DOS for a divalent RX chalcogenide. A narrow f-peak is situated in the gap between anion p-states and rare earth d-states. The Fermi level is situated in the energy gap between the fully occupied f-peak and the empty d-states.
Download figure:
Standard image High-resolution image

**Figure 9.** SIC-LSD DOS for divalent EuTe (a) without and (b) with transition state implemented. Note that the majority (minority) spin component is shown along the positive (negative) direction of the second axis.
Download figure:
Standard image High-resolution image

Other first-principles approaches have similarly been applied to the Eu chalcogenides. With respect to the structural properties, the agreement between LSDA/GGA studies and experiment tends to be rather good [86], indicating that the fully occupied majority (and minority) band of the Eu²⁺ configuration can be reasonably described without taking into account the localized character of the f-electrons. However, as mentioned earlier, the LSDA usually positions the f-band states at the Fermi level, which can result in an unphysical metallic behaviour [87]. Calculations, based on the Slater exchange potential [88], showed that a reduced exchange potential can give rise to the correct energy gaps and relative f-band positions. The more recent calculations explicitly address the correlated nature of the 4f-electrons and, given a reasonable value for the U parameter, methodologies such as LDA + U [87, 89], DMFT [90], or QSGW + U [91], are able to accurately reproduce the spectroscopic features of EuX at ambient pressure.

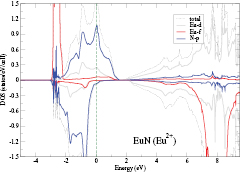
In the rare earth pnictides, the three unoccupied anion p-orbitals favour a trivalent ground state which, however—in the case of Eu and Yb pnictides—competes with the increased trend towards localization due to the associated filling of the narrow f-peak. Localizing fully the entire f-manifold requires emptying some of the broad band states originating from the p-orbitals, as shown in the example of divalent EuN in figure 10. This localization, according to the SIC-LSD calculations, turns out to be energetically unfavourable for all Eu pnictides, except for EuBi. For the Yb pnictides a fully localized configuration is never favourable, but the trend from solidly trivalent YbN to divalent/trivalent, almost degenerate, YbBi indicates increasing localization with anion size, in line with experimental observations [92]. Interestingly, the pnictides characterized by small or negative total energy differences, 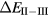$\Delta {{E}_{\text{II}-\text{III}}}$ , such as EuSb, YbBi, and EuBi, in reality do not crystallize in the NaCl structure investigated here [78], indicating a link between f-electron localization/delocalization and structural properties. For the remaining Eu and Yb compounds the ground state stays trivalent, i.e. Eu³⁺ (f⁶) and Yb³⁺ (f¹³), with large densities of states resulting from a partially filled f-peak pinned to the Fermi level.

**Figure 10.** SIC-LSD DOS for divalent EuN which is energetically unfavourable.
Download figure:
Standard image High-resolution image

The Yb monopnictides are described as semi-metallic compounds with low carrier concentration [93], seemingly at odds with the large DOS at the Fermi level predicted by the SIC-LSD calculations. The experimentally observed large specific heat coefficient in these systems has been interpreted as heavy fermion behaviour by some authors [93, 94], while others have explained it in terms of the Kondo effect [95, 96]. Since the SIC-LSD calculations are based on the effective one-electron theory, they cannot adequately describe the many-body physics of these compounds. However, the large peak at the Fermi level that is calculated in the trivalent configuration indicates strong pf-mixing, i.e. a prerequisite of the hybridization between the narrow f-peak and the sea of conduction electrons, underpinning the Kondo effect. Experimental measurements by Degiorgi et al [97] find YbN to be a self-compensated semi-metal and the anomaly in the specific heat observed near 5K is interpreted in terms of the Kondo effect resulting from p − f hybridization. In an earlier study Ott et al [94] have interpreted this same anomaly as being due to a high DOS at the Fermi level with the resulting heavy electron behaviour.

According to SIC-LSD, in the Ce monopnictides, 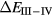$\Delta {{E}_{\text{III}-\text{IV}}}$ becomes the relevant energy scale, indicating the potential for an additional f-electron to delocalize. The Ce monopnictides are low-carrier density strongly correlated electron systems [98]. With the exception of CeN, which tends toward the mixed-valence regime, the rest of the compounds show semi-metallic behaviour, yet with pronounced hybridization effects in the excitation spectra [99]. The proximity to delocalization thus can be interpreted as the representation of a localized f-peak hybridizing with the sea of conduction electrons, reminiscent of the suggested heavy-fermion or Kondo behaviour in the Yb monopnictides. Lægsgaard and Svane [99] have calculated the excitation spectra of the Ce monopnictides using a lattice model including the Hubbard U on the 4f-orbitals. The model has been treated within DMFT, with the non-crossing approximation used for solving the impurity problem. The model has been found to account qualitatively for all the features of the experimental spectra.

The good agreement between experiment and theory, especially for the chalcogenides, indicates that the 'beyond-LDA' methodologies are well suited for describing the ground state electronic properties of Eu and Yb compounds in the localized limit. Consequently, these approaches are relied on when investigating a range of interesting materials properties, not least the change in magnetic ordering from ferromagnetic EuO to anti-ferromagnetic EuTe [90, 100], and the change in electronic structure under pressure [101].

3.3.2. Sm and Tm compounds: the localized/delocalized frontier.

In the chalcogenide part of the phase diagram in figure 3, the white/light blue regions indicate compounds situated at the boundary of a localization–delocalization transition driven by the combined effect of lanthanide contraction and anion size. Most interesting in this respect are the Sm and Tm chalcogenides. With the f-electrons less localized than in their Eu and Yb counterparts, the ground state is determined by the alloying anion, and a trivalent to divalent transition is observed when moving down the phase diagram from the oxide to the telluride.

The SIC-LSD calculations predict an insulating divalent ground state for SmS, SmSe, and SmTe, but with divalent-trivalent energy differences that are considerably smaller than the corresponding values for EuX. Especially for SmS, a fairly small energy difference of 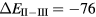$\Delta {{E}_{\text{II}-\text{III}}}=-76$ meV (erroneously specified as −5.6 eV in [5]) seems to point to a divalent semiconductor, susceptible of undergoing a localization–delocalization transition under pressure [55], as observed experimentally [102]. For SmO, the calculated positive energy difference, 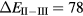$\Delta {{E}_{\text{II}-\text{III}}}=78$ meV, predicts a marginally trivalent ground state. The small energy differences between configurations (within 0.1 eV) imply their near degeneracy, pointing toward intermediate-valent states rather than a clearly preferred f⁶ ground state for SmS, and f⁵ ground state for SmO. Optical absorption/reflectivity measurements [103, 104] determine absorption edges of 0.15, 0.46 and 0.63 eV respectively for SmS, SmSe, and SmTe. Quite similarly to the Eu chalcogenides [79, 88], the corresponding transition is observed to be the 4f-5d one. Early calculations on Sm chalcogenides, assuming a divalent 4f⁶ configuration for the Sm ion, and using the fully relativistic Korringa–Kohn–Rostoker (KKR) approach, with the Slater approximation for the local exchange potential, reproduced an electronic structure characterized by an f-band situated in the gap between the chalcogenide p-valence band and Sm sd-conduction band [105, 106].

In the late rare earths, the Tm chalcogenides display a very similar trend as a function of alloying element, with XPS measurements revealing TmS to be metallic trivalent, TmSe intermediate-valent, and TmTe semiconducting divalent [107, 108]. With the divalent-trivalent energy differences, 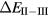$\Delta {{E}_{\text{II}-\text{III}}}$ , of about 0.52, 0.33, 0.1, and −0.1 eV for, respectively, TmO, TmS, TmSe, and TmTe, the ground state sequence predicted by SIC-LSD is in good agreement with experiment. Similarly to SmO and SmS, the small energy differences for TmSe and TmTe (within 0.1 eV) indicate near degeneracy between configurations, and the corresponding ground state can be more adequately described as intermediate-valent (highlighted as IV in figure 6). From their calculations using the fully relativistic LMTO method with the LSDA + U approach, Antonov et al [109, 110] observe that with respect to the band structure, both TmS and TmSe are characterized by 12 fully occupied f-bands, and a partially occupied 13th f-band state. The change in occupation number of the latter, from 0.12 for TmS to 0.27 for TmSe is interpreted in terms of a trivalent to mixed valent ground state transition. TmTe is predicted to be a divalent semiconductor with 13 completely occupied f-band states. In these calculations, using a Hubbard U of 6 eV, the calculated positions of the f-states are found in overall good agreement with both photoemission and inverse photoemission measurements. The optical and magneto-optical spectra have furthermore been investigated using a weighted sum of the LDA + U 4 f¹¹ and 4 f¹² densities of states, in order to mimic multiplet structures. Calculations based on SIC-LDA and using the Hubbard-I approximation were able to correctly describe the detailed multiplet structures of the experimental photoemission spectra with, respectively, a pure f¹² ground state of TmS, a mixed 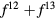${{f}^{12}}+{{f}^{13}}$ ground state of TmSe, and a pure f ¹³ configuration of TmTe [111].

3.3.3. Nitrides: Semimetallic versus semiconducting.

Comprehensive reviews of the R nitrides have recently been presented by Natali et al [112] and Wachter [113]. A major interest in these compounds originates from the fact that a number of them might turn out to be ferromagnetic semiconductors which would make them potential candidates for applications in spintronics and magneto-resistive devices. However, in spite of many studies, especially on GdN, the overall findings from both experiment and theory remain inconclusive as to their insulating character.

From theoretical calculations it has emerged that the band structure of the rare earth nitrides is characterized by a rather large direct band gap at the X point (≈1 eV), combined with an indirect 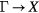$\Gamma\to X$ band gap which, depending on the nitride under investigation, is either extremely small (semi-conductor) or vanishes altogether (semi-metal). The size of the energy band gap (order of meV) challenges the level of precision that can be reached within electronic structure calculations and makes the results dependent on the underlying approximations (ASA radii, choice of Hubbard-U, hybrid functional used, etc). This explains some of the disagreements encountered between the different theoretical studies.

For GdN, by far the most investigated compound among these nitrides, the magnetic ground state remains somewhat controversial [114–116], and there is as yet no consensus as to whether it is a semiconductor or a semimetal. The band structure calculated in the LSD approximation predicts GdN to be semimetallic [117], as shown in figure 11. An early APW study using Slater's exchange potential predicted an energy band gap of less than 0.2 eV [118], similarly to recent SIC-LSD calculations [5]. In their HSE hybrid functional study, Schlipf et al [119] predict below T_c a marginal insulator (with gap of 0.01 eV) at the experimental lattice parameter, and a semi-metal at a slightly smaller theoretical lattice parameter. In the paramagnetic phase above T_c, a band gap of 0.9 eV is predicted. Band structure calculations using a semi-empirical quasi-particle correction [120] find GdN to be semiconducting as do also the more recent QSGW calculations [61] that find GdN with a band gap of 0.22 eV, but situated close to a metal-insulator transition. With respect to the LDA/GGA + U calculations, a dependence on both lattice parameter and the Hubbard U is observed, and the results range from semiconductor [117, 48] to half-metal [121, 122].

**Figure 11.** Band structure of GdN as obtained within the LSD approximation. The majority and minority spin contributions are indicated by red solid and green dotted lines respectively. The Fermi energy is at 0 eV.
Download figure:
Standard image High-resolution image

The situation is not more clear in the experimental studies on the ground state of GdN, where both insulating [123–125] and semi-metallic [115, 116, 126] behaviours have been reported. Wachter [116] has pointed out that this confusion about the ground state electronic structure of GdN is likely due to differences in preparation and the resulting purity of the samples. The fact that even small variations in stoichiometry might have such a profound effect on the electronic properties of GdN seems to give support to the theoretical calculations in their overall prediction of an extremely small or vanishing energy band gap. Nevertheless, the optical gap seems to be well established by now, at 1.3 eV in the paramagnetic phase, decreasing to 0.9 eV for the low temperature ferromagnetic phase [127]. For the larger gapped paramagnetic phase above T_c the calculations tend to agree on a semiconducting character for GdN [119].

Compared to the large number of investigations on GdN, relatively few studies have focused on the remaining nitrides. From their conductivity measurements Didchenko et al determined all the rare earth nitrides to be semi-metallic [128], the only exception being YbN which appeared to be semi-conducting. However, as noted earlier for GdN, it is difficult to assess the level of off-stoichiometry in those early measurements, which would likely influence the resistivity behaviour. The theoretical studies, as well as the more recent experimental investigations reveal a somewhat more varied energy gap behaviour throughout the nitride series. From the LDA + U calculations by Larson et al [48], it emerges that the overall picture of both a larger direct gap and a small/vanishing indirect gap applies to all the nitrides. The calculated direct band gaps are found in reasonable agreement with the optical gaps. In figure 12 the corresponding LSDA + U indirect 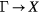$\Gamma\to X$ gaps, calculated for 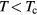$T<{{T}_{\text{c}}}$ , are compared to the energy band gaps obtained within SIC-LSD. The two sets of results agree on the semiconducting nature of NdN, GdN, TbN, DyN, HoN, and ErN, as well as on the semi-metallic character of SmN and PrN, but disagree regarding the ground states of PmN, TmN, and YbN. Whilst these electronic structure calculations predict DyN to be semi-conducting and SmN to be semi-metallic [5, 48], the resistivity measurements determine both compounds to be semiconductors [129]. In contradistinction to Larson et al [48], Jakobsen et al [130], also using LDA + U, determine TbN to be half-metallic, indicating that the calculated energy gap might be sensitive to the U value, as also observed for GdN. Using both LDA + U and DMFT in the form of the Hubbard-I approximation, Peters et al [131] similarly predict a semi-metallic DOS for TbN. These authors furthermore discussed the spectral properties of TbN, with predicted atomic multiplets that, however, still require experimental confirmation.

**Figure 12.** Energy gaps calculated respectively with LSDA + U and SIC-LSD.
Download figure:
Standard image High-resolution image

For EuN, Johannes et al derive a semi-metallic ground state from their LDA + U calculations [132], in agreement with the recent LSDA + U and DMFT calculations by Richter et al [133]. Similarly, as seen in figure 13, SIC-LSD predicts a metallic trivalent ground state configuration with a large DOS at the Fermi level, as a result of closing the band gap between N-p and Eu-sd states and a partially occupied f-peak [5].

**Figure 13.** The SIC-LSD density of states of EuN in the trivalent, ground state, configuration.
Download figure:
Standard image High-resolution image

The QSGW results [133], however, predict a small gap semiconductor at the boundary to a metal-insulator transition. The direct band gap of 0.9 eV at X, obtained from these QSGW calculations, is in agreement with the optical transmittance measurements. Experimentally, it appears that Eu is largely trivalent, with some Eu²⁺ impurities [134] associated with N vacancies, but no clear evidence for a semiconducting state has emerged yet.

First-princples calculations clearly, to a large degree, capture the complexities of the electronic structure underpinning the rare earth nitrides, but fail to reach the level of precision required to distinguish between a semiconductor with a vanishingly small band gap and a semi-metal. As said earlier, this is due to uncertainties in the various approximations to the strongly correlated electron behaviour required within LDA + U-, hybrid-functional- or SIC-LSD-approaches. Even within the same approximation different choices can influence the predicted energy band gap. In the earlier SIC-LSD calculations by Aerts et al [135], only TbN, DyN, and HoN were predicted to be semiconductors, whilst GdN was calculated to be semi-metallic, in contradistinction to the later result [5]. A possible reason for the discrepancy could be differences in the choice of the ASA radii or the spin–orbit coupling effect which was not taken into account in the earlier study. One should mention here, however, that Hasegawa et al [118] in their calculations only noticed a marginal effect on the band structure when taking relativistic effects into account.

3.3.4. Oxides and oxidation.

EuO is the only monoxide whose existence under ambient conditions is well established. All the remaining rare earth oxides have only been observed under high pressure or as surface layers. Leger et al [136], using pressures in the range of 15–18 kbar and temperatures in the range of 500–1200 °C, were able to synthesize NaCl structured Ce-, Pr-, Nd-, Sm-, and Yb-monoxides. Meier et al [137] reported the formation of YbO thin film on Yb(111) surfaces. Earlier observations reported NaCl structured ErO [138] thin films. The reported zinc blende structured GdO and SmO [139] were revealed to be hybrid phases.

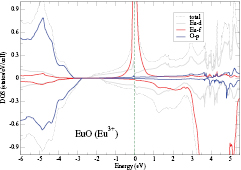
Photoemission studies [79] on EuO reveal an electronic structure characterized by the localized Eu-f states situated in the semiconducting gap, separating the O-2p valence band from the Eu-6s5d conduction band (≈4.3 eV). At ambient temperature, the observed optical absorption edge places the occupied f-level at around 1.0 eV below the unoccupied d states. From optical absorption measurements at 20 K [140], it has been established that EuO remains semiconducting below the Curie temperature, although the shift of the absorption edge to lower energies indicates an energy gap that is reduced by roughly 0.3 eV. The redshift has been subsequently explained by the onset of exchange interactions below T_c that split the conduction band spin-up and spin-down states, resulting in a reduced energy band gap between the f-states and the conduction band [141], also confirmed by recent spin-resolved x-ray absorption measurements [80].

As discussed earlier, in connection with localization in the rare earth chalcogenides, the SIC-LSD calculations predict the divalent Eu²⁺ (f ⁷) ground state configuration for EuO. The corresponding DOS, shown in figure 14, displays an O-p to Eu-d gap of 2.6 eV, with the occupied f-peak appearing at −4 eV, rather than at −1 eV below the conduction band minimum as observed experimentally. The large moment on the Eu ions results in the splitting between spin-up and spin-down d states at the bottom of the conduction band. The calculated value for the exchange splitting (≈0.59 eV) is in good agreement with experiment [80]. Numerous other first-principles calculations have been instrumental in explaining the experimental findings and evolving the current understanding of EuO. Whilst applying the LSD approximation results in a metallic behaviour [87], it was shown in early calculations, based on the Slater exchange potential [88], that a reduced exchange potential gives rise to the correct energy band gaps and relative f-band positions. More recently, a number of advanced studies by means of LDA + U [87, 89, 142], DMFT [90], and QSGW + U [91], were able to accurately reproduce the spectroscopic features of EuO at ambient pressure. With respect to the LSDA/GGA + U calculations, apart from the question of which value of U best to use, some discussion is centered on the issue of whether to correct both the f and d states [87, 142] or only apply the correction to the f-states [89, 91]. In the 'LSDA + U_f + U_d' approach the direct (X) and indirect (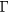 $\Gamma$ -X) gaps are almost the same, whilst in the 'LSDA + U_f' approach the gap is indirect 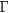$\Gamma$ -X, similar to what is observed in QSGW + U. Furthermore, compared to the LSDA + U calculations, the O-p states are lowered by roughly 2.5 eV in the QSGW + U calculations, which results in overall very good agreement of the latter with experiment.

**Figure 14.** The SIC-LSD density of states of EuO in the divalent configuration.
Download figure:
Standard image High-resolution image

Whilst EuO, not least due to a very rare ferromagnetic insulating ground state [143], has been extensively investigated both theoretically and experimentally, only a few studies have tried to address the other rare earth monoxides [5, 66, 91, 144]. SIC-LSD calculations predict YbO to be the only other divalent insulating monoxide, in agreement with a recent DFT + U calculation based on the modified Becke–Johnson LDA [145], as well as experimental measurements where an f − d gap of 0.32 eV is observed [146]. The small divalent-trivalent energy difference (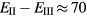 ${{E}_{\text{II}}}-{{E}_{\text{III}}}\approx 70$ meV) calculated in SIC-LSD for SmO indicates an intermediate valent ground state, in line with experimental observations. The predictions of metallic behaviour for the remaining rare earth monoxides have furthermore been confirmed experimentally for CeO, PrO and NdO [136].

The trivalent monoxides turn out to be unstable towards further oxidation, as the delocalized f-states facilitate the uptake of oxygen [147, 148], resulting in the sesquioxides (R₂O₃) being the stable rare earth oxides. All the rare earth sesquioxides occur in nature, crystallizing either in the La₂O₃ or Mn₂O₃ structure, and according to SIC-LSD prefer the trivalent ground state configuration [147, 149]. Oxidation towards R⁴⁺ requires delocalizing an additional f-electron, which is energetically favourable only for the early rare earths and Tb (Tb⁴⁺ is stabilized by the half-filled shell). Therefore only a few rare earth dioxides are found to occur naturally, namely CeO₂, PrO₂, and TbO₂.

4. Pressure induced phase transitions

The divalent rare earth chalcogenides are of particular interest due to the fact that an insulator to metal transition can be brought about by changes in the external parameters, such as pressure, temperature, or alloying. Valence transitions under pressure have been observed in Tm [111], Yb [74], Eu [73], and Sm chalcogenides [104]. In general, features such as the occurrence of an isostructural phase transition upon compression, or an anomalous pV curve, are distinct signatures of valence transformations. A well known example is the 'black-gold' phase transition in SmS at about 0.65 GPa [104] that has been mentioned earlier. These electronic transitions do compete with structural changes, since under pressure, a large majority of RX compounds, similarly to the alkaline earth chalcogenides [150], undergo a transition from the sixfold coordinated NaCl(B1) to the eightfold coordinated CsCl(B2) structure.

4.1. Tellurides

For SmTe, with increasing pressure a continuous isostructural valence change from Sm²⁺ to Sm³⁺ is observed, although the various measurements differ somewhat regarding the onset and range of the transition (roughly within 2–8 GPa) [77, 151–154]. At a pressure of around 12 GPa, SmTe (now in the trivalent phase) is seen to undergo a transition from the NaCl to the CsCl structure [151, 153]. We use a combined structure/valence notation to denote these two transitions as B1²⁺ → B1³⁺ and B1³⁺ → B2³⁺ respectively. The first-principles results are found to be in overall very good agreement with these findings. The SIC-LSD total energy calculations predict an isostructural valence transition to occur around 9.5 GPa, with a volume collapse of 7.6%, accompanying the associated insulator to metal transition [155]. The sluggishness of the experimentally observed valence transitions is not found in the theoretical studies, and might reflect a finite temperature effect. A structural transition from NaCl to CsCl is predicted to occur with increasing pressure at 12.3 GPa.

In the neighbouring EuTe, a structural NaCl to CsCl transition is observed at pressures above 10 GPa, but with the exception of an early measurement by Rooymans [157] no indication of a valence transition has been detected up to the pressure of 30 GPa [73, 158, 159]. A number of different first-principles predictions [86] have been able to model the structural transition, with the calculated pressures ranging from 10 to 17 GPa, depending on the approximation used [86]. Using for example the standard LDA gives a transition pressure of 9.9 GPa [160], compared to 12 GPa when using GGA + Hubbard-I [90]. The SIC-LSD calculations predict a structural B1²⁺ → B2²⁺ transition at 13 GPa, followed by an isostructural B2²⁺ → B2³⁺ valence transition at 47 GPa [155]. We have seen earlier that due to the lanthanide contraction, the degree of f-electron localization increases from SmTe to EuTe. Conversely, under pressure it is harder to delocalize f-electrons in EuTe than in SmTe, which has a noticeable effect on the order in which the structural and electronic transitions will occur. Thus in EuTe the degree of localization is such that under pressure the structural transition occurs prior to the f-electron delocalization, whilst the somewhat less localized f-electrons in SmTe start delocalizing at rather low pressure, and hence the valence transition occurs before the structural transition.

According to the SIC-LSD calculations [155], a similar switch between transitions is predicted to occur from TmTe to YbTe. Thus for TmTe an insulator to metal transition in the NaCl phase is predicted at around 3 GPa, followed by a structural transition to the CsCl phase at around 15 GPa, whilst for YbTe with slightly more localized f-electrons, the structural transition at 17 GPa precedes the valence transition at 31 GPa in the CsCl structure. For TmTe the SIC-LSD results are resumed in figure 15(a), where the transition pressures between phases are indicated at the crossing of the corresponding enthalpies. With respect to experiment, at pressure of around 2 GPa, an isostructural transition occurs, associated with a valence change from the divalent Tm²⁺ configuration to an intermediate-valent Tm²⁺ /Tm³⁺ metallic state. The intermediate-valent state is characterized by Kondo-like behaviour and f − d hybridization [156, 161], with possibly reentrant insulating behaviour at around 7 GPa [156]. At 8 GPa a structural transition to a tetragonal metallic phase is observed [162, 163]. The latter is characterized as close to trivalent [156]. The theoretical predictions for the valence transitions are in overall good agreement with experiment as can be seen for example from the pressure–volume relation in figure 15(b). Whilst the SIC-LSD calculations predict the B1 to B2 transition at around 15 GPa, a simulation of a transition to the real, experimentally observed, tetragonal structure has not been attempted. The experimental data on YbTe remain controversial with no reported observation of an NaCl to CsCl transition for pressures up to 48 GPa, and disagreement on a possible valence transition [164–168].

**Figure 15.** The theoretical behaviour of TmTe under pressure. (a) The enthalpies of the structures B1 and B2 with Tm configuration 3+or 2+. The enthalpy of B2(3+) is used as reference. The calculated transition pressures for B1(2+) → B1(3+) and for B1(3+) → B2(3+) are quoted. (b) The calculated p − V relation of TmTe. The full lines give the predicted sequence of B1(2+), B1(3+) and B2(3+) phases, while the dashed lines are extensions of the p − V relations beyond the respective transition pressures. The experimental data of Jarrige *et al* [156] are shown with pink circles. Figures are reproduced with permission from [155].
Download figure:
Standard image High-resolution image

From both theory and experiment it emerges that whilst intermediate-valent behaviour is induced at moderate pressure (or by chemical alloying) in the SmX and TmX compounds, the EuX and YbX tend to be more stable in their divalent configuration, requiring relatively larger pressures to initiate the transition [75]. Since the degree of f-electron localization determines the behaviour under pressure, it is to be expected that apart from the lanthanide contraction also the increasing localization from oxide to telluride will influence the corresponding phase transitions. For the Sm chalcogenides for example, with increasing anion size, i.e. from SmS to SmTe, first-principles calculations find a tendency towards increasing B1(2+) → B1(3+) transition pressures [55, 64, 169, 170], in agreement with experiment [153, 154, 171]. Upon further increase of pressure, similar to what is observed in SmTe, the valence transition in SmS and SmSe is followed by a structural NaCl to CsCl transition [153, 170].

4.2. EuO

In contrast to EuTe, where both the anion size and the lanthanide contraction conspire to localize the f-electrons, in EuO the competition between the increased localization, due to the lanthanide contraction (and half-filled shell effect), and the increased hybridization, due to the smaller anion size, results in a rather more complex set of phase transitions under pressure. Thus the SIC-LSD calculations predict a sequence of three transitions, respectively an isostructural B1²⁺ → B1³⁺ transition at 49 GPa, a structural B1–B2 transition, combined with a reentrant $3+\to 2+$ valence transition (i.e. B1³⁺ → B2²⁺) at around 60 GPa, and a further isostructural divalent to trivalent transition, now in the B2 phase, at 70 GPa [101]. In figure 16 the enthalpies of the B1 and B2 structures, each with both the 2 + and 3 + Eu configurations, are shown as functions of pressure. Below 40 GPa, the B1²⁺ phase has a significantly lower enthalpy than any of the other phases, while above 80 GPa the B2³⁺ phase has distinctly the lowest enthalpy. In the pressure range between 40 and 80 GPa, the lowest enthalpy phase changes with increasing pressure as B1²⁺ , B1³⁺ , B2²⁺ , and B2³⁺.

**Figure 16.** EuO under pressure. Enthalpy as a function of pressure for the different phases of EuO relative to that of the B1³⁺ phase (blue). The B1²⁺ is shown in red, the B2²⁺ in black, and the B2³⁺ in green. The 0.24 eV shift refers to an ASA related energy shift of the B2 phase relative to the B1 phase required in order to align the structural transition pressure with the experimentally observed 60 GPa. Figure is reproduced with permission from [101].
Download figure:
Standard image High-resolution image

With respect to underlying electronic structure, the transition form NaCl to CsCl leads to a sudden increase in the Eu-O distance, and consequently a decrease in the overlap between O-p and Eu-d states. The associated reduction in hybridization leads to the filling of the f-peak and makes the trivalent configuration relatively less favourable, resulting in the reentrant transition to a divalent ground state. In their pressure experiments Souza-Neto et al [172] observe a coexistence of the trivalent (Eu³⁺) NaCl phase and divalent (Eu²⁺) CsCl phase in the range between 44 and 60 GPa, and a complete transition to the divalent CsCl structure above 60 GPa, which altogether is in good agreement with the theoretical picture emerging from the SIC-LSD calculations.

First-principles calculations correctly predict valence and structural transitions in the RX compounds, but the associated changes in electronic structure remain the subject of debate. The SIC-LSD approach compares total energies in the divalent and trivalent configurations, and the transition turns out to be strongly linked to the number of electrons occupying the narrow f-peak in the trivalent scenario as demonstrated for EuO in figure 17. At zero pressure, this peak is almost completely filled, with a marginal gain in band formation energy, and it is overall energetically favourable for the f-electron to localize instead, with the resulting divalent ground state configuration shown in figure 14. Under pressure, on the other hand, the f-peak becomes gradually less occupied due to f − d transfer. Compared to filling the narrow f-peak, the gain in binding energy associated with filling the much broader d-states is rather large, overcoming the gain in the SIC energy, and eventually the trivalent configuration depicted in figure 17 becomes energetically favourable.

**Figure 17.** The SIC-LSD density of states of EuO in the trivalent configuration.
Download figure:
Standard image High-resolution image

Rather than an f-electron delocalization under pressure, a large number of studies interpret the valence transition in terms of a 4f → 5d promotion [173]. As discussed earlier, photoemission measurements indicate that in the divalent chalcogenide compounds the localized f states are situated in the gap separating the occupied anion p from the unoccupied rare earth 5d states. The accepted view is that under pressure the f − d gap starts closing, and that at the transition point where the gap closes, f → d transfer or f − d mixing brings about a change in valence. Experiments have shown that this valence change is not sudden and complete from 2 + to 3+, but rather to an intermediate valence [151, 156, 174], gradually increasing with increasing pressure. This $f\to d$ promotion picture for example underlies a number of studies of EuO under pressure, although the views differ as to whether the closure is gradual [175] rather than sudden [176], or whether it results in a hybridization gap [177] rather than a metal-insulator transition [175, 176], and finally whether the collapsed phase is intermediate-valent rather than integer-valent. Zimmer et al [175] estimated that the gradually increasing valence observed in their experiments would reach ∼2.5 at pressures of around 35 GPa. In their electronic structure calculations using a constant U within their LSD + Hubbard-I scheme, Wan et al [90] have attempted to reproduce this evolution in electronic structure under pressure. They find that the gap between f and d states closes at around 10 GPa, but no change in the 4f occupation and no sign of valence instability for pressures up to 40 GPa. According to SIC-LSD, the isostructural B1²⁺ → B1³⁺ transition results in an effective valence of roughly 2.35 [101].

4.3. Summary

It emerges that our understanding of the underlying physics of valence transitions in the rare earth chalcogenides under pressure remains incomplete. This is particularly obvious for SmS where the experimentally observed [102, 104, 178, 179] semiconductor ('black phase') to metal ('golden phase') transition, at a relatively modest pressure of 0.65 GPa, has been extensively studied by means of such methods as LDA [154, 180], LDA + SIC [55, 181], LDA + U [182, 183], and LDA + DMFT [184], with interpretations ranging from f-electron delocalization and f − d promotion to topological phase transition.

Finally, we should note that the large majority of the rare earth compounds are trivalent in their ground state, and undergo B1–B2 structural transitions under pressure. The delocalization of a second f-electron, i.e. from R³⁺ → R⁴⁺ , tends to be energetically unfavourable, except for some of the light rare earths, such as the Cerium chalcogenides and pnictides, where in both CeP and CeS electronic structure transitions are observed in the B1 phase at respectively 10 and 12.5 GPa [174]. The observed transitions are quantitatively reproduced in the SIC-LSD calculations, which also predict the structural B1–B2 transition energetically favourable for the heavier Ce compounds, in agreement with experiment [185–187].

5. Conclusions

In this article we have attempted to overview a number of different ab initio descriptions of rare earth monopnictides and monochalcogenides, in comparison with the available experimental evidence. The focus has been on trends and systematics, but a few families of monopnictides and monochalcogenides have been discussed in some detail, both in equilibrium and under pressure, with the interest and relevance for new technologies in mind. We have concentrated on the global picture of and trends in the electronic structure properties, provided mostly by the SIC-LSD calculations performed for 140 RX compounds. SIC-LSD is likely the only first-principles method that is reasonably fast and capable to treat both localized and itinerant electron systems on equal footing. The ground state valence and valence transitions of RX have been identified across the whole RX family, starting from tetravalency, through trivalency to divalency, when moving from early to late R, in correlation with the ligands. Important links have been uncovered between the underlying electronic structure, valence and physical properties, ranging from semiconducting, semi-metallic, metallic and even heavy fermion-like behaviour. Since SIC-LSD is an orbital dependent effective one electron theory, the predicted electronic phase diagram should be seen mostly as a guide, rather than a complete map of the observed areas distinguishing particular electronic/physical properties among all the studied RX compounds. It seems especially true in the IV and heavy fermion-like areas, where more accurate, dynamical, treatment of many-body interactions would most likely introduce refinements into the physical trends predicted by SIC-LSD among others.

With respect to future studies on the rare earth pnictides and chalcogenides it will be highly relevant to investigate the effect on the underlying properties from doping the RX system on either the cation or anion site. Although there exist a number of experimental studies on this subject [141, 188], with respect to first principles calculations relatively few attempts have been made so far to address these strongly correlated alloys [91]. Studying the changes in materials properties as a function of dopant concentration will help to better understand the role of chemistry in these compounds, and investigate their potential for use in functional materials. Finally, as discussed in the previous section, one can envisage that future experimental and theoretical studies will also seek improved insight into the underlying physics of valence transitions in the rare earth compounds under pressure, as it is far from complete or established.

Acknowledgment

This work was supported by EPSRC through a service level agreement with STFC's Scientific Computing Department.

Rare-earth pnictides and chalcogenides from first-principles

Article metrics

Submit

Permissions

Author e-mails

Author affiliations

Dates

Peer review information

Abstract

1. Introduction