Atomistic spin model simulations of magnetic nanomaterials

The extended Heisenberg spin model encapsulates the essential physics of a magnetic material at the atomic level, where the energetics of a system of interacting atomic moments is given by a spin Hamiltonian (which neglects non-magnetic effects such the as the Coulomb term). The spin Hamiltonian $\mathcal {H}$ typically has the form:

$$\begin{equation}\label {eq:spinhamiltonian} \mathcal {H} = \mathcal {H}_{{\rm exc}} + \mathcal {H}_{{\rm ani}} + \mathcal {H}_{{\rm app}} \end{equation} \tag{ 1 }$$

denoting terms for the exchange interaction, magnetic anisotropy, and externally applied magnetic fields respectively.

The dominant term in the spin Hamiltonian is the Heisenberg exchange energy, which arises due to the symmetry of the electron wavefunction and the Pauli exclusion principle [60] which governs the orientation of electronic spins in overlapping electron orbitals. Due to its electrostatic origin, the associated energies of the exchange interaction are around 1–2 eV, which is typically up to 1000 times larger than the next largest contribution and gives rise to magnetic ordering temperatures in the range 300–1300 K. The exchange energy for a system of interacting atomic moments is given by the expression

$$\begin{equation} \mathcal {H}_{{\rm exc}} = -\sum _{i\ne j} {J_{ij}} {\mathbf {S}}_i \boldsymbol {\cdot } {\mathbf {S}}_j \label {eq:HJij} \end{equation} \tag{ 2 }$$

where J_ij is the exchange interaction between atomic sites i and j, S_i is a unit vector denoting the local spin moment direction and S_j is the spin moment direction of neighbouring atoms. The unit vectors are taken from the actual atomic moment $\boldsymbol {\mu }_{{\rm s}}$ and given by ${\mathbf {S}}_i = \boldsymbol {\mu }_{{\rm s}}/|\boldsymbol {\mu }_{{\rm s}}|$. It is important to note here the significance of the sign of J_ij. For ferromagnetic materials where neighbouring spins align in parallel, J_ij > 0, and for antiferromagnetic materials where the spins prefer to align anti-parallel J_ij < 0. Due to the strong distance dependence of the exchange interaction, the sum in equation (2) is often truncated to include nearest neighbours only. This significantly reduces the computational effort while being a good approximation for many materials of interest. In reality the exchange interaction can extend to several atomic spacings [29, 30], representing hundreds of pairwise interactions.

In the simplest case the exchange interaction J_ij is isotropic, meaning that the exchange energy of two spins depends only on their relative orientation, not their direction. In more complex materials, the exchange interaction forms a tensor with components:

$$\begin{equation} \mathbf {J}_{ij}^{\mathrm {M}} = \begin{bmatrix} J_{xx}&J_{xy}&J_{xz}\\ J_{yx}&J_{yy}&J_{yz} \\ J_{zx}&J_{zy}&J_{zz} \end{bmatrix} , \label {eq:HJijM} \end{equation} \tag{ 3 }$$

which is capable of describing anisotropic exchange interactions, such as two-ion anisotropy [29] and the Dzyaloshinskii–Moriya interaction (off-diagonal components of the exchange tensor). In the case of tensorial exchange $\mathcal {H}_{{\rm exc}}^{{\rm M}}$, the exchange energy is given by the product:

$$\begin{equation} \mathcal {H}_{{\rm exc}}^{{\rm M}} = -\sum _{i \ne j}\begin{bmatrix}S_x^i S_y^i S_z^i\end{bmatrix} \begin{bmatrix} J_{xx}&J_{xy}&J_{xz}\\ J_{yx}&J_{yy}&J_{yz} \\ J_{zx}&J_{zy}&J_{zz} \end{bmatrix} \begin{bmatrix}S_x^j \\S_y^j \\ S_z^j\end{bmatrix} . \label {eq:HJijSMS} \end{equation} \tag{ 4 }$$

Obtaining the components of the exchange tensor may be done phenomenologically, or via ab initio methods such as the relativistic torque method [62–65] or the spin-cluster expansion technique [30, 66–68]. The above expressions for the exchange energy also exclude higher-order exchange interactions such as three-spin and four-spin terms. In most materials the higher-order exchange terms are significantly smaller than the leading term and can safely be neglected.

While the exchange energy gives rise to magnetic ordering at the atomic level, the thermal stability of a magnetic material is dominated by the magnetic anisotropy, or preference for the atomic moments to align along a preferred spatial direction. There are several physical effects which give rise to anisotropy, but the most important is the magnetocrystalline anisotropy (namely the preference for spin moments to align with particular crystallographic axes) arising from the interaction of atomic electron orbitals with the local crystal environment [69, 70].

The simplest form of anisotropy is of the single-ion uniaxial type, where the magnetic moments prefer to align along a single axis, $\boldsymbol {e}$, often called the easy axis and is an interaction confined to the local moment. Uniaxial anisotropy is most commonly found in particles with elongated shape (shape anisotropy), or where the crystal lattice is distorted along a single axis as in materials such as hexagonal Cobalt and L1₀ ordered FePt. The uniaxial single-ion anisotropy energy is given by the expression:

$$\begin{equation} \mathcal {H}_{{\rm ani}}^{{\rm uni}} = -{k_{{\rm u}}} \sum _i \left ({\mathbf {S}}_i \boldsymbol {\cdot } \boldsymbol {e} \right )^2 \end{equation} \tag{ 5 }$$

where k_u is the anisotropy energy per atom. Materials with a cubic crystal structure, such as iron and nickel, have a different form of anisotropy known as cubic anisotropy. Cubic anisotropy is generally much weaker than uniaxial anisotropy, and has three principal directions which energetically are easy, hard and very hard magnetization directions respectively. Cubic anisotropy is described by the expression:

$$\begin{equation} \mathcal {H}_{{\rm ani}}^{{\rm cub}} = \frac {k_{{\rm c}}}{2} \sum _i \left (S_x^4+S_y^4+S_z^4\right ) \end{equation} \tag{ 6 }$$

where k_c is the cubic anisotropy energy per atom, and S_x, S_y, and S_z are the x, y, and z components of the spin moment S respectively.

Most magnetic problems also involve interactions between the system and external applied fields, denoted as H_app. External fields can arise in many ways, for example a nearby magnetic material, or as an effective field from an electric current. In all cases the applied field energy is simply given by:

$$\begin{equation} \mathcal {H}_{{\rm app}} = - \sum _i {\mu _{{\rm s}}} {\mathbf {S}}_i \boldsymbol {\cdot } {\mathbf {H}}_{{\rm app}}. \end{equation} \tag{ 7 }$$

The subject of magnetic units is controversial due to the existence of multiple competing standards and historical origins [60]. Starting from the atomic level however, the dimensionality of units is relatively transparent. Atomic moments are usually accounted for in multiples of the Bohr magneton (μ_B), the magnetic moment of an isolated electron, with units of J T⁻¹. Given a number of atoms of moment μ_s in a volume, the moment per unit volume is naturally in units of J T m⁻³, which is identical to the SI unit of A m⁻¹. However, the dimensionality (moment per unit volume) of the unit A m⁻¹ is not as obvious as J T⁻¹m⁻³, and so the latter form is used herein.

Applied magnetic fields are hence defined in Tesla, which comes naturally from the derivative of the spin Hamiltonian with respect to the local moment. The unit of Tesla for applied field is also beneficial for hysteresis loops, since the area enclosed a typical M–H loop is then given as an energy density (J m⁻³). A list of key magnetic parameters and variables and their units are shown in table 1.

Ab initio density functional theory (DFT) calculations utilize the Hohenberg–Kohn–Sham theory [71, 72] which states that the total energy E of a system can be written solely in terms the electron density, ρ. Thus, if the electron density is known then the physical properties of the system can be found. In practice, the both electron density and the spin density are used as fundamental quantities in the total energy expression for spin-polarized systems [73]. In many implementations DFT-based methods only consider the outer electrons of a system, since the inner electrons play a minimal role in the bonding and also partially screen the effect of the nuclear core. These effects are approximated by a pseudopotential which determines the potential felt by the valence electrons. In all-electron methods, however, the core electron density is also relaxed. By energy minimization, DFT enables the calculation of a wide range of properties, including lattice constants, and in the case of magnetic materials localized spin moments, magnetic ground state and the effective magnetocrystalline anisotropy. Standard software packages such as VASP [74], CASTEP [75, 76] and SIESTA [77] make such calculations readily accessible. At present determining site resolved properties such as anisotropy constants and pairwise exchange interactions is more involved and requires ab initio Green's functions techniques such as the fully relativistic Korringa–Kohn–Rostoker method [78, 79] or the LMTO method [80, 81] in conjunction with the magnetic force theorem [62]. An alternative approach for the calculation of exchange parameters is the utilization of the generalized Bloch theorem for spin-spiral states in magnetic systems [82] together with a Fourier transformation of k-dependent spin-spiral energies [83, 84].

A number of studies have determined atomic magnetic properties from first principles calculations by direct mapping onto a spin model, including the principal magnetic elements Co, Ni and Fe [81], metallic alloys including FePt [29], IrMn [31], oxides [85] and spin glasses [86], and also bilayer systems such as Fe/FePt [87]. Such calculations give detailed insight into microscopic magnetic properties, including atomic moments, long-ranged exchange interactions, magnetocrystalline anisotropies (including surface and two-ion interactions) and other details not readily available from phenomenological theories. Combined with atomistic models it is possible to determine macroscopic properties such as the Curie temperature, temperature-dependent anisotropies, and magnetic ground states, often in excellent agreement with experiment. However, the computational complexity of DFT calculations also means that the systems which can be simulated with this multi scale approach are often limited to small clusters, perfect bulk systems and 2D periodic systems, while real materials of course often contain a plethora of defects disrupting the long range order. Some studies have also investigated the effects of disorder in magnetic systems combined with a spin model mapping, such as dilute magnetic semiconductors [88] and metallic alloys [89].

Magnetic properties calculated at the electronic level have a synergy with atomistic spin models, since the electronic properties can often be mapped onto a Heisenberg spin model with effective local moments. This multiscale electronic and atomistic approach avoids the continuum approximations of micromagnetics and treats magnetic materials at the natural atomic scale.

The alternative approach to multiscale atomistic/density-functional-theory simulations is to derive the parameters from experimentally determined values. This has the advantage of speed and lower complexity, whilst foregoing microscopic details of the exchange interactions or anisotropies. Another key advantage of generic parameters is the possibility of parametric studies, where parameters are varied explicitly to determine their importance for the macroscopic properties of the system, such as has been done for studies of surface anisotropy [17] and exchange bias [13].

Unlike micromagnetic simulations, the fundamental thermodynamic approach of the atomistic model means that all parameters must be determined for zero temperature. The spin fluctuations then determine the intrinsic temperature dependence of the effective parameters which are usually put into micromagnetic simulations as parameters. Fortunately determination of the atomic moments, exchange constants and anisotropies from experimental values is relatively straightforward for most systems.

3.2.1. Atomic spin moment

The atomic spin moment μ_s is related to the saturation magnetization simply by:

$$\begin{equation} {\mu _{{\rm s}}} = \frac {{M_{{\rm s}}} a^3}{n_{{\rm at}}} \end{equation} \tag{ 8 }$$

where M_s is the saturation magnetization at 0 K in J T⁻¹m⁻³, a is the unit cell size (m), and n_at is the number of atoms per unit cell. We also note the usual convention of expressing atomic moments in multiples or fractions of the Bohr magneton, μ_B owing to their electronic origin. Taking BCC iron as an example, the zero temperature saturation magnetization is 1.75 MA m⁻¹ [90], unit cell size of a = 2.866 Å, this gives an atomic moment of 2.22 μ_B/atom.

3.2.2. Exchange energy

For a generic atomistic model with z nearest neighbour interactions, the exchange constant is given by the mean-field expression:

$$\begin{equation} {J_{ij}} = \frac {3 k_{\mathrm {B}} {T_{{\rm c}}}}{\epsilon z} \label {eq:JijTc} \end{equation} \tag{ 9 }$$

where k_B is the Boltzmann constant and T_c is the Curie temperature z is the number of nearest neighbours. is a correction factor from the usual mean-field expression which arises due to spin waves in the 3D Heisenberg model [91]. Because of this is also dependent on the crystal structure and coordination number, and so the calculated T_c will vary slightly according to the specifics of the system. For Cobalt with a T_c of 1388 K and assuming a hexagonal crystal structure with z = 12, this gives a nearest neighbour exchange interaction J_ij = 6.064 × 10⁻²¹ J/link.

3.2.3. Anisotropy energy

The atomistic magnetocrystalline anisotropy k_u is derived from the macroscopic anisotropy constant K_u by the expression:

$$\begin{equation} {k_{{\rm u}}} = \frac {{K_{{\rm u}}} a^3}{n_{{\rm at}}} \end{equation} \tag{ 10 }$$

where K_u in given in J m⁻³. In addition to the atomistic parameters, it is also worth noting the analogous expressions for the anisotropy field H_a for a single domain particle:

$$\begin{equation}H_{{\rm a}} = \frac {2{K_{{\rm u}}}}{{M_{{\rm s}}}} = \frac {2{k_{{\rm u}}}}{{\mu _{{\rm s}}}} \end{equation} \tag{ 11 }$$

where symbols have their usual meaning. At this point it is worth mentioning that the measured anisotropy is a free energy difference. While the intrinsic k_u remains (to a first approximation) temperature independent, at a non-zero temperature the free energy in the easy/hard directions is increased/decreased due to the magnetization fluctuations. Thus the macroscopic anisotropy value decreases with increasing temperature, vanishing at T_c. The thermodynamic basis of atomistic models makes them highly suitable for the investigation of such phenomena, as we show later. Applying the above, parameters for the key ferromagnetic elements are given in table 2.

3.2.4. Ferrimagnets and antiferromagnets

In the case of ferrimagnets and antiferromagnets the above methods for anisotropy and moment determination do not work due to the lack of macroscopic measurements, although the estimated exchange energies apply equally well to the Néel temperature provided no magnetic frustration (due to lattice symmetry) is present. In general, other theoretical calculations or formalisms are required to determine parameters, such as mean-field approaches [9] or density functional theory calculations [31].

Table 2.  Table of derived constants for the ferromagnetic elements Fe, Co, Ni and Gd.

	Fe	Co	Ni	Gd	Unit
Crystal structure	bcc	hcp	fcc	hcp	—
Unit cell size a	2.866	2.507	3.524	3.636	Å
Interatomic spacing rij	2.480	2.507	2.492	3.636	Å
Coordination number z	8	12	12	12	—
Curie temperature Tc	1043	1388	631	293	K
Spin-wave MF correction [91, 92]	0.766	0.790	0.790	0.790	—
Atomic spin moment μs	2.22	1.72	0.606	7.63	μB
Exchange energy Jij	7.050 × 10−21	6.064 × 10−21	2.757 × 10−21	1.280 × 10−21	J/link
Anisotropy energy [93] k	5.65 × 10−25	6.69 × 10−24	5.47 × 10−26	5.93 × 10−24	J/atom

In addition to determining the parameters of the spin Hamiltonian, an essential part of the atomistic model is the determination of the nuclear, or atomic, positions in the system. In the multiscale approach utilizing ab initio parameterization of the system, the spin Hamiltonian is intrinsically tied to the atomic positions. The additional detail offered by first principles calculations is highly desirable even for perfect crystals and atomically sharp interfaces, however the computational complexity of the calculations limits the ability to parameterize a spin Hamiltonian for systems of extended defects over 10 nm+ length scales, including physical effects such as vacancies, impurities, dislocations and even amorphous materials.

For systems modelled using the nearest neighbour approximation, the atomic structures are much less restricted, allowing for simulations of material defects such as interface roughness [13] and intermixing [21], magnetic multilayers [94], disordered magnetic alloys [9], surface [17] and finite size effects [57]. VAMPIRE includes extensive functionality to generate such systems, the details of which are included in appendix B. In addition to crystallographic and molecular systems [95, 96] it is also possible to investigate magnetic effects in disordered materials and nanoparticles by incorporating the results of Molecular Dynamics simulations [19, 20, 97].

The first understanding of spin dynamics came from ferromagnetic resonance experiments, where the time-dependent behaviour of a magnetic materials is described by the equation derived by Landau and Lifshitz [98], and in the modern form given by:

$$\begin{equation}\label {eqn:LL} \frac {\partial \mathbf {m}}{\partial t} = -\gamma [\mathbf {m} \times \mathbf {H} + \alpha \mathbf {m} \times (\mathbf {m} \times \mathbf {H})] \end{equation} \tag{ 12 }$$

where m is a unit vector describing the direction of the sample magnetization, H is the effective applied field acting on the sample, γ is the gyromagnetic ratio and α is a phenomenological damping constant which is a property of the material. The physical origin of the Landau–Lifshitz (LL) equation arises due to two distinct physical effects. The precession of the magnetization (first term in equation (12)) arises due to the quantum mechanical interaction of an atomic spin with an applied field. The relaxation of the magnetization (second term in equation (12)) is an elementary formulation of energy transfer representing the coupling of the magnetization to a heat bath which aligns the magnetization along the field direction with a characteristic coupling strength determined by α. In the LL equation the relaxation rate of the magnetization to the field direction is a linear function of the damping parameter, which was shown by Gilbert to yield incorrect dynamics for materials with high damping [99]. Subsequently Gilbert introduced critical damping, with a maximum effective damping for α = 1, to arrive at the Landau–Lifshitz–Gilbert (LLG) equation. Although initially derived to describe the dynamics of the macroscopic magnetization of a sample, the LLG is the standard equation of motion used in numerical micromagnetics, describing the dynamics of small magnetic elements.

The same equation of motion can also be applied at the atomistic level. The precession term arises quantum mechanically for atomic spins and the relaxation term now describes direct angular momentum transfer between the spins and the heat bath, which includes contributions from the lattice [100] and the electrons [101]. A distinction between the macroscopic LLG and the atomistic LLG now appears in terms of the effects included within the damping parameter. In the macroscopic LLG, α includes all contributions, both intrinsic (such as spin–lattice and spin–electron interactions) and extrinsic (spin-spin interactions arising from demagnetization fields, surface defects [102], doping [103] and temperature [50]), while the atomistic LLG only includes the local intrinsic contributions. To distinguish the different definitions of damping we therefore introduce a microscopic damping parameter λ. Although the form of the LLG is identical for atomistic and macroscopic length scales, the microstructural detail in the atomistic model allows for calculations of the effective damping including extrinsic effects, such as rare-earth doping [103]. Including a microscopic damping λ the atomistic Landau–Lifshitz–Gilbert equation is given by

$$\begin{equation}\label {eqn:LLG} \frac {\partial {\mathbf {S}}_i }{\partial t} = -\frac {\gamma }{(1+\lambda ^{2})}[{\mathbf {S}}_i \times {\mathbf {H}}^i_{{\rm eff}} + \lambda {\mathbf {S}}_i \times ({\mathbf {S}}_i \times {\mathbf {H}}^i_{{\rm eff}})] \end{equation} \tag{ 13 }$$

where S_i is a unit vector representing the direction of the magnetic spin moment of site i, γ is the gyromagnetic ratio and ${\mathbf {H}}^i_{{\rm eff}}$ is the net magnetic field on each spin. The atomistic LLG equation describes the interaction of an atomic spin moment i with an effective magnetic field, which is obtained from the negative first derivative of the complete spin Hamiltonian, such that:

$$\begin{equation}\label {eqn:Heff} {\mathbf {H}}^i_{{\rm eff}} = -\frac {1}{{\mu _{{\rm s}}}}\frac {\partial \mathcal {H}}{\partial {\mathbf {S}}_i} \end{equation} \tag{ 14 }$$

where μ_s is the local spin moment. The inclusion of the spin moment within the effective field is significant, in that the field is then expressed in units of Tesla, given a Hamiltonian in Joules. Given typical energies in the Hamiltonian of 10 μeV –100 meV range. This gives fields typically in the range 0.1–1000 T, given a spin moment of the same order as the Bohr magneton (μ_B).

In its standard form the LLG equation is strictly only applicable to simulations at zero temperature. Thermal effects cause thermodynamic fluctuations of the spin moments which at sufficiently high temperatures are stronger than the exchange interaction, giving rise to the ferromagnetic-paramagnetic transition. The effects of temperature can be taken into account by using Langevin Dynamics, an approach developed by Brown [104]. The basic idea behind Langevin Dynamics is to assume that the thermal fluctuations on each atomic site can be represented by a Gaussian white noise term. As the temperature is increased, the width of the Gaussian distribution increases, thus representing stronger thermal fluctuations. The established Langevin Dynamics method is widely used for spin dynamics simulations and incorporates an effective thermal field into the LLG equation to simulate thermal effects [105–107]. The thermal fluctuations are represented by a Gaussian distribution $\boldsymbol {\Gamma }(t)$ in three dimensions with a mean of zero. At each time step the instantaneous thermal field on each spin i is given by:

$$\begin{equation} {\mathbf {H}}^{i}_{{\rm th}} = \boldsymbol {\Gamma }(t) \sqrt {\frac {2 \lambda {k_{{\rm B}}} T}{\gamma {\mu _{{\rm s}}} \Delta t}} \end{equation} \tag{ 15 }$$

where k_B is the Boltzmann constant, T is the system temperature, λ is the Gilbert damping parameter, γ is the absolute value of the gyromagnetic ratio, μ_s is the magnitude of the atomic magnetic moment, and Δt is the integration time step. The effective field for application in the LLG equation with Langevin Dynamics then reads:

$$\begin{equation}\label {eqn:Heffth} {\mathbf {H}}^i_{{\rm eff}} = -\frac {1}{{\mu _{{\rm s}}}}\frac {\partial \mathcal {H}}{\partial {\mathbf {S}}_i} + {\mathbf {H}}^{i}_{{\rm th}}. \end{equation} \tag{ 16 }$$

Given that for each time step three Gaussian distributed random numbers are required for every spin, efficient generation of such numbers is essential. VAMPIRE makes use the Mersenne Twister [108] uniform random number generator and the Ziggurat method [109] for generating the Gaussian distribution.

It is useful at the this point to address the applicability of the atomistic LLG equation to slow and fast problems respectively. In reality the thermal and magnetic fluctuations are correlated at the atomic level, arising from the dynamic interactions between the atoms and lattice/electron system. These correlations may be important in terms of the thermal fluctuations experienced by the atomistic spins. In the conventional Langevin dynamics approach described above, the noise term is completely uncorrelated in time and space. For short timescales however, the thermal fluctuations are correlated in time, and so the noise is coloured [110]. The effect of the coloured noise is to lessen the effect of sudden temperature changes on the magnetization dynamics. However, the existence of ultrafast magnetization dynamics [11, 44], and that it is driven by a thermal rather than quantum mechanical process [111], requires that the effective correlation time is short, with an upper bound of around 1 fs. Given that the correlation time is close to the integration timestep, the applicability of the LLG to problems with timescales ≥ 1 fs is sound. There will be a point however where the LLG is no longer valid, where direct simulation of the microscopic damping mechanisms will be necessary. Progress has been made in linking molecular dynamics and spin models [100, 112, 113] which enables the simulation of spin–lattice interactions, which is particularly relevant for slow problems, such as conventional magnetic recording where switching occurs over nanosecond timescales. However, it is also essential to consider spin–electron effects [101, 114] necessary for ultrafast demagnetization processes, although the physical origins are still currently debated [115].

In order to determine the time evolution of a system of spins, it is necessary to solve the stochastic LLG equation, as given by equations (13) and (16), numerically. The choice of solver is limited due to the stochastic nature of the equations. Specifically, it is necessary to ensure convergence to the Stratonovich solution. This has been considered in detail by Garcia-Palacios [105], but the essential requirement [116] is that the solver enforces the conservation of the magnitude of the spin, either implicitly or by renormalization. The most primitive integration scheme uses Euler's method, which assumes a linear change in the spin direction in a single discretized time step, Δt. An improved integration scheme, known as the Heun method [105] is commonly used, which allows the use of larger time steps because of its use of a predictor–corrector algorithm. Other more advanced integration schemes have been suggested, such as the midpoint method [117] and modified predictor–corrector midpoint schemes [103, 118]. The principal advantage of the midpoint scheme is that the length of the spin vector is preserved during the integration which allows larger time steps to be used. However for the midpoint scheme the significant increase in computational complexity outweighs the benefits of larger time steps [118]. Modified predictor–corrector schemes [103, 118] reduce the computational complexity of the midpoint scheme, but with a loss of accuracy, particularly in the time-dependent dynamics [103]. For valid integration of the stochastic LLG equation it is also necessary for the numerical scheme to converge to the Stratonovich solution [105, 119]. Although proven for the midpoint and Heun numerical schemes, the validity of the predictor–corrector midpoint schemes for the stochastic LLG have yet to be confirmed. On balance the Heun scheme, despite its relative simplicity, is sufficiently computationally efficient that it is still the most widely used integration scheme for stochastic magnetization dynamics, and so we proceed to describe its implementation in detail.

In the Heun method, the first (predictor) step calculates the new spin direction, ${\mathbf {S}}_i'$, for a given effective field ${\mathbf {H}}_{{\rm eff}}^i$ by performing a standard Euler integration step, given by:

$$\begin{equation} {\mathbf {S}}_i'= {\mathbf {S}}_i + \Delta {\mathbf {S}} \Delta t \end{equation} \tag{ 17 }$$

where

$$\begin{equation} \Delta {\mathbf {S}} = - \frac {\gamma }{(1+\lambda ^{2})}[{\mathbf {S}}_i \times {\mathbf {H}}_{{\rm eff}}^i + \lambda {\mathbf {S}}_i \times ({\mathbf {S}}_i \times {\mathbf {H}}_{{\rm eff}}^i)]{\rm .} \end{equation} \tag{ 18 }$$

The Heun scheme does not preserve the spin length and so it is essential to renormalize the spin unit vector length S_i after both the predictor and corrector steps to ensure numerical stability and convergence to the Stratanovich solution. After the first step the effective field must be re-evaluated as the intermediate spin positions have now changed. It should be noted that the random thermal field does not change between steps. The second (corrector) step then uses the predicted spin position and revised effective field ${\mathbf {H}}_{{\rm eff}}^{i'}$ to calculate the final spin position, resulting in a complete integration step given by:

$$\begin{equation} {\mathbf {S}}_i^{t + \Delta t} = {\mathbf {S}}_i + \tfrac {1}{2}\left [\Delta {\mathbf {S}} + \Delta {\mathbf {S}}' \right ]\Delta t \end{equation} \tag{ 19 }$$

where

$$\begin{equation} \Delta {\mathbf {S}}' = -\frac {\gamma }{(1+\lambda ^{2})}[{\mathbf {S}}_i' \times {\mathbf {H}}^{i'}_{{\rm eff}} + \lambda {\mathbf {S}}_i' \times ({\mathbf {S}}_i' \times {\mathbf {H}}^{i'}_{{\rm eff}})]{\rm .} \end{equation} \tag{ 20 }$$

The predictor step of the integration is performed on every spin in the system before proceeding to evaluate the corrector step for every spin. This is then repeated many times so that the time evolution of the system can be simulated. Although the Heun scheme was derived specifically for a stochastic equation with multiplicative noise, in the absence of the noise term the Heun method reduces to a standard second order Runge–Kutta method [120]. In order to test the implementation of the Heun integration scheme, it is possible to compare the calculated result with the analytical solution for the LLG. For the simple case of a single spin initially along the x-axis in an applied field along the z-axis, the time evolution [121] is given by:

$$\begin{eqnarray} &&\begin{array}{lll} S_{x} (t) = {\rm sech} \left (\displaystyle \frac {\lambda \gamma H}{1+\lambda ^2}t\right ) \cos \left (\displaystyle \frac {\gamma H}{1+\lambda ^2}t\right ) \\ [1pc] S_{y} (t) = {\rm sech} \left (\displaystyle \frac {\lambda \gamma H}{1+\lambda ^2}t\right ) \sin \left (\displaystyle \frac {\gamma H}{1+\lambda ^2}t\right ) \\ [1pc] S_{z} (t) = \tanh \left (\displaystyle \frac {\lambda \gamma H}{1+\lambda ^2}t\right ). \label {eq:analytic_LLG} \end{array} \end{eqnarray} \tag{ 21 }$$

The expected and simulated time evolution for a single spin with H = 10 T, Δt = 1 × 10⁻¹⁵ s and λ = 0.1,0.05 is plotted in figure 1. Superficially the simulated and expected time evolution agree very well, with errors around 10⁻⁶. The error gives a characteristic trace the size and shape of which is indicative of a correct implementation of the Heun integration scheme.

Zoom In Zoom Out Reset image size

Ideally one would like to use the largest time step possible so as to simulate systems for the longest time. For micromagnetic simulations at zero temperature, the minimum time step is a well defined quantity since the largest field (usually the exchange term) essentially defines the precession frequency. However, for atomistic simulations using the stochastic LLG equation with Langevin dynamics, the effective field becomes temperature dependent. The consequence of this is that for atomistic models the most difficult region to integrate is in the immediate vicinity of the Curie point. Errors in the integration of the system will be apparent from a non-converged value for the average magnetization. This gives a relatively simple case which can then be used to test the stability of integration schemes for the stochastic LLG model. A plot of the mean magnetization as a function of temperature is shown in figure 2 for a representative system consisting of 22 × 22 × 22 unit cells with generic material parameters of FePt with an fcc crystal structure, nearest neighbour exchange interaction of J_ij = 3.0 × 10⁻²¹ J/link and uniaxial anisotropy of 1.0 × 10⁻²³ J/atom. The system is first equilibrated for 10 ps at each temperature and then the mean magnetization is calculated over a further 10 ps.

Zoom In Zoom Out Reset image size

First, comparing the effect of temperature on the minimum allowable time step, the data show that for low temperatures reasonably large time steps of 1 × 10⁻¹⁵ give the correct solution of the LLG equations, while near the Curie point (690 K) the deviations from the correct equilibrium value are significant. Consequently for simulations studying high temperature reversal processes time steps of 1 × 10⁻¹⁶ s are necessary. It should be noted that the time steps which can be used are material-dependent—specifically if a material with higher Curie temperature is used then the usable time steps will be correspondingly lower due to the increased exchange field.

From a practical perspective a significant advantage of the spin dynamics method is the ability to parallelize the integration system by domain decomposition, details of which are given in appendix C. This allows the efficient simulation of relatively large systems consisting of tens or hundreds of grains or nano structures with dimensions greater than 100 nm for nanosecond timescales, with typical numbers of spins in the range 10⁶–10⁸.

While spin dynamics are particularly useful for obtaining dynamic information about the magnetic properties or reversal processes for a system, they are often not the optimal method for determining the equilibrium properties, for example the temperature-dependent magnetization. The Monte Carlo Metropolis algorithm [122] provides a natural way to simulate temperature effects where dynamics are not required due to the rapid convergence to equilibrium and relative ease of implementation.

The Monte Carlo metropolis algorithm for a classical spin system proceeds as follows. First a random spin i is picked and its initial spin direction S_i is changed randomly to a new trial position ${\mathbf {S}}_i'$, a so-called trial move. The change in energy $\Delta E = E({\mathbf {S}}_i') - E({\mathbf {S}}_i)$ between the old and new positions is then evaluated, and the trial move is then accepted with probability

$$\begin{equation}P = {\rm exp} \left ({-\frac {\Delta E}{{k_{{\rm B}}} T}}\right ) \label {eq:AMCP} \end{equation} \tag{ 22 }$$

by comparison with a uniform random number in the range 0–1. Probabilities greater than 1, corresponding with a reduction in energy, are accepted unconditionally. This procedure is then repeated until N trial moves have been attempted, where N is the number of spins in the complete system. Each set of N trial moves comprises a single Monte Carlo step.

The nature of the trial move is important due to two requirements of any Monte Carlo algorithm: ergodicity and reversibility. Ergodicity expresses the requirement that all possible states of the system are accessible, while reversibility requires that the transition probability between two states is invariant, explicitly $P({\mathbf {S}}_i \rightarrow {\mathbf {S}}_i') = P({\mathbf {S}}_i' \rightarrow {\mathbf {S}}_i)$. From equation (22) reversibility is obvious since the probability of a spin change depends only on the initial and final energy. Ergodicity is easy to satisfy by moving the selected spin to a random position on the unit sphere, however this has an undesirable consequence at low temperatures since large deviations of spins from the collinear direction are highly improbable due to the strength of the exchange interaction. Thus at low temperatures a series of trial moves on the unit sphere will lead to most moves being rejected. Ideally a move acceptance rate of around 50% is desired, since very high and very low rates require significantly more Monte Carlo steps to reach a state representative of true thermal equilibrium.

One of the most efficient Monte Carlo algorithms for classical spin models was developed by Hinzke and Nowak [123], involving a combinational approach using a mixture of different trial moves. The principal advantage of this method is the efficient sampling of all available phase space while maintaining a reasonable trial move acceptance rate. The Hinzke–Nowak method utilizes three distinct types of move: spin flip, Gaussian and random, as illustrated schematically in figure 3.

Zoom In Zoom Out Reset image size

The spin flip move simply reverses the direction of the spin such that ${\mathbf {S}}_i' = - {\mathbf {S}}_i$ to explicitly allow the nucleation of a switching event. The spin flip move is identical to a move in Ising spin models. It should be noted that spin flip moves do not by themselves satisfy ergodicity in the classical spin model, since states perpendicular to the initial spin direction are inaccessible. However, when used in combination with other ergodic trial moves this is quite permissible. The Gaussian trial move takes the initial spin direction and moves the spin to a point on the unit sphere in the vicinity of the initial position according to the expression

$$\begin{equation} {\mathbf {S}}'_i = \frac {{\mathbf {S}}_i + \sigma _{{\rm g}}\boldsymbol {\Gamma }} {|{\mathbf {S}}_i + \sigma _{{\rm g}}\boldsymbol {\Gamma }|} \label {eq:MCgaussian} \end{equation} \tag{ 23 }$$

where $\boldsymbol {\Gamma }$ is a Gaussian distributed random number and σ_g is the width of a cone around the initial spin S_i. After generating the trial position ${\mathbf {S}}_i'$ the position is normalized to yield a spin of unit length. The choice of a Gaussian distribution is deliberate since after normalization the trial moves have a uniform sampling over the cone. The width of the cone is generally chosen to be temperature dependent and of the form

$$\begin{equation} \sigma _{{\rm g}} = \frac {2}{25}\left (\frac {{k_{{\rm B}}} T}{{\mu _{{\rm B}}}}\right )^{1/5}. \label {eq:MCgaussianSigma} \end{equation} \tag{ 24 }$$

The Gaussian trial move thus favours small angular changes in the spin direction at low temperatures, giving a good acceptance probability for most temperatures.

The final random trial move picks a random point on the unit sphere according to

$$\begin{equation} {\mathbf {S}}'_i = \frac {\boldsymbol {\Gamma }}{|\boldsymbol {\Gamma }|} \label {eq:MCrandom} \end{equation} \tag{ 25 }$$

which ensures ergodicity for the complete algorithm and ensures efficient sampling of the phase space at high temperatures. For each trial step one of these three trial moves is picked randomly, which in general leads to good algorithmic properties.

To verify that the random sampling and Gaussian trial moves give the expected behaviour, a plot of the calculated trial moves on the unit sphere for the different algorithms is shown in figure 4. The important points are that the random trial move is uniform on the unit sphere, and that the Gaussian trial move is close to the initial spin direction, along the z-axis in this case.

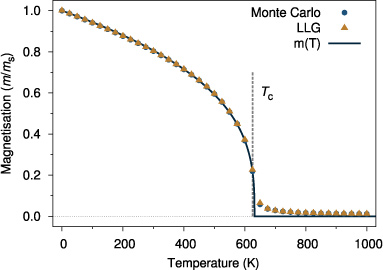
Zoom In Zoom Out Reset image size

At this point it is worthwhile considering the relative efficiencies of Monte Carlo and spin dynamics for calculating equilibrium properties. Figure 5 shows the simulated temperature-dependent magnetization for a test system using both LLG spin dynamics and Monte Carlo methods. Agreement between the two methods is good, but the spin dynamics simulation takes around twenty times longer to compute due to the requirements of a low time step and slower convergence to equilibrium. However, Monte Carlo algorithms are notoriously difficult to parallelize, and so for larger systems LLG spin dynamic simulations are generally more efficient than Monte Carlo methods.

Zoom In Zoom Out Reset image size

Assuming a correct implementation of an integration scheme as described in the previous section, the first test case of interest is the correct implementation of uniaxial magnetic anisotropy. For a single spin in an applied field and at zero temperature, the behaviour of the magnetization is essentially that of a Stoner–Wohlfarth particle, where the angular variation of the coercivity, or reversing field, is well known [125]. This test serves to verify the static solution for the LLG equation by ensuring an easy axis loop gives a coercivity of H_k = 2k_u/μ_s as expected analytically. For this problem the Hamiltonian reads

$$\begin{equation} \mathcal {H} = -{k_{{\rm u}}} S_z^2 -{\mu _{{\rm s}}} {\mathbf {S}} \boldsymbol {\cdot } {\mathbf {H}}_{{\rm app}} \end{equation} \tag{ 26 }$$

where k_u is the on-site uniaxial anisotropy constant and H_app is the external applied field. The spin is initialized pointing along the applied field direction, and then the LLG equation is solved for the system, until the net torque on the system S ×H_eff ≤|10⁻⁶| T, essentially a condition of local minimum energy.

The field strength is decreased from saturation in steps of 0.01 H/H_k and solved again until the same condition is reached. A plot of the calculated alignment of the magnetization to the applied field (${\mathbf {S}} \boldsymbol {\cdot } {\mathbf {H}}_{{\rm app}}$) for different angles from the easy axis is shown in figure 6. The calculated hysteresis curve conforms exactly to the Stoner–Wohlfarth solution.

Zoom In Zoom Out Reset image size

To quantitatively test the thermal effects in the model and the correct implementation of the stochastic LLG or Monte Carlo integrators, the simplest case is that of the Boltzmann distribution for a single spin with anisotropy (or applied field), where the probability distribution is characteristic of the temperature and the anisotropy energy. The Boltzmann distribution is given by:

$$\begin{equation}\label {eqn:boltz} P(\theta ) \propto \sin \theta \exp \left (-\frac {{k_{{\rm u}}} \sin ^2\theta } {k_{{\rm B}} T}\right ) \end{equation} \tag{ 27 }$$

where θ is the angle from the easy axis. The spin is initialized along the easy axis direction and the system is allowed to evolve for 10⁸ time steps after equilibration, recording the angle of the spin to the easy axis at each time. Since the anisotropy energy is symmetric along the easy axis, the probability distribution is reflected and summed about π/2, since at low temperatures the spin is confined to the upper well (θ < π/2). Figure 7 shows the normalized probability distribution for three reduced temperatures.

Zoom In Zoom Out Reset image size

The agreement between the calculated distributions is excellent, indicating a correct implementation of the stochastic LLG equation.

Tests such as the Stoner–Wohlfarth hysteresis or Boltzmann distribution are helpful in verifying the mechanical implementation of an algorithm for a single spin, but interacting systems of spins present a significant challenge in that no analytical solutions exist. Hence it is necessary to calculate some well-defined macroscopic property which ensures the correct implementation of interactions in a system. The Curie temperature T_c of a nanoparticle is primarily determined by the strength of the exchange interaction between spins and so makes an ideal test of the exchange interaction. As discussed previously the bulk Curie temperature is related to the exchange coupling by the mean-field expression given in equation (9). However, for nanoparticles with a reduction in coordination number at the surface and a finite number of spins, the Curie temperature and criticality of the temperature-dependent magnetization will vary significantly with varying size [57].

To investigate the effects of finite size and reduction in surface coordination on the Curie temperature, the equilibrium magnetization for different sizes of truncated octahedron nanoparticles was calculated as a function of temperature. The Hamiltonian for the simulated system is

$$\begin{equation} \mathcal {H} = -\sum _{i\ne j} {J_{ij}} {\mathbf {S}}_i \boldsymbol {\cdot } {\mathbf {S}}_j \end{equation} \tag{ 28 }$$

where J_ij = 5.6 × 10⁻²¹ J/link, and the crystal structure is face-centred-cubic, which is believed to be representative of Cobalt nanoparticles. Given the relative strength of the exchange interaction, anisotropy generally has a negligible impact on the Curie temperature of a material, and so the omission of anisotropy from the Hamiltonian is purely for simplicity. The system is simulated using the Monte Carlo method with 10 000 equilibration and 20 000 averaging steps. The system is heated sequentially in 10 K steps, with the final state of the previous temperature taken as the starting point of the next temperature to minimize the number of steps required to reach thermal equilibrium. The mean temperature-dependent magnetization for different particle sizes is plotted in figure 8.

Zoom In Zoom Out Reset image size

From equation (9) the expected Curie temperature is 1282 K, which is in agreement with the results for the 10 nm diameter nanoparticle. For smaller particle sizes the magnetic behaviour close to the Curie temperature loses its criticality, making T_c difficult to determine. Traditionally the Curie point is taken as the maximum of the gradient dm/dT [57], however this significantly underestimates the actual temperature at which magnetic order is lost (which is, by definition, the Curie temperature). Other estimates of the Curie point such as the divergence in the susceptibility are probably a better estimate for finite systems, but this is beyond the scope of the present article. Another effect visible for very small particle sizes is the appearance of a magnetization above the Curie point, an effect first reported by Binder [126]. This arises from local moment correlations which exist above T_c. It is an effect only observable in nanoparticles where the system size is close to the magnetic correlation length.

For systems larger than the single domain limit [33] and systems which have one dimension significantly different from another, the demagnetizing field can have a dominant effect on the macroscopic magnetic properties. In micromagnetic formalisms implemented in software packages such as OOMMF [37], MAGPAR [38] and NMAG [39], the calculation of the demagnetization fields is calculated accurately due to the routine simulation of large systems where such fields dominate. Due to the long-ranged interaction the calculation of the demagnetization field generally dominates the compute time and so computational methods such as the fast-Fourier-transform [127, 128] and multipole expansion [129] have been developed to accelerate their calculation.

In large-scale atomistic calculations, it is generally sufficient to adopt a micromagnetic discretization for the demagnetization fields, since they only have a significant effect on nanometre length scales [7]. Additionally due to the generally slow variation of magnetization, the timescales associated with the changes in the demagnetization field are typically much longer than the time step for atomistic spins. Here we present a modified finite difference scheme for calculating the demagnetization fields, described as follows.

Zoom In Zoom Out Reset image size

The complete system is first discretized into macrocells with a fixed cell size, each consisting of a number of atoms, as shown in figure 9(a). The cell size is freely adjustable from atomistic resolution to multiple unit cells depending on the accuracy required. The position of each macrocell p_mc is determined from the magnetic 'centre of mass' given by the expression

$$\begin{equation}p^{\alpha }_{{\rm mc}} = \frac {\sum _i^n \mu _i p_i^{\alpha }}{\sum _i^n \mu _i} \label {eq:macrocellpos} \end{equation} \tag{ 29 }$$

where n is the number of atoms in the macrocell, μ_i is the local (site-dependent) atomic spin moment and α represents the spatial dimension x, y, z. For a magnetic material with the same magnetic moment at each site, equation (29) corrects for partial occupation of a macrocell by using the mean atomic position as the origin of the macrocell dipole, as shown in figure 9(b). For a sample consisting of two materials with different atomic moments, the 'magnetic centre of mass' is closer to the atoms with the higher atomic moments, as shown in figure 9(c). This modified micromagnetic scheme gives a good approximation of the demagnetization field without having to use computationally costly atomistic resolution calculation of the demagnetization field.

The total moment in each macrocell m_mc is calculated from the vector sum of the atomic moments within each cell, given by

$$\begin{equation}m_{{\rm mc}}^{\alpha } = \sum _i^n \mu _i S_i^{\alpha }{\rm .} \end{equation} \tag{ 30 }$$

Depending on the particulars of the system, the macrocell moments can vary significantly depending on position, composition and temperature. At elevated temperatures close to the Curie point, the macrocell magnetization becomes small, and so the effects of the demagnetizing field are much less important. Similarly in compensated ferrimagnets consisting of two competing sublattices the overall macrocell magnetization can also be small again leading to a reduced influence of the demagnetizing field.

The demagnetization field within each macrocell p is given by

$$\begin{equation} {\mathbf {H}}_{{\rm demag}}^{{\rm mc},p} = \frac {\mu _0}{4\pi }\left (\sum _{p \ne q}\frac {3({\mathbf {m}_{{\rm mc}}}^q\boldsymbol {\cdot } \hat {\mathbf {r}})\hat {\mathbf {r}}-{\mathbf {m}_{{\rm mc}}}^q}{r^3}\right ) - \frac {\mu _0}{3}\frac {{\mathbf {m}_{{\rm mc}}}^p}{V_{{\rm mc}}^p}\label {eq:demag} \end{equation} \tag{ 31 }$$

where r is the separation between dipoles p and q, $\hat {\mathbf {r}}$ is a unit vector in the direction p→q, and $V_{{\rm mc}}^p$ is the volume of the macrocell p. The first term in equation (31) is the usual dipole term arising from all other macrocells in the system, while the second term is the self-demagnetization field of the macrocell, taken here as having a demagnetization factor 1/3. Strictly this is applicable only for the field at the centre of a cube. However, the non-uniformity of the field inside a uniformly magnetized cube is not large and the assumption of a uniform demagnetization field is a reasonable approximation. The self-demagnetization term is often neglected in the literature, but in fact is essential when calculating the field inside a magnetic material. Once the demagnetization field is calculated for each macrocell, this is applied uniformly to all atoms as an effective field within the macrocell. It should be noted however that the macrocell size cannot be larger than the smallest sample dimension, otherwise significant errors in the calculation of the demagnetizing field will be incurred.

The volume of the macrocell V_mc is an effective volume determined from the number of atoms in each cell and given by

$$\begin{equation}V_{{\rm mc}} = n^{{\rm a}}_{{\rm mc}} V_{{\rm atom}} = n^{{\rm a}}_{{\rm mc}} \frac {V_{{\rm uc}}}{n^{{\rm a}}_{{\rm uc}}} \label {eq:mc_volume} \end{equation} \tag{ 32 }$$

where $n^{{\rm a}}_{{\rm mc}}$ is the number of atoms in the macrocell, $n^{{\rm a}}_{{\rm uc}}$ is the number of atoms in the unit cell and V_uc is the volume of the unit cell. The macrocell volume is necessary to determine the magnetization (moment per volume) in the macrocell. For unit cells much smaller than the system size, equation (32) is a good approximation, however for a large unit cell with significant free space, for example a nanoparticle in vacuum, the free space contributes to the effective volume which reduces the effective macrocell volume.

5.4.1. Demagnetizing field of a platelet

To verify the implementation of the demagnetization field calculation it is necessary to compare the calculated fields with some analytic solution. Due to the complexity of demagnetization fields analytical solutions are only available for simple geometric shapes such cubes and cylinders [130], however for an infinite perpendicularly magnetized platelet the demagnetization field approaches the magnetic saturation − μ₀M_s. To test this limit we have calculated the demagnetizing field of a 20 nm × 20 nm × 1 nm platelet as shown in figure 10. In the centre of the film agreement with the analytic value is good, while at the edges the demagnetization field is reduced as expected.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

5.4.2. Performance characteristics

In micromagnetic simulations, calculation of the demagnetization field usually dominates the runtime of the code and generally it is preferable to have as large a cell size as possible. For atomistic calculations however, additional flexibility in the frequency of updates of the demagnetization field is permitted due to the short time steps used and the fact that the magnetization is generally a slowly varying property.

To investigate the effects of different macrocell sizes and the time taken between updates of the demagnetization field we have simulated hysteresis loops of a nanodot of diameter 40 nm and height of 1.4 nm. Figure 11(a) shows hysteresis loops calculated for different macrocell sizes for the nanodot. For most cell sizes the results of the calculation agree quite well, however, for a cell size of 4 unit cells, the calculated coercivity is significantly larger, owing to the creation of a flat macrocell (with dimensions 4 × 4 × 1 unit cells). This illustrates that for systems with small dimensions, extra care must be taken when specifying the macro cell size in order to avoid non-cubic cells. In general, the problem with asymmetric macrocells is not trivial to solve within the finite difference formalism, since the problem arises due to a modification of both the intracell and intercell contributions to the demagnetizing field.

Figure 11(b) shows the runtime for a single update of the demagnetizing field on a single CPU for different macrocell size discretizations. Noting the logarithmic scale for the simulation time, single unit cell discretizations are computationally costly while not giving significantly better results than larger macrocell discretizations. Although the demagnetization field calculation is an $n_{{\rm mc}}^2$ problem, it is possible to pre-calculate the distances between the macrocells at the cost of increased memory usage. Due to the computational cost of calculating the position vectors, this method is often much faster than the brute force calculation. However, due to the fact that memory usage increases proportionally to $n_{{\rm mc}}^2$, fine discretizations for large systems can require many GBs of memory.

By collating terms in equation (31) it is possible to construct the following matrix M_pq for each pairwise interaction:

$$\begin{eqnarray} \mathbf {M}_{pq} = \begin{bmatrix} (3r_x r_x-1)/r_{pq}^3 -1/3 & 3r_x r_y & 3r_xr_z \\ 3r_xr_y & (3r_yr_y-1)/r_{pq}^3 -1/3 & 3r_yr_z \\ 3r_xr_z & 3r_yr_z & (3r_zr_z-1)/r_{pq}^3 -1/3 \end{bmatrix}\nonumber \\ \end{eqnarray} \tag{ 33 }$$

where r_x, r_y, r_z are the components of the unit vector in the direction p→q, and r_pq is the separation of macrocells. Since the matrix is symmetric along the diagonal only six numbers need to be stored in memory. The total demagnetization field for each macrocell p is then given by:

$$\begin{equation} {\mathbf {H}}_{{\rm demag}}^{{\rm mc},p} = \frac {\mu _0}{4\pi } \left (\sum _{p \ne q}\mathbf {M}_{pq} \boldsymbol {\cdot } {\mathbf {m}_{{\rm mc}}}^q\right ) - \frac {\mu _0}{3}\frac {{\mathbf {m}_{{\rm mc}}}^p}{V_{{\rm mc}}^p}.\label {eq:demag-fast} \end{equation} \tag{ 34 }$$

The relative performance of the matrix optimization is plotted for comparison in figure 11(b), showing a significant reduction in runtime. Where the computer memory is sufficiently large, the recalculated matrix should always be employed for optimal performance.

In addition to variable macrocell sizes, due to the small time steps employed in atomistic models and that the magnetization is generally a slowly varying property, it is not always necessary to update the demagnetization fields every single time step. Hysteresis loops for different times between updates of the demagnetization field are plotted in figure 11(c). In general hysteresis calculations are sufficiently accurate with a picosecond update of the demagnetizing field, which significantly reduces the computational cost.

In general good accuracy for the demagnetizing field calculation can be achieved with coarse discretization and infrequent updates, but fast dynamics such as those induced by laser excitation require much faster updates, or simulation of domain wall processes in high anisotropy materials requires finer discretizations to achieve correct results.

5.4.3. Demagnetizing field in a prolate ellipsoid

Since the macrocell approach works well in platelets and nanodots, it is also interesting to apply the same method to a slightly more complex system: a prolate ellipsoid. An ellipsoid adds an effective shape anisotropy due to the demagnetization field, and so for a particle with uniaxial magnetocrystalline anisotropy along the elongated direction (z), the calculated coercivity should increase according to the difference in the demagnetization field along x and z, given by:

$$\begin{equation}H_{{\rm dm}}^{{\rm shape}} = +\Delta N \mu _{0} {M_{{\rm s}}} \end{equation} \tag{ 35 }$$

where ΔN = N_z − N_x. The demagnetizing factors N_x, N_y, and N_z are known analytically for various ellipticities [131], and here we assume a/c = b/c = 0.5, where a, b, and c are the extent of the ellipsoid along x, y and z respectively.

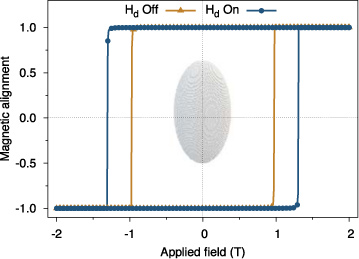
To verify the macrocell approach gives the same expected increase of the coercivity we have simulated a generic ferromagnet with atomic moment 1.5 μ_B, an FCC crystal structure with lattice spacing 3.54 Å and anisotropy field of H_a = 1 T. The particle is cut from the lattice in the shape of an ellipsoid, of diameter 10 nm and height of 20 nm, as shown inset in figure 12. A macrocell size of 2 unit cells is used, which is updated every 100 time steps (0.1 ps).

Zoom In Zoom Out Reset image size

As expected the coercivity increases due to the shape anisotropy. From [131] the expected increase in the coercivity is $H_{{\rm dm}}^{{\rm shape}}=0.37\ {\rm T}$ which compares well to the simulated increase of 0.33 T.

The most trivial form of parallelism is batch or statistical, where the statistical properties of a system are determined by a series of independent calculations, each of which can be run in parallel. Statistical parallelism has the prime advantage that the division of work leads to an ideal scaling behaviour, since each of the runs are entirely independent and require no intercommunication.

In magnetic simulations, the most common applications of statistical parallelism are sweeps of the parameter space for a particular system, or in determining thermodynamic averages. For the former, a given system is calculated for different values of key parameters, for example, anisotropy or exchange constants; for the latter, the same system is simulated, but each run is given a different seed for the random number generator. This leads to a different thermodynamic evolution, which can provide information about the statistical behaviour of the system. It should be noted that the correct seeding of the random number generator, where a number of uncorrelated random number sequences are generated, is quite complex [108]. For magnetic simulations, the chaotic nature of the system, whereby a small change in the time evolution rapidly leads to a significantly different result, means that crude sequential number seeding is quite satisfactory.

Although statistical parallelism is useful for some types of simulation, it has one significant limitation: it can only be applied to relatively small systems, as the entire problem must be solved on a single processor. For larger systems it is necessary to divide the system into smaller parts for parallel execution. The most efficient method for such parallelization is generally geometric decomposition, where the space is divided into cells, and each processor is assigned a cell to simulate. If well implemented, geometric decomposition can be scaled to run on thousands of CPUs, and this is one of the key aims of our implementation.

The starting point for geometric decomposition is efficiently dividing the space to run on N_CPU CPUs. In order to achieve this, we have devised an algorithm which takes into account the physical system dimensions and which searches for a solution where

$$\begin{equation}\label {eqn:nxnynz} n_x \cdot n_y \cdot n_z = N_{{\rm CPU}} \end{equation} \tag{ C.1 }$$

while minimizing the surface to volume ratio. If the dimensions of the overall system are given by l_x, l_y, and l_z, then the volume of each cell is:

$$\begin{equation}V_{{\rm cell}} = \frac {l_x}{n_x} \cdot \frac {l_y}{n_y} \cdot \frac {l_z}{n_z} \end{equation} \tag{ C.2 }$$

and the surface area of each cell is:

$$\begin{equation}A_{{\rm cell}} = 2\left [\frac {l_x l_y}{n_x n_y} + \frac {l_y l_z}{n_y n_z} + \frac {l_x l_z}{n_x n_z} \right ]. \end{equation} \tag{ C.3 }$$

The surface to volume ratio is then given by:

$$\begin{equation} \frac {A_{{\rm cell}}}{V_{{\rm cell}}} = 2\left [\frac {n_z}{l_z} + \frac {n_y}{l_y} + \frac {n_x}{l_x} \right ]{\rm .} \end{equation} \tag{ C.4 }$$

It is clear that the minimum in the surface to volume ratio occurs for n_α/l_α = 1 for all three dimensions, essentially showing that longer dimensions parallelize better with more CPUs.

Given that the dimensions of the system are fixed, the only free variables are the number of CPUs in each dimension, n_x, n_y, and n_z. These are further constrained by equation (C.1). In order to find the optimal solution for a given number of CPUs, the starting point is $n_{\alpha } = \frac {l_x}{\sqrt {N_{{\rm CPU}}}}$. Exact solutions for n_x, n_y and n_z are then searched for and the one with the lowest surface to volume ratio is selected. This approach is very flexible and allows for efficient decomposition for any number of CPUs. The only problematic solution is for prime numbers of CPUs, where only one exact solution exists, though this is a rare occurrence for large numbers of CPUs. A visualization of a cubic system decomposed into 48 blocks is shown in figure 15.

Zoom In Zoom Out Reset image size

Having decomposed the system, each CPU is allocated a cell which defines its own spatial domain. In order to maintain maximum scalability, each CPU generates its own portion of the complete system, and all associated data. This has the advantage of minimizing the memory footprint and also parallelizing the system creation, which can become a significant bottleneck for very large numbers of processors. Once the local atoms have been generated it is necessary to know which atoms on remote processors (halo atoms) are potentially interacting with atoms on the local processor (boundary atoms), as well as which atoms are interacting locally only (core atoms). This essentially defines three distinct regions, as shown schematically in figure 16.

Zoom In Zoom Out Reset image size

The maximum interaction range of the atoms is known globally, and so provided all atoms in this range are included, generation of the neighbour list is trivially the same as the serial case. In practice this is implemented by a global broadcast of each processor's domain, i.e., which regions of space are 'owned' by each processor. Each processor then looks at each atom in its boundary region, and then dispatches a copy of the atom to the appropriate neighbouring processors. This method has the advantage that it is quite general, and can be applied to any decomposition method, not necessarily cubes. At this point parallel periodic boundary conditions are easily implemented in the same manner, by copying atoms at the edge of the system to the desired processors. Once all boundary atoms have been sent, and all halo atoms have been received, the neighbour list is generated in the usual fashion with a linked-cell algorithm. After the actual neighbour list has been generated, it is likely that some of the copied halo atoms are in fact not needed, and so these atoms are deleted. Similarly some atoms in the in the boundary region may not interact with the halo, and these atoms are re-assigned to the core region. Following this book-keeping exercise, parallel simulation of the system can begin.

The method we have adopted for parallel simulation of the system makes use of latency hiding, where requests for data from other processors are made prior to a locally compute-intensive period, after which the requested data should have arrived. Such latency hiding is an important consideration when running the code on many processors. In practice atoms on each processor are ordered according to their interaction classification, i.e.: core; boundary; and finally halo atoms. The integration of the system proceeds as follows:

• A request is made for all halo data from other processors.
• The core region is then integrated.
• If the halo data has not arrived, then wait for it.
• Integrate the boundary region.
• Global synchronization.

The parallel integration is repeated the desired number of times during the simulation.

For continuous systems, geometric decomposition provides an efficient way of parallelizing the calculation. However, for sparse systems geometric decomposition can be inefficient due to poor load balancing, where some processors have many more atoms than others. This means some processors spend a significant amount of time waiting for others to complete the integration step, leading to a reduction in scalability. In magnetism, such systems are typically granular, consisting of a small number of grains. One solution to sparse systems is to utilize a replicated data approach, where each processor has a complete copy of all data, similar to the statistical parallelism method. Each processor then simulates (1/n_cpu)th of the total system, without any constraints on spatial locality. The atoms are classified in a similar way to the geometric decomposition approach, as core, boundary, and halo, and integrated in exactly the same way.

The principal disadvantages of the replicated data approach are the increased memory footprint (each processor must generate a complete copy of the system), and the tendency to have a high proportion of boundary spins. The latter can be mitigated by re-ordering spins in memory to ensure some degree of spatial locality. For granular systems this is fact trivial, since the assignment of each spin to a grain provides the necessary geometric information, and so the spins are ordered by a unique grain identification, which is also spatially correlated. In addition to its use in simulation of sparse systems, the replicated data approach is also the strategy adopted for the parallel calculation of the long-ranged demagnetization fields. The method for the parallel code is identical to that described earlier, where the spins are allocated to macrocells which then interact with each other. Since the calculation of the demagnetization field in each cell requires knowledge of all other cells, replicated data is the logical choice for the parallelization. The demagnetization field calculation proceeds as follows:

• The macrocell moments are initialized to zero on all processors.
• Each processor determines the contribution of its spins to each macrocell.
• The macrocell moments are summed globally, so that each processor has a complete copy of the macrocell magnetizations.
• Each processor calculates the demagnetization field only for macrocells which contain local spins.
• The local demagnetization field on each spin is determined from its macrocell demagnetization field.

This approach leads to excellent scaling, as for reasonable macrocell sizes the communication costs are minimal, and for ≫1 macrocell per processor the method scales linearly with n_cpu. Fine macrocell discretizations (≪27 unit cells/macrocell) can lead to significant memory and computation costs, but in general this is unnecessary for most atomic scale calculations.

Zoom In Zoom Out Reset image size

VAMPIRE has already been shown to scale well for a generic system with nearest neighbour exchange interactions, but in order to verify the general usefulness of the parallelization we have also considered an extended system including the demagnetization field calculation, and a system using ab initio parameters for FePt [29] which includes a long-ranged exchange interaction extending over several unit cells, as shown in figure 17.

The simulations in figure 17(a) including the demagnetizing fields use a 2 × 2 unit cell macrocell size, updated every 10 steps, for system sizes of approximately 10⁴, 10⁵ and 10⁶ spins respectively. The high spatial and temporal resolution of the demagnetizing field calculation are in some sense a worst case scenario as these are probably not needed for most problems, and so for these simulations, calculation of the demagnetizing fields dominates the run time. Nevertheless, the scaling of the code remains very good, showing the effectiveness of the parallelization of the demagnetizing field calculation. For small system sizes the scaling breaks down as the number of macrocells approaches the number of processors. Here the scaling is limited by the time required to update all of the cell magnetizations and the time required to calculate the contributions of the reduced number of local macrocells. For all problem sizes scaling begins to reduce somewhat due to limitations in the network bandwidth.

For the long-ranged exchange interactions shown in figure 17(b) the scaling is only good within a single node (up to 8 processors). Above that, the larger the system the worse the scaling. This arises due to the large amount of data which has to be shared between processors. For the long-ranged exchange interaction, each atom to be simulated must know the spin configurations of over 1000 neighbouring atoms. In a parallel simulation these spin directions must be passed between processors twice per time step, which is a bandwidth intensive operation. Thus, the reduced scaling, particularly with larger system size, is due to saturation of the network link. Due to the long range nature of the exchange interaction, memory use also becomes an issue in terms of storing the neighbour list. For the largest simulation size of around 1.6 × 10⁶ atoms, 33GB of RAM is required to store all the interactions. However, due to the parallel system generation this divides nicely between all of the processors, so the memory required per processor is quite reasonable for larger numbers of processors.