Abstract
A full dynamical simulation shows that the charge transfer between the amine and the phenyl moieties of the cation of the bifunctional molecule 2-phenylethyl-N,N-dimethylamine can be induced and subsequently probed by two ultrashort photoionizations. The first ionization of the pump–probe scheme is by a 1.5 fs UV or 6 fs IR pulse that ionizes the neutral. The pump pulse can be tailored to produce a coherent superposition of the electronic states of the cation that differ in their energy and spatial localization of their electron density. The time-dependent amplitudes of the states of the superposition means that the state of the cation is not stationary and we show that it is beating between the two ends of the molecule. This beating is next probed by a second attosecond XUV pulse. The ultrafast photoionization of the cation to the dication probes the spatial charge reorganization in the cation. We use the computed time-dependent molecular frame photoelectron angular distributions as a quantitative measure of the charge migration. The computation of the dynamics are carried out by a coupled equation scheme that includes an electronic manifold for the three charge states: neutral, cation and dication, the coupling to the ionization continua of the cation and the dication and the dynamics induced by the pump and the probe pulses.
Export citation and abstract BibTeX RIS
1. Introduction
The recent developments in the generation of optical attopulses [1–6] suggest that it will soon become experimentally feasible to induce and directly probe ultrafast charge transfer between the end moieties of bifunctional molecules using two ultrafast ionizations [7, 8]. The suggestion for a fast to ultrafast charge migration between the two ends of a bifunctional molecule goes back to the pioneering experiments of Weinkauf and Schlag on the selective prompt fragmentation at the nitrogen end of tetrapeptide cations resulting from a local ionization at the carboxylic aromatic chromophore [9]. The prompt and selective fragmentation was interpreted as resulting for the ultrafast migration to the amine end of the hole created by ionization at the chromophore end [9]. The possibility of charge induced reactivity has since received a lot of attention and has been the subject of several theoretical investigations [7, 10–24].
Recently, an ultrafast pump–probe experimental study on an amino-acid provided evidence for an ultrafast charge migration on a fs time-scale [25]. In this experiment, as in the initial Weinkauf–Schlag experiment and recent ones on small diatomic and medium size molecules [26–32], the probing of the charge motion is indirect, through the monitoring of the ionic fragments of the system, which implies a coupling between the electronic and nuclear degrees of freedom.
Our aim is to demonstrate the existence of a purely electronic time-scale [7], before the coupling to the nuclei takes place. This is a pre-Born–Oppenheimer regime where the electronic states are not stationary. Subsequently we aim to understand how controlling this purely electronic motion can be used to trigger a selective motion of the nuclei thereby implementing charge directed reactivity. We have proposed that the probing of the ultrafast electronic reorganization in a tetrapeptide cation was feasible using a pump–probe scheme where one ultrashort pulse photoionizes the neutral to the cation and a second ultrashort pulse probes the cation by ionizing it to the dication [8]. This early study, and the more recent ones [13, 33] show that time-resolved photoelectron spectra and molecular frame photoelectron angular distributions (MFPAD) are reliable probes of the time-dependent localization of the electron density. These earlier studies use the approximation of a sudden ionization and do not take into account the dynamics that occurs during the photoionization step. The sudden approximation limit is expected to be valid when two ultrashort UV or EUV pulses are used to pump and probe the system. Up to now however, the available experimental set-ups are typically using an IR-UV or an UV-IR scheme. In the case of an IR pulse, the approximation of a one photon sudden ionization breaks down and one needs to include the ionization dynamics in calculation. We have recently developed a coupled equation scheme for computing the electronic dynamics in the neutral and cation subspaces in a pump–probe scheme as well as the photoelectron spectra and MFPAD as a function of the pump–probe delay [34]. This formalism allows us to fully take into account the dynamics in the electronic states that occurs during the photoionization process, which is particularly important in the case when one of the pulses is an IR pulse.
We use here this formalism to study the electronic dynamics in the lowest energy extended conformer of the bifunctional 2-phenylethyl-N,N-dimethylamine (PENNA) molecule. PENNA is a precursor of neurotransmitter that possesses a phenyl moiety linked to a dimethyl amine by an ethyl spacer. PENNA can therefore be viewed as a model for the larger tetrapeptide cations. Indeed PENNA was investigated by Weinkauf and coworkers [35–37] who provided evidence for an ultrafast charge migration (upper bound 80 fs ± 24 fs [37]) between the two end moieties in this system. From a computational point of view, its smaller size makes PENNA more suitable for carrying out accurate studies. The hole motion in the bound electronic states of the PENNA cation resulting from the sudden ionization of a molecular orbital of the neutral has previously been investigated at the equilibrium geometry of the neutral by Cederbaum and coworkers [38, 39] using the algebraic diagrammatic construction (ADC) propagator approach.
Our study goes beyond the sudden approximation ionization limit and describes the electronic dynamics occurring during a full pump–probe experiment, starting from the ground state (GS) of the neutral and ending in the GS and excited states of the dication, as schematically shown in figure 1. We use the partitioning technique within a coupled equation scheme to describe the dynamics in the neutral, cation and dication subspaces that results from the interaction of the molecule with the strong pump and the probe pulses to all orders. The partitioning formalism is outlined in section 2 with technical details of the methodology given in the supplementary materials (available from stacks.iop.org/JPhysB/47/124011/mmedia). In section 3, we give details on the PENNA electronic structure. Several conformers coexist at room temperature. In our computations, as well as previously reported [36, 38], the extended antisymmetric conformer is found to be the lowest in energy and the computations reported here are for its geometry. Time-dependent density functional theory (TD-DFT) is used to compute the manifolds of field-free electronic states of the three species (neutral, cation and dication) and their expansion in Kohn–Sham determinants is used as a basis set for the coupled equation scheme. The accuracy of this computational level is supported by comparison with multi-configuration complete active space-self-consistent field (CAS-SCF) computations of the lowest excited states of each species as well as with the available experimental results [35, 37, 40]. TD-DFT is one of the few methods that allows computation of a band of states of the neutral that is wide enough in energy to describe realistically the multiphoton-ionization process by an IR pulse.
Figure 1. Scheme of the simulated pump–probe experiment for an oriented PENNA molecule. (a) A first pulse is used to ionize the ground state of the system and launch the dynamics in the cationic states. This dynamics is subsequently probed by a second probe pulse at a pump–probe delay, τ. (b) Energy level diagram of the 30 neutral, ten cationic and two dicationic electronic states used for the dynamical simulation. Each electronic state is written as an expansion of Kohn–Sham determinants. Each cationic and dicationic state of the core carries an ionization continuum. The arrows indicate which photoionization channels are open for the photoionization of the neutral ground state and for the photoionization of the cationic states to the two dicationic states. All the photoionization channels are open but for clarity, in the case of the cation, we only show arrows for the three lowest excited states.
Download figure:
Standard image High-resolution imagePENNA is an ideal system to induce and probe charge motion because its GS cation has a hole localized on the amine end while in the next two lowest electronic states, 0.6 eV and 1.0 eV respectively above the GS, the hole is localized on the phenyl group. In a coherent superposition of these three states, the electronic density beats between the two ends on a fs time-scale that corresponds to their energy gap. We find that the GS of the dication is a triplet diradical, with one hole on the phenyl and one hole on the nitrogen end. It is almost degenerate (0.26 eV) with the first triplet excited state, which has also a hole on the phenyl and the nitrogen ends. These two states are well separated from higher triplet excited states and the singlet manifold. There are therefore optimal final states for probing the motion of the electronic density in the cation.
The examples presented in section 4 show that both a UV and an IR ultrashort photoionization of the oriented neutral molecule lead to a beating motion of the electronic density between the two ends of cation. This motion is reflected in the oscillating of the component of the dipole moment of the cation parallel to the molecular backbone. Photoionization by a short XUV probe pulse to the dication states reflects the spatial localization of the electronic density at the time of ionization. We first report on the electronic dynamics induced by a resonant 1.4 fs UV pump pulse that ionizes the neutral and builds a clean superposition of the three lowest states of the cation. The charge migration is then probed by a single XUV attosecond pulse of 400 as that photoionizes the cation almost instantaneously. We next show that a multiphoton ionization by a 6 fs IR pump pulse can be used to induce robust charge migration in the states of the cation, even though in addition to the three lowest states of the cation, higher electronic states are also accessed but photoionize much faster than the lowest states so that they are not significantly populated at the end of the pump pulse. Furthermore, we show that the charge migration can be probed efficiently with a longer 1.4 fs XUV probe pulse. In this second example, both the pump and the probe pulses are within actual experimental capabilities.
2. Electronic dynamics by a partitioning and coupled equation scheme
The description of the electronic dynamics in strong field is challenging and a variety of methods were attempted. These include grid methods [41–44], many body S matrix theory [45], multiconfiguration time-dependent Hartree–Fock [46–48] and time-dependent multi-configuration self-consistent field [49–51]. The more accurate methods are often limited to small molecules and electronic dynamics for frozen nuclei but some also include the nuclear dynamics [41, 48, 52–55]. Direct TD-DFT [56, 57] allows simulation of the ultrafast electron-nuclear dynamics at the mean field level using Ehrenfest dynamics for the centroid motion of the nuclei.
Here we use a coupled equation scheme based on the partitioning technique [27, 55, 58–62]. We compute the purely electronic dynamics for a fixed position of the nuclei, clamped at equilibrium geometry of the neutral GS. We therefore describe the purely electronic dynamics that takes place before the onset of significant nuclei motion. On the ultrashort time-scale of 10–15 fs investigated here, we expect that the dephasing of the electronic wave packet due to the coupling with nuclear motion will remain small. We already applied this method to describe electronic dynamics in the neutral and ionization in strong field for the LiH molecule. Here we show that for medium sized polyatomic molecules the partitioning technique and the coupled equation scheme can be efficiently extended to three orthogonal and physically distinct subspaces, the bound states of the neutral, and the ionized states of the cation and dication, as shown in figure 1.
The electronic Hamiltonian, H(t), includes the pump and the probe ionizing pulses. The coupling with the electric field, E(t), is described in the dipole approximation and included to all orders
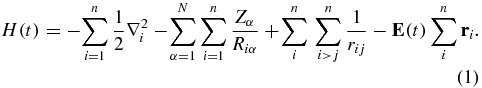
Atomic units are used throughout the paper. In equation (1), N is the number of nuclei, n the number of electrons, R the fixed nuclear coordinates and r the electronic ones. The time-dependent electric field of the pump and probe pulses is given by
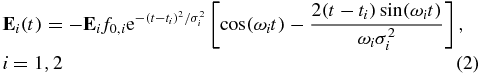
where Ei is the orientation of the electric field in the laboratory frame and f0, i its magnitude. σi is the width of the Gaussian envelope and ti the time at which it is centred. The pulse wavelength is given by ωi.
We solve numerically the time-dependent Schrödinger equation using the partitioning technique. We need to partition the total space into three orthogonal subspaces. The manifold of the electronic states of the neutral, Q, the manifold of cationic states of PENNA+ populated by the pump ionizing pulse, P1, and the manifold of the states of the dication, PENNA2+, P2, which are accessed by the probe ionizing pulse are shown in figure 1(b). As long as the UV field strength is not very high one can exclude higher ionized states and then 1 = Q+P1+P2.
The time evolution of the different components of the wave function of the system, QΨ(t), P1Ψ(t), and P2Ψ(t), is then described by the following set of coupled equations. A detailed derivation can be found in the supplementary material (available from stacks.iop.org/JPhysB/47/124011/mmedia)
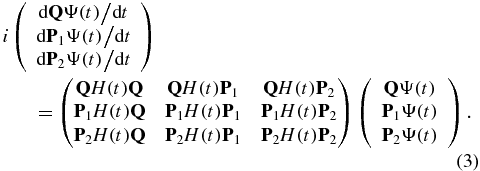
In equation (3), the dipole coupling induces electronic dynamics within each subspace, through the diagonal matrices, QH(t)Q, P1H(t)P1 and P2H(t)P2. The main role of the coupling induced by the field is the photoionization process that couples Q and P1 and P1 and P2 through the matrices QH(t)P1 and P1H(t)P2. We assume that there is no direct coupling between the neutral and dication states, QH(t)P2 = 0, which is realistic for the strengths and the wavelengths of the two pulses that we use in the examples below. We therefore describe a sequential double ionization process, where a first pulse ionizes the neutral to the cation and after a delay, τ, a second pulse ionizes the coherent superposition of states of the cation resulting from the first ionization to the dication. In the results presented below, the two pulses do not overlap in time.
The projector on the bound subspace, 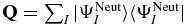 , is composed of the field-free electronic states,
, is composed of the field-free electronic states,  , of PENNA. The field-free states are the eigenstates of the field-free Hamiltonian,
, of PENNA. The field-free states are the eigenstates of the field-free Hamiltonian, 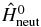 , which is the time-independent part of the total Hamiltonian of equation (1) and these states need only to be computed once. The time-dependent Hamiltonian in the subspace, Q, can be expressed as follows:
, which is the time-independent part of the total Hamiltonian of equation (1) and these states need only to be computed once. The time-dependent Hamiltonian in the subspace, Q, can be expressed as follows:
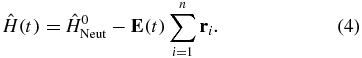
The QH(t)Q term in equation (3) describes the electronic dynamics in the bound states. It is non-diagonal since the electric field induces coupling between the states. The coupling matrix element between two field-free states I and J is given by 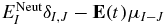 , where
, where 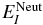 is the field-free energy of the electronic state I and μI − J is the transition dipole moments between the states I and J.
is the field-free energy of the electronic state I and μI − J is the transition dipole moments between the states I and J.
The projector of the singly ionized states,  , is composed of anti-symmetrized products of the field-free cationic electronic states of PENNA+,
, is composed of anti-symmetrized products of the field-free cationic electronic states of PENNA+, , and the wavefunction of the ionized electron,
, and the wavefunction of the ionized electron,  , that is normalized within a box of size, L, and orthogonalized to the MOs of the neutral [63–65] thereby ensuring QP1 = 0. We discretized the ionization continua so that each ionized electron,
, that is normalized within a box of size, L, and orthogonalized to the MOs of the neutral [63–65] thereby ensuring QP1 = 0. We discretized the ionization continua so that each ionized electron,  , is defined by an energy |k1|2/2 and an orientation Ω1 that is defined by a set of points in 3D. This spherical grid is more efficient than sampling on a Cartesian grid. The n electron Hamiltonian of the ionized states is assumed to be separable into a n−1 cationic Hamiltonian and the one electron Hamiltonian of the ionized electron
, is defined by an energy |k1|2/2 and an orientation Ω1 that is defined by a set of points in 3D. This spherical grid is more efficient than sampling on a Cartesian grid. The n electron Hamiltonian of the ionized states is assumed to be separable into a n−1 cationic Hamiltonian and the one electron Hamiltonian of the ionized electron
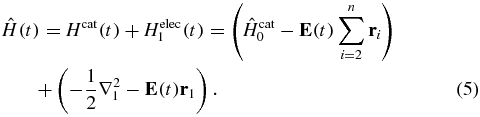
In equation (5), the coupling between the cation and the ionized electron is neglected [66, 67]. This implies that the multipolar coupling between the electron and the remaining core is not inducing internal states dynamics of the cation. The cation-ionizing electron coupling is expected to play a more important role in tunnel ionization [68, 69] than in the photoionization processes considered here. The field-induced dynamics in the cation ionized states P1 is described by the matrix P1H(t)P1:
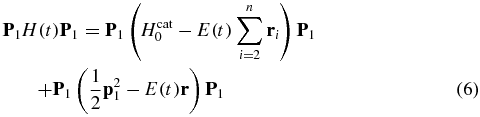
P1H(t)P1 is highly non-diagonal due to the dipole coupling during the pulse. In the first term on the rhs of equation (6) the dipole coupling affects the bound states of the cation and is computed from the transition dipole matrix elements between the field-free states. The second term can be brought to a diagonal form using a time-dependent unitary transformation [34], see the supplementary material (available from stacks.iop.org/JPhysB/47/124011/mmedia) for more details.
The doubly ionized states are defined as anti-symmetrized products of the field-free electronic states of the PENNA2+ dication, 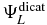 , and two plane waves,
, and two plane waves, 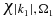 , and
, and  , normalized and orthogonalized to the MOs of the neutral to ensure P1P2 = 0 and QP2 = 0. The projector P2 is written
, normalized and orthogonalized to the MOs of the neutral to ensure P1P2 = 0 and QP2 = 0. The projector P2 is written  . We further assume that the n electron Hamiltonian is separable into the time-dependent Hamiltonian of the dication and two one electron Hamiltonians for the ionized electrons
. We further assume that the n electron Hamiltonian is separable into the time-dependent Hamiltonian of the dication and two one electron Hamiltonians for the ionized electrons
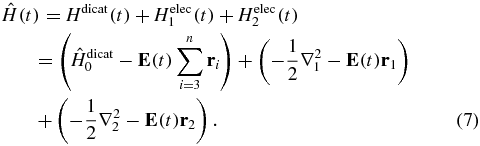
The matrix P2H(t)P2 is of a form similar to that of P1H(t)P1 discussed above and also highly non-diagonal because of the dipole coupling:
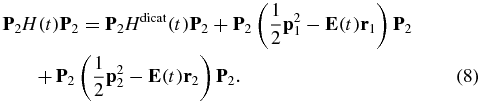
The last two terms on the rhs of equation (8) represent the first and second ionizations that are separated by a delay time τ. These terms can be brought to a diagonal form using a double time-dependent unitary transformation, see the supplementary material (available from stacks.iop.org/JPhysB/47/124011/mmedia) for more details. The dipole non-diagonal terms in the first term are computed using the transition dipole matrix elements between the field-free states of the dication.
The three subspaces, Q, P1 and P2 are coupled by the time-dependent electric field, which is represented in equation (3) by the rectangular matrices QH(t)P1 and P1H(t)P2. There is no direct coupling from the neutral to the dication since such ionization does not take place at the field strengths used in the simulations below. The matrix QH(t)P1 accounts for the photoionization of the neutral states and the matrix coupling elements can be reduced to a one electron integral,  , involving the dipole coupling between an orthogonalized plane wave and the Dyson orbital [33, 70–73],
, involving the dipole coupling between an orthogonalized plane wave and the Dyson orbital [33, 70–73], 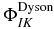 , computed as the overlap between the n electron state of the neutral, I and the n−1 electron state of the cation, K [74].
, computed as the overlap between the n electron state of the neutral, I and the n−1 electron state of the cation, K [74]. 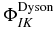 represents the wavefunction of the ionized electron. The photoionization of the cationic states is described by P1H(t)P2. The coupling matrix elements are given by
represents the wavefunction of the ionized electron. The photoionization of the cationic states is described by P1H(t)P2. The coupling matrix elements are given by  where
where  is the Dyson orbital between the cationic state K and the dicationic state L.
is the Dyson orbital between the cationic state K and the dicationic state L.
We integrate numerically the time-dependent Schrödinger equation using a sixth order Runge–Kutta algorithm and an electronic basis of 30 neutral states, ten cationic states and two dicationic states. Note that the dimension of the P1 and P2 subspaces are much larger than that of Q since in addition to the bound states of the cation and the dication, the P1 and P2 subspaces include one and two discretize continuum respectively. For each state of the cation, we use a grid of 900 points for the continuum states 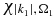 and 900 grid points for
and 900 grid points for 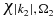 . The electronic structure of the neutral and two charge states of the PENNA molecule is detailed in section 3 below.
. The electronic structure of the neutral and two charge states of the PENNA molecule is detailed in section 3 below.
The motion of the electron density in the cation states is reflected by the oscillations of the component of the mean value of the dipole moment along the molecular axis [32, 33, 70, 75–77]. Its expression is given by:
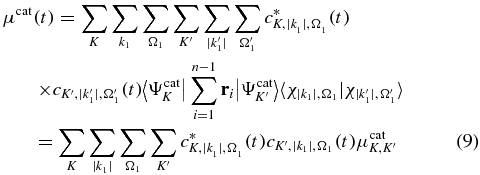
where  is the dipole moment between the two cationic states K and K'.
is the dipole moment between the two cationic states K and K'.
The photoelectron spectra shown below are computed by integrating the population of the ionized states, 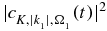 at the end of the pulse over all the orientations for each kinetic energy. We also report below heatmaps of the anisotropy parameter,
at the end of the pulse over all the orientations for each kinetic energy. We also report below heatmaps of the anisotropy parameter, 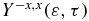 resulting from the photoionization by the second pulse.
resulting from the photoionization by the second pulse.  is defined as:
is defined as:
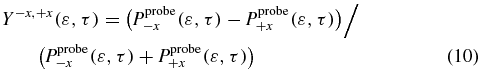
where  and
and  are given by
are given by
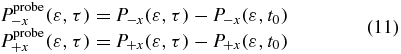
t0 is the time at the end of the first pulse.  and
and  represent the yield of the ionized electrons by the second pulse in the +x and −x direction, at the amine end and at the phenyl end respectively, removing the ionization background by the pump pulse. P+x(ε, τ) and P−x(ε, τ) are the yields in ionized electrons with a kinetic energy ε in the direction +x and −x for a pump–probe delay τ. The yields are computed by integration of the populations,
represent the yield of the ionized electrons by the second pulse in the +x and −x direction, at the amine end and at the phenyl end respectively, removing the ionization background by the pump pulse. P+x(ε, τ) and P−x(ε, τ) are the yields in ionized electrons with a kinetic energy ε in the direction +x and −x for a pump–probe delay τ. The yields are computed by integration of the populations, 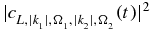 , in the states of the dication at a kinetic energy,
, in the states of the dication at a kinetic energy, 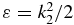 , for positive (P+x(ε, τ)) and negative, P−x(ε, τ), values of the x component of the momentum vector corresponding to Ω2. We report in section 4 below heatmaps of the anisotropy parameter,
, for positive (P+x(ε, τ)) and negative, P−x(ε, τ), values of the x component of the momentum vector corresponding to Ω2. We report in section 4 below heatmaps of the anisotropy parameter,  , computed as a function of the delay time, τ, and kinetic energy, ε.
, computed as a function of the delay time, τ, and kinetic energy, ε.
3. Electronic structure of the different charge states of the PENNA molecule
Several conformers (folded and unfolded) of PENNA were previously reported to coexist at room temperature [36]. The electronic structure of the neutral PENNA was computed for the non-symmetric unfolded anti conformer. In this study, we use the density functional with the long range corrected wB97xD functional [78] and the 6–311++G(d,p) basis set in the implementation of the quantum chemistry suites of programs Gaussian 09 [79]. At this level, we find that the extended non-symmetric conformer is the lowest in energy, in agreement with [36]. Three other stable conformers, two extended and one folded are found within 400 cm−1 above the most stable one, also in agreement with the results of [36]. The geometries of these four conformers, as well as the values of their permanent dipole moments, are reported in figure S1 and table S1 of the supplementary material (available from stacks.iop.org/JPhysB/47/124011/mmedia). All four conformers will coexist at room temperature. They have large permanent dipole moments and can be oriented in a strong field [80, 81]. The total dipole moment of the extended conformers (0.67, 0.72 and 0.62 au) are about two times larger than for the folded conformer (0.32 au). In the rest of this study, we report results for the equilibrium geometry of the most stable extended conformer shown in figure 1(a).
Isoamplitude contours of the three highest occupied Kohn–Sham orbitals: HOMO, HOMO-1 and HOMO-2 are shown in figure 2(a). The HOMO is localized on the amine part while the HOMO-1 and HOMO-2 are π type orbitals localized on the phenyl ring, separated by 0.3 eV. The gap between HOMO and HOMO-1 is 0.69 eV. In HOMO-1, the density localized on the phenyl has a nodal plane parallel to the molecular backbone while the nodal plane on the phenyl group in HOMO-2 is perpendicular to the molecular backbone. These three orbitals are separated from the lower occupied MOs by more than 3 eV.
Figure 2. (a) Isoamplitude contours (0.02 Å−3) of the three highest occupied Kohn–Sham orbitals of the ground state of PENNA at the equilibrium geometry. The positive amplitudes are in yellow and the negative in blue. (b) Dyson orbitals for the ionization of the ground state of the neutral to the three lowest states of the cation. The same isoamplitude contour of 0.02 Å−3 is used for the Dyson orbitals. (c) Dyson orbitals for the ionization of the three lowest states of the cation to the ground and first excited states of the dication.
Download figure:
Standard image High-resolution imageThe TD-DFT [82] excitation energies of the lowest excited states of the neutral and two charge states of PENNA, computed at the equilibrium geometry of the neutral GS with the same basis set, are reported in table 1, as well as the values of their permanent dipoles.
Table 1. Excitation energies, ΔE in eV, and permanent dipole moments along the x-direction, μx, (parallel to the molecular backbone) of the five lowest states in PENNA, PENNA+ and PENNA2+ computed in TD-DFT with the wB97xD functional and the 6–311++G(d,p) basis set.
| Neutral | Cation | Dication | ||||
|---|---|---|---|---|---|---|
| ΔE | µx (au) | ΔE | µx (au) | ΔE | µx (au) | |
| GS | 0.00 | −0.35 | 0.00 | −5.48 | 0.00 | −2.33 |
| 1ES | 5.45 | −1.85 | 0.62 | 4.35 | 0.25 | −2.01 |
| 2ES | 5.70 | 1.42 | 0.99 | 3.81 | ||
| 3ES | 6.09 | −1.44 | 3.05 | 3.38 | ||
| 4ES | 6.29 | −0.93 | 3.14 | 5.89 | ||
The electronic structure of cation and its excited states were computed using a multi-configuration CAS-SCF (Molpro) [83] with the same basis set 6–311++G(d,p). At the state average CAS-SCF level, a double weight is given to the GS compared to the two lowest excited states. The active space comprises eleven electrons and ten orbitals. The CAS-SCF excitation energies, reported in table 2, are in good agreement with the TD-DFT ones and the experimental data. Furthermore, we observe an excellent agreement between CASSCF and TD-DFT for the transition dipole moments. The computed vertical IP for the ionization of the neutral at CAS-SCF and DFT (table 3) levels are in good agreement with the experimental vertical IP [40].
Table 2. Excitation energies (ΔE in eV, experimental [40] and computed), dipole moments (au) and transition dipole moments (au) along the x- and z-directions in the molecular frame computed at CAS-SCF and TD-DFT levels.
| Experimental | CAS-SCF | TDDFT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ΔE | ΔE | μx | 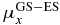 |
μz | 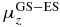 |
ΔE | μx | 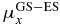 |
μz |  |
|
| GS | −4.64 | 0.39 | −5.48 | 0.68 | |||||||
| 1ES | 0.60 | 0.61 | 3.97 | 1.29 | 0.36 | 0.02 | 0.62 | 4.35 | 1.29 | 0.87 | −0.04 |
| 2ES | 0.92 | 0.82 | 4.12 | −0.56 | 0.34 | 0.01 | 0.99 | 3.81 | −0.50 | 0.63 | 0.02 |
Table 3. Comparison of the computed vertical ionization potential (IP in eV) in DFT and CAS-SCF with the experimental vertical IP [40].
| wB97xD ΔSCF IP | CAS ΔSCF IP | Experimental | |
|---|---|---|---|
| Neutral-cation | 8.18 | 8.14 | 8.35 ± 0.14 |
| Cation-dication | 11.94 | 11.46 |
In the dynamical simulations, we used the TD-DFT excited states expressed as expansions of Kohn–Sham determinants. TD-DFT is one of the few methods allowing computing the large band of electronic states required to describe the IR pumping of this relatively large molecule. A band of 30 excited states of the neutral was used to describe the bound subspace. It was kept the same throughout.
There is very little electronic relaxation in the lowest states of the cation and the MOs of the neutral and of the cation are very similar. The GS cation's main configuration is similar to that of the resulting one from removing an electron from the HOMO. It has a hole on the amine part. The isocontours of the Dyson orbital for an ionization of the GS neutral to the GS of the cation correspond to those of the HOMO of the neutral, see figures 2(a) and (b). The two first excited states, ES1 and ES2, are only 0.62 eV and 0.99 eV above the GS and correspond to configurations where an electron is missing on the phenyl group. The Dyson orbitals from the GS of the neutral to ES1 and ES2 correspond to the HOMO-1 and HOMO-2 of the neutral (see figures 2(a) and (b)). In summary, the hole resulting from the ionization of the GS of the neutral will be localized either on the amine part for an ionization to the GS of the cation or on the phenyl part for an ionization to the two lowest excited states of the cation.
The triplet GS of the dication is 1.94 eV lower than the singlet and corresponds to an electronic configuration where two electrons are missing, one in a MO localized on the amine part and one in a MO localized on the phenyl part respectively. The triplet GS of the dication is also found to be more stable than the singlet at the CAS-SCF level. The IPs computed for the ionization of the cation in TD-DFT and in CAS-SCF are in good agreement, see table 3. The first dicationic excited triplet state is only 0.26 eV above the GS. Its main configuration corresponds to a hole in the HOMO and in the HOMO-2, the other component of the π MO localized on the phenyl part, see figure 2. The MOs of the dication remain similar to that of the neutral and the cation. The Dyson orbitals for the ionization of the three lowest states of the cation to the GS and the first excited states of the dication are shown in figure 2(c). The GS of the cation ionizes to the two lowest dicationic states. In the two lowest excited states of the cation, an electron has already been removed from the phenyl so the next electron to be ionized is the one on the amine part. Figure 2(c) shows that the first excited state of the cation ionizes selectively to the GS of the dication while the second excited state of the cation ionizes selectively to the first excited state of the dication, see also figure 1. Higher triplet excited states of the dication are computed to be higher in energy, above 2.7 eV.
4. Simulation of the dynamics of the electronic density of the cation
We report simulations for two different pump–probe experiments. In the first one, we model an ideal femtosecond UV pump–attosecond XUV probe experiment. The pump pulse ionizes the GS of the neutral and builds a coherent superposition primarily of the three lowest states of the cation (GS, 1ES and 2ES). This leads to a motion of the electronic density from one side of the molecule to the other. The dynamics can then be probed by a single attosecond XUV pulse and the angular distribution of the ionized electron records the dynamics at the time of ionization. In the second example we report on a more realistic IR pump–XUV probe scheme with pulses similar to those used in the experiment of Belshaw et al on the migration of charge in amino acid [25]. We show that such pulses can also be used to trigger and probe the electronic dynamics in the cation.
In the first example, a weak 1.4 fs UV pulse (134 nm) is used to ionize the neutral molecule. The initial state of the simulation is the GS of the neutral. All the states of the neutral and the cation are coupled during the first pulse, according to the strength of their transition dipoles. The ionizing pulse is polarized along +z direction, roughly perpendicular to the molecular backbone. A pump pulse polarized along z leads to a coherent superposition of the three lowest states of the cation (GS, 1ES and 2ES) without accessing higher cationic excited states (figure 3(a)). We chose a polarization along z and adjusted the pulse strength to avoid accessing the threshold of the dication states by multiphoton ionization during the pump pulse. A pump polarized along the x direction leads to significantly larger ionization yields, both to the states of the cation and the dication. The photoelectron spectrum resulting from the pump pulse is shown in figure 3(b). The high intensity peak close to threshold corresponds to the resonant one photon ionization of the GS of the neutral to the three lowest states of the cation (GS, ES1 and ES2). The small peak at 5 eV is the result of non-resonant contributions of these channels, which have the maximum of their photoionization cross section around 5 eV, as well as from the photoionization of the transient higher excited states of the neutral that occurs while the pump pulse is on. At the end of the first pulse, there is 0.1% of the population in the excited states of the neutral, 4.1% in the cation. 0.01% of population reached the dication by sequential double ionization, which is negligible. Compared to the electronic density of the neutral GS, the hole is about equally localized on the two moities. The coherent superposition of the three populated cationic states (GS, 1ES and 2ES) induces a motion of the one electron density along the molecular backbone and this motion is reflected in the oscillation of the dipole moment of the cation, see equation (9) above. When the pump pulse is over, the populations,  , of each state are stationary. However the interference terms continue to beat even when the pulse is over. The x component of the time-dependent dipole moment shown in figure 4(a) exhibits two main frequencies corresponding to the transition frequencies GS-1ES and GS-2ES, which is confirmed by the Fourier transform (FT) of the dipole moment plotted in figure 4(b). The transition frequency ES1–ES2 does not appear because the transition dipole μES1 − ES2 is small, see table 2.
, of each state are stationary. However the interference terms continue to beat even when the pulse is over. The x component of the time-dependent dipole moment shown in figure 4(a) exhibits two main frequencies corresponding to the transition frequencies GS-1ES and GS-2ES, which is confirmed by the Fourier transform (FT) of the dipole moment plotted in figure 4(b). The transition frequency ES1–ES2 does not appear because the transition dipole μES1 − ES2 is small, see table 2.
Figure 3. (a) Time evolution of the populations of the ground and excited states of the cation during the photoionization by a 1.4 fs 134 nm UV pump pulse with a spectral width of 3.2 eV (in equation (2), ω1 = 0.33 au (9.0 eV), σ1 = 30 au and f0, 1 = 0.01 au (3.5 1012 W cm−2) polarized in the +z direction). At the end of the pulse, the evolution is field-free and the population are stationary. (b) The photoelectron spectrum resulting from the ionization by the pump.
Download figure:
Standard image High-resolution imageFigure 4. (a) Variation of the x component of the time-dependent dipole moment (equation (9)) computed for the superposition of states built by the UV pump pulse (red) and the IR pump pulse (black). The beatings of μx(t) resulting from an IR photoionization are more complex because of the multiphoton process. This is reflected in the Fourier transform of the dipole moment shown in panel (b). (b) Fourier transform of the dipole moments plotted in panel (a), UV photoionization (black) and IR photoionization (red). Higher transition frequencies appear in the FT of the dipole moment resulting from the IR photoionization because the multiphoton process populates higher cationic excited states.
Download figure:
Standard image High-resolution imageThe oscillations of the dipole moment of the cation shown in figure 4 reflect the oscillation of the charge density. The amplitudes of the oscillations are governed by the values of the transition dipoles. From table 2, one can see that these are much larger along the molecular backbone, in the x direction, than along z. In turn, the values of the transition dipoles directly reflect the spatial localization of the transition density matrices shown in figure 5(a). Negative transition densities are represented in blue and positive ones in yellow. One can see that it is mainly the transition density between the GS and 1ES, ρGS − 1ES, that is responsible for the electronic density motion along the molecular backbone from the phenyl part to the nitrogen part. In figure 5(b), we show the differences, ρ(t) − ρ(t0), where t0 corresponds to the end of the pulse. The values of the times t were chosen when the dipole moment is maximum or minimum. At the end of the pump pulse, at time t0, the hole is about equally localized on the amine and phenyl ends but the electronic density is non-stationary because a coherent superposition of states has been built. When the dipole moment is maximum (μx ≈ 0.0) at t =3.9, t = 10.3, t = 17 fs, there is accumulation of electronic density (yellow) on the amine part compared to the distribution at time t0 while for the minimum (μx ≈ −1.0), at t = 7.4, t = 12.5, t = 20.1 fs, there is a decrease (blue) of the electronic density on the amine part. This corresponds to a transfer of 4% of electronic density in the cation that is added or removed from the amine part. The motion of the density on the phenyl part is more complex because it involves the transition densities ρGS − 2ES and ρ1ES − 2ES.
Figure 5. (a) Transition densities between the three lowest states of the cation. (b) Isocontour plots (5 10−5 Å−3) of the electronic density difference in the cation, ρ(t) − ρ(t0), for a pump by the UV pulse with t0 = 2.5 fs computed for time values when the dipole moment is maximum or minimum. 4% of the electronic density of the cation is transferred from the phenyl to the amine and vice versa. Yellow corresponds to an accumulation of electronic density and blue to a decrease. At the end of the pulse (time t0), compared to the density of the neutral GS, the hole is about equally localized on the two moieties.
Download figure:
Standard image High-resolution imageThe electronic dynamics in the cationic states induced by the pump pulse can be probed by an ultrashort 0.4 fs XUV (93 nm) pulse (ω2 = 0.49 au (13.3eV), σ2 = 10 au and f0, 2 = 0.015 au polarized in the +z direction) that ionizes the cationic states to the two lowest states of the dication. Ionization to higher excited states of the dication is in principle possible because of the 8.7 eV bandwidth of the XUV pulse but they are computed to have much smaller photoionization widths from the three lowest states of the cation. The interaction with the second pulse also induces ionization from the neutral and dynamics in the neutral or cationic states and these processes are fully taken into account by the coupled equation scheme. Despite the complex dynamics, our computations show that one can reliably probe the motion of the electron density in the states of the cation by photoionization. The anisotropy parameter, 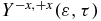 given by equation (10), is a good probe of the oscillations of the electron density between the two ends of the molecule.
given by equation (10), is a good probe of the oscillations of the electron density between the two ends of the molecule. 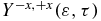 is defined to be positive when the ionization yield from the amine part is larger than from the phenyl part. It is plotted as a heatmap in figure 6(b). By comparing with figure 4(a), one can see that at delay times 7.4, 12.5 and 20.1 fs, when the dipole moment is negative, indicating that the centre of negative charge is on the phenyl end,
is defined to be positive when the ionization yield from the amine part is larger than from the phenyl part. It is plotted as a heatmap in figure 6(b). By comparing with figure 4(a), one can see that at delay times 7.4, 12.5 and 20.1 fs, when the dipole moment is negative, indicating that the centre of negative charge is on the phenyl end,  is close to zero. The fact that
is close to zero. The fact that 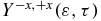 is not negative is because the probing of the charge localization is modulated by the relative yields of ionization of the states of the cation to the states of the dication. The corresponding Dyson orbitals are shown in figure 2(c). On the other hand,
is not negative is because the probing of the charge localization is modulated by the relative yields of ionization of the states of the cation to the states of the dication. The corresponding Dyson orbitals are shown in figure 2(c). On the other hand, 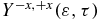 is positive, which indicates a preferential ionization from the amine end when the dipole moment is close to zero, which indicates that there is more negative charge on the amine end. These trends are in agreement with the isocontour of the electronic density shown in figure 5. One can also analyse the average value of the anisotropy parameter in a given energy range of the photoelectron. For values of the kinetic energy between 1.0 and 3.5 eV,
is positive, which indicates a preferential ionization from the amine end when the dipole moment is close to zero, which indicates that there is more negative charge on the amine end. These trends are in agreement with the isocontour of the electronic density shown in figure 5. One can also analyse the average value of the anisotropy parameter in a given energy range of the photoelectron. For values of the kinetic energy between 1.0 and 3.5 eV, 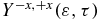 oscillates with one main frequency that corresponds to the transition frequency GS-1ES (see figure 6(c) and FT in figure 6(d)). For values of the kinetic energies above 5 eV, the beatings are more complex (figures 6(c) and (d)). Two frequencies, corresponding the transition frequencies GS-1ES and GS-2ES respectively, appear in the FT shown in figure 6(d). The analysis of the beating frequencies of the anisotropy parameters therefore clearly reflects the electronic states that are present in the cationic electronic wave packet. Information about the spatial localization of the electronic density requires the angular distribution of the photoelectron to be resolved and is not easily extractable from the photoelectron spectrum integrated over all space shown in figure 6(c).
oscillates with one main frequency that corresponds to the transition frequency GS-1ES (see figure 6(c) and FT in figure 6(d)). For values of the kinetic energies above 5 eV, the beatings are more complex (figures 6(c) and (d)). Two frequencies, corresponding the transition frequencies GS-1ES and GS-2ES respectively, appear in the FT shown in figure 6(d). The analysis of the beating frequencies of the anisotropy parameters therefore clearly reflects the electronic states that are present in the cationic electronic wave packet. Information about the spatial localization of the electronic density requires the angular distribution of the photoelectron to be resolved and is not easily extractable from the photoelectron spectrum integrated over all space shown in figure 6(c).
Figure 6. (a) Photoelectron spectrum resulting from the probe of the electronic dynamics in the cationic states. (b) Heatmap of the anisotropy parameter,  (equation (10)) computed as a function of the delay time, τ, between the two pulses and the magnitude of the kinetic energy, ε, for the ionization by the probe XUV pulse with a spectral width of 8.7 eV (ω2 = 0.49 au (13.3 eV), σ2 = 10 au and f0, 2 = 0.015 au polarized in the +z direction, see equation (2)). (c) Anisotropy parameter for ε ranging from 1.0 to 3.5 eV (red) and 5.0 to 9 eV (black). (d) Fourier transform of the anisotropy parameter plotted in panel (c). Only the GS-ES1 transition frequency of the cation is present for low values of the kinetic energy (between 1 and 3.5 eV). For kinetic energies above 5 eV, both transition frequencies, GS-ES1 and GS-ES2 appear in the FT of the anisotropy parameter.
(equation (10)) computed as a function of the delay time, τ, between the two pulses and the magnitude of the kinetic energy, ε, for the ionization by the probe XUV pulse with a spectral width of 8.7 eV (ω2 = 0.49 au (13.3 eV), σ2 = 10 au and f0, 2 = 0.015 au polarized in the +z direction, see equation (2)). (c) Anisotropy parameter for ε ranging from 1.0 to 3.5 eV (red) and 5.0 to 9 eV (black). (d) Fourier transform of the anisotropy parameter plotted in panel (c). Only the GS-ES1 transition frequency of the cation is present for low values of the kinetic energy (between 1 and 3.5 eV). For kinetic energies above 5 eV, both transition frequencies, GS-ES1 and GS-ES2 appear in the FT of the anisotropy parameter.
Download figure:
Standard image High-resolution imageWe next simulate a more realistic 6 fs IR pump–1.4 fs XUV probe experiment, similar to the set-up of [25] and show that in this case too, it is possible to probe the charge migration of the electron density between the two moieties along the molecular backbone. First, a 6 fs 800 nm IR pulse is used to ionize the neutral. Similarly to the UV pump pulse, it creates coherent superposition of cationic states mainly composed of the GS, 1ES and 2ES but also of the higher excited states as expected for a multiphoton ionization process, see figure 7(a). The photoelectron spectrum plotted in figure 7(b) is broader than in the UV case (figure 3(b)) and small peaks spaced by 1.6 eV, one 800 nm IR photon, are present at higher energy. The bouncing of the one electron density of the cation between the two ends of the molecule is shown in figure 8 where the difference ρ(t) − ρ(t0) is plotted for extrema of the values of the dipole moment of the cation, see figure 4(a). Because several excited states of the cation are accessed during the multiphoton IR ionization, the time dependence of the dipole moment is more complex than in the case of an ionization by a UV pulse as shown in figure 3. Several transition frequencies between excited states appear in the FT of the cation dipole shown in figure 4(b). For example the peak in figure 4(b) at 3.2eV corresponds to the transition frequency between the 1ES and the 7ES.
Figure 7. (a) Time evolution of the populations of the ground and excited states of the cation during the photoionization by a 6 fs 800 nm IR pump pulse with a spectral width of 0.6 eV. The pump parameters in equation (2) are ω1 = 0.057 au (1.55 eV), σ1 = 150 au and f0, 1 = 0.02 au polarized in the +z direction. Compared to figure 3(a), there is a significant amount of population in the higher excited states of the cation (b). The photoelectron spectrum resulting from the ionization by the IR pump pulse.
Download figure:
Standard image High-resolution imageFigure 8. Isocontour plots (5 10−5 Å−3) of the density difference, ρ(t) − ρ(t0), for a pump by the IR pulse with t0 = 6 fs computed for time values when the dipole moment is maximum or minimum, which correspond to a transfer of 6% of the electronic density of the cation from the amine to the phenyl or vice versa. At the end of the pulse (time t0), compared to the density of the neutral GS, the hole is about equally localized on the two moieties.
Download figure:
Standard image High-resolution imageTo probe the cationic dynamics, we use a 1.4 fs XUV pulse (ω2 = 0.49 au (13.3eV), σ2 = 30 au and f0, 2 = 0.005 au polarized in the +z direction). The anisotropy parameter is shown in figure 9(b) as a function of the pump–probe delay, τ, and the kinetic energy of the ionized electron. As for the UV pump–XUV probe scheme discussed above, the sign of the anisotropy parameter correlates with the localization of the electron density and the value of the dipole moment at the time of ionization. When the dipole moment is positive, at delay times 9, 16.1 and 21.2 fs, the electronic density is on amine and the ionization yield is positive, reflecting the preferential ionization from the amine side. When we average 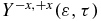 over a kinetic energy varying from 1 to 3.5 eV, we observe a beating with a period corresponding the transition frequency between the GS-1ES as was the case for the photoionization by a UV pulse shown in figure 6. However for a higher kinetic energy range, there is a complex variation of
over a kinetic energy varying from 1 to 3.5 eV, we observe a beating with a period corresponding the transition frequency between the GS-1ES as was the case for the photoionization by a UV pulse shown in figure 6. However for a higher kinetic energy range, there is a complex variation of 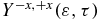 coming from the ionization of a superposition of a larger number of cationic states. Nevertheless, the frequencies of the beatings GS-1ES and GS-2ES dominate, which is shown by the two broad peaks in the FT of the anisotropy parameter (figure 9(d)).
coming from the ionization of a superposition of a larger number of cationic states. Nevertheless, the frequencies of the beatings GS-1ES and GS-2ES dominate, which is shown by the two broad peaks in the FT of the anisotropy parameter (figure 9(d)).
Figure 9. (a) Photoelectron spectrum resulting from the probe of the electronic dynamics in the cationic states. (b) Heatmap of the anisotropy parameter, 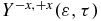 (equation (10)) computed for the ionization of the electronic dynamics triggered by the IR pump pulse. A XUV probe pulse of 1.4 fs with a spectral width of 3.0 eV (ω2 = 0.49 au (13.3 eV), σ2 = 30 au and f0, 2 = 0.005 au polarized in the +z direction, see equation (2)) is used to probe the electronic dynamics. (c) Anisotropy parameter for ε ranging from 1.0 to 3.5 eV (red) and 5.0 to 9 eV (black). (d) Fourier transform of the anisotropy parameters plotted in panel (c). Only the GS-ES1 transition frequency of the cation is present for low values of the kinetic energy (between 1 and 3.5 eV) as is observed in the UV pump–XUV probe experiment. For kinetic energies above 5 eV, the transition frequencies GS-ES1 and GS-ES2 dominate the FT of the anisotropy parameter but the peaks are broader than in the UV-XUV case shown in figure 6 above due to the more complex superposition of cationic states that is built by the IR pump.
(equation (10)) computed for the ionization of the electronic dynamics triggered by the IR pump pulse. A XUV probe pulse of 1.4 fs with a spectral width of 3.0 eV (ω2 = 0.49 au (13.3 eV), σ2 = 30 au and f0, 2 = 0.005 au polarized in the +z direction, see equation (2)) is used to probe the electronic dynamics. (c) Anisotropy parameter for ε ranging from 1.0 to 3.5 eV (red) and 5.0 to 9 eV (black). (d) Fourier transform of the anisotropy parameters plotted in panel (c). Only the GS-ES1 transition frequency of the cation is present for low values of the kinetic energy (between 1 and 3.5 eV) as is observed in the UV pump–XUV probe experiment. For kinetic energies above 5 eV, the transition frequencies GS-ES1 and GS-ES2 dominate the FT of the anisotropy parameter but the peaks are broader than in the UV-XUV case shown in figure 6 above due to the more complex superposition of cationic states that is built by the IR pump.
Download figure:
Standard image High-resolution image5. Concluding remarks
We demonstrate by dynamical simulations of full pump–probe experiments with realistic pulse parameters that the charge migration in the cation of a modular molecule after the photoionization of the neutral molecule by the pump pulse can be reliably probed by a second photoionization to the states of the dication. In a large molecule like PENNA, the nuclear motion is expected to play a significant role after the first dozen of femtoseconds or so. We report on the purely electronic dynamics taking place before the onset of significant nuclear motion and show that the first bouncings of the electronic density between the amine and the phenyl groups is reflected in the beatings of the anisotropy of the ionization yields at the two moieties. We suggest that these beating could be experimentally observed in PENNA or in similar modular systems.
Acknowledgments
FR and BM gratefully acknowledge support of the Fonds de la Recherche Fondamentale Collective, FRFC 2.4545.12 and of the Fonds National de la Recherche Scientifique (FNRS, Belgium). FR and RDL thank the Einstein Foundation of Berlin.








