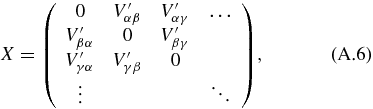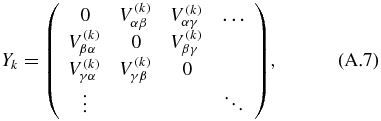Abstract
We present a theoretical investigation of the multiphoton resonance dynamics driven by intense frequency-comb and cavity-mode fields inside a femtosecond enhancement cavity (fsEC). The many-mode Floquet theorem is employed to provide a nonperturbative and exact treatment of the interaction between a quantum system and laser fields. The quasienergy structure driven by the frequency-comb laser field is modified by coupling the cavity-mode field and the multiphoton resonance processes between modified quasienergy states, resulting in the generation of even-order harmonics. The high-order harmonic generation (HHG) from a two-level system driven by the laser fields can be coherently controlled by tuning the laser parameters. In particular, the tuning intensity of the cavity-mode field allows one to coherently control the HHG power spectra without changing the absolute positions of comb frequencies.
Export citation and abstract BibTeX RIS
1. Introduction
In the last decade, the development of the phase-stabilized optical frequency comb from a femtosecond laser has played a remarkable role in the field of metrology of optical frequencies, owing to its ability to provide a precise and direct link between optical and microwave frequencies [1, 2]. The generation of extreme ultraviolet (XUV) and vacuum ultraviolet (VUV) frequency combs have led to the advancement in test of quantum electrodynamics [3–6], the development of the optical atomic clock [7–12] and high-precision optical frequency spectroscopy [13–20]. The latter two applications require the repetition rate of laser fields >100 MHz and the generation of phase coherent and low noise combs with the power per comb element as high as possible. Significantly higher repetition rates with suitable pulse energies can be achieved using a femtosecond enhancement cavity (fsEC) with full control of the carrier-envelope phase (CEP) [21]. In 2005, coherent XUV [22] and VUV [23] radiations at a repetition frequency of more than 100 MHz, a 1000-fold improvement over previous experiments, have been generated via high-order harmonic generation(HHG) inside fsECs. More recently, Cingöz et al [20] reported the generation of XUV frequency combs up to the 27th harmonic order (wavelength of 40 nm), by coupling a high-power near-infrared frequency comb to a robust fsEC.
The behaviour of the frequency-comb structure and coherence in HHG in the VUV–XUV regimes was first explored theoretically by means of the accurate solution of TDSE and time-frequency spectrum [24, 25]. The nested comb structure within each of the harmonics was found to range from the first harmonic all the way to the cutoff harmonic. It has experimentally been shown that, the frequency-comb structure and coherence can indeed survive in very high-order harmonics and in the presence of substantial ionization [4, 20, 26, 27]. In addition, Son and Chu [28] have recently presented a theoretical extension of the many-mode Floquet theory (MMFT) [29, 30] for the nonperturbative treatment of the coherent control of multiphoton resonance dynamics and the enhancement of HHG driven by an intense frequency-comb laser field. They showed that HHG driven by an intense frequency-comb laser field has a comb structure with the same repetition frequency and different offset frequencies for each harmonic. Moreover, the HHG can be dramatically enhanced by tuning the CEP shift due to multiphoton resonance with all the comb frequencies. This multiphoton-resonant enhancement approach promises an alternative method for achieving a powerful frequency-comb structure in the VUV and/or XUV region, without increasing the intensity of the driving frequency-comb laser field.
In previous investigations, the generating frequency-comb structure is restricted in odd harmonics due to opposite parities of the two levels involved. The enhancement of the spectra intensities of comb frequencies is achieved by tuning the CEP shift of the frequency-comb laser field. In this way, however, absolute positions of comb frequencies are simultaneously changed [28]. In this paper, we present an ab initio investigation of the multiphoton resonance dynamics by coupling an intense frequency-comb laser field with a cavity-mode field inside a fsEC. With the assistance of the cavity-mode field, multiphoton resonance processes with an even number of photons of the carrier frequency take place in a driven two-level system. As a result, even-order harmonics can be radiated by the two-level system. We also show that the HHG power spectra can be enhanced via tuning the intensity of the cavity-mode field without varying the CEP shift of the frequency-comb laser field. It means that the generating comb frequencies in harmonics can be enhanced without changing their absolute positions.
The paper is organized as follows. In section 2, we present the MMFT for the treatment of the interaction between a quantum system and an intense frequency-comb laser field coupled with a cavity-mode field inside a fsEC. In section 3, we apply the MMFT to study the coherent control of multiphoton-resonant dynamics by means of laser fields. This is followed by a conclusion in section 4.
2. MMFT treatment of multiphoton excitation driven by intense frequency-comb and cavity-mode fields inside a fsEC
We consider the interaction between an atomic or molecular system and frequency-comb and cavity-mode fields inside a fsEC.
A frequency-comb laser field generated by the pulse circulating in a fsEC can be written in the form
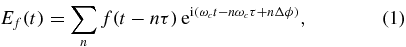
where ωc is the carrier frequency, τ is the time interval between pulses, Δϕ is the CEP shift from pulse to pulse,  is the envelope function for each pulse, f0 is the peak amplitude and σ is the standard deviation of a Gaussian function. Equation (1) can also be expressed as the summation of components of discrete comb frequencies [28],
is the envelope function for each pulse, f0 is the peak amplitude and σ is the standard deviation of a Gaussian function. Equation (1) can also be expressed as the summation of components of discrete comb frequencies [28],
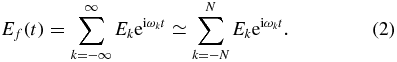
The comb frequencies ωk can be written as

with the repetition frequency ωr = 2π/τ and the main angular frequency
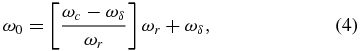
where [ ] is the round function and the offset frequency ωδ = Δϕ/τ. In equation (2), individual amplitudes of frequencies ωk are given by
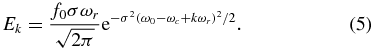
The infinite summation over k in equation (2) is done with the truncation approximation; a finite integer number N is chosen to approximately reproduce the frequency-comb field and make sure the calculation is accessible and convergent. In our calculation, N is chosen such that Ek < 1 × 10−15 au (corresponding to intensity 3.51 × 10−14 W cm−2) when |k| > N.
On the other hand, there are many eigenmodes of a cavity. Suppose that only the eigenmode of the smallest angular frequency of the fsCE is excited to couple with the frequency-comb laser field. Then the total electric field can be expressed as
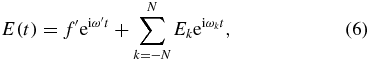
where f' and ω'( = ωr) are the amplitude and angular frequency of the cavity-mode field, respectively. If both the frequency-comb and the cavity-mode fields are linearly polarized along the z-axis, the Hamiltonian is given by

where  is the unperturbed Hamiltonian of an atomic or molecular system, μ(r) is the electric dipole moment operator and μz is the component parallel to the polarization axis. Note that the time-dependent Hamiltonian in equation (7) is bichromatic, containing two independent frequencies ω0 and ωr.
is the unperturbed Hamiltonian of an atomic or molecular system, μ(r) is the electric dipole moment operator and μz is the component parallel to the polarization axis. Note that the time-dependent Hamiltonian in equation (7) is bichromatic, containing two independent frequencies ω0 and ωr.
By employing the MMFT [29, 30], the time-dependent Schrödinger equation with the Hamiltonian (7) can be converted into an equivalent time-independent generalized Floquet matrix eigenvalue problem. Because all the comb frequencies can be represented by two variables, ω0 and ωr, we can employ the basis vectors in the two-mode Floquet formalism
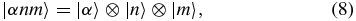
where α is the system index and n and m are the Fourier components of ω0 and ωr, respectively. In the representation spanned by the basis vectors {|αnm〉}, we can write the time-independent generalized Floquet matrix eigenvalue equation as
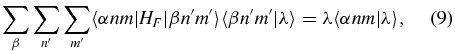
where λ is the quasienergy eigenvalue and |λ〉 is the corresponding eigenvector. Solving the eigenvalue problem, we can obtain a set of quasienergies λγnm and corresponding eigenvectors |λγnm〉 which satisfy the orthonormality condition [31]. Details of the Floquet matrix are given in the appendix.
After solving the eigenvalue problem in equation (9), the time-averaged transition probability can be computed from the quasienergy eigenvectors [29],
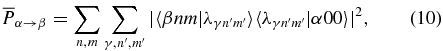
which has the maximum values of  at the avoided crossings of quasienergies that are associated with multiphoton resonance transitions [30].
at the avoided crossings of quasienergies that are associated with multiphoton resonance transitions [30].
The induced dipole moment can be expanded in double Fourier series [28],
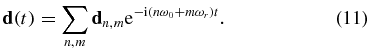
Given values of n and m, the angular frequency ω is determined by ω = nω0 + mωr. The harmonic generation spectra in the length form can be expressed by
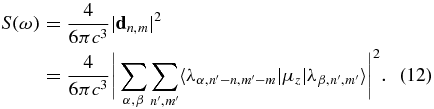
Here the harmonic order is defined by ω/ωc and can be a fractional number because of the comb structure of frequencies.
3. Results and discussions
In the following, we first study the multiphoton resonance dynamics of a two-level system driven by frequency-comb and cavity-mode fields inside a fsEC. The parameters of the frequency-comb field are peak intensity 2.5 × 1015 W cm−2, carrier frequency 563.5 THz (corresponding to ωc = 0.085 6454 au and wavelength 532 nm) and repetition frequency 10 THz (corresponding to ωr = 1.519 83 × 10−3 au and pulse separation τ = 0.1 ps), which are generated from a train of Gaussian pulses with 20 fs full width at half maximum (FWHM). The parameters of the cavity-mode field are intensity 1 × 1012 W cm−2 and carrier frequency 10 THz (i.e. ω' = ωr). For the two-level system, the transition dipole moment 〈α|μz|β〉 = 0.1 au is used.
Figures 1(a) and (b) show the two-mode quasienergies and the time-averaged transition probabilities as a function of the energy separation of the two-level system, ℏωαβ = εβ − εα, varying from 0.0 to 0.38 au, respectively. As a comparison, figures 1(c) and (d) present the two-mode quasienergies and time-averaged transition probabilities for the two-level system driven by the frequency-comb laser field alone, respectively. By increasing the energy separation, avoided crossings of quasienergies occur. Around each avoided crossing, a cluster of resonant transitions are observed due to the comb structure of frequencies of the laser fields. When the two-level system is driven by the frequency-comb field alone, (multiphoton) resonant transitions are only found near odd times of ωc (figure 1(d)). When coupled with the cavity-mode field of frequency ω' = ωr, multiphoton resonance peaks appear near even times of ωc (figure 1(b)). Thus even-harmonic resonances happen.
Figure 1. (a) Quasienergies and (b) time-averaged transition probabilities as a function of energy separation, for the two-level system driven by frequency-comb and cavity-mode fields. (c) Quasienergies and (d) time-averaged transition probabilities as a function of energy separation, for the two-level system driven by the frequency-comb field alone. The parameters of the frequency-comb field are peak intensity 2.5 × 1015 W cm−2, carrier frequency 563.5 THz and repetition frequency 10 THz of 20 fs FWHM Gaussian pulses. The parameters of the cavity-mode field are intensity 1 × 1012 W cm−2 and carrier frequency 10 THz.
Download figure:
Standard image High-resolution imageThe appearance of even-harmonic resonances never means that the dipole transition rule has been broken. In the MMFT, the laser dressed states are written as the linear superposition of the states (8). Dipole transitions between two dressed states are composed of various dipole transitions among the states (8). When driven by the frequency-comb field alone, there are only photons of comb frequencies ω0 + kωr. The quasiperiodic structure of the quasienergies can be represented by
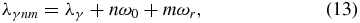
where λγ are the eigenvalues of equation (9) and n and m are integers. Quasienergy levels |γn1m1〉 can only be populated by absorbing an odd number (n1 − n2) of photons of comb frequencies from levels |γ'n2m2〉 with γ' ≠ γ. Thus only the odd-harmonic resonances are allowed (figure 1(d)). When coupling the frequency-comb field with the cavity-mode field, there are not only photons of comb frequencies ω0 + kωr, but also photons of the cavity-mode frequency ωr. New quasienergy levels |γnm'l〉 with quasienergies
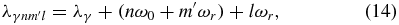
appear. These levels are degenerate with the levels |γnm〉 (m = m' + l), which are generated by the frequency-comb field alone. However, transitions with both an odd- and an even-number of photons of comb frequencies are allowed among the new quasienergy levels. For instance, quasienergy levels |γn1m1l1〉 can be populated by the transitions from levels |γ'n2m2l2〉 with γ' ≠ γ. In the transition, an odd number (n1 − n2) of photons of comb frequencies plus an even number (l1 − l2) of photons of the cavity-mode frequency are absorbed. At the same time, |γn1m1l1〉 can also be populated from levels |γ'n3m3l3〉 with γ' ≠ γ. In the transition, an even number (n1 − n3) of photons of comb frequencies plus an odd number (l1 − l3) of photons of the cavity-mode frequency are absorbed. Since the cavity-mode frequency is much smaller than the comb frequencies, multiphoton resonance transitions can be found in the vicinities of both odd- and even-harmonics of ωc (figure 1(b)).
The presence of the resonance transitions with an even number of photons of comb frequencies implies that even-order harmonics can be generated when the system is driven by the frequency-comb and cavity-mode fields. In the following, we investigate the generation and coherent control of the HHG power spectra of the two-level system with an energy separation in the vicinity of the even-harmonics of ωc. Son and Chu [28] have shown that HHG can be dramatically enhanced by reaching multiphoton resonance among all the comb frequencies. Since the AC stark effect is dependent on the intensities and frequencies of the driving fields, the resonance condition is usually hard to reach. However, once the intensities and frequencies of the driving fields are fixed, the resonance position will be retained and much easier to reach by varying the CEP shift [28]. Generalized to our investigation, when driven by the frequency-comb and the cavity-mode fields, the n-harmonic resonance condition is expressed as
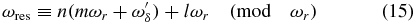
where ωres is the resonance frequency between two laser-dressed states and  is the offset frequency of the frequency-comb field. Equation (15) means the reminders of ωres and
is the offset frequency of the frequency-comb field. Equation (15) means the reminders of ωres and  are the same when divided by ωr. Then the CEP shifts for n-harmonic resonance are
are the same when divided by ωr. Then the CEP shifts for n-harmonic resonance are
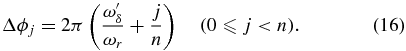
As varying the CEP shift Δϕ from 0 to 2π, the resonance can be achieved n times when the CEP shift satisfies equation (16). In equations (15) and (16), n can be an odd or even number due to the coupling of the cavity-mode field. Figures 2(a) and (b) show the quasienergies and the time-averaged transition probabilities as a function of the CEP shift, respectively. The energy separation ωαβ is fixed at 0.17 au, corresponding to the two-harmonic dominant resonance regime (ωαβ ≈ 2ωc) and Δϕ is varied from 0 to 2π. Other parameters are the same as those in figures 1(a) and (b). It is observed that: time-averaged transition probabilities reach the maximum value  at Δϕ/2π = 0.198 787 and 0.698 787. The two peaks separated by π appear exactly at the avoided crossings of quasienergies.
at Δϕ/2π = 0.198 787 and 0.698 787. The two peaks separated by π appear exactly at the avoided crossings of quasienergies.
Figure 2. (a) Plots of quasienergies and (b) time-averaged transition probabilities as a function of the CEP shift Δϕ. Two resonance positions separated by π due to two-harmonic dominant resonance.
Download figure:
Standard image High-resolution imageIn figure 3, the enhancement of the HHG power spectra is shown with various values of CEP shift, Δϕ/2π = 0.1 (off-resonance), 0.198 and 0.198 787 (near-resonance). The energy separation is fixed at 0.17 au. As discussed above, the emission of odd-order harmonics is generated by the transition from |γnml〉 to |γ'n'm'l'〉, where γ ≠ γ', (n − n') is an odd number and (l − l') is an even number. The transition is far-off-resonance with the chosen energy separation. The resonance cannot be reached by varying the CEP shift. Therefore, the emission of odd-order harmonics is insensitive to the change of the CEP shift. On the other hand, the emission of even-order harmonics is related to the transition from |γnml〉 to |γ'n'm'l'〉, where γ ≠ γ', (n − n') is an even number and (l − l') is an odd number. The transition is near-on-resonance with the chosen energy separation. Thus the resonance can be achieved by varying the CEP shift, leading to the dramatically enhanced emission of even-order harmonics, as shown in figure 3.
Figure 3. Enhancement of HHG by varying the CEP shift. The intensity of the cavity-mode field is 1 × 108 W cm−2. Other parameters are the same as those in figure 1. For clarity, HHG peaks of the comb structure are connected by a line.
Download figure:
Standard image High-resolution imageIt is a good approach to enhance the HHG power spectra by tuning the CEP shift of the frequency-comb field. However, absolute positions of generating comb frequencies are simultaneously changed as the CEP shift is varied. What has been considered is whether it is possible to achieve the enhancement of HHG power spectra without changing absolute positions of the generating comb frequencies. The left side of the resonance condition (equation (15)) is the Stark shifted energy separation and the right side is the comb frequencies. The Stark shifted energy separation is dependent on the intensities, as well as the frequencies, of frequency-comb and cavity-mode fields, but independent of the CEP shift. So there are two options to achieve n-harmonic resonance: one is to meet the Stark shifted energy separation by tuning the CEP shift but fixing the intensities of laser fields. The other one is to meet the right side of equation (15) by tuning the intensities of fields but fixing the absolute positions of generating comb frequencies.
We now investigate the coherent control of the HHG power spectra at a fixed CEP shift, by tuning the intensity of the cavity-mode field. Figures 4(a)–(c) show the quasienergies, the time-averaged transition probabilities and the HHG power spectra as a function of the intensity of the cavity-mode field, respectively. The energy separation ωαβ is fixed at 0.17 au, corresponding to the two-harmonic dominant resonance regime. The CEP shift Δϕ is fixed at 0.4385 × 2π, which is off-resonance for the peak intensity 1 × 1014 W cm−2. As a comparison, we also present the case with the energy separation ωαβ = 0.25 au, corresponding to the three-harmonic dominant resonance regime. The results are presented in figure 5 with the CEP shift Δϕ = 0.1684 × 2π, which is off-resonance for the peak intensity 1 × 1014 W cm−2. In both cases, the quasienergies are shifted due to an increasing intensity of the cavity-mode field (figures 4(a) and 5(a)); the multiphoton-resonant condition is achieved at the avoided crossing of quasienergies (figures 4(b) and 5(b)). The HHG power spectra (figures 4(c) and 5(c)) are dramatically enhanced when the n-harmonic resonance condition is reached. Here we note that the enhancement of the HHG power spectra via tuning the intensity of the cavity-mode field is achieved without changing the CEP shift of frequency-comb field.
Figure 4. (a) Quasienergies and (b) time-averaged transition probabilities as a function of the intensity of the cavity-mode field. The resonance position is at 1.489 × 1011 W cm−2. (c) The enhancement of HHG power spectra by tuning the intensity of the cavity-mode field. For clarity, HHG peaks of the comb structure are connected by a line. The energy separation is fixed at ωαβ = 0.17 au. The CEP shift is fixed at Δϕ = 0.4385 × 2π. The parameters of the frequency-comb field are peak intensity 1 × 1014 W cm−2, carrier frequency 563.5 THz and repetition frequency 10 THz of 20 fs FWHM Gaussian pulses. The carrier frequency of the cavity-mode field is 10 THz.
Download figure:
Standard image High-resolution imageFigure 5. (a) Quasienergies and (b) time-averaged transition probabilities as a function of the intensity of the cavity-mode field. The resonance position is at 4.395 × 1011 W cm−2. (c) The enhancement of the HHG power spectra by tuning the intensity of the cavity-mode field. For clarity, HHG peaks of the comb structure are connected by a line. The energy separation is fixed at ωαβ = 0.25 au. The CEP shift is fixed at Δϕ = 0.1684 × 2π. Other parameters used are the same as those in figure 4.
Download figure:
Standard image High-resolution image4. Conclusion
In conclusion, we present a theoretical investigation of multiphoton resonance dynamics driven by frequency-comb and cavity-mode fields. The interaction between a quantum system and the laser fields are treated accurately by employing the many-mode Floquet theory. The cavity-mode field contributes additional photons of cavity-mode frequency. Although the frequency of the cavity-mode field is much smaller than the carrier frequency of the frequency-comb field, the cavity-mode photons can assist the electric-dipole-allowed multiphoton resonance transitions, which are related to photon absorptions with an odd number of cavity-mode photons, and an even number of photons of the carrier frequency. These transitions lead to the generation of even-order harmonics of the carrier frequency. We also investigate the coherent control of the HHG power spectra by tuning the CEP shift of the frequency-comb laser field and the intensity of the cavity-mode field. We found that the HHG power spectra can be enhanced without changing the absolute positions of comb frequencies by tuning the intensity of the cavity-mode field. This approach provides a new method for the optimal control of the frequency-comb structures generated via HHG with desired absolute comb frequencies. An extension of this work to the study of the coherent control of atomic and molecular processes is in process.
Acknowledgments
This work was partially supported by the National Basic Research Program of China (973 Program) No 2010CB923102, the Special Prophase Project on the National Basic Research Program of China (Grant No 2011CB311807) and the National Nature Science Foundation of China (Grant No 11074199). S-IC was partially supported by the Chemical Sciences, Geosciences and Biosciences Division of the Office of Basic Energy Sciences, Office of Sciences, US Department of Energy.
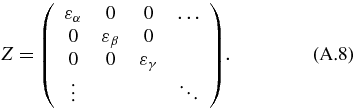
Appendix.: The structure of the Floquet matrix
The two-mode Floquet matrix HF is constructed by
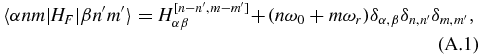
where
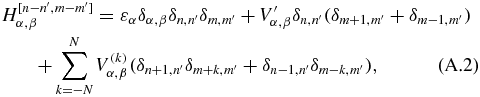
with  ,
,  and
and  . Due to the interaction between the cavity-mode field and the system, i.e. the second term of
. Due to the interaction between the cavity-mode field and the system, i.e. the second term of ![$H_{\alpha ,\beta }^{[n-n^{\prime },m-m^{\prime }]}$](https://content.cld.iop.org/journals/0953-4075/46/14/145403/revision1/jpb464914ieqn10.gif) , the structure of HF is different from that presented by Son and Chu [28]. The HF matrix for the case of linearly polarized fields can be constructed as follows:
, the structure of HF is different from that presented by Son and Chu [28]. The HF matrix for the case of linearly polarized fields can be constructed as follows:
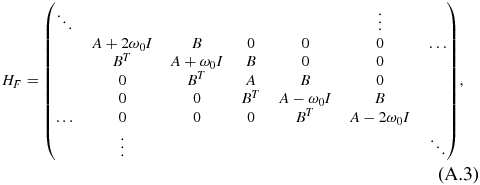
where
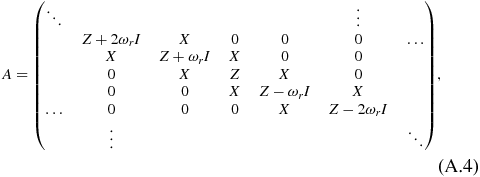
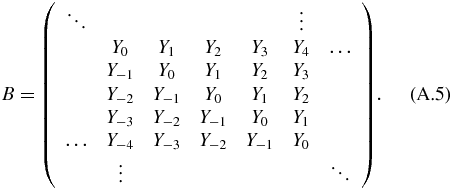
The matrices of X, Yk and Z which form blocks in A and B have the following forms: