Arnold diffusion for smooth convex systems of two and a half degrees of freedom

In the present note we announce a proof of a strong form of Arnold diffusion for smooth convex Hamiltonian systems. Let 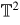${\mathbb T}^2$ be a 2-dimensional torus and B² be the unit ball around the origin in 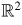${\mathbb R}^2$. Fix ρ > 0. 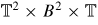Our main result says that for a 'generic' time-periodic perturbation of an integrable system of two degrees of freedom $H_0(p)+\varepsilon H_1(\theta,p,t),\quad \ \theta\in {\mathbb T}^2,\ p\in B^2,\ t\in {\mathbb T}={\mathbb R}/{\mathbb Z}$, with a strictly convex H₀, there exists a ρ-dense orbit (θ_ε, p_ε, t)(t) in ${\mathbb T}^2 \times B^2 \times {\mathbb T}$, namely, a ρ-neighborhood of the orbit contains ${\mathbb T}^2 \times B^2 \times {\mathbb T}$.

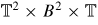Our proof is a combination of geometric and variational methods. The fundamental elements of the construction are the usage of crumpled normally hyperbolic invariant cylinders from [9], flower and simple normally hyperbolic invariant manifolds from [36] as well as their kissing property at a strong double resonance. This allows us to build a 'connected' net of three-dimensional normally hyperbolic invariant manifolds. To construct diffusing orbits along this net we employ a version of the Mather variational method [41] equipped with weak KAM theory [28], proposed by Bernard in [7].