Abstract
The higher derivatives of motion are rarely discussed in the teaching of classical mechanics of rigid bodies; nevertheless, we experience the effect not only of acceleration, but also of jerk and snap. In this paper we will discuss the third and higher order derivatives of displacement with respect to time, using the trampolines and theme park roller coasters to illustrate this concept. We will also discuss the effects on the human body of different types of acceleration, jerk, snap and higher derivatives, and how they can be used in physics education to further enhance the learning and thus the understanding of classical mechanics concepts.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
We are exposed to a wide variety of external motion and movement on a daily basis. From driving a car to catching an elevator, our bodies are repeatedly exposed to external forces acting upon us, leading to acceleration.
Being exposed to changes in motion and movement can have significant biomechanical effects on the human body and, in general we try to minimise our exposure to movement. Most transportation devices are designed to reduce acceleration as much as is reasonably practicable. Amusement rides on the other hand, are unique in that they are deliberately designed to expose us to large and changing types of motion.
We are all familiar with the terms displacement, velocity and acceleration. We experience velocity when we move and acceleration when we change the velocity at which we move. Our body does not feel velocity, but only the change of velocity i.e. acceleration, brought about by the force exerted by an object on our body. For example, a passenger in a constantly accelerating car will feel a constant force from the seat on his or her body.
Excluding the force of gravity that we are all exposed to minute by minute the concept of a constant force is rare in our daily lives. The accelerations that we normally experience and thus feel are not constant. When we are in a car and accelerate as the lights change to green, our acceleration is not constant. In this situation our acceleration is changing, so the motion sensation we are feeling is more likely jerk and even snap since there is a change in the jerk. As concrete illustrations of the concepts, we present in some detail examples for roller coasters and trampolines, using authentic data.
There is no agreement of the names of higher order derivatives [1]. The term snap will be used throughout this paper to denote the fourth derivative of displacement with respect to time. Another name for this fourth derivative is jounce. The fifth and sixth derivatives with respect to time are referred to as crackle and pop respectively.
2. Jerk, snap and higher derivatives
The terms jerk and snap mean very little to most people, including physicists and engineers. What are jerk and snap? Mathematically jerk is the third derivative of our position with respect to time and snap is the fourth derivative of our position with respect to time.
Acceleration without jerk is just a consequence of static load. Jerk is felt as the change in force; jerk can be felt as an increasing or decreasing force on the body. Consider the following. Velocity does not suddenly switch on, but instead grows from zero. So, there must be some acceleration involved. Similarly, acceleration does not suddenly switch on, but instead grows from zero. So, there must be some jerk involved. But the jerk does not suddenly switch on, it also grows from zero. So there must be some snap involved. But the snap does not suddenly switch on, it also grows from zero. So, there must be some crackle involved. But the crackle does not suddenly switch on, it also grows from zero. So, there must be some pop involved, and so on.
We know the terms displacement,  , velocity,
, velocity,  , and acceleration,
, and acceleration,  , where
, where  , and
, and  . A change in velocity must thus be accompanied by a force affecting every part of the body, although the damping of the human body leads to some attenuation of rapid changes.
. A change in velocity must thus be accompanied by a force affecting every part of the body, although the damping of the human body leads to some attenuation of rapid changes.
Students are taught Newton's second law at school, commonly in the form  , where m is the mass and a is the acceleration. What students are generally not taught is that the precise wording that Newton used was Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur. (Law II: A change in motion is proportional to the motive force impressed and takes place along the straight line in which that force is impressed.) [2]. This wording can also be interpreted as the impulse force where the force acts over a period of time
, where m is the mass and a is the acceleration. What students are generally not taught is that the precise wording that Newton used was Lex II: Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur. (Law II: A change in motion is proportional to the motive force impressed and takes place along the straight line in which that force is impressed.) [2]. This wording can also be interpreted as the impulse force where the force acts over a period of time  . If the force is impulsive it follows that the acceleration cannot be constant (if the mass of the body remains unchanged).
. If the force is impulsive it follows that the acceleration cannot be constant (if the mass of the body remains unchanged).
A change in force leads to a change in acceleration, that can be expressed, e.g. as j = da/dt = (dF/dt)/m, where we have introduced the jerk, j. Similarly we can define snap, s, crackle, c, and pop, p, as:



What, physically, are snap, crackle and pop? Below, we consider numerical examples in connection with a few familiar situations.
3. Roller coaster acceleration
Most rides that we embark upon such as riding in a lift, catching a train, sailing in a ship, or flying in an aeroplane are deliberately designed to minimise the biomechanical effects on us. Not so with roller coaster rides. Roller coaster rides are deliberately designed to stimulate the human sensory system, primarily visual, auditory and vestibular. Users of amusement rides are purposely subjected to elevated acceleration where the magnitude, duration and rate of change of the acceleration are controlled. These biomechanical variables are increased to enhance the sensory stimulation but also limited to ensure ride safety [3].
The biomechanical effects of elevated accelerations do not all lead to pleasure. If a roller coaster ride was inadequately designed or faulty the biomechanical effects would result in a feeling of discomfort or even harm to the health of the passengers.
The ability of the human body to handle extreme g-forces was experimentally validated in the late 1940s by Col. John Stapp of the US Air Force [4, 5]. Stapp planned and conducted a series of tests on himself using a rocket-powered sled, known as the 'Gee Whiz' or 'Sonic Wind'. He strapped himself into the sled facing rearward, refusing anaesthetic because he wanted to study his reactions first-hand. Travelling at speeds greater than 65 m s−1 he was brought to an abrupt stop in less than 6 ms as he was crushed against the seat back. He is credited with proving that the human body can withstand elevated g-forces and survived a  impact, although in the process he suffered headaches, concussion, a fractured rib and wrist, and a haemorrhaged retina [3, 5].
impact, although in the process he suffered headaches, concussion, a fractured rib and wrist, and a haemorrhaged retina [3, 5].
Figure 1 illustrates the coordinate system used to describe the forces acting on a passenger. For example, as a roller coaster accelerates at launch we experience 'eyes back' or  that presses our body into the seat backward. The total force, X on the body from the roller coasters also needs to compensate for the force of gravity, so that the total acceleration will be
that presses our body into the seat backward. The total force, X on the body from the roller coasters also needs to compensate for the force of gravity, so that the total acceleration will be  , whereas the load on the body is characterised by
, whereas the load on the body is characterised by  . In contexts of biomechanical effects it is still customary to refer to
. In contexts of biomechanical effects it is still customary to refer to  as 'acceleration'.
as 'acceleration'.
Figure 1. Three-axis acceleration coordinate system for a seated roller coaster passenger based on [6]. The coordinate axes in the figure are commonly referred to as 'vertical' (z), 'longitudinal' (x) and 'lateral' (y) and rotate together with the rider, as illustrated in the picture to the right (the concluding heartline roll of the roller coaster helix [7]). It should be noted that the external force on the rider,  , is given by
, is given by  , and that it is customary to refer to
, and that it is customary to refer to  as 'acceleration'.
as 'acceleration'.
Download figure:
Standard image High-resolution imageTable 1 gives the maximum admissible acceleration to which a passenger should be exposed seated in a roller coaster—or in a space craft. For example, at launch a passenger could be exposed to a constant linear ax acceleration of  for more than 12 s or alternatively to a constant linear ax acceleration of
for more than 12 s or alternatively to a constant linear ax acceleration of  for no more than 1.5 s. This type of extended periods of constant large acceleration is unlikely in roller coasters, but would apply during launch of a space craft. It could also be achieved in a carousel moving with constant angular velocity, with the rider facing the centre, such as the classical rotor ride, or on the NASA 20g Ames Research Center's centrifuge.
for no more than 1.5 s. This type of extended periods of constant large acceleration is unlikely in roller coasters, but would apply during launch of a space craft. It could also be achieved in a carousel moving with constant angular velocity, with the rider facing the centre, such as the classical rotor ride, or on the NASA 20g Ames Research Center's centrifuge.
Table 1. Admissible amusement rides accelerations (i.e. values for a–g) for the x-, y- and z-directions depending on the time of exposure [6].
| Admissible acceleration | 0.2 s | 1.5 s |

|
|||
|---|---|---|---|---|---|---|
| min | max | min | max | min | max | |
| ax | −2.0g | +6.0g | −1.5g | +5.0g | −1.5g | +2.5g |
| ay | −3.0g | +3.0g | −2.5g | +2.5g | −2.0g | +2.0g |
| az | −2.0g | +6.0g | −1.5g | +5.0g | −1.1g | +2.0g |
Figures 2 and 3 are acceleration versus time onset graphs depicting the recommended acceleration exposures for different values of az and ax. Importantly they depict the threshold for admissible acceleration onset or jerk as  . Figure 4 depicts a typical acceleration versus time data plot of a roller coaster with the appropriate acceleration versus time onset (jerk) envelopes overlaid.
. Figure 4 depicts a typical acceleration versus time data plot of a roller coaster with the appropriate acceleration versus time onset (jerk) envelopes overlaid.
Figure 2. Recommended maximum acceleration durations for  and
and  as well as the negative values,
as well as the negative values,  and
and  . Also shown are the recommended maximum (dashed) and miniumum (solid) rates of onset or jerk, based on [6].
. Also shown are the recommended maximum (dashed) and miniumum (solid) rates of onset or jerk, based on [6].
Download figure:
Standard image High-resolution imageFigure 3. Recommended maximum acceleration duration for  and
and  as well as the negative values,
as well as the negative values,  and
and  . Also shown are the recommended maximum (dashed) and miniumum (solid) rates of onset or jerk, based on [6].
. Also shown are the recommended maximum (dashed) and miniumum (solid) rates of onset or jerk, based on [6].
Download figure:
Standard image High-resolution imageFigure 4. An example of analysis of a 'vertical' (+z) acceleration versus time diagram for a ride close to the back in the roller coaster helix [7]. The thin horizontal lines represent maximum allowed duration, whereas the thicker horizontal lines represent actual exposure at that level. The solid sloping lines represent average acceleration during the event. The dashed lines represent maximum and minimum onset of acceleration. According to [6] 'the acceleration exposure of a patron must always be beneath the envelop formed by the trapezium which is drawn by applying the onset acceleration, the maximum constant acceleration, and trailing edge acceleration'.
Download figure:
Standard image High-resolution imageReal roller coasters are complex three-dimensional contorted beasts with curves, loops and helixes and the engineer needs to combine all the accelerations and ensure that the passengers' exposure remains within tolerable design limits. Note that the coordinate axes in table 1 are fixed to the person, as shown in figure 1, and move and rotate together with the rider during a ride.
In most roller coasters, curves are banked to minimize lateral forces (ay). As long as the position of the body is essentially with the 'vertical' (z) axis (spine) orthogonal to the track, forces in the x direction are relatively small, apart from during launches and brakes. In other types of rides or in roller coasters, where e.g. riders rotate relative to the track, it is of particular importance to account for the combinations of the acceleration vectors. The maximum allowable acceleration exposure in each direction, shown in table 1, is then reduced by the combination, as indicated in the 'egg graphs' in figure 5. It can be noted that both ax and ay reach much smaller values than az.
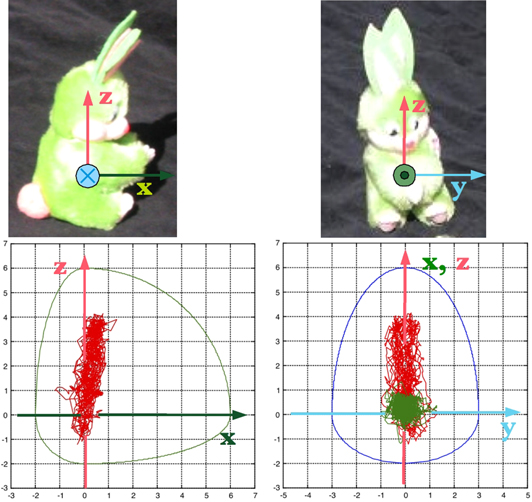
Figure 5. 'Egg graphs' showing the allowable combined effect of ax, ay and az accelerations for durations below t = 0.2 s, together with rabbits to illustrate the coordinates. The first graph shows the combinations for az and ax, whereas the second graph shows the combinations of ay with az, which is identical to the egg graph for the combination of ay with ax. In addition, accelerometer data from a ride in the middle of the train in the roller coaster helix, collected with a WDSS sensor [8] have been included for illustration. The slight slope of the data in the graph on the left may reflect a non-perfectly aligned sensor, causing leakage between the z and x components.
Download figure:
Standard image High-resolution imageThe 'egg' graphs depicted in figure 5 are usually defined as an assembly of elliptical curves.
4. Jerk and snap are common and can be dangerous and/or destructive
Consider the following statements: 'She jerked the phone out of his hands'; 'The bus jerked to a halt'; or 'The carriages jerked and jolted along as the train moved forward'. What do they tell us?
Driving in a car we can observe effects of velocity, acceleration and higher order derivatives. A more experienced driver accelerates smoothly, whereas a learner may produce a jerky ride. Changing gears with a manual clutch can cause the car to shudder along the road inducing both jerk and snap.
Jerk and snap can be observed in various areas of physics and engineering. In physics and engineering jerk and snap should always be considered when vibration occurs and particularly when this excitation induces multi-resonant modes of vibration. They should also be considered at all times when a transition occurs such as: start up and shutdown; take-off and landing; and accelerating and decelerating.
Acceleration without jerk is just a static load, and therefore constant acceleration alone could never cause vibration. In a machine shop, a toolmaker can damage the mill or the job if the setup starts vibrating. This vibration happens because of jerk and snap.
In mechanical engineering it is important in automotive design to ensure that the cam-follower does not jump off the camshaft. It is also important in manufacturing processes as rapid changes in acceleration of a cutting tool can lead to premature tool wear and result in an uneven and rough surface finish.
In civil engineering railway train tracks and roads should be designed for a smooth exit from a straight section into a curve, and it is common to use a transition called a clothoid, which is part of a Cornu spiral (also referred to as an Euler spiral). When a clothoid is implemented the change in acceleration is not abrupt and the levels of jerk and possibly snap are significantly reduced. If the transition between different radii of curvature is sudden, the transition is uncomfortable for passengers and potentially dangerous as it could cause the car or train to be thrown off the road or track. With good physics design engineers are attempting to produce a gradual jerk and constant snap, which gives a smooth increase in radial acceleration, or preferably a zero snap, constant jerk, and linear increase in radial acceleration. Just as road and railway engineers design out jerk and snap using the clothoid transition so, too, do roller coaster designers when they design loops and helices for the roller coasters [11, 12].
In greyhound racing the velocity can be more than 18 m s−1 and the abrupt transition from the straight to a circular bend results in a greater frequency of accidents and injuries.
5. Trampoline acceleration, jerk, snap and crackle
5.1. Theoretical model: free fall and harmonic oscillator motion
In a previous paper, trampoline jumps were analysed as a combination of free fall and harmonic oscillator motion [9]. The maximum upward force from the trampoline on the body with mass m is expressed as  , giving a maximum acceleration of
, giving a maximum acceleration of  . From the theoretical model in [9], combining harmonic motion with free fall, the total time between two jumps can then be expressed, using the parameter N as
. From the theoretical model in [9], combining harmonic motion with free fall, the total time between two jumps can then be expressed, using the parameter N as

where  is the period for small bounces, where the feet do not leave the mat.
is the period for small bounces, where the feet do not leave the mat.
As the feet reach the mat, the acceleration increases as part of a sine function which passes zero, as the jumper passes the equilibrium position (at the moment where the acceleration is 0 and the force from the mat is mg, compensating for gravity).
For the part of the jumping cycle where the trampolinist is in the air, acceleration is constant,  , and the jerk and all higher derivatives are zero. While the gymnast is in contact with the trampoline, the jerk can be described by a harmonic function, and each additional derivative adds a factor of ω and shifts sine to cosine or cosine to negative sine, respectively. The value of the jerk is zero when the acceleration is maximum. As the acceleration passes zero, the jerk has its maximum value
, and the jerk and all higher derivatives are zero. While the gymnast is in contact with the trampoline, the jerk can be described by a harmonic function, and each additional derivative adds a factor of ω and shifts sine to cosine or cosine to negative sine, respectively. The value of the jerk is zero when the acceleration is maximum. As the acceleration passes zero, the jerk has its maximum value  as the gymnast is on the way down, and a maximum negative value
as the gymnast is on the way down, and a maximum negative value  when the gymnast is on the way up. There may be a very small lag due to the inherent damping within the trampoline system.
when the gymnast is on the way up. There may be a very small lag due to the inherent damping within the trampoline system.
In the theoretical model, the jerk becomes a step function, in the moments when the feet reach or leave the mat. This leads to singularities in the higher derivatives. The derivative of the step function can formally be described by a Dirac delta function, which can be implemented using a number of different analytical functions. Each successive derivative of the delta function brings an additional maximum or minimum. The width and height of the approximate delta function and its derivatives depend on the implementation.
5.2. Authentic trampoline data
Figure 6 shows accelerometer data, together with its derivative, jerk, for five consecutive jumps on a gymnastic trampoline where force on the jumper reaches  (and the acceleration reaches
(and the acceleration reaches  ).
).
Figure 6. Acceleration (blue, in units of g) and jerk (red, in  s) during five consecutive bounces on a gymnastic trampoline. The red dots show the raw jerk data. Note that the acceleration is −|g| when the gymnast is airborne and at a maximum when the mat is a bottom-dead-centre. The snap and crackle are shown together with acceleration and jerk in figure 7.
s) during five consecutive bounces on a gymnastic trampoline. The red dots show the raw jerk data. Note that the acceleration is −|g| when the gymnast is airborne and at a maximum when the mat is a bottom-dead-centre. The snap and crackle are shown together with acceleration and jerk in figure 7.
Download figure:
Standard image High-resolution imageFrom equation (1) we find that a maximum force of around  corresponds to a ratio of about 3 between cycle time and the period for small oscillations. Figure 6 shows 4 periods in about 6.5 s, giving a period of 0.54 s for small bounces or
corresponds to a ratio of about 3 between cycle time and the period for small oscillations. Figure 6 shows 4 periods in about 6.5 s, giving a period of 0.54 s for small bounces or  , which is also the factor added for each successive derivative.
, which is also the factor added for each successive derivative.
The accelerometer data were collected with a sampling frequency of 100 Hz using a GPS Sports device and the derivative at a given time was obtained from the data points collected just before and after that time. These raw jerk data are shown as points in figure 6 and show large fluctuations, whereas the smoother solid line shows a 10 point running average.
Two jerk maxima were observed per jump cycle. The contacting or leading edge maximum where jerk maximum was positive and occurred nearly immediately after the trampolinist's feet contacted the mat, and the separating or trailing edge maximum where the jerk maximum was negative and occurred prior to the trampolinist's feet separating from the mat. From theoretical consideration we would expect a maximum around  , whereas, the five contacting maxima in the raw jerk data were between
, whereas, the five contacting maxima in the raw jerk data were between  and
and  . The averaging leads to slower rise than in the raw data, and also to smaller peak values for the jerk.
. The averaging leads to slower rise than in the raw data, and also to smaller peak values for the jerk.
Figure 7 shows the 10-point running averages for the higher derivatives snap and crackle for one of the jumps. As expected, each derivative brings an additional factor to the maximum of around ω: a snap minimum is of approximately  , is observed, as expected, when the acceleration is at a maximum, whereas the crackle has minimum and maximum values around
, is observed, as expected, when the acceleration is at a maximum, whereas the crackle has minimum and maximum values around  .
.
Figure 7. Acceleration in units of g (blue, solid), jerk in  (red, dashed, – –), snap
(red, dashed, – –), snap  (green, dotted, ···), crackle
(green, dotted, ···), crackle  (magenta, dash-dotted, ·–·–) during one bounce on a gymnastic trampoline. Note that the maximum snap occurred when the gymnast first made contact with the mat, i.e. during the transition period, although a larger negative snap values, occurs when the acceleration is largest, with a theoretical value
(magenta, dash-dotted, ·–·–) during one bounce on a gymnastic trampoline. Note that the maximum snap occurred when the gymnast first made contact with the mat, i.e. during the transition period, although a larger negative snap values, occurs when the acceleration is largest, with a theoretical value  . The acceleration and jerk for the same data set are graphed in figure 6.
. The acceleration and jerk for the same data set are graphed in figure 6.
Download figure:
Standard image High-resolution imageIn addition to these expected maxima and minima, we find two side maxima for the snap around the transition from air to mat or vice versa, and one snap minimum around the time the feet make contact with the mat and a maximum as the feet leave the mat. The averaging procedure makes the jerk and higher derivatives 'spill over' into the time interval when the gymnast is in the air. The values outside the contact time are results of the numerical procedures for derivation and averaging and can also be seen as approximation of the Dirac delta function (for jerk) and its derivatives (for jerk, crackle).
6. Jerks on roller coasters
Roller coasters involve transitions between many different types of motion. If the radius of curvature in a transition changes abruptly, it also leads to a sudden change in acceleration—a jerk. As an example, we consider a hypothetical circular loop suddenly changing to a straight track, which would mean changing from (at least)  to about
to about  at the bottom, in a very short time (and vice versa on the way into the loop). For a 20 m high loop, the speed would be at least 20 m s−1 at the bottom. For distance between wheel axles which is typically around 1 m, this would give a change in vertical force of at least
at the bottom, in a very short time (and vice versa on the way into the loop). For a 20 m high loop, the speed would be at least 20 m s−1 at the bottom. For distance between wheel axles which is typically around 1 m, this would give a change in vertical force of at least  in 0.05 s, corresponding jerk of about 80g s−1. In addition, there would be a sudden change in angular velocity, from
in 0.05 s, corresponding jerk of about 80g s−1. In addition, there would be a sudden change in angular velocity, from  to 0, giving an angular acceleration
to 0, giving an angular acceleration  . This combination was known to lead to whiplash injuries in the early 20th century roller coaster loop-the-loop coasters, e.g. at Coney Island [10]. Roller-coaster designer Werner Stengel has described how the clothoid was introduced to avoid sudden changes of radius of curvature [11]. Also other mathematical shapes are used where all derivatives are continuous [11, 12].
. This combination was known to lead to whiplash injuries in the early 20th century roller coaster loop-the-loop coasters, e.g. at Coney Island [10]. Roller-coaster designer Werner Stengel has described how the clothoid was introduced to avoid sudden changes of radius of curvature [11]. Also other mathematical shapes are used where all derivatives are continuous [11, 12].
Mechanical brakes in older roller coasters often lead to abrupt stops. In these cases, not only the rapid changes in force on the body contribute to a possibly uncomfortable experience, but also the uneven distributions of the forces over the torso of the rider. High jerk and snap within roller coasters also reduces the life of both the structure and cars. Also the gradients of the force on the body may be worth considering.
7. Conclusion
Jerk is a common everyday experience, but rarely mentioned in the teaching of mechanics. Still, minimising jerk is an important consideration from smooth driving of a car or bus to the design of roller coasters and other rides. The human tolerance to acceleration has been measured and is well understood. The human tolerance to jerk and snap is not well understood. Nevertheless, designers of roller coaster rides limit these to improve the passenger comfort of their rides. Roller coaster passengers need time to sense acceleration changes and adjust their muscle tension or suffer conditions such as whiplash. Even when human safety is not an issue physicists and engineers expend considerable design effort optimising jerk and eliminating snap within roller coaster rides to reduce maintenance and extend the life of the ride.