Abstract
We consider the fluid dynamics of the chocolate fountain. Molten chocolate is a mildly shear-thinning non-Newtonian fluid. Dividing the flow into three main domains—the pumped flow up the centre, the film flow over each dome, and the freely falling curtain flow between the domes—we generate a wide-ranging study of Newtonian and non-Newtonian fluid mechanics. The central pumped flow is a benchmark to elucidate the effects of shear-thinning. The dome flow can be modelled as a thin-film flow with the leading-order effects being a simple balance of gravity and viscosity. Finally, the curtain flow is analytically intractable but is related to the existing theory of water bells (both inviscid and viscous). In pipe flow, Newtonian fluids exhibit a parabolic velocity profile; shear-thinning makes the profile more blunted. In thin-film flow over the dome, gravitational and viscous effects balance and the dome shape is not important beyond the local slope. We find that the chocolate thins and slows down as it travels down the dome. Finally, in the curtain flow, we predict the shape of the falling sheet for an inviscid fluid, and compare this with the literature to predict the shape for a viscous fluid, having shown that viscous forces are too great to ignore. We also find that the primary effect driving the shape of the curtain (which falls inwards towards the axis of the fountain) is surface tension. We find that the three domains provide excellent introductions to non-Newtonian mechanics, the important mathematical technique of scaling, and how to manipulate existing data to make our own predictions. We also find that the topic generates interest among the public in our engagement work.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Chocolate fountains (see figure 1(a)) are a popular feature at special events. From table-top machines that are 30 cm tall, to large displays several metres tall, fountains normally consist of a series of stacked dome-shaped tiers over which melted chocolate flows, after being pumped up through a central tube from a basin at the bottom. The tiers are set far enough apart so that chocolate aficionados can enjoy dipping small food items (typically pieces of fruit or marshmallows) in the falling curtains of chocolate.
Figure 1. (a) The table chocolate fountain used for our experiments and the inside structure. (b) Our model of the fountain. Useful dimensions given in table 1.
Download figure:
Standard image High-resolution imageHow well the chocolate runs through the fountain is largely dictated by the viscosity of the fondue. Indeed, in order to keep it flowing smoothly and generating aesthetic curtains, operators are often seen to add liquids such as vegetable oil. The resulting mixture of chocolate fondue poses an interesting fluid mechanics problem, as it is non-Newtonian: this is to say, its viscosity depends on how it moves through the fountain.
The journey of the chocolate through the fountain consists of three distinct stages (see figure 1): being pumped to the top through the pipe, flowing as a thin film over the tiered domes, and falling freely as a curtain. The balance of forces experienced by the chocolate in each case is different, leading to three distinct dynamical regimes which can be investigated.
This project, then, offers the opportunity to introduce non-Newtonian fluid mechanics at an undergraduate level in a tasty and tactile way. It also introduces, at a more accessible level, the principles of mathematical modelling that are essential to applied mathematics: identifying different regimes (here, in the fountain) and then modelling these dynamical systems separately.
We perform easy experiments on an affordable table-top chocolate fountain2 (costing about £30) and then aim to use this data in models of liquid chocolate used by professional chocolatiers to make predictions of fluid profiles, and to answer questions that are not easily answered by observation. For example,
- What is the shape of the velocity profile inside the tube?
- Where is the chocolate falling fastest down the dome-shaped tier?
- When the chocolate falls, why does it fall inwards slightly, rather than straight down?
Since we use a few different models of chocolate, we also aim to discover when a simpler model captures enough of the desired features of the more complex model that it is 'good enough': an important consideration for any industrial modelling.
At a high school and popular mathematics level, we have used the results of this study of the fountain to introduce the aforementioned principles of mathematical modelling as well as generating interest in the scientific properties of other easily accessible, non-Newtonian foodstuffs. Fountains are found with other fondue choices (e.g. cheese or ketchup), and by classifying foods by their rheological properties, we try to identify other possible fondues!
In this paper, we investigate each regime in turn: the upwards flow through the centre of the fountain (see section 3); the film flow over each dome (see section 4); and the freely falling curtain flow (see section 5). We present results within each section, and our overall conclusions in section 6.
The mathematics of each section come from different eras: pressure-driven flow through a pipe starts in 1846 [19], thin-film flows from 1886 [21], and falling shapes of fluid from 1959 [23]. But these problems continue in current research: for example, there is recent work in both screw-driven pipe flows [4] and in curtain flows [10]. More sophisticated understanding of the mechanics of the chocolate fountain requires delving into more modern results, which this project allows.
2. Modelling chocolate
The motion of any fluid is governed by the Navier–Stokes equations,
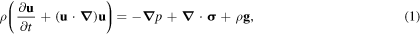
which are Newton's second law for a fluid. In every section it is this equation which we will be looking to solve. The terms on the left represent acceleration, and those on the right represent forces. The external force here is gravity,  and the internal forces are split into the pressure gradient,
and the internal forces are split into the pressure gradient,  and those due to viscosity, which are represented in the stress tensor,
and those due to viscosity, which are represented in the stress tensor,  Primarily, at any point in the fluid, the stress tensor is a function of the differences in velocity around that point, or how quickly the fluid is being sheared in each direction. These differences are represented by the rate of strain tensor,
Primarily, at any point in the fluid, the stress tensor is a function of the differences in velocity around that point, or how quickly the fluid is being sheared in each direction. These differences are represented by the rate of strain tensor,  which is defined in terms of the fluid velocity,
which is defined in terms of the fluid velocity,  as
as

Its magnitude, the shear rate,  is defined as
is defined as

where  is the (i, j)th component of the rate of strain tensor
is the (i, j)th component of the rate of strain tensor 
It is the definition of the stress tensor in terms of the rate of strain tensor—the constitutive equation—which gives rise to different fluid models. The relationship between the two may be as simple as being directly proportional, or it may include additional terms representing temperature, time, and historical values of all these quantities.
Using household multimeter temperature probes, we observed that in our fountain, the temperature of the chocolate remains constant at 40 ± 0.5 °C throughout its journey, so long as the fountain has been running for long enough (about thirty minutes). Wollny [25] states that to within one degree, the viscosity of chocolate should fluctuate between 5% and 10%. This allows us to treat the chocolate as isothermal, i.e. in our models, we do not have to include terms which relate to changes of temperature3 .
A fluid like ketchup exhibits time-dependence, or thixotropy, in the amount of time it takes, after shearing, for the microstructure of the fluid to realign to regain its viscosity. This is observable after shaking a bottle of ketchup: it remains pourable for about a minute. Only chocolate with a fat content of less than 30% exhibits thixotropy [2], and as the chocolate we use in our fountain4 has a fat content of 38%, we can neglect its effects here.
These observations pave the way for us to use models, plotted in figure 2, where the stress is merely a function of the rate of strain. The simplest fluid model we shall be using is the Newtonian model, where there is proportionality between these two quantities. First described in Newton's Principia, with the following history described in Franco and Partal [11], the scalar form is

where our viscosity, μn, (using a subscript 'n' for 'Newtonian') is constant. We shall use a representative viscosity of chocolate at 40 °C , at a typical observed shear rate of 10 s−1, of 14 Pa s [20]. The viscosity of honey is about 10 Pa s [18] so this is a plausible value.
Figure 2. The three constitutive equations we are using, equation (7): Newtonian (blue, —); power-law (red, – –), fitted from Radosasvljevic et al [20] (red, ◦); and Casson (green, ---), fitted from Wollny [25] (green, •); plotted with parameters from table 1. Data points were converted from graphs to data using the online WebPlotDigitizer program.
Download figure:
Standard image High-resolution imageThe typical observed shear rate here can be seen by simple ruler-and-stopwatch calculations, calculating the speed of a bubble on the surface of the chocolate as it falls over the dome. Assuming no-slip on the surface, the shear rate is estimated by dividing the speed by the thickness of the chocolate, also measurable with a ruler.
In Casson [8], another constitutive equation is provided, originally designed for printing ink, as

with parameters from industrial experiments with chocolate [17] given in table 1. Casson's model is a modification of the Newtonian model, requiring the stress to exceed a yield value, σy, before motion can occur (see that when plotted in figure 2,  for
for  ). In the limit of zero yield stress, it returns to the Newtonian model. It was recommended by the International Confectionery Association to model chocolate from 1973 until 2000, when Aeschlimann and Beckett [1] found that at low shear rates, it does not fit the experimental rheology data well. As such it was difficult to find repeatability, and so interpolation data was recommended instead [3, 22].
). In the limit of zero yield stress, it returns to the Newtonian model. It was recommended by the International Confectionery Association to model chocolate from 1973 until 2000, when Aeschlimann and Beckett [1] found that at low shear rates, it does not fit the experimental rheology data well. As such it was difficult to find repeatability, and so interpolation data was recommended instead [3, 22].
Table 1. Table of values found experimentally which we will use in comparison and scaling analysis.
| Pipe radius | a | 0.02 m |
|---|---|---|
| Dome radius | R | 0.07 m |
| Density of chocolate [24] | ρ | 1270 kg m−3 |
| Surface tension of chocolate [13] | γs | 0.0226 N m−1 |
| Characteristic dome film thickness | H | 0.001 m |
| Characteristic dome velocity | U | 0.1 m s−1 |
| Typical dome leaving velocity | u0 | 0.1 m s−1 |
| Characteristic sheet film thickness | H | 0.002 m |
| Estimated flux on dome | Q | 1.4 × 10−5 m3 s−1 |
| Gravitational acceleration | g | 10 m s−2 |
| Drop height | ℓ | 0.07 m |
| Newtonian apparent viscosity [20] | μn | 14 Pa s |
| Power-law flow consistency index [20] | μp | 64.728 Pa sn |
| Power-law flow behaviour index [20] | n | 0.3409 |
| Casson apparent viscosity [25] | μc | 5.60 Pa s |
| Yield stress of chocolate [25] | σy | 8.01 Pa |
Such interpolation data typically takes the form of a power-law model, where

Typical values for chocolate at 40 °C are, from industrial experiments [20], μp = 65Pa sn and n = 0.34. Fluids with 0 < n < 1, as our chocolate is, are called shear-thinning, and include ceiling paint and toothpaste among them. Fluids with n > 1 are called shear-thickening, of which a paste of cornflour and water is the best known. When n = 1, this model reduces to the Newtonian model. Observe that negative values of n are unphysical, as this implies infinite stress at no shear.
The three constitutive equations we will work with, then, now written in tensorial form [16], are



where  is the scalar shear rate defined in equation (3), and σ is the magnitude of the stress tensor,
is the scalar shear rate defined in equation (3), and σ is the magnitude of the stress tensor,  contracted in the same way.
contracted in the same way.
The scalar forms of these equations are plotted with values from table 1 in figure 2, along with data points from two different sources. Notice how different the models are, and how different the two sets of data points are, since we have no control over the ingredients of the chocolate tested in each case. These differences will run us into trouble later.
3. Pumped pipe flow
In this section, we introduce non-Newtonian fluids by examining the velocity profiles we would expect to see in a pipe, and comparing these to what we would see for a Newtonian fluid. Generating these profiles requires solving the governing Navier–Stokes equations, equation (1), after symmetry simplifications, and is a typical exercise in a undergraduate fluids course. This, therefore, provides a natural introduction to the topic, as well as being relevant to the chocolate fountain.
In our table chocolate fountain, chocolate is heated in the dish at the base of the machine, and is then transported to the top using a screw pump. The flow of the chocolate is driven by the moving boundary of the screw, but this internal motion of the fluid is noticeable only by a small amount of rotation as the chocolate exits the pipe, which quickly dissipates. On larger display fountains, the chocolate is instead driven through the vertical pipe by a pressure pump. While the mechanics of the screw pump are interesting (see Alves et al [4] for recent advances in this problem), choosing to model the pipe as a pump with a constant pressure gradient allows us to introduce relevant non-Newtonian fluid models within a domain that is familiar and well-understood.
3.1. Solving the governing equations
We attempt to solve the Navier–Stokes equations, then, equation (1), along with mass conservation for an incompressible fluid,

The radius of the pipe is a, and the natural choice is to use cylindrical coordinates (r, θ, z), so  etc.
etc.
Symmetry in the problem leads us to expect no motion in the r- or θ-directions, and to expect axial velocity to be merely a function of radial position, uz = uz(r). Furthermore, searching for steady flow solutions sets all time derivatives to zero. Under these conditions, the only non-zero components of shear rate are

and hence the only non-constant components of stress in all of our models are σrz = σzr.
These observations, along with denoting the constant pressure gradient,  by −G, reduce the Navier–Stokes equations to
by −G, reduce the Navier–Stokes equations to

Integrating equation (10) with the boundary condition from symmetry that σzr(0) = 0, and introducing the wall stress constant,

we see that the momentum equation is reduced to

where the relation between σzr and uz will depend on which model we choose.
In all our models, velocity boundary conditions on the pipe will be the no-slip condition, and a symmetry observation,

3.2. Expressions for the velocity
3.2.1. Newtonian model
In the Newtonian model, the stress term is

which when substituted into equation (12) and integrated with boundary conditions, equation (13), gives us the velocity profile we expect for Poiseuille flow,

Note that we should not be worried that r2 − a2 is negative: in the absence of a pressure gradient G, we would expect fluid to flow down the tube, in the negative z-direction.
With constant values from table 1, figure 3(a) shows this parabolic velocity profile.
Figure 3. (a) Velocity profiles of Newtonian (blue, —), power-law (red, – –) and Casson (green, - - -) pipe flows with an upward pressure of G = 2ρg and walls at r = ±2 cm. (b) Same profiles, as a percentage of their maximum.
Download figure:
Standard image High-resolution image3.2.2. Power-law model
In the power-law model, the stress term is given by

since  and
and  are the only non-zero components of the shear rate tensor. When substituted into equation (12), rearranged and integrated with boundary conditions, equation (13), we have the velocity profile
are the only non-zero components of the shear rate tensor. When substituted into equation (12), rearranged and integrated with boundary conditions, equation (13), we have the velocity profile

In the case  n = 1, this reduces to our Newtonian result. With constant values from table 1, the velocity profile is also shown in figure 3(a).
n = 1, this reduces to our Newtonian result. With constant values from table 1, the velocity profile is also shown in figure 3(a).
3.2.3. Casson's model
Substituting equation (12) into Casson's model, we have

for σzr > σy. We solve for uz by rearranging and integrating (with the boundary conditions, equation (13), again), and, specifying the yield stress,  we find
we find
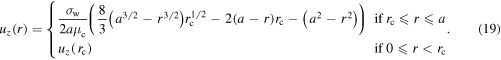
Rearranging equation (12) and using values from table 1 gives us an estimate for the critical radius rc of 2.4 mm, only 12% of the radius of the pipe. This velocity profile has been illustrated in figure 3(a).
3.3. Discussion of results
The Newtonian model exhibits the well-known parabolic velocity profile. In our shear-thinning models—the power-law and Casson models—the profile is more blunted and eventually a 'plug' of high-viscosity fluid forms in the centre of the channel. The plug flows with nearly uniform velocity, while the velocity gradients are confined to regions close to the wall.
Scaling all the profiles on their maxima to compare their shapes (see figure 3(b)), we see that with small rc, the Casson profile looks very similar to the parabola seen in the Newtonian case, with a slight flatness at the centre: indeed, equation (19) reduces to the Newtonian expression, equation (15), in the limit  With larger rc, it resembles much more closely the power-law profile, with the plug flow in the centre. However, in the Casson model, the flatness seen is a genuine plug: it is truly flat, with
With larger rc, it resembles much more closely the power-law profile, with the plug flow in the centre. However, in the Casson model, the flatness seen is a genuine plug: it is truly flat, with  in this area. In the power-law profile, the profile towards the centre is only approximately flat, forming instead a 'pseudo-plug', the flatness of which increases with the strength of shear-thinning of the fluid (as
in this area. In the power-law profile, the profile towards the centre is only approximately flat, forming instead a 'pseudo-plug', the flatness of which increases with the strength of shear-thinning of the fluid (as  ).
).
The maximum speed of the power-law fluid is 40% of the Newtonian maximum, which is itself 24% of the Casson fluid. These differences are to be expected and are not features of the models themselves, but rather because the parameters have been sourced from different industrial experiments. These results in the pipe will be compared with those from dome flow in the next section, and the similarity will allow us to disregard Casson's model from here on in, since its profile shape falls between the other two models.
4. Dome flow
In this section we aim to find, as the chocolate moves over the domed tiers of the fountain, the thickness of the chocolate at any given point, and the speed of the chocolate at any given point, just by using the measurable parameters from table 1.
How the chocolate moves on the dome is typical of the flow seen in a multitude of natural and technological applications, such as rain falling down a window, lava flowing down a volcano, or the coating of manufactured products: fluid thickness is much smaller than its other dimensions, the flow is predominantly in one of these other directions, and an external force (gravity) is driving the flow. This is an opportunity to show the power of scaling arguments, a very useful technique, but which is slightly awkward for the non-Newtonian model.
We model the dome as the top half of a sphere, but show that the analysis (and result) would work for any smooth shape, since the global curvature of the dome does not affect the motion of the fluid (mirroring other thin-film flows).
The two expressions we are looking for—thickness and speed—turn out to be interlinked, so we approach the problem in one go, starting from solving the governing equations.
4.1. Reducing the problem using scaling
Since we are modelling the dome as the top half of a sphere, we set up spherical coordinates (r, θ, ϕ) where θ is the inclination angle, 0 ≤ θ < π, and ϕ is the azimuthal angle, 0 ≤ ϕ < 2π. We label the radius of the sphere R, and the film thickness h. We expect axisymmetric flow so we can observe h = h(θ).
Again we are attempting to solve the Navier–Stokes equations, equation (1), expecting steady, axisymmetric flow, so we can set uϕ, and derivatives with respect to ϕ and time, to zero. Even with the simplifications afforded by this (e.g.  ) and our constitutive equations (e.g. hence
) and our constitutive equations (e.g. hence  ), scaling arguments need to be made to attempt an analytical solution.
), scaling arguments need to be made to attempt an analytical solution.
Scaling is an important technique that gives access to solving difficult problems by providing a rigorous method of deciding when variables are insignificant compared to others. The method is, for each variable, to divide through by a typical (characteristic) value, so that the resultant 'scaled', dimensionless, variables are all of the same order. Then we can compare terms by looking at the sizes of the resulting dimensionless groups of these characteristic values.
We introduce scaled variables (with hats) as follows:
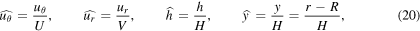
where y is a shifted (but still dimensional) radial coordinate which emphasizes the physical nature of the problem: the fluid occupies the space 0 ≤ y ≤ h. U and V are characteristic speeds in the θ- and r-direction respectively, H is a characteristic film thickness, and R is our already-established dome radius.
The continuity equation, equation (8), written in spherical coordinates, is
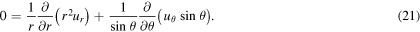
Substituting in the scaled variables gives us
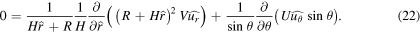
Then, since the two terms in the sum balance each other, the characteristic values should balance each other as well. Noting that  (since
(since  ), the characteristic values of both terms, respectively, are
), the characteristic values of both terms, respectively, are

Rearranged, this tells us

(since H/R is small) which tells us how these characteristic values interact with each other. In particular, it tells us what we already know: flow is predominantly in the θ-direction.
We then use the same scaling technique on the Navier–Stokes (momentum) equations in spherical coordinates. For example, the θ-momentum equation is
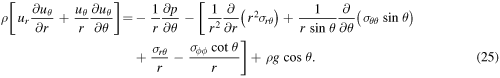
Introducing the scaled variables, we find that the sizes of these terms are

where we have marked by (?) the size of terms that we do not know. Dividing through by μ U/H2, the relative sizes are

where  and
and  is the Reynolds number: a non-dimensional number which is large in fast, low-viscosity flows; and is small in slow, high-viscosity flows. For a power-law fluid, the Reynolds number, is defined to be
is the Reynolds number: a non-dimensional number which is large in fast, low-viscosity flows; and is small in slow, high-viscosity flows. For a power-law fluid, the Reynolds number, is defined to be

since the viscosity is given by  Using the values from table 1, we find that for the Newtonian data,
Using the values from table 1, we find that for the Newtonian data,  and for the power-law data,
and for the power-law data,  Both of these are of the order we expect.
Both of these are of the order we expect.
In fact, here we have the 'reduced Reynolds number',  which is familiar in thin-film problems. Since the Reynolds number is of order 1, we are able to not only discount those viscous terms on the right-hand side of equation (27) which are multiplied by
which is familiar in thin-film problems. Since the Reynolds number is of order 1, we are able to not only discount those viscous terms on the right-hand side of equation (27) which are multiplied by  , but also the inertial terms on the left-hand side.
, but also the inertial terms on the left-hand side.
Using this process on the r-equation at this point, we can deduce the scaling for the pressure term using the same method as with the continuity equation, finding it to be negligible.
Putting this into the θ-equation, we continue our scaling analysis until we are left with

i.e., the viscosity term balances with the gravity term. This is what we would expect from a fluid with a low Reynolds number.
4.2. Solving the resultant equation
Recalling  we can substitute this into equation (29) and perform similar scaling arguments to arrive at
we can substitute this into equation (29) and perform similar scaling arguments to arrive at
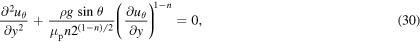
with boundary conditions

By writing  and defining
and defining  the differential equation becomes separable5
the differential equation becomes separable5

with solution

Integrating this with our boundary conditions, (31), gives us the expression for flow down the dome as
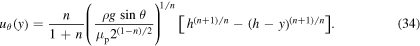
4.3. Using flux to solve our problem
Although we have found the expression for the velocity, equation (34), as desired, it relies on knowing the film thickness, h(θ), which is itself a function of angle down the dome. Fortunately we can introduce a constant, measurable quantity which allows to us find the thickness function h(θ). Once we have found this, we can put it back into our velocity expression.
This constant quantity is the flux. For this we have to assume that the flow is steady, i.e. there are no variations in the amount of chocolate being pumped out of the top of the pipe. Then at any time, since the chocolate falls down smoothly, the amount of chocolate passing through all points on the dome with some angle, is the same as the amount passing through any other set of points with another angle. In particular, at any given time, the amount of chocolate being pumped onto the top of the dome is the same as the amount of chocolate falling off the dome.
Mathematically, the flux, Q, is described by the velocity of the chocolate, integrated over the area it is passing through:

where the sin θ term before the integral comes from the 'flat radius' of the dome at any given angle θ, which varies through the chocolate from  to
to 
This integration appears unwieldy but requires simply an integration by parts. However, doing this would leave us unable to find an explicit expression for the film thickness h(θ). Instead we once again make the observation that the film thickness is much smaller than the radius of the dome, y ≤ h ≪ R, and so our flux expression becomes


where

Since we can measure the film thickness at any angle θ with simply a ruler, we choose to measure it at the base of the dome (θ = π/2). Using the measured value of 2 mm, as well as the other relevant parameters from table 1, the Newtonian model estimates a flux of 2.1 ml s−1, and the power-law model estimates 0.015 ml s−1: a considerable difference. Some intuition suggests this these are both too small: we can directly measure the flux by capturing all the chocolate that falls in a 10 s timeframe, measuring the volume, and dividing by 10 s. Doing so gives us a measured flux of 14 ml s−1.
Rearranging equation (37) to find an equation for the film thickness h(θ), having set our constant value of Q to be when θ = π/2, we find that

The simplicity of this result is surprising and satisfying: the film thickness for a power-law fluid at any angle is given by a single trigonometric function, scaled on the (easily measurable) final film thickness. This equation for both models has been plotted in figure 4, with final thickness h(π/2) = 2 mm.
Figure 4. Thickness profile of chocolate flowing over the dome (thick line) for the Newtonian (blue, —) and power-law (red, – –) models.
Download figure:
Standard image High-resolution imageWe also now use these expressions for film thickness, h, in our expression for the velocity of each fluid, uθ(y, θ), equation (34). Since the expression for velocity includes rheological parameters (from table 1), in order to compare the two models we have set the flux to be, in both cases, that which we measured in experiment.
The velocity has been plotted as a function of angle, at some film thicknesses, in figure 5; and at a fixed angle, at varying thicknesses, in figure 6.
Figure 5. Velocity of chocolate for the Newtonian (blue, —) and power-law (red, – –) models at a fixed flux, at, increasingly, heights y = h/8, h/4, h/2 and h.
Download figure:
Standard image High-resolution imageFigure 6. Velocity of chocolate for the Newtonian (blue, —) and power-law (red, – –) models at a fixed flux and angle, as a function of the fraction of the way through the thickness of chocolate. Observe the similarity to figure 3(b).
Download figure:
Standard image High-resolution image4.4. Discussion of results
We have found results which, from looking at figures 4 and 5 seem sensible. But the severe underestimate of the flux in equation (37) is troubling. Such a low estimate for the flux suggests that the parameters and boundary conditions we have used lead to very slow flow. Indeed, equation (34) suggests a velocity at the upper surface of the chocolate, when it is about to fall off, of 17 μm s−1 for the power-law case, many orders of magnitude smaller than the observed speed of 10 cm s−1.
We should note, though, the sensitivity to our measurements. Our expression for the flux, equation (37), shows that  In our power-law model, n = 1/3, so we have Q ∝ h5: clearly this expression for the flux is highly sensitive to the accuracy of our height measurement. However, the height of the film was measured quite crudely, by placing some paper in the film and measuring the height of the chocolate left on the paper. A measured final height of 1 mm leads to a power-law final velocity of 1 μm s−1, whereas a final height of 2 mm leads to a velocity of 17 μm s−1: a significant difference which we need to be careful about when we have such primitive measurements. Indeed, this is a typical problem when data-fitting for strongly shear-thinning fluids.
In our power-law model, n = 1/3, so we have Q ∝ h5: clearly this expression for the flux is highly sensitive to the accuracy of our height measurement. However, the height of the film was measured quite crudely, by placing some paper in the film and measuring the height of the chocolate left on the paper. A measured final height of 1 mm leads to a power-law final velocity of 1 μm s−1, whereas a final height of 2 mm leads to a velocity of 17 μm s−1: a significant difference which we need to be careful about when we have such primitive measurements. Indeed, this is a typical problem when data-fitting for strongly shear-thinning fluids.
A likely inaccuracy is the 'no-slip condition', the first statement in equation (31): it may be that the chocolate is slipping over the dome surface. If we instead knew this speed on the boundary, our theory would provide higher speeds, perhaps better matching the observed flux.
Another source of inaccuracy is our rheological parameters. Despite extracting data from sources for milk chocolate at 40 °C , there is still a large variety of different chocolates, made in different ways and with different proportions of ingredients. The large difference in the two pieces of data in figure 2 is typical of what we find when trying to source rheological data. That the prediction for the fluid is so small, suggests that the chocolate is not as viscous as our data suggests. Indeed, in section 3, figure 3(b) showed that the parameters in the Casson model—a model since discounted as displaying intermediate behaviour between the Newtonian and power-law models—predict much higher speeds in the pipe, which would transfer to higher flow speeds here as well.
Rather than take the data to predict the speed and thickness, it would be nice to be able to measure these to infer the rheological parameters. With accurate measuring equipment, it should be possible to solve equation (37) for the power-law parameters, μp and n, if we can measure accurately the height of the fluid in two places on the dome. However, without such equipment to test it ourselves, this is the best we can do, and so it serves as a useful lesson on the uncertainty of rheological measurements.
A final source of error could be that we assume that the chocolate runs steadily down the dome. On closer observation, it tends to come down in waves, as it is pushed out of the top of the pipe. However, this should not account for the wildly small velocity prediction.
Problems aside, let us have a look at the results. The velocity profiles for each fluid from equation (34), when plotted at different film thicknesses in figure 6, match the velocity profiles for half a pipe flow from the previous section. The plug flow seen for the power-law model is also seen in the dome flow. This is not surprising, as when we arrive at equation (29), we see that the curvature of the problem has disappeared. The balance of viscosity and gravity is what we would find for a fluid travelling down an flat inclined plane at an angle, θ, to the horizontal. In other words, to leading order in the film aspect ratio, the fluid does not experience the curvature of the substrate. Although we have modelled the dome as a hemisphere, we could choose any smooth shape for the dome and the velocity profiles would still describe the flow for each locally sloped piece of surface.
The velocity profiles in figure 5 show that the shear-thinning power-law fluid is slower than the Newtonian fluid at varying film thicknesses throughout the majority of flow (matching our observation in the pipe) although close to the surface of the dome, it begins to match it.
In figure 4, we can see that both models give qualitatively the same thickness profile, well up to high enough on the dome where the flow would be affected by the previous part of the fountain. Given the complication of the power-law model for no further insight, use of the Newtonian model for further work here would be sufficient.
5. Curtain flow
This section is driven by the questions 'why does the chocolate sheet fall inwards?' and 'can we predict how far inwards it will fall?'.
When we look at our table fountain, we see that when the chocolate is running smoothly, it falls inwards around 3 cm for every 10 cm it falls. Such curtain flow is a difficult problem and is often found in industrial coating [10]. The difficulties come from three main sources:
- (1)the sheet has two free boundaries,
- (2)the relation between sheet thickness and distance along the sheet is unknown,
- (3)the locations of the sheet's free surfaces are also unknown.
When watching the fountain, we can see that the curtain moves inwards and outwards erratically. Holes appear and disappear at the bottom of the sheet continuously while it fluctuates, ranging in height from less than a centimetre to the full height of the drop.
In order to start on this interesting problem, the way in we propose here is through the analysis of water bells (see figure 7(a)). These are inverted-teardrop-shaped water features that form from water which is jetted onto a small disc (typically the size of a small coin) and then forced outwards: essentially the 'water hitting a spoon' effect. If left to continue, the water bell is pulled back round by surface tension, to close at the bottom. It is the bottom half of the bell which reminds us of the fountain (see figure 7(b)).
Figure 7. (a) A water bell made in the kitchen: this experiment is unexpectedly easy to perform, requiring just a tap, a pen, a coin secured to the top of the pen, and something to stand the pen up in. (b) Fitting the chocolate fountain (dotted) into the setup of the water bell. In this way we use the bottom half of the bell to represent the falling sheet of chocolate.
Download figure:
Standard image High-resolution imageTreating the fountain as a water bell means making a lot of assumptions: that the flow is smooth and continuous, that it is not affected by the shape of the rim of the dome, and that the liquid is inviscid. Despite finding Reynolds numbers in section 4.1 of  or 2.9 (depending on the model), which indicate viscous flow, it is not clear that these values apply to curtain flow. The Reynolds number, when defined in section (28), uses the dome radius, R, as a typical lengthscale that the fluid travels. In a general curtain flow, the fluid falls as a sheet for an unspecified distance, so it is not obvious what the relevant lengthscale should be. Ideally the lengthscale should be one over which the flow varies, but it is not clear how the velocity varies in the sheet: if we took the lengthscale to be the typical sheet thickness of 2 mm (from table 1), then
or 2.9 (depending on the model), which indicate viscous flow, it is not clear that these values apply to curtain flow. The Reynolds number, when defined in section (28), uses the dome radius, R, as a typical lengthscale that the fluid travels. In a general curtain flow, the fluid falls as a sheet for an unspecified distance, so it is not obvious what the relevant lengthscale should be. Ideally the lengthscale should be one over which the flow varies, but it is not clear how the velocity varies in the sheet: if we took the lengthscale to be the typical sheet thickness of 2 mm (from table 1), then  or 0.08, values for which an inviscid model might be appropriate. Furthermore, an inviscid approach allows us to analytically derive a solution, whereas finding a viscous prediction requires numerical work which is beyond the scope of the project.
or 0.08, values for which an inviscid model might be appropriate. Furthermore, an inviscid approach allows us to analytically derive a solution, whereas finding a viscous prediction requires numerical work which is beyond the scope of the project.
Although we start by solving the inviscid problem, we are still able to achieve an appropriate viscous, Newtonian prediction. Numerical work by Gilio et al [12] gives a relationship between an inviscid and an appropriate, viscous prediction. We choose parameters in their results which map our inviscid prediction onto theirs, thereby reading off a viscous prediction. This is described in section 5.2.
Finding an inviscid result will require extensive scaling arguments, as this is another example of thin-film flow, this time driven by gravity and surface tension.
5.1. Solving the water bell problem
The water bell problem was first investigated by Taylor and Howarth [23], where they derived an equation of motion for a water bell trajectory. Assuming the flow to be axisymmetric, we can take a vertical slice of the curtain (see figure 8) and consider the forces acting on a fluid element: gravity, surface tension, and internal and external pressure difference.
Figure 8. The balance of forces acting on a vertical slice of the falling curtain.
Download figure:
Standard image High-resolution imageThe form of the gravitational force is as we would expect (mass of the fluid element multiplied by acceleration due to gravity); and the pressure force is given by multiplying the volume of the element by the pressure difference, set in the direction normal to the curtain. The force due to surface tension is given by the Young–Laplace equation, again multiplied by the volume of the element and set in the normal direction.
By balancing these forces and resolving (with suitable non-dimensionalization in the style of the previous chapter), Taylor and Howarth found a relationship between the velocity, u(z), and distance of the sheet from the pipe in the centre of the bell, r(z), both functions of vertical distance below the bottom of the dome, z. Some later trigonometric simplifications by Brenner [5, equations (13)–(15)] lead to

the process of which is explained fully in Button [7, ch 5].
This equation has some given initial conditions: r(0) = r0, the scaled radius of the dome; and r'(0) = v0, specifying the angle at which the curtain begins its fall. The problem depends on two physical parameters: α accounts for the effect of the inside–outside pressure difference, and β accounts for gravity. They are discussed more in section 5.3.2, but are given by
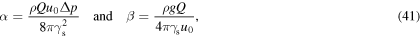
where we can see they are composed of terms we would expect from the three forces we are balancing: γs is surface tension; Δp is the pressure difference between the inside and outside of the sheet; and g is the acceleration due to gravity. We also have u0, our initial velocity; and Q, the (constant) flux.
We assume that the sheet is sufficiently thin so that we can assume the velocity to be constant through a cross-section at a given height. Since the surface of the liquid film is itself a streamline and this model is for inviscid fluid, we can use Bernoulli's equation for any arbitrary point along a streamline where gravity is constant:

noting that we have switched the sign on the  term from the usual convention, as we are measuring z downwards.
term from the usual convention, as we are measuring z downwards.
Since the streamline is also a free surface, the pressure, p, on it is constant, so it can be absorbed into the right-hand side. With the non-dimensionalized boundary conditions u = 1 at z = 0, Bernoulli's equation reduces to

which expresses the increase of momentum in the direction of the flow due to the acceleration of gravity.
We are left with the complete governing equations, equations (40) and (43), to solve. Analytically this is only possible where α = β = 0. Since we do not expect any significant pressure difference between the inside and outside of the sheet, we can set α = 0. However, we cannot say this for β, since this is the Bond number (or Eötvös number), which represents the balance of gravitational forces to surface tension forces which we are left with from figure 8. With values from table 1, we find β = 6.3.
An approach we can take is to consider the β ≫ 1 limit, where the the flow is dominated by gravity rather than surface tension. In this limit, the curtain, starting at r(0) = r0 (the scaled radius of the dome), falls further downwards than it does inwards, and we can express r as a regular series in 

Differentiating, we have

and substituting this into equation (40) and taking the leading order terms, we have

Rearranging for  and taking the leading order term from equation (45), we are left with
and taking the leading order term from equation (45), we are left with

which we can substitute into equation (43).
Integrating the resulting equation with the boundary condition r(0) = r0, we have an expression for the sheet profile r(z),

This equation (in dimensional form) has been plotted in figure 9, with data from table 1.
Figure 9. Falling sheet profile predictions for inviscid (orange, ––) and viscous (blue, —) cases, as well as the observed falling profile over 7 cm (pink, ⋯).
Download figure:
Standard image High-resolution image5.2. Mapping the inviscid result onto viscous data
Finding an equivalent profile for even a Newtonian viscous liquid requires numerical work, and we were pleased to find Gilio et al [12], where they study both inviscid and viscous two-dimensional, falling, nonsteady liquid sheets. They derive governing equations using a different method, and solve their viscous equations numerically, using finite-difference methods.
In their viscous model they use a fluid with Newtonian viscosity 10 Pa s, close to our chocolate value of 14 Pa s. We were able to manipulate our inviscid graph, from equations (40) and (43) to fit theirs, to find an equation governing the viscous velocity.
We do this by scaling the velocity plots from [12, figure 6] to match our inviscid results in equation (43). The viscous profile is remarkably linear and can be extracted from their graph, in non-dimensional form, as

We can substitute this velocity into equation (47) to find an equation governing the position of the viscous sheet, namely

In this way we now have a viscous prediction for the profile of our falling sheet, and this has also been plotted (in dimensional form) on figure 9.
5.3. Discussion of the results
The inviscid velocity profile, equation (43), is somewhat validated by the results of Brunet et al [6]. They use a silicon oil with similar density and surface tension to chocolate (ρ = 970 kg m−3, γs = 20.4 mN m−1), but with a viscosity of 0.2 Pa s, which is smaller than that of chocolate (but considerably higher than water). They find by direct measurements that equation (43) is a reasonable approximation of their results.
Comparing the inviscid sheet profile with the observed falling profile in figure 9, we see that the sheet falls inwards due to surface tension with slope of the same order we expect. However, it predicts that the sheet falls in about 3 cm over the 7 cm drop, when we measure in experiment about half of that. Secondly, in our observations, the sheet starts falling at a slant, rather than downwards, and we have lost the ability to set r'(0) in performing the perturbation analysis in equation (5.1), which reduced the order of the governing equation. The viscous sheet prediction, however, falls 1.5 cm inwards, better matching our observations.
5.3.1. Validity of inviscid approximation
Having derived profiles from two models, we now show that we expect the inviscid model to fare poorly, since the viscous effects are expected to be significant. We compare the total energy in the system with the amount used in the work done by viscous forces in the falling fluid. We find that even in the least-possible case for the viscous forces, they are of comparable size, meaning that ignoring viscous forces, as we have done in our inviscid approximation, is unlikely to give us good results.
We start by finding the total energy in the system, i.e. the sum of kinetic and gravitational energy. The velocity in our sheet is predominantly vertical, occupying in cylindrical polar coordinates the (dimensional) region V, given by R ≤ r ≤ R + h, 0 ≤ θ < 2π, 0 ≤ z ≤ ℓ, recalling that the z-axis points downwards. Then the kinetic energy EK in the system is given by
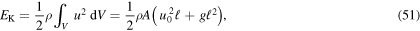
where

the cross-sectional area of a horizontal slice of the curtain.
The gravitational potential energy EP of the system is given by

Therefore the total energy instantaneously in the falling sheet, when we plug in the parameters from table 1, is EK + EP = 0.044 J.
We want to compare this with the amount of energy dissipated as the sheet falls. Cauchy's energy equation for the rate of energy dissipation, K, due to viscosity in a viscous Newtonian fluid of volume V and viscosity μ is given by [15]

Here,  is the scalar shear rate, first introduced in equation (3). Given that the velocity in our sheet is predominantly vertical, we say that the dominant rate of strain tensor component is
is the scalar shear rate, first introduced in equation (3). Given that the velocity in our sheet is predominantly vertical, we say that the dominant rate of strain tensor component is  given by du/dz. In dimensional form, equation (43) is given by
given by du/dz. In dimensional form, equation (43) is given by

which we can differentiate to find, substituting in 

Incompressibility in the fluid ( ) requires that the shear rate tensor is traceless. We then have some flexibility with values of the other diagonal rate of strain elements
) requires that the shear rate tensor is traceless. We then have some flexibility with values of the other diagonal rate of strain elements  and
and  The least energy change rate in equation (54) occurs when
The least energy change rate in equation (54) occurs when  and the most when
and the most when  and
and  Given that we are looking for a lower bound on the energy dissipation, we take the least-case scenario and after substituting into equation (54), we get
Given that we are looking for a lower bound on the energy dissipation, we take the least-case scenario and after substituting into equation (54), we get
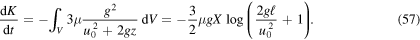
Again with the parameters from table 1, we find that in a tenth of a second, an estimate for how long it takes chocolate to complete its fall, in the least-case scenario, the energy dissipated by viscous forces K is 0.046 J.
We have shown that, if we use an inviscid model to predict the fluid velocity of our viscous fluid, the dissipation we have neglected is as large as the total energy in the system. Though our energy estimates are rough, it is clear that the neglect of viscous effects is not justifiable, and we can expect the inviscid approximation to give poor predictions.
5.3.2. Importance of physical parameters
The governing equation for our sheet position and velocity profiles, equation (40), relies on the physical parameters α and β, given in equation (41).
Since the pressure difference is negligible, given that the falling sheet never forms an airtight seal, we set α = 0, but we can see that the Bond number, β, depends on physical parameters of the chocolate.
Figure 10 shows the profile of the falling sheets in the inviscid and viscous cases for substances with different values of β. Lower values of β, corresponding primarily to increased surface tension since the densities are of similar order, bring the sheet in further. Interestingly, it affects the viscous sheet more than the inviscid sheet, with the viscous sheet falling further inwards in the higher surface tension case than the inviscid prediction.
Figure 10. Falling sheet profile predictions for viscous (blue, —) and inviscid (orange, ––) cases for fluids with different values of β: (i, light) water at 25 °C (β = 1.5, since  , ρ = 997 kg m−3); (ii, dark) chocolate (β = 6.3); (iii, light) liquid nitrogen at −196 °C (β = 10.1, since γs = 8.9 mN m−1, ρ = 806 kg m−3) [9]. Dotted line (pink, ⋯) represents observed chocolate profile, as in figure 9.
, ρ = 997 kg m−3); (ii, dark) chocolate (β = 6.3); (iii, light) liquid nitrogen at −196 °C (β = 10.1, since γs = 8.9 mN m−1, ρ = 806 kg m−3) [9]. Dotted line (pink, ⋯) represents observed chocolate profile, as in figure 9.
Download figure:
Standard image High-resolution image6. Conclusions
6.1. Physical conclusions
From our analyses in the three separate domains of the fountain, we have found how the chocolate moves round the fountain under different models, and were able to compare them to what we see with our actual fountain. In short:
- Pumped pipe flow. For power-law flows, plug flow is expected in a pipe with a pressure gradient. For Newtonian flows, a parabolic flow is expected. The analysis here allows us to narrow our choice of models to just two.
- Dome flow. Gravitational and viscous effects balance, and the dome shape is not important beyond the local slope. The chocolate thins and slows down as it travels over the dome. The Newtonian model performs as well as the power-law model in predicting the thickness of the chocolate.
- Curtain flow. Surface tension is the dominating factor in pulling the sheet inwards. An inviscid model is not expected to predict well how far inwards the sheet will fall, but a viscous one would.
6.2. Pedagogical conclusions
We have taken a novelty, engaging consumer item and presented a project which uses it to introduce the world of non-Newtonian fluid mechanics. Moreover, we have found that it works particularly well in bringing this exciting area of research to many different levels of technical ability.
The process of deriving the key results is necessarily mathematical, and highly suited to a final-year undergraduate course or project. Breaking the fountain into its three natural components, we see that each serves a distinct and valuable educational purpose.
- Pumped pipe flow. Pressure-driven flow in a pipe is a simple flow problem, ideal for developing the theory of non-Newtonian fluid flow and investigating the phenomenology of different model fluids. Students will have met this problem for Newtonian flow before in a fluids course, so it serves as a reminder as well as an interesting extension.
- Dome flow. Thin-film flow over the dome provides an introduction to lubrication theory, by the use of scaling, an important technique which may have been seen already in a different area of applied mathematics. With very mild constitutive assumptions, analytical solutions can be calculated for power-law as well as Newtonian fluids.
- Curtain flow. Finally, the curtain or sheet region in which the molten chocolate falls freely under gravity is intractable analytically (and beyond the scope of an undergraduate level project to solve numerically). However, perturbation analysis allowed us to find a first prediction. After this, we moved onto finding and interpreting relevant existing literature, working out how to convert existing numerical results to our situation by scaling for our values of viscosity, film thickness and speed. At a research level, the falling sheet leaves the greatest opportunity for further work.
Although the level of mathematics required to derive this is high, the results, however, we have found to be very much of interest to the general public in our engagement work. That general foodstuffs can be divided into different rheological classes based on whether they are shear-thinning, shear-thickening, or simply Newtonian, is interesting; but that we can describe them all mathematically with the power-law model, simply by changing the parameter n, shows the power of mathematics. We have found that showing audiences the effect of varying n on viscosity–shear rate graphs allows them to appreciate why mathematics is important in describing the world. Also, that surface tension brings the chocolate fountain inwards as it falls, settles a debate which chocolate enthusiasts have long wondered about.
The subject matter is intrinsically attractive (tasty, even!) and we hope that others get the opportunity to learn about this area of mathematics with their own chocolate fountain.
Footnotes
- 2
- 3
For thin-film dome flow with a non-isothermal Newtonian fluid, see Leslie et al [14].
- 4
- 5
We would like to thank the reviewer for this observation.











