Abstract
I present a brief review of the Landau Fermi-liquid theory of the normal and superfluid phases of liquid  , with emphasis on its philosophy, its successes and its limitations.
, with emphasis on its philosophy, its successes and its limitations.
Export citation and abstract BibTeX RIS
Invited by Laura Greene
1. Introduction
When I was asked to write an article for this volume, the provisional title I was given was 'Foundations of correlations in Fermi liquids: origins in 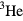 '. Now it is certainly true that liquid
'. Now it is certainly true that liquid 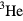 is historically the first strongly interacting system of fermions of which we have been able to obtain a semi-quantitative description in the low-temperature limit; however, this pleasant state of affairs seems likely to be due, first, to the rather simple degrees of freedom characterizing it, and secondly to a serendipitous separation of energy scales. So it is not entirely clear how far our understanding of the low-temperature behavior of liquid
is historically the first strongly interacting system of fermions of which we have been able to obtain a semi-quantitative description in the low-temperature limit; however, this pleasant state of affairs seems likely to be due, first, to the rather simple degrees of freedom characterizing it, and secondly to a serendipitous separation of energy scales. So it is not entirely clear how far our understanding of the low-temperature behavior of liquid 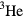 (which I will try to quantify below) will assist us in our attempts to grapple with that of more complex systems where neither of these features may be realized. At any rate, in this article I shall try to review what we do and do not understand quantitatively about liquid
(which I will try to quantify below) will assist us in our attempts to grapple with that of more complex systems where neither of these features may be realized. At any rate, in this article I shall try to review what we do and do not understand quantitatively about liquid 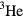 , on the basis of Landau's Fermi-liquid theory and its generalization to the superfluid phases.
, on the basis of Landau's Fermi-liquid theory and its generalization to the superfluid phases.
One thing should be emphasized at the start: when we say that we have a 'semi-quantitative' understanding of the properties of liquid 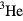 , this claim is really justified only over a rather small region of the parameter space. To define this region, let us consider a gas of noninteracting fermions with the same mass and density as real liquid
, this claim is really justified only over a rather small region of the parameter space. To define this region, let us consider a gas of noninteracting fermions with the same mass and density as real liquid 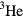 at saturated vapor pressure. Then the Fermi wave vector qF is approximately 1 Å−1, and the corresponding Fermi energy EF and Fermi temperature TF respectively approximately
at saturated vapor pressure. Then the Fermi wave vector qF is approximately 1 Å−1, and the corresponding Fermi energy EF and Fermi temperature TF respectively approximately 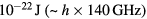 and 7 K. Then the theory to be described below is believed to be quantitatively valid only when the temperature, and the wave vector q and frequency ω of the probe applied to the liquid, satisfy the conditions
and 7 K. Then the theory to be described below is believed to be quantitatively valid only when the temperature, and the wave vector q and frequency ω of the probe applied to the liquid, satisfy the conditions
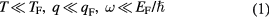
Moreover, the probe in question should be sufficiently weak that it can be treated in linear approximation, and the magnetic field B (if any) should satisfy 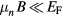 . Over the (much larger) remainder of the parameter space when the above conditions are not satisfied, the theory gives at best a qualitative picture. In practice, it seems to agree quantitatively with experiment only for
. Over the (much larger) remainder of the parameter space when the above conditions are not satisfied, the theory gives at best a qualitative picture. In practice, it seems to agree quantitatively with experiment only for 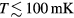
In section 2 I describe the physical characteristics of the system and briefly compare and contrast it with other strongly correlated Fermi systems. In section 3 I review our understanding of the normal phase of the liquid, and in section 4 do the same for the superfluid phase (or rather phases). Section 5 is a brief conclusion. I assume familiarity with the BCS theory of superconductivity as presented in standard textbooks. Very little of the discussion below is original (indeed, much of it is more than 40 years old!), and the bibliography is certainly not intended to be exhaustive.
2. Physical properties of liquid 3He [1]
Apart perhaps from gaseous hydrogen and its heavier and more plentiful cousin 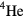 , a collection of
, a collection of  atoms is probably the simplest many-body system actually found in nature. The electronic groundstate of the
atoms is probably the simplest many-body system actually found in nature. The electronic groundstate of the 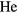 atom (of either species) is (1s)2 1S0 and thus has no orientational degrees of freedom associated with it; the lowest excited state has excitation energy ~20 eV, so that its probability of occurrence at any temperature where the system is liquid is completely negligible. The interaction potential between two
atom (of either species) is (1s)2 1S0 and thus has no orientational degrees of freedom associated with it; the lowest excited state has excitation energy ~20 eV, so that its probability of occurrence at any temperature where the system is liquid is completely negligible. The interaction potential between two 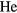 atoms has been the subject of many calculations, of which the most sophisticated output is probably the Aziz [2] potential; for our purposes it will be enough to represent it by a simple van der Waals form with a minimum of depth
atoms has been the subject of many calculations, of which the most sophisticated output is probably the Aziz [2] potential; for our purposes it will be enough to represent it by a simple van der Waals form with a minimum of depth 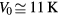 at distance
at distance 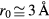 . Since the density of
. Since the density of 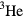 at melting pressure is
at melting pressure is 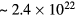 atms cm−3, this means that the ratio of
atms cm−3, this means that the ratio of  to the interparticle spacing is ~0.85, and the ratio of
to the interparticle spacing is ~0.85, and the ratio of 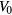 to the Fermi energy calculated for the corresponding noninteracting gas is ~1.6. Thus, liquid
to the Fermi energy calculated for the corresponding noninteracting gas is ~1.6. Thus, liquid 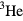 is indeed a 'strongly interacting' system.
is indeed a 'strongly interacting' system.
The nucleus of the 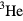 atom differs from that of
atom differs from that of 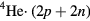 by containing two protons but only one neutron and has spin 1/2; hence, in consequence of the standard spin-statistics relation, a system of
by containing two protons but only one neutron and has spin 1/2; hence, in consequence of the standard spin-statistics relation, a system of 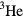 atoms obeys Fermi statistics. rather than the Bose variety obeyed by
atoms obeys Fermi statistics. rather than the Bose variety obeyed by  . A second difference is that associated with the spin is a small magnetic moment
. A second difference is that associated with the spin is a small magnetic moment 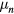 (
(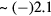 nuclear magnetons), and this gives rise to an additional interatomic interaction which has the standard dipole–dipole form
nuclear magnetons), and this gives rise to an additional interatomic interaction which has the standard dipole–dipole form 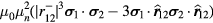 . The absolute magnitude of this term (
. The absolute magnitude of this term (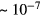 K at
K at 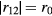 ) is very small compared to the spin-independent van der Waals term, but since unlike the latter it is not invariant under rotation of the spin and orbital coordinates separately, it turns out to have spectacular effects in the superfluid phases (see section 4).
) is very small compared to the spin-independent van der Waals term, but since unlike the latter it is not invariant under rotation of the spin and orbital coordinates separately, it turns out to have spectacular effects in the superfluid phases (see section 4).
Most other strongly correlated Fermi systems lack the simplicity of liquid 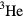 . The nucleons in nuclear matter, while less strongly interacting, are subject to tensor (spin–orbit) forces which are comparable in strength to the spin-independent ones, and in addition possess an extra degree of freedom (isotopic spin). The electrons in solids interact with the crystal lattice and thus lack the property of translation invariance enjoyed by
. The nucleons in nuclear matter, while less strongly interacting, are subject to tensor (spin–orbit) forces which are comparable in strength to the spin-independent ones, and in addition possess an extra degree of freedom (isotopic spin). The electrons in solids interact with the crystal lattice and thus lack the property of translation invariance enjoyed by 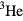 ; in addition, in many cases crystal-field and other effects strongly break rotational invariance even of the spin degree of freedom. The only currently realized Fermi system which might claim a simplicity comparable to that of liquid
; in addition, in many cases crystal-field and other effects strongly break rotational invariance even of the spin degree of freedom. The only currently realized Fermi system which might claim a simplicity comparable to that of liquid 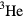 is (electronically) spin-polarized gaseous deuterium (but this is actually a spin-1 Fermi system, see e.g. [3]). Thus
is (electronically) spin-polarized gaseous deuterium (but this is actually a spin-1 Fermi system, see e.g. [3]). Thus 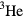 appears to be rather unique.
appears to be rather unique.
3. The normal state
In the regime of low temperatures, long wavelengths and small frequencies and low magnetic fields (see section 1 for a more precise statement) an excellent description of the behavior of liquid 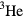 is given by the classic 'Fermi-liquid' theory of Landau [4]. This theory has been exhaustively reviewed in many articles and textbooks, in particular in the very comprehensive treatise of Nozières [5], but it seems appropriate to rehearse the essential output here as a basis for commentary. I follow here the intuitive approach of Landau's first paper [4] rather than his subsequent field-theoretic discussion [6], which seems to me to add little extra physical insight. In the context of the present section I shall ignore the nuclear dipole–dipole-interaction, so that the Hamiltonian of the system is invariant not only under translation but under rotation of the spin and orbital coordinates separately.
is given by the classic 'Fermi-liquid' theory of Landau [4]. This theory has been exhaustively reviewed in many articles and textbooks, in particular in the very comprehensive treatise of Nozières [5], but it seems appropriate to rehearse the essential output here as a basis for commentary. I follow here the intuitive approach of Landau's first paper [4] rather than his subsequent field-theoretic discussion [6], which seems to me to add little extra physical insight. In the context of the present section I shall ignore the nuclear dipole–dipole-interaction, so that the Hamiltonian of the system is invariant not only under translation but under rotation of the spin and orbital coordinates separately.
The fundamental insight underlying Landau's Fermi-liquid theory is that most of the qualitative properties of the noninteracting Fermi gas, in particular the extreme scarcity of many-body states of low energy, can be adiabatically extrapolated to the strongly interacting system. Consider a noninteracting Fermi gas of atoms of mass and number density n equal to those of real 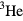 ; then the single-particle states can be labelled by their momentum
; then the single-particle states can be labelled by their momentum 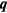 and spin projection σ, and will be fully occupied for
and spin projection σ, and will be fully occupied for 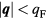 , where the Fermi wave vector qF is equal to
, where the Fermi wave vector qF is equal to 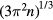 . We note that the density of single-particle states per unit energy at the Fermi surface is
. We note that the density of single-particle states per unit energy at the Fermi surface is 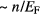 (actually
(actually 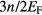 ). Now imagine that we add one extra particle in state
). Now imagine that we add one extra particle in state 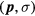 where
where 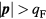 ; it is convenient to introduce a notation for the many-body states such that
; it is convenient to introduce a notation for the many-body states such that 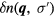 specifies the difference in occupation number of the state
specifies the difference in occupation number of the state 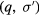 from the groundstate value
from the groundstate value 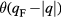 , so that in this case we have
, so that in this case we have
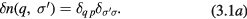
Had we removed an atom from a state 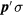 with
with 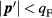 , the corresponding notation would have been
, the corresponding notation would have been
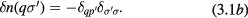
So far, the ('simple') excited state we have created is, trivially, an eigenstate of the many-body Hamiltonian. Now let us turn on a very weak inter-particle interaction which we designate schematically as V. The effect of this will be twofold: First, it will mix in other many-body states (e.g. of the kind discussed below) virtually into the wave function of the 'simple' state (3.1); this effect is not particularly sensitive to its energy. Secondly, it will cause real transitions between the 'simple' state (3.1) and others having more complicated forms of 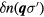 ; the simplest such state will be one in which we have
; the simplest such state will be one in which we have 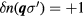 for two different states with
for two different states with 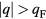 and
and 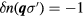 for one state with
for one state with 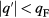 , or in more informal language two extra particles and one hole. Now the crucial point is that (assuming V to be translation-invariant and spin-independent) the transition ('decay') process must conserve momentum, spin and, most importantly, energy. If the energy of the original extra particle relative to the Fermi energy was
, or in more informal language two extra particles and one hole. Now the crucial point is that (assuming V to be translation-invariant and spin-independent) the transition ('decay') process must conserve momentum, spin and, most importantly, energy. If the energy of the original extra particle relative to the Fermi energy was  , the two-final-state particles must have energy
, the two-final-state particles must have energy 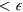 and the hole
and the hole 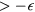 , so the total number of many-body states with energy (relative to the groundstate)
, so the total number of many-body states with energy (relative to the groundstate) 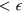 is
is  and the differential with respect to
and the differential with respect to  (which is what comes into the 'golden-rule' formula for the transition probability)
(which is what comes into the 'golden-rule' formula for the transition probability) 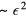 . In fact, a straightforward calculation yields the result for the decay rate
. In fact, a straightforward calculation yields the result for the decay rate 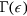
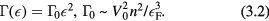
Evidently more complicated processes (involving final states with 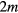 particles and
particles and 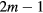 holes) will give a decay rate proportional to
holes) will give a decay rate proportional to 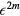 and so can be neglected for
and so can be neglected for 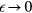 . The upshot is that states with a single extra particle are extremely long-lived in the limit
. The upshot is that states with a single extra particle are extremely long-lived in the limit  , and the same is true for states containing a single hole. Moreover, a fortiori, the original groundstate will be unable to 'decay' at all.
, and the same is true for states containing a single hole. Moreover, a fortiori, the original groundstate will be unable to 'decay' at all.
Now, following Landau, imagine that we gradually increase the strength of the interaction until it is equal to that in real-life liquid 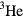 , and follow the evolution of (e.g.) the simple 'single-particle' state (3.1a). At each stage, although it will be progressively 'dressed' by more complicated many-body states, provided the time elapsed is
, and follow the evolution of (e.g.) the simple 'single-particle' state (3.1a). At each stage, although it will be progressively 'dressed' by more complicated many-body states, provided the time elapsed is  it will be unable to undergo a real transition and hence will as it were preserve its identity; the same is true a fortiori for the original many-body groundstate. This then enables us to label the groundstate and low-lying excited states of the interacting many-body Fermi system by the states of the noninteracting system from which they have adiabatically evolved, i.e. by the set of quantities
it will be unable to undergo a real transition and hence will as it were preserve its identity; the same is true a fortiori for the original many-body groundstate. This then enables us to label the groundstate and low-lying excited states of the interacting many-body Fermi system by the states of the noninteracting system from which they have adiabatically evolved, i.e. by the set of quantities 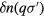 . (From now on I will change the notation to coincide with that standard in the literature and write these as
. (From now on I will change the notation to coincide with that standard in the literature and write these as 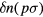 ). It should be noted that in this approach the statement that the Fermi momentum pF of the fully interacting system is equal to that of the noninteracting system (a special case of 'Luttinger's theorem') is true by definition. (The above argument is analyzed much more formally and carefully in the book [5] by Nozières).
). It should be noted that in this approach the statement that the Fermi momentum pF of the fully interacting system is equal to that of the noninteracting system (a special case of 'Luttinger's theorem') is true by definition. (The above argument is analyzed much more formally and carefully in the book [5] by Nozières).
One important caveat is necessary at this point: it is implicit in this argument that the many-body system indeed follows the gradual switching-on of the interaction adiabatically, and in particular that it does not undergo a first-order phase transition at any point during the process. Obviously, this assumption fails at pressure >35 atm, since at those pressures we know from experiment that the groundstate of a set of  atoms is a solid! A second point to note (though it is irrelevant in the
atoms is a solid! A second point to note (though it is irrelevant in the 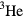 context) is that while the conservation of energy is an essential ingredient in the argument, conservation of momentum and spin is not: the only role of these conservation laws is to ensure that (e.g.) the final many-body state which has evolved from (3.1a) indeed has total momentum p and spin σ, and then can legitimately be described as containing 'a single quasiparticle of momentum p and spin of σ'. (This is essentially a definition of the notion of 'quasiparticle'.) Were spin and/or momentum not conserved, the characterization of the 'quasiparticles' would just be that bit more complicated.
context) is that while the conservation of energy is an essential ingredient in the argument, conservation of momentum and spin is not: the only role of these conservation laws is to ensure that (e.g.) the final many-body state which has evolved from (3.1a) indeed has total momentum p and spin σ, and then can legitimately be described as containing 'a single quasiparticle of momentum p and spin of σ'. (This is essentially a definition of the notion of 'quasiparticle'.) Were spin and/or momentum not conserved, the characterization of the 'quasiparticles' would just be that bit more complicated.
It is easy to extend the above considerations to low-lying many-body states derived from states of the noninteracting gas with several of the quantities 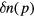 different from zero. In this case the total particle number (relative to the groundstate)
different from zero. In this case the total particle number (relative to the groundstate) 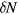 , total spin
, total spin 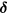 and total momentum P are given by the intuitively plausible formulae
and total momentum P are given by the intuitively plausible formulae


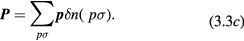
Note that since the spin current
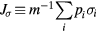
is not conserved by the interaction, we do not have
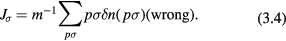
The actual situation regarding the spin current will be investigated below.
For only a few quasiparticles excited the considerations concerning decay continue to hold, so that the decay rate of any one quasiparticle is still given by (3.2) but with 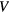 now taking its value for real
now taking its value for real 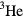 . However, at finite temperatures, a large number of quasiparticles will be thermally excited; one effect of this is to 'smear out' the Fermi surface over an energy scale
. However, at finite temperatures, a large number of quasiparticles will be thermally excited; one effect of this is to 'smear out' the Fermi surface over an energy scale 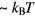 , and consideration of this circumstance in the argument leading to (3.2) leads to an additional term on the RHS proportional to
, and consideration of this circumstance in the argument leading to (3.2) leads to an additional term on the RHS proportional to 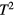 .
.
Having found an appropriate parametrization (namely that given by the quantities  ) for the low-lying energy eigenstates of the system, we now proceed to investigate the general structure of the dependence of the energy on
) for the low-lying energy eigenstates of the system, we now proceed to investigate the general structure of the dependence of the energy on 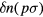 . We make a Taylor expansion:
. We make a Taylor expansion:

where
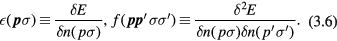
For weak (external or thermal) excitation terms of third and higher order in the 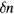 's can be neglected. Following Landau, we argue that invariance under spin and orbital rotation separately requires
's can be neglected. Following Landau, we argue that invariance under spin and orbital rotation separately requires 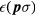 to be a function only of
to be a function only of 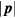 , and furthermore that
, and furthermore that 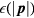 can be expanded in a Taylor series around
can be expanded in a Taylor series around 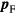 . (This last step is perhaps not entirely obvious: it can be justified by noting that it is true to any order in perturbation theory, or more satisfactorily by a field-theoretic analysis [5]. Then writing
. (This last step is perhaps not entirely obvious: it can be justified by noting that it is true to any order in perturbation theory, or more satisfactorily by a field-theoretic analysis [5]. Then writing 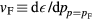 we find that the first-order term in (3.5) is parametrized by a single number, the 'effective mass'
we find that the first-order term in (3.5) is parametrized by a single number, the 'effective mass'

Similarly, rotational invariance implies that the two-quasiparticle interaction function 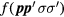 can be a function only of the variables
can be a function only of the variables 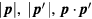 and
and  (or more accurately
(or more accurately 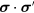 ). Again we take the lowest nonvanishing term in a Taylor expansion in
). Again we take the lowest nonvanishing term in a Taylor expansion in 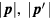 around
around  , in this case the zeroth-order one; thus we take
, in this case the zeroth-order one; thus we take 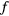 to be a function only of the variables
to be a function only of the variables 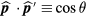 and
and 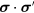 . Multiplying by the single-quasiparticle density of states
. Multiplying by the single-quasiparticle density of states 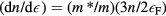 so as to obtain a dimensionless quantity and expanding in Legendre polynomials
so as to obtain a dimensionless quantity and expanding in Legendre polynomials 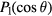 , we finally obtain (in modern notation1)
, we finally obtain (in modern notation1)
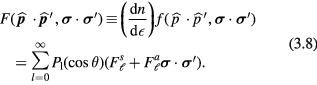
Thus the two-quasi-particle interaction is parameterized by an infinite double set of dimensionless 'Landau parameters' 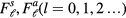 Fortunately, as we shall see, the formulas obtained for quantitites of experimental interest are either given exactly or well approximated by expressions which involve only a few of the
Fortunately, as we shall see, the formulas obtained for quantitites of experimental interest are either given exactly or well approximated by expressions which involve only a few of the 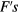 .
.
An appealing way of visualizing the effect of the two-quasiparticle interaction is in terms of an infinite set of generalized 'molecular fields'. Using the definitions (3.5) and (3.8), and expanding 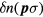 in spherical harmonics
in spherical harmonics  , we see that this term can be rewritten in the form
, we see that this term can be rewritten in the form
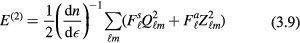
where
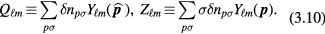
In a few cases (corresponding to the conserved quantities of equations (3.3a)–(3.3c)), the quantity 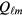 or
or 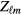 has a simple physical interpretation: e.g.
has a simple physical interpretation: e.g. 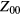 is just the total spin of the liquid, and
is just the total spin of the liquid, and 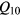 is the total z-component of momentum divided by
is the total z-component of momentum divided by 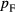 ; however, more general terms (such as
; however, more general terms (such as 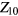 ) have no such simple interpretation (see equation (3.4)). Despite this, we can use intuition derived from the simple cases to construct a general prescription for calculating the response of a Fermi liquid to an arbitrary weak external (generalized) field, which schematically goes as follows: Simply calculate the 'bare' response of the system, i.e. the response of gas of free (quasi)particles of mass
) have no such simple interpretation (see equation (3.4)). Despite this, we can use intuition derived from the simple cases to construct a general prescription for calculating the response of a Fermi liquid to an arbitrary weak external (generalized) field, which schematically goes as follows: Simply calculate the 'bare' response of the system, i.e. the response of gas of free (quasi)particles of mass 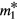 , but pretend that it is responding to a total field which is the sum of the external field and a set of 'molecular fields'
, but pretend that it is responding to a total field which is the sum of the external field and a set of 'molecular fields' 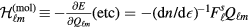 , where
, where 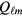 is the self-consistently calculated response. Let's illustrate this for the simple case in which the external field is a real magnetic field
is the self-consistently calculated response. Let's illustrate this for the simple case in which the external field is a real magnetic field 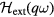 and we set all the
and we set all the 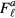 equal to zero for
equal to zero for 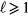 (from symmetry, the
(from symmetry, the 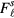 cannot play a role): if
cannot play a role): if 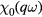 is the bare response and we set the nuclear magnetic moment equal to 1 for notational simplicity, we get
is the bare response and we set the nuclear magnetic moment equal to 1 for notational simplicity, we get
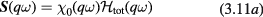
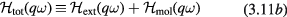
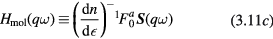
which on solution yield for the true susceptibility 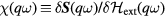
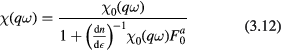
In particular, since the static susceptibility 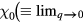
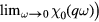 of the noninteracting quasiparticle gas is just
of the noninteracting quasiparticle gas is just 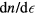 in our units, we find the well-known result that the effect of the quasiparticle interaction term is to multiply
in our units, we find the well-known result that the effect of the quasiparticle interaction term is to multiply 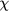 by the Stoner-like factor
by the Stoner-like factor 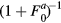 . Had we taken into account a nonzero Landau parameter
. Had we taken into account a nonzero Landau parameter  (but set
(but set 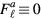 for
for  ), we would need to keep in mind that for general
), we would need to keep in mind that for general 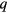 and
and 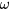 excitation of the spin density leads also to excitation of a nonzero 'pseudo-spin-current' term
excitation of the spin density leads also to excitation of a nonzero 'pseudo-spin-current' term 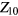 and thus of the corresponding molecular field: the result is to make in equation(3.12) the replacement (see e.g. [7])
and thus of the corresponding molecular field: the result is to make in equation(3.12) the replacement (see e.g. [7])
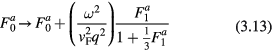
(a correction which clearly vanishes in the static limit). Quite generally, the results of treating the response to an external field in the way just outlined are completely equivalent to those obtained by the more standard Boltzmann-equation technique.
One advantage of the 'generalized molecular field' method is that it makes it rather straightforward to see which kinds of physical quantity will be independent of the values of the Landau parameters and which will be sensitive to them. The general rule is straightforward: if the quantity in question either (a) corresponds to all 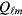 and
and  being zero, or (b) to a value such that the corresponding value of
being zero, or (b) to a value such that the corresponding value of 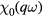 is much smaller than
is much smaller than 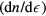 , then the Landau parameters have negligible effect. An example of case (a) is the specific heat: warming the system does not induce a nonzero value of any of the
, then the Landau parameters have negligible effect. An example of case (a) is the specific heat: warming the system does not induce a nonzero value of any of the 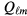 or
or 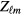 , and thus the specific heat is given by the standard quasiparticle-gas formula
, and thus the specific heat is given by the standard quasiparticle-gas formula 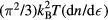 . An example of (b) is the transport coefficients, provided they are expressed in the form of conductivities rather than diffusivities; in this case, application of the Kubo formula shows that the relevant
. An example of (b) is the transport coefficients, provided they are expressed in the form of conductivities rather than diffusivities; in this case, application of the Kubo formula shows that the relevant 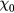 's are proportional to
's are proportional to 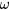 and thus vanish in the relevant limit
and thus vanish in the relevant limit 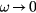 . (Details of the argument are given in [8]). Of course, to obtain finite transport coefficients at all it is necessary to add to the noninteracting-gas model some account of the process of mutual (real) scattering of quasiparticles; in general these involve large-
. (Details of the argument are given in [8]). Of course, to obtain finite transport coefficients at all it is necessary to add to the noninteracting-gas model some account of the process of mutual (real) scattering of quasiparticles; in general these involve large-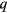 components of the effective inter-quasiparticle potential, which is the absence of a specific model cannot be simply related to the Landau parameters; however, it is clear that the standard temperature-dependences for a degenerate Fermi gas (e.g. viscosity
components of the effective inter-quasiparticle potential, which is the absence of a specific model cannot be simply related to the Landau parameters; however, it is clear that the standard temperature-dependences for a degenerate Fermi gas (e.g. viscosity 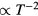 ) are preserved in the strongly interacting system. Qualitatively similar remarks attach to the behavior at values of
) are preserved in the strongly interacting system. Qualitatively similar remarks attach to the behavior at values of 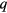 and
and 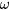 of the order of
of the order of  and
and 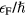 respectively, where the Landau theory cannot be expected to give a quantitatively accurate account.
respectively, where the Landau theory cannot be expected to give a quantitatively accurate account.
One might ask at this point: how 'strongly interacting' is real-life liquid 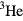 ? Within the framework of Fermi-liquid theory, a reasonable estimate may be obtained from the values of the ratio
? Within the framework of Fermi-liquid theory, a reasonable estimate may be obtained from the values of the ratio 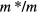 and of the Landau parameters
and of the Landau parameters  . Both are quite strongly pressure-dependent,
. Both are quite strongly pressure-dependent, 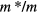 ranges from
ranges from  at svp to
at svp to 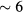 at the melting curve. Of the
at the melting curve. Of the 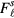 , by far the largest appears to be
, by far the largest appears to be  , which is
, which is 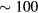 at the melting pressure; of the
at the melting pressure; of the 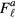 , the largest in absolute magnitude is probably
, the largest in absolute magnitude is probably  which is
which is 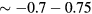 , thus not too far from a ferromagnetic instability. Thus we are very far from the simple noninteracting Fermi gas.
, thus not too far from a ferromagnetic instability. Thus we are very far from the simple noninteracting Fermi gas.
Actually, there is a rather different way of trying to estimate how similar or different real liquid 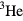 is from a noninteracting Fermi gas. Consider the linear response function
is from a noninteracting Fermi gas. Consider the linear response function 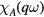 corresponding to some physical quantity
corresponding to some physical quantity 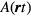 . If
. If 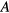 corresponds to a conserved quantity (total particle number, spin or momentum) then the quantity
corresponds to a conserved quantity (total particle number, spin or momentum) then the quantity 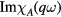 must vanish in the limit
must vanish in the limit 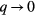 then
then 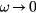 ; equivalently in this limit it can have contributions only from the low-lying many-body states which are expressible in terms of the quasiparticle picture. If on the other hand
; equivalently in this limit it can have contributions only from the low-lying many-body states which are expressible in terms of the quasiparticle picture. If on the other hand 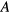 is not conserved, then even in this limit
is not conserved, then even in this limit 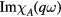 can have contributions from states with
can have contributions from states with 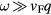 which in general cannot be expressed in quasiparticle language, and it is interesting to ask how important a contribution comes from this 'incoherent background'? It turns out that in the case of the spin current one can actually answer this question, since in this case
which in general cannot be expressed in quasiparticle language, and it is interesting to ask how important a contribution comes from this 'incoherent background'? It turns out that in the case of the spin current one can actually answer this question, since in this case 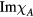 must obey a sum rule, and one can work out the contribution to the latter from the quasiparticle states. The answer is that the incoherent background contributes about 80% of the sum rule! Thus, the 'dressing' of the original
must obey a sum rule, and one can work out the contribution to the latter from the quasiparticle states. The answer is that the incoherent background contributes about 80% of the sum rule! Thus, the 'dressing' of the original 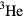 atom to form a quasiparticle is by no means a trivial effect.
atom to form a quasiparticle is by no means a trivial effect.
Two general remarks about the Landau Fermi-liquid theory of liquid 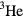 : First, not only does it not in itself guarantee that the system indeed satisfies the postulate of adiabatic evolution (as noted above, it does not for
: First, not only does it not in itself guarantee that the system indeed satisfies the postulate of adiabatic evolution (as noted above, it does not for 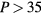 atm!), but even given that it does, it says nothing about the values of the effective mass
atm!), but even given that it does, it says nothing about the values of the effective mass 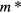 or the Landau parameters
or the Landau parameters 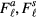 (except for the limits imposed by the necessity of avoiding Pomeranchuk instabilities). Moreover, it says virtually nothing about the many-body wave function expressed in the original atomic coordinates; in particular the output of the theory seems insensitive as to whether or not this wave function contains a long-wavelength Jastrow factor (as it presumably should). In the normal phase which is the subject of this section, the sum rules are satisfied either way (in the superfluid phase this point would require separate discussion).
(except for the limits imposed by the necessity of avoiding Pomeranchuk instabilities). Moreover, it says virtually nothing about the many-body wave function expressed in the original atomic coordinates; in particular the output of the theory seems insensitive as to whether or not this wave function contains a long-wavelength Jastrow factor (as it presumably should). In the normal phase which is the subject of this section, the sum rules are satisfied either way (in the superfluid phase this point would require separate discussion).
Secondly, one might ask whether the theory has any real content? Indeed, when the present author was a graduate student in Oxford in the early 60s and the theory had begun to be somewhat known in the West, a not uncommon reaction among experimentalists was that it is essentially vacuous, since 'every time you measure a new quantity you just postulate a new parameter to fit it'. Fifty years later, I don't think this pessimistic view holds up. In the first place, the theory predicts qualitatively new features such as transverse zero sound [9] which, unlike the longitudinal variety, have not even a remote analog in the weakly interacting gas. Secondly, even in the normal phase (and as we shall see more spectacularly in the superfluid phase) there are phenomena where a whole gamut of behavior can be quantitatively accounted for by invoking only one previously unknown Landau parameter; a prime example is the anomalous spin diffusion observed in a high magnetic field [10] ('Leggett–Rice effect'), where at the cost of treating the single Landau parameter 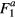 as a fitting parameter one can account for the full dependence of the signal on magnetic field, temperature and tipping angle. In the light of the above I do not think one can reasonably claim that the Landau theory is vacuous.
as a fitting parameter one can account for the full dependence of the signal on magnetic field, temperature and tipping angle. In the light of the above I do not think one can reasonably claim that the Landau theory is vacuous.
4. The superfluid phases
In the analysis of the onset and characteristics of superfluidity in liquid 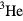 , one circumstance plays an overwhelmingly dominant role: By the time we reach the temperature at which, experimentally, superfluidity is found to occur,
, one circumstance plays an overwhelmingly dominant role: By the time we reach the temperature at which, experimentally, superfluidity is found to occur, 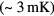 , the normal state is extremely well described by the Landau Fermi-liquid theory reviewed in section 3. Formally this is reflected in the fact that the ratio
, the normal state is extremely well described by the Landau Fermi-liquid theory reviewed in section 3. Formally this is reflected in the fact that the ratio 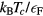 (or what is roughly equivalent,
(or what is roughly equivalent, 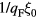 where
where 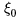 is the pair radius) is only
is the pair radius) is only 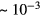 . Thus we may confidently describe all the states of the many body system which can be relevant to the superfluid state in terms of the quasiparticle (quasihole) occupation numbers, and introduce the corresponding fermionic creation and annihilation operators
. Thus we may confidently describe all the states of the many body system which can be relevant to the superfluid state in terms of the quasiparticle (quasihole) occupation numbers, and introduce the corresponding fermionic creation and annihilation operators  ; it is irrelevant that in the absence of a microscopic model we do not know how to express the
; it is irrelevant that in the absence of a microscopic model we do not know how to express the 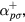 etc, in terms of the original real-particle operators
etc, in terms of the original real-particle operators 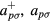 . Of course, such a procedure will fail when the quasiparticle energies (relative to the Fermi energy) reach some value, typically of the order of but appreciably smaller than,
. Of course, such a procedure will fail when the quasiparticle energies (relative to the Fermi energy) reach some value, typically of the order of but appreciably smaller than, 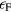 , whose order of magnitude we denote below by
, whose order of magnitude we denote below by 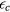 ; but as long as
; but as long as 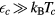 , this does not matter.
, this does not matter.
When we express the effective Hamiltonian describing the low-energy many body states in terms of the quasiparticle operators  , we expect in general to get terms involving the simultaneous creation and destruction of one, two, three...quasiparticles. (The conservation of (quasi) particle number expressed by equation (3.3a) guarantees that the number of creation operators must equal that of annihilation operators). Terms involving creation and destruction of three or more quasiparticles turn out to give corrections of higher order in the small parameters
, we expect in general to get terms involving the simultaneous creation and destruction of one, two, three...quasiparticles. (The conservation of (quasi) particle number expressed by equation (3.3a) guarantees that the number of creation operators must equal that of annihilation operators). Terms involving creation and destruction of three or more quasiparticles turn out to give corrections of higher order in the small parameters  and thus will be neglected in the present context (see the remarks at the end of section 1). The single-quasiparticle term is, from conservation of spin and momentum, exactly as in equation(3.5): in terms of the
and thus will be neglected in the present context (see the remarks at the end of section 1). The single-quasiparticle term is, from conservation of spin and momentum, exactly as in equation(3.5): in terms of the  's,
's,

The full two-quasiparticle term is however more complicated than in equation (3.5):
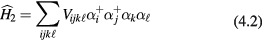
where for brevity we set 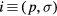 , and where of course conservation of spin and momentum places certain constraints on the matrix element
, and where of course conservation of spin and momentum places certain constraints on the matrix element 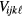 which we do not write out. As we have seen, in the normal phase the effect of those terms in (4.2) which are not diagonal in the quantities
which we do not write out. As we have seen, in the normal phase the effect of those terms in (4.2) which are not diagonal in the quantities 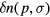 and which are not incorporated in the second term in (3.8) is in some sense small: they give a quasiparticle decay rate which is proportional to
and which are not incorporated in the second term in (3.8) is in some sense small: they give a quasiparticle decay rate which is proportional to 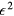 and hence vanishes relative to the quasiparticle energy
and hence vanishes relative to the quasiparticle energy  as
as 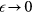 , and their only major role is in guaranteeing that for any given nonzero
, and their only major role is in guaranteeing that for any given nonzero 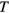 the transport coefficients are finite.
the transport coefficients are finite.
However, just as in the case of a weakly interacting gas, there is a class of terms which need special attention, namely those involving scattering of quasiparticles of opposite momentum (in the above condensed notation, those for which 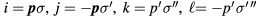 ). If the corresponding matrix element (or more accurately any spherical harmonic of it) is attractive, than these terms can lead just as in the weakly interacting gas, to the formation of Cooper pairs and in consequence to superfluidity. Indeed, the analysis of the possibility of instability due to such pair formation goes through exactly as in that case and leads to the prediction
). If the corresponding matrix element (or more accurately any spherical harmonic of it) is attractive, than these terms can lead just as in the weakly interacting gas, to the formation of Cooper pairs and in consequence to superfluidity. Indeed, the analysis of the possibility of instability due to such pair formation goes through exactly as in that case and leads to the prediction
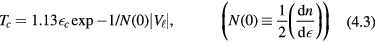
where 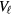 is the most negative spherical harmonic of the pairing interaction, and we have arbitrarily taken the upper cutoff on the energy integral which occurs in the BCS gap equation to be equal to the energy at which, as discussed above, the quasiparticle description ceases to be good. (This is of course only defined to an order of magnitude, so the prefactor in (4.3) should not be taken too seriously).
is the most negative spherical harmonic of the pairing interaction, and we have arbitrarily taken the upper cutoff on the energy integral which occurs in the BCS gap equation to be equal to the energy at which, as discussed above, the quasiparticle description ceases to be good. (This is of course only defined to an order of magnitude, so the prefactor in (4.3) should not be taken too seriously).
In some sense equation (4.3) in itself has no real content, since in the absence of a concrete microscopic model one does not have a quantitative estimate of the parameter 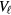 . However, this situation is no different from that which holds (or at least held until quite recently) in the theory of superconductivity in metals. In the latter case a common strategy is to take
. However, this situation is no different from that which holds (or at least held until quite recently) in the theory of superconductivity in metals. In the latter case a common strategy is to take 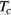 for the metal of interest directly from experiment, and then observe that as a function of the reduced temperature
for the metal of interest directly from experiment, and then observe that as a function of the reduced temperature 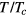 the properties of the superconducting state are given quite precisely and quantitatively by the BCS theory. And indeed it turns out that with three important qualifications to be discussed below, the same is true for the superfluid phases of liquid
the properties of the superconducting state are given quite precisely and quantitatively by the BCS theory. And indeed it turns out that with three important qualifications to be discussed below, the same is true for the superfluid phases of liquid 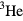 . Thus, the fact that attempts to derive
. Thus, the fact that attempts to derive 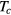 for that system from first principles have not been spectacularly successful (indeed, in advance of the event were rather spectacularly unsuccessful!) should not be of major concern.
for that system from first principles have not been spectacularly successful (indeed, in advance of the event were rather spectacularly unsuccessful!) should not be of major concern.
Before addressing the qualifications, let us review briefly the standard identification of the three different superfluid phases of liquid 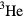 described in experiment. (A much more detailed discussion can be found in e.g. [11]). According to this scheme, all three phases correspond to formation of pairs with
described in experiment. (A much more detailed discussion can be found in e.g. [11]). According to this scheme, all three phases correspond to formation of pairs with 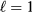 and thus in a triplet spin state; they differ in the population of the 9 different Zeeman substates. In zero or weak (say
and thus in a triplet spin state; they differ in the population of the 9 different Zeeman substates. In zero or weak (say 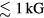 ) magnetic fields, the bulk of the phase diagram in the
) magnetic fields, the bulk of the phase diagram in the  plane below
plane below  is occupied by the B phase. This phase is identified with the so-called BW phase originally predicted on theoretical grounds by Vdovin and independently by Balian and Werthamer, in which the pairs form (prima facie, see below) in what in molecular physics would be called a
is occupied by the B phase. This phase is identified with the so-called BW phase originally predicted on theoretical grounds by Vdovin and independently by Balian and Werthamer, in which the pairs form (prima facie, see below) in what in molecular physics would be called a 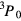 state; intuitively speaking, the orbital angular momentum of each pair is oppositely oriented to its spin, so that the total angular momentum
state; intuitively speaking, the orbital angular momentum of each pair is oppositely oriented to its spin, so that the total angular momentum 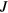 is zero. (In the 'd-vector' rotation which has become standard for the discussion of triplet superfluidity (see e.g. [11]), this state is written
is zero. (In the 'd-vector' rotation which has become standard for the discussion of triplet superfluidity (see e.g. [11]), this state is written 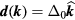 ). In such a state, the fermionic (Bogoliubov) excitations have an energy gap
). In such a state, the fermionic (Bogoliubov) excitations have an energy gap 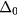 which is independent of direction on the Fermi surface, so from the point of view of thermodynamics the BW state is equivalent to an ordinary BCS (
which is independent of direction on the Fermi surface, so from the point of view of thermodynamics the BW state is equivalent to an ordinary BCS (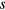 -wave) superconductor. Actually it turns out that any state which is obtained from the BW state by rotation of the Cooper-pair spins relative to their orbital angular momenta
-wave) superconductor. Actually it turns out that any state which is obtained from the BW state by rotation of the Cooper-pair spins relative to their orbital angular momenta 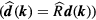 is degenerate with it as regards the 'gross' energies in the problem (kinetic, van der Waals, hard core), which are invariant under such a rotation, but may do better in minimizing the nuclear dipole energy, and it is thus this energy, tiny as it is, which determines the actual groundstate configuration of
is degenerate with it as regards the 'gross' energies in the problem (kinetic, van der Waals, hard core), which are invariant under such a rotation, but may do better in minimizing the nuclear dipole energy, and it is thus this energy, tiny as it is, which determines the actual groundstate configuration of 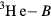 , which is believed to correspond to a rotation of
, which is believed to correspond to a rotation of  around the direction of the magnetic field. While this detail is crucial to the interpretation of the NMR data, it is irrelevant to most of the other properties of the system, and for most purposes we may safely identify the
around the direction of the magnetic field. While this detail is crucial to the interpretation of the NMR data, it is irrelevant to most of the other properties of the system, and for most purposes we may safely identify the 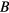 phase of liquid
phase of liquid 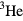 with the original
with the original 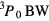 phase.
phase.
In zero magnetic field a small sliver of the 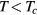 phase diagram, near melting pressure and
phase diagram, near melting pressure and 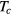 (and at higher fields a larger region, in fact for
(and at higher fields a larger region, in fact for 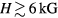 almost the whole) is occupied by the
almost the whole) is occupied by the 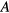 phase. This phase is identified with the so called ABM phase originally studied by Anderson and Morel and subsequently by Anderson and Brinkman, in which the Cooper pair wave function (order parameter) is a product of spin and orbital fractions. The orbital wave function corresponds formally to relative orbital angular momentum
phase. This phase is identified with the so called ABM phase originally studied by Anderson and Morel and subsequently by Anderson and Brinkman, in which the Cooper pair wave function (order parameter) is a product of spin and orbital fractions. The orbital wave function corresponds formally to relative orbital angular momentum 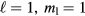 along a particular direction usually labeled
along a particular direction usually labeled 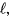 while the spin wave function describes a so-called 'ESP' (equal spin pairing) state, that is one in which with the z-axis chosen say along the external magnetic field, the pairs form in the states
while the spin wave function describes a so-called 'ESP' (equal spin pairing) state, that is one in which with the z-axis chosen say along the external magnetic field, the pairs form in the states 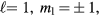 with equal amplitude but in general different phase. (In the
with equal amplitude but in general different phase. (In the 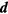 -vector notation, this corresponds to
-vector notation, this corresponds to 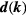 independent of
independent of 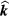 and lying perpendicular to the magnetic field). An issue which has been controversial in the literature for more than 40 years concerns the total angular momentum of a given sample of
and lying perpendicular to the magnetic field). An issue which has been controversial in the literature for more than 40 years concerns the total angular momentum of a given sample of 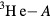 : does the fact that the relative wave function of the
: does the fact that the relative wave function of the 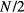 Cooper pairs corresponds to an apparent orbital angular momentum of
Cooper pairs corresponds to an apparent orbital angular momentum of 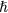 imply that the liquid as a whole has an angular momentum
imply that the liquid as a whole has an angular momentum 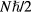 (or perhaps some power of
(or perhaps some power of 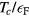 times this)? Even in 2015, neither theory nor experiment appears to have definitively settled this question. (see [12] for the 'standard' theoretical approach, and for some reservations about the latter, appendix to chapter 6 of [13])
times this)? Even in 2015, neither theory nor experiment appears to have definitively settled this question. (see [12] for the 'standard' theoretical approach, and for some reservations about the latter, appendix to chapter 6 of [13])
Finally, in a magnetic field of the order of a few 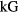 , the so-called
, the so-called 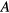 -phase appears as a thin wedge separating the
-phase appears as a thin wedge separating the  and normal phases. This phase is similar to the A phase but with only one Zeeman state (e.g.
and normal phases. This phase is similar to the A phase but with only one Zeeman state (e.g. 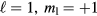 ) populated; this raises some intriguing questions about the relation between the spin and 'phase' degrees of freedom, see e.g. [14].
) populated; this raises some intriguing questions about the relation between the spin and 'phase' degrees of freedom, see e.g. [14].
So far, nothing I have said about the superfluid phases of liquid 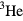 would be inconsistent with the idea that the system is simply a system of spin
would be inconsistent with the idea that the system is simply a system of spin 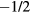 fermions with a weak attractive interaction. Where does the 'strongly correlated' nature of the normal phase come in? I believe in at least three ways, which I will now try to outline.
fermions with a weak attractive interaction. Where does the 'strongly correlated' nature of the normal phase come in? I believe in at least three ways, which I will now try to outline.
The first concerns the effect of the Landau molecular-field terms in (3.9), which are absent in the weakly interacting gas. As previously remarked, these only come into play when a nonzero value at least one of the 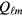 or
or 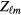 is excited; consequently, they do not affect the calculation of the transition temperature, nor of the superconducting-state specific heat, which is thus expected (and found) to be given satisfactorily by the BCS theory. However, they do affect the response to external fields. Thus, for example, following through the calculation outlined in equations (3.11) and (3.12), we find for the spin susceptibility in the superconducting state
is excited; consequently, they do not affect the calculation of the transition temperature, nor of the superconducting-state specific heat, which is thus expected (and found) to be given satisfactorily by the BCS theory. However, they do affect the response to external fields. Thus, for example, following through the calculation outlined in equations (3.11) and (3.12), we find for the spin susceptibility in the superconducting state
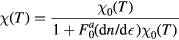
where 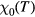 is the susceptibility of the weakly interacting quasiparticle gas. Since in the BW phase the latter is equal to
is the susceptibility of the weakly interacting quasiparticle gas. Since in the BW phase the latter is equal to 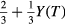 (Y(T) = Yosida function) multiplied by the normal-state susceptibility, which in our units is
(Y(T) = Yosida function) multiplied by the normal-state susceptibility, which in our units is 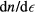 , we find
, we find
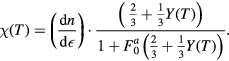
Inserting the experimental value 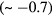 of the Landau parameter
of the Landau parameter 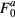 , we find that the B-phase susceptibility drops considerably more rapidly than that for the weakly interacting gas, and at
, we find that the B-phase susceptibility drops considerably more rapidly than that for the weakly interacting gas, and at  is approximately
is approximately  rather than the 'gas' value of 2/3 for the BW state; this is confirmed experimentally. (The approximately 1/2 reduction is a numerical accident). Similarly, the expression for the normal fraction
rather than the 'gas' value of 2/3 for the BW state; this is confirmed experimentally. (The approximately 1/2 reduction is a numerical accident). Similarly, the expression for the normal fraction 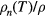 , which for a 'gas-like' BW phase is again given by
, which for a 'gas-like' BW phase is again given by 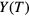 , now becomes
, now becomes
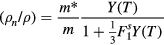
and since the Landau parameter 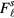 is positive and reasonably large
is positive and reasonably large 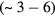 , the curve is less steep than that of the superfluid gas. Similar results, generalized to take account of the anisotropy of the superfluid-gas normal component, hold for the A phase. Again, this is confirmed by experiment.
, the curve is less steep than that of the superfluid gas. Similar results, generalized to take account of the anisotropy of the superfluid-gas normal component, hold for the A phase. Again, this is confirmed by experiment.
The second point, which in some sense goes beyond the FL theory, relates to the origin of the effective attraction which induces the formation of Cooper pairs. In the case of a metallic superconductor described by the BCS theory, this is primarily due to the exchange of virtual phonons; since the properties of the phonon system are very insensitive to the onset of superconductivity, the attraction may be regarded as constant below 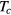 . In liquid
. In liquid 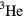 , by contrast, the effective attraction very likely has an important (in fact perhaps dominant) contribution from the exchange of virtual fluctuations of the liquid itself (in particular, of long-lived spin fluctuations ('paramagnons')). Since the onset of Cooper pairing can change the structure of these fluctuations, the strength of the attraction may itself change in the superfluid state. As pointed out by Anderson and Brinkman [15], this likely explains the one feature of the experimental phase diagram which appears qualitatively impossible to explain within a simple superfluid-gas theory, namely that the ABM phase is ever stable with respect to the BW phase: what happens, very crudely, is that because of the different spin and orbital structure of their order parameters, the pairing attraction in the BW phase is weakened by the 'feedback' effect described above, while that in the ABM phase is (slightly paradoxically) actually strengthened. A more exhaustive and systematic analysis of these feedback effects has been carried out by Rainer and Serene [16].
, by contrast, the effective attraction very likely has an important (in fact perhaps dominant) contribution from the exchange of virtual fluctuations of the liquid itself (in particular, of long-lived spin fluctuations ('paramagnons')). Since the onset of Cooper pairing can change the structure of these fluctuations, the strength of the attraction may itself change in the superfluid state. As pointed out by Anderson and Brinkman [15], this likely explains the one feature of the experimental phase diagram which appears qualitatively impossible to explain within a simple superfluid-gas theory, namely that the ABM phase is ever stable with respect to the BW phase: what happens, very crudely, is that because of the different spin and orbital structure of their order parameters, the pairing attraction in the BW phase is weakened by the 'feedback' effect described above, while that in the ABM phase is (slightly paradoxically) actually strengthened. A more exhaustive and systematic analysis of these feedback effects has been carried out by Rainer and Serene [16].
A third complication relative to the case of a nearly-free Fermi gas occurs when one tries to calculate not susceptibilities but the equilibrium averages of various physical quantities; very typically, such averages have important contributions from atomic configurations in which a pair of atoms is close together, corresponding to wave vectors of order 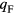 . This is precisely the regime in which the Fermi liquid picture fails, and since in the absence of a detailed microscopic model one does not have much idea how the many-body wave function looks when expressed in real atomic coordinates it is difficult to obtain quantitative results. This problem actually occurs in the calculation of
. This is precisely the regime in which the Fermi liquid picture fails, and since in the absence of a detailed microscopic model one does not have much idea how the many-body wave function looks when expressed in real atomic coordinates it is difficult to obtain quantitative results. This problem actually occurs in the calculation of 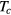 , but as we have seen in that case can be swept under the rug by regarding the latter as an experimentally fitted parameter. A rather similar situation arises when one needs to calculate the expectation value of the nuclear dipole interaction energy, something which is necessary to get a quantitative account of the NMR behavior; since the contribution to this energy is proportional to the inverse cube of the internuclear separation, the dominating contribution is again from regimes not quantitatively describable by FL theory, and a more phenomenological approach is necessary (see e.g. [17]), but again, any uncertainties refer only to the overall constant and drop out in e.g. the temperature-dependence of the shifts in the A and B phases and their ratio.
, but as we have seen in that case can be swept under the rug by regarding the latter as an experimentally fitted parameter. A rather similar situation arises when one needs to calculate the expectation value of the nuclear dipole interaction energy, something which is necessary to get a quantitative account of the NMR behavior; since the contribution to this energy is proportional to the inverse cube of the internuclear separation, the dominating contribution is again from regimes not quantitatively describable by FL theory, and a more phenomenological approach is necessary (see e.g. [17]), but again, any uncertainties refer only to the overall constant and drop out in e.g. the temperature-dependence of the shifts in the A and B phases and their ratio.
One should be aware that the remarks above to the effect that the (zero-field) thermodynamics of the superfluid phases of liquid 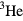 is identical to that of the corresponding superfluid gas is true only to the extent that it is completely dominated by the fermionic (Bugoliubov quasiparticle) excitations. This is always true for the A phase, but for the B phase, with its everywhere nonzero energy gap, one has only to go down to a temperature
is identical to that of the corresponding superfluid gas is true only to the extent that it is completely dominated by the fermionic (Bugoliubov quasiparticle) excitations. This is always true for the A phase, but for the B phase, with its everywhere nonzero energy gap, one has only to go down to a temperature  (just becoming accessible in the laboratory) for a fermionic contribution to effectively freeze out and the bosonic excitations, in particular the spin waves [11], to become the dominant component. In fact, it seems likely that in this ultra-low-temperature regime not just the thermodynamics but the transport coefficients will be 'boson-dominated'—a state of affairs which has no analog in the superfluid-gas model. I believe this may be the next frontier in experimental low-temperature physics.
(just becoming accessible in the laboratory) for a fermionic contribution to effectively freeze out and the bosonic excitations, in particular the spin waves [11], to become the dominant component. In fact, it seems likely that in this ultra-low-temperature regime not just the thermodynamics but the transport coefficients will be 'boson-dominated'—a state of affairs which has no analog in the superfluid-gas model. I believe this may be the next frontier in experimental low-temperature physics.
Finally, it should be re-emphasized that even at 'temperatures' 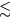 100 mK, the good quantitative understanding of liquid
100 mK, the good quantitative understanding of liquid  given by the Landau theory applies only to the behavior in or close to equilibrium. The behavior under grossly non-equilibrium conditions is much more controversial, see [18].
given by the Landau theory applies only to the behavior in or close to equilibrium. The behavior under grossly non-equilibrium conditions is much more controversial, see [18].
5. Conclusion
Viewed from the standpoint of 2015, Landau's theory of a Fermi liquid may be regarded as a small-scale instantiation of the Kuhnian idea of a 'paradigm shift' [19]; it really re-oriented the sense of the condensed-matter community as to what were the legitimate questions to ask and what kinds of answer to them were acceptable. In this chapter I have reviewed its application to the system for which it was originally devised, namely the normal and (after an extension which Landau himself did not live to see) the various superfluid phases of liquid 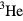 . As noted in the introduction, this system is in some sense specially favorable for the application of Fermi-liquid theory because of its simple nature and the serendipitous separation of energy scales
. As noted in the introduction, this system is in some sense specially favorable for the application of Fermi-liquid theory because of its simple nature and the serendipitous separation of energy scales 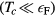 . However, given this we have seen that the theory produces a remarkably detailed and quantitative account of the low-temperature, long-wavelength and low-frequency properties of both the normal and the superfluid phase(s). It is no accident that the general philosophy embodied in Landau's approach (don't try to calculate from first principles, rather try to relate different properties of the system) is now so standard and ubiquitous in all areas of condensed-matter physics that we tend to forget that at one time it was novel and revolutionary.
. However, given this we have seen that the theory produces a remarkably detailed and quantitative account of the low-temperature, long-wavelength and low-frequency properties of both the normal and the superfluid phase(s). It is no accident that the general philosophy embodied in Landau's approach (don't try to calculate from first principles, rather try to relate different properties of the system) is now so standard and ubiquitous in all areas of condensed-matter physics that we tend to forget that at one time it was novel and revolutionary.
Footnotes
- 1
For brevity I ignore, here, some technical complications connected with the operator nature of the
 's.
's.



