Abstract
Using a quantum kinetic description, we establish a general expression for the dispersion relation of electron plasma waves in the presence of an arbitrary spectrum of electromagnetic waves. This includes both electron and photon Landau damping. The quantum kinetic description allows us to compare directly these two distinct processes, and to show that they are indeed quite similar. The present work also extends previous results on photon Landau damping onto the quantum domain.
Export citation and abstract BibTeX RIS
1. introduction
Wave propagation in quantum plasma has been considered by several authors in recent years [1–3]. This problem can be relevant to different areas, such as laser acceleration [4], laser fusion [5] and astrophysical plasmas [6], where quantum effects in dense plasmas can eventually become relevant. Quantum dispersion effects are indeed relevant to the theory of free electron lasers [7], and to several other aspects of quantum physics associated with intense laser-plasma interactions [8].
Here, we provide a quantum kinetic description of electron plasma wave propagation in quantum plasmas, in the presence of an arbitrary spectrum of transverse electromagnetic waves. Both electron and photon Landau damping of electron plasma waves will be considered. Electron Landau damping in a quantum plasma has been recently discussed [9, 10]. On the other hand, photon Landau damping in a classical plasma was first considered by [11], using the geometric optics approximation, and extended to exact wave propagation in [12]. Recoil photon effects were identified in this exact formulation, which are formally identical to quantum electron recoil. This somewhat surprising result can however be understood by noting that the classical electromagnetic theory is the theoretical counterpart of the first quantization theory of the electron probability field. In the present work, both photon and electron recoil effects are described on a similar basis.
Our quantum plasma description is based on the Wigner–Moyal approach [13, 14]. This will be applied to both the electron probability field and the electromagnetic photon field. The contents of this paper is the following. In section 2, we establish the wave-kinetic equation describing the evolution of the electron quasi-distribution, where spin effects are ignored. However, spin contributions to the equilibrium electron distribution will be retained. It should be noticed that the electron quasi-distribution is a Wigner function, which can take negative as well as positive values, but tends to the usual electron distribution function in the classical limit. In section 3 we discuss the case of electron plasma waves and the well known quantum expressions for the electron Landau damping. In section 4 we examine the case of electromagnetic waves in a plasma and derive the corresponding photon wave-kinetic equation. This will allow us to derive a new dispersion relation, for electron plasma waves in the presence of radiation which includes both electron and photon Landau damping, as discussed in sections 5 and 6.
It should be noticed that a quantum plasma is usually characterized by a set of standard parameters, such as the coupling and the degeneracy parameters. The coupling parameter is defined as the ratio between the average potential and kinetic energy per particle,  , and measures the Coulomb coupling strength. For
, and measures the Coulomb coupling strength. For  the system is strongly coupled. On the other hand, the degree of degenerescence is measured by the parameter
the system is strongly coupled. On the other hand, the degree of degenerescence is measured by the parameter  , which gives the ratio between the Fermi and the plasma temperatures. For
, which gives the ratio between the Fermi and the plasma temperatures. For  , the plasma has to be described as a quantum system. Here, we consider a weakly coupled quantum plasma.
, the plasma has to be described as a quantum system. Here, we consider a weakly coupled quantum plasma.
A quantum plasma approach is needed to describe both electron and photon responses in a similar formal way, and to derive the corresponding susceptibilities. Such a formal similarity results from the use of a quantum wave description for the electron kinetics, which is the particle counterpart of the wave description of the photon field. That is the reason why only a quantum plasma description is able to compare photon and electron Landau damping processes. But, as will be shown, the kinetic photon and electron susceptibilities do not simply add to each other. Instead, they are connected in a completely new dispersion term which contains both electron and photon contributions. This results from the fact that the photon contribution to the electron plasma wave dispersion is mediated by the electron response. Finally, in section 7, we state some conclusions.
2. Quantum kinetic equation
We assume high frequency waves in a quantum plasma, and assume immobile ions. The electrons are degenerate, in the sense that their de Broglie wavelength is larger than the inter-particle distance, or equivalently, the electron temperature is of the order or lower than the Fermi temperature,  . The electron population can then be described by a Wigner quasi-distribution
. The electron population can then be described by a Wigner quasi-distribution  , satisfying the wave-kinetic equation
, satisfying the wave-kinetic equation
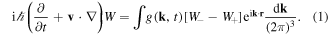
Here,  is the spatial Fourier transform of the electromagnetic potential function, defined as
is the spatial Fourier transform of the electromagnetic potential function, defined as

where  and
and  are the scalar and vector potentials. In equation (1), we have also used the displaced quantities
are the scalar and vector potentials. In equation (1), we have also used the displaced quantities  . A detailed derivation of equations (1) and (2) can be found in [15], for the more general case of relativistic quantum plasmas. The potentials are determined by the equations
. A detailed derivation of equations (1) and (2) can be found in [15], for the more general case of relativistic quantum plasmas. The potentials are determined by the equations
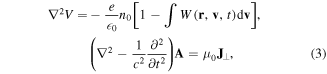
where  is the divergence free current satisfying
is the divergence free current satisfying  , and we are using the Coulomb gauge, such that
, and we are using the Coulomb gauge, such that  . In equation (3) we have assumed that the equilibrium electron density is equal to the background ion density n0. Alternative forms of the wave-kinetic equation can be found in [1]. It is also useful to consider the quasi-classical approximation valid for
. In equation (3) we have assumed that the equilibrium electron density is equal to the background ion density n0. Alternative forms of the wave-kinetic equation can be found in [1]. It is also useful to consider the quasi-classical approximation valid for  . In that case, we obtain the equation
. In that case, we obtain the equation
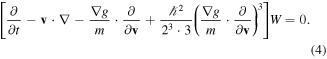
In the classical limit,  , this reduces to the Vlasov equation for the electron distribution function,
, this reduces to the Vlasov equation for the electron distribution function,  .
.
3. Electron plasma waves
We first discuss the case of electrostatic waves, such that  , and
, and  . We can assume an infinitesimal perturbation
. We can assume an infinitesimal perturbation  , where the equilibrium quasi-distribution W0 is normalized as
, where the equilibrium quasi-distribution W0 is normalized as  . Linearizing equation (1) with respect to that perturbation, we get
. Linearizing equation (1) with respect to that perturbation, we get
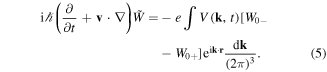
The electrostatic potential associated with the perturbation is determined by
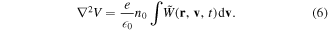
We now focus on a single component of the  spectrum, evolving with a time-varying frequency ω, such that a linear dispersion relation can be satisfied. We define
spectrum, evolving with a time-varying frequency ω, such that a linear dispersion relation can be satisfied. We define  and
and  . Replacing this in equations (5) and (6), we can easily derive the dispersion relation
. Replacing this in equations (5) and (6), we can easily derive the dispersion relation
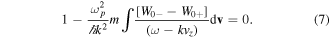
It is useful to consider the parallel quasi-distribution  . Replacing this in equation (7), we are led to a different expression for the dispersion relation
. Replacing this in equation (7), we are led to a different expression for the dispersion relation
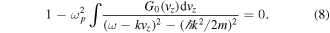
This can also be written as
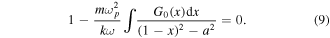
With the auxiliary quantities
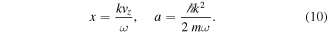
Let us consider the case of a quantum plasma, in equilibrium, at a temperature  , where TF is the Fermi temperature. In that case, the equilibrium distribution can be described by a Fermi–Dirac distribution, where the electron states are equally occupied for velocities less than the Fermi velocity,
, where TF is the Fermi temperature. In that case, the equilibrium distribution can be described by a Fermi–Dirac distribution, where the electron states are equally occupied for velocities less than the Fermi velocity,  , and they are empty for
, and they are empty for  . Using energy units such that kB = 1, we can write
. Using energy units such that kB = 1, we can write  , and
, and
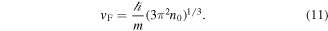
Using for the equilibrium distribution
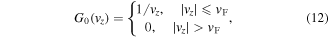
we can transform equation (9) into
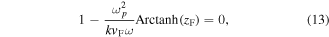
where  , and
, and  . Using the expansion
. Using the expansion  , valid for
, valid for  , we can derive the approximate result
, we can derive the approximate result
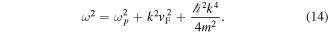
This is the well known dispersion relation for electron plasma waves in a quantum plasma [1]. Let us now consider the quantum Landau damping. Returning to equation (8), and retaining the contributions of the two poles, we obtain the damping coefficient
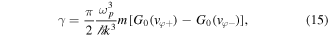
with

In the classical limit, this will reduce to the familiar expression
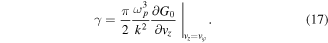
A detailed discussion of the nonlinear regimes of quantum Landau damping, and of electron quantum trapping, can be found in [10]. Most of these results have been described one way or another in the literature. In the following sections we introduce an additional ingredient and consider the influence of electromagnetic radiation on electron plasma wave dispersion.
4. Photon kinetic equation
We now use the second equation (3), with the current given by  . Going back to equation (1), with V = 0, and
. Going back to equation (1), with V = 0, and  , we get for the perturbed quantity
, we get for the perturbed quantity  , associated with an electromagnetic perturbation, the following evolution equation
, associated with an electromagnetic perturbation, the following evolution equation
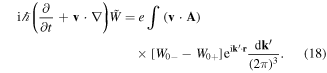
To avoid confusion with the electrostatic waves, we use the notation  for frequencies and wavevectors of transverse waves. Using a single mode solution behaving as
for frequencies and wavevectors of transverse waves. Using a single mode solution behaving as  , we obtain
, we obtain
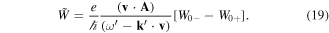
Using  , where the unit polarization vector
, where the unit polarization vector  is transverse to the direction of wave propagation,
is transverse to the direction of wave propagation,  , we can derive from equations (18) and (19), the dispersion relation
, we can derive from equations (18) and (19), the dispersion relation
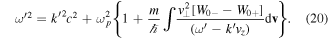
Again, we have assumed wave propagation along the z-axis. This can also be written in terms of the parallel electron quasi-distribution  as
as
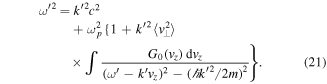
For high frequency waves, such that  , this can be simplified to
, this can be simplified to
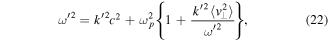
where  . The kinetic term is therefore of order
. The kinetic term is therefore of order  , and can be neglected for
, and can be neglected for  . Let us now assume that the electron plasma density is perturbed by the presence of a spectrum of electron plasma waves. We then have to add to the second equation (3) the current contributions associated with
. Let us now assume that the electron plasma density is perturbed by the presence of a spectrum of electron plasma waves. We then have to add to the second equation (3) the current contributions associated with  such as
such as
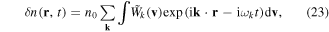
where  satisfy the dispersion relation (8) or (13), and
satisfy the dispersion relation (8) or (13), and  are the associated perturbations of the electron quasi-distribution. Applying the Wigner–Moyal procedure [13] to the second equation (3), with
are the associated perturbations of the electron quasi-distribution. Applying the Wigner–Moyal procedure [13] to the second equation (3), with ![${{\bf{J}}}_{\perp }=-e[{n}_{0}+\delta n({\bf{r}},t)]{{\bf{v}}}_{\perp }$](https://content.cld.iop.org/journals/1402-4896/91/9/095601/revision1/psaa3350ieqn49.gif) , we can derive a wave-kinetic equation of the form (see [16] for a recent discussion on wave-kinetics)
, we can derive a wave-kinetic equation of the form (see [16] for a recent discussion on wave-kinetics)
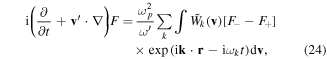
where  is the photon (group) velocity and
is the photon (group) velocity and  is the photon quasi-distribution, as defined by
is the photon quasi-distribution, as defined by
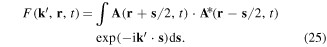
In equation (24), we have assumed that the group velocity  corresponds to traverse wave modes
corresponds to traverse wave modes  , satisfying the dispersion relation (21). We have also used
, satisfying the dispersion relation (21). We have also used  . Notice that F is the photon equivalent to the electron quasi-probability W, and that equation (24) is the photon equivalent to the electron wave-kinetic equation (1).
. Notice that F is the photon equivalent to the electron quasi-probability W, and that equation (24) is the photon equivalent to the electron wave-kinetic equation (1).
5. Electrostatic waves in two quantum fluids
Let us now consider the more complicated situation where an electron plasma wave propagates in a time-varying plasma in the presence of an arbitrary spectrum of electromagnetic waves. We can assume that this is equivalent to the case where the electron plasma wave is coupled to two different quantum fluids, the electron and the photon fluid, each of them described by a corresponding wave-kinetic equation. The total scalar potential Vtot acting on the electrons can now be written as
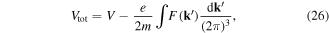
where V is the usual electrostatic potential, as determined by the first of equations (3), and  is the photon quasi-distribution, as defined above. This allows us to write a generalized Poisson's equation for the total potential, of the form
is the photon quasi-distribution, as defined above. This allows us to write a generalized Poisson's equation for the total potential, of the form
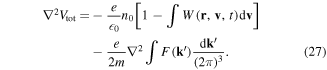
We now consider an electron plasma wave perturbation, of the form  . Using the linearized versions of equations (24) and (5), we can derive the corresponding values for the perturbations of the photon quasi-distribution
. Using the linearized versions of equations (24) and (5), we can derive the corresponding values for the perturbations of the photon quasi-distribution  and electron quasi-distribution
and electron quasi-distribution  , as
, as

and
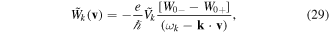
where  is the total electrostatic wave perturbation, as determined by the above generalized Poisson's equation. These two equations show remarkable similarities, but also some important differences. They both describe quantum-like recoil effects, for electrons and photons, as evidenced by the recoil functions
is the total electrostatic wave perturbation, as determined by the above generalized Poisson's equation. These two equations show remarkable similarities, but also some important differences. They both describe quantum-like recoil effects, for electrons and photons, as evidenced by the recoil functions  and
and  . They also display electron and photon Landau resonances, for different values of the phase velocity. The well-known electron resonance appears in equation (29), for
. They also display electron and photon Landau resonances, for different values of the phase velocity. The well-known electron resonance appears in equation (29), for  , while the photon resonance [12] appears in equation (28), for
, while the photon resonance [12] appears in equation (28), for  . The position of the two resonances in the corresponding velocity space is clearly distinct. Replacing equations (28) and (29) in the potential equation (26), we obtain an expression for the potential perturbation, as
. The position of the two resonances in the corresponding velocity space is clearly distinct. Replacing equations (28) and (29) in the potential equation (26), we obtain an expression for the potential perturbation, as
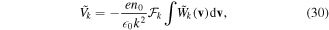
where we have introduced the quantity
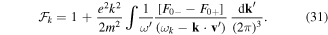
From here we can finally derive a new dispersion relation for electron plasma waves, of the form

The first term in the quantity  describes the electron dispersion, while the second term is due to photon dispersion. The similarities of the electron and photon dispersion properties are very striking. But, more interestingly, the electron and photon susceptibilities do not simply add to each other. On the contrary, the resulting coupling term, as stated by the above dispersion relation, is quite surprising. In a non-relativistic plasma,
describes the electron dispersion, while the second term is due to photon dispersion. The similarities of the electron and photon dispersion properties are very striking. But, more interestingly, the electron and photon susceptibilities do not simply add to each other. On the contrary, the resulting coupling term, as stated by the above dispersion relation, is quite surprising. In a non-relativistic plasma,  , electron Landau damping will be dominant for low phase velocities,
, electron Landau damping will be dominant for low phase velocities,  , while photon Landau damping usually dominates for high phase velocities such that
, while photon Landau damping usually dominates for high phase velocities such that  . However, this will change if the photon spectrum is very close to cuff-off,
. However, this will change if the photon spectrum is very close to cuff-off,  , where the photon group velocity is considerably reduced and the two damping processes could occur simultaneously. The same is true for a relativistic quantum plasma, with
, where the photon group velocity is considerably reduced and the two damping processes could occur simultaneously. The same is true for a relativistic quantum plasma, with  , which however cannot be described by the present nonrelativistic model.
, which however cannot be described by the present nonrelativistic model.
6. Instabilities and damping
Let us discuss the dispersion relation (32) in more detail. In order to understand its significance, we first write it in another form, as
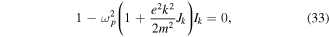
where we have introduced the auxiliary integrals:

Due to the existence of poles, these two integrals are generally complex, and can be written in terms of their real and imaginary parts, as  and
and  , as a result of the two Landau poles. Let us first ignore the imaginary parts. We then write the dispersion relation as
, as a result of the two Landau poles. Let us first ignore the imaginary parts. We then write the dispersion relation as
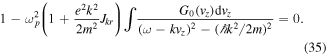
Here we assumed wave propagation along the z-axis,  , and used the equilibrium parallel electron distribution
, and used the equilibrium parallel electron distribution  . Assuming that
. Assuming that  , we can determine the quantity
, we can determine the quantity  with
with
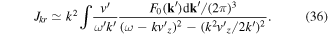
In order to illustrate equation (35), we consider the case of a cold photon beam associated, for instance, to an incident laser beam. It can be described by using  , where a0 is the maximum amplitude of the vector potential. This leads to
, where a0 is the maximum amplitude of the vector potential. This leads to
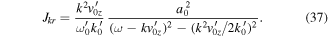
Defining θ as the angle between the wavector  , the parallel photon group velocity is
, the parallel photon group velocity is  , where
, where  . We have also used the photon frequency
. We have also used the photon frequency  . In order to simplify the dispersion relation further, we consider a cold plasma, such that
. In order to simplify the dispersion relation further, we consider a cold plasma, such that  . Equation (35) is then reduced to
. Equation (35) is then reduced to
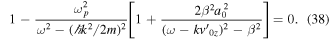
Here we have used the normalized photon field amplitude  , and introduced the auxiliary frequency
, and introduced the auxiliary frequency  . This new dispersion relation for electron plasma waves in the presence of electromagnetic radiation contains photon and electron recoil effects. It shows the occurrence of a photon beam instability, associated with the photon beam amplitude a0. A classical version of this instability was previously considered [12, 13]. In order to find the maximum growth rates, we can define the wave frequency as
. This new dispersion relation for electron plasma waves in the presence of electromagnetic radiation contains photon and electron recoil effects. It shows the occurrence of a photon beam instability, associated with the photon beam amplitude a0. A classical version of this instability was previously considered [12, 13]. In order to find the maximum growth rates, we can define the wave frequency as  , with
, with  , and assume a double resonance condition such that
, and assume a double resonance condition such that
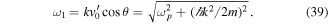
Replacing in equation (38), we can establish the instability growth rate  as
as
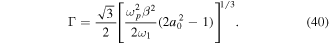
We can see that the photon beam instability has an amplitude threshold, such that  , which is due to recoil effects. Let us now consider the electron kinetic effects. Going back to equation (35), we obtain an expression for the electron Landau damping of the form
, which is due to recoil effects. Let us now consider the electron kinetic effects. Going back to equation (35), we obtain an expression for the electron Landau damping of the form
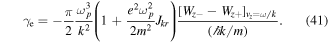
Here, we have  . In the presence of a cold photon beam, the quantity
. In the presence of a cold photon beam, the quantity  is determined by equation (37). We can see that the presence of the photon field modifies the electron Landau damping, and not just the real part of the wave dispersion. In the classical limit, we would have get
is determined by equation (37). We can see that the presence of the photon field modifies the electron Landau damping, and not just the real part of the wave dispersion. In the classical limit, we would have get
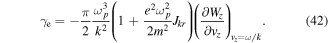
We can see the correction introduced in the electron Landau damping by the presence of electromagnetic radiation. We can similarly establish the photon Landau damping, which takes the form
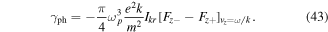
Here, we have used the parallel photon quasi-distribution  , which is defined by
, which is defined by
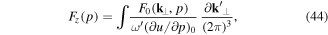
where p is the parallel component of the photon wave vector, as determined by  , and u the parallel component of the group velocity, such that
, and u the parallel component of the group velocity, such that  . The derivative of u in the denominator is taken at the resonant value
. The derivative of u in the denominator is taken at the resonant value  , where the photon parallel group velocity u becomes equal to the phase velocity of the electrostatic wave
, where the photon parallel group velocity u becomes equal to the phase velocity of the electrostatic wave  . We have also used the corresponding resonant values of the photon frequency, as defined by
. We have also used the corresponding resonant values of the photon frequency, as defined by  . In the classical (or geometric optics) limit, we would get
. In the classical (or geometric optics) limit, we would get
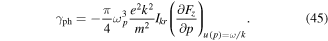
In order to complete our discussion, we should notice that in these expressions we can use
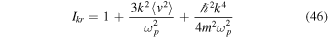
where we have defined the electron square mean velocity as  . Here we can see that the electron quantum effects will contribute to photon Landau damping. These results are illustrated in figure 1, where the total damping rate
. Here we can see that the electron quantum effects will contribute to photon Landau damping. These results are illustrated in figure 1, where the total damping rate  is represented for an electron plasma wave in the presence of a moderately strong photon beam. We can see that, although slow electron plasma waves are mainly damped by electron Landau damping, for fast waves photon Landau damping becomes dominant. In the photon dominated regime, an unstable region corresponding to positive values of γ is also present. This is the kinetic version of the photon beam instability described above, and can be associated to a stimulated Raman scattering process [13].
is represented for an electron plasma wave in the presence of a moderately strong photon beam. We can see that, although slow electron plasma waves are mainly damped by electron Landau damping, for fast waves photon Landau damping becomes dominant. In the photon dominated regime, an unstable region corresponding to positive values of γ is also present. This is the kinetic version of the photon beam instability described above, and can be associated to a stimulated Raman scattering process [13].
Figure 1. Total Landau damping,  , as a function of the normalized wave number
, as a function of the normalized wave number  , in the quasi-classical limit. Equations (42) and (45) were used, with
, in the quasi-classical limit. Equations (42) and (45) were used, with  and
and  . Both the electron and the photon Landau damping regions can be identified, where for slow waves the electron kinetic effects dominate, while for fast waves the photon kinetic effects become important. In this case, an instable region is also present.
. Both the electron and the photon Landau damping regions can be identified, where for slow waves the electron kinetic effects dominate, while for fast waves the photon kinetic effects become important. In this case, an instable region is also present.
Download figure:
Standard image High-resolution image7. Conclusions and remarks
We have considered the process of electron plasma wave propagation in quantum plasmas. This could eventually be relevant in different physical situations, such as the early universe, the interior of dense stars, or a laser compressed target. We have established a new dispersion relation for electron plasma waves in the presence of an arbitrary spectrum of transverse electromagnetic waves.
The wave dispersion properties depend on the response of both electron and photon populations, as determined by a new form of dispersion equation. In this new dispersion relation, the kinetic effects of both electrons and photons are included. We have shown that, in a quantum plasma, electron and photon Landau damping can be described by very similar expressions where quantum recoil effects can be identified. As noted in our previous work [12], recoil effects are not exclusive to quantum physics, as they are a general property of wave phenomena. The similarities between these two dispersion effects are due to the similarities between a quantum description of the plasma electrons and a wave description of the photon field.
Another remarkable and unexpected property of our new dispersion relation for electron plasma waves is that the kinetic effects of electron and photons do not simply add to each other, as they are contained in a single kinetic dispersion term. Extension to a relativistic quantum plasma could be interesting, due to a possible overlap between the two Landau resonances, and will be considered in a future work.
Acknowledgments
We would like to acknowledge the support of the European project PIRSES-GA-2013-612506.



