Abstract
Propagation of a gel/glass transition boundary in a polymer is considered in the context of drug release. Drug molecules are assumed to undergo subdiffusive motion in the gel and be quiescent in the glass region. Exact self-similar solutions for the drug concentration are constructed, and the amount of released drug is determined as a function of time.
Export citation and abstract BibTeX RIS
1. Introduction
The advection-diffusion transport in random velocity fields often exhibits a non-standard behavior [1] which is referred to as anomalous diffusion. The essence of the phenomenon of the anomalous diffusion is the violation of the relation 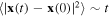 for a random motion x = x(t) of a molecule. Instead, the mean square displacement of the particle scales as
for a random motion x = x(t) of a molecule. Instead, the mean square displacement of the particle scales as 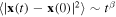 , where the exponent β is either larger than 1 (superdiffusion) or smaller than 1 (subdiffusion). Numerous examples of both kinds of anomalous diffusion in flows can be found in review paper [2]. In addition to turbulent convection [3], plasma turbulence [4, 5], and atmospheric turbulence [6], anomalous diffusion has been detected in contaminant transport [7], transport in heterogeneous porous media [8] and gels [9–12].
, where the exponent β is either larger than 1 (superdiffusion) or smaller than 1 (subdiffusion). Numerous examples of both kinds of anomalous diffusion in flows can be found in review paper [2]. In addition to turbulent convection [3], plasma turbulence [4, 5], and atmospheric turbulence [6], anomalous diffusion has been detected in contaminant transport [7], transport in heterogeneous porous media [8] and gels [9–12].
Anomalous diffusion in gels has potential applications in the problem of controlled drug delivery. Mathematical modeling of controlled drug delivery has been attracting much attention of scientists [13–19]. Analysis of the drug delivery process is often based on traditional models that typically involve a standard Fickian diffusion equation. Due to the scaling properties of this equation, the flux of a drug released from a pill decreases with time as t−1/2. In applications, it is desirable to release the drug with a nearly constant rate. Anomalous diffusion in gels has been suggested as a mechanism that would provide a slower decrease of the drug flux than in the case of normal diffusion [20–24].
In the present paper we consider drug release from a polymer matrix that undergoes a gel/glass transition. Drug molecules are assumed to perform a subdiffusive motion in the gel and be quiescent in the glass region. We construct an exact self-similar solution for the drug concentration and determine the amount of released drug as a function of time.
2. Mathematical model
Before formulating the problem, we note that subdiffusive transport of the drug in the gel can be described by a fractional diffusion equation for the drug concentration C(x, t)
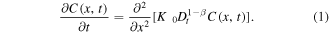
The equation can be derived by means of probabilistic methods [25]. Here
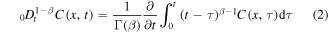
is the Riemann–Liouville fractional derivative and K is a constant fractional diffusion coefficient. One can rewrite equation (1) as

where
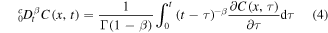
is the Caputo fractional derivative. Equation (1) can be also written in the form of a conservation law
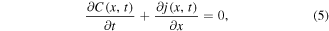
where the subdiffusive flux
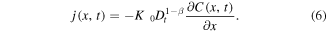
Let us assume now that the polymer in the state of gel, where the subdiffusion of a drug takes place, occupies the region 0 < x < s(t), while in the region 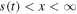 the polymer is in the state of glass with a vanishing diffusion coefficient. Assume also that the glass/gel transition front moves to the right, and it passes any point x at a certain time instant tf (x), so that s(tf (x)) = x. Then the subdiffusive flux in the gel is
the polymer is in the state of glass with a vanishing diffusion coefficient. Assume also that the glass/gel transition front moves to the right, and it passes any point x at a certain time instant tf (x), so that s(tf (x)) = x. Then the subdiffusive flux in the gel is
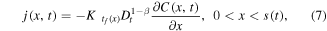
which leads to the subdiffusion equation

We note the difference between the generic expression for the subdiffusive flux (6) and the expression (7) that we are using. In (6), the history of a drug molecule motion (i.e., the lower limit of integration in the Riemann–Liouville derivative) starts at t = 0. In (7), the history starts at the time t = tf (x) when the molecule enters the gel region since no motion of the molecule occurs in the glass region. This difference is discussed in greater detail in [26].
At the left boundary of the gel region, x = 0, we assume full consumption of the drug

At the front of the glass/gel transition, we expect a jump of the drug concentration due to a restricted solubility of the drug in the solvent:

The conservation of the drug mass leads to the following Stefan boundary condition:
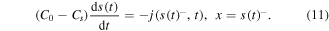
In the glass region
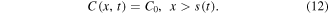
The initial conditions are:
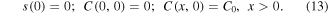
We remark that while in the case of the normal diffusion, β = 1, the system (8)–(13) has a self-similar solution which describes propagation of the transition front with s(t) ∼ t1/2 and a finite ∂C/∂x at the front, in the case of subdiffusion, where the flux is determined by the memory integral (7), j(s(t)−, t) = 0, unless ∂C/∂x is singular as x → s(t)−. In order to determine the limiting value of j(x, t) as x → s(t)−, we derive equations that determine the self-similar subdiffusive solution.
Taking into account the scaling properties of the system, we assume
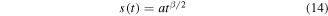
and introduce the self-similar variable

For the self-similar solution C(x, t) = f (u), we find:
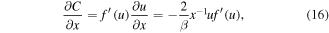

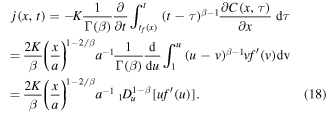
Substituting (17), (18) into (5), we obtain the following equation for the self-similar solution f(u):
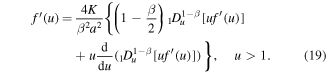
It is convenient to rewrite this equation in terms of the function 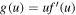 as
as
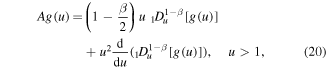
where
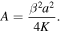
Boundary conditions (9) and (10) give

respectively, from which
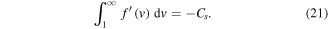
Finally, the boundary condition (11) yields
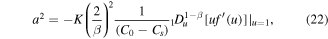
which can be written as
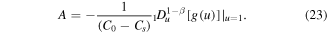
The solution g(u) of equation (20) can be written in the form

where rj(u) are analytic functions that can be expanded in powers of u − 1, with  . All the coefficients of the expansions can be determined in terms of k, while k is arbitrary as it should be since equation (20) is a linear homogeneous equation. We reiterate that for u close to 1
. All the coefficients of the expansions can be determined in terms of k, while k is arbitrary as it should be since equation (20) is a linear homogeneous equation. We reiterate that for u close to 1
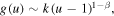
so that
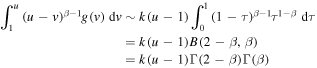
and
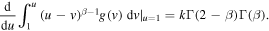
We can rewrite (23) as
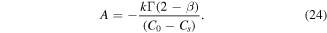
Rather than attempting to solve (20) by the series expansion, we solve it by using the Laplace transform. We rewrite (20) for the function y(ξ) = g(u), ξ = u − 1 to obtain

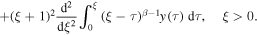
Applying the Laplace transform to (25) and using

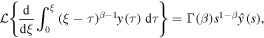
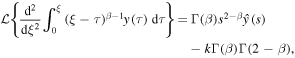
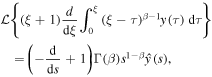
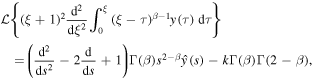
we reduce the equation to
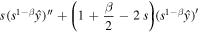
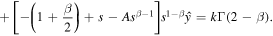
Two linearly independent solutions of the homogeneous equation are
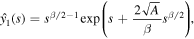
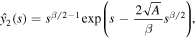
so that using variation of parameters we find the general solution as
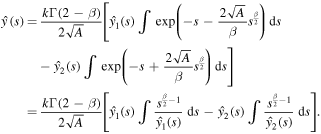
We are interested in the solution that decays as 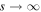 . This solution can be written in the form
. This solution can be written in the form
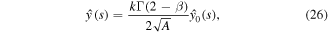
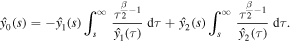
Next, we determine the coefficient k by using the condition (21). We observe that
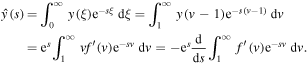
Thus
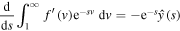
and integrating with respect to s from s to infinity yields

Evaluating at s = 0, we get
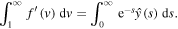
Using the condition (21) and the expression (26) for 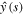 in the above equation results in the formula for k
in the above equation results in the formula for k
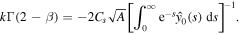
Using this result in (24), we obtain an equation for A
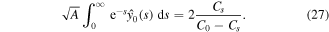
The equation can be simplified. Indeed

Thus, equation (27) simplifies to
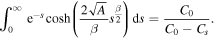
Recalling the definition of A, we get
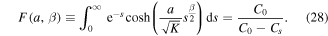
Since the right-hand side of (28) is greater than 1 and the left-hand side monotonically increases from 1 to infinity as a goes from zero to infinity, there is a unique solution of the equation for any β, 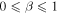 . Note that in the case of normal diffusion, β = 1, the integral on the left-hand side can be computed yielding the well known result
. Note that in the case of normal diffusion, β = 1, the integral on the left-hand side can be computed yielding the well known result
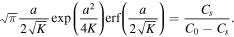
In the limiting case β → 0, we obtain from (28) that

We remark that the function F(a, β) monotonically increases with β, 0 ≤ β ≤ 1, so that a is a decreasing function of β.
The total amount of drug Q(t) released from the polymer by the time t, which is an important characteristic of the process, can be found using (18) as

where
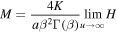
and
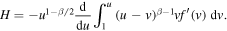
To calculate M, we observe that H can be written as
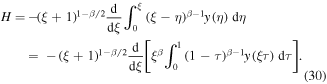
We have to compute the limit of H as  .To determine the limit, we note that asymptotic behavior of y(η) for large η can be found from the behavior of the Laplace transform
.To determine the limit, we note that asymptotic behavior of y(η) for large η can be found from the behavior of the Laplace transform 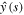 for small s. The expression (26) for
for small s. The expression (26) for 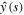 gives for
gives for 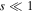
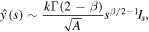
where
so that for η ≫ 1
and accounting for the definition of A and relation (24), we simplify the expression for M yielding
In the case of normal diffusion, β = 1, the integral Is in (32) can be evaluated and (32) reduces to the square root dependence
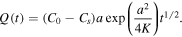
3. Discussion
We studied a Stefan problem which describes propagation of a gel/glass transition front in a polymer in the context of drug-release devices. In our model, there is no transport of drug molecules through the glass region, while in the gel region the evolution of drug concentration is governed by a subdiffusion equation. We constructed an exact self-similar solution for the drug concentration and determined the amount of drug released from the glass region with time.
There are several other works in which anomalous diffusion in the gel is studied for drug-release devices [20–24]. The models considered in these papers differ from our model. For example, in [20] the authors obtain a self-similar solution of equation (3), which is equivalent to (1), with the fractional derivative 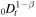 rather than
rather than 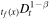 . In [21, 22], in addition, the boundary condition (11) is replaced with
. In [21, 22], in addition, the boundary condition (11) is replaced with
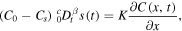
which is not equivalent to (11). In [24], the amount of released drug Q(t) is calculated as proportional to t1 − β/2 (see (32)) as a result of using the normal diffusion flux through the boundary x = 0 rather than a subdiffusive flux,which should be used in the subdiffusion case.
According to our predictions, the drug flux from a subdiffusive gel will decrease with time as tβ/2 − 1, i.e., faster than in the case of normal diffusion. Therefore, gel subdiffusion cannot be considered as a way to provide a nearly constant drug release, which is desirable in applications. Actually, there are other explanations of the deviation from the Fickian scaling observed in experiments (see, e.g., [27] and the references therein) due to polymer swelling, dissolution, erosion, etc. Analysis of these mechanisms of a non-Fickian drug release is beyond the scope of the present paper.
Acknowledgments
The work has been partially supported by the US-Israel Binational Science Foundation (grant No. 2008122). VAV gratefully acknowledges the support of NSF grant DMS 1108624.



