Abstract
Two-photon transitions in H- and He-like heavy ions in the presence of an external static electric field are explored using a relativistic Greens function approach and an independent particle model. The effects of Stark mixing on angular correlations, spectral distributions and total transition rates are analyzed in detail. Special emphasis is placed on the 2p1/2 → 1s1/2 two-photon transition in H-like ions and the 1s1/22p1/2:23P0 → 1s21/2:11S0 and 1s1/22s1/2:21S0 → 1s21/2:11S0 two-photon transitions in He-like ions.
Export citation and abstract BibTeX RIS
1. Introduction
In the last decades two-photon transitions have gained interest as a sensitive tool to study the electronic structure of highly charged heavy ions. Such studies could lead to new insights into various phenomena such as relativistic, quantum electrodynamics, or parity non-conservation effects in ions. Apart from spontaneous two-photon decay which was addressed in most of the previous studies [1–3], much of the current interest is focused on laser-induced transitions. For heavy ions, high-intensity lasers are required to perform such studies [4]. These high laser intensities, however, may affect the electronic structure of the ions and, hence, the properties of the two-photon transitions. In order to estimate the importance of such electronic structure changes we will consider two-photon decay under one of the simplest perturbation of the electronic structure of ions, the mixing of different parity states due to the linear Stark effect. A preliminary non-relativistic study of the effects of electric fields on two-photon transitions in hydrogen has been performed by Solovyev et al [5]. Here we extend this study to highly charged H-like and He-like ions.
In this work we examine the angular and spectral distributions of two-photon transitions as well as the total decay rates in H-like and He-like heavy ions in the presence of a static electric field. To perform this study, we use a relativistic Greens function approach based on Dirac theory and an independent particle model (IPM). The effect of the electric field is included using first order non-degenerate perturbation theory. The properties of the 2p1/2 → 1s1/2 two-photon transition in H-like ions and the 1s1/22p1/2:23P0 → 1s21/2:11S0 and 1s1/22s1/2:21S0 → 1s21/2:11S0—or shorter the 23P0 → 11S0 and 21S0 → 11S0—two-photon transitions in He-like ions in the presence of an external electric field are discussed in detail.
In our calculations we used atomic units.
2. Theoretical background
2.1. Two-photon transitions in one- and two-electron atoms
Two-photon transitions in atoms and ions have been studied extensively for many decades [1, 3, 6]. Their properties are usually traced back to the second order transition amplitude given by
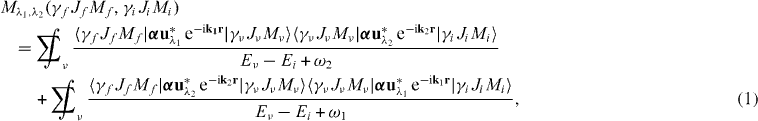
where Ji,ν,f and Mi,ν,f are the total angular momenta and the magnetic quantum numbers of the initial, virtual intermediate and final states. The γi,ν,f characterize all other quantum numbers necessary to uniquely define the states. In the numerator the operator α u*λ e−i k r describes the relativistic coupling of the electron with photons of the polarization uλ. In the denominators the Ei and Eν are the energies of the initial and intermediate states. The ω1 and ω2 are the energies of the two photons. Due to the energy conservation, these energies are related to the transition energy like Ei − Ef = ω1 + ω2. It is convenient, therefore, to introduce the energy sharing parameter x = ω1/(Ei − Ef), 0 ⩽ x ⩽ 1 that indicates which portion of the transition energy is taken away by the 'first' photon.
The amplitude (1) contains summations over the complete spectrum γν,Jν,Mν. We treat this summations by introducing the Greens function of the system: 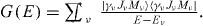 For H-like ions with a point-like nucleus there exist several representations of the Greens function that allow the analytical evaluation of the transition amplitude. In this work we use the Sturmian representation of the Greens function [3].
For H-like ions with a point-like nucleus there exist several representations of the Greens function that allow the analytical evaluation of the transition amplitude. In this work we use the Sturmian representation of the Greens function [3].
For the treatment of He-like systems we use an IPM. In IPM, the He-like states are products of H-like states with coupled angular momenta. Some shielding of the nuclear charge is included by introducing an effective nuclear charge. With this IPM the transition amplitude for He-like systems can be written in terms of H-like transition amplitudes [7].
2.2. The Stark perturbed two-photon transition amplitude
In equation (1) the initial, final and intermediate states |γiJiMi〉, |γfJfMf〉 and |γνJνMν〉 are states with well defined angular momentum properties, symmetries and parity. If the ion is placed in an electric field these states can be mixed with nearby opposite parity levels. This mixing may affect the properties of the two-photon decay. In order to study these effects we recall the basic formulas describing the linear Stark mixing.
We characterize the Stark mixing of the states using non-degenerate first order perturbation theory [5, 8]. The perturbed state 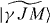 can be expressed in terms of the original state |γJM〉 and the perturbing states |γμJμMμ〉 using
can be expressed in terms of the original state |γJM〉 and the perturbing states |γμJμMμ〉 using
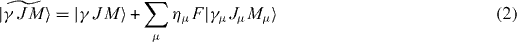
with F being the electric field strength and ημ the mixing parameter [9, 10]. By adopting the quantization (z-)axis along the electric field, we can simplify the summation in equation (2) and obtain for this mixing parameter

where ΔEμ = E − Eμ is the energy difference between the original and induced initial states, Γμ = Γ + Γ0μ their combined line widths, and z the z-component of the position operator.
In the chosen coordinate system the Stark mixing coefficient is only non-zero when the quantum numbers of the unperturbed and the perturbing states fulfill: ΔL = 0, ΔS = 0, ΔM = 0. For some original states the ΔM = 0 condition leads to a selection of magnetic quantum numbers in the perturbing states. As a result the Stark mixing depends on the choice of the coordinate system and thus on the direction of electric field. Some consequences of this dependence will be discussed in the next section.
By inserting the perturbed wavefunctions (2) into equation (1) we can derive the transition amplitude, describing the two-photon decay in the presence of an external electric field. Generally the calculation of this amplitude is rather difficult since initial, final and intermediate states may be affected by the Stark mixing. For some transitions, however, the evaluation can be significantly simplified. For example, when we consider the 2p1/2 → 1s1/2, the 21S0 → 11S0, and the 23P0 → 11S0 transitions in H-like and He-like ions, the initial states have usually a single perturbing state with a particular small energy difference ΔEμ. This contribution dominates the perturbation of the initial state. The final state and its closest perturbing state on the other hand has a much larger energy splitting ΔEμ than the initial state and its perturbing state and can therefore be neglected.
The mixing of the intermediate state require some deeper analysis. Additional to the one Greens function in the transition amplitude (1), the intermediate state contributions contain a second Greens function  at the energies E = Ei − ω1,2. As a first estimation these contributions are dominated by the summands
at the energies E = Ei − ω1,2. As a first estimation these contributions are dominated by the summands  for which the energy difference ΔEν = Eν − E becomes minimal. However, for non-resonant transitions 0 ≠ x ≠ 1 like the ones we consider here, the minimal energy difference ΔEν is still much larger than the energy splitting of the initial state. Therefore we can ignore the intermediate parts and focus on the dominant perturbation of the initial state. We call the dominant initial perturbing state
for which the energy difference ΔEν = Eν − E becomes minimal. However, for non-resonant transitions 0 ≠ x ≠ 1 like the ones we consider here, the minimal energy difference ΔEν is still much larger than the energy splitting of the initial state. Therefore we can ignore the intermediate parts and focus on the dominant perturbation of the initial state. We call the dominant initial perturbing state  and its mixing parameter
and its mixing parameter  .
.
2.3. Angular correlation, spectral distribution and total transition rate
In the last section we discussed the evaluation of the perturbed two-photon transition amplitude in leading order. We use this perturbed transition amplitude as a 'building block' to compute all two-photon transition properties. For example the triple differential decay rate—differential in the photon emission directions Ω1 = (θ1,ϕi), Ω2 = (θ2,ϕ2) and the energy sharing of the photons x—is given by
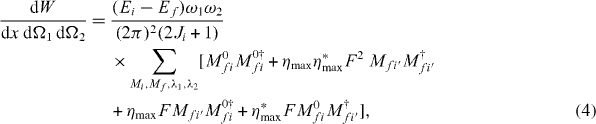
with the abbreviations M0fi = Mλ1,λ2(γfJfMf,γiJiMi) and 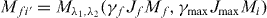 . The differential decay rate (4) is proportional to the two-photon angular correlation. We will use this proportionality in the upcoming analysis to study the angular correlation in terms of the differential decay rate.
. The differential decay rate (4) is proportional to the two-photon angular correlation. We will use this proportionality in the upcoming analysis to study the angular correlation in terms of the differential decay rate.
In (4) we see that the differential decay rate of the Stark quenched system consists of a F independent part, an induced part quadratic in F and interference terms which are linear in F. We will discuss the interplay of these parts in more detail in the next section.
The spectral distribution and the total decay rate are obtained by integrating the angular correlation over all photon emission angles and for the total rate by additionally integrating over the energy sharing of the photons.
3. Results and discussion
Based on equation (4) we are able to discuss how the properties of two-photon decay are affected by an external static electric field. To estimate the region of the electric field strength where our perturbative approach is valid, we introduce a critical field strength 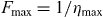 .
. 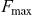 defines a natural field strength scale for linear Stark mixing. It is convenient to express field strengths in fractions of it. In the following listing we present
defines a natural field strength scale for linear Stark mixing. It is convenient to express field strengths in fractions of it. In the following listing we present 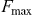 for the transitions considered in this text. The upper index indicates the perturbed and the dominant perturbing initial states.
for the transitions considered in this text. The upper index indicates the perturbed and the dominant perturbing initial states.
For hydrogen the value of 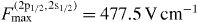 is in good agreement with previous calculations [5]. In highly charged uranium
is in good agreement with previous calculations [5]. In highly charged uranium 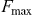 is of the same order of magnitude as electric fields that would be expected in the experiments involving laser induced transitions mentioned in the introduction, i.e. we have
is of the same order of magnitude as electric fields that would be expected in the experiments involving laser induced transitions mentioned in the introduction, i.e. we have 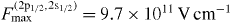 in U91+ and
in U91+ and 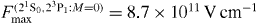 and
and 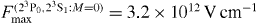 in U90+.
in U90+.
At the start of our analysis of the external field effects, we note that in the integration procedure to obtain the spectral distribution and the total decay rate the interference terms in equation (4) vanish and only the terms independent and quadratic in F play a role. For the total decay rate this means that within the limits of applicability of our approach 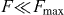 the perturbed rate only differs considerably for initial states that have a decay rate similar as or smaller than the leading perturbing contribution. The transitions we consider here fulfill this condition.
the perturbed rate only differs considerably for initial states that have a decay rate similar as or smaller than the leading perturbing contribution. The transitions we consider here fulfill this condition.
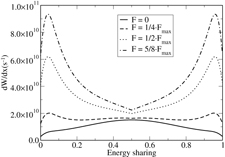
For a more detailed inspection of the Stark mixing effects we calculated the spectral distribution of the 23P0 → 11S0 decay of He-like Uranium for various external electric field strengths F. These spectral distributions are shown in figure 1. As seen from the figure, even if the strength is a quarter of  , a strong alternation of the spectral distribution can be observed. This alternation can be understood from equation (4) and the last paragraph which suggests that the perturbed energy differential decay rate can be seen as a superposition of the spectral distributions of the F-independent 'unperturbed' 23P0 → 11S0 transition and the 'Stark induced' 23S1(M = 0) → 11S0 transition proportional to F2. Since the spectral distributions of these two transitions are drastically different the spectral distribution of the resulting perturbed 23P0 → 11S0 transition strongly depends on F.
, a strong alternation of the spectral distribution can be observed. This alternation can be understood from equation (4) and the last paragraph which suggests that the perturbed energy differential decay rate can be seen as a superposition of the spectral distributions of the F-independent 'unperturbed' 23P0 → 11S0 transition and the 'Stark induced' 23S1(M = 0) → 11S0 transition proportional to F2. Since the spectral distributions of these two transitions are drastically different the spectral distribution of the resulting perturbed 23P0 → 11S0 transition strongly depends on F.
Figure 1. Spectral distribution of the 23P0 → 11S0 two-photon transition of U90+ in the presence of an electric field F given in fractions of 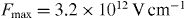 .
.
Download figure:
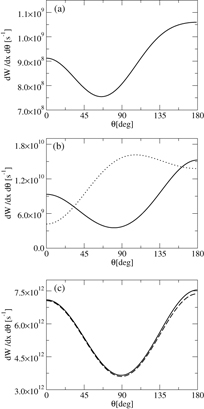
Standard image High-resolution imageIn contrast to the total decay rate and the spectral distribution, the (triple) differential decay rate d3W/dE dΩ1 dΩ2 is affected by all contributions in equation (4). Furthermore since the Stark mixing has some dependence on the direction of the electric field, we expect a similar dependence of the field induced contributions of the angular correlation. To illustrate these effects, we present in figure 2 the differential decay rate of the perturbed 2p1/2 → 1s1/2 transition in H-like Uranium and the 23P0 → 11S0 and 21S0 → 11S0 transitions in He-like Uranium. Different angles between the electric field and the emitted photons are taken into account by considering angular correlations where one of the photons is emitted 'parallel' or 'antiparallel' to the electric field or where both photons are emitted 'perpendicular' to it. The angle between the two-photons is called θ.
Figure 2. Triple differential decay rates of two-photon transitions in an external electric field for different angles between the emitted photons and the electric field. The solid lines show the differential decay rates for 'parallel' emission of the photons, the dashed lines the rates for 'antiparallel' emission, and the dotted lines the rates for 'perpendicular' emission. The field strengths F and energy sharing x were optimized for contrast. We have in (a) the 2p1/2 → 1s1/2 two-photon transition in U91+ with x = 1/4, 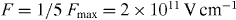 , in (b) the 23P0 → 11S0 transition in U90+ for x = 1/4,
, in (b) the 23P0 → 11S0 transition in U90+ for x = 1/4, 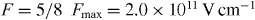 and in (c) the 21S0 → 11S0 transition in U90+ for
and in (c) the 21S0 → 11S0 transition in U90+ for 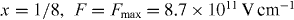 .
.
Download figure:
Standard image High-resolution imageIn figure 2 (a) we see that the angular correlation of the Stark perturbed 2p1/2 → 1s1/2 transition is not dependent on the direction of the electric field. This non-dependence can be explained by vanishing interference terms in equation (4). It is caused by the fact that for this transition the contributions to the interference terms from the different Mi and Mf cancel each other.
Figure 2(b) shows the differential decay rate of the 23P0 → 11S0 transition. In this panel the 'parallel' and 'antiparallel' angular correlations coincide while the 'perpendicular' one deviates from them. To understand this fact, it is useful to remember the direction dependence arising from the ΔM = 0 condition for the mixing parameter. It is caused by the fact that for the 23P0 initial state, the perturbing initial state 23S1:(M = 0) can be considered 'oriented'. This 'orientation' leads to a direction dependence of the perturbed differential decay rate similar to angular dependencies in the decay of 'oriented' states.
Finally we have in figure 2 (c) the differential decay rate of the 21S0 → 11S0 decay in an external field. In this decay the 'antiparallel' and 'parallel' angular correlations differ at θ → 180°. This effect hints to the linear dependence of non-negligible interference terms cf equation (99) in [5].
4. Summary and outlook
We studied the angular correlations, the spectral distributions and the total two-photon decay rates of heavy few-electron ions in the presence of external electric fields. We found that all analyzed properties of two-photon transitions can be strongly affected by the Stark mixing. These effects become most pronounced when the unperturbed two-photon decay rate is smaller than the two-photon decay rate of the largest perturbative contribution and the electric field is relatively large compared to the critical field strength where the perturbative approach breaks down 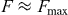 .
.
The outcome of our study shows the importance of including Stark mixing effects in the analysis of two-photon transitions in the presence of external electric fields. In particular such effects may arise in the analysis of induced two-photon transitions. The analysis of these transitions is currently underway and will be presented in a following publication.