Abstract
The MHD–kinetic hybrid toroidal stability code MARS-K (Liu et al 2008 Phys. Plasmas 15 112503) is applied to study the shaping effects on magnetohydrodynamic (MHD) stabilities in reversed field pinch (RFP) plasmas, where both elongation and triangularity are taken into account. The ideal wall β (the ratio of the gaso-kinetic to magnetic pressures) limit set by the ideal kink mode/resistive wall mode in shaped RFP is investigated first, followed by a study of the kinetic damping on the resistive wall mode. Physics understanding of the results is provided by a systematic numerical analysis. Furthermore, the stability boundary of the linear resistive tearing mode in shaped RFP plasmas is computed and compared with that of the circular case. Finally, bootstrap currents are calculated for both circular and shaped RFP plasmas. Overall, the results of these studies indicate that the current circular cross-section is an appropriate choice for RFP devices, in the sense that the plasma shaping does not bring an appreciable advantage to the RFP performance in terms of macroscopic stabilities. In order to reach a steady-state operation, future RFP fusion reactors will probably need a substantial fraction of external current drives, due to the unfavourable scaling for the plasma-generated bootstrap current in the RFP configuration.
Export citation and abstract BibTeX RIS
1. Introduction
The optimization of the geometrical shape for toroidal fusion plasmas is an important issue. For example, it is well known that for an advanced tokamak design, the appropriate D-shaped cross-section can result in a higher performance towards high-β, steady-state fusion plasmas. In tokamaks, shaping often helps to increase the favourable curvature region which is inherently stabilizing for a few magnetohydrodynamic (MHD) modes. In addition, elongation normally helps to increase the total plasma current I, by a factor (1 + κ2)/2, with the same q(a) value, where κ is the elongation factor and q(a) is the plasma edge safety factor. A larger current normally yields a better confinement. Furthermore, since the no-wall beta limit βN (βN = βT(aBT/I),
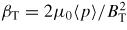 , 〈p〉 is the average plasma pressure, μ0 is the vacuum permeability and BT is the strength of the toroidal magnetic field) for the ideal kink instability in tokamak is related to the total current [1–3], increasing current implies the possibility of maximizing the βT value for an advanced tokamak, without changing other parameters such as βN, a and BT. The value of βN is often determined by the radial profiles of equilibrium quantities such as the plasma pressure and current, and can be largely independently controlled from the total plasma current.
, 〈p〉 is the average plasma pressure, μ0 is the vacuum permeability and BT is the strength of the toroidal magnetic field) for the ideal kink instability in tokamak is related to the total current [1–3], increasing current implies the possibility of maximizing the βT value for an advanced tokamak, without changing other parameters such as βN, a and BT. The value of βN is often determined by the radial profiles of equilibrium quantities such as the plasma pressure and current, and can be largely independently controlled from the total plasma current.
As an alternative fusion experimental device, reversed field pinch (RFP) has toroidal axisymmetry as well [4]. Nevertheless, all of the existing RFPs possess a circular cross-section. There is no experimental evidence showing whether shaped plasmas in an RFP can bring an advantage for its performance. Recently, significant progress has been made in RFP studies both in experiments and theory [5, 6]. The question of how to improve the RFP design towards an advanced fusion device is placed on the agenda. The macroscopic MHD instabilities in RFP plasmas are often categorized into resonant and non-resonant modes, depending on whether the mode's rational surface is located inside (resonant) or outside (non-resonant) the plasma. It is also conventional to divide the instabilities into internal and external modes, depending on whether the mode is located inside or outside the toroidal field reversal radius. The plasma shaping effect has previously been studied in an early work [7], with the main conclusion that plasma shaping does not have a significant effect on the stability of the resonant ideal modes and the interchange modes, either with or without a finite plasma pressure. The study assumed an ideal wall surrounding the plasma. On the other hand, the resonant ideal kink modes have been experimentally observed being stable in RFP plasmas due to the self-organized relaxation process. It is now understood that the most important (and/or commonly observed) instabilities in RFP plasmas are the (internal and external) non-resonant ideal modes (the resistive wall modes, RWMs) and the resonant resistive modes (the tearing modes, TMs) [8, 9]. The latter is responsible for the necessary dynamo effect to maintain the RFP magnetic configuration. The pressure-driven interchange mode can be unstable when the Mercier criterion is violated, which is a rather localized mode due to the high magnetic shear in the RFP configuration. It may not be the most dangerous mode to set the β limit for RFP plasmas. In this work, we systematically investigate the shaping effects on the most prominent MHD instabilities—the RWM and the TM—observed in RFPs, with the aim to find whether shaping can bring an advantage for improving the performance of RFPs. Moreover, this work includes the following key aspects: (i) an in-depth physics understanding of the shaping effects based on the detailed energy analysis of the modes; (ii) the drift kinetic effects on the RWMs in the presence of shaping, following a non-perturbative approach; (iii) the shaping induced multiple trapping and modification of bootstrap fraction. Both plasma elongation and triangularity are taken into account. The kinetic–MHD hybrid toroidal stability code MARS-K is modified and adopted for the RFP study [10, 11].
We first consider the stabilities of the non-resonant ideal kink mode and related RWM, which are commonly observed in RFPs [12–22], in shaped plasmas. Both fluid theory and the kinetic effects of the high-β thermal particles are considered. The RFP magnetic configuration is characterized by the reversed toroidal magnetic field BT near the edge and a large poloidal field Bp, which has the strength of the same order as the toroidal field. Compared with the tokamak configuration with the same BT at the magnetic axis, RFP has a much higher plasma current, which in turn can provide sufficiently large ohmic heating, allowing the possibility of reaching the fusion reaction [4, 21, 22]. However, a large current often causes a current-driven RWM (basically an ideal kink mode instability), which can be unstable even at vanishing plasma pressure, thus leading to a zero no-wall β limit
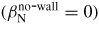 . Furthermore, the strong poloidal magnetic field Bp gives a dominant contribution to the magnetic curvature, implying that bad magnetic curvatures exist everywhere along the poloidal angle. The plasma shaping does not change this fundamental feature. On the other hand, shaping does cause a significant variation of the field strength along the poloidal angle, resulting in an enhancement of the poloidal mode coupling and an occurrence of multiple trapping regions, as we shall show. Consequently, the shaping effect on the RFP plasmas is generally quite different from that on tokamak plasmas.
. Furthermore, the strong poloidal magnetic field Bp gives a dominant contribution to the magnetic curvature, implying that bad magnetic curvatures exist everywhere along the poloidal angle. The plasma shaping does not change this fundamental feature. On the other hand, shaping does cause a significant variation of the field strength along the poloidal angle, resulting in an enhancement of the poloidal mode coupling and an occurrence of multiple trapping regions, as we shall show. Consequently, the shaping effect on the RFP plasmas is generally quite different from that on tokamak plasmas.
In this work, we find that the ideal-wall β limit (i.e. the ideal kink stability threshold) is reduced by shaping for both internally and externally non-resonant modes. The kinetic effects of thermal particles become more significant in the shaped RFP, stabilizing the RWM at relatively lower β values than that in a circular RFP. However, the required plasma rotation frequency for the mode suppression is still in the ion acoustic range as being found in circular RFPs [10]. We report a detailed physics understanding on the mechanisms underlying these results.
Next, we study the linear stability of the resistive TMs, which are responsible for the dynamo effects in RFPs, in shaped plasmas and compare the results with that of the circular cases. Finally, the effect of shaping on the bootstrap currents of RFP plasmas is also preliminarily studied and discussed. We observe that the shaping effects with respect to all these aspects do not result in a notable change of the RFP performance.
The paper is organized as follows. Section 2 discusses the shaping model, the relevant MARS-K formulations used in this work. Section 3 investigates the β limit set by the ideal kink and the RWM in shaped plasmas. In section 4, kinetic damping on the RWM in a shaped RFP is studied. In section 5, the results of shaping effects on the resistive TM instability in low-β RFP plasmas are presented. Section 6 discusses the bootstrap current fraction in both circular and shaped RFP plasmas. The conclusion and a brief discussion are given in section 7.
2. Models and formulations
2.1. Elliptic, triangular and D-shaped RFP plasmas
The shape of the plasma boundary is described by the following formulae:


where R and Z are the Cartesian coordinates with the origin at the centre of the torus, R0 is the major radius, ε is the inverse aspect ratio, κ is the elongation and δ is the triangularity. The RFP equilibria are computed by solving the Grad–Shafranov equation using the CHEASE code [23], given the plasma current and pressure profiles as the input, together with the plasma boundary specified above. Figure 1 shows examples of the computed equilibrium flux surfaces with various shaped cross-sections: circular (κ = 1.0, δ = 0.0), elliptic (κ = 1.3, δ = 0.0), triangular (κ = 1.0, δ = 0.3) and D-shaped (κ = 1.3 and δ = 0.3). In order to make sensible comparisons between different shaping parameters on the RFP physics, we keep the areas of the cross-sections invariant for different types of shaping, meaning that all types of cross-sections have the same area as that of the circular case, πa2. In addition, the following parameters have the same values for various shapes in the computation: the safety factor at the magnetic axis q(0), the field reversal parameter F and the total plasma current I. Here F is defined as F = BT(a)/〈BT〉, where 〈···〉 is the average over the plasma volume.
Figure 1. Plots of the shaped poloidal magnetic flux surfaces of RFP equilibria for F = −0.06 q(0) = 0.1448 and βp = 0.12: (a) circular RFP with aspect ratio ε = a/R = 0.2295, elongation κ = 1.0 and triangularity δ = 0.0; (b) elliptic, κ = 1.3 and δ = 0.0, and ε = 0.2012; (c) triangular, κ = 1.0 and δ = 0.3, ε = 0.2308; (d) D-shaped, κ = 1.3 and δ = 0.3, ε = 0.2024. All types of cross-sections have the same area as the area in (a).
Download figure:
Standard image High-resolution image2.2. Toroidal self-consistent MHD–kinetic hybrid model
The MARS-K code numerically solves the linearized, single-fluid MHD equations with self-consistent inclusion of drift kinetic resonances in toroidal geometry [24]. For a given curvilinear flux coordinate system (s, χ, φ), and by assuming that all the perturbations have the form A(s, χ, φ, t) = A(s, χ)e−iωt−inφ, the MHD equations are written in the Eulerian frame in the code:





where s is the normalized radial coordinate, labelling the equilibrium flux surface, and χ is a generalized poloidal angle. ω = iγ − ωr is the complex eigenvalue of the mode (γ being the mode growth rate, ωr the mode rotation frequency in the laboratory frame). The mode frequency is corrected by a Doppler shift in Ω, with n being the toroidal mode number, Ω the plasma rotation frequency in the toroidal direction φ. ξ, v, Q, j and p represent the perturbed quantities: the plasma displacement, the perturbed velocity, magnetic field, current and pressure tensor, respectively. ρ is the unperturbed plasma density, η is the plasma resistivity, R is the plasma major radius and
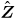 is the unit vector in the vertical direction. B, J and P denote the equilibrium magnetic field, current and pressure, respectively. A conventional unit system is assumed with the vacuum permeability μ0 = 1. For the RWM study, a set of vacuum equations for the perturbed magnetic field Q, and the resistive wall equation based on the thin-shell approximation, are solved together with equations (3)–(7) [25].
is the unit vector in the vertical direction. B, J and P denote the equilibrium magnetic field, current and pressure, respectively. A conventional unit system is assumed with the vacuum permeability μ0 = 1. For the RWM study, a set of vacuum equations for the perturbed magnetic field Q, and the resistive wall equation based on the thin-shell approximation, are solved together with equations (3)–(7) [25].
The drift kinetic effects from the thermal particles are self-consistently coupled to the MHD equations, as detailed in [24]. The key element in this formulation is the wave–particle resonance operator, expressed as follows:
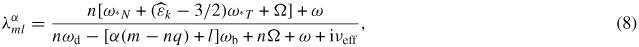
where
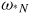 and
and
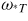 are the diamagnetic drift frequencies due to the plasma density and temperature gradients, respectively. In this drift kinetic formulation, it has been assumed that the effect of finite radial excursion width of particles across magnetic surfaces is negligible. q is the safety factor, νeff is the effective collision frequency and
are the diamagnetic drift frequencies due to the plasma density and temperature gradients, respectively. In this drift kinetic formulation, it has been assumed that the effect of finite radial excursion width of particles across magnetic surfaces is negligible. q is the safety factor, νeff is the effective collision frequency and
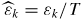 is the particle kinetic energy normalized by the temperature. ωd is the bounce-orbit-averaged precession drift frequency. For trapped particles, α = 0, and ωb is the bounce frequency. For passing particles, α = 1, and ωb represents the transit frequency. In further discussions we also use notation ωp for the transit frequency, in order to distinguish from the bounce frequency. Equation (8) includes particle bounce, transit, as well as magnetic precession drift resonances with the mode. The imaginary part of the resonant operator represents damping physics resulted from the energy transfer between the mode and particles.
is the particle kinetic energy normalized by the temperature. ωd is the bounce-orbit-averaged precession drift frequency. For trapped particles, α = 0, and ωb is the bounce frequency. For passing particles, α = 1, and ωb represents the transit frequency. In further discussions we also use notation ωp for the transit frequency, in order to distinguish from the bounce frequency. Equation (8) includes particle bounce, transit, as well as magnetic precession drift resonances with the mode. The imaginary part of the resonant operator represents damping physics resulted from the energy transfer between the mode and particles.
2.3. Quadratic energy terms
In order to gain a better physical understanding, we compute various components of the quadratic energy form, for both fluid and drift kinetic energy perturbations, from the self-consistent solution. As is well known, the quadratic energy form can be constructed by multiplying equation (4) by
 and integrating over the plasma volume VP. We define the following energy components of the fluid potential energy δWF [21, 26] and the kinetic potential energy δWk :
and integrating over the plasma volume VP. We define the following energy components of the fluid potential energy δWF [21, 26] and the kinetic potential energy δWk :


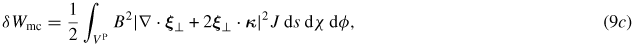
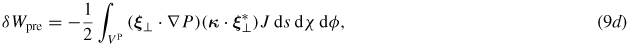
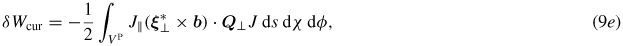
where J is the Jacobian of the flux coordinates. δWmb is the magnetic bending term representing the energy required to bend magnetic field lines, δWmc responds to the energy necessary to compress the magnetic field. Both terms are positive and give stabilizing contributions. δWpre and δWcur represent potential sources of instability, and are referred to as the pressure-driven and the current-driven terms, respectively. Both δWpre and δWcur can be negative. We consider cases with vanishing perturbed surface current, where the surface terms in the potential energy disappear. In the energy calculation, we neglect the centrifugal and the Coriolis force terms in the RHS of equation (4), assuming a slow equilibrium flow. The kinetic energy term is then obtained as

where the surface term
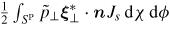 is negligible if we assume that the equilibrium pressure vanishes at the plasma edge P(a) = 0 (the perturbed kinetic pressure is roughly proportional to the equilibrium pressure). Sp here is the plasma surface, Js = |∇s|J is the surface Jacobian and n is an outward normal vector to the vacuum region.
is negligible if we assume that the equilibrium pressure vanishes at the plasma edge P(a) = 0 (the perturbed kinetic pressure is roughly proportional to the equilibrium pressure). Sp here is the plasma surface, Js = |∇s|J is the surface Jacobian and n is an outward normal vector to the vacuum region.
We also compute the vacuum energy
 and δWvb, without wall and with an ideal wall at the minor radius b, respectively:
and δWvb, without wall and with an ideal wall at the minor radius b, respectively:
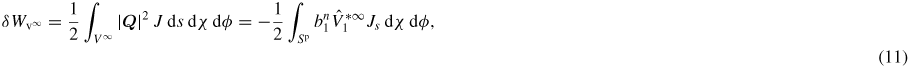

where
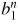 is the normal magnetic field perturbation, and is related to the perturbed magnetic components Q1 with
is the normal magnetic field perturbation, and is related to the perturbed magnetic components Q1 with
 [27]; the component Q1 is essentially the perturbed flux function.
[27]; the component Q1 is essentially the perturbed flux function.
 is the complex conjugate of the perturbed magnetic scalar potential, which is determined by the ideal wall position and
is the complex conjugate of the perturbed magnetic scalar potential, which is determined by the ideal wall position and
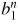 at the plasma surface [21]. The two vacuum energy terms are associated with the vacuum magnetic field perturbation, induced by the plasma instability. They are always positive and play a stabilizing role for the RWM.
at the plasma surface [21]. The two vacuum energy terms are associated with the vacuum magnetic field perturbation, induced by the plasma instability. They are always positive and play a stabilizing role for the RWM.
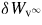 and δWvb can be written either in a volume integral, or in a surface integral, as shown in equations (11) and (12).
and δWvb can be written either in a volume integral, or in a surface integral, as shown in equations (11) and (12).
Equations (9a)–(9e) to (12) are implemented in the MARS-K code [10, 11], and applied for the energy analysis of the RWM physics in this work.
3. Shaping effect on the β limit of the RWM
3.1. Instability spectrum of the RWM in RFPs
With respect to tokamaks, the RFP plasmas are easier to be 'kinking' due to the weaker toroidal field in the configuration. As a result, the RWM, being a potentially disruptive instability, grows whenever the duration of the discharge is longer than the wall penetration time, even in the absence of the plasma pressure.
Furthermore, due to the toroidal field reversal, resulted from the relaxation process, RFPs can operate in a stable regime of the 'resonant' (with rational surface being inside the plasma) ideal kink modes. The observed RWM instabilities always have their rational surfaces outside the plasma. They are the so-called 'externally non-resonant' modes (ENRM), if the rational surfaces are located at q < q(a) < 0 (q(a) is the safety factor at the plasma edge r = a), or the 'internally non-resonant' modes (INRM), if the rational surfaces are located at q > q(0) > 0 [12, 19, 20]. In the following, we use n < 0 to denote the INRM, and n > 0 to represent the ENRMs. The experimentally observed resonant modes (with the resonant surface inside the plasma) are TMs, which are generally believed to be responsible for the dynamo generation in RFPs. We use n < 0 to denote the TM with the rational surface inside the BT reversal position, and vice versa.
Shown in figure 2 is the plot of the RWM growth rate as a function of the toroidal mode numbers n, where both INRM and ENRM are computed by MARS-K in a circular, zero β RFP plasma without plasma flow. The wall position of b/a = 1.12 and the inverse aspect ratio of ε = 0.23 are taken from the RFX-mod [28] parameters. The wall time is taken as τw/τA ≈ 6.4 × 103, where τw is the penetration time of the resistive wall and τA is the Alfvén time calculated at the magnetic axis. As we already observed previously [20], a shallower reversal (a smaller negative F value) results in a larger growth rate of the INRM and a smaller growth of ENRM, and vice versa. The modes with n < −6 (e.g. n = −7, −8 ...) are resonant modes, and are observed experimentally as TMs.
Figure 2. Mode growth rates versus the toroidal mode number n plotted for different F(= −0.06, −0.1, −0.26, −0.4, −0.8, −0.9, −1.0) values. Two groups of RWMs, INRMs (n < 0) and EXRMs (n > 0) are plotted. The fluid model with βp = 0.0, q(0) = 0.1448, Ω0 = 0.0, and b/a = 1.12, ε = 0.23 is used in the circular RFP. The poloidal Fourier harmonics from m = −10 to m = 10 are taken into the calculation.
Download figure:
Standard image High-resolution image3.2. Ideal-wall β limit of RWM (ideal kink instability)
In RFP plasmas, all RWMs are current-driven modes, therefore the no-wall βp limit
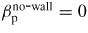 (βp = (8π/I2Ro)〈p〉 Vtot, 〈p〉 is the volume-averaged plasma pressure, 2π Vtot is the total plasma volume [23]), whilst the ideal-wall βp limit,
(βp = (8π/I2Ro)〈p〉 Vtot, 〈p〉 is the volume-averaged plasma pressure, 2π Vtot is the total plasma volume [23]), whilst the ideal-wall βp limit,
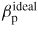 , is finite for a given wall position at the minor radius rb = b. When
, is finite for a given wall position at the minor radius rb = b. When
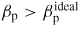 , the non-resonant ideal kink mode becomes unstable with the ideal wall at rb = b. For
, the non-resonant ideal kink mode becomes unstable with the ideal wall at rb = b. For
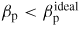 , the RWM instability appears if the ideal wall is replaced by a resistive wall.
, the RWM instability appears if the ideal wall is replaced by a resistive wall.
When the plasma elongation and triangularity are introduced, it is found that the shaping induces a strong poloidal coupling, which increases the mode growth rate and reduces the ideal-wall β limit for both the INRM and the ENRM. Figure 3 shows the RWM eigenfunctions (the perturbed magnetic field in the normal direction)
 of various poloidal harmonics for (a) a circular case, (b) a case with elongation only, κ = 1.3 and δ = 0.0, (c) a case with triangularity only, κ = 1.0, δ = 0.3. It shows that in a circular toroidal RFP plasma (figure 3(a)), the m = 1 mode has a dominant amplitude, and the m = 2, 3 ... modes appear with low amplitudes due to the weak coupling by toroidicity [11]. Note that RWMs in circular RFP plasmas have much weaker toroidal coupling than that in tokamaks due to the weaker poloidal asymmetry induced by the strong poloidal field. The elongation (figure 3(b)) induces the variation of the magnetic field strength along the poloidal angle, which in turn enhances the mode coupling between m = 1 and m = ±2. As a result, the m = −1 and m = 3 modes have much larger amplitudes with respect to the circular case. The triangularity (figure 3(c)) induces multiple coupling between m = 1 and m = ±1, m = ±2 and m = ±3 modes, such that multiple modes appear due to the coupling, but with less increments of the amplitudes compared with the elongation-induced mode coupling.
of various poloidal harmonics for (a) a circular case, (b) a case with elongation only, κ = 1.3 and δ = 0.0, (c) a case with triangularity only, κ = 1.0, δ = 0.3. It shows that in a circular toroidal RFP plasma (figure 3(a)), the m = 1 mode has a dominant amplitude, and the m = 2, 3 ... modes appear with low amplitudes due to the weak coupling by toroidicity [11]. Note that RWMs in circular RFP plasmas have much weaker toroidal coupling than that in tokamaks due to the weaker poloidal asymmetry induced by the strong poloidal field. The elongation (figure 3(b)) induces the variation of the magnetic field strength along the poloidal angle, which in turn enhances the mode coupling between m = 1 and m = ±2. As a result, the m = −1 and m = 3 modes have much larger amplitudes with respect to the circular case. The triangularity (figure 3(c)) induces multiple coupling between m = 1 and m = ±1, m = ±2 and m = ±3 modes, such that multiple modes appear due to the coupling, but with less increments of the amplitudes compared with the elongation-induced mode coupling.
Figure 3. Eigenfunctions of various poloidal harmonics
 (real parts of the perturbed magnetic component in the normal direction) for n = −6 RWM plotted as a function of magnetic flux coordinate s for different shapes of RFP plasmas, where m = −10 to 10 are taken into account. The mode amplitudes are normalized by the maximum absolute value
(real parts of the perturbed magnetic component in the normal direction) for n = −6 RWM plotted as a function of magnetic flux coordinate s for different shapes of RFP plasmas, where m = −10 to 10 are taken into account. The mode amplitudes are normalized by the maximum absolute value
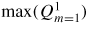 : (a) circular, κ = 1.0 and δ = 0.0; (b) elliptic, κ = 1.3 and δ = 0.0; (c) triangular, κ = 1.0 and δ = 0.3. Other parameters are F = −0.06, q(0) = 0.1448, βp = 0.0, b/a = 1.12 and Ω0 = 0.0.
: (a) circular, κ = 1.0 and δ = 0.0; (b) elliptic, κ = 1.3 and δ = 0.0; (c) triangular, κ = 1.0 and δ = 0.3. Other parameters are F = −0.06, q(0) = 0.1448, βp = 0.0, b/a = 1.12 and Ω0 = 0.0.
Download figure:
Standard image High-resolution imageFigure 4 shows the RWM growth rate plotted as a function of the elongation with different values of triangularity. The normalized mode growth rate (normalized by ωA) increases with κ, showing a destabilizing role played by elongation. This destabilization is also consistent with the decrease in the ideal-wall beta limit, as will be shown in figure 5(a). The triangularity itself slightly increases the RWM growth rate in the absence of elongation (κ = 1). When the triangularity is combined with elongation, it causes a slight cancellation of the destabilizing effect due to the elongation. The net effect still leads to an increase in the RWM growth rate.
Figure 4. Growth rates of the n = −6 RWMs versus elongation parameter κ plotted for various triangularities: δ = 0.0 (solid line); δ = 0.3 (dashed line); δ = 0.5 (dashed–dotted line), with the same parameters as in figure 3.
Download figure:
Standard image High-resolution imageFigure 5. Beta limits of RWMs versus wall position plotted for various toroidal mode numbers: (a) INRMs (n = −6, −5, −4, F = −0.06) for an RFP plasma with circular shape (lines with solid points), elongation κ = 1.3 (dashed–dotted lines with empty points) and triangularity δ = 0.3 (dotted line with stars); (b) EXRMs (n = 4, 3, 2, F = −0.9) for an RFP plasma with circular shape (lines with solid points), elongation κ = 1.3 (dashed–dotted lines with empty points) and triangularity δ = 0.3 (dotted line with stars). The other parameters are the same as in figure 3.
Download figure:
Standard image High-resolution imageFigure 5 plots the computed ideal-wall βp limits with varying wall position, for different toroidal harmonics of the RWMs. The INRMs with n = −6, −5 and −4 are plotted in (a), and the ENRMs with n = 4, 3, 2 are plotted in (b). Each line indicates the stability boundary of the ideal kink mode. This boundary depends on both the βp value and the normalized wall position b/a. The unstable domains are located above and to the right of the lines, and the (ideal mode) stable domains below and to the left of the lines. For κ = 1.3, the
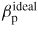 values are largely reduced with respect to the circular case. For the most unstable RWM observed in RFX-mod, with n = −6, which sets the most severe
values are largely reduced with respect to the circular case. For the most unstable RWM observed in RFX-mod, with n = −6, which sets the most severe
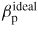 limit and the closest fitting wall position among all the RWMs, the circular plasma model gives
limit and the closest fitting wall position among all the RWMs, the circular plasma model gives
 ; the elongation reduces this value to
; the elongation reduces this value to
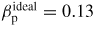 with the same wall position. Other toroidal harmonics such as n = −5, −4 and n = 4, 3, 2 have relatively smaller growth rates than that of n = −6, thus setting higher βp limits and moderately closer wall positions. The triangularity δ = 0.3 is also considered for the n = −6 mode in figure 5(a) and for the n = 4 mode in (b) showing a similar, but less significant destabilizing effect than the elongation. The results in figure 5 indicate that, for a given plasma βp, the shaped RFP requires a closer fitting wall to stabilize the ideal kink mode than the circular case; this effect is found extremely significant for ENRMs, as shown in figure 5(b).
with the same wall position. Other toroidal harmonics such as n = −5, −4 and n = 4, 3, 2 have relatively smaller growth rates than that of n = −6, thus setting higher βp limits and moderately closer wall positions. The triangularity δ = 0.3 is also considered for the n = −6 mode in figure 5(a) and for the n = 4 mode in (b) showing a similar, but less significant destabilizing effect than the elongation. The results in figure 5 indicate that, for a given plasma βp, the shaped RFP requires a closer fitting wall to stabilize the ideal kink mode than the circular case; this effect is found extremely significant for ENRMs, as shown in figure 5(b).
3.3. A physical understanding of the results on β limits
For the purposes of a better physics understanding, we perform further numerical analysis, including the calculation of the perturbed energy components. The following analysis shows that the strong poloidal mode coupling, induced by shaping in the RFP, causes the reduction of the vacuum potential energy δWvb, which is an important stabilizing factor for the ideal kink mode. Consequently, the shaping-enhanced mode coupling destabilizes the RWM and reduces the ideal-wall β limits for the ideal kink modes.
The well-known dispersion relation for the RWM, in the absence of the kinetic effects, can be expressed as [29, 30]

where γ is the mode growth rate and
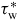 characterizes the penetration time of the resistive wall. The ideal-wall β limit corresponds to the ideal kink marginal stability, which can be determined by the following condition:
characterizes the penetration time of the resistive wall. The ideal-wall β limit corresponds to the ideal kink marginal stability, which can be determined by the following condition:

where δWF < 0, dominated by the current-driven energy δWcur and pressure-driven energy δWpre as expressed in equations (9a)–(9e), and δWvb > 0, which plays an important stabilizing role. As described in equation (12), δWvb is determined by the perturbed magnetic field (including all poloidal harmonics m) in the normal direction on the plasma surfaces
 , where
, where
 , and
, and
 . As an example, in figure 6 we plot the magnetic perturbation in the normal direction, for various poloidal harmonics
. As an example, in figure 6 we plot the magnetic perturbation in the normal direction, for various poloidal harmonics
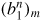 as functions of the poloidal angle χ for the n = −6 mode and elongation κ = 1.3, at the plasma surface. Both the real and imaginary parts of each
as functions of the poloidal angle χ for the n = −6 mode and elongation κ = 1.3, at the plasma surface. Both the real and imaginary parts of each
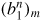 are shown in the figure. It is clear that the m = 2 coupling, induced by the elongation, leads to the cancellation of the imaginary parts between the m = 1, 3 and the m = −1, −3 harmonics. This ultimately results in a reduction of the total magnitude of
are shown in the figure. It is clear that the m = 2 coupling, induced by the elongation, leads to the cancellation of the imaginary parts between the m = 1, 3 and the m = −1, −3 harmonics. This ultimately results in a reduction of the total magnitude of
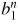 at the plasma surface. Figure 7 shows (a) the real, and (b) the imaginary parts of
at the plasma surface. Figure 7 shows (a) the real, and (b) the imaginary parts of
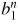 as the Fourier summation of all 21 poloidal harmonics
as the Fourier summation of all 21 poloidal harmonics
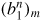 , m from −10 to 10, for κ = 1.0, 1.3 and 1.6, respectively. The amplitude
, m from −10 to 10, for κ = 1.0, 1.3 and 1.6, respectively. The amplitude
 is plotted in (c). The elongation significantly reduces the imaginary part of the amplitude of the magnetic perturbation, Im
is plotted in (c). The elongation significantly reduces the imaginary part of the amplitude of the magnetic perturbation, Im
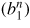 , at the plasma surface, whilst bringing only a slight change to the amplitude of Re
, at the plasma surface, whilst bringing only a slight change to the amplitude of Re
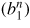 . The eventual effect is a significant decrease in
. The eventual effect is a significant decrease in
 along most part of the poloidal angle, as shown in (c). As a result, the vacuum perturbation energy δWvb correspondingly decreases. Shown in figure 8 are the various perturbed energy components of the RWM instability under the shaping assumptions of (a) elongation κ = 1.3 and 1.6, δ = 0.0, (b) triangularity δ = 0.3, κ = 1.0, and compared with the circular plasma κ = 1.0 and δ = 0.0.
along most part of the poloidal angle, as shown in (c). As a result, the vacuum perturbation energy δWvb correspondingly decreases. Shown in figure 8 are the various perturbed energy components of the RWM instability under the shaping assumptions of (a) elongation κ = 1.3 and 1.6, δ = 0.0, (b) triangularity δ = 0.3, κ = 1.0, and compared with the circular plasma κ = 1.0 and δ = 0.0.
Figure 6. Various poloidal harmonics of the n = −6 RWM perturbed magnetic fields in the normal direction
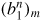 (here
(here
 ) at the plasma edge with elongation κ = 1.3 plotted along the poloidal angle χ. Among m = −10 to m = 10, five most important harmonics m = −3, −1, 0, 1, 3 modes are plotted: (a) the real parts; (b) the imaginary parts. The other parameters are the same as in figure 3.
) at the plasma edge with elongation κ = 1.3 plotted along the poloidal angle χ. Among m = −10 to m = 10, five most important harmonics m = −3, −1, 0, 1, 3 modes are plotted: (a) the real parts; (b) the imaginary parts. The other parameters are the same as in figure 3.
Download figure:
Standard image High-resolution imageFigure 7. Total normal component of the n = −6 RWM perturbed magnetic fields
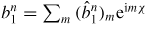 at the plasma edge with various elongation κ = 1.0, 1.3, 1.6 along poloidal angle χ: (a) the real parts; (b) the imaginary parts; (c) the absolute value abs
at the plasma edge with various elongation κ = 1.0, 1.3, 1.6 along poloidal angle χ: (a) the real parts; (b) the imaginary parts; (c) the absolute value abs
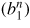 . The other parameters are the same as in figure 3, where the poloidal Fourier harmonics m are taken from m = −10 to m = 10.
. The other parameters are the same as in figure 3, where the poloidal Fourier harmonics m are taken from m = −10 to m = 10.
Download figure:
Standard image High-resolution imageFigure 8. Potential energy components of the RWMs, which are normalized by the driven term δWcur + δWpre, plotted for n = −6 modes in RFP plasmas: (a) comparison between the different elongations: group (1) is for the circular cross-section, group (2) is for elongated shape with κ = 1.3 and group (3) is with κ = 1.6. The corresponding growth rates are γ1 = 6.07 × 10−4, γ2 = 1.02 × 10−3, γ3 = 9.15 × 10−3, respectively; (b) comparison between the circular RFP plasma (δ = 0.0 in group (1)), and triangle shaped RFP (δ = 0.3 in group (2)), the growth rates are γ1 = 6.07 × 10−4 and γ2 = 8.45 × 10−4. The other parameters are F = −0.06, q(0) = 0.1448, βp = 0.07 and b/a = 1.12.
Download figure:
Standard image High-resolution imageThe energy components are presented in several groups of columns as marked in the figure. In each group, the first column denotes the current-driven terms δWcur and the pressure-driven terms δWpre. The second column presents the stabilizing terms δWmc and δWmb. The third group presents the vacuum energy, δWvb, with an ideal wall at the minor radius b and vacuum energy,
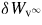 , without a wall. The fourth group is the total plasma fluid potential energy δWF. The last column is δWb and δW∞, as expressed in equation (13). Figure 8(a) presents the elongation effect on various energy components. Increasing the elongation significantly reduces δWvb, but only slightly reduces |δWF| (mainly due to enhancement of the magnetic bending). Therefore, the value of δWb = δWF + δWvb (δWb > 0) is reduced by the elongation. Figure 8(a) also shows that, although
, without a wall. The fourth group is the total plasma fluid potential energy δWF. The last column is δWb and δW∞, as expressed in equation (13). Figure 8(a) presents the elongation effect on various energy components. Increasing the elongation significantly reduces δWvb, but only slightly reduces |δWF| (mainly due to enhancement of the magnetic bending). Therefore, the value of δWb = δWF + δWvb (δWb > 0) is reduced by the elongation. Figure 8(a) also shows that, although
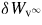 is slightly reduced (less notable than δWvb), the no-wall energy perturbation
is slightly reduced (less notable than δWvb), the no-wall energy perturbation
 almost does not change with increasing κ. Following the dispersion relation (13) and (14), we find that an increase in the elongation κ leads to an increase in the RWM growth rate, and to a reduction in the ideal-wall βp limit. Figure 8(b) presents the triangularity effect, which is similar to that by the elongation, except that the decrease in δWvb appears less significant than that caused by the elongation.
almost does not change with increasing κ. Following the dispersion relation (13) and (14), we find that an increase in the elongation κ leads to an increase in the RWM growth rate, and to a reduction in the ideal-wall βp limit. Figure 8(b) presents the triangularity effect, which is similar to that by the elongation, except that the decrease in δWvb appears less significant than that caused by the elongation.
4. Kinetic stabilization of RWM in shaped RFP plasmas
4.1. Multiple trapping regions
An interesting observation is that, due to Bp ∼ BT in RFPs, the shaping effect causes a significant variation of the field strength along the poloidal angle, resulting in multiple trapping regions along the poloidal angle. Figure 9 is a 2D plot of the values of the total magnetic field strength | B| on the shaped RFP cross-section with κ = 1.3 and δ = 0.3. The new areas where the lower magnetic strength appears due to the shaping are marked regions 1, 2 and 3, respectively, in the figure. The strength of the normal field due to the toroidicity is not shown in this figure; the trapped fraction due to the toroidicity will be shown in figure 10(a) and denoted as '0'. Three new regions of the trapped particles appear in the shaped RFP plasmas, which are shown in figure 10, where we plot the fractions of the trapped particle density (ntrap/ntotal, ntrap is the local trapped particle density and ntotal is the local total densities including the trapped particles and passing particles) in these regions on the cross-section: (a) the fraction of the usual trapping due to the toroidicity, which we denote as 'trap 0'. (b) and (c) present the fractions of 'traps 1 and 3' and 'trap 2' resulted from both elongation and triangularity. Obviously, the shaping effect increases the total fraction of trapped particles due to the appearance of the multiple trapping regions. Figure 11 shows the radial profiles of various fractions of the trapped particles in a shaped RFP, where the total trapped fraction and passing fraction are also presented as a function of the magnetic flux coordinates. The data of figure 11 are obtained by taking average over each magnetic flux surface. It shows that the total trapped fraction keeps increasing towards the edge of the shaped plasma, contrary to the circular cross-section case where the total trapped fraction decreases towards the plasma edge [31]. Figure 12 plots the radial profiles of the bounce frequencies of trapped particles in different regions. The new trapped regions are located in a rather narrow area along the poloidal angle near the plasma edge, having higher bounce frequency than the nominal case. In particular, the particles of traps 1 and 3 have bounce frequencies comparable to or even larger than the transit frequency of the passing particles. The precession frequencies for both ions and electrons are also shown in the figure. The new trapped particles do not have substantially different precession frequencies w.r.t. the particles in 'trap 0'.
Figure 9. 2D plots of the strength of total equilibrium magnetic field with κ = 1.3 and δ = 0.3. It shows that new trapped particle regions (1, 2, 3) can appear, where relatively weak magnetic field strengths exist. The other parameters are F = −0.06, q(0) = 0.1448, βp = 0.12.
Download figure:
Standard image High-resolution imageFigure 10. Fractions of trapped particle density (ntrap/ntotal) in the multiple regions plotted with the same parameters used in figure 9: (a) nominal trapping region (trap 0) by toroidicity in circular RFP; (b) new trapping regions, trap 1 and trap 3; (c) the new equatorial trapping region in the low-field side, trap 2.
Download figure:
Standard image High-resolution imageFigure 11. Radial profiles of the fraction of passing and trapped particles in various regions (using the same notation as in figure 10 to distinguish the trapping regions). The fraction profiles of regions 1 and 3 are the same. It also shows the total particle fraction (equal to 1.0) and the sum of all trapping fractions. The other parameters are the same as in figure 10.
Download figure:
Standard image High-resolution imageFigure 12. Radial profiles of the various frequencies of passing and trapped thermal particles in various regions (using the same region numbers as in figure 10). The other parameters are βp = 0.12, κ = 1.3 and δ = 0.3. The transit frequency (m − nq)ωp/n of the passing particles, the bounce frequencies of trapped particles in various regions, denoted as ωb−0, ωb−1&3 and ωb−2 ; the precession frequencies of trapped ion ωdi and electron ωde are presented. The embedded figure describes details of the precession frequencies contributed by various trapped regions,
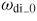 , ωdi_1&3 and
, ωdi_1&3 and
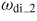 are for trapped ions and
are for trapped ions and
 , ωde_1&3 and
, ωde_1&3 and
 are for trapped electrons.
are for trapped electrons.
Download figure:
Standard image High-resolution image4.2. Kinetic damping on RWMs in shaped RFPs
By taking into account the particle–wave resonance effects, the stabilization condition of RWMs can be written as [32]

As expressed in equation (10), the kinetic energy δWk consists of the resonant (imaginary) part
 and the non-resonant (real) part
and the non-resonant (real) part
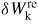 ,
,
 . Generally, the imaginary part always gives a stabilizing effect. The real part can be either stabilizing or destabilizing. For RWMs, the first term in equation (15) is negative, i.e. δW∞δWb < 0, which is the most important destabilizing term contributed by the fluid effects. The kinetic energy δWk usually has a smaller value than the fluid energy components. In such cases the kinetic effects can play a significant role only when δW∞ or δWb is very small (which leads to the first destabilizing term (δWbδW∞) being small). This conclusion has already been obtained by a previous analysis [11]. In RFPs, the shaping leads to a smaller δWb, therefore, the kinetic effects become more significant than those in the circular case. Earlier studies [10, 11] found that the RWMs in RFP could be kinetically stabilized mainly by the transit resonance of passing (thermal) ions for a high-βp plasma, due to the ion acoustic Landau damping. The required plasma rotation frequency for the stabilization is in the ion acoustic wave frequency range. Considering the shaping effects, we find that the transit resonance of passing ions is still the main mechanism for the kinetic stabilization of the RWM in RFPs. The (more significant) kinetic effects result in a lower β value, required for the full stabilization, than that required in the circular case. As for the plasma rotation needed for the stabilization, the elongation leads to a slightly smaller rotation frequency; whilst the triangularity leads to a slightly larger rotation frequency for the mode stabilization, compared with that of the circular RFP. Figure 13 plots the mode growth rate versus the normalized plasma rotation frequency Ωo (Ωo = Ω/ωA, where ωA is the Alfvén frequency calculated at the magnetic axis) under various kinetic effects, such as the transit resonance of passing ions, the precession and bounce resonances of trapped particles, and the full kinetic contributions from both passing and trapped particles. The results of the fluid theory are also plotted for comparison. Figure 13(a) is for the circular plasma and (b) is for a plasma with elongation κ = 1.3. It is found that the stabilization of the RWM for the n = −6 mode in the circular plasma requires a higher βp value, βp = 0.15, and a rotation at Ωo = 0.025 under the full kinetic effects, whilst for the shaped plasma with κ = 1.3, the required βp value is lower, with the stabilization found at βp = 0.12. The critical rotation frequency for full stabilization is also slightly decreased from 0.025 to 0.024. The transit resonance of passing ions is the dominant kinetic stabilization mechanism for both cases. The new trapped regions enhance the damping by enhanced bounce resonances, as shown in figure 13(b). On the other hand, the stabilization by these new bounce resonance regimes requires a higher rotation frequency than the transit damping; we do not consider these new regimes as the principal mechanism for stabilizing the RWM in RFP. However, the multiple trapped regions may become a significant factor to be considered, when the fast ions produced by neutral beam injection or alpha particles are taken into account.
. Generally, the imaginary part always gives a stabilizing effect. The real part can be either stabilizing or destabilizing. For RWMs, the first term in equation (15) is negative, i.e. δW∞δWb < 0, which is the most important destabilizing term contributed by the fluid effects. The kinetic energy δWk usually has a smaller value than the fluid energy components. In such cases the kinetic effects can play a significant role only when δW∞ or δWb is very small (which leads to the first destabilizing term (δWbδW∞) being small). This conclusion has already been obtained by a previous analysis [11]. In RFPs, the shaping leads to a smaller δWb, therefore, the kinetic effects become more significant than those in the circular case. Earlier studies [10, 11] found that the RWMs in RFP could be kinetically stabilized mainly by the transit resonance of passing (thermal) ions for a high-βp plasma, due to the ion acoustic Landau damping. The required plasma rotation frequency for the stabilization is in the ion acoustic wave frequency range. Considering the shaping effects, we find that the transit resonance of passing ions is still the main mechanism for the kinetic stabilization of the RWM in RFPs. The (more significant) kinetic effects result in a lower β value, required for the full stabilization, than that required in the circular case. As for the plasma rotation needed for the stabilization, the elongation leads to a slightly smaller rotation frequency; whilst the triangularity leads to a slightly larger rotation frequency for the mode stabilization, compared with that of the circular RFP. Figure 13 plots the mode growth rate versus the normalized plasma rotation frequency Ωo (Ωo = Ω/ωA, where ωA is the Alfvén frequency calculated at the magnetic axis) under various kinetic effects, such as the transit resonance of passing ions, the precession and bounce resonances of trapped particles, and the full kinetic contributions from both passing and trapped particles. The results of the fluid theory are also plotted for comparison. Figure 13(a) is for the circular plasma and (b) is for a plasma with elongation κ = 1.3. It is found that the stabilization of the RWM for the n = −6 mode in the circular plasma requires a higher βp value, βp = 0.15, and a rotation at Ωo = 0.025 under the full kinetic effects, whilst for the shaped plasma with κ = 1.3, the required βp value is lower, with the stabilization found at βp = 0.12. The critical rotation frequency for full stabilization is also slightly decreased from 0.025 to 0.024. The transit resonance of passing ions is the dominant kinetic stabilization mechanism for both cases. The new trapped regions enhance the damping by enhanced bounce resonances, as shown in figure 13(b). On the other hand, the stabilization by these new bounce resonance regimes requires a higher rotation frequency than the transit damping; we do not consider these new regimes as the principal mechanism for stabilizing the RWM in RFP. However, the multiple trapped regions may become a significant factor to be considered, when the fast ions produced by neutral beam injection or alpha particles are taken into account.
Figure 13. The n = −6 RWM growth rates γ versus plasma rotation frequency Ω0 (= Ω/ωA) plotted for (a) the circular RFP κ = 1.0, βp = 0.15 and (b) the elongation RFP κ = 1.3, βp = 0.12. Different types of kinetic effects are included: full kinetic (dashed–dotted line); transit (solid line); precession (line with squares); bounce (line with triangles). The other parameters are the same as in figure 3.
Download figure:
Standard image High-resolution imageFigure 14 shows a comparison between an elongated and a circular RFP on the stability windows (shaded area) induced by the kinetic effects, in the βp − b/a plane (b/a is the normalized wall radial position). The INRMs with n = −6, −5 are presented in (a), and a typical ENRM with n = 4 is in (b). For each stability window, the solid lines represent the ideal-wall beta limit
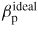 , while the dashed lines represent the boundary of the stability windows opened by kinetic damping. Thereby, the area above and to the right of the shaded area represents the unstable region of the ideal kink (with ideal wall at r = b); the area below and to the left of the shaded area represents unstable RWMs. For a given wall position, each RWM, with toroidal harmonic n, has the stability window opened along the βp-axis. For a given βp value, each n mode has a stability window in the b/a-axis. Within stable windows, if both βp and b/a are given, only one critical rotation frequency Ωc (normalized by ωA) will be found correspondingly. The critical rotation frequencies Ωc marked in the figures correspond to the required rotation at the smallest b/a points (highest βp) of the dashed lines. More complete data of each stability boundary are listed in table 1. It is shown that elongation makes the kinetic damping more efficient, and thus the stability window opened in the lower βp region with a slightly lower rotation frequency than the circular one. For INRMs, elongation leads to narrower stability windows in both βp and b/a parameter spaces. For ENRMs, shown in (b), the kinetic effects provide a rather wide stability window except at a very low βp, where a rather fast plasma rotation is required for the mode stabilization. For n = 4 mode, Ωc is around 0.17–0.285 with a wall at b/a = 1.35 for the circular RFP, and Ωc ∼ 0.26–0.32 with b/a = 1.2 for the κ = 1.3 non-circular case. Higher critical rotation Ωc is required if the wall is closer to the plasma. These rotation ranges are much faster than that of the currently operating RFP plasmas without external momentum sources such as that from the tangential neutral beam injection.
, while the dashed lines represent the boundary of the stability windows opened by kinetic damping. Thereby, the area above and to the right of the shaded area represents the unstable region of the ideal kink (with ideal wall at r = b); the area below and to the left of the shaded area represents unstable RWMs. For a given wall position, each RWM, with toroidal harmonic n, has the stability window opened along the βp-axis. For a given βp value, each n mode has a stability window in the b/a-axis. Within stable windows, if both βp and b/a are given, only one critical rotation frequency Ωc (normalized by ωA) will be found correspondingly. The critical rotation frequencies Ωc marked in the figures correspond to the required rotation at the smallest b/a points (highest βp) of the dashed lines. More complete data of each stability boundary are listed in table 1. It is shown that elongation makes the kinetic damping more efficient, and thus the stability window opened in the lower βp region with a slightly lower rotation frequency than the circular one. For INRMs, elongation leads to narrower stability windows in both βp and b/a parameter spaces. For ENRMs, shown in (b), the kinetic effects provide a rather wide stability window except at a very low βp, where a rather fast plasma rotation is required for the mode stabilization. For n = 4 mode, Ωc is around 0.17–0.285 with a wall at b/a = 1.35 for the circular RFP, and Ωc ∼ 0.26–0.32 with b/a = 1.2 for the κ = 1.3 non-circular case. Higher critical rotation Ωc is required if the wall is closer to the plasma. These rotation ranges are much faster than that of the currently operating RFP plasmas without external momentum sources such as that from the tangential neutral beam injection.
Figure 14. Stability windows in the plane of the poloidal beta βp versus wall position b/a plotted for both INRMs and ENRMs: (a) INRMs n = −6, −5 with κ = 1.0 and 1.3, δ = 0.0, F = −0.06 q(0) = 0.1448 and (b) EXRMs n = 4 with κ = 1.0 and 1.3, δ = 0.0, F = −0.9, q(0) = 0.1448. The solid lines present the ideal-wall beta limits
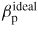 and the dashed lines express the boundaries of the stability window opened by kinetic damping. The Ωc values marked in the figures are the required rotation frequencies corresponding to the points having the smallest b/a on the dashed lines. More complete data including all other points are listed in table 1.
and the dashed lines express the boundaries of the stability window opened by kinetic damping. The Ωc values marked in the figures are the required rotation frequencies corresponding to the points having the smallest b/a on the dashed lines. More complete data including all other points are listed in table 1.
Download figure:
Standard image High-resolution imageTable 1. List of data corresponding to figure 14. The results of the ideal-wall beta limit (includes
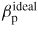 , b/a and Ω0 = 0.0) and the stability boundary by kinetic stabilization (includes βp, b/a and Ωc) for INRMs n = −6, −5 and ENRM n = 4 are presented.
, b/a and Ω0 = 0.0) and the stability boundary by kinetic stabilization (includes βp, b/a and Ωc) for INRMs n = −6, −5 and ENRM n = 4 are presented.
| κ = 1.0 | κ = 1.3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ideal-wall βp limit (Ω0 = 0.0) | Boundary of kinetic stabilization | Ideal-wall βp limit (Ω0 = 0.0) | Boundary of kinetic stabilization | |||||||
| b/a | βp | b/a | βp | Ωc | b/a | βp | b/a | βp | Ωc | |
| n = −6 | 1.125 | 0.16 | 1.125 | 0.136 | 0.036 | 1.125 | 0.13 | 1.125 | 0.11 | 0.034 |
| 1.15 | 0.145 | 1.175 | 0.112 | 0.034 | 1.15 | 0.11 | 1.225 | 0.049 | 0.031 | |
| 1.225 | 0.1 | 1.225 | 0.086 | 0.0328 | 1.225 | 0.055 | ||||
| 1.3 | 0.05 | 1.3 | 0.043 | 0.0292 | ||||||
| n = −5 | 1.275 | 0.3 | 1.275 | 0.2025 | 0.148 | 1.275 | 0.165 | 1.275 | 0.1075 | 0.09 |
| 1.325 | 0.24 | 1.3 | 0.18 | 0.152 | 1.325 | 0.08 | 1.3 | 0.08 | 0.0785 | |
| 1.375 | 0.18 | 1.35 | 0.14 | 0.122 | ||||||
| 1.45 | 0.1 | |||||||||
| n = 4 | 1.375 | 0.12 | 1.35* | 0.09 | 0.17 | 1.25 | 0.12 | 1.2* | 0.12 | 0.26 |
| 1.3375 | 0.21 | 1.35* | 0.04 | 0.21 | 1.2125 | 0.24 | 1.2* | 0.03 | 0.31 | |
| 1.35 | 0.01 | 0.285 | 1.2 | 0.015 | 0.32 | |||||
The data with sign '*' correspond to the points located inside the stability windows.
5. Shaping effects on resistive modes
In this section, we present toroidal results on the stability of the linear resistive modes in shaped RFP plasmas. Only fluid theory with constant resistivity is considered. The kinetic effect is ignored, MARS-F is applied for these computations. For an RFP plasma with a circular cross-section, the computation shows that the behaviour of current-driven resistive modes in RFP can appear as either a resistive tearing or a resistive kink mode. This can be judged from the scaling of the mode growth rate w.r.t. the value of the Lundquist number S. The TM obeys a scaling law of γ ∝ S−3/5, and the resistive kink mode has a growth rate scaling as γ ∝ S−1/3. Computations with the RFX-mod equilibrium at zero β find that, for the most long wavelength modes (mode's rational surface is near the magnetic axis) such as the n = −7 and n = −8 modes, the growth rates approximately follow the tearing scaling law when S > 106, and the resistive kink scaling when S < 106. As for the shorter wavelength modes, such as n = −11, −12 ..., the mode growth rates almost follow the tearing scaling only. In the following analysis, we will not distinguish these two, simply labelling them the resistive mode.
The shaping effect can also enhance the poloidal mode coupling for the resistive mode. In this case, the resonant TM (m = 1) coupled mostly with the non-resonant modes (rational surfaces outside the plasma), e.g. m = 2, −1, −2, etc. We find that shaping can moderately increase the mode's growth rate, but cannot significantly change the stability boundary in the F–Θ plane. Shown in figure 15 is the growth rate of the n = −8 mode at S = 105 and zero β, plotted as a function of the pinch parameter Θ (a larger Θ value implies a more peaked current profile, Θ = Bp(a)/〈BT〉). An ideal wall at b/a = 1.12 is assumed. Both elongation and triangularity result in a larger growth rate than the circular case. The stability boundaries are also investigated and compared with experimental data. It is necessary to point out that, for each RFP machine, the parameters F and Θ cannot change independently for all discharges. It has been found that all the discharges follow a fixed F–Θ curve (F is a monotonic function of Θ) [19, 20, 33, 34]. We selected four points of experimental data on the F–Θ curve, as presented in [20], which have the reversal parameter F = −0.05, −0.1, −0.15, −0.2; and the corresponding Θ values on the curve are Θ = 1.42, 1.49, 1.57, 1.63, as plotted in figure 16. The n = −8 resistive mode's stability boundary is computed by MARS-F, and compared among several cases: circular (κ = 1.0, δ = 0.0), elongated (κ = 1.3, δ = 0.0) and D-shaped (κ = 1.3, δ = 0.5). A cylindrical code is also used for a reference. The figure shows that the RFP experiments operate near the TM stability boundary (marginally stable TM). This is agreed with the previous observations [35]. Since the TMs are considered as the dynamo modes, this can be understood as the results of the self-organized relaxation in RFP plasmas through the dynamo effects. As shown in figure 16, the shaping effects do not significantly change the stability boundary in the F–Θ plane, and hence cannot significantly influence the operating state of the dynamo system. The eigenfunctions
 of the n = −8 resistive mode are plotted in figure 17, with elongation of κ = 1.3 and various wall conditions: without wall, with an ideal wall and with a resistive wall with the penetration time of τw/τA ∼ 6.4 × 103(τA = 1/ωA). The corresponding growth rates (normalized by ωA) of the modes are γ = 3.246 × 10−2, γ = 4.99 × 10−4 and 1.275 × 10−3, respectively. It is obvious that the ideal wall results in the smallest growth rate, the no-wall condition gives the largest growth rate, and the resistive wall result stays in the middle.
of the n = −8 resistive mode are plotted in figure 17, with elongation of κ = 1.3 and various wall conditions: without wall, with an ideal wall and with a resistive wall with the penetration time of τw/τA ∼ 6.4 × 103(τA = 1/ωA). The corresponding growth rates (normalized by ωA) of the modes are γ = 3.246 × 10−2, γ = 4.99 × 10−4 and 1.275 × 10−3, respectively. It is obvious that the ideal wall results in the smallest growth rate, the no-wall condition gives the largest growth rate, and the resistive wall result stays in the middle.
Figure 15. Growth rate of the n = −8 TM versus pinch parameter Θ plotted for F = −0.05 and −0.15 with different shaped RFPs: circular, κ = 1.0, δ = 0.0 (line with dots); elongation, κ = 1.3, δ = 0.0 (line with triangles); and D-shaped, κ = 1.3, δ = 0.5 (line with squares). Other parameters are βp = 0.0 with ideal wall at b/a = 1.12, Lundquist number S = 105, and no plasma rotation.
Download figure:
Standard image High-resolution imageFigure 16. Stability boundary of the n = −8 TM plotted in the F–Θ plane obtained by MARS-F. For circular cross-section κ = 1.0, δ = 0.0 (dashed–dotted line), elongation κ = 1.3, δ = 0.0 (triangle point), and D-shaped κ = 1.3, δ = 0.5 (diamond point) RFPs. Experimental data (dots) and the results from cylindrical code (solid line) are also plotted for comparison. Other parameters used are the same as in figure 15.
Download figure:
Standard image High-resolution imageFigure 17. Eigenfunctions of perturbed magnetic fields in the normal direction for the n = −8 TM with elongation κ = 1.3 plotted for different wall conditions such as no-wall (dotted line) with the growth rate γ = 3.246 × 10−2, ideal wall (solid line) γ = 4.99 × 10−4, and resistive wall (dashed–dotted line) γ = 1.275 × 10−3. Various poloidal harmonics are shown. The embedded figure presents the whole eigenfunctions for the no-wall case. The parameters are F = −0.05, q(0) = 0.15, Θ = 1.43.
Download figure:
Standard image High-resolution imageThis can also be seen from the derivative jumps of the eigenfunction
 (the radial component of the magnetic perturbation). Assuming the same values of
(the radial component of the magnetic perturbation). Assuming the same values of
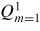 at the rational surfaces for all the three cases, the no-wall boundary condition gives a much larger amplitude of the perturbation outside the rational surface.
at the rational surfaces for all the three cases, the no-wall boundary condition gives a much larger amplitude of the perturbation outside the rational surface.
We point out that the marginal TM state obtained by MARS-F has a slight discrepancy with the experimental data. This may be due to the fact that the model equilibrium current profile used by MARS-F does not perfectly match the real experimental current profile, which currently cannot be directly measured yet. However, the conclusion of the shaping effects on the tearing stability boundary is not altered by this fact.
6. Shaping on bootstrap current in RFPs
In RFPs, the bootstrap current fraction is much smaller than that in tokamaks, due to the strong poloidal field Bp. For the same on-axis BT amplitude, the poloidal field Bp and hence the total current Itotal in a circular RFP are approximately one order of O(ε−1) larger than a circular tokamak with the same geometry. Furthermore, it is well known that the density of the bootstrap current jBT is proportional to
 , jBT ∝ (1/Bp)(dp/dr), hence for a given pressure profile, the total plasma bootstrap current IBT is scaled to
, jBT ∝ (1/Bp)(dp/dr), hence for a given pressure profile, the total plasma bootstrap current IBT is scaled to
 too. However, the total plasma current is scaled as Itotal ∝ Bp. Therefore, the fraction of the bootstrap current IBT/Itotal should approximately satisfy the scaling of
too. However, the total plasma current is scaled as Itotal ∝ Bp. Therefore, the fraction of the bootstrap current IBT/Itotal should approximately satisfy the scaling of
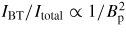 . Considering the fact that the pressure gradient (dp/dr) can generally be of the same order in both RFPs and tokamaks, the fraction of trapped particles in a circular RFP is smaller than that in a circular tokamak with the same geometry [31], we arrive at a conclusion that the bootstrap current fraction of the RFP is at least O(ε2) smaller than the fraction of the circular tokamak with the same BT at the axis:
. Considering the fact that the pressure gradient (dp/dr) can generally be of the same order in both RFPs and tokamaks, the fraction of trapped particles in a circular RFP is smaller than that in a circular tokamak with the same geometry [31], we arrive at a conclusion that the bootstrap current fraction of the RFP is at least O(ε2) smaller than the fraction of the circular tokamak with the same BT at the axis:
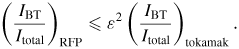
The shaping effect can increase the fraction of the bootstrap current. The results of computation by the CHEASE code, using the Hirshman model [36], are presented in figure 18, showing the profiles of the normalized total current density and the bootstrap current density under various types of shaping, and comparing with the circular case results. The bootstrap current fractions IBT/Itotal are also marked in the figure. Only a very small fraction bootstrap current, around a few per cent, can be achieved in RFP. Shaping increases this fraction by 10–30% more than the circular value. However, the eventual fraction remains of the same order. Similar results showing a very small BT fraction are obtained by previous calculations in circular RFP plasmas using different models [31, 37]. We point out that these characteristics have resulted from the intrinsic nature of the RFP configuration. The speculation about a significant enhancement of BT fraction by increasing the temperature of RFP plasmas seems not realizable due to the unfavourable scaling for the plasma-generated BT current. Therefore, in future RFP fusion reactors, for a steady-state operation, external current drives will be probably necessary.
Figure 18. Normalized radial profiles of the bootstrap current density 〈J · B〉BT (with different shaped RFP plasmas) plotted to compare with the total plasma current density 〈J · B〉total. The total current is expressed by the solid line, and the bootstrap currents under different shapes are expressed by 30 times amplification: circular cross-section κ = 1.0, δ = 0.0 (short dashed–dotted line); elongation κ = 1.3, δ = 0.0 (dashed–dotted line); triangularity κ = 1.0, δ = 0.3 (dotted line); and D-shaped κ = 1.3, δ = 0.5 (dashed line). IBT/Itotal represents the fraction of the bootstrap current. The parameters used in the calculation are F = −0.06, q(0) = 0.1448, and βp = 0.12.
Download figure:
Standard image High-resolution imageThe regime of the new multiple trapping regions is not considered in this calculation. This may lead to a slight underestimation of the fraction of the bootstrap current, but will not result in any significant change of the conclusion.
7. Summary and conclusion
We have studied the shaping effects on RFP plasmas by using the MHD–kinetic hybrid toroidal stability code MARS-K. Both elongation and triangularity effects are investigated. The studies focus on the most important MHD modes in RFPs. The first topic is the βp limit set by the RWM (the ideal kink mode) instability, where the ideal-wall β limit and the stabilization by drift kinetic damping are studied, and an in-depth analysis is carried out for physics understanding. The second topic is on the linear stability of the resistive mode (the dynamo modes) under shaping effects in the low-β RFP plasmas, and a comparison with the circular case. Finally, we report a computational result on the bootstrap fraction in shaped RFP plasmas.
The RFP magnetic configuration is characterized by a strong poloidal magnetic field and reversed toroidal field. Shaping effects in RFPs induce a stronger poloidal mode coupling than the circular case, due to the variation of the poloidal field strength along the poloidal angle. Moreover, shaping also introduces multiple trapped regions. As a consequence, the shaping effects lead to quite a different conclusion from that of a tokamak. Detailed results are summarized as follows.
For the RWM, shaping yields a lower ideal-wall β limit, and increases the growth rate of the mode due to the reduction in the vacuum energy component δWvb. In this case, the kinetic damping becomes more significant than the circular case, meaning that the kinetic stabilization requires a lower βp value, and possibly also a slightly slower rotation. However, the kinetic contribution is still dominant by the ion acoustic Landau damping of passing particles, thus requiring a critical plasma rotation still in the ion acoustic frequency range. Furthermore, the stabilization windows in a shaped RFP become narrower in both βp and b/a parameter spaces. The appearance of multiple trapping regions due to the shaping can enhance the bounce resonance damping, which, nevertheless, is not the dominant damping mechanism for the RWM in thermal RFP plasmas.
For the linear resistive modes in low-β RFPs, shaping-induced poloidal coupling only moderately increases the growth rate, without significantly influencing the stability boundary of the mode in the F–Θ plane. The self-organized RFX plasma in a relaxation process operates along a fixed F–Θ curve, which is near the marginal stable state of the tearing modes. Since the shaping effects do not give a notable change to the stability boundary, we may conclude that shaping in RFPs cannot introduce a notable change to the state of the dynamo system.
The RFP configuration yields a much smaller (order of (ε2)) fraction of the bootstrap current than that in tokamaks. Although shaping can increase the bootstrap fraction by up to 30%, the eventual fraction in shaped plasmas remains of the same order as that in a circular RFP. Therefore, in order to reach steady-state RFP fusion reactors, a substantial fraction of external current drives would be necessary, because of the unfavourable scaling for the plasma-generated bootstrap current in the RFP configuration.
Based on the results from the above studies, we conclude that the present circular cross-section design for RFPs is an appropriate choice, in the sense that no notable improvement for the RFP performance seems to be gained by shaping the plasma cross-section. The major physics reason is the strong poloidal field in the RFP (compared with the toroidal field), which plays an important role in the poloidal mode coupling and the particle dynamics, in particular, prevents the access to a substantially improved good averaged curvature by shaping.
New multiple trapped regions appear in the shaped RFP configuration. Although these regions do not significantly modify the RWM stability in thermal plasmas, they can still be the notable phenomena which may influence the energetic particle physics and the other kinetic-driven instabilities in a shaped RFP.
The resistive tearing mode studied in this work is only for very low β RFP plasmas. The effects of high β and energetic particles, as well as the corresponding kinetic effects, have not been taken into account. These will be studied in a future work. The behaviour of the nonlinear dynamics of the resistive tearing mode under the shaping effects is still unknown, which is beyond the scope of this work. In particular, the variation of the single helical phase due to shaping is an interesting topic to be studied.
Acknowledgments
One of the authors (S.C. Guo) would like to acknowledge helpful discussions with T. Bolzonella, M.E. Puiatti, M. Valisa, P. Zaccaria and P. Sonato.
This work was supported by the Euratom Communities under the contract of Association between EURATOM and ENEA, and part-funded by The RCUK Energy Programme under Grant No EP/I501045 and the European Communities under the contract of Association between EURATOM and CCFE. The views and opinions expressed herein do not necessarily reflect those of the European Commission.




















