ABSTRACT
The solar dynamo is known to be associated with several periodicities, with the nearly 11/22 yr cycle being the most pronounced one. Even though these quasiperiodic variations of solar activity have been attributed to the underlying dynamo action in the Sun's interior, a fundamental theoretical description of these cycles is still elusive. Here, we present a new possible direction in understanding the Sun's cycles based on resonant nonlinear interactions among magnetohydrodynamic (MHD) Rossby waves. The WKB theory for dispersive waves is applied to magnetohydrodynamic shallow-water equations describing the dynamics of the solar tachocline, and the reduced dynamics of a resonant triad composed of MHD Rossby waves embedded in constant toroidal magnetic field is analyzed. In the conservative case, the wave amplitudes evolve periodically in time, with periods on the order of the dominant solar activity timescale (∼11 yr). In addition, the presence of linear forcings representative of either convection or instabilities of meridionally varying background states appears to be crucial in balancing dissipation and thus sustaining the periodic oscillations of wave amplitudes associated with resonant triad interactions. Examination of the linear theory of MHD Rossby waves embedded in a latitudinally varying mean flow demonstrates that MHD Rossby waves propagate toward the equator in a waveguide from −35° to 35° in latitude, showing a remarkable resemblance to the structure of the butterfly diagram of the solar activity. Therefore, we argue that resonant nonlinear magnetohydrodynamic Rossby wave interactions might significantly contribute to the observed cycles of magnetic solar activity.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
The magnetic activity of the Sun exhibits several approximately periodic cycles, the 11/22 yr cycle (Schwabe/Hale cycle) being the most pronounced one. This cycle is associated with both reversals in the magnetic polarity of the dipolar mode of the Sun's magnetic field and the sunspots. Other cycles with a wide range of periodicities have been investigated in the literature, including 2 yr, 80 yr, and 200 yr cycles (Jager & Dahau 2011). A fundamental question is, how do these well-defined periods emerge from the turbulent flows in the solar interior?
In this context, modeling of solar activity has largely been based on kinematic dynamo models, in which the feedback of the Lorentz force on the velocity field is neglected. This approach has successfully simulated the Sun's periodic cycles, being capable of reproducing the spatiotemporal behavior of the solar activity depicted in the butterfly diagram (Charbonneau 2010). On the other hand, global simulations of the full magnetohydrodynamic equations have failed to reproduce the main features of solar magnetic activity (Guerrero et al. 2013). From this point of view, a fundamental theoretical description of these reversals is still elusive, and a fully magnetohydrodynamic basis for describing the solar activity is still needed.
In the kinematic interpretation of the solar dynamo, the trapping of sunspot activity and its respective migration toward the equator, represented by the butterfly diagram, can be understood as a result of the propagation of dynamo waves (Schmitt & Schüssler 2004). However, in the system of coupled magnetohydrodynamic equations, dynamo waves no longer exist as linear eigenmodes. In contrast, the purely magnetic oscillation of dynamo waves in this case should be coupled to the hydrodynamic component of the model, yielding a magnetohydrodynamic wave mode. Hence, a relevant question in the transition from a kinematic to a magnetohydrodynamic interpretation of the solar activity is, what kind of magnetohydrodynamic wave does inherit the equatorward migration properties of dynamo waves? This is a problem addressed in Section 3 of the present paper.
Another main observational constraint, which is relevant for the modeling of the cyclic behavior of the solar activity, is that cyclic oscillations are reflected in several spherical harmonic coefficients of the solar magnetic field, both axisymmetric (m = 0) and nonaxisymmetric (Knaack & Stenflo 2005). According to Knaack & Stenflo (2005), fluctuations in the spherical harmonic coefficients have shown a dominant periodicity of 22 yr as well as second (11 yr) and third (7 yr) harmonics, but a pronounced periodicity of 2–2.5 yr is also observed in some coefficients. In addition, Knaack's harmonic analysis also shows that oscillations of different harmonics of the magnetic field are out of phase and have the same period, indicating a possible nonlinear energy exchange among different harmonics of the magnetic field. Here, we present a possible theoretical explanation for these observed periodic modulations of nonaxisymmetric harmonic coefficients of the solar magnetic field based on resonant nonlinear interactions among magnetohydrodynamic Rossby waves. This theoretical description of the cyclic activity of the Sun's magnetic field may open up a new perspective to construct a more comprehensive theory of the solar cycle.
The magnetic activity of the Sun is believed to have its origin in the solar tachocline, a thin layer in the base of the convection zone and above the rigid interior of the Sun (Spiegel & Zahn 1992) at about 0.7 solar radii. Because the thickness of the tachocline is small compared to the radius of the Sun, a suitable approximation for the dynamics of this layer is the so-called shallow-water magnetohydrodynamic (MHD) approximation (Gilman 2000). This approximation is valid for motions whose vertical scales are small compared with their horizontal ones, and, consequently, magnetic and velocity fields are assumed to be two- dimensional vector fields. This is the MHD analog to the well-known shallow-water approximation applied to the Earth's ocean and atmosphere (Pedlosky 1986). The only difference is the inclusion of the magnetic field effects.
The shallow-water MHD approximation has been widely used in the study of both waves and instabilities in the solar tachocline (Gilman & Dikpati 2002; Dikpati & Gilman 2005). In particular, Rossby-like waves arise as one of the possible eigensolutions of the governing equations either in spherical geometry or in the beta-plane approximation (Zaqarashvili et al. 2007, 2010). The effect of Rossby wave motion in the context of the Sun was studied by Gilman (1969), who analyzed a kinematic MHD model where the hydrodynamic component is considered as a prescribed background flow for the magnetic field evolution. He obtained oscillatory behavior with periods on the order of a few years. However, Zaqarashvili et al. (2007), by including the feedback effect of the magnetic field on the hydrodynamic component of the model represented by the Lorentz force, showed the existence of a lower-frequency branch that was not present in Gilman's analysis. Zaqarashvili et al. (2007) studied MHD Rossby waves through the shallow-water MHD equations linearized around a resting and constant toroidal magnetic field background state, and Zaqarashvili et al. (2010) augmented this linear theory to include a latitudinal variation of the background magnetic field and a zonal mean flow represented by a differential rotation in order to analyze the possible role of wave instability in Rieger-type periodicities. The possible role of Rossby waves as a mechanism for the dynamo alpha effect in thick shells because of its helical structure, was highlighted by Avalos-Zuniga (2009). Here, we extend the MHD Rossby wave theory of Zaqarashvili et al. (2007) in order to take into account the effect of nonlinearity. For this purpose, the weakly nonlinear Wentzel–Kramers–Brillouin (WKB) theory for dispersive waves has been applied to MHD Rossby waves embedded in a resting and constant toroidal magnetic field. In order to further demonstrate the potentiality of the present nonlinear theory in describing the observed spatial–temporal variability of solar activity, we have also analyzed a particular case of the linear theory of MHD Rossby waves embedded in a latitudinally varying background state presented by Zaqarashvili et al. (2010) and investigated possible waveguides of MHD Rossby waves.
The weakly nonlinear theory of dispersive waves has been extensively studied in the context of plasma physics (Davidson 1972) and geophysical fluid dynamics (Majda 2003). According to this theory, the effect of nonlinearity is to break down the independence of wave eigenmodes, allowing their amplitudes to evolve slowly in time through energy exchanges among resonant modes. For quadratic nonlinearities, as is usually the case in most geophysical fluid dynamics and MHD problems, wave coupling takes place in a triad configuration, where the energy exchanges occur only if the modes satisfy the well-known resonant triad interaction conditions in which the wavenumbers and time frequencies of the triad components both add to zero. In this context, the nonlinear energy exchanges are described by a set of coupled ordinary differential equations in the case of a discrete spectrum of wave eigenmodes and by a set of coupled nonlinear Schrödinger equations in the case of wave packets (see, for instance, Majda 2003; Craik 1985 and references therein).
Here we apply the weakly nonlinear WKB method to the shallow-water MHD equations and analyze the reduced dynamics of a single resonant triad of MHD Rossby wave modes. In addition, we have assumed a discrete spectrum associated with periodic boundary conditions so that the wave amplitudes are described by a Hamiltonian set of three coupled ordinary differential equations, the so-called triad equations. In the absence of forcing, these equations are integrable and can be solved analytically in terms of Jacobian elliptic functions (Bretherton 1964; Craik 1985). In this case, the period of energy modulations depends on the coupling constants and the initial mode amplitudes. The coupling constants, in turn, represent the intrinsic nonlinear coupling among the triad components and depend on the background magnetic field, the wavenumbers, and the eigenfrequencies of the modes composing the resonant triad and on the density and magnetic permeability. For a representative example of a resonant triad explored here, which is composed of two magnetic and one hydrodynamic Rossby modes, more expressive energy exchanges among the triad components were found to occur for a parameter regime of the solution in which the period of the energy modulations is close to the 11 yr period or even longer periods of the solar cycle. Thus, we argue that the wave interaction mechanism explored here might be relevant for the nearly 11 yr cycle as well as for longer timescale cycles of solar magnetic activity. In the presence of convective forcing, the time evolution of the wave amplitudes of the resonant triad exhibits a growth/decay asymmetry similar to that observed in the magnetic field during the solar dynamo cycle. Also, the linear divergence terms of both the vorticity and magnetic density current equations that work as parametric forcings for MHD disturbances may potentially balance the dissipative terms and, consequently, appear to be crucial to sustain the quasiperiodic fluctuations associated with the resonant triad interactions against dissipative actions. Thus, we believe that convective forcings, possibly related to thermal inhomogeneities throughout the tachocline's boundaries, might be important in triggering and sustaining the resonant triad interactions explored here.
The analysis of the linear MHD Rossby wave theory, including a latitudinally varying mean flow performed here, points out the existence of a waveguide between 35°S and 35°N for the magnetic branch, with a maximum of the refraction index at the equator. Therefore, according to our theoretical results, the observed evolution of solar activity emerging at midlatitudes and migrating toward the equator, which is often represented by the so-called butterfly diagram, is associated with a waveguide at the equator that is due to the differential rotation of the Sun. Beyond the WKB limit, the solar differential rotation, as well as the background toroidal magnetic field of the solar tachocline, may be unstable and consequently excite planetary-scale MHD Rossby mode disturbances. Thus, apart from convective forcings related to thermal inhomogeneities along the tachocline's boundaries, global instabilities of both solar differential rotation and toroidal magnetic field can also be accounted for by another energy source that prevents resonant triad interactions of MHD Rossby modes from declining because of viscous and ohmic dissipative actions. Therefore, we argue here that the magnetic branch of Rossby waves might be a good candidate for replacing the dynamo waves in a magnetohydrodynamic interpretation. In addition, our results suggest that the observed time modulation of sunspots with a nearly 11 yr period might be associated with energy exchanges among MHD Rossby modes in resonant triad interactions.
2. SHALLOW-WATER MHD EQUATIONS WITH CONVECTIVE FORCING
The shallow-water equation model governs the dynamics of a homogeneous and incompressible fluid under hydrostatic balance. It constitutes an appropriate approximation of the full Navier–Stokes equations for quasi-horizontal motions in a thin layer and has long been used in studies of Earth's ocean and atmosphere (Pedlosky 1986). Its magnetohydrodynamic extension was introduced by Gilman (2000). For the sake of simplicity, we make use of Cartesian coordinates with the so-called beta-plane approximation, in which the dependence of the Coriolis parameter on latitude is given by a linear function (Pedlosky 1986). In this context, the shallow-water MHD equations are written as
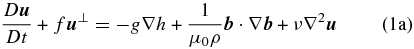
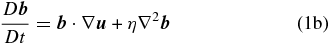


where 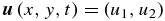 is the two-dimensional velocity field,
is the two-dimensional velocity field, 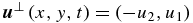 ,
, 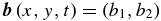 represents the two-dimensional magnetic field, and the scalar field h(x, y, t) refers to the thickness of the fluid layer; g is the gravity acceleration, ρ is the density, μ0 refers to the magnetic permeability, and f(y) = f0 + βy corresponds to the Coriolis parameter, with both f0 and β being assumed to be constant. The parameters η and ν are magnetic diffusivity and viscosity, respectively. Equation (1d) is the constraint associated with the requirement that the magnetic field be parallel to the upper free surface (Gilman 2000).
represents the two-dimensional magnetic field, and the scalar field h(x, y, t) refers to the thickness of the fluid layer; g is the gravity acceleration, ρ is the density, μ0 refers to the magnetic permeability, and f(y) = f0 + βy corresponds to the Coriolis parameter, with both f0 and β being assumed to be constant. The parameters η and ν are magnetic diffusivity and viscosity, respectively. Equation (1d) is the constraint associated with the requirement that the magnetic field be parallel to the upper free surface (Gilman 2000).
Because we aim to adopt model Equations (1) to study MHD Rossby waves, it is convenient to take the curl of Equations (1a) and (1b), where the two-dimensional vorticity and the magnetic density current are defined as ζ = (∂u2/∂x) − (∂u1/∂y) and j = (∂b2/∂x) − (∂b1/∂y), respectively. Therefore, we obtain the following scalar equations for the vorticity and the magnetic density current:
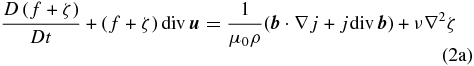
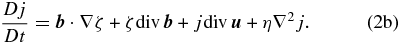
Because our analysis focuses on planetary-scale perturbations (Rossby waves), to a first approximation, both velocity and magnetic fields could be assumed as divergenceless. However, we will retain the divergence of both velocity and magnetic fields in the equations above as small forcing terms associated with thermal anomalies in the boundaries of the solar tachocline. In fact, because in an incompressible fluid the continuity equation may be approximated as
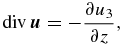
with u3 representing the vertical velocity field, an upwelling fluid parcel in a confined layer will result in horizontal divergence; hence horizontal divergence can be used as a measure of thermal convection. In order to keep the effect of thermal convection without dealing with the thermodynamic equations, we define 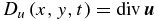 as a prescribed term representing a Rossby wave convective source. This assumption of keeping the horizontal divergence as a prescribed Rossby wave source has been extensively used in geophysical fluid dynamics in the study of teleconnection patterns in the atmosphere (see, for instance, Hoskins & Karoly 1981; Hoskins & Ambrizzi 1993 and many others). In addition, these numerical studies of atmospheric teleconnection patterns using the vorticity equation have disregarded the term
as a prescribed term representing a Rossby wave convective source. This assumption of keeping the horizontal divergence as a prescribed Rossby wave source has been extensively used in geophysical fluid dynamics in the study of teleconnection patterns in the atmosphere (see, for instance, Hoskins & Karoly 1981; Hoskins & Ambrizzi 1993 and many others). In addition, these numerical studies of atmospheric teleconnection patterns using the vorticity equation have disregarded the term 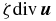 based on arguments of scale analysis. However, as shall be discussed in Section 5, this parametric forcing term of the vorticity balance is important in our nonlinear analysis because it can potentially balance the dissipative terms and, consequently, sustain the nonlinear oscillations in the presence of dissipation. Thus, we will consider here the effect of both prescribed (
based on arguments of scale analysis. However, as shall be discussed in Section 5, this parametric forcing term of the vorticity balance is important in our nonlinear analysis because it can potentially balance the dissipative terms and, consequently, sustain the nonlinear oscillations in the presence of dissipation. Thus, we will consider here the effect of both prescribed (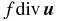 ) and parametric (
) and parametric ( ) forcing terms of the vorticity equation.
) forcing terms of the vorticity equation.
Similarly, the divergence of the horizontal magnetic field in Equations (2a)–(2b) will also be assumed as a prescribed function representing magnetic anomalies associated with inhomogeneities in the boundaries of the solar tachocline. In fact, from Equation (1d) the divergence of the horizontal magnetic field can be written as
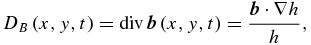
which shows that this prescribed forcing can be particularly important in the case of a variable tachocline thickness (see Guerrero et al. 2007 for a discussion on the effects of a prolate tachocline).
Therefore, with the assumptions mentioned above, Equations (2) become
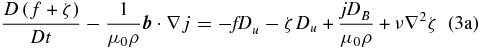
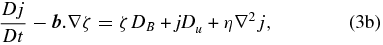
where Du(x, y, t) =  and DB(x, y, t) =
and DB(x, y, t) = 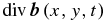 .
.
3. LINEAR THEORY
3.1. Resting and Constant Magnetic Field Background State
MHD Rossby waves are eigensolutions of the linearized and unforced version of Equations (3). Let us consider, for instance, the linearized and unforced version of (3) for a background state with no motion and a constant toroidal magnetic field. Note that this background state represents an exact stationary solution of Equation (3). Thus, considering infinitesimal amplitude perturbations around a background state at rest and with a constant toroidal magnetic field (i.e.,  ), the linearized and unforced (Du = DB ≡ 0) problem governing the time evolution of these perturbations can be written in terms of stream function ψ and vector potential A as
), the linearized and unforced (Du = DB ≡ 0) problem governing the time evolution of these perturbations can be written in terms of stream function ψ and vector potential A as
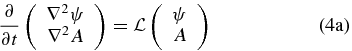
where the linear differential operator  is given by
is given by

and the streamfunction ψ and vector potential A satisfy the relations ∇2ψ = ζ and ∇2A = j, respectively. Taking the Fourier transform of  , we obtain the algebraic operator
, we obtain the algebraic operator
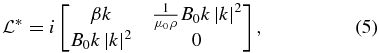
whose eigenvalues correspond to the two possible branches of the MHD Rossby wave dispersion relation and are determined by the characteristic equation
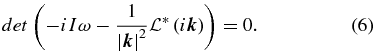
In the equations above,  is the vector wavenumber. The two solutions of the characteristic Equation (6) are given by
is the vector wavenumber. The two solutions of the characteristic Equation (6) are given by
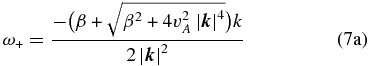
and
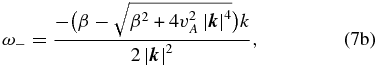
where  refers to the Alfvén wave speed. The branches ω+ and ω− refer to the fast hydrodynamic mode and the slow magnetic mode, respectively (Zaqarashvili et al. 2007). In fact, for small wavenumbers such that
refers to the Alfvén wave speed. The branches ω+ and ω− refer to the fast hydrodynamic mode and the slow magnetic mode, respectively (Zaqarashvili et al. 2007). In fact, for small wavenumbers such that  , the dispersion relations of the two branches can be approximated by
, the dispersion relations of the two branches can be approximated by 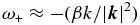 and
and 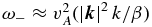 . Thus, the asymptotic form of ω+in the long-wave limit corresponds to the dispersion relation of purely hydrodynamic Rossby waves, whereas the asymptotic form of ω− in the same limit corresponds to the dispersion relation of Alfvén waves. For this reason we shall label mode "−" as the magnetic mode and mode "+'' as the hydrodynamic mode. In the calculations displayed in this paper we have set the parameters β = 0, 95.10−13 m−1 s−1, and vA = 200 m s−1.
. Thus, the asymptotic form of ω+in the long-wave limit corresponds to the dispersion relation of purely hydrodynamic Rossby waves, whereas the asymptotic form of ω− in the same limit corresponds to the dispersion relation of Alfvén waves. For this reason we shall label mode "−" as the magnetic mode and mode "+'' as the hydrodynamic mode. In the calculations displayed in this paper we have set the parameters β = 0, 95.10−13 m−1 s−1, and vA = 200 m s−1.
The corresponding right eigenvectors of matrix 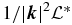 are given by
are given by

and
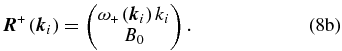
For each wavenumber 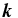 , the eigenvectors defined above form an orthogonal basis in
, the eigenvectors defined above form an orthogonal basis in 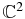 space under a suitable inner product defined by
space under a suitable inner product defined by
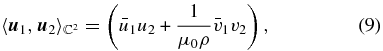
where  and
and  represent arbitrary elements of
represent arbitrary elements of  vector space and the over bar denotes the complex conjugate. The norm defined by this inner product represents the energy of a given eigenmode.
vector space and the over bar denotes the complex conjugate. The norm defined by this inner product represents the energy of a given eigenmode.
3.2. Latitudinally Varying Mean Zonal Flow and Waveguides for MHD Rossby Waves
Schmitt & Schüssler (2004) have shown that dynamo waves, propagating oscillations that arise as eigensolutions of the induction equation, can reproduce the equatorward migration of the solar activity represented in the butterfly diagram. Here we argue that the magnetic branch of MHD Rossby waves might be a good magnetohydrodynamic counterpart of the dynamo waves because they are confined in a belt around the equator and are refracted toward the equator, as will be shown in this section.
Waveguides associated with westerly jet streams play a central role in the propagation of Rossby wave disturbances and, consequently, in establishing the main teleconnection patterns in Earth's atmosphere (Hoskins & Ambrizzi 1993; Hoskins & Karoly 1981). In addition, latitudinally varying shear flows constitute an essential ingredient of the Sun's dynamics, and, as a consequence, solar MHD Rossby waves are seldom embedded in a resting background state. Thus, in this subsection we examine the linear theory of MHD Rossby waves embedded in a latitudinally varying background state presented by (Zaqarashvili et al. 2010) to investigate possible MHD Rossby waveguides in the solar dynamo. For simplicity, we consider the special case of a latitudinally varying zonal flow and a constant toroidal magnetic field.
In this context, let us now consider infinitesimal amplitude disturbances embedded in a background state characterized by a constant magnetic field in the x direction and by a slowly varying zonal flow 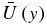 . In this case, according to the WKB approximation, the MHD Rossby wave dispersion relation is given by
. In this case, according to the WKB approximation, the MHD Rossby wave dispersion relation is given by
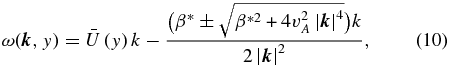
where 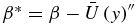 is the meridional gradient of absolute vorticity.
is the meridional gradient of absolute vorticity.
For simplicity in exposition, we consider the asymptotic forms of the two branches in the long-wave limit introduced in the last section. For the hydrodynamic branch  , and the total wavenumber is given by
, and the total wavenumber is given by
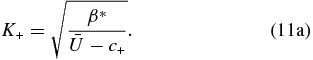
On the other hand, for the magnetic branch 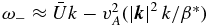 , and the total wavenumber is
, and the total wavenumber is
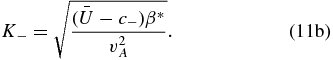
In the equations above, c± = ω±/k refers to the zonal phase speed of the modes. Wave propagation is allowed only where the total wavenumber K is real because in the latitudes where the total wavenumber K is imaginary, the solution is evanescent.
In general, the phase speed of Rossby waves is smaller in magnitude than the velocity of the background flow. Consequently, a usual approximation of the equations above is the assumption of a stationary wave (c = 0). In this case, the total wavenumber defined above is replaced by the stationary wavenumber Ks. The concept of stationary wavenumber Ks has been extensively used in geophysical fluid dynamics problems to determine possible Rossby waveguides in the presence of realistic background zonal flows and has been successfully used to interpret some model results on the atmospheric response to heat or orographic forcing in a qualitative fashion (e.g., Hoskins & Karoly 1981; Hoskins et al. 1977; Hoskins & Ambrizzi 1993).
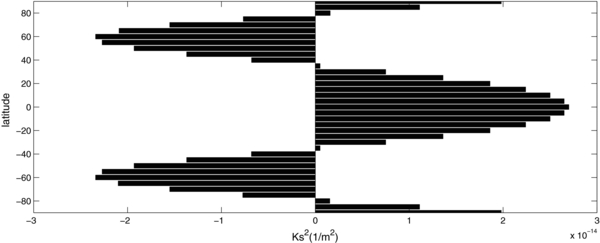
Figure 1 shows the latitudinal profile of Ks2 referred to the magnetic branch for a zonal flow  (y) obtained from a theoretical profile of the solar differential rotation taken from MacGregor & Charbonneau (1997). One notices in Figure 1 the existence of critical latitudes at around 80° and 35° in both hemispheres. These critical latitudes refer to regions where the solution changes from a wave propagation (Ks2 > 0) regime to an evanescent (Ks2 < 0) regime. This is in agreement with observations of solar magnetic activity, which show that sunspots are present in the tropical belt. Furthermore, for the magnetic branch, the stationary wavenumber Ks is maximal at the equator. According to the WKB theory of Rossby wave propagation in a slowly varying medium (Bühler 2009; Held 1983; Hoskins & Ambrizzi 1993, Section 2), Rossby waves are refracted toward regions of maximum stationary wavenumber such that these regions work as waveguides. Thus, according to the result displayed in Figure 1, in the solar dynamo context the equator acts as a waveguide for the magnetic branch of MHD Rossby waves such that waves generated at the critical latitudes around ±35° are refracted toward this latitude of maximum stationary wavenumber. This feature is also consistent with observations of the solar activity whose latitude versus time structure is depicted by the butterfly diagram.
(y) obtained from a theoretical profile of the solar differential rotation taken from MacGregor & Charbonneau (1997). One notices in Figure 1 the existence of critical latitudes at around 80° and 35° in both hemispheres. These critical latitudes refer to regions where the solution changes from a wave propagation (Ks2 > 0) regime to an evanescent (Ks2 < 0) regime. This is in agreement with observations of solar magnetic activity, which show that sunspots are present in the tropical belt. Furthermore, for the magnetic branch, the stationary wavenumber Ks is maximal at the equator. According to the WKB theory of Rossby wave propagation in a slowly varying medium (Bühler 2009; Held 1983; Hoskins & Ambrizzi 1993, Section 2), Rossby waves are refracted toward regions of maximum stationary wavenumber such that these regions work as waveguides. Thus, according to the result displayed in Figure 1, in the solar dynamo context the equator acts as a waveguide for the magnetic branch of MHD Rossby waves such that waves generated at the critical latitudes around ±35° are refracted toward this latitude of maximum stationary wavenumber. This feature is also consistent with observations of the solar activity whose latitude versus time structure is depicted by the butterfly diagram.
Figure 1. Meridional distribution of the squared stationary wavenumber Ks2 for the magnetic branch. The calculations were performed for a zonal flow obtained from a theoretical profile of the solar differential rotation taken from MacGregor & Charbonneau (1997).
Download figure:
Standard image High-resolution imageThe behavior described above has a striking agreement with the structure of the activity zones (drifting groups of sunspots) as described by Joy's law (Hale et al. 1919). Joy's law predicts that the tilt of a bipolar activity zone will vary from approximately 15° as they appear around 35° of latitude and will decrease as the activity zone approaches the equator, becoming parallel to the equator at 0° of latitude. This suggests that activity zones might be traveling MHD Rossby waves and Joy's law might represent the ray of the Rossby wave as it travels in the slowly varying medium due to differential rotation.
4. WEAKLY NONLINEAR WAVE INTERACTION THEORY: IDEAL CASE
In this section we present the nonlinear MHD Rossby wave interaction theory as a fundamental theoretical description of observed periodic cycles of nonaxisymmetric components of solar magnetic activity. For simplicity, we consider wave disturbances embedded in the background state at rest and with a constant toroidal magnetic field 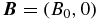 . Let us consider, for instance, finite amplitude perturbations around the background state described above in the unforced and inviscid version of model Equations (3). In this case, the governing equations for these perturbations are obtained by restoring the quadratic nonlinear terms into Equations (4):
. Let us consider, for instance, finite amplitude perturbations around the background state described above in the unforced and inviscid version of model Equations (3). In this case, the governing equations for these perturbations are obtained by restoring the quadratic nonlinear terms into Equations (4):
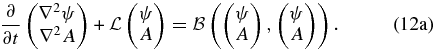
In Equation (12),  is the linear operator given by Equation (4b) and
is the linear operator given by Equation (4b) and  corresponds to the quadratic nonlinear operator, given by
corresponds to the quadratic nonlinear operator, given by
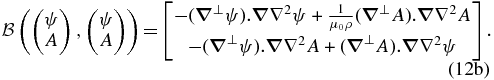
The standard asymptotic treatment of Equation (12) in the weakly nonlinear regime requires elimination of secular terms that are due to resonances arising in the right-hand side of Equation (12a). To eliminate secular solutions, we enforce conditions for the slow evolution of the wave amplitudes given by the Fredholm alternative (Majda 2003, Chapter 5). For a set of three modes whose wavenumbers  ,
,  , and
, and  and corresponding eigenfrequencies
and corresponding eigenfrequencies  ,
,  , and
, and  satisfy the resonance conditions
satisfy the resonance conditions
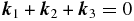
and
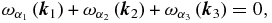
the respective wave amplitudes Ω1, Ω2, and Ω3 evolve in time according to
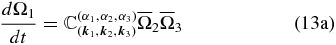
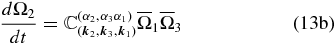

In the equations above, αi, i = 1, 2, 3, refers to the branch (αi = + for hydrodynamic branch and αi = − for magnetic branch), the over bar indicates the complex conjugate, and  ,
,  , and
, and  are the nonlinear interaction coefficients, given by
are the nonlinear interaction coefficients, given by
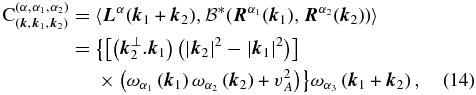
where  stands for the left eigenvector of the linear operator
stands for the left eigenvector of the linear operator and 〈〉 represents the inner product (9).
and 〈〉 represents the inner product (9).
Equations (13) are integrable and can be solved analytically in terms of Jacobian elliptic functions (Craik 1985). In general, the solution of Equation (13) is periodic, except for the special case of m = 1, as will be shown below.
To obtain the analytical solution of system (13), let us consider mode 1 as the one with the highest absolute value interaction coefficient and mode 3 as having the smallest absolute value interaction coefficient, that is,
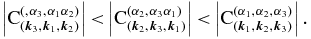
From Equation (14) one notices that the interaction coefficients are proportional to their respective eigenfrequencies, so the condition above implies that
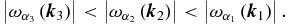
The conditions above, or equivalently  , represent a characteristic feature of conservative resonant triads (Craik 1985). In this context, for the initial condition Ω1(t = 0) = 0, Ω2(t = 0) = Ω2(0), and Ω3(t = 0) = Ω3(0),1 the solution can be written as (Domaracki & Loesch 1977)
, represent a characteristic feature of conservative resonant triads (Craik 1985). In this context, for the initial condition Ω1(t = 0) = 0, Ω2(t = 0) = Ω2(0), and Ω3(t = 0) = Ω3(0),1 the solution can be written as (Domaracki & Loesch 1977)
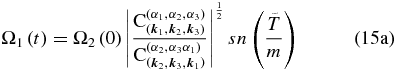
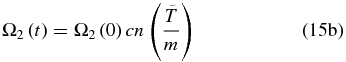
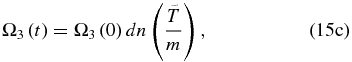
where sn, cn, and dn are the Jacobian elliptic functions, with the argument corresponding to the rescaled time  , given by
, given by
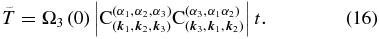
Also, the parameter m of the Jacobian elliptic functions above is written as
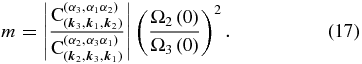
In the limiting case of m = 0, the solution (15) reduces to
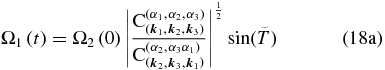

The m = 0 case occurs for resonant triads whose interaction coefficient of the third component (13c) is zero, which in turn refers to the case where 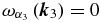 (zero-frequency wave). For such triads, the amplitude of the third wave does not change in time. Consequently, this mode acts as a catalyst for the interaction of the other two waves, which exchange energy periodically in time, with the period of the energy exchange varying linearly with the amplitude of the third wave. In this case, the higher the amplitude of mode 3, the shorter the interaction period.
(zero-frequency wave). For such triads, the amplitude of the third wave does not change in time. Consequently, this mode acts as a catalyst for the interaction of the other two waves, which exchange energy periodically in time, with the period of the energy exchange varying linearly with the amplitude of the third wave. In this case, the higher the amplitude of mode 3, the shorter the interaction period.
According to the dispersion relation of MHD Rossby waves (Equation (7)), the modes with zerofrequency are those having an axisymmetric x structure (k = 0). For instance, dipole modes (i.e., the two branches of the MHD Rossby mode with zonal wavenumber k = 0 and meridional wavenumber l = 1) constitute an example of such stationary modes. Thus, the present theory points out that the dipole meridional structure MHD Rossby modes, which might contribute to the dipole harmonic of the Sun's magnetic field, can act as a catalyst for nonaxisymmetric propagating MHD Rossby modes to interact and exchange energy with each other. An example of such a resonant triad is composed of hydrodynamic Rossby waves with corresponding wave numbers (0, 1) (zero-frequency mode) and (1, 8) and (1, 9), both with frequency of approximately 8.45 × 10−6 Hz.
According to Equation (17), Equations (18) can also be obtained for resonant triads containing only propagating modes as the asymptotic limit of Equations (15) when |Ω2(0)| ≪ |Ω3(0)|. However, in this case, Equation (18) shows that modes 1 and 2 exchange energy, but their amplitudes remain small compared with the amplitude of mode 3, that is, |Ω1, 2(t)| ≪ |Ω3(0)| for all t > 0. Consequently, the triad interaction in this case does not yield significant changes in the dynamical fields 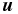 and
and  . Thus, we believe that the MHD Rossby wave interactions in this regime, whose interaction period is on the order of a few years or shorter, might not be relevant for the observed cycles of solar magnetic activity.
. Thus, we believe that the MHD Rossby wave interactions in this regime, whose interaction period is on the order of a few years or shorter, might not be relevant for the observed cycles of solar magnetic activity.
In the other limit (m = 1), the amplitude of mode 1 grows rapidly in time at the expense of the amplitude decrease of modes 2 and 3. After mode 1 achieves its maximum amplitude level, the solution attains a stationary regime where the amplitudes of the three waves do not change in time. Hence, for resonant triads involving three propagating MHD Rossby modes, the period of the wave amplitude modulations can be arbitrarily long for m → 1 or short for m → 0, with the parameter m depending crucially on the interaction coefficients and on the initial condition.
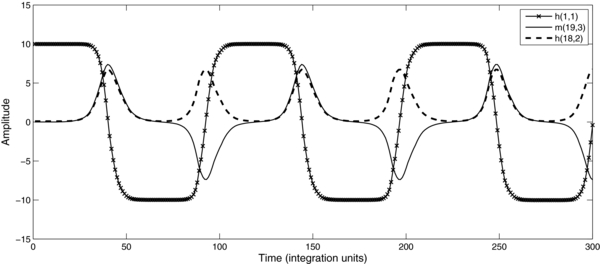
In general, the initial amplitudes and the interaction coefficients are such that 0 < m < 1, with the three modes undergoing significant energy modulations in this regime (Domaracki & Loesch 1977). In fact, Raupp et al. (2008) have shown that the resonant triad interactions among equatorial atmospheric waves in this parameter regime are capable of yielding significant amplitude modulations in the wind and pressure fields. Thus, we illustrate our analysis with a representative example of a resonant triad in the present model for the initial amplitudes of modes 2 and 3 chosen to fall into this regime. This representative example of a resonant triad in the present model is displayed in Table 1. This triad is composed of two hydrodynamic modes and one magnetic mode. For this triad illustrated in Table 1, one notices that the coupling coefficients do satisfy the relation  , which ensures that the modes exchange energy but the total energy of the triad remains constant. Figure 2 displays the time evolution of mode amplitudes for the triad illustrated in Table 1 composed of three propagating MHD Rossby modes. In this resonant triad interaction, mode 1 is a hydrodynamic mode with zonal wavenumber k = 1 and meridional wavenumber l = 1, essentially representing a planetary-scale wave mode. Although mode 1 does not have an axisymmetric x structure, it exhibits a dipole meridional structure. Hence, this mode might contribute to the observed dipole mode activity of the Sun's magnetic field. The remaining modes of the triad have more complex meridional structures, contributing to the energetics of higher harmonics of the Sun's magnetic field; namely, mode 2 is a hydrodynamic mode with zonal wavenumber 2 and meridional wavenumber l = 18; mode 3 is a magnetic mode with meridional wavenumber 19 and zonal wavenumber 3. For this triad interaction involving two hydrodynamic and one magnetic modes, the planetary-scale hydrodynamic mode is the highest frequency mode and, consequently, the unstable mode of the triad. Consequently, its energy (amplitude) always changes in time in the opposite direction of the remaining triad components; that is, this mode always supplies energy to or receives energy from the remaining two waves. When the initial state is projected only onto modes 2 and 3 (Figure 2), the planetary-scale hydrodynamic wave is excited, and its amplitude (energy) grows in time at the expense of the remaining modes of the triad. When the planetary-scale hydrodynamic Rossby mode attains its maximum energy level, this mode begins to excite the shorter-scale waves again; that is, its amplitude begins to decrease in time at the expense of the amplitude growth of modes 2 and 3. After mode 1 attains its minimum energy level again (Ω1(t) = 0), its amplitude grows again but in the opposite polarity, in detriment of the energy loss of modes 2 and 3. The complete cycle, including the two polarities (positive and negative amplitudes of the dipolar wave mode), has a period on the order of 20 yr, whereas the period of the energy (which is proportional to the amplitude squared) modulation is one-half of the period of the amplitude modulation.
, which ensures that the modes exchange energy but the total energy of the triad remains constant. Figure 2 displays the time evolution of mode amplitudes for the triad illustrated in Table 1 composed of three propagating MHD Rossby modes. In this resonant triad interaction, mode 1 is a hydrodynamic mode with zonal wavenumber k = 1 and meridional wavenumber l = 1, essentially representing a planetary-scale wave mode. Although mode 1 does not have an axisymmetric x structure, it exhibits a dipole meridional structure. Hence, this mode might contribute to the observed dipole mode activity of the Sun's magnetic field. The remaining modes of the triad have more complex meridional structures, contributing to the energetics of higher harmonics of the Sun's magnetic field; namely, mode 2 is a hydrodynamic mode with zonal wavenumber 2 and meridional wavenumber l = 18; mode 3 is a magnetic mode with meridional wavenumber 19 and zonal wavenumber 3. For this triad interaction involving two hydrodynamic and one magnetic modes, the planetary-scale hydrodynamic mode is the highest frequency mode and, consequently, the unstable mode of the triad. Consequently, its energy (amplitude) always changes in time in the opposite direction of the remaining triad components; that is, this mode always supplies energy to or receives energy from the remaining two waves. When the initial state is projected only onto modes 2 and 3 (Figure 2), the planetary-scale hydrodynamic wave is excited, and its amplitude (energy) grows in time at the expense of the remaining modes of the triad. When the planetary-scale hydrodynamic Rossby mode attains its maximum energy level, this mode begins to excite the shorter-scale waves again; that is, its amplitude begins to decrease in time at the expense of the amplitude growth of modes 2 and 3. After mode 1 attains its minimum energy level again (Ω1(t) = 0), its amplitude grows again but in the opposite polarity, in detriment of the energy loss of modes 2 and 3. The complete cycle, including the two polarities (positive and negative amplitudes of the dipolar wave mode), has a period on the order of 20 yr, whereas the period of the energy (which is proportional to the amplitude squared) modulation is one-half of the period of the amplitude modulation.
Figure 2. Time evolution of the mode amplitudes for the resonant triad composed of two hydrodynamic modes with wavenumbers (1, 1) and (2, 18) and a magnetic mode with wavenumber (3, 19). Time is dimensionless, with the solar rotation period as the characteristic timescale. The period of energy exchange in this triad is around 11 yr.
Download figure:
Standard image High-resolution imageTable 1. Example of Resonant Triad Wave Numbers, Angular Frequencies, and Respective Interaction Coefficients of a Triad Composed of One Magnetic and Two Hydrodynamic Rossby Waves
| Hid. Mode | Hid. Mode | Mag. Mode | |
|---|---|---|---|
| K | 1 | 18 | 19 |
| L | 1 | 2 | 3 |
| Frequency (×10E−5 Hz) | −2.25 | −1.23 | 1.02 |
Download table as: ASCIITypeset image
The scenario described above may explain in a simplified fashion certain global magnetic patterns on the Sun that are part of the dynamo, such as the so-called active longitudes (Dikpati & Gilman 2005 and references therein). The active longitudes refer to some specific longitude intervals where the cyclic magnetic activity of the Sun is more pronounced. A possible conjecture for the existence of such specific longitude intervals of pronounced periodic signals is that nonaxisymmetric modes of magnetic activity may be responsible for or amplify (some pre-existing) magnetic oscillations. This theoretical conjecture is supported by the observational evidence of Knaack & Stenflo (2005), who found significant periodic oscillations in nonaxisymmetric spherical harmonic coefficients of the solar magnetic field. According to the theory described here, these observed periodic modulations of nonaxisymmetric spherical harmonic coefficients of the solar magnetic field presented by Knaack & Stenflo (2005) are due to resonant triad interactions containing nonaxisymmetric MHD Rossby waves. In fact, according to the results displayed in Figure 2, when the dipole harmonic (l = 1) of the meridional structure of the solar magnetic field is at its maximum amplitude level, the higher meridional harmonics reach their minimum amplitude level and vice versa.
5. EFFECTS OF FORCING, DISSIPATION, AND INSTABILITIES ON THE WAVE INTERACTION THEORY
5.1. Constant Convective Forcing
Let us consider now the same finite amplitude analysis carried out in the previous section but with the inclusion of the prescribed divergence term (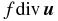 ) in the vorticity balance equation. This approach of considering only (
) in the vorticity balance equation. This approach of considering only ( ) as a prescribed Rossby wave source is in the spirit of theoretical and modeling studies on the impact of thermal or topographic forcings on the large-scale atmospheric dynamics, as previously discussed. In this context, Equation (12a) is replaced by
) as a prescribed Rossby wave source is in the spirit of theoretical and modeling studies on the impact of thermal or topographic forcings on the large-scale atmospheric dynamics, as previously discussed. In this context, Equation (12a) is replaced by
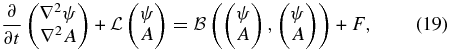
where the operators  and
and  are given by Equations (4b) and (12b), respectively; F corresponds to the prescribed forcing vector defined according to
are given by Equations (4b) and (12b), respectively; F corresponds to the prescribed forcing vector defined according to
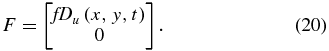
In the equations above, the forcing  is required to have a zero average in order to ensure conservation of angular momentum, meaning that there will always be a region of divergence and a region of convergence. By expanding F in a Fourier basis, it is readily seen that this prescribed forcing will be composed of a series of wavepatterns, each one with a positive and a negative region of divergence.
is required to have a zero average in order to ensure conservation of angular momentum, meaning that there will always be a region of divergence and a region of convergence. By expanding F in a Fourier basis, it is readily seen that this prescribed forcing will be composed of a series of wavepatterns, each one with a positive and a negative region of divergence.
A possible source of divergence in the tachocline is the baroclinic instability, an important process for the generation of vorticity through conversion of potential energy (Ghil & Childress 1987). Baroclinic instability was recently shown to occur on modes with a global scale (wavenumbers 1 and 2; Dikpati & Gilman 2014). Different from the barotropic Rossby waves described here, baroclinic Rossby waves are associated with horizontally divergent motions, so the prescribed divergence term in Equation (20) could be seen as a representation of the net effect of baroclinic motions on barotropic modes, especially motions associated with unstable modes that will mostly contribute to horizontal divergence.
The asymptotic treatment of Equation (19) in the weakly nonlinear and weak forcing regime yields the following reduced equations for the amplitudes of three resonantly interacting waves:
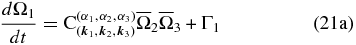
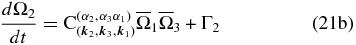
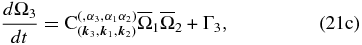
where the coupling coefficients 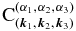 ,
, 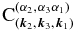 , and
, and  are given by Equation (14) and Γ1, Γ2, and Γ3 correspond to the projection of forcing vector F onto modes 1, 2, and 3, respectively, meaning that only the special scales of the divergence corresponding to the spatial scale of waves 1, 2, and 3 will be relevant to our analysis.
are given by Equation (14) and Γ1, Γ2, and Γ3 correspond to the projection of forcing vector F onto modes 1, 2, and 3, respectively, meaning that only the special scales of the divergence corresponding to the spatial scale of waves 1, 2, and 3 will be relevant to our analysis.
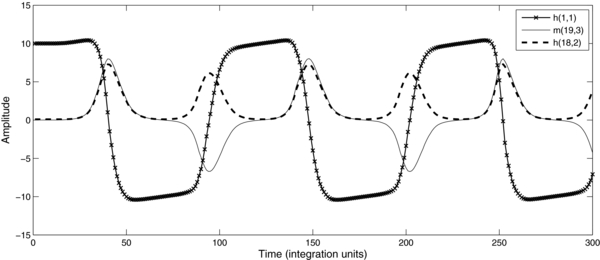
Figure 3 shows the time evolution of the mode amplitudes of the same resonant triad and initial condition as in Figure 2, but with the inclusion of a Rossby wave source F = [fD(x, y, t), 0]T that projects only onto the unstable mode of the triad (mode 1, the large-scale dipole mode). According to the dynamics of periodically forced resonant triads, this situation where the forcing resonates only with the unstable mode is the condition for total energy to remain bounded in time (Raupp & Dias 2009; Harris et al. 2012). Apart from producing a period doubling in the time evolution of the amplitude of mode 3, from Figure 3 one notices that the effect of the forcing on this resonant interaction is to yield an asymmetry between the growth and decay phases of the mode amplitudes. This growth and decay asymmetry is also an observed characteristic of the time evolution of solar magnetic activity. Thus, the results suggest that a vorticity source on the most unstable mode may lead sunspots to alternate small and large energy peaks during the solar cycle.
Figure 3. Same as Figure 2, but with the inclusion of a vorticity source projecting onto mode 1.
Download figure:
Standard image High-resolution image5.2. Combined Effect of Linear Forcing and Dissipation
In a realistic scenario, the flows in the solar interior are subjected to dissipation, which may contribute to the amplitude modulations associated with the nonlinear wave interactions discussed thus far to die out with time. However, as mentioned in Section 2, the fluid at the tachocline is also heated from below, which may act as a forcing mechanism for MHD Rossby waves, preventing them from vanishing through dissipative losses. Thus, in what follows, we describe the effects of the interaction of the complete divergence forcing and dissipation on the nonlinear MHD Rossby wave interactions.
For this purpose, we consider the same finite-amplitude perturbation analysis performed thus far but add the linear divergence and dissipative terms of Equation (3). In this way, the governing equations for the MHD disturbances are
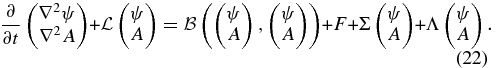
In Equation (22), the operators  ,
,  , and F are defined according to Equations (4b), (12b), and (20), respectively, and Σ and Λare the linear operators representing the parametric divergence forcing and dissipation, respectively, given by
, and F are defined according to Equations (4b), (12b), and (20), respectively, and Σ and Λare the linear operators representing the parametric divergence forcing and dissipation, respectively, given by
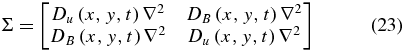

Consequently, the general form of the wave amplitude equations in a forced-dissipative resonant triad of model Equations (22) is

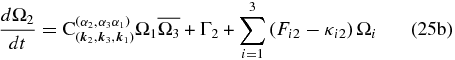
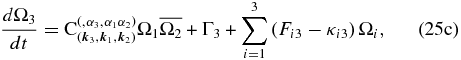
where
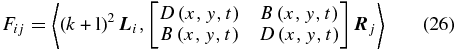
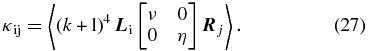
One notices that the linear divergence terms in both the vorticity balance and induction equations compete with the dissipative terms so that the last term in the right-hand side of Equation (25) can work in different ways for the three-wave interacting dynamics. If Fij − κij has positive eigenvalues, it will lead to instability. In this context, the pattern of the convective cells will determine the most excited modes, which in turn will be the most energetic waves. On the other hand, if Fij − κij has only negative eigenvalues, it will work as an effective damping. Finally, if the eigenvalues of Fij − κij are purely imaginary, the last term in the right-hand side of Equation (25) yields a resonant coupling between two of the three modes of the triad, contributing to the oscillatory behavior of the wave amplitudes. Consequently, the different ways by which the competition between the linear forcing and dissipation can interact with nonlinearity makes the dynamics of system (25) rather complex, exhibiting a rich variety of behaviors depending on the parameters, including transitions between regular (i.e., periodic) and chaotic regimes. For a comprehensive account of the bifurcation structure of these equations, see (Wersinger et al. 1980a, 1980b). Chian et al. (2000) analyzed a special case of system (25) in the context of plasma physics, where the combination of the last two terms in the right-hand side of Equation (25) acts as a linear parametric forcing for the unstable mode (mode 1) and as a dissipation mechanism for the remaining modes of the triad. They showed that the three-wave interacting dynamics in this scenario undergoes transitions from regular to chaotic behaviors via either the period-doubling route or the type I Pomeau–Manneville intermittency route. Here we stick to the case where the dissipative terms are slightly greater than linear divergence forcing in order to demonstrate the potentiality of these thermal convection parametric forcing terms to sustain, against dissipative losses, the amplitude oscillations related to the nonlinear coupling among the MHD Rossby modes.
In fact, the dynamical system governed by Equation (25) can be conservative provided it preserves volume in phase space, which is accomplished if Equation (25) satisfies the Liouville property:
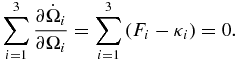
An unbalance between forcing and dissipation will lead the phase space volume to shrink (dissipation is greater than forcing), or to expand in the opposite situation.
Figure 4 shows an example of a numerical solution of system (25), for the same triad presented previously, representing the situation in which the forcing is greater than dissipation on the dipole scale, and dissipation is stronger on a small scale. This is reasonable because dissipation varies linearly with the wavenumber, being therefore more effective for the small-scale disturbances. We use parameters (F1 − κ1) = 0.1, (F2 − κ2) = −0.4, (F3 − κ3) = 0.45, discarding diagonal terms. In order to obtain this numerical solution, we have adopted the fourth-order Runge–Kuta numerical scheme. In Figure 4, we see that this combination of forcing and dissipation will alter the frequency of oscillation, where in this particular case the solution obtained seems to represent an attractor corresponding to a periodic orbit.
Figure 4. Same as Figure 2, but with the inclusion of a vorticity source projecting onto mode 1, linear forcing and dissipation being mode 1 with a positive balance between forcing and dissipation; modes 2 and 3 have a negative balance (dissipation is greater than forcing). Oscillations are sustained against dissipation; amplitudes and periods of exchange of energy, however, are altered compared to Figures 1 and 2 because of the appearance of a periodic attractor.
Download figure:
Standard image High-resolution image5.3. Interaction with Differential Rotation and Nonuniform Zonal Magnetic Field
Apart from the convective forcing that excites MHD Rossby waves through the divergent circulation associated with the vertical motion, instabilities of either the differential rotation or the toroidal magnetic field might constitute another energy source for MHD Rossby waves in the solar tachocline. Recall that the meridionally varying background flow associated with solar differential rotation can trap the magnetic branch of MHD Rossby waves within the latitudinal belt between around ±35° and refract them toward the equator, as demonstrated earlier. However, here we shall perform an alternative analysis of the effect of a latitudinally varying background state on MHD Rossby waves in order to elucidate how instabilities associated with either solar differential rotation or toroidal magnetic fields of a solar tachocline might interact with resonant nonlinear interactions among the MHD Rossby waves discussed in this paper. For this purpose, let us analyze here how a meridionally varying background flow combined with a meridionally varying toroidal magnetic field can modify the eigenmodes of the homogeneous operator  defined by Equation (4b). Thus, for clarity in exposition, we consider the linearized and unforced (Du = DB = 0) version of Equations (3) for perturbations around a background state defined according to
defined by Equation (4b). Thus, for clarity in exposition, we consider the linearized and unforced (Du = DB = 0) version of Equations (3) for perturbations around a background state defined according to

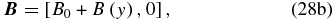
with B0 being a constant. In this context, the time evolution of the infinitesimal amplitude perturbations around the background state defined above can be written in terms of stream function ψ and vector potential A as
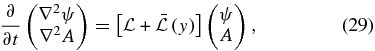
where  is the homogenous linear operator given by Equation (4b) and
is the homogenous linear operator given by Equation (4b) and  is the linear differential operator with variable coefficients, given by
is the linear differential operator with variable coefficients, given by
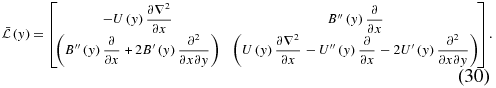
To analyze how the nonhomogeneous operator  modifies the eigenmodes of the homogeneous operator
modifies the eigenmodes of the homogeneous operator  , let us assume that the perturbed fields in Equation (29) are composed of a single mode:
, let us assume that the perturbed fields in Equation (29) are composed of a single mode:
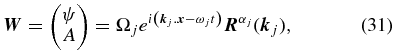
where Ωj refers to an arbitrary constant amplitude and 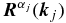 corresponds to the normalized right eigenvector of
corresponds to the normalized right eigenvector of  . Inserting the ansatz (31) into Equation (29) yields
. Inserting the ansatz (31) into Equation (29) yields
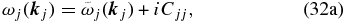
where
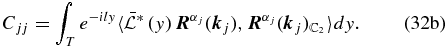
In Equation (32b), l is the meridional wavenumber,  refers to the inner product defined according to Equation (9),
refers to the inner product defined according to Equation (9),  is the operator obtained from
is the operator obtained from  by replacing ∂/∂x by ik and ∂/∂y by il, and
by replacing ∂/∂x by ik and ∂/∂y by il, and  corresponds to the eigenvalue of the homogeneous operator
corresponds to the eigenvalue of the homogeneous operator  associated with eigenvector
associated with eigenvector 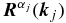 and is given by Equation (7). From Equation (32) one can notice that the nonhomogeneous operator
and is given by Equation (7). From Equation (32) one can notice that the nonhomogeneous operator  can either modify the time frequency of MHD Rossby modes from their eigenvalues (7) or generate instabilities or exponential growth of these modes. In this context, the imaginary part of coefficient Cjj is responsible for the Doppler-shift effect on the propagation of MHD Rossby modes, whereas the real part of Cjj yields either exponential growth (Re(Cjj) < 0) or decay (Re(Cjj) > 0) of the amplitude of these modes.
can either modify the time frequency of MHD Rossby modes from their eigenvalues (7) or generate instabilities or exponential growth of these modes. In this context, the imaginary part of coefficient Cjj is responsible for the Doppler-shift effect on the propagation of MHD Rossby modes, whereas the real part of Cjj yields either exponential growth (Re(Cjj) < 0) or decay (Re(Cjj) > 0) of the amplitude of these modes.
Thus, according to the linear dynamics represented by Equation (29), if a particular infinitesimal amplitude mode j is unstable (Re(Cjj) < 0),its amplitude will grow exponentially in time. However, after a certain time, the amplitude growth of the unstable mode leads the linear approximation to break down, and the quadratic nonlinearities must be restored for a satisfactory description of system (3) in this regime. In this case, the role of the quadratic nonlinearities is to yield saturation for the amplitude growth of the unstable mode j. In this scenario, we believe that the nonlinear saturation is mostly due to resonant triad interactions in which mode j participates as the pump mode (the triad member with the highest absolute value of nonlinear coupling coefficient). In fact, if we restore the quadratic nonlinear and dissipative terms in Equation (29), the resulting dynamical system governing the resonant three-wave interacting dynamics in this case will be identical to system (25), but with the coefficients Fij as given by Equation (26) being replaced by Re(Cij) as given by Equation (32b). In this case, the modes composing the resonant triad would match the usual resonant triad interaction conditions for their wavenumbers and the real part of their time–frequencies, whereas the imaginary part of their time–frequencies would appear as linear forcing coefficients in the right-hand side of Equation (25).
A linear instability analysis of MHD shallow-water equations describing the dynamics of a solar tachocline has been investigated by Dikpati & Gilman (2005) for the profiles U(y) and B(y), representative of solar differential rotation and toroidal magnetic field bands in the solar tachocline, respectively. They show that the most unstable modes represent planetary-scale disturbances with a wavenumber 1–2 spatial structure. As demonstrated in Section 4, the hydrodynamic branch of wavenumber 1–2 MHD Rossby modes, in turn, can work as a pumpwave in resonant triad interactions with shorter-wavelength MHD Rossby modes. On the other hand, dissipation is believed to be small for planetary-scale disturbances and to have its effect enhanced as wavenumber increases. As a consequence, in the presence of a background state represented by Equation (28), with U(y) and B(y) representing the solar differential rotation and toroidal magnetic field of the solar tachocline, respectively, for resonant triad interactions involving a hydrodynamic MHD Rossby mode with zonal and meridional wavenumbers one or two and shorter spatial-scale MHD Rossby modes, we would expect that dissipation is weaker than linear forcing for the planetary-scale pump mode and stronger than linear forcing for the shorter spatial-scale modes. Hence, for this kind of resonant triad of MHD Rossby modes, the competition between linear forcing and dissipation yields an effective linear forcing for the pump mode and an effective damping for the remaining modes of the triad. As demonstrated by Chian et al. (2000) for the nonlinear triad interaction involving Langmuir, whistler, and Alfvén waves in the context of planetary magnetospheres, the nonlinear triad interaction in this case is capable of saturating the exponential growth of the unstable mode, with the solution of the three-wave interaction equations undergoing either periodic or chaotic behaviors. Thus, we believe that the resonant triad interactions described in Section 4, when embedded in a background state characterized by a differential rotation mean zonal flow and the toroidal magnetic field of the solar tachocline, might be capable of saturating the exponential growth of the unstable planetary-scale mode and yielding nonaxisymmetric periodic modulations in the solar magnetic activity. Saturation of global instabilities by nonlinear waves at the solar tachocline is also suggested by numerical simulations of the full hydrodynamic shallow-water equations performed by Dikpati (2012).
Therefore, apart from convective sources related to thermal inhomogeneities along a tachocline's boundaries, we have pointed out in the present part of this section that global instabilities of both solar differential rotation and toroidal magnetic field can also be accounted for by potentially important energy sources that prevent resonant triad interactions of MHD Rossby modes from declining through viscous and Ohmic dissipative actions. In addition, we believe that such instabilities might be the natural triggering for the resonant interactions of the MHD Rossby waves analyzed in Section 4.
6. ROSSBY WAVES AND MERIDIONAL CIRCULATION
6.1. Generation of Waves Due to Meridional Circulation
Meridional circulation has been established in recent decades as an essential process for the solar cycle. In fact, this process is of particular importance for the determination of the specific periods of the solar cycle in kinematic dynamo models (Dikpati & Charbonneau 1999). Therefore, we present here a few remarks on the possible role of meridional circulation on the nonlinear wave theory of MHD Rossby waves developed in this paper. The first view, explored in the present subsection, is that the meridional flow is a process separated from Rossby waves and is provided by preexisting cells in the upper layer that will force the motion at the tacholine. In the following subsection, we consider the meridional flow generated by Rossby waves themselves.
In a purely hydrodynamic context, meridional circulation is known to be a source of Rossby waves because, according to the Kelvin circulation theorem (Pedlosky 1986), a meridional displacement of a fluid parcel yields a disturbance in the vorticity field. Thus, a possible conjecture to including the effect of the meridional circulation on the nonlinear wave interaction theory developed here would be that the effect of the meridional circulation appears as a stationary forcing in the right-hand side of the vorticity Equation (3a), though this conjecture cannot be directly generalized to the MHD context because MHD equations have a different set of invariants (Dellar 2002). However, the meridional displacement of a fluid parcel may alter the cross-helicity field instead and therefore may be responsible for the generation of MHD Rossby waves.
Another possible conjecture on the effect of meridional circulation on the wave interaction theory described here would be that the meridional circulation accounted for the background state in which MHD Rossby waves are embedded. In this sense, the meridional circulation may change both the propagation and instability of MHD Rossby waves. An example of the impact of a meridional mean circulation on Rossby wave propagation can be found in Freitas & Ambrizzi (2012) for a purely hydrodynamic context, where they analyzed the effect of changes in the tropical Hadley cell on stationary Rossby waveguides in the atmospheric dynamics.
The heuristic arguments mentioned above appear to be crucial points in establishing the relation between Rossby waves and the solar cycle and need further investigation in future research.
6.2. Meridional Flows Due to Rossby Waves
In view of the success of transport-flux dynamos, we briefly discuss a possible connection with Rossby waves. As discussed in Schmitt & Schüssler (2004), it is difficult to distinguish between a dynamo wave mechanism and an advection explanation for the structure of the butterfly diagram, a distinction that could only be made by helioseismological observation of the properties of the meridional flow at tachocline depths, but Zhao et al. (2013) suggest that the equatorial return of meridional circulation occurs at depths shallower than the tachocline. In Section 3.2 we provide a mechanism that can be considered as an MHD generalization of the dynamo waves that keep the desired properties. Here we show that Rossby waves might also help explain longitudinally dependent structures in the currently prevalent view of equatorward flux transport. Our arguments could be adapted to near-surface poleward advection of poloidal magnetic fields.
Letting![$\psi = A{\rm exp} [ {i ({{\boldsymbol k}.{\boldsymbol x} - \omega t} )} ]$](https://content.cld.iop.org/journals/0004-637X/799/1/78/revision1/apj505657ieqn73.gif) be the stream function associated with a Rossby wave, the corresponding flow will be
be the stream function associated with a Rossby wave, the corresponding flow will be
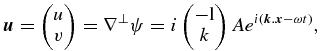
where we see that for all Rossby waves with nonzero zonal wavenumber k (nonaxisymmetric) there will be a meridional flow associated with them. Supposing that the horizontal velocity field  is composed of a superposition of resonantly interacting Rossby waves, in a particularly interesting case one of the waves is axisymmetric, providing a zonal flow, and one is not axisymmetric, providing a meridional flow. A cubic mechanism is needed to couple such waves; see Burzlaff et al. (2008) for details. When the amplitude of the axisymmetric wave is maximal, the zonal flow (differential rotation) is maximal, and when the amplitude of the nonaxisymmetric wave is maximal, the meridional flow has maximum velocity. Therefore, resonantly coupled Rossby waves can provide a mechanism for oscillatory behavior of both zonal and meridional flows; the oscillation can be in or out of phase depending on the modes involved and on their respective amplitudes at a given time (i.e., initial conditions). This mechanism can be associated with observed variations in the meridional flow throughout a cycle (Javaraiah et al. 2006 see also Dikpati et al. 2004 and references therein for details).
is composed of a superposition of resonantly interacting Rossby waves, in a particularly interesting case one of the waves is axisymmetric, providing a zonal flow, and one is not axisymmetric, providing a meridional flow. A cubic mechanism is needed to couple such waves; see Burzlaff et al. (2008) for details. When the amplitude of the axisymmetric wave is maximal, the zonal flow (differential rotation) is maximal, and when the amplitude of the nonaxisymmetric wave is maximal, the meridional flow has maximum velocity. Therefore, resonantly coupled Rossby waves can provide a mechanism for oscillatory behavior of both zonal and meridional flows; the oscillation can be in or out of phase depending on the modes involved and on their respective amplitudes at a given time (i.e., initial conditions). This mechanism can be associated with observed variations in the meridional flow throughout a cycle (Javaraiah et al. 2006 see also Dikpati et al. 2004 and references therein for details).
Because of the continuity of the radial shear, the meridional flow of the Rossby waves must match the meridional flow of the layers above. An interaction of Rossby waves at the tachocline and the meridional flow at the convection zone will occur; this combination will affect the preexisting meridional flow by adding a longitudinal structure to it. This effect might combine with the traditional interpretation of equatorward flux transport to explain longitudinally dependent structures, such as preferred longitudes (Dikpati & Gilman 2005).
7. FINAL COMMENTS
Here we have presented a possible fundamental theoretical description of the cyclic oscillations of solar magnetic activity based on resonant nonlinear interactions among MHD Rossby waves in the solar tachocline. According to our theory, planetary-scale modes having a meridional structure of a nonaxisymmetric dipole mode of the Sun's toroidal magnetic field can act as a pump wave in resonant triad interactions, supplying energy to and receiving energy from shorter-scale modes in a periodic fashion, and the energy exchanges resulting from this parametric instability yield periodic oscillations of the polarity of the pump mode with a period close to the nearly 11 yr period of the solar cycle. These periodic oscillations are in phase with the maximum energy level of the remaining shorter-scale waves of the triad. To demonstrate a closer fidelity of our theory with observations, we have also examined the linear theory of MHD Rossby waves embedded in a latitudinally varying zonal flow mimicking the solar differential rotation. In this context, we have computed the parameters associated with wave propagation and found that in the solar dynamo the equator can act as a waveguide for the magnetic branch such that waves generated in midlatitudes are refracted toward the equator. In a more realistic model that takes into account instabilities of the background state, as these waves propagate they may cause disturbances on the surrounding magnetic field, which would possibly trigger instabilities. This could account for the appearance of sunspots as the waves propagate throughout the equatorial waveguide. The path followed by the waves could explain the format of the butterfly diagram, in which there is magnetic activity appearing at around 35° and propagating toward the equator. This feature is in agreement with Joy's law for activity sunspot zones, suggesting that activity zones could be determined by Rossby waves. The modulation of this wave activity in a nearly 11 yr cycle observed in the butterfly diagram could be explained by resonant nonlinear interactions of these waves with larger-scale modes representing the dipole meridional structure of the magnetic field.
We would like to stress the fact that nearly periodic coherent phenomena are rather common in the context of turbulent systems. This was perhaps first noticed in the classic work of Fermi and collaborators on a chain of coupled oscillators (Fermi et al. 1955), the so-called Fermi–Pasta–Ulam paradox. The counterintuitive result of Fermi and collaborators is that despite the high dimensionality and nonlinearity of their problem, there is a violation of ergodicity, and the final states of the system are characterized by the energy being concentrated in a few modes that exchange energy periodically through nonlinear resonance. In our view, the situation of the solar cycle is analogous, as may become evident by examining the evolution of the amplitudes of spherical harmonic coefficients of the solar magnetic field (Knaack & Stenflo 2005). The present article is therefore a first attempt to put the periodic nature of the solar cycle in this context.
In summary, we believe that this "quasi-geostrophic MHD" picture could help in clarifying the interpretation of several aspects of the magnetic activity of the Sun, including periodicities and spatio-temporal evolution, particularly the features with longitudinal structure.
In order to develop a complete theory explaining both the butterfly structure of sunspots and its decadal modulation, we need to put the arguments presented in Section 5.3 on resonant MHD Rossby wave triads embedded in a latitudinally varying background state into a quantitative form, as well as augment this theory for a continuous spectrum of wave packets. We intend to develop this theory in future work. Further generalization of this model to spherical geometry might be important as well because, in the spherical geometry, Rossby waves can generate zonal jets at higher orders of amplitude, as suggested by Burzlaff et al. (2008), permitting exchange of energy with zero-frequency modes. A closer fidelity of our results with the observed temporal evolution of solar activity might also be achieved by augmenting our nonlinear theory to include coupled resonant triads as well as parametric forcings that could yield either exponential growth or a linear resonant coupling. These points will be investigated in a future paper.
The work of Carlos F. M. Raupp is supported by FAPESP, and Breno Raphaldini was supported by CAPES. We also thank the anonymous reviewer for his or her fruitful comments for improving this manuscript.
Footnotes
- 1
Although it might seem artificial to force mode 1 to have zero initial amplitude, it is in fact general because the solution is periodic and, thus, mode 1 will have zero amplitude infinitely many times.