ABSTRACT
The cosmic ray mean free path in a large-scale nonuniform guide magnetic field with superposed magnetostatic turbulence is calculated to clarify some conflicting results in the literature. A new, exact integro-differential equation for the cosmic-ray anisotropy is derived from the Fokker–Planck transport equation. A perturbation analysis of this integro-differential equation leads to an analytical expression for the cosmic ray anisotropy and the focused transport equation for the isotropic part of the cosmic ray distribution function. The derived parallel spatial diffusion coefficient and the associated cosmic ray mean free path include the effect of adiabatic focusing and reduce to the standard forms in the limit of a uniform guide magnetic field. For the illustrative case of isotropic pitch angle scattering, the derived mean free path agrees with the earlier expressions of Beeck & Wibberenz, Bieber & Burger, Kota, and Litvinenko, but disagrees with the result of Shalchi. The disagreement with the expression of Shalchi is particularly strong in the limit of strong adiabatic focusing.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
The transport and acceleration of energetic particles in partially turbulent cosmic magnetic fields is typically described using the Fokker–Planck equation for the particle distribution function (for a recent derivation, see Schlickeiser 2011). The diffusion approximation for the particle density is a well-known simplified form of the Fokker–Planck equation, which results when turbulent pitch-angle scattering is strong enough to ensure that the scale of the particle density variation is significantly greater than the particle mean free path (Jokipii 1966; Hasselmann & Wibberenz 1968, 1970; Earl 1974). Numerical studies confirmed the accuracy of the diffusion approximation in a uniform mean (guide) magnetic field (Kota et al. 1982).
Large-scale guide magnetic fields such as the interplanetary magnetic field, however, are often nonuniform. Roelof (1969), Earl (1976), and Kunstmann (1979) identified the effect of adiabatic focusing on particle transport in spatially varying magnetic fields, resulting from the parallel component of the mirror force in nonuniform guide fields (Schlickeiser & Jenko 2010). Focused transport equations have been used extensively to model the propagation of energetic particles in interplanetary space following large solar flares (e.g., Bieber et al. 2002; Saiz et al. 2008; Dröge et al. 2010; Artmann et al. 2011). Besides causing coherent spatial particle streaming along the guide field in magnetostatic turbulence, the presence of adiabatic focusing modifies the spatial diffusion coefficients of cosmic ray particles κ = vλ/3 parallel to the mean magnetic field, where v is the particle speed and λ the scattering mean free path. In the limit of weak focusing with |ξ| = λ0/|L| ≪ 1, where the focusing length
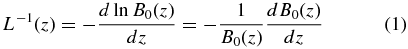
is positive (negative) in a diverging (converging) guide field and where λ0 denotes the mean free path in an uniform (|L| = ∞) guide field, Beeck & Wibberenz (1986), Bieber & Burger (1990), and Kota (2000) calculated this modification to

for the case where the magnetostatic fluctuations have vanishing cross (Hc = 0) and magnetic (σ = 0) helicities, i.e., forward- and backward-propagating plasma waves have equal intensities and polarizations. Litvinenko (2012a) investigated the influence of non-zero cross and magnetic helicity values.
The case of arbitrarily strong focusing ξ ∈ [0, ∞] was recently studied by Shalchi (2011), Litvinenko (2012a, 2012b), and Shalchi & Danos (2013), claiming different results. It is the purpose of the present manuscript to recalculate the cosmic-ray mean free path for arbitrarily strong focusing. As most authors before, we consider the case of magnetostatic turbulence with vanishing cross and magnetic helicities.
2. COSMIC-RAY TRANSPORT WITH ADIABATIC FOCUSING
We start from the Fokker–Planck equation for the gyrotropic cosmic-ray distribution function f0(z, p, μ, t), which incorporates the effects of adiabatic focusing and scattering in particle pitch-angle cosine (μ = cos θ; Schlickeiser & Shalchi 2008):
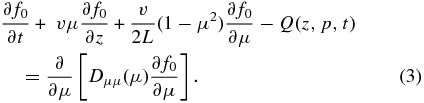
We restrict our analysis to spatially point-like isotropic source terms Q(z, p, t) = q(p, t)δ(z). Here, z denotes the spatial variable along the magnetic guide field B0(z), and effects due to perpendicular spatial diffusion are ignored. For magnetostatic turbulence, the pitch-angle scattering coefficient Dμμ(μ) is the only non-vanishing Fokker–Planck coefficient.
Now it is convenient to introduce the linear phase space density f(z, p, μ, t) = f0(z, p, μ, t)/B0(z), providing
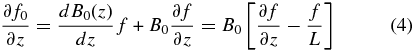
Consequently, Equation (3) leads to
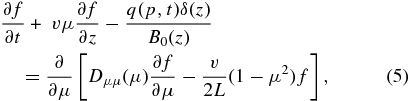
the Fokker–Planck equation for the gyrotropic linear phase space density.
For dominating pitch-angle scattering, described by Dμμ(μ), the gyrotropic phase space distribution functions adjust very rapidly to a quasi-equilibrium that is close to the isotropic equilibrium distribution F(z, p, t), in excellent agreement with the often observed high isotropy of cosmic rays. We therefore split the gyrotropic cosmic-ray phase space density into its average in pitch-angle cosine and an anisotropic part, i.e.,
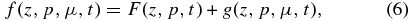
where
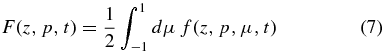
and
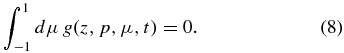
In contrast to the diffusion approximation (Jokipii 1966; Skilling 1975; Schlickeiser 1989), we do not assume that |g| ≪ F. Inserting Equation (6) into the Fokker–Planck equation (5) then yields
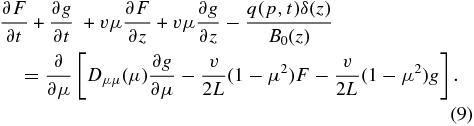
Next, we integrate this equation over μ, making use of the regularity of Dμμ(μ = ±1) = 0 so that
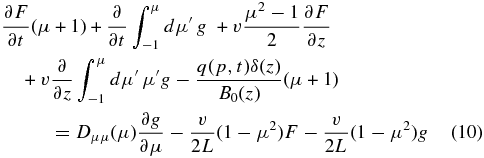
Taken at μ = 1, using Dμμ(μ = 1) = 0, this equation with Equation (8) yields
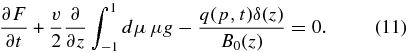
Subtracting Equation (11) from Equation (10) provides
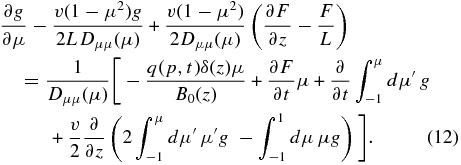
This equation can be expressed as

where we introduce the integrating function
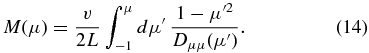
Equations (11) and (14) are still exact.
If we are outside the source region (z ≠ 0) and ignore the time derivatives on the right-hand side for stationary cases, the anisotropy equation (13) simplifies to
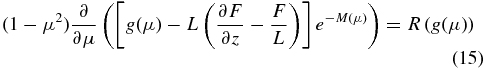
with the function
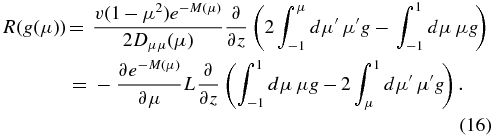
Equation (15) still is an exact integro-differential equation for the anisotropy g(μ) for the stationary case.
2.1. Approximate Anisotropy in Stationary State
In accordance with all earlier studies, we assume that the right-hand side of Equation (15) is much smaller than the left-hand side, which can be checked a posteriori. We then set R(μ) = 0 so that Equation (15) readily integrates to
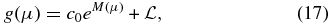
where we introduce
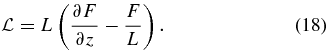
The integration constant c0 can be determined from condition (8), providing
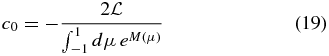
so that the anisotropy (17) reads
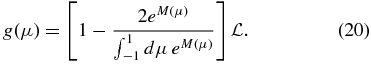
2.2. Spatial Diffusion Coefficient and Mean Free Path
The first moment of the anisotropy (20) needed in Equation (11) is then given by

so that Equation (11) reduces to the time-dependent spatial transport equation for the isotropic part of the linear phase space density
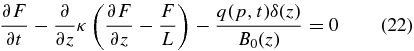
with the parallel spatial diffusion coefficient
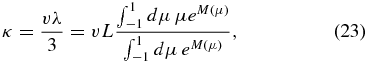
corresponding to the scattering mean free path
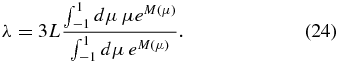
Expressing the isotropic part of the linear phase space density F(z, p, t) = F0(z, p, t)/B0(z) by the isotropic part of the phase space density gives
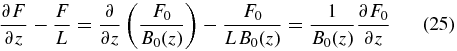
so that the transport equation (22) becomes
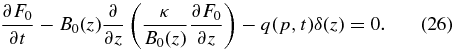
For the second term, we obtain
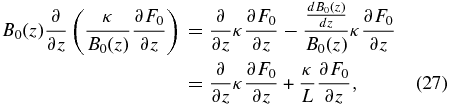
where we use definition (1) of the focusing length L(z). Consequently, the time-dependent spatial transport equation for the isotropic part of the phase space density becomes
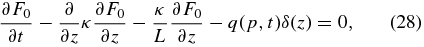
which agrees with the focused transport equation of Earl (1976) containing the coherent spatial particle streaming along the guide field.
Equations (28), (23) and (24), together with Equation (14), are the central results of this investigation. In the following sections, we derive various limits of the mean free path (24).
3. NEGLIGIBLE ADIABATIC FOCUSING
We first consider the limit of negligible adiabatic focusing |L| → ∞. We note that the function (14) can be written as
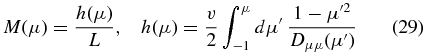
so that the mean free path (24) becomes
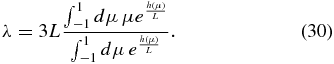
For very large |L| ≫ 1, we expand the exponential functions to first order in their arguments, providing
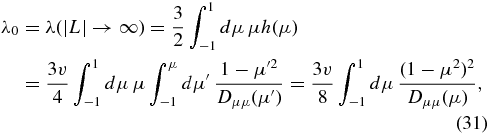
after partial integration in the last step. Equation (31) is the correct limit.
4. ISOTROPIC SCATTERING
Now we consider the case of isotropic scattering with Dμμ(μ) = D0(1 − μ2) with a constant D0. Here, functions (14) and (29) simplify to

so that we obtain for Equation (31)

Introducing the ratio

as a measure for weak (|ξ| ≪ 1) and strong (|ξ| ≫ 1) focusing, the function (32) reads

We then find for the anisotropy (20)
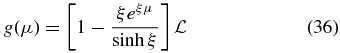
and the mean free path (24)
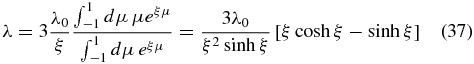
after elementary integrations. Consequently, we obtain the ratio
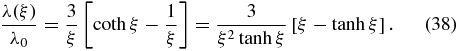
We note the symmetry λ(− ξ) = λ(ξ) so that the mean free path is independent from the sign of the focusing length L. Equation (38) implies for the spatial diffusion coefficient
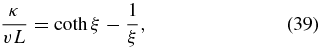
in agreement with the earlier expressions of Beeck & Wibberenz (1986), Kota (2000), and Litvinenko (2012a).
However, Equation (38) disagrees with Equation (33) of Shalchi (2011), who gives
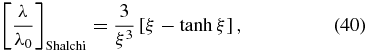
although the differences at small ξ ≪ 1 are small as tanh ξ ≃ ξ. This disagreement leads to different behaviors in the weak (ξ ≪ 1) and strong (ξ ≫ 1) focusing limits, which we consider next. As an aside, we note that Equation (62) in Shalchi & Danos (2013) agrees exactly with our result (38). We conclude that Equation (33) of Shalchi (2011) is incorrect.
4.1. Weak and Strong Focusing Limit
With the known asymptotic approximations of the  function, we obtain the weak focusing limit (ξ ≪ 1) for the mean free path (38)
function, we obtain the weak focusing limit (ξ ≪ 1) for the mean free path (38)
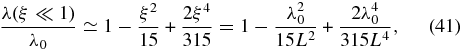
valid up to fourth order in ξ ≪ 1, which reproduces exactly Equation (2) in second order, but differs from Equation (35) of Shalchi (2011).
Likewise, in the strong focusing limit (ξ ≫ 1), we find
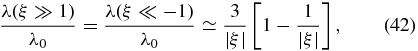
in strong contradiction to Equation (37) of Shalchi (2011), who obtained λ/λ0 = 3ξ−2 from his incorrect expression in this case.
4.2. Consistency Check
For the case of isotropic scattering with Dμμ(μ) = D0(1 − μ2), we use the anisotropy (36) to derive for the residual function (16) with
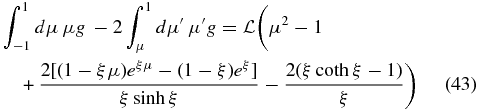
so that
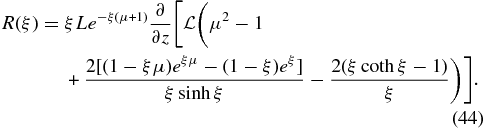
We use
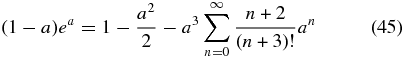
to infer
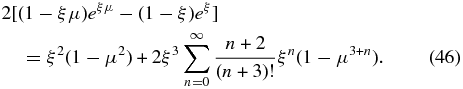
In the weak scattering limit (|ξ| ≪ 1), we find the lowest order in ξ:
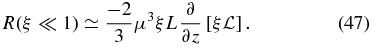
Moreover, with definition (18) and Equation (25), we find
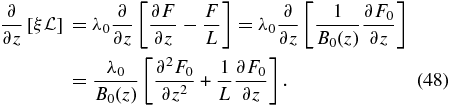
The steady-state transport equation (28) yields
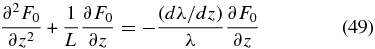
so that with the limit (41),

Collecting terms we find for the residual function (47) in the weak scattering limit,
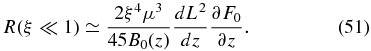
For the often considered case of a spatially constant focusing length L, the residual function (51) vanishes, making our perturbational approach to the integro-differential equation (15) an exact approach.
For spatially varying L(z), as in Artmann et al. (2011), the residual function (51) is of fourth-order R(ξ ≪ 1)∝ξ4. In the same limit, the anisotropy (36)
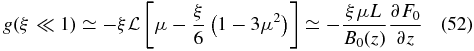
is of first-order g(ξ ≪ 1)∝ξ. Therefore, in the weak scattering limit R(ξ ≪ 1) ≪ g(ξ ≪ 1), which justifies a posteriori our approximation (17), at least in this limit.
5. SUMMARY AND CONCLUSIONS
We recalculated the cosmic ray mean free path in a large-scale nonuniform guide magnetic field with superposed magnetostatic turbulence to clarify some conflicting results in the literature. We derive a new exact integro-differential equation for the cosmic-ray anisotropy from the Fokker–Planck transport equation, which incorporates the effects of adiabatic focusing and pitch-angle scattering. A perturbation analysis of this integro-differential equation leads to an analytical expression for the cosmic ray anisotropy and the focused transport equation for the isotropic part of the cosmic ray distribution function. The derived parallel spatial diffusion coefficient and the associated cosmic ray mean free path include the effect of adiabatic focusing and reduce to the standard forms in the limit of an uniform guide magnetic field.
For the illustrative case of isotropic pitch-angle scattering, the derived mean free path agrees with the earlier expressions of Beeck & Wibberenz (1986), Bieber & Burger (1990), Kota (2000), and Litvinenko (2012a, 2012b), but disagrees with the result of Shalchi (2011). The disagreement with the expression of Shalchi (2011) is particularly strong in the limit of strong adiabatic focusing. The consistency check in the limit of weak adiabatic focusing indicates that the perturbation solution is exact in the case of a spatially constant focusing length and a good approximation to the integro-differential equation in the case of weak focusing.
This work was partially supported by grants Schl 201/23-1 and Schl 201/29-1 of the Deutsche Forschungsgemeinschaft. H.-Q.H. gratefully acknowledges the partial support of the National Natural Science Foundation of China under grants 41204130, 41321003, and 41131066; the National Important Basic Research Project under grant 2011CB811405; and the International Postdoctoral Exchange Fellowship Program of China under grant 20130023.


