AN EXACT SOLUTION FOR MAGNETIC ANNIHILATION IN A CURVED CURRENT SHEET

Magnetic reconnection is invoked to explain a wide range of astrophysical phenomena, from geomagnetic substorms and solar flares to flare stars and accretion disks (Priest & Forbes 2000). Flux pileup magnetic reconnection is one of the few reconnection models amenable to analytical treatment. Reconnection is a complicated nonlinear phenomenon, and so exact solutions that illustrate its key features—a small thickness of the current sheet, flux pileup at the entrance to the sheet, Alfvénic outflows—have educational and practical value, despite their well-known limitations (Litvinenko et al. 1996).

Exact analytical solutions for annihilation (merging) of planar magnetic fields in an incompressible resistive plasma were discovered by Clarke (1964), Parker (1973), and Sonnerup & Priest (1975). Craig and coworkers obtained more general solutions that describe magnetic reconnection in two and three dimensions (Craig & Henton 1995; Craig & Fabling 1996; Craig et al. 1995, 1997). More recent models incorporated various physical effects, such as the Hall electric field (Dorelli 2003), electron inertia (Watson & Porcelli 2004), and viscosity (Besser et al. 1990; Litvinenko 2005; for a recent summary, see Craig & Litvinenko 2012).

A common feature of the available analytical models for flux pileup merging is that they describe magnetic annihilation or reconnection in current sheets, sustained by a stagnation-point flow. It is natural to ask whether analytical models based on other types of flows can be constructed. This paper gives a positive answer to this question. Specifically, a solution is presented for magnetic merging, driven by an axisymmetric stagnation flow on a cylinder (Wang 1974).

Watson & Craig (2002) also obtained magnetic merging solutions in cylindrical geometry, but the geometry of the solution presented here is entirely different. Notably, the new solution remains valid in the presence of both the isotropic and parallel (Braginskii 1965) viscosity.

The governing magnetohydrodynamic (MHD) equations for the velocity v and magnetic field B in an incompressible resistive viscous plasma are as follows: the momentum equation

$$\begin{equation} \partial _t {\bf v} + ({\bf v} \cdot \nabla) {\bf v} = - \nabla p + (\nabla \times {\bf B}) \times {\bf B} + \nu \nabla ^2 {\bf v}, \end{equation} \tag{ 1 }$$

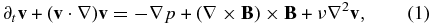
the induction equation

$$\begin{equation} \partial _t {\bf B} = \nabla \times ({\bf v} \times {\bf B}) + {\eta } {\nabla ^2} {\bf B}, \end{equation} \tag{ 2 }$$

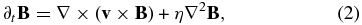
the continuity equation

$$\begin{equation} \nabla \cdot {\bf v} = 0, \end{equation} \tag{ 3 }$$

and the magnetic field equation

$$\begin{equation} \nabla \cdot {\bf B} = 0. \end{equation} \tag{ 4 }$$

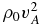The equations are written in dimensionless form by adopting reference values of the magnetic field B₀, plasma density ρ₀, and length L. The speed is measured in units of the Alfvén speed $v_A = B_0 / \sqrt{4\pi \rho _0}$, and the pressure p is measured in units of $\rho _0 v_A^2$. The dimensionless electric current density is given by j = ∇ × B. The dimensionless parameters ν and η are the plasma viscosity and resistivity, normalized by v_AL and 4πv_AL/c², respectively, where c is the speed of light. Although the usual isotropic viscosity is assumed, the solution to be presented turns out to be valid for an anisotropic (parallel) viscosity as well.

Wang (1974; see also Drazin & Riley 2006) discovered an axisymmetric stagnation flow of the form

$$\begin{equation} {\bf v} = -\alpha \left(r - \frac{a^2}{r} \right) {\bf \hat{\boldsymbol {r}}} + 2 \alpha z {\bf \hat{\boldsymbol {z}}}, \end{equation} \tag{ 5 }$$

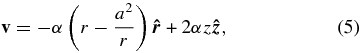
where α and a are constants. Although the expression is formally valid everywhere, in practice it may be advisable to consider it for r ⩾ r₁ > 0. The singularity at the origin corresponds to a source if α > 0 and a sink if α < 0. When a > 0, the flow stagnation takes place on a circle of radius a which is the intersection of the xy-plane and a circular cylinder whose generators are parallel to the z-axis. In the limit a = 0, the flow reduces to the stagnation-point flow.

Assuming α > 0, consider a steady magnetic field of the form

$$\begin{equation} {\bf B} = B(r) {\bf \hat{\boldsymbol {z}}}. \end{equation} \tag{ 6 }$$

It is straightforward to check that both v and B are solenoidal. Furthermore, ∇ × v = 0, and so ∇²v = 0. Consequently, the volumetric force due to viscosity vanishes. The magnetic field satisfies $\nabla \times {\bf B} = -B^{\prime }(r) {\bf \hat{\boldsymbol {\theta }}}$ and $(\nabla \times {\bf B}) \times {\bf B} = -BB^{\prime } {\bf \hat{\boldsymbol {r}}}$. Now the steady momentum equation is integrated without much trouble to yield the pressure profile:

$$\begin{equation} p (r, z) = {\rm const} - \frac{1}{2} v^2 - \frac{1}{2} B^2. \end{equation} \tag{ 7 }$$

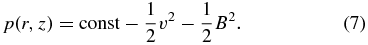
The steady induction equation reduces to

$$\begin{equation} \eta \left(B^{\prime \prime } + \frac{1}{r} B^{\prime } \right) + \frac{\alpha }{r} [ (r^2-a^2) B]^{\prime } = 0, \end{equation} \tag{ 8 }$$

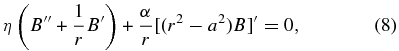
which defines the magnetic field profile B(r). In the limit a = 0, this equation has a well-known solution for a magnetic tube of Gaussian profile (Moffatt 1978):

$$\begin{equation} B (r) = B(0) \exp (-\alpha r^2 / 2 \eta). \end{equation} \tag{ 9 }$$

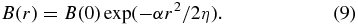
Kambe (1985) pointed out that a unidirectional vorticity can be added to the stagnation-point solution, leading to an MHD generalization of the Burgers vortex.

Integration of Equation (8) yields

$$\begin{equation} \eta (r B^{\prime } - a J) + \alpha (r^2 - a^2) B = 0, \end{equation} \tag{ 10 }$$

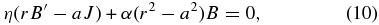
where an integration constant is expressed in terms of J = B'(a). This equation is Ohm's law in MHD. The electric field is given by

$$\begin{equation} {\bf E} = \eta J \frac{a}{r} {\bf \hat{\boldsymbol {\theta }}}, \end{equation} \tag{ 11 }$$

which of course satisfies ∇ × E = 0. Note that, although the plasma velocity is singular at the origin, the magnetic field remains finite:

$$\begin{equation} B(0) = -\frac{\eta J}{\alpha a}. \end{equation} \tag{ 12 }$$

Now another integration gives the magnetic field profile:

$$\begin{equation} B(r) = r^{\alpha a^2 / \eta } \exp \left(-\frac{\alpha r^2}{2 \eta } \right) f(r), \end{equation} \tag{ 13 }$$

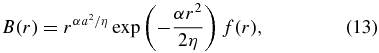
where

$$\begin{equation} f(r) = a J \int r^{-1 -\alpha a^2 / \eta } \exp \left(\frac{\alpha r^2}{2 \eta } \right) dr. \end{equation} \tag{ 14 }$$

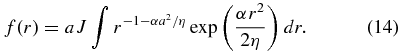
Alternatively, the solution can be formally expressed in terms of known functions:

$$\begin{eqnarray} B(r) &=& \left[ C r^{\alpha a^2 / \eta } - \frac{aJ}{2} \left(-\frac{\alpha r^2}{2 \eta } \right)^{\alpha a^2 / 2 \eta } \Gamma \left(-\frac{\alpha a^2}{2 \eta }, -\frac{\alpha r^2}{2 \eta } \right) \right] \nonumber\\ &&\times \exp \left(-\frac{\alpha r^2}{2 \eta } \right)\!, \end{eqnarray} \tag{ 15 }$$

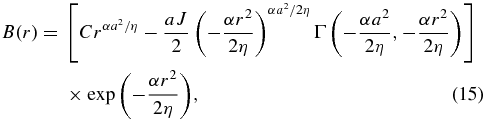
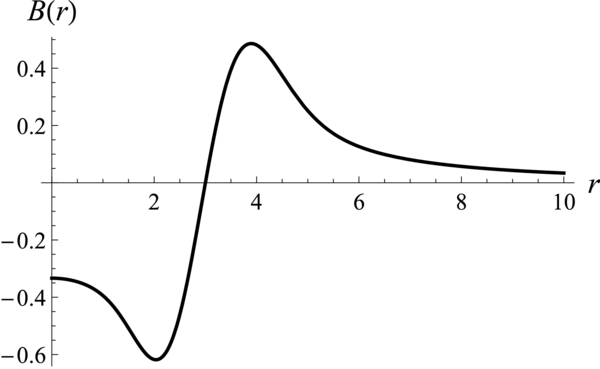
where C is an integration constant, determined from B(a) = 0 for a current sheet located in the flow stagnation region, and Γ is the incomplete gamma function (e.g., Oldham et al. 2009). Figure 1 shows the resulting profile B(r) of the merging magnetic field.

Zoom In Zoom Out Reset image size

Near the current sheet, |1 − r/a| ≪ 1, Equation (10) can be approximated by

$$\begin{equation} B^{\prime } + \frac{2 \alpha }{\eta } (r-a) B = J, \end{equation} \tag{ 16 }$$

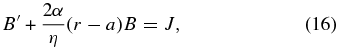
whose solution, specified by B(a) = 0, is

$$\begin{equation} B(r) = J \left(\frac{\eta }{\alpha } \right)^{1/2} {\rm daw} \left[ \left(\frac{\alpha }{\eta } \right)^{1/2} (r-a) \right]\!, \end{equation} \tag{ 17 }$$

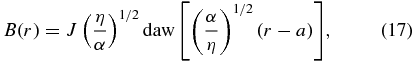
where daw denotes Dawson's integral (e.g., Oldham et al. 2009). The effect of curvature is small if r ≈ a, so it is not surprising that the merging magnetic field profile near the current sheet has the same functional form as that in the planar geometry solution (Sonnerup & Priest 1975; Craig & Henton 1995).

If the dimensionless current sheet thickness l ≪ 1, simple expressions for l and the magnetic field B_s at the entrance to the sheet follow from a boundary-layer argument. The advective term v × B is negligible in the stagnation region. Hence the induction equation simplifies to rB' ≈ aJ, and so the inner solution for the magnetic field is

$$\begin{equation} B_i (r) \approx J(r-a). \end{equation} \tag{ 18 }$$

Far from the sheet, the resistive term in the diffusion equation is negligible, and the outer solution for the magnetic field is

$$\begin{equation} B_o (r) \approx \frac{a \eta J}{\alpha (r^2 - a^2)}, \end{equation} \tag{ 19 }$$

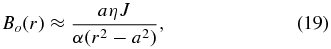
where the value of B_o(0) is in fact exact. Now the sheet thickness is defined by the condition B_i(l) ≈ B_o(l):

$$\begin{equation} l \approx \left(\frac{\eta }{2 \alpha } \right)^{1/2}, \end{equation} \tag{ 20 }$$

and the magnetic field B_s at the entrance to the sheet follows from B_s ≈ Jl.

Therefore, the salient features of the new solution for magnetic merging in cylindrical geometry are as follows. A curved current sheet of thickness l ∼ η^1/2 is sustained by a large-scale stagnation flow. Fast merging, characterized by E(a) = ηJ ≃ 1, can be achieved in a current sheet with B_s ∼ η^−1/2, as long as the merging rate does not exceed a pressure-imposed limit (Litvinenko et al. 1996). Thus the new solution extends the earlier results, derived in a planar geometry (Sonnerup & Priest 1975; Craig & Henton 1995) and emphasizes the key requirement of flux pileup (B_s > 1) if the merging rate ηJ is to be higher than the Sweet–Parker rate E ≃ η^1/2.

The viscous force in Equation (1) is based on the isotropic viscous stress tensor. Its use is appropriate, for instance, in the solar convection zone where the magnetic field is relatively weak (e.g., Rüdiger & Kitchatinov 1997). Viscous stresses, however, are highly anisotropic in a strongly magnetized plasma (Braginskii 1965; see also Lifshitz & Pitaevskii 1981). The leading term in the viscous stress tensor in a magnetized plasma, known as the ion parallel viscosity, is as follows (e.g., Hollweg 1986):

$$\begin{equation} S_{ij} = \nu \left(\delta _{ij} - 3 \frac{B_i B_j}{B^2} \right) \left(\frac{B_k B_l}{B^2} \frac{\partial v_k}{\partial x_l} - {1 \over 3} \nabla \cdot {\bf v} \right)\!. \end{equation} \tag{ 21 }$$

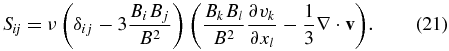
It is the parallel viscosity that should be used, for instance, for modeling the plasma dynamics in a flaring solar corona (e.g., Litvinenko 2005).

It is notable that the new merging solution remains valid when the parallel viscosity is taken into account. Because the magnetic field is directed along the z-axis, the only nonzero components of the viscous stress tensor are given by

$$\begin{equation} S_{xx} = S_{yy} = \nu \frac{\partial v_z}{\partial z} = 2 \alpha \nu, \quad S_{zz} = -2 S_{xx}. \end{equation} \tag{ 22 }$$

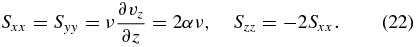
The volumetric force due to viscosity, defined as the negative of the divergence of S_ij, vanishes since ∂S_ij/∂x_j = 0. To sum up, the viscous force in Equation (1) vanishes whether the plasma viscosity is isotropic or anisotropic (parallel). As emphasized by Hollweg (1986) in his analysis of planar flux pileup merging, even though viscosity does not affect the momentum equation, viscous plasma heating is generally present. The heating is ultimately caused by unbalanced viscous stresses at the boundaries of the system.

Exact MHD solutions for magnetic reconnection illustrate its key features and may provide a standard for checking the accuracy of a computer code or an empirical approximation. Until now, analytical models for flux pileup merging were based on stagnation-point flows in two or three dimensions. This paper presents a solution for magnetic merging, driven by a three-dimensional axisymmetric stagnation flow on a cylinder. The new solution describes magnetic merging in a curved current sheet, located at r = const, and thus demonstrates that the previously obtained analytical results for flux pileup merging are not limited to the idealized geometry of a flat current sheet.

Watson & Craig (2002) and Tassi et al. (2002) gave the only other analytical example of magnetic merging in a curved current sheet, although their solution was based on a stagnation-point flow. The key difference with the present solution is that, while the velocity and magnetic field are co-planar in their solution, the magnetic field in the new solution is perpendicular to the plane in which the plasma flow stagnates. The tubular current profile of the present solution resembles that in the spine solution of Craig et al. (1995, 1997). In sharp contrast to spine merging, however, the current maximum of the new solution is not localized at the origin. This fact has important consequences for the energetics of magnetic reconnection. Suppose that a ≃ 1, η ≪ 1, and merging is fast, so that a characteristic dimensionless speed α ≃ 1. Then the volume in which the magnetic energy release takes place, which scales as a(η/α)^1/2, is much greater than the corresponding volume for spine merging, which scales as η/α. Consequently, the magnetic energy dissipation rate can exceed the dissipation rate for spine merging by a factor a(α/η)^1/2 ≫ 1.

The new solution is formally valid in any range of the azimuthal angle θ, which was not the case for the solutions of Watson & Craig (2002) and Tassi et al. (2002). In practice, however, it may make sense to consider the new solution in a finite annular region defined by r₁ ⩽ r ⩽ r₂ and θ₁ ⩽ θ ⩽ θ₂. Similarly, all merging models, based on stagnation-point flows, should be restricted to a finite spatial region to avoid infinite velocities.

As to possible applications of the new solution, its geometry may make it particularly useful in modeling the photospheric flux cancellation on the Sun. Magnetic reconnection, driven by converging convective flows, is believed to cause the observed convergence and mutual cancellation of photospheric magnetic fragments of opposite polarity (Martin et al. 1985). The magnetic field in the merging solution of this paper is perpendicular to the plane z = 0 in which the flow stagnation takes place. The plane can be identified with the solar photosphere and the field with the photospheric magnetic field. Flux pileup can be large in the dense photospheric plasma where the gas pressure significantly exceeds the magnetic pressure. Hence flux pileup merging can be sufficiently rapid to explain the observed cancellation rates (Litvinenko et al. 1996, 2007).

A possible problem with this idea, noted by the referee, is that the solar atmosphere is highly stratified. The photosphere separates low-beta and high-beta plasma regions, and so the application of an incompressible MHD model to photospheric flux cancellation may seem questionable. Litvinenko (1999) addressed this concern by arguing that the vertical extent of a photospheric current sheet should be limited by the atmospheric pressure scale height, implying that the neglect of z-dependence of the magnetic field and density in the sheet could be justified to a reasonable degree of accuracy. A difficulty remains, however. Although reconnection is believed to cause the observed flux cancellation, the height range in the solar atmosphere where such reconnection could occur has not been constrained either theoretically or observationally (for a recent review, see Chae 2012).

Numerous useful discussions with Professor Ian Craig are gratefully acknowledged. An anonymous referee's report was prompt and helpful.